Как решаются производные – как найти, вычислить и понять с нуля

Производные простых тригонометрических функций

Для нахождения производной тригонометрической функции нужно пользоваться таблицей производных, а именно производными 6-13.

При нахождении производных простых тригонометрических функций во избежание распространённых ошибок следует обращать внимание на следующие моменты:

• в выражении функции часто одно из слагаемых представляет собой синус, косинус или другую тригонометрическую функцию не от аргумента функции, а от числа (константы), поэтому производная этого слагаемого равна нулю;
• почти всегда нужно упростить выражение, полученное в результате дифференцирования, а для этого нужно уверенно пользоваться знаниями по действиям с дробями;
• для упрощения выражения почти всегда нужно знать тригонометрические тождества, например, формулу двойного угла и формулу единицы как сумму квадратов синуса и косинуса .

Пример 1. Найти производную функции

.

Решение. Допустим, с производной косинуса всё понятно, скажут многие, начинающие изучать производные. А как быть с производной синуса двенадцати, делённых на пи? Ответ: считать равной нулю! Здесь синус (функция всё-таки!) — ловушка, потому что аргумент — не переменная икс или любая другая переменная, а просто число. То есть, синус этого числа — тоже число. А производная числа (константы), как мы знаем из таблицы производных, равна нулю. Итак, оставляем только минус синус икса и находим его производную, не забывая про знак:

.

Ответ:

.

Пример 2. Найти производную функции

.

Решение. Второе слагаемое — тот же случай, что и первое слагаемое в предыдущем примере. То есть, число, а производная числа равна нулю. Находим производную второго слагаемого как производную частного:

Ответ:

Пример 3. Найти производную функции

.

Решение. Это уже другая задача: здесь в первом слагаемом нет ни арксинуса, ни другой тригонометической функции, но есть икс, а значит, это функция от икса. Следовательно, дифференцируем её как слагаемое в сумме функций:

Здесь потребовались навыки в действиях с дробями, а именно — в ликвидации трёхэтажности дроби.

Пример 4. Найти производную функции

.

Решение. Здесь буква «фи» играет ту же роль, что «икс» в предыдущих случаях (и в большинстве других, но не во всех) — независимой переменной. Поэтому, когда будем искать производную произведения функций, не будем спешить объявлять равной нулю производную корня от «фи». Итак:

Но на этом решение не заканчивается. Так как в двух скобках собраны подобные члены, от нас ещё требуется преобразовать (упростить) выражение. Поэтому умножаем скобки на вынесенные за них множители, а далее приводим слагаемые к общему знаменателю и выполняем другие элементарные преобразования:

Пример 5. Найти производную функции

.

Решение. В этом примере от нас потребуется знание того факта, что существует такая тригонометрическая функция — секанс — и её формулы через косинус. Дифференцируем:

Пример 6. Найти производную функции

.

Решение. В этом примере от нас потребуется помнить из школьного курса формулу двойного угла. Но сначала дифференцируем:

Далее применяем следующие тригонометрические тождества:

,

(это и есть формула двойного угла)

и получаем:

.

Пример 7. Найти производную функции

.

Решение. В этом примере от нас потребуется всего-то лишь умение сокращать дроби. И внимание — не забыть, что дробь нужно сократить. Это сделано на последнем шаге решения:

В решении применено тригонометрическое тождество:

.

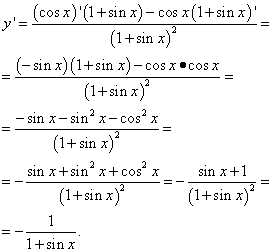
Поделиться с друзьями

Весь блок «Производная»

function-x.ru

Вычисление производных первого порядка.

Определение: Производной первого порядка функции $y=f(x)$ в точке $x_0$ называется предел 

$$f'(x_0)=\lim\limits_{\Delta x\rightarrow 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}.$$

Основные формулы для вычисления производных.

$c’=0,\quad c=const;$

$(x^\alpha)’=\alpha x^{\alpha-1},$      $x\in\mathbb{R}, \alpha\neq 0;$ 

$(a^x)’=a^x\ln a,\quad a>0, a\neq 1, x\in \mathbb{R};$

$(e^x)’=e^x;$

$(\log_a x)’=\frac{1}{x\ln a}, \quad x>0;$

$(\log_a|x|)’=\frac{1}{x\ln a},\quad x\neq 0;$

$(\ln x)’=\frac{1}{x},\quad x>0;$

$(\sin x)’=\cos x, \quad x\in \mathbb{R};$

$(\cos x)’=-\sin x\quad x\in \mathbb{R};$

$(tg x)’=\frac{1}{\cos^2 x},$     $x\neq\frac{\pi}{2}(2n+1),\,\, n\in\mathbb{Z};$ 

$(ctg x)’=-\frac{1}{\sin^2 x},$  $x\neq\pi n,\,\, n\in\mathbb{Z};$ 

$(\arcsin x)’=\frac{1}{\sqrt{1-x^2}},\quad |x|<1;$

$(\arccos x)’=-\frac{1}{\sqrt{1-x^2}},\quad |x|<1;$

$(arctg x)’=\frac{1}{1+x^2},\quad x\in\mathbb{R};$

$(arcctg x)’=-\frac{1}{1+x^2},\quad x\in\mathbb{R};$

 

Правила вычисления производных.

1) Пусть $f=c_1 f_1+c_2f_2+…+c_nf_n.$ Тогда $f’=c_1f’_1+c_2f’_2+…+c_nf’_n.$

2) Пусть $f=f_1\cdot f_2.$ Тогда $f’=f’_1f_2+f_1f’_2.$

3) Если $f=f_1/f_2,$ то $f’=\frac{f’_1f_2-f’_2f_1}{f_2^2}.$

4) Если функция $y=f(x)$ имеет производную в точке $x_0,$ а функция $z=g(y) $ — в точке $y_0=f(x_0),$ то сложная функция $z=\varphi(x)=g(f(x)),$ также имеет производную в точке $x_0,$ причем $\varphi'(x_0)=g'(y_0)f'(x_0).$

Примеры.

Найти производную функции $y(x)$

1) ${ y=x^3+x^2+x+1}$

Решение.

$y’=3x^2+2x+1.$

 

2) ${ y=7x^{13}+13x^{-7}}$

Решение.

$y’=7\cdot 13x^{12}+13({-7})x^{-8}=91x^{12}-91x^{-8}=91(x^{12}-x^{-8}).$

 

3) ${y=\frac{x^2-5x+6}{x^2+x+7}}$

Решение.

$$y’=\frac{(x^2-5x+6)'(x^2+x+7)-(x^2+x+7)'(x^2-5x+6)}{(x^2+x+7)^2}=$$ $$=\frac{(2x-5)(x^2+x+7)-(2x+1)(x^2-5x+6)}{(x^2+x+7)^2}=$$ $$\frac{2x^3+2x^2+14x-5x^2-5x-35-2x^3+10x^2-12x-x^2+5x-6}{(x^2+x+7)^2}=$$ $$=\frac{6x^2+2x-41}{(x^2+x+7)^2}.$$

 {jumi[*4]}

 

4) ${y=(x+1)tg x;}$

Решение.

$y’=(x+1)’tg x+(x+1)(tg x)’=tg x+\frac{x+1}{\cos^2 x};$

 

5) ${ y=(a+bx)^\alpha}$

Решение.

$y’=\alpha(a+bx)^{\alpha-1}(a+bx)’=$ $\alpha(a+bx)^{\alpha-1}b;$

 

6) ${y=\sqrt[3]{\frac{1-x^3}{1+x^3}}.}$

Решение.

$$y’=\frac{1}{3}\left(\frac{1-x^3}{1+x^3}\right)^{-\frac{2}{3}}\frac{(-3x^2)(1+x^3)-3x^2(1-x^3)}{(1+x^3)^2}$$

 

7) ${y=\ln\ln(x/2)}$

Решение.

$$y’=\frac{1}{\ln(x/2)}\cdot(\ln(x/2))’=\frac{1}{\ln(x/2)}\cdot\frac{2}{x}\cdot\frac{1}{2}=\frac{1}{x\log(x/2)}.$$

8) $y=\ln\frac{x^2+a}{\sqrt{x^4+b^2}}+\frac{a}{b}arctg\frac{x^2}{b}$ 

Решение.

 

$$y’=\frac{\sqrt{x^4+b^2}}{x^2+a}\cdot\left(\frac{x^2+a}{\sqrt{x^4+b^2}}\right)’+\frac{a}{b}\frac{1}{1+\frac{x^4}{b^2}}\cdot\left(\frac{x^2}{b}\right)’=$$

$$\frac{\sqrt{x^4+b^2}}{x^2+a}\cdot\frac{2x\sqrt{x^4+b^2}-1/2(x^4+b^2)^{-1/2}\cdot4x^3(x^2+a)}{x^4+b^2}+\frac{a}{b}\frac{1}{1+\frac{x^4}{b^2}}\cdot\frac{2x}{b}=$$

$$=\frac{2x(x^4+b^2)-2x^3(x^2+a)+2xa(x^2+a)}{(x^2+a)(x^4+b^2)}=\frac{2x(a^2+b^2)}{(x^2+a)(x^4+b^2)}.$$

 

9) ${y=x^x}$

Решение.

$y’=(x^x)’=(e^{\ln x^x})’=(e^{x\ln x})’=e^{x\ln x}(x\ln x)’=e^{x\ln x}(\ln x+x\cdot\frac{1}{x})=$ $=x^x(\ln x+1).$

 

10) ${y=\log_x 7}$

Решение.

$$y’=(\log_x 7)’=\left(\frac{1}{\log_7 x}\right)’=(\log_7^{-1} x)’=-\log_7^{-2}x\cdot\frac{1}{x\ln 7}=$$

$$-\frac{1}{(\frac{\ln x}{\ln 7})^2}\cdot\frac{1}{x\ln 7}=-\frac{1}{x\ln x\cdot\frac{\ln x}{\ln 7}}=-\frac{1}{x\ln x\log_7 x}.$$

 

Производная функции заданной параметрически.

Пусть функции $x=x(t)$ и $y=y(t)$ определены в некоторой окрестности точки $t_0$ и параметрически задают в окрестности точки $x_0=x(t_0) $ функцию $y=f(x).$ Тогда, если $x(t)$ и $y(t)$ имеют в точке $t_0$ производные и если $\frac{dx(t_0)}{dt}\neq 0,$ то функция $y=f(x)$ в точке $x_0$ также имеет производную, которая может быть задана по формуле 

$\frac{df(x_0)}{dx}=\frac{\frac{dy(t_0)}{dt}}{\frac{dx(t_0)}{dt}},$  $y’_x(x_0)=\frac{y’_t(t_0)}{x’_t(t_0)}.$   

Примеры.

1) ${ x=\sin^2 t,\,\, y=\cos^2 t,\quad t\in(0,\pi/2). }$

Решение.

$x’_t=2\sin t\cdot(\sin t)’=2\sin t\cdot\cos t;$

$y’_t=2\cos t\cdot(\cos t)’=2\cos t\cdot(-\sin t).$

$$y’_x=\frac{2\cos t\cdot(-\sin t)}{2\sin t\cdot\cos t}=-1.$$

2) ${ x=e^{-t}; \,\, y=t^3 \quad t\in (-\infty;\, +\infty) .}$

Решение.

$$y’_x=\frac{3t^2}{-e^{-t}}=-3t^2e^t.$$

3) ${ x=a\cos t;\,\, y=b\sin t,\quad t\in(0,\pi). }$

Решение.

$$y’_x=\frac{b\cos t}{-a\sin t}-\frac{b}{a}ctg t.$$

4) ${ x=(t^3-2t^2+3t-4)e^t,\,\, y=(t^3-2t^2+4t-4)e^t. }$

Решение.

$$y’_x=\frac{(3t^2-4t+4)e^t+e^t(t^3-2t^2+4t-4)}{(3t^2-4t+3)e^t+e^t(t^3-2t^2+3t-4)}=$$ $$\frac{t^3+t^2}{t^3+t^2-t-1}=\frac{t^2(t+1)}{t^2(t+1)-(t+1)}=\frac{t^2}{t^2-1}.$$

5) $x=ctg 2t,\,\, y=\frac{2\cos 2t-1}{2\cos t}\quad t\in (0, \pi/2).$ $x’_y -?$ 

Решение.

$$x’_y=-\frac{2}{\sin^2 2t}\cdot\frac{4\cos^2 t}{-4\sin 2t\cdot2\cos t+2\sin t(2\cos 2t-1))}=$$ $$\frac{-1}{\sin^2 t(-8\sin t\cos^2 t+\sin t(2(1-2\sin^2 t)-1))}=$$

$$\frac{-1}{-8\sin^3 t\cos^2 t-4\sin^5 t+2\sin^3 t-\sin^3 t}=$$
$$\frac{1}{\sin^3 t(8\cos^2 t+4\sin^2t-2+1)}=\frac{1}{\sin^3 t(4\cos^2 t+3)}.$$

 

Производная функции заданной неявно.

Если дифференцируемая на некотором интервале функция $y=y(x)$ задана неявно уравнением $F(x,y)=0,$ то ее производную $y'(x)$ можно найти из уравнения $\frac{d}{dx}F(x,y)=0.$

 Примеры.

Найти производную функции $y'(x).$

1) ${ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 }$

Решение. 
$$\frac{d}{dx}\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\right)=0$$
$$\frac{2x}{a^2}+\frac{2y}{b^2}y’=0, \Rightarrow\quad y’=-\frac{b^2 x}{a^2 y}.$$

2) ${ y^5+y^3+y-x=0 }$

Решение.
$$\frac{d}{dx}(y^5+y^3+y-x)=0 \Rightarrow 5y^4y’+3y^2y’+y’-1=0\,\,\Rightarrow\,\,$$ $$\Rightarrow y’=\frac{1}{5y^4+3y^2+1}.$$

3) $ y-x=\varepsilon\sin y $

Решение.

$$\frac{d}{dx}(y-x-\varepsilon\sin y)=0\Rightarrow\,\, y’-1-\varepsilon\cos y\cdot y’=0 \Rightarrow y’=\,\frac{1}{1-\varepsilon\cos y}.$$

mathportal.net

таблица производных | математика-повторение

На этом занятии мы будем учиться применять формулы и правила дифференцирования.

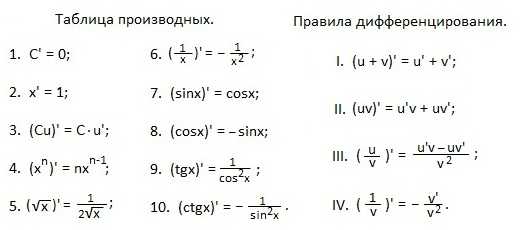
Примеры. Найти производные функций.

1. y=x⁷+x⁵-x⁴+x³-x²+x-9. Применяем правило I, формулы 4, 2 и 1. Получаем:

y’=7x⁶+5x⁴-4x³+3x²-2x+1.

2. y=3x⁶-2x+5. Решаем аналогично, используя те же формулы и формулу 3.

y’=3∙6x⁵-2=18x⁵-2.

Применяем правило I,  формулы 3, 5 и 6 и 1.

 

 Применяем правило IV, формулы 5 и 1.

 

В пятом примере по правилу I производная суммы равна сумме производных,  а производную 1-го слагаемого мы только что находили (пример 4), поэтому, будем находить производные  2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.

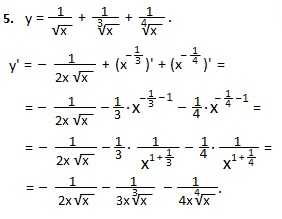Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.

Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.

Решим шестой пример и выведем еще одну  формулу.

Используем правило IV и формулу 4. Получившиеся дроби сократим.

Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:

Учим новые формулы!

 

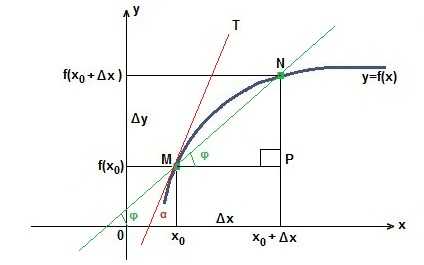В координатной плоскости хОу рассмотрим график функции y=f (x). Зафиксируем точку М(х₀; f (x₀)). Придадим абсциссе х₀ приращение Δх. Мы получим новую абсциссу х₀+Δх. Это абсцисса точки N, а ордината будет равна f (х₀+Δх). Изменение абсциссы повлекло за собой изменение ординаты. Это изменение называют приращение функции и обозначают Δy.

Δy=f (х₀+Δх) — f (x₀).  Через точки M и N проведем секущую MN, которая образует угол φ с положительным направлением оси Ох. Определим тангенс угла φ из прямоугольного треугольника MPN.

Пусть Δх стремится к нулю. Тогда секущая MN будет стремиться занять положение касательной МТ, а угол φ станет углом α. Значит, тангенс угла α есть предельное значение тангенса угла φ:

Определение производной. Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю, называют производной функции в данной точке:

Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:

Смотрите видео 10.3. Определение производной. Геометрический смысл производной.

Примеры.

1. Найти приращение аргумента и приращение функции y=x², если начальное значение аргумента было равно 4, а новое  —4,01.

Решение.

Новое значение аргумента х=х₀+Δx. Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх=4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х₀+Δх) — f (x₀).  Так как у нас функция y=x²,  то Δу=(х₀+Δx)²— (х₀)²=(х₀)²+2x₀ · Δx+(Δx)²— (х₀)²=2x₀ · Δx+(Δx)²=

=2 · 4 · 0,01+(0,01)²=0,08+0,0001=0,0801.

Ответ: приращение аргумента Δх=0,01; приращение функции Δу=0,0801.

Можно было приращение функции найти по-другому: Δy=y (х₀+Δx) -y (х₀)=у(4,01) -у(4)=4,01²-4²=16,0801-16=0,0801.

2. Найти угол наклона касательной к графику функции y=f (x) в точке х₀, если f ‘(х₀) = 1.

Решение.

Значение производной в точке касания х₀ и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f ‘(х₀) = tgα = 1  → α = 45°,   так как  tg45°=1.

Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45°.

3. Вывести формулу производной функции y=xⁿ.

Смотрите видео: «10.3.0. Вывод формулы производной степени».

Дифференцирование — это действие нахождения производной функции.

При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же,  как мы вывели формулу производной степени: (xⁿ)’ = nx^n-1.

Вот эти формулы.     

Таблицу производных легче будет заучить, проговаривая словесные формулировки:

 

1. Производная постоянной величины равна нулю.

2. Икс штрих равен единице.

3. Постоянный множитель можно вынести за знак производной.

4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.

5. Производная корня равна единице, деленной на два таких же корня.

6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.

7. Производная синуса равна косинусу.

8. Производная косинуса равна минус синусу.

9. Производная тангенса равна единице, деленной на квадрат косинуса.

10. Производная котангенса равна минус единице, деленной на квадрат синуса.

Учим правила дифференцирования.

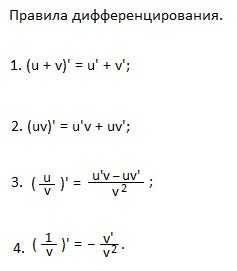1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.

2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.

3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».

4. Частный случай формулы 3.

Учим вместе!

 

www.mathematics-repetition.com