Вычисление тройных интегралов: теория и примеры
Тройные интегралы – это аналог двойного интеграла для функции трёх переменных, заданной как f(M) = f(x, y, z).
Записывается тройной интеграл так:
.
Здесь V – пространственная (трёхмерная) фигура, ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.
Вычислить тройной интеграл — значит найти число, равное объёму тела V или, что то же самое — области V.
Практически каждый может понять смысл вычисления тройного интеграла «на своей шкуре». Точнее — «под шкурой», а ещё точнее — по своим органам дыхания — лёгким. Вне зависимости от того, знаете ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол — пузырьковых образований, оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так: объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое «огромное количество малостей» математически как раз и формулируется понятие тройного интеграла.
Почему именно тройной интеграл служит для нахождения объёма тела V? Пусть область V разбита на n произвольных областей Δvi, причём под этим обозначением подразумевается не только каждая маленькая область, но и её объём. В каждой такой маленькой области выбрана произвольная точка Mi, а f(Mi) — значение функции f(M) в этой точке. Теперь будем максимально увеличивать число таких маленьких областей, а наибольший диаметр Δvi — наоборот, уменьшать. Можем составить интегральную сумму вида
.
Если функция f(M) = f(x, y, z) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом.
В этом случае функция f(M) = f(x, y, z) называется интегрируемой в области V; V — областью интегрирования; x, y, z — переменными интегрирования, dv (или dx dy dz) — элементом объёма.
Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.
Рассмотрим трёхмерную область V. Снизу и сверху (то есть по высоте) эта область ограничена поверхностями z = z1(x, y) и z = z2(x, y). С боковых сторон (то есть по ширине) область ограничена поверхностями y = y1(x) и y = y2(x). И, наконец, по глубине (если Вы смотрите на область в направлении оси Ox) — поверхностями x = a и x = b
Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область V была правильной. Она правильна тогда, когда прямая, параллельная оси Oz, пересекает границу области V не более чем в двух точках. Правильными трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже — прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.
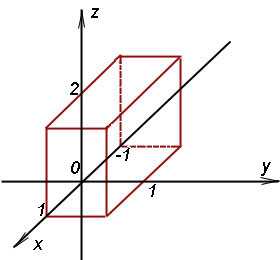
Чтобы наглядно представить отличие правильности от неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На рисунке ниже — пример неправильной области V — однополостный гиперболоид, поверхность которого прямая, параллельная оси Oz (красного цвета), пересекает более чем в двух точках.
Мы будем рассматривать только правильные области.
Итак, область V — правильная. Тогда для любой функции f(x, y, z), непрерывной в области V, справедлива формула
Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению
внутреннего определённого интеграла по переменной
Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:
Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.
Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому внешнему (по переменной x). Для удобства восприятия последовательности вычислений три «вложенных» интеграла можно записать так:
.
Из этой записи уже однозначно видно, что:
- сначала нужно интегрировать функцию f(x, y, z) по переменной z, а в качестве пределов интегрирования взять уравнения z = z1(x, y) и z = z2(x, y) поверхностей ограничивающих область V снизу и сверху;
- получившийся на предыдущем шаге результат интегрировать по переменной y, а в качестве пределов интегрирования взять уравнения y = y1(x) и y = y2(x) поверхностей, ограничивающих область V с боковых сторон;
- получившийся на предыдущем шаге результат интегрировать по переменной x, а в качестве пределов интегрирования взять уравнения x = a и x = b поверхностей, ограничивающих область V по глубине.
Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу
последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.
Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:
.
Вычислим второй интеграл — по переменной y:
.
Теперь вычисляем самый внешний интеграл — по переменной x:
.
Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.
Пример 2. Вычислить тройной интеграл
,
где V — параллелепипед, ограниченный плоскостями x = − 1, x = + 1, y = 0, y = 1, z = 0, z = 2.
Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем интеграл «в серединке» — по переменной y. Получаем;
.
Теперь вычисляем самый внешний интеграл — по переменной x:
Ответ: данный тройной интеграл равен -2.
Пример 3. Вычислить тройной интеграл
,
где V — пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0, y = 0, z = 0. Область V проецируется на плоскость xOy
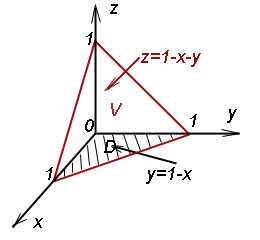
Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0. Чтобы получить верхний предел, выразим z из x + y + z = 1. Получаем 1 − x − y. Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0. Для получения верхнего предела выразим y из x + y + z = 1, считая при этом, что z = 0 (так как линия расположена в плоскости xOy). Получаем: 1 − x.
Сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной y. Получаем:
Наконец, вычисляем самый внешний интеграл — по переменной x:
Ответ: данный тройной интеграл равен 1/8.
Вычислить тройной интеграл самостоятельно, а затем посмотреть решение
Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление
интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к
последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность.
В первом примере область интегрирования V представляла собой параллелепипед,
с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно
заданы уравнениями плоскостей. Во втором примере — пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область
Начнём с примера «пострашнее», чтобы почувствовать «обстановку, приближенную к боевой».
Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V — эллипсоид
.
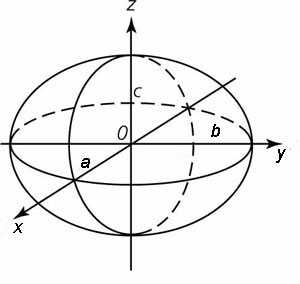
Решение. Пусть центр эллипсоида — начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу. Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена ниже плоскости xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение со знаком минус будет нижним пределом интегрирования по переменной z:
.
Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z:
.
Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:
.
Чтобы получить нижний предел интегрирования по переменной y, нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:
.
Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:
.
Что касается интегрирования по переменной x, то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a: x1 = − a и x2 = a.
Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:
,
где «игрек первое», «игрек второе», «зет первое» и «зет второе» — полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc/3.
Следующие примеры — не такие страшные, как только что рассмотренный. При этом они предполагают не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте, чему вы научились, следя за решением «страшного» примера. Думать при расстановке пределов всё равно придётся.
Пример 6. Вычислить тройной интеграл
,
если область интегрирования ограничена плоскостями x + y = 1, x + 2y = 4, y = 0, y = 1, z = 1, z = 5.
Решение. «Курортный» пример по сравнению с примером 5, так как пределы интегрирования по «игрек» и «зет» определены однозначно. Но придётся разобраться с пределами интегрирования по «иксу». Проекцией области интегрирования на плоскость xOy является трапеция ABCD.
В этом примере выгоднее проецировать трапецию на ось Oy, иначе, чтобы вычислить тройной интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по «иксу» чисто алгебраически. Для этого выразим «икс» из первого и второго уравнений, данных в условии примера. Из первого уравения получаем нижний предел 1 − y, из второго — верхний 4 − 2y. Сведём данный тройной интеграл к последовательности трёх определённых интегралов:
.
Внимание! В этом примере самый внешний интеграл — не по переменной «икс», а по переменной «игрек», а «средний» — по переменной «икс»! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox, на на ось Oy.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной x. Получаем:
.
Наконец, вычисляем самый внешний интеграл — по переменной y:
Ответ: данный тройной интеграл равен 43.
Пример 7. Вычислить тройной интеграл
,
если область интегрирования ограничена поверхностями x = 0, y = 0, z = 2, x + y + z = 4.
Решение. Область V (пирамида MNRP) является правильной. Проекцией области V на плоскость xOy является треугольник AOB.
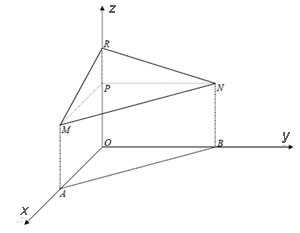
Нижние пределы интегрирования по всем переменным заданы в условии примера. Найдём верхний предел интегирования по «иксу». Для этого выразим «икс» из четвёртого уравнения, считая «игрек» равным нулю, а «зет» равным двум. Получаем x = 2. Найдём верхний предел интегирования по «игреку». Для этого выразим «игрек» из того же четвёртого уравнения, считая «зет» равным двум, а «икс» — переменной величиной. Получаем y = 2 − x. И, наконец, найдём верхний предел интегрирования по переменной «зет». Для этого выразим «зет» из того же четвёртого уравнения, считая «игрек» и «зет» переменными величинами. Получаем z = 4 − x − y.
Сведём данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной y. Получаем:
.
Вычисляем самый внешний интеграл — по переменной x и окончательно находим данный тройной интеграл:
Ответ: данный тройной интеграл равен 2.
Если проекцией области интегрирования на какую-либо из координатных плоскостей является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами (r, φ, z), где r — расстояние от начала координат до проекции N точки M на плоскость xOy, φ — угол между вектором ON и положительным направлением оси Ox, z — аппликата точки M (рисунок ниже).
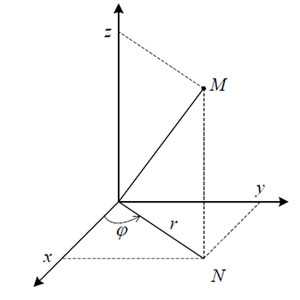
Прямоугольные координаты x, y, z с цилиндрическими координатами r, φ, z связывают формулы
x = rcosφ,
y = rsinφ,
z = z.
Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r, φ, z:
.
То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:
.
Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:
Если область интегрирования в тройном интеграле представляет собой шар или часть шара, то проще вычислить тройной интеграл в сферических координатах. В сферических координатах точку M характеризуют три величины (ρ, φ, θ), где ρ — расстояние от точки M до начала координат 0, φ — угол между вектором ON и положительным направлением оси Ox (N — проекция точки M на плоскость xOy), θ — угол между вектором OM и положительным направлением оси Oz.
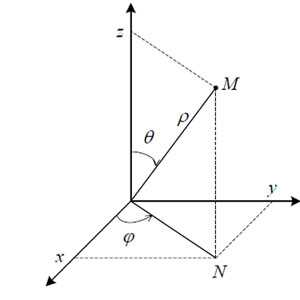
Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями
x = ρsinθcosφ,
y = ρsinθsinφ,
z = ρcosθ.
Элемент объёма в сферических координатах выражается следующим образом:
.
Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к сферическим координатам осуществляется по формуле:
Чтобы вычислить тройной интеграл в сферических координатах, нужно поступить так же, как при вычислениях в прямоугольных декартовых и цилиндрических координатах — перейти к повторным интегралам (последовательности трёх определённых интегралов):
Пример 9. Вычислить тройной интеграл
переходом к сферическим координатам, где V — область, ограниченная неравенствами и .
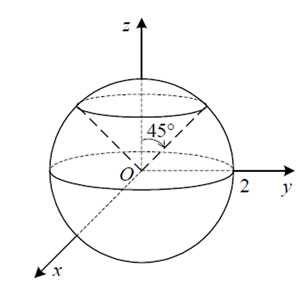
Решение. Снизу область интегрирования ограничена конической поверхностью , а сверху — сферой . Так как область интегирования представляет собой часть шара, перейдём к сферическим координатам. Перепишем подынтегральную функцию:
Учитывая, что , получаем
Расставим пределы интегрирования и перепишем последний полученный интеграл в виде трёх повторных интегралов. По рисунку видно, что , , . Поэтому
Итак, тройной интеграл вычислен. Так как все три интеграла — независисмые друг от друга, мы смогли интегрировать каждый отдельно и результаты перемножить.
Вычисление объёма тела. Объём области V равен тройному интегралу по этой области, если подынтегральная функция равна 1:
.
Вычисление массы неоднородного тела. Массу неоднородного тела с плотностью ρ = ρ(x, y, z) можно вычислить по формуле:
.
Статические моменты материального тела. Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:
Моменты инерции материального тела. Моменты инерции относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:
Моменты инерции относительно осей Ox, Oy, Oz определяются по формулам:
Центр тяжести материального тела. Координаты центра массы C(xc, yc, zc) материального тела с плотностью ρ = ρ(x, y, z) определяются по формулам:
Кратные и криволинейные интегралы
Поделиться с друзьями
function-x.ru
5.3. Примеры
Пример 5.1. Вычислить интеграл в цилиндрических координатах:
.
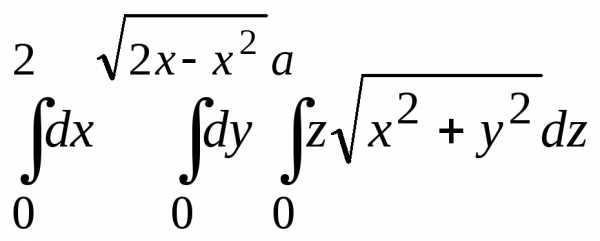Решение.
Восстановим область интегрирования 
по известным пределам интегрирования:
Область 
(проекция области
на плоскость
)
расположена в первой четверти и ограничена
прямой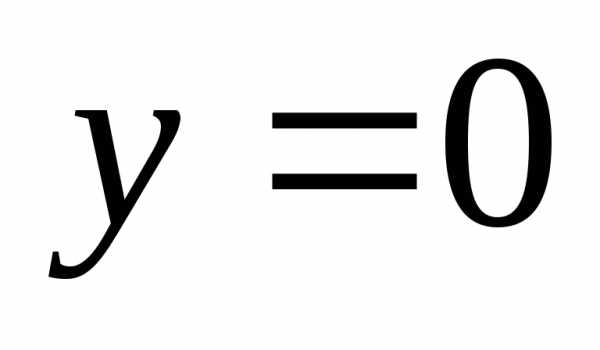
и линией
.
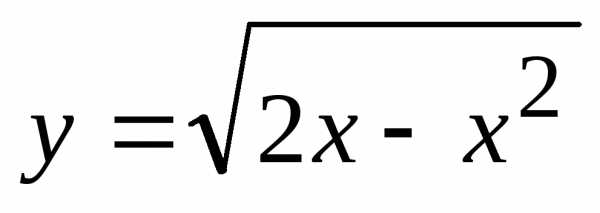Преобразуем последнее выражение. После возведения в квадрат получим
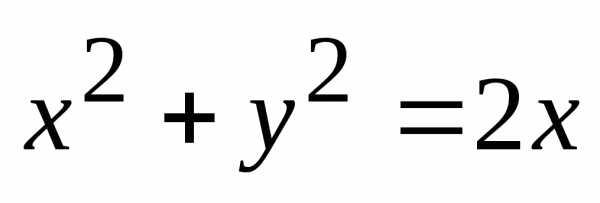, (5.3)
а после простых преобразований будем иметь
.
Это
уравнение окружности радиусом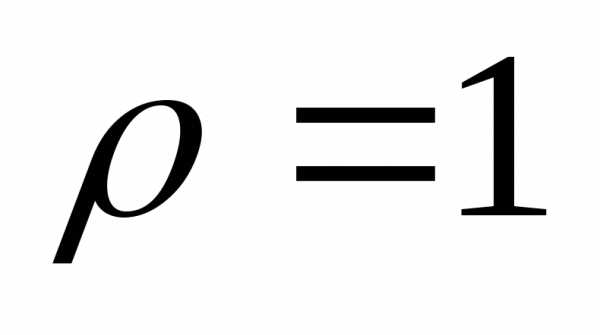 
,
центр которой смещён в положительную
сторону по оси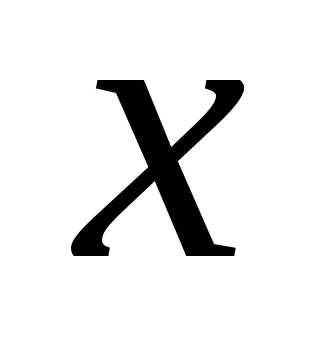
на радиус. Границей области
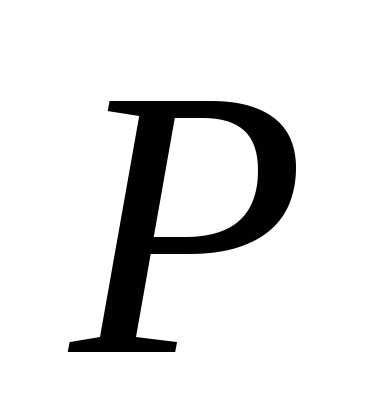является правая половина этой окружности.
Рис. 5.9
Уравнение окружности в цилиндрических координатах получим, подставив в (5.3) соотношения:
; ;
или .
Точка
пробегает правую половину окружности
при изменении угла 
от 0 до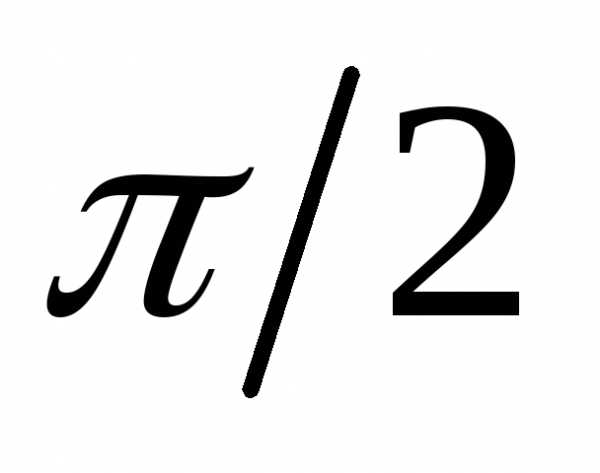
;
подынтегральное выражение в цилиндрических
координатах имеет вид:
.
Тело 
изображено на рис. 5.9.
Интеграл вычисляем в цилиндрических координатах:
.
Пример 5.2. Вычислить интеграл:
,
если
область интегрирования 
ограничена сферой
.
Уравнение сферы простыми преобразованиями приводится к виду
.
Это
– сфера радиусом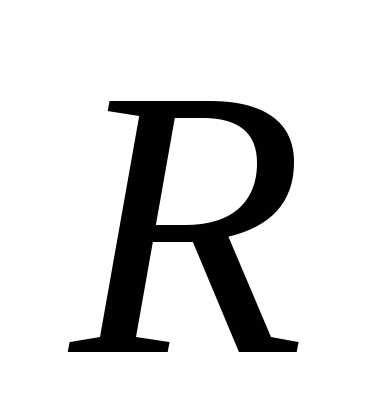 
,
смещенная вверх по оси
на радиус (рис. 5.10).
Рис. 5.10
Решение. Вычисления проведём в сферических координатах. Уравнение границы области преобразуем, подставив в уравнение сферы соотношения
.
, или .
Подставив те же соотношения в подынтегральное выражение, получим
.
Области изменения переменных:
.
Интеграл в сферических координатах легко вычислить:
.
Объём тела удобно вычислять тройным интегралом:
.
В цилиндрических координатах интеграл принимает вид:
.
В сферических координатах:
.
Пример 5.3. Вычислить объём тела, ограниченного сферой
и
конусом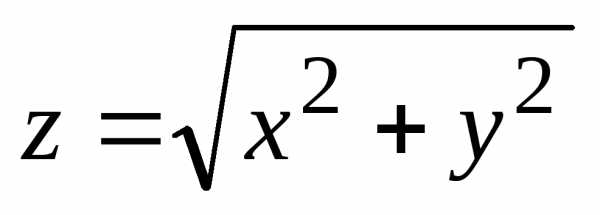 
(рис.
5.11).
Решение. Уравнение сферы простыми преобразованиями приводится к виду:
.
В сферических координатах уравнение сферы
.
Уравнение конуса
.
Области изменения переменных
.
Рис. 5.11
Искомый объём вычислим в сферических координатах:
.
Вычисление интеграла в данной задаче можно произвести в цилиндрических координатах.
Преобразуем уравнения сферы и конуса, подставив в них соотношения
.
Уравнение верхней половины сферы
.
Уравнение верхней половины конуса
.
Проекция
объёма 
на плоскость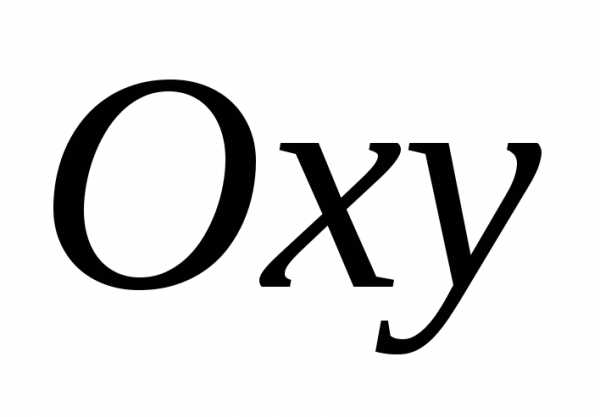
круг радиусом 
.
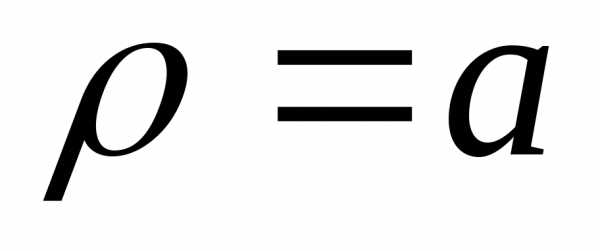Области
изменения переменных
.
Эти данные позволяют расставить пределы в повторных интегралах и вычислить искомый объём:
.
Пример 5.4. Вычислить объём тела Вивиани, образованного пересечением сферы
и цилиндра с вертикальными образующими
.
(На рис. 5.12 приведено изображение только верхней половины тела Вивиани.)
Рис. 5.12
Решение. Вычислим интеграл в цилиндрических координатах. Преобразуем уравнения сферы и цилиндра, подставив в них соотношения
.
Уравнение сферы
.
Уравнение цилиндра
.
Вычислим объём четверти тела Вивиани, лежащей в первом октанте, и результат умножим на 4, что возможно, так как тело симметрично.
Области изменения переменных
.
Вычисление тройного интеграла сведется к вычислению трех повторных интегралов, пределы интегрирования в которых соответствуют данным, приведенным выше:
.
Решить самостоятельно: [1] № 3590, 3592, 3593.
studfiles.net
Примеры применения цилиндрических и сферических координат / Тройной интеграл / 3dstroyproekt.ru
Как и в случае перехода к полярным координатам в двойном интеграле, дать однозначный рецепт того, когда следует применять цилиндрические или сферические координаты, нельзя, это дело опыта. Можно попробовать применить цилиндрические координаты, если подынтегральная функция и/или уравнения поверхностей, ограничивающих объём $\mathbf { \textit { V } } $, зависят от комбинации $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } $; сферические — если эти уравнения зависят от $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } $. Рассмотрим ряд примеров.
Пример 1
Найти объём $\mathbf { \textit { V } } $ общей части двух шаров, ограниченных сферами
$\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } =\mathbf { \textit { R } } ^ { 2 } $, $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } $ = 2$\mathbf { \textit { Rz } } ^ { } $.
Решение:
Пересечение сфер находится на уровне $2Rz=R^2\Rightarrow z=R/2$ и представляет собой круг радиуса $R\frac { \sqrt 3 } { 2 } $. Объём $\mathbf { \textit { V } } $ограничен сверху поверхностью $z=\sqrt { R^2-x^2-y^2 } $, снизу — поверхностью $z=R-\sqrt { R^2-x^2-y^2 } $. Вычисления в декартовых координатах дают $V=\iiint\limits_V { dv } =\iiint\limits_V { dxdydz } =\int\limits_ { -R\frac { \sqrt 3 } { 2 } } ^ { R\frac { \sqrt 3 } { 2 } } { dx\int\limits_ { -\sqrt { \frac { 3 } { 4 } R^2-x^2 } } ^ { \sqrt { \frac { 3 } { 4 } R^2-x^2 } } { dy\int\limits_ { R-\sqrt { R^2-x^2-y^2 } } ^ { \sqrt { R^2-x^2-y^2 } } { dz } } } $ — достаточно громоздкие выкладки.
В цилиндрических координатах объём $\mathbf { \textit { V } } $ ограничен сверху поверхностью $z=\sqrt { R^2-r^2 } $, снизу — поверхностью $z=R-\sqrt { R^2-r^2 } $, поэтому
$V=\iiint\limits_V { dv } =\iiint\limits_V { rdrd\varphi dz } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { R\frac { \sqrt 3 } { 2 } } { rdr\int\limits_ { R-\sqrt { R^2-r^2 } } ^ { \sqrt { R^2-r^2 } } { dz } } } =2\pi \int\limits_0^ { R\frac { \sqrt 3 } { 2 } } { \left[ { 2\sqrt { R^2-r^2 } -R }\right]rdr } =$ $ =2\pi \left. { \left[ { -\frac { 2 } { 3 } \sqrt { \left( { R^2-r^2 }\right)^3 } -R\frac { r^2 } { 2 } }\right] }\right|_0^ { R\frac { \sqrt 3 } { 2 } } =2\pi \left[ { \frac { 2 } { 3 } R^3-\frac { 2 } { 3 } \sqrt { \left( { R^2/4 }\right)^3 } -\frac { 3R^3 } { 8 } }\right]=2\pi R^3\left( { \frac { 2 } { 3 } -\frac { 2 } { 24 } -\frac { 3 } { 8 } }\right)=\frac { 5 } { 12 } \pi R^3. $
В сферических координатах уравнение нижней сферы принимает вид $r=R$, верхней — $r^2=2Rr\cos \theta \Rightarrow r=2R\cos \theta $, их пересечение соответствует значению $\cos \theta =1/2\Rightarrow \theta =\pi /3$. В интервале $0\leqslant \theta \leqslant \pi /3 \quad \mathbf { \textit { r } } $ меняется от $0$ до $\mathbf { \textit { R } } $, в интервале $\pi /3\leqslant \theta \leqslant \pi /2 \quad \mathbf { \textit { r } } $ меняется от $0$ до $2R\cos \theta $, поэтому
$V=\iiint\limits_V { dv } =\iiint\limits_V { r^ { 2 } \sin\theta drd\varphi d\theta } = \int_0^ { 2\pi } d \phi \int_0^ { \pi/3 } \sin \theta d\theta \int_0^R r^2 dr + \int_0^ { 2\pi } d \phi \int_ { \pi/3 } ^ { \pi/2 } \sin \theta d\theta \int_0^ { 2R\cos \theta } r^2 dr = 2\pi \frac { R^3 } { 3 } (-\cos\theta) =\\ =2\pi \frac { R^3 } { 3 } \left. { \left( { -\cos \theta }\right) }\right|_0^ { \frac { \pi } { 3 } } +2\pi \frac { 8R^3 } { 3 } \int\limits_ { \frac { \pi } { 3 } } ^ { \frac { \pi } { 2 } } { \cos ^3\theta \sin \theta d\theta } =\frac { \pi R^3 } { 3 } -\frac { 16\pi R^3 } { 3 } \cdot \left. { \frac { \cos ^4\theta } { 4 } }\right|_ { \frac { \pi } { 3 } } ^ { \frac { \pi } { 2 } } = $ $ =\frac { \pi R^3 } { 3 } +\frac { \pi R^3 } { 3\cdot 4 } =\frac { 5\pi R^3 } { 12 } . $
В этом примере трудоёмкость вычислений в цилиндрических и сферических координатах примерно одинакова.
Пример 2
$I=\iiint\limits_V { (x+y+z)dxdydz } ;\quad V:\left[{ \begin{array} { l } x=2-y^2-z^2, \\ x^2=y^2+z^2,\;x\geqslant 0. \\ \end{array} }\right.$
Решение:
Параболоид и конус пересекаются в плоскости $x=2-x^2\Rightarrow x=1$ по кругу радиуса 1. Осью симметрии объёма $\mathbf { \textit { V } } $ служит ось $\mathbf { \textit { Ох } } $, поэтому цилиндрические координаты вводим формулами $x=x,\quad y=r\cos \varphi ,\quad z=r\sin \varphi ; \quad I=\iiint\limits_V { (x+y+z)dxdydz } =\iiint\limits_V { (x+r\cos \varphi +r\sin \varphi )rdxdrd\varphi } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^1 { rdr\int\limits_r^ { 2-r^2 } { (x+r\cos \varphi +r\sin \varphi )dx } } } =$ $ =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^1 { \left. { \frac { x^2 } { 2 } }\right|_r^ { 2-r^2 } rdr } } +\int\limits_0^ { 2\pi } { (\cos \varphi +\sin \varphi )d\varphi \int\limits_0^1 { \left. x \right|_r^ { 2-r^2 } r^2dr } } =\pi \int\limits_0^1 { \left( { 4-5r^2+r^4 }\right)dr } =\frac { 38\pi } { 15 } . $ Применение сферических координат в этом примере нецелесообразно { громоздкое уравнение для параболоида } .
Пример 3
$I=\iiint\limits_V { \sqrt { x^2+y^2+z^2 } dxdydz } ;\quad V:\left[{ x^2+y^2+z^2=z. }\right.$
Решение:
Здесь область интегрирования — шар радиуса 1/2, сдвинутый по оси $\mathbf { \textit { Оz } } $ на 1/2 единицы, подынтегральная функция зависит от выражения $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } $, поэтому применим сферические координаты. Уравнение сферы $x^2+y^2+z^2=z\Rightarrow r^2=r\cos \theta \Rightarrow r=\cos \theta \left( { \Rightarrow 0\leqslant \theta \leqslant \pi /2 }\right)$ , поэтому $I=\iiint\limits_V { \sqrt { x^2+y^2+z^2 } dxdydz } =\iiint\limits_V { r\cdot r^2\sin \theta drd\varphi d\theta } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \pi /2 } { \sin \theta d\theta } \int\limits_0^ { \cos \theta } { r^3dr } } =\frac { 2\pi } { 4 } \int\limits_0^ { \pi /2 } { \left. { r^4 }\right|_0^ { \cos \theta } \sin \theta d\theta } = \\ =\frac { 2\pi } { 4 } \int\limits_0^ { \pi /2 } { \cos ^4\theta \sin \theta d\theta } =-\frac { 2\pi } { 4\cdot 5 } \left. { \cos ^5\theta }\right|_0^ { \pi /2 } =\frac { \pi } { 10 } $.
Пример 4
Вычислить объём тела, ограниченного поверхностью $\left( { x^2+y^2+z^2 }\right)^ { \,2 } =a^3z,\;a=const>0$
Решение:
Здесь тоже для того, чтобы понять, как устроено тело, и найти его объём, надо перейти к сферическим координатам { на это указывает комбинация $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } =\mathbf { \textit { r } } ^ { 2 } )$. Уравнение поверхности $\left( { x^2+y^2+z^2 }\right)^ { \,2 } =a^3z\Rightarrow r^4=a^3r\cos \vartheta \Rightarrow r=a\sqrt[3] { \cos \vartheta } \;\left( { \Rightarrow 0\leqslant \theta \leqslant \pi /2 }\right)$. По этому уравнению поверхность построить уже можно; отсутствие координаты $\varphi $ в уравнении показывает, что это — тело вращения вокруг оси $\mathbf { \textit { Oz } } $. Находим объём: $ V=\iiint\limits_V { r^2\sin \theta drd\varphi d\theta } =\int\limits_0^ { 2\pi } { d\varphi \int\limits_0^ { \pi /2 } { \sin } } \theta d\theta \int\limits_0^ { a\sqrt[3] { \cos \theta } } { r^2dr } =\frac { 2\pi } { 3 } \int\limits_0^ { \pi /2 } { \left. { r^3 }\right|_0^ { a\sqrt[3] { \cos \theta } } \sin \theta d\theta = } $ $ =\frac { 2\pi a^3 } { 3 } \int\limits_0^ { \pi /2 } { \cos \theta \sin \theta d\theta = } \frac { \pi a^3 } { 3 } . $
Пример 5
Вычислить интеграл $\iiint\limits_U { \left( { { x^4 } + 2 { x^2 } { y^2 } + { y^4 } }\right)dxdydz } ,$ где область (U) ограничена поверхностью ( { x^2 } + { y^2 } \le 1) и плоскостями (z = 0,) (z = 1).
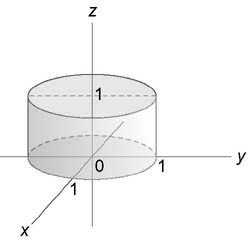
Решение:
Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость (Oxy) представляет собой круг ( { x^2 } + { y^2 } \le 1) или (0 \le \rho \le 1).
Заметим, что подынтегральное выражение записывается в виде $ { \left( { { x^4 } + 2 { x^2 } { y^2 } + { y^4 } }\right) } = { { \left( { { x^2 } + { y^2 } }\right)^2 } } = { { \left( { { \rho ^2 } }\right)^2 } = { \rho ^4 } } $
Тогда интеграл будет равен $I = \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } \rho d\rho } \int\limits_0^1 { dz } .$
Здесь во втором интеграле добавлен множитель (\rho) якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга.
В результате тройной интеграл легко вычисляется: $ { I = \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } \rho d\rho } \int\limits_0^1 { dz } } = { 2\pi \int\limits_0^1 { { \rho ^5 } d\rho } \int\limits_0^1 { dz } } = { 2\pi \cdot 1 \cdot \int\limits_0^1 { { \rho ^5 } d\rho } } = { 2\pi \left. { \left( { \frac { { { \rho ^6 } } } { 6 } }\right) }\right|_0^1 } = { 2\pi \cdot \frac { 1 } { 6 } = \frac { \pi } { 3 } . } $
Пример 6
Вычислить интеграл $\iiint\limits_U { \left( { { x^2 } + { y^2 } }\right)dxdydz } ,$ где область (U) ограничена поверхностями ( { x^2 } + { y^2 } = 3z,) (z = 3)
Решение:
Область интегрирования изображена на рисунке
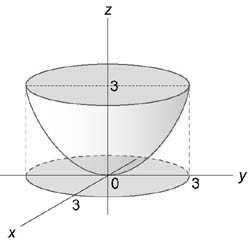
Для вычисления интеграла перейдем к цилиндрическим координатам: $ { x = \rho \cos \varphi , } \;\; { y = \rho \sin \varphi , } \;\; { z = z. } $ Дифференциал при этом равен $dxdydz = \rho d\rho d\varphi dz\;\;\left( { \rho — \text { якобиан } }\right).$
Уравнение параболической поверхности принимает вид: $ { \rho ^2 } { \cos ^2 } \varphi + { \rho ^2 } { \sin^2 } \varphi = 3z\;\;\text { или } \;\; { \rho ^2 } = 3z.$ Проекция области интегрирования (U) на плоскость (Oxy) представляет собой окружность ( { x^2 } + { y^2 } \le 9) радиусом (\rho = 3).
Координата (\rho) изменяется в пределах от (0) до (3,) угол (\varphi) от (0) до (2\pi) и координата (z) от (\large\frac { { { \rho ^2 } } } { 3 } \normalsize) до (3.)
В результате интеграл будет равен $ { I = \iiint\limits_U { \left( { { x^2 } + { y^2 } }\right)dxdydz } } = { \iiint\limits_ { U’ } { { \rho ^2 } \cdot \rho d\rho d\varphi dz } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^3 { { \rho ^3 } d\rho } \int\limits_ { \frac { { { \rho ^2 } } } { 3 } } ^3 { dz } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^3 { { \rho ^3 } d\rho } \cdot \left[ { \left. z \right|_ { \frac { { { \rho ^2 } } } { 3 } } ^3 }\right] } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^3 { { \rho ^3 } \left( { 3 — \frac { { { \rho ^2 } } } { 3 } }\right)d\rho } } = \\ = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^3 { \left( { 3 { \rho ^3 } — \frac { { { \rho ^5 } } } { 3 } }\right)d\rho } } = { \int\limits_0^ { 2\pi } { d\varphi } \cdot \left[ { \left. { \left( { \frac { { 3 { \rho ^4 } } } { 4 } — \frac { { { \rho ^6 } } } { { 18 } } }\right) }\right|_0^3 }\right] } = { \left( { \frac { { 3 \cdot 81 } } { 4 } — \frac { { 729 } } { { 18 } } }\right)\int\limits_0^ { 2\pi } { d\varphi } } = { \frac { { 81 } } { 4 } \cdot 2\pi = \frac { { 81\pi } } { 2 } . } $
Пример 7
Используя цилиндрические координаты, найти значение интеграла $ I = \int\limits_ { — 2 } ^2 { dx } \int\limits_ { — \sqrt { 4 — { x^2 } } } ^ { \sqrt { 4 — { x^2 } } } { dy } \int\limits_0^ { 4 — { x^2 } — { y^2 } } { { y^2 } dz } $
Решение:
Область интегрирования (U) изображена на рисунке:
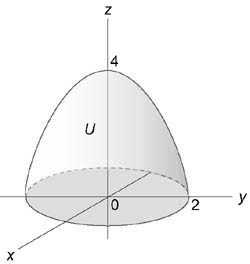
Ее проекция на плоскость (Oxy) представляет собой круг ( { x^2 } + { y^2 } = { 2^2 } ):
Новые переменные в цилиндрических координатах будут изменяться в пределах $ { 0 \le \rho \le 2, } \;\; { 0 \le \varphi \le 2\pi , } \;\; { 0 \le z \le 4 — { \rho ^2 } . } $
Подставляя (x = \rho \cos \varphi ) и (x = \rho \sin \varphi,) найдем значение интеграла: $ { I = \int\limits_ { — 2 } ^2 { dx } \int\limits_ { — \sqrt { 4 — { x^2 } } } ^ { \sqrt { 4 — { x^2 } } } { dy } \int\limits_0^ { 4 — { x^2 } — { y^2 } } { { y^2 } dz } } = { \iiint\limits_U { { y^2 } dxdydz } } = { \iiint\limits_ { U’ } { { { \left( { \rho \sin \varphi }\right) } ^2 } \rho d\rho d\varphi dz } } = { \iiint\limits_ { U’ } { { \rho ^3 } { { \sin } ^2 } \varphi d\rho d\varphi dz } } = { \int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } \int\limits_0^2 { { \rho ^3 } \left( { 4 — { \rho ^2 } }\right)d\rho } } = \\ = { \int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } \int\limits_0^2 { \left( { 4 { \rho ^3 } — { \rho ^5 } }\right)d\rho } } = { \int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } \cdot \left[ { \left. { \left( { \frac { { 4 { \rho ^4 } } } { 4 } — \frac { { { \rho ^6 } } } { 6 } }\right) }\right|_0^2 }\right] } = { \left( { { 2^4 } — \frac { { { 2^6 } } } { 6 } }\right)\int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } } = { \frac { { 16 } } { 3 } \int\limits_0^ { 2\pi } { { { \sin } ^2 } \varphi d\varphi } } = { \frac { { 16 } } { 3 } \int\limits_0^ { 2\pi } { \frac { { 1 — \cos 2\varphi } } { 2 } d\varphi } } = \\ = { \frac { 8 } { 3 } \int\limits_0^ { 2\pi } { \left( { 1 — \cos 2\varphi }\right)d\varphi } } = { \frac { 8 } { 3 } \left[ { \left. { \left( { \varphi — \frac { { \sin 2\varphi } } { 2 } }\right) }\right|_0^ { 2\pi } }\right] } = { \frac { 8 } { 3 } \cdot 2\pi = \frac { { 16\pi } } { 3 } . } $
Пример 8
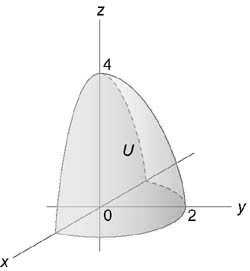
Вычислить интеграл, используя цилиндрические координаты: $\iiint\limits_U { \sqrt { { x^2 } + { y^2 } } dxdydz } .$ Область (U) ограничена параболоидом (z = 4 — { x^2 } — { y^2 } ,) цилиндром ( { x^2 } + { y^2 } = 4) и плоскостями (y = 0,) (z = 0)
Решение:
Изобразив схематически область интегрирования (U,) находим, что ее проекция на плоскость (Oxy) { область (D) } представляет собой полукруг радиусом (\rho = 2).
Перейдем к цилиндрическим координатам, применяя подстановки $ { x = \rho \cos \varphi , } \;\; { y = \rho \sin \varphi , } \;\; { z = z, } \;\; { dxdydz = \rho d\rho d\varphi dz. } $
Новые переменные будут изменяться в пределах $ { 0 \le \rho \le 2, } \;\; { 0 \le \varphi \le \pi , } \;\; { 0 \le z \le 4 — { \rho ^2 } . } $
Теперь вычисляем интеграл: $ { I = \iiint\limits_U { \sqrt { { x^2 } + { y^2 } } dxdydz } } = { \iiint\limits_ { U’ } { \rho \cdot \rho d\rho d\varphi dz } } = { \iiint\limits_ { U’ } { { \rho ^2 } d\rho d\varphi dz } } = { \int\limits_0^\pi { d\varphi } \int\limits_0^2 { { \rho ^2 } d\rho } \int\limits_0^ { 4 — { \rho ^2 } } { dz } } = { \int\limits_0^\pi { d\varphi } \int\limits_0^2 { { \rho ^2 } d\rho } \cdot \left[ { \left. z \right|_0^ { 4 — { \rho ^2 } } }\right] } = { \int\limits_0^\pi { d\varphi } \int\limits_0^2 { { \rho ^2 } \left( { 4 — { \rho ^2 } }\right)d\rho } } = \\ = { \int\limits_0^\pi { d\varphi } \int\limits_0^2 { \left( { 4 { \rho ^2 } — { \rho ^4 } }\right)d\rho } } = { \int\limits_0^\pi { d\varphi } \left[ { \left. { \left( { \frac { { 4 { \rho ^3 } } } { 3 } — \frac { { { \rho ^5 } } } { 5 } }\right) }\right|_0^2 }\right] } = { \left( { \frac { 4 } { 3 } \cdot { 2^3 } — \frac { { { 2^5 } } } { 5 } }\right)\int\limits_0^\pi { d\varphi } } = { \frac { { 64 } } { { 15 } } \int\limits_0^\pi { d\varphi } } = { \frac { { 64 } } { { 15 } } \cdot \left[ { \left. \varphi \right|_0^\pi }\right] = \frac { { 64\pi } } { { 15 } } . } $
Пример 9
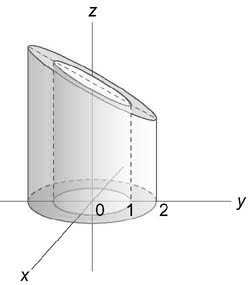
Найти интеграл $\iiint\limits_U { ydxdydz } ,$ где область (U) ограничена плоскостями (z = x + 1,) (z = 0) и цилиндрическими поверхностями ( { x^2 } + { y^2 } = 1,) ( { x^2 } + { y^2 } = 4)
Решение:
Вычислим данный интеграл в цилиндрических координатах. Из условия $0 \le z \le x + 1$ следует, что $0 \le z \le \rho \cos \varphi + 1.$ Область интегрирования в плоскости (Oxy) представляет собой кольцо, ограниченное окружностями ( { x^2 } + { y^2 } = 1) и ( { x^2 } + { y^2 } = 4)
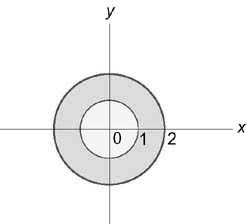
Следовательно, переменные (\rho) и (\varphi) изменяются в интервале $1 \le \rho \le 2,\;\;0 \le \varphi \le 2\pi .$
Находим интеграл: $ { I = \iiint\limits_U { ydxdydz } } = { \iiint\limits_ { U’ } { \rho \sin \varphi \cdot \rho d\rho d\varphi dz } } = { \iiint\limits_ { U’ } { { \rho ^2 } \sin \varphi d\rho d\varphi dz } } = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \int\limits_0^2 { { \rho ^2 } d\rho } \int\limits_0^ { \rho \cos \varphi + 1 } { dz } } = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \int\limits_0^2 { { \rho ^2 } d\rho } \cdot \left[ { \left. z \right|_0^ { \rho \cos \varphi + 1 } }\right] } = \\ = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \int\limits_0^2 { { \rho ^2 } \left( { \rho \cos \varphi + 1 }\right)d\rho } } = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \int\limits_0^2 { \left( { { \rho ^3 } \cos \varphi + { \rho ^2 } }\right)d\rho } } = { \int\limits_0^ { 2\pi } { \sin \varphi d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^4 } } } { 4 } \cos \varphi + \frac { { { \rho ^3 } } } { 3 } }\right) }\right|_ { \rho = 1 } ^ { \rho = 2 } }\right] } = \\ = { \int\limits_0^ { 2\pi } { \sin \varphi \left[ { \left( { 4\cos \varphi + \frac { 8 } { 3 } }\right) — \left( { \frac { { \cos \varphi } } { 4 } + \frac { 1 } { 3 } }\right) }\right]d\varphi } } = { \int\limits_0^ { 2\pi } { \sin \varphi \left( { \frac { { 15 } } { 4 } \cos \varphi + \frac { 7 } { 3 } }\right)d\varphi } } = { \int\limits_0^ { 2\pi } { \left( { \frac { { 15 } } { 4 } \sin \varphi \cos \varphi + \frac { 7 } { 3 } \sin \varphi }\right)d\varphi } } = \\ = { \int\limits_0^ { 2\pi } { \left( { \frac { { 15 } } { 8 } \sin 2\varphi + \frac { 7 } { 3 } \sin \varphi }\right)d\varphi } } = { \left. { \left( { — \frac { { 15 } } { { 16 } } \cos 2\varphi — \frac { 7 } { 3 } \cos \varphi }\right) }\right|_0^ { 2\pi } = 0. } $
Этот результат закономерен, поскольку область (U) симметрична относительно плоскости (Oxz,) а подынтегральная функция является четной.
Пример 10
Найти интеграл (\iiint\limits_U { \sqrt { { x^2 } + { y^2 } + { z^2 } } dxdydz } ,) где область интегрирования (U) шар, заданный уравнением ( { { x^2 } + { y^2 } + { z^2 } } = 25.)
Решение:
Поскольку область (U) представляет собой шар, и к тому же подынтегральное выражение является функцией, зависящей от $f\left( { { x^2 } + { y^2 } + { z^2 } }\right),$ то перейдем к сферическим координатам.
Сделаем замену: $ { x = \rho \cos \varphi \sin \theta , } \;\; { y = \rho \sin \varphi \sin \theta , } \;\; { z = \rho \cos \theta , } $ Новые переменные изменяются в пределах: $ { 0 \le \rho \le 5, } \;\; { 0 \le \varphi \le 2\pi , } \;\; { 0 \le \theta \le \pi . } $
Учитывая якобиан ( { \rho ^2 } \sin \theta,) записываем интеграл в виде: $ { I = \iiint\limits_U { \sqrt { { x^2 } + { y^2 } + { z^2 } } dxdydz } } = { \iiint\limits_ { U’ } { \rho \cdot { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^5 { { \rho ^3 } d\rho } \int\limits_0^\pi { \sin \theta d\theta } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^5 { { \rho ^3 } d\rho } \left[ { \left. { \left( { — \cos \theta }\right) }\right|_0^\pi }\right] } = \\ = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^5 { { \rho ^3 } d\rho } \left( { — \cos \pi + \cos 0 }\right) } = { 2\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^5 { { \rho ^3 } d\rho } } = { 2\int\limits_0^ { 2\pi } { d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^4 } } } { 4 } }\right) }\right|_0^5 }\right] } = \\ = { 2\int\limits_0^ { 2\pi } { d\varphi } \cdot \frac { { { 5^4 } } } { 4 } } = { \frac { { 625 } } { 2 } \int\limits_0^ { 2\pi } { d\varphi } } = { \frac { { 625 } } { 2 } \cdot 2\pi = 625\pi . } $
Пример 11
Вычислить интеграл $\iiint\limits_U { { e^ { { { \left( { { x^2 } + { y^2 } + { z^2 } }\right) } ^ { \frac { 3 } { 2 } } } } } dxdydz } ,$ где область (U) представляет собой единичный шар ( { { x^2 } + { y^2 } + { z^2 } } \le 1.)
Решение:
Центр данного шара расположен в начале координат. Следовательно, в сферических координатах область интегрирования (U) описывается неравенствами $ { 0 \le \rho \le 1, } \;\; { 0 \le \varphi \le 2\pi , } \;\; { 0 \le \theta \le \pi . } $
Записывая интеграл в сферических координатах, получаем $ { I = \iiint\limits_U { { e^ { { { \left( { { x^2 } + { y^2 } + { z^2 } }\right) } ^ { \frac { 3 } { 2 } } } } } dxdydz } } = { \iiint\limits_ { U’ } { { e^ { { { \left( { { \rho ^2 } }\right) } ^ { \frac { 3 } { 2 } } } } } { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = { \iiint\limits_ { U’ } { { e^ { { \rho ^3 } } } { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = { \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { e^ { { \rho ^3 } } } { \rho ^2 } d\rho } \int\limits_0^\pi { \sin \theta d\theta } . } $
Как видно, тройной интеграл вырождается в произведение трех однократных интегралов, каждый из которых вычисляется независимо. В результате находим $ { I = \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { e^ { { \rho ^3 } } } { \rho ^2 } d\rho } \int\limits_0^\pi { \sin \theta d\theta } } = { \left[ { \left. \varphi \right|_0^ { 2\pi } }\right] \cdot \int\limits_0^1 { \left( { { e^ { { \rho ^3 } } } \cdot \frac { 1 } { 3 } d { \rho ^3 } }\right) } \cdot \left[ { \left. { \left( { — \cos \theta }\right) }\right|_0^\pi }\right] } = { 2\pi \cdot \frac { 1 } { 3 } \left[ { \left. { \left( { { e^ { { \rho ^3 } } } }\right) }\right|_ { { \rho ^3 } = 0 } ^ { { \rho ^3 } = 1 } }\right] \cdot \left( { — \cos \pi + \cos 0 }\right) } = { \frac { { 2\pi } } { 3 } \cdot \left( { e — 1 }\right) \cdot 2 } = { \frac { { 4\pi } } { 3 } \left( { e — 1 }\right). } $
Пример 12
Вычислить интеграл (\iiint\limits_U { xyzdxdydz } ,) где область (U) представляет собой часть шара ( { x^2 } + { y^2 } + { z^2 } \le { R^2 } ,) расположенную в первом октанте (x \ge 0, y \ge 0, z \ge 0.)
Решение:
Перейдем к сферическим координатам. Сделаем замену переменных: $ { x = \rho \cos \varphi \sin \theta , } \;\; { y = \rho \sin \varphi \sin \theta , } \;\; { z = \rho \cos \theta , } \;\; { dxdydz = { \rho ^2 } \sin \theta d\rho d\varphi d\theta . } $ Новые переменные будут изменяться в пределах: $ { 0 \le \rho \le R, } \;\; { 0 \le \varphi \le \frac { \pi } { 2 } , } \;\;0 { \le \theta \le \frac { \pi } { 2 } . } $ Тогда интеграл в сферических координатах равен $ { I = \iiint\limits_U { xyzdxdydz } } = { \iiint\limits_ { U’ } { \left[ { \rho \cos \varphi \sin \theta \cdot \rho \sin \varphi \sin \theta \cdot \rho \cos \theta \cdot { \rho ^2 } \sin \theta d\rho d\varphi d\theta }\right] } } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \cos \varphi \sin \varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { { { \sin } ^3 } \theta \cos \theta d\theta } } = \\ = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \left( { \frac { 1 } { 2 } \sin 2\varphi d\varphi }\right) } \int\limits_0^R { { \rho ^5 } d\rho } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { { { \sin } ^3 } \theta \cos \theta d\theta } } = \\ = { \frac { 1 } { 2 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { { { \sin } ^3 } \theta d\left( { \sin \theta }\right) } } = { \frac { 1 } { 2 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \cdot \left[ { \left. { \left( { \frac { { { { \sin } ^4 } \theta } } { 4 } }\right) }\right|_ { \theta = \\ = 0 } ^ { \theta = \large\frac { \pi } { 2 } \normalsize } }\right] } = { \frac { 1 } { 8 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \cdot \left( { { { \sin } ^4 } \frac { \pi } { 2 } — { { \sin } ^4 } 0 }\right) } = \\ = { \frac { 1 } { 8 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \int\limits_0^R { { \rho ^5 } d\rho } \cdot 1 } = { \frac { 1 } { 8 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin 2\varphi d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^6 } } } { 6 } }\right) }\right|_0^R }\right] } = { \frac { { { R^6 } } } { { 48 } } \left[ { \left. { \left( { — \frac { { \cos 2\varphi } } { 2 } }\right) }\right|_0^ { \large\frac { \pi } { 2 } \normalsize } }\right] } = { \frac { { { R^6 } } } { { 96 } } \left( { — \cos \pi + \cos 0 }\right) } = { \frac { { { R^6 } } } { { 96 } } \cdot 2 } = { \frac { { { R^6 } } } { { 48 } } . } $
Пример 13
Найти тройной интеграл $\iiint\limits_U { \left( { \frac { { { x^2 } } } { { { a^2 } } } + \frac { { { y^2 } } } { { { b^2 } } } + \frac { { { z^2 } } } { { { c^2 } } } }\right)dxdydz } ,$ где область (U) ограничена эллипсоидом $ { \frac { { { x^2 } } } { { { a^2 } } } + \frac { { { y^2 } } } { { { b^2 } } } + \frac { { { z^2 } } } { { { c^2 } } } } = 1.$
Решение:
Для вычисления интеграла перейдем к обобщенным сферическим координатам путем следующей замены переменных: $ { x = a\rho \cos \varphi \sin \theta , } \;\; { y = b\rho \sin \varphi \sin \theta , } \;\; { z = c\rho \cos \theta . } $ Модуль якобиана данного преобразования равен (\left| I \right| = abc { \rho ^2 } \sin \theta .) Поэтому для дифференциалов справедливо соотношение $dxdydz = abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta .$ В новых координатах интеграл принимает вид: $ { I = \iiint\limits_U { \left( { \frac { { { x^2 } } } { { { a^2 } } } + \frac { { { y^2 } } } { { { b^2 } } } + \frac { { { z^2 } } } { { { c^2 } } } }\right)dxdydz } } = { \iiint\limits_ { U’ } { \left[ { \frac { { { { \left( { a\rho \cos \varphi \sin \theta }\right) } ^2 } } } { { { a^2 } } } + \frac { { { { \left( { b\rho \sin \varphi \sin \theta }\right) } ^2 } } } { { { b^2 } } } + \frac { { { { \left( { c\rho \cos \theta }\right) } ^2 } } } { { { c^2 } } } }\right]abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = \\ = { \iiint\limits_ { U’ } { \left[ { { \rho ^2 } { { \cos } ^2 } \varphi \, { { \sin } ^2 } \theta + { \rho ^2 } { \sin^2 } \varphi \, { { \sin } ^2 } \theta + { \rho ^2 } { { \cos } ^2 } \theta }\right]abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = \\ = { \iiint\limits_ { U’ } { \left[ { { \rho ^2 } { { \sin } ^2 } \theta \underbrace { \left( { { { \cos } ^2 } \varphi + { \sin^2 } \varphi }\right) } _1 + { \rho ^2 } { { \cos } ^2 } \theta }\right]abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = \\ = { \iiint\limits_ { U’ } { { \rho ^2 } \underbrace { \left( { { \sin^2 } \theta + { { \cos } ^2 } \theta }\right) } _1abc { \rho ^2 } \sin \theta d\rho d\varphi d\theta } } = { abc\iiint\limits_ { U’ } { { \rho ^4 } \sin \theta d\rho d\varphi d\theta } . } $
Область интегрирования (U’) в сферических координатах представляет собой параллелепипед и определяется неравенствами $ { 0 \le \rho \le 1, } \;\; { 0 \le \varphi \le 2\pi , } \;\; { 0 \le \theta \le \pi . } $ Тогда тройной интеграл становится равным $ { I = abc\iiint\limits_ { U’ } { { \rho ^4 } \sin \theta d\rho d\varphi d\theta } } = { abc\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } d\rho } \int\limits_0^\pi { \sin \theta d\theta } } = { abc\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } d\rho } \cdot \left[ { \left. { \left( { — \cos \theta }\right) }\right|_0^\pi }\right] } = \\ = { abc\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } d\rho } \cdot \left( { — \cos \pi + \cos 0 }\right) } = { 2abc\int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^1 { { \rho ^4 } d\rho } } = { 2abc\int\limits_0^ { 2\pi } { d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^5 } } } { 5 } }\right) }\right|_0^1 }\right] } = \\ = { \frac { { 2abc } } { 5 } \int\limits_0^ { 2\pi } { d\varphi } } = { \frac { { 2abc } } { 5 } \cdot \left[ { \left. \varphi \right|_0^ { 2\pi } }\right] } = { \frac { { 2abc } } { 5 } \cdot 2\pi = \frac { { 4abc\pi } } { 5 } . } $
Пример 14
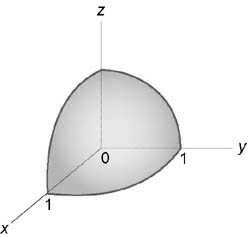
Вычислить интеграл $\int\limits_0^1 { dx } \int\limits_0^ { \sqrt { 1 — { x^2 } } } { dy } \int\limits_0^ { \sqrt { 1 — { x^2 } — { y^2 } } } { { { \left( { { x^2 } + { y^2 } + { z^2 } }\right) } ^2 } dz } ,$ используя сферические координаты.
Решение:
Область интегрирования представляет собой часть шара, расположенная в первом октанте и, следовательно, ограничена неравенствами $ { 0 \le \rho \le 1, } \;\; { 0 \le \varphi \le \frac { \pi } { 2 } , } \;\; { 0 \le \theta \le \frac { \pi } { 2 } . } $
Учитывая, что подынтегральное выражение равно $ { { \left( { { x^2 } + { y^2 } + { z^2 } }\right)^2 } } = { { \left[ { { { \left( { \rho \cos \varphi \sin \theta }\right) } ^2 } + { { \left( { \rho \sin \varphi \sin \theta }\right) } ^2 } + { { \left( { \rho \cos \theta }\right) } ^2 } }\right]^2 } } = \\ = { { \left[ { { \rho ^2 } { { \cos } ^2 } \varphi \, { { \sin } ^2 } \theta + { \rho ^2 } { \sin^2 } \varphi \, { { \sin } ^2 } \theta + { \rho ^2 } { { \cos } ^2 } \theta }\right]^2 } } = { { \left[ { { \rho ^2 } { { \sin } ^2 } \theta \underbrace { \left( { { { \cos } ^2 } \varphi + { \sin^2 } \varphi }\right) } _1 + { \rho ^2 } { { \cos } ^2 } \theta }\right]^2 } } = { { \left[ { { \rho ^2 } { { \sin } ^2 } \theta + { \rho ^2 } { { \cos } ^2 } \theta }\right]^2 } } = \\ = { { \left[ { { \rho ^2 } \underbrace { \left( { { { \sin } ^2 } \theta + { { \cos } ^2 } \theta }\right) } _1 }\right]^2 } } = { { \rho ^4 } , } $
а дифференциалы связаны соотношениями $dxdydz = { \rho ^2 } \sin \theta d\rho d\varphi d\theta ,$ получаем $ { I = \int\limits_0^1 { dx } \int\limits_0^ { \sqrt { 1 — { x^2 } } } { dy } \int\limits_0^ { \sqrt { 1 — { x^2 } — { y^2 } } } { { { \left( { { x^2 } + { y^2 } + { z^2 } }\right) } ^2 } dz } } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \int\limits_0^1 { \left( { { \rho ^4 } \cdot { \rho ^2 } d\rho }\right) } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { \sin \theta d\theta } } = \\ = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \int\limits_0^1 { { \rho ^6 } d\rho } \cdot \left[ { \left. { \left( { — \cos \theta }\right) }\right|_0^ { \large\frac { \pi } { 2 } \normalsize } }\right] } = \\ = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \int\limits_0^1 { { \rho ^6 } d\rho } \cdot \left( { — \cos \frac { \pi } { 2 } + \cos 0 }\right) } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \int\limits_0^1 { { \rho ^6 } d\rho } \cdot 1 } = { \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } \cdot \left[ { \left. { \left( { \frac { { { \rho ^7 } } } { 7 } }\right) }\right|_0^1 }\right] } = \\ = { \frac { 1 } { 7 } \int\limits_0^ { \large\frac { \pi } { 2 } \normalsize } { d\varphi } } = { \frac { 1 } { 7 } \cdot \left[ { \left. \varphi \right|_0^ { \large\frac { \pi } { 2 } \normalsize } }\right] } = { \frac { 1 } { 7 } \cdot \frac { \pi } { 2 } } = { \frac { \pi } { { 14 } } . } $
3dstroyproekt.ru
Тройной интеграл, вычисление объема тела. Примеры решения задач
Тройной интеграл, вычисление объема тела
Задача1. Вычислить тройной интеграл ,
где область ограничена поверхностями , , , . Поверхности, ограничивающие область интегрирования, являются плоскостями, а область является тетраэдром, который определяется системой неравенств
Изобразим область .
Проекцией области на плоскость является прямоугольный треугольник,
определяемый системой неравенств
Задача2
С помощью тройного интеграла вычислить объём тела, ограниченного координатными плоскостями и плоскостью . Изобразить данное тело и его проекцию на плоскость.
Решение
Если , то где V — объём области интегрирования.
Изобразим данное тело и его проекцию на плоскости.
Задача 3. Найти объем тела, заданного ограничивающими его поверхностями. www.matem96.ru
Лекции Тройной интеграл
Скачать с Depositfiles
Тройной интеграл.
Контрольные вопросы.
Тройной интеграл, его свойства.
Вычисление тройного интеграла в декартовых координатах.
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
Вычисление тройного интеграла в сферических координатах.
Пусть функция u = f(x,y,z) определена в ограниченной замкнутой области V пространства R3. Разобьём область V произвольным образом наn элементарных замкнутых областей V1, … , Vn, имеющих объемы V1, …, Vn соответственно. Обозначим d – наибольший из диаметров областей V1, … , Vn. В каждой области Vk выберем произвольную точку Pk (xk , yk , zk) и составим интегральную сумму функции f(x, y, z)
S =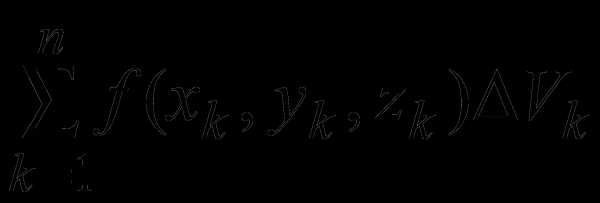 
Определение. Тройным интегралом от функции f(x, y, z) по области V называется предел интегральной суммы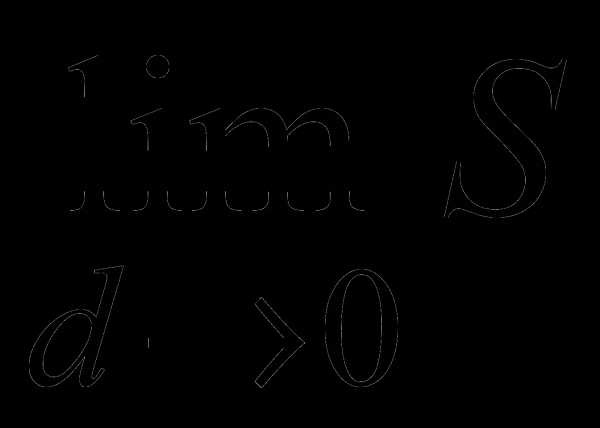 
, если он существует.
Таким образом,
(1)
Замечание. Интегральная сумма S зависит от способа разбиения области V и выбора точек Pk (k=1, …, n). Однако, если существует предел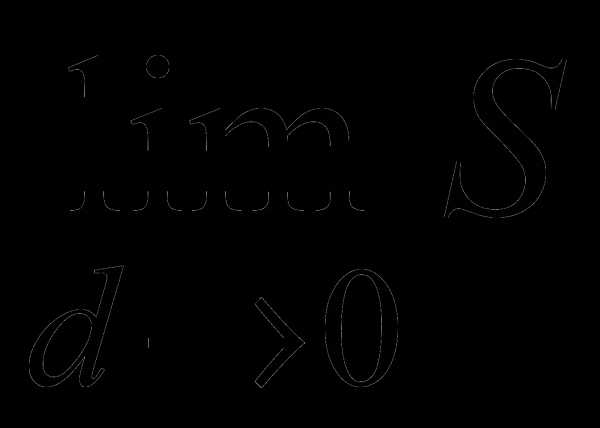
, то он не зависит от способа разбиения области V и выбора точек Pk . Если сравнить определения двойного и тройного интегралов, то легко увидеть в них полную аналогию.
Достаточное условие существования тройного интеграла. Тройной интеграл (13) существует, если функция f(x, y, z) ограничена в V и непрерывна в V, за исключением конечного числа кусочно-гладких поверхностей, расположенных в V .
В дальнейшем будем считать, что все рассматриваемые тройные интегралы существуют.
Некоторые свойства тройного интеграла.
1) Если С – числовая константа, то
3) Аддитивность по области. Если область V разбита на области V1 и V2, то
.
4) Объем тела V равен
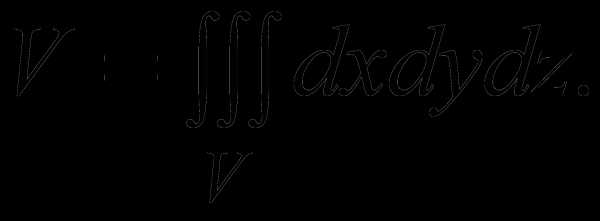(2)
Вычисление тройного интеграла в декартовых координатах.
Пусть D проекция тела V на плоскость xOy, поверхности z=φ1(x, y), z=φ2(x, y) ограничивают тело V снизу и сверху соответственно. Это значит, что
V = {(x, y, z): (x, y)
D, φ1(x, y) ≤ z ≤ φ2(x, y)} .
Такое тело назовем z-цилиндрическим. Тройной интеграл (1) по z-цилиндрическому телу V вычисляется переходом к повторному интегралу, состоящему из двойного и определенного интегралов:
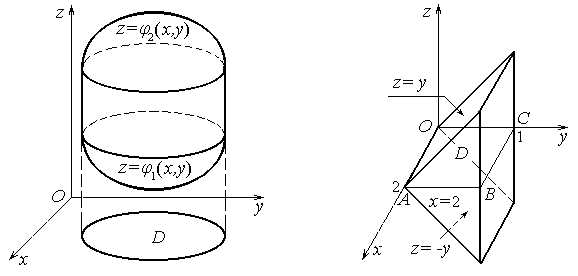
(3)
В этом повторном интеграле сначала вычисляется внутренний определенный интеграл по переменной z, при этом x, y считаются постоянными. Затем вычисляется двойной интеграл от полученной функции по области D.
Если V x-цилиндрическое или y-цилиндрическое тело, то верны соответственно формулы
В первой формуле D проекция тела V на координатную плоскость yOz, а во второй на плоскость xOz
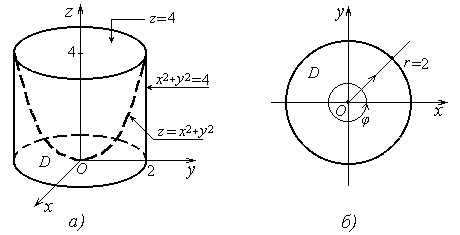
Примеры. 1) Вычислить объем тела V, ограниченного поверхностями z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. Вычислим объём при помощи тройного интеграла по формуле (2)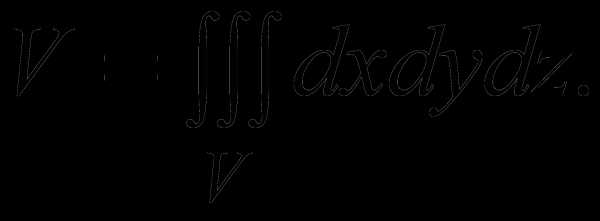 
Перейдем к повторному интегралу по формуле (3).
Пусть D круг x2 + y2 ≤ 4, φ1(x, y) = 0, φ2(x, y)= x2 + y2 . Тогда по формуле (3) получим
Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }.
2) Тело V ограничено поверхностями z=y, z= –y, x=0 , x=2, y=1. Вычислить
Плоскости z = y, z = –y ограничивают тело соответственно снизу и сверху, плоскости x=0 , x=2 ограничивают тело соответственно сзади и спереди, а плоскость y=1 ограничивает справа. V – z-цилиндрическое тело, его проекцией D на плоскость хОу является прямоугольник ОАВС. Положим φ1(x, y) = –y, φ2(x, y)= y и применим формулу (3):
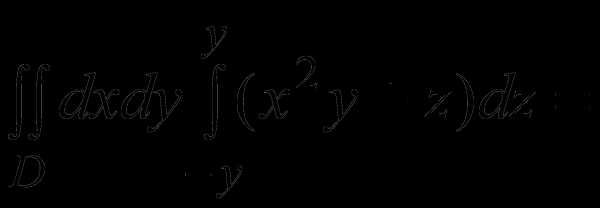
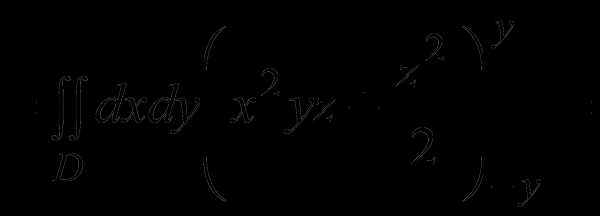
greleon.ru
ТРОЙНЫЕ ИНТЕГРАЛЫ
ρ ≥ 0, ϕ [0,2π] z — любое. Цилиндрические координаты связаны с
декарторыми соотношениями: |
|
x = ρ cosϕ,y = ρ sinϕ,z = z . | (2.7) |
Преобразование тройного интеграла от декартовых | координат |
x , y, z к цилиндрическим координатамϕ, ρ, z осуществляется по
следующей формуле перехода
∫∫∫ f(x, y, z)dxdydz=∫∫∫ f(ρ cosϕ, ρsin ϕ, z)ρdρdϕdz,
V V
где dv = ρdρdϕdz — элемент объема в цилиндрических координатах.
Выразим уравнения нижней и верхней частей поверхности S , ограничивающей данную областьV , в цилиндрических координатах —
z = z1(ρ,ϕ) иz = z2 (ρ,ϕ) соответственно и запишем формулу для вычисления интеграла в цилиндрических координатах, аналогичную (2.3)
∫∫∫ f (ρ cosϕ,ρsinϕ,z)ρdρdϕdz = ∫∫ρdρdϕ | z2 (ρ,ϕ) |
| ||
∫ f (ρ cosϕ,ρsinϕ,z)dz, | ||||
V |
| D | z1 (ρ,ϕ) |
|
где D есть проекция областиV на плоскостьxOy.Воспользовавшись |
| |||
заданием плоской области D в полярных координатах (пункт 1.4) получим | ||||
| z2 | ( ρ,ϕ) |
|
|
∫∫ρdρdϕ | ∫ f (ρ cosϕ,ρsinϕ,z)dz = |
| ||
D | z1 (ρ,ϕ) |
|
| |
β | ρ2 (ϕ) | z2 (ρ,ϕ) |
|
|
= ∫dϕ | ∫ ρdρ | ∫ f (ρ cosϕ,ρsinϕ,z)dz . | (2.8) | |
αρ1 (ϕ)z1 (ρ,ϕ)
Формулу (2.8) удобно использовать, если область V проектируется в круг или часть круга.
Пример 2.3. Вычислить∫∫∫(x2 + y2 )dxdydz по области, ограни-
V
ченной плоскостью z = 2 и параболоидомx2 + y2 = 2z.
Решение. ОбластьV (рис. 2.4) снизу ограничена параболоидомx2 + y2 = 2z , сверху
плоскостью z = 2 . Эта область проектируется на плоскостьxOy в облстьD , ограниченную
| окружностью | x2+ y2= 4, | уравнение которой | ||
| получено | при | исключении | переменной z | из |
| уравнений | параболоида | x2+ y2= 2z | и | |
Рис. 2.4 | плоскости z = 2 . | x2+ y2= ρ2, |
| ||
Введем цилиндрические координаты. Так как | то | ||||
studfiles.net
Тройные интегралы. Вычисление объема тела
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: [email protected]
Мы в социальных сетях
Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам
ВКонтакте >
Что такое Myslide.ru?
Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.
Для правообладателей >
myslide.ru