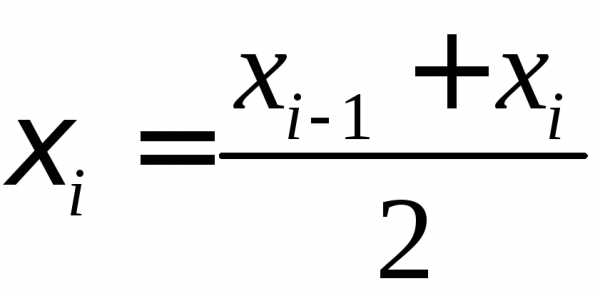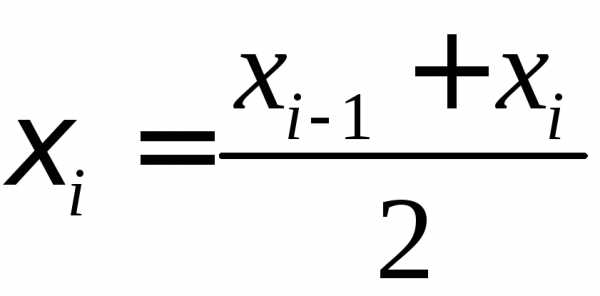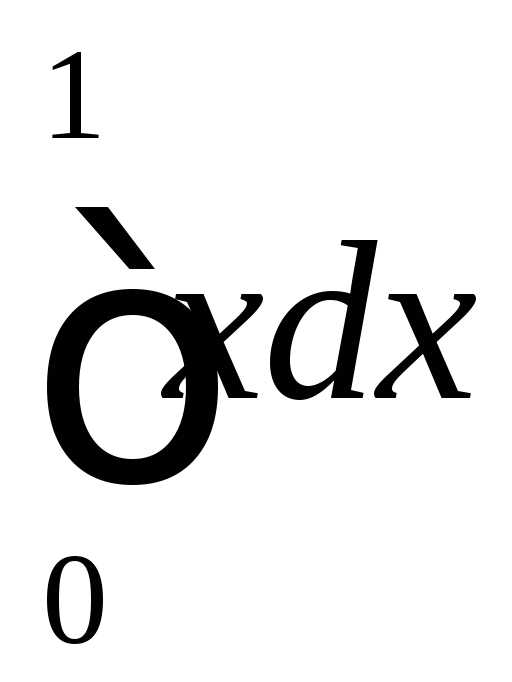Виды интегралов
Неопределенный и определенный интегралы
ОПРЕДЕЛЕНИЕ Неопределенный интеграл – это множество всех первообразных некоторой функции :
Например.
Подробнее про неопределенные интегралы читайте по ссылке.
ОПРЕДЕЛЕНИЕ Определённый интеграл от функции на отрезке – предел интегральных сумм при стремлении диаметра разбиения к нулю, если он существует независимо от разбиения и выбора точек внутри элементарных отрезков:
Например.
Подробнее про определенные интегралы читайте по ссылке.
Собственный и несобственный интегралы
ОПРЕДЕЛЕНИЕ Собственный интеграл – это определенный интеграл, для которого ограниченной является как подынтегральная функция, так и область интегрирования.Например.
ОПРЕДЕЛЕНИЕ Несобственный интеграл – определенный интеграл, для которого неограниченна либо подынтегральная функция, либо область интегрирования, либо и то, и другое вместе.Пусть функция определена на полуоси и интегрируема на любом отрезке . Предел интеграла при называется несобственным интегралом первого рода функции от a до и обозначается :
Например.
Подробнее про несобственные интегралы читайте по ссылке.
Сходящийся и расходящийся интегралы
ОПРЕДЕЛЕНИЕ Если предел существует и конечен, то несобственный интеграл первого рода называется сходящимся.Например.
В противном случае несобственный интеграл первого рода называется расходящимся.
Например.
ОПРЕДЕЛЕНИЕ Если предел конечен, то несобственный интеграл первого рода называется сходящимся.Например.
ОПРЕДЕЛЕНИЕЕсли предел не существует или бесконечен, то несобственный интеграл второго рода называется расходящимся.
Например.
ОПРЕДЕЛЕНИЕ Кратным или многократным интегралом называется множество интегралов, взятых от переменных:
Например.
Криволинейные и поверхностные интегралы
Например. , где
ОПРЕДЕЛЕНИЕ Если на кривой определены функции и , то криволинейным интегралом второго рода называется интеграл вида .Например. , где
Подробнее про криволинейные интегралы читайте по ссылке.
ОПРЕДЕЛЕНИЕ Поверхностным интегралом первого рода от функции по некоторой поверхности называется интеграл .Например. , где − часть плоскости , лежащая в первом октанте.
ОПРЕДЕЛЕНИЕ Поверхностным интегралом второго рода по фиксированной стороне двусторонней поверхности называется интеграл вида .Например. , где − часть внутренней поверхности эллипсоида
Например.
ОПРЕДЕЛЕНИЕ Интеграл называется интегралом, зависящим от параметра .Например.
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Интегралы в математике, основные понятия и определения
Функция будет первообразной для функции , если будем иметь место равенство . Проверим его выполнение:То есть действительно является первообразной функции .
Аналогично проверим выполнение равенства :
Итак, равенство выполняется, а тогда функция – первообразная для функции . Неопределенные интегралы от некоторых функций не берутся в элементарных функциях.
Что и требовалось доказать.
ru.solverbook.com
Интегралы вида ,
где хотя бы одно из чисел m или n нечетное целое число
Пусть, например, – нечетно. Тогда
(замена ),
то есть интеграл сводится к сумме табличных интегралов от степеней.
Интегралы вида ,
где m и n четные целые числа
Если m и n четные целые положительные числа, то используем формулы понижения степени
Интегралы от произведений синусов и косинусов
различных аргументов
Для их вычисления используются тригонометрические формулы
.
.
.
Примеры решения задач
Вычислить
 .
.
◄ Сделаем универсальную подстановку . Используя формулы , получаем
.►
Вычислить .
◄
►
Вычислить
 .
.
◄
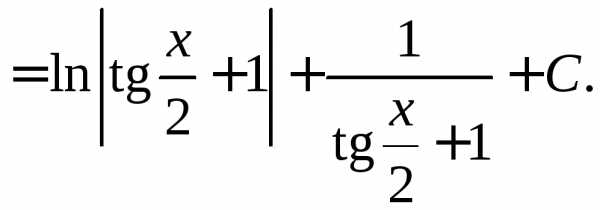 ►
►
Вычислить
 .
.
◄ Так
как 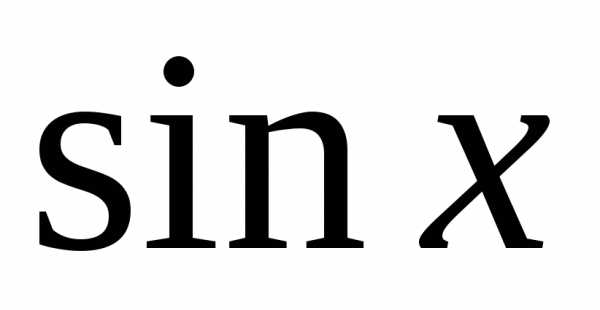 и
и входят в подынтегральную функцию в
чётных степенях, то можно сделать
подстановку
,
входят в подынтегральную функцию в
чётных степенях, то можно сделать
подстановку
, 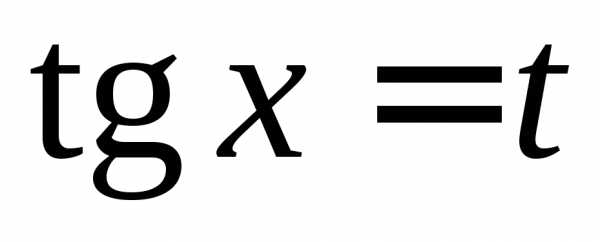 .
Используя формулы , получаем
.
Используя формулы , получаем
►
Вычислить
 .
.
◄
►
Вычислить
 .
.
◄
.►
Вычислить .
◄ Используем то обстоятельство, что косинус стоит в нечётной степени.
.►
Вычислить .
◄ Для вычисления этого интеграла от произведения синуса и косинуса в чётных степенях используем формулы понижения степени .
. ►
Вычислить .
◄ Используем формулу :
►
Задачи для самостоятельного решения
Вычислить интегралы.
Интегрирование некоторых иррациональных функций
7.1. Сведения из теории
Далее будем обозначать – рациональную функцию аргументов.
7.1.1. Интегралы вида ,
где
– целые числа, с помощью подстановки
где n – общий
знаменатель дробей 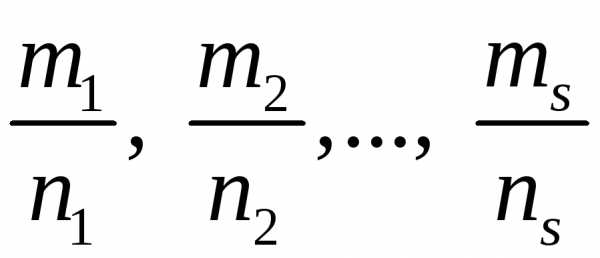 сводятся к интегралам от рациональных
функций переменнойt.
сводятся к интегралам от рациональных
функций переменнойt.
7.1.2. Интегралы вида
;
;
с помощью тригонометрических подстановок, соответственно,
в , в и 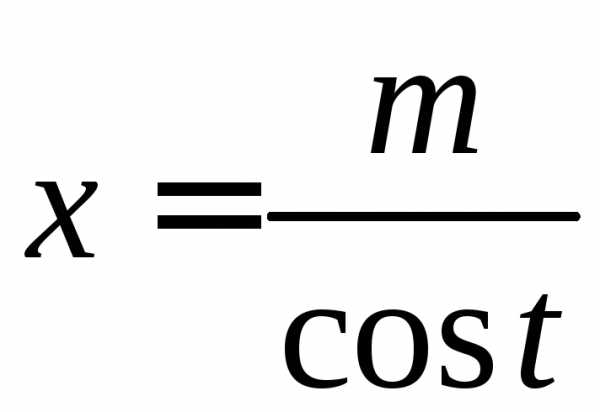 в
в
приводятся к тригонометрическим интегралам вида , рассмотренным в п.6.
7.1.3. Интегралы вида
Выделив полный квадрат в квадратном трёхчлене
и
сделав замену переменных 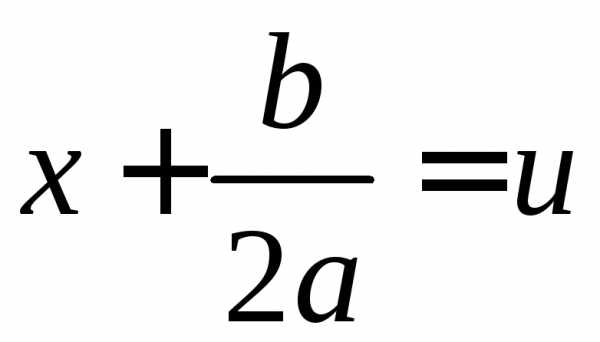 ,
получим интеграл одного из видов ,
или .
,
получим интеграл одного из видов ,
или .
Примеры решения задач
Вычислить
 .
.
◄ 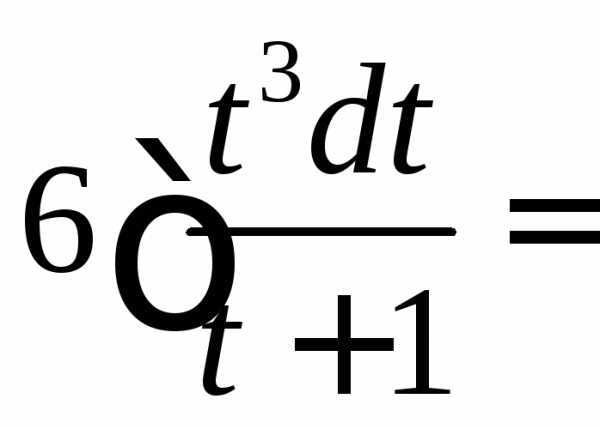
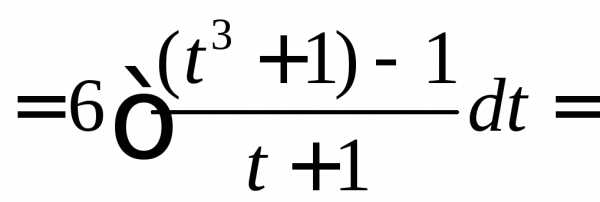
. ►
Вычислить
 .
.
◄ =
. ►
Вычислить
 .
.
◄ Рассматриваемый интеграл имеет вид . Поэтому делаем тригонометрическую подстановку ,.
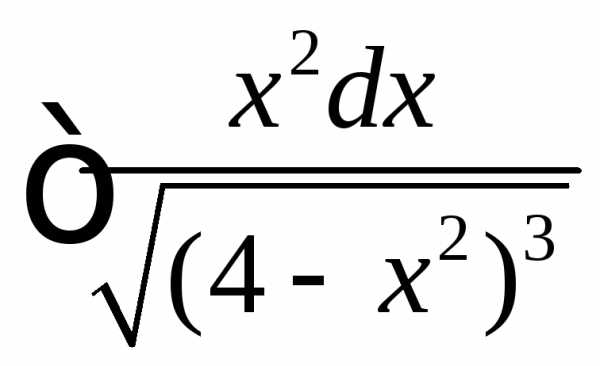 =
=
►
Вычислить
.
◄ Рассматриваемый
интеграл имеет вид . Поэтому делаем
тригонометрическую подстановку 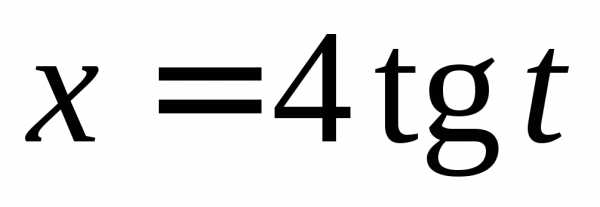 ,.
,.
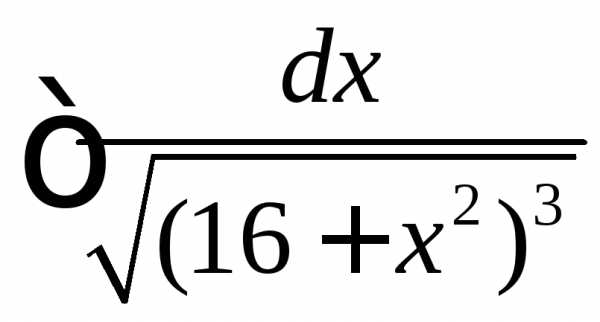 =
=
. ►
Вычислить
 ,
, .
.
◄ Рассматриваемый
интеграл имеет вид . Поэтому делаем
тригонометрическую подстановку 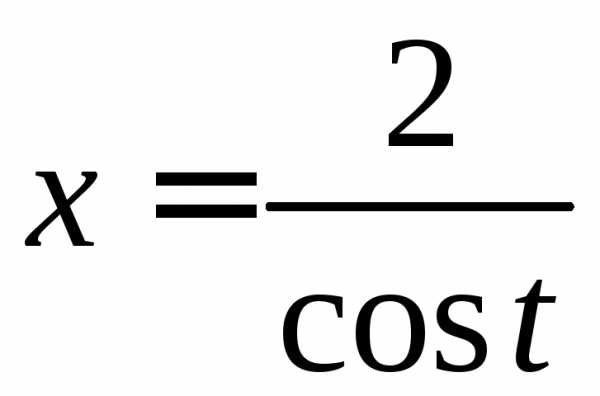 (.
(.
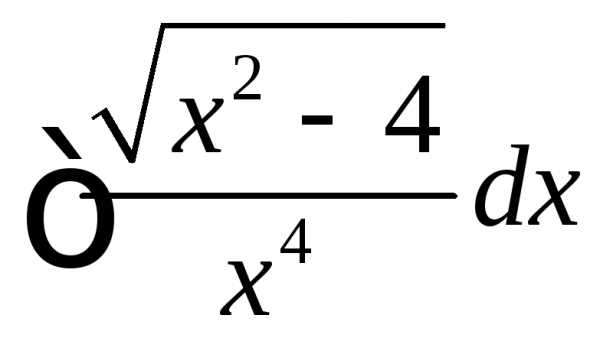
. Произведем обратную замену:
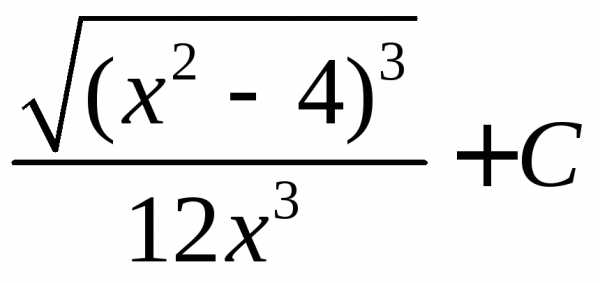 .
►
.
►
Вычислить
 .
.
◄
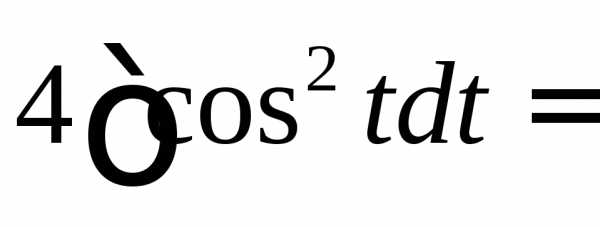
.►
Задачи для самостоятельного решения
Вычислить интегралы от иррациональных функций.
Понятие определенного интеграла.
Приближенное вычисление определенного интеграла
Основные понятия и формулы (и аналогично в дальнейшем ?)
Пусть
функция 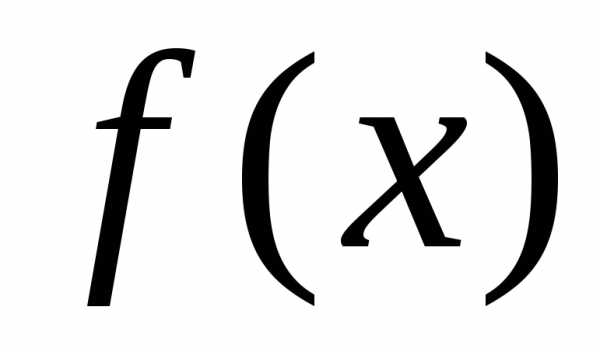 определена на отрезке
определена на отрезке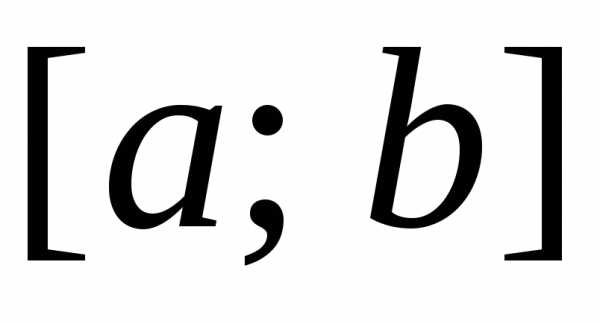 .
Разобьем этот отрезок точкамина частичные отрезки
.
Разобьем этот отрезок точкамина частичные отрезки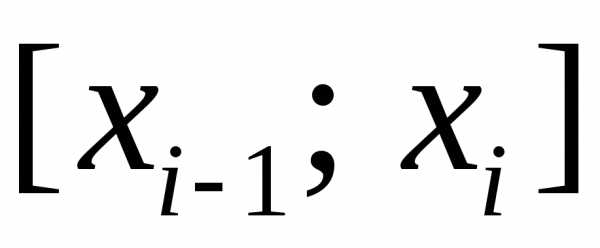 ,,
длины.
Наибольшую из этих длин
,,
длины.
Наибольшую из этих длин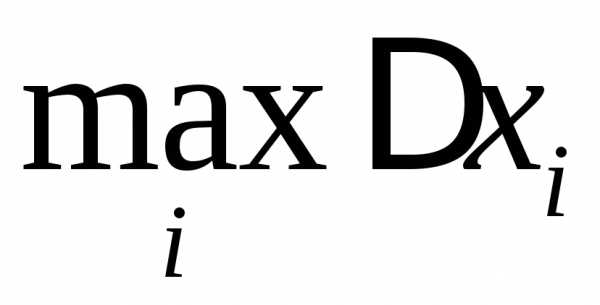 назовеммелкостью
разбиения.
В каждом из частичных отрезков
назовеммелкостью
разбиения.
В каждом из частичных отрезков 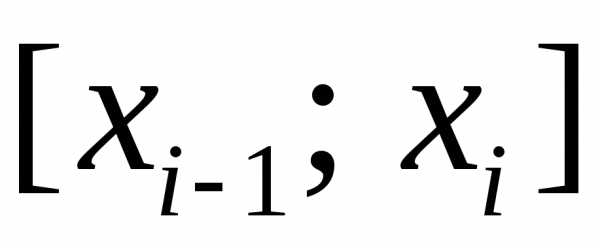 выберем точку
выберем точку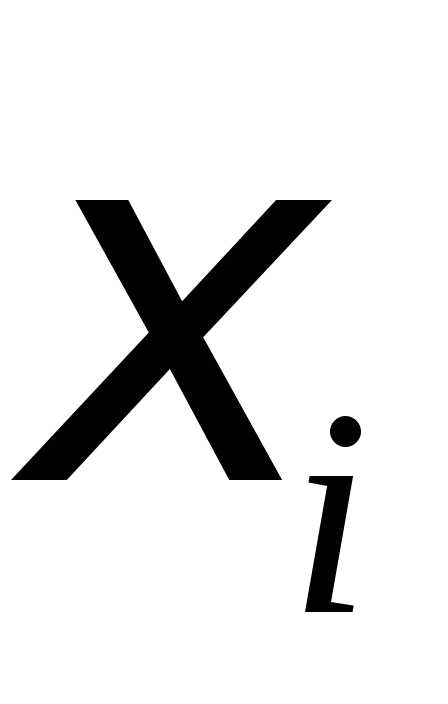 (рис. 1). Составим интегральную сумму
(рис. 1). Составим интегральную сумму
.
Определенным
интегралом от функции 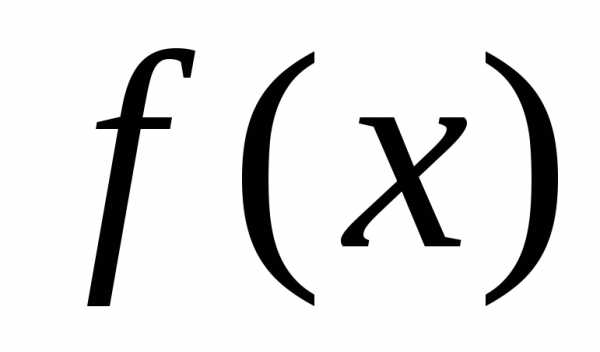 по отрезку (в пределах от
по отрезку (в пределах от до
до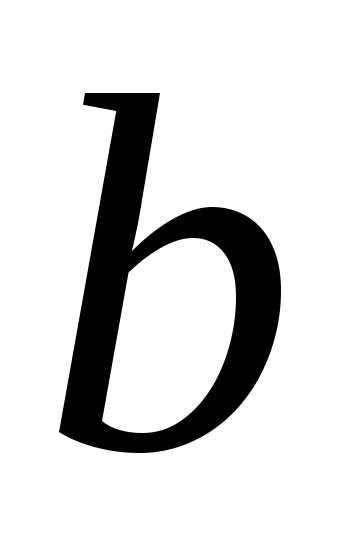 )
называется число (оно обозначается
)
называется число (оно обозначается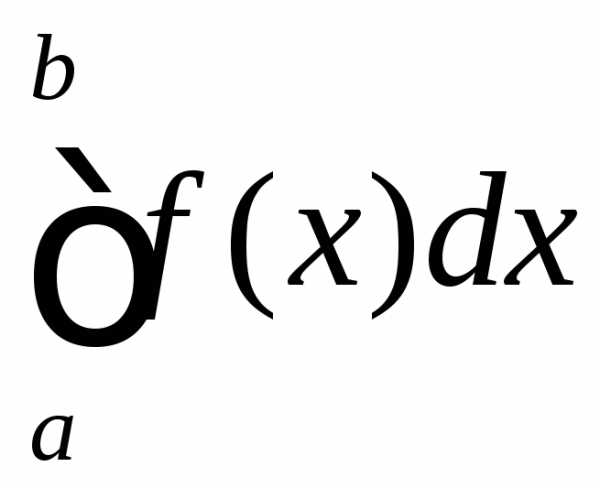 ),
равное пределу интегральных сумм при
неограниченном измельчении разбиения:
),
равное пределу интегральных сумм при
неограниченном измельчении разбиения:
.
Точно
это означает следующее: для любого  найдется такое
найдется такое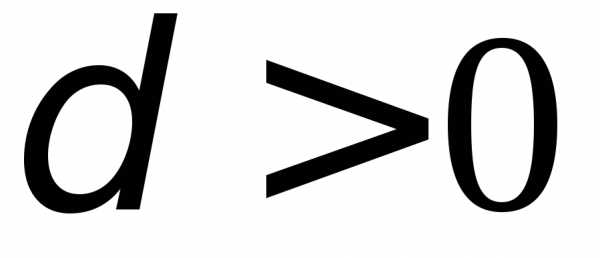 ,
что для любого разбиения с мелкостью
,
что для любого разбиения с мелкостью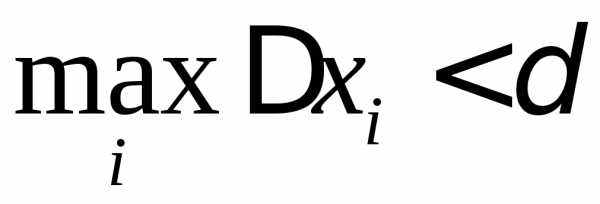 при любом выборе точек
при любом выборе точек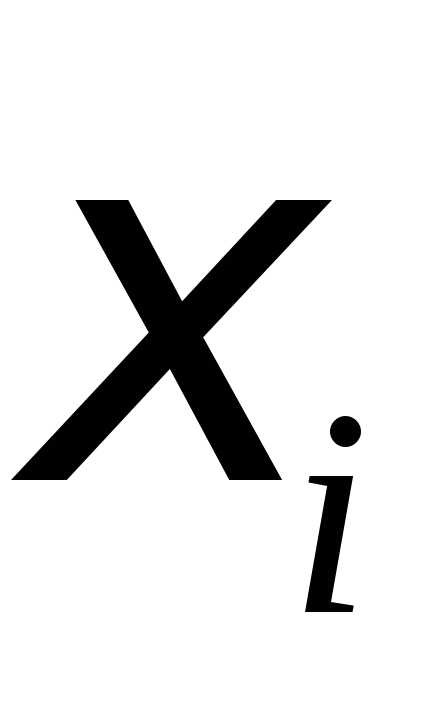 выполняется неравенство
выполняется неравенство
.
Для
функций, непрерывных или кусочно-непрерывных
на отрезке 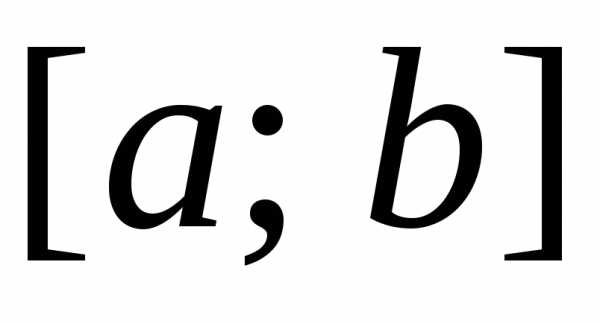 ,
определенный интеграл по этому отрезку
существует –функция
интегрируема по отрезку
,
определенный интеграл по этому отрезку
существует –функция
интегрируема по отрезку 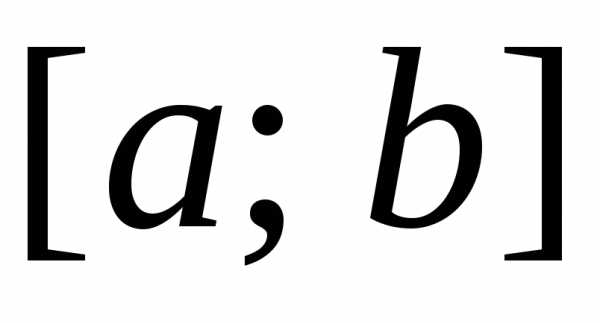 .
.
Полагают также, что
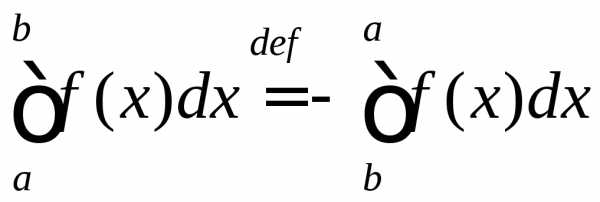 при
при  ;
и
;
и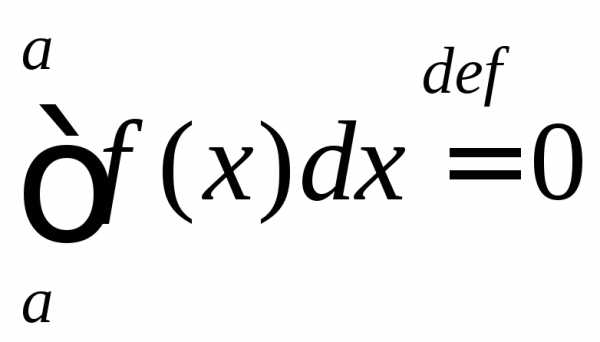 .
.
Из
определения интеграла следует и
простейший метод его приближенного
вычисления – метод
прямоугольников.
Разбиваем отрезок 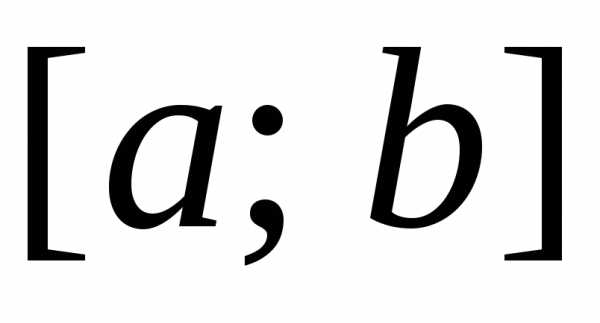 на достаточно большое число
на достаточно большое число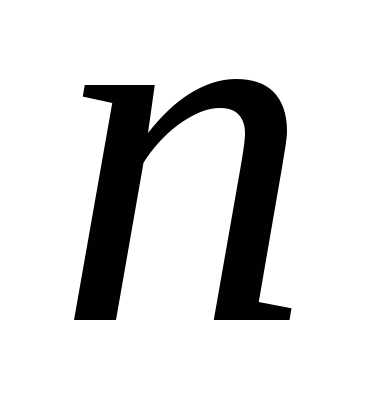 равных отрезков длины
равных отрезков длины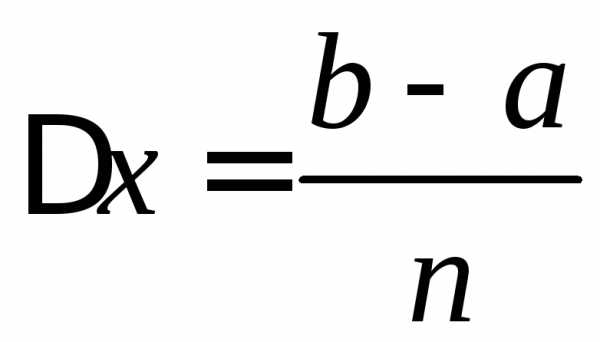 ,
за
,
за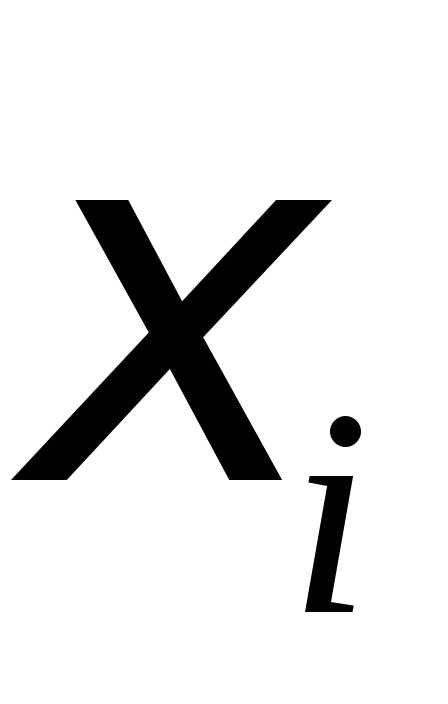 берем середину
берем середину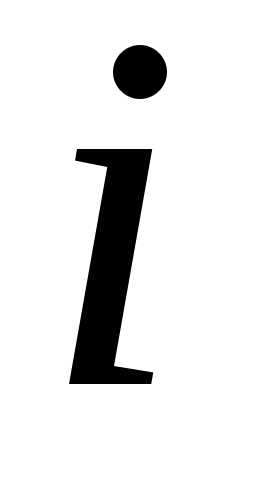 -го
отрезка1
-го
отрезка1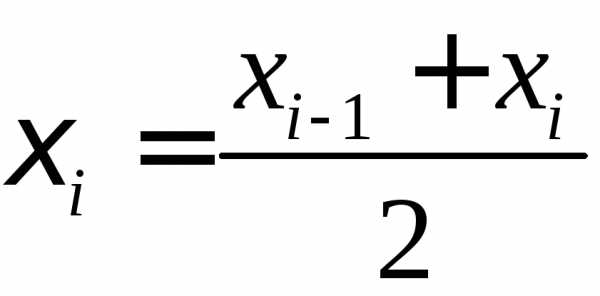 .
В качестве приближенного значения
интеграла принимаем интегральную сумму:
.
В качестве приближенного значения
интеграла принимаем интегральную сумму:
.
Каждое
слагаемое в интегральной сумме является
площадью прямоугольника с высотой 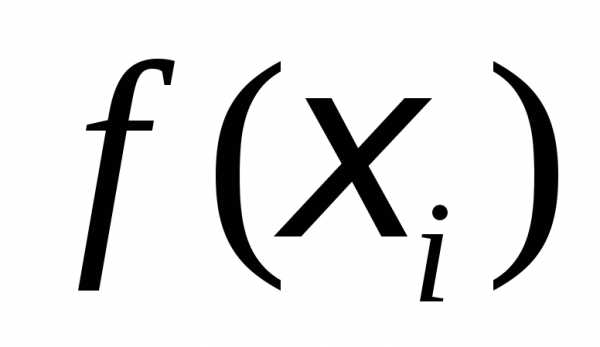 и основанием(рис.1),
откуда и происходит название метода.
и основанием(рис.1),
откуда и происходит название метода.
Оценка
точности метода прямоугольников:
если при некотором значении 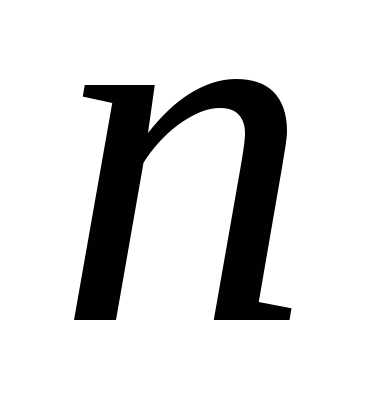 ,
то
,
то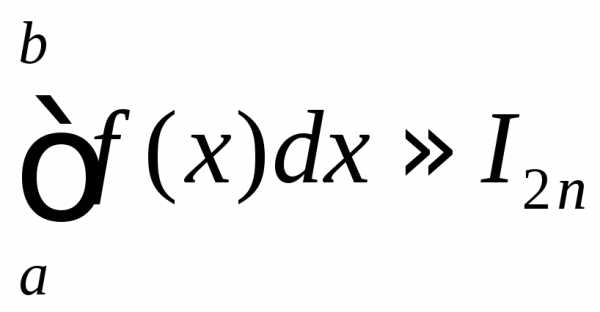 с точностью до
с точностью до .
.
Примеры решения задач
Вычислить
 по определению, как предел интегральных
сумм.
по определению, как предел интегральных
сумм.
◄ Отрезок
интегрирования 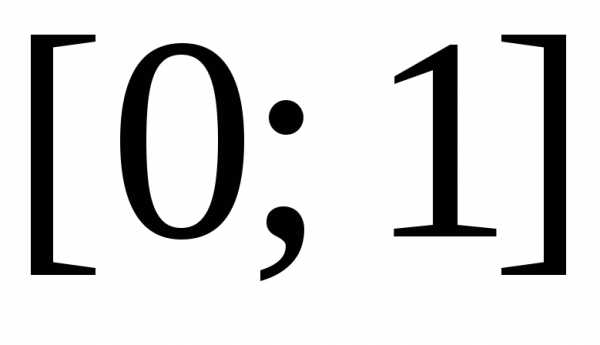 разобьем точками
разобьем точками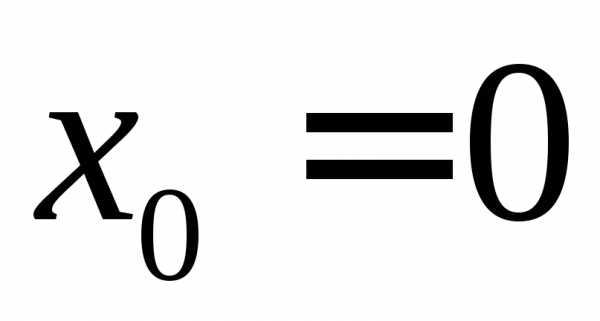 ,
,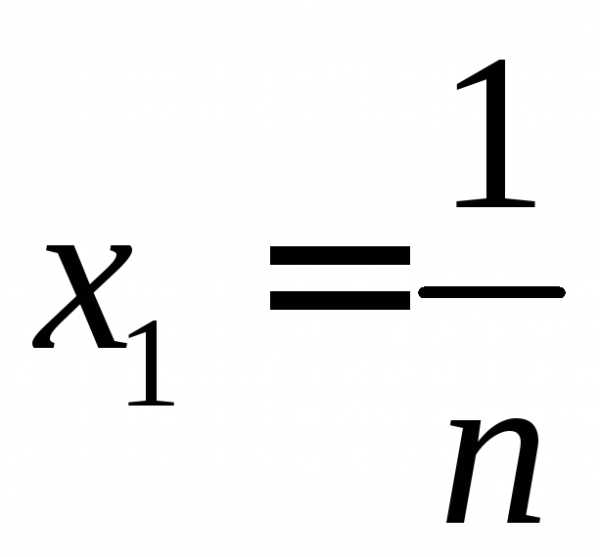 ,на частичные отрезки
,на частичные отрезки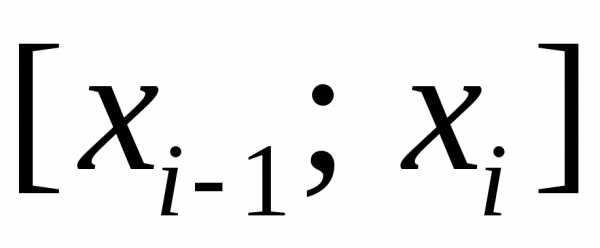 ,,
одинаковой длины
,,
одинаковой длины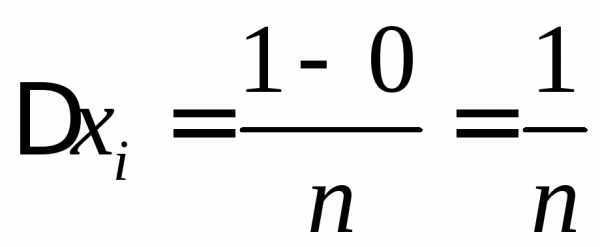 .
Возьмем
.
Возьмем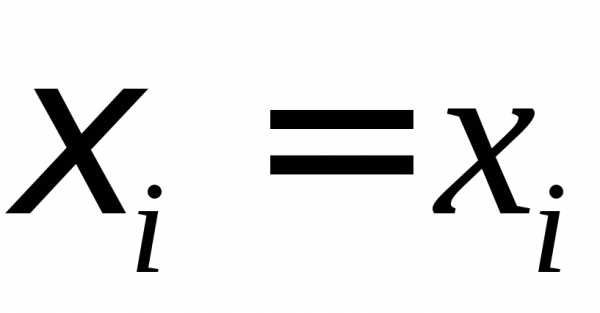 ,.
Составим интегральную сумму для функции
,.
Составим интегральную сумму для функции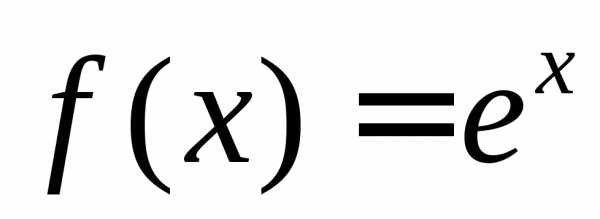
.
В
скобках стоит сумма первых 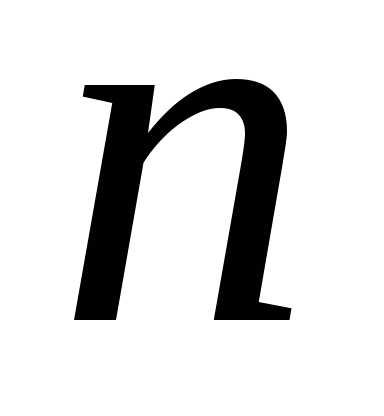 членов геометрической прогрессии со
знаменателем
членов геометрической прогрессии со
знаменателем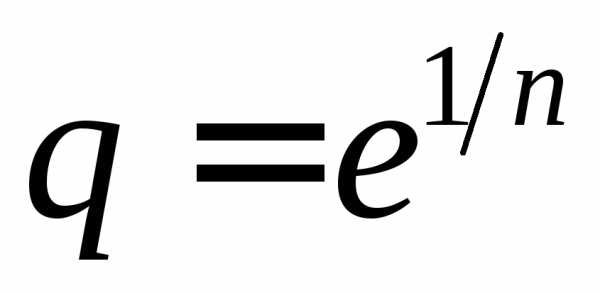 и первым членом
и первым членом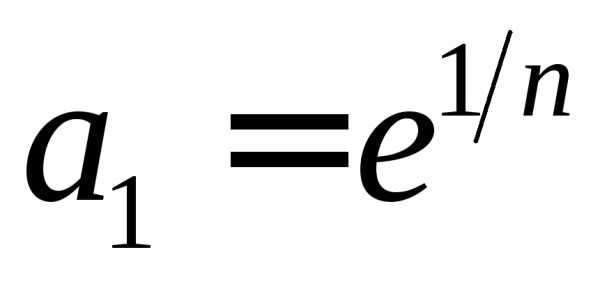 .
Она равна
.
Она равна
.
Поэтому интегральная сумма
.
Вычислим
теперь интеграл как предел интегральных
сумм при 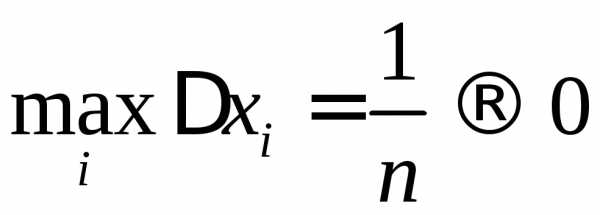 ().
().
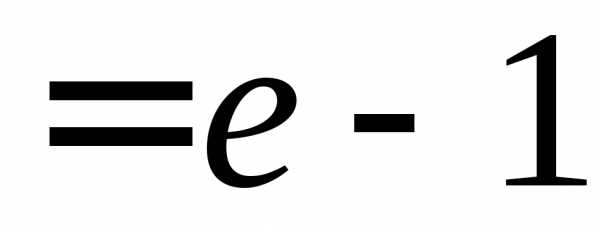 .►
.►
Вычислить приближенно
 методом прямоугольников (методом
средних) с точностью до.
методом прямоугольников (методом
средних) с точностью до.
◄ Разобьем
отрезок 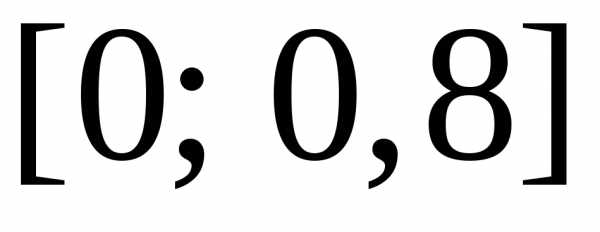 на
на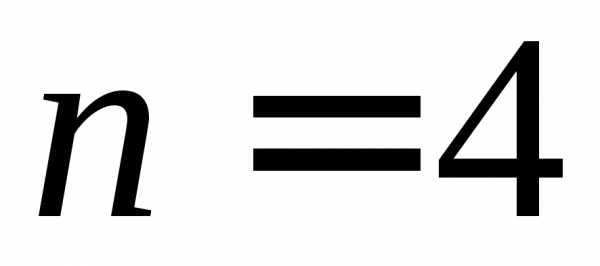 равных отрезков. Их длина
равных отрезков. Их длина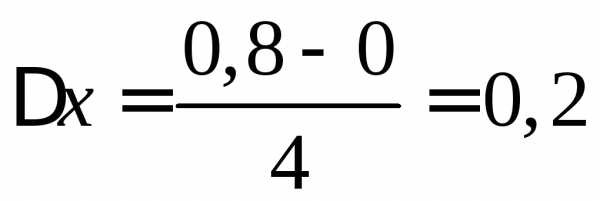 .
Поэтому точки деления
.
Поэтому точки деления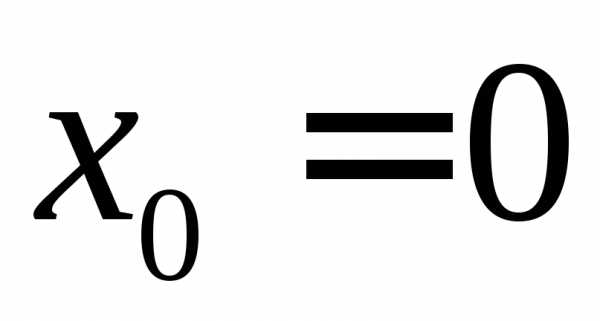 ,
,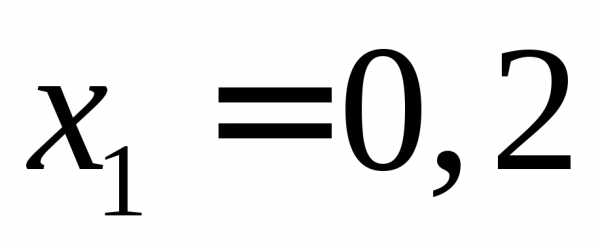 ,
,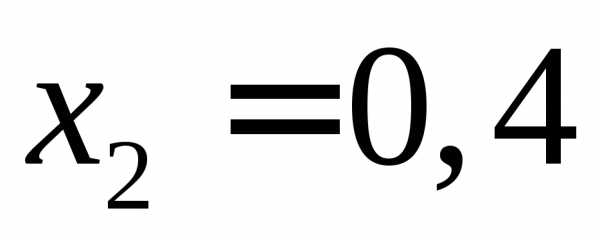 ,
,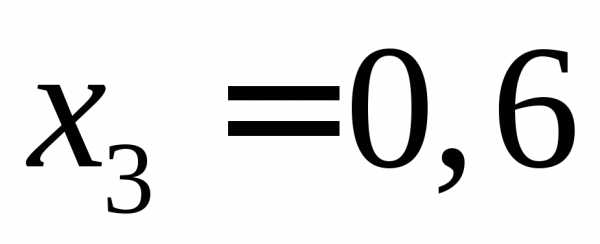 ,
,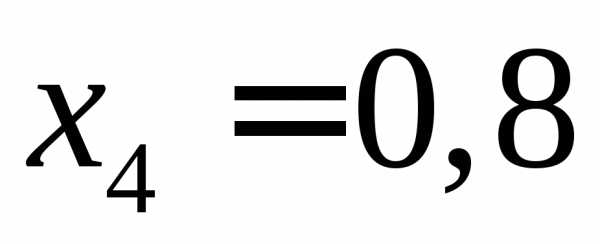 .
Составим табл. 1.
.
Составим табл. 1.
Таблица 1
|
| |
1 | 0,1 | 1, 0005 |
2 | 0,3 | 1,0134 |
3 | 0,5 | 1,0607 |
4 | 0,7 | 1,1589 |
По формуле прямоугольников
.
Разобьем
отрезок 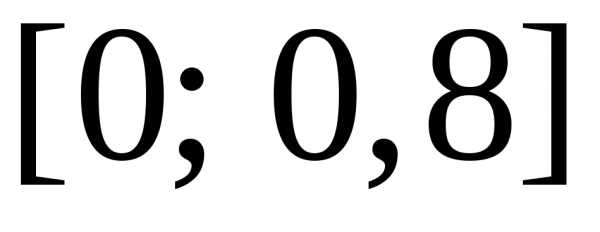 на
на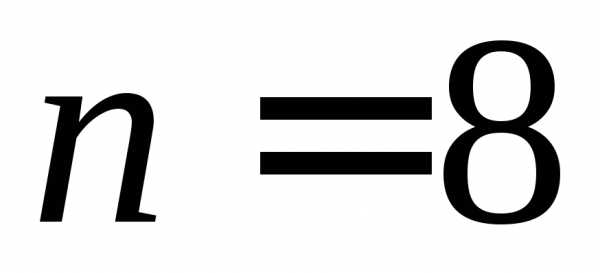 равных отрезков. Их длина
равных отрезков. Их длина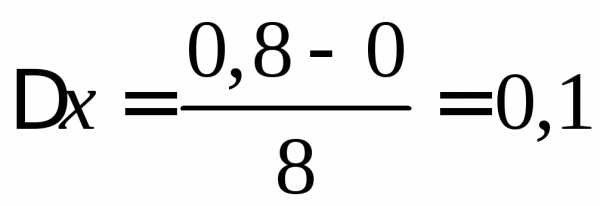 .
Поэтому точки деления
.
Поэтому точки деления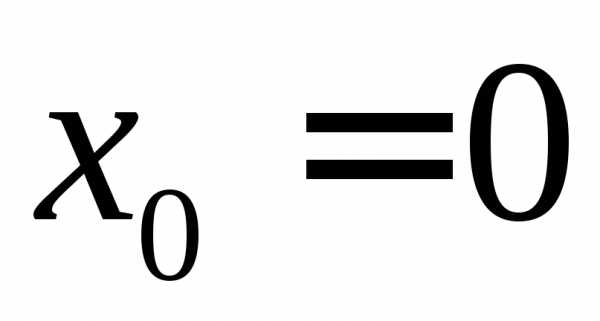 ,,
,,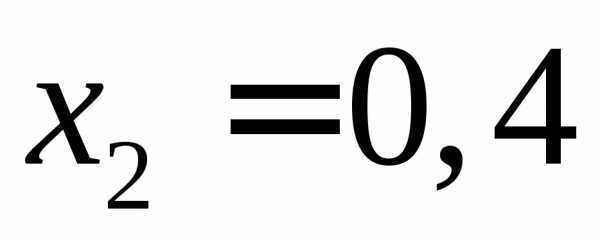 ,
…,
,
…,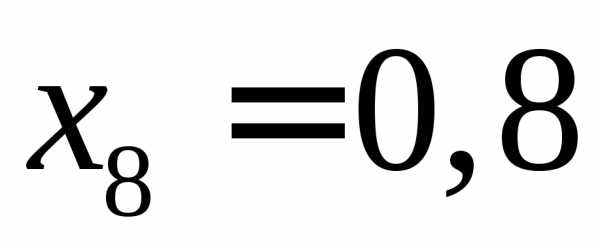 .
Составим табл. 2.
.
Составим табл. 2.
Таблица 2
|
| |
1 | 0,05 | 1,0001 |
2 | 0,15 | 1,0017 |
3 | 0,25 | 1,0078 |
4 | 0,35 | 1,0212 |
5 | 0,45 | 1,0446 |
6 | 0,55 | 1,0800 |
7 | 0,65 | 1,1290 |
8 | 0,75 | 1,1924 |
По формуле прямоугольников
.
Поскольку
,
то с точностью до.
Округляя до сотых, получаем окончательно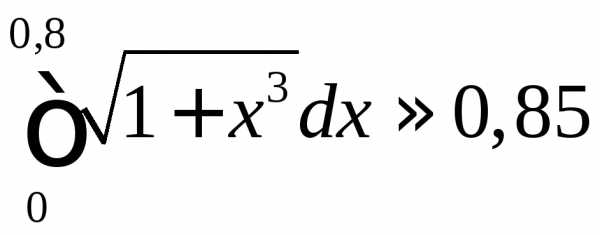 .
.
Замечание.
Для другой подынтегральной функции или
при другом  могло бы оказаться, что.
Тогда для достижения заданной точности
могло бы оказаться, что.
Тогда для достижения заданной точности следует продолжить вычисление интегральных
сумм
следует продолжить вычисление интегральных
сумм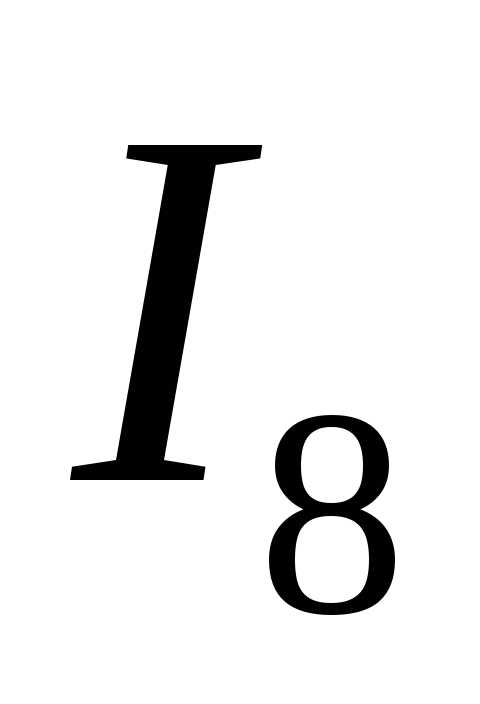 ,
,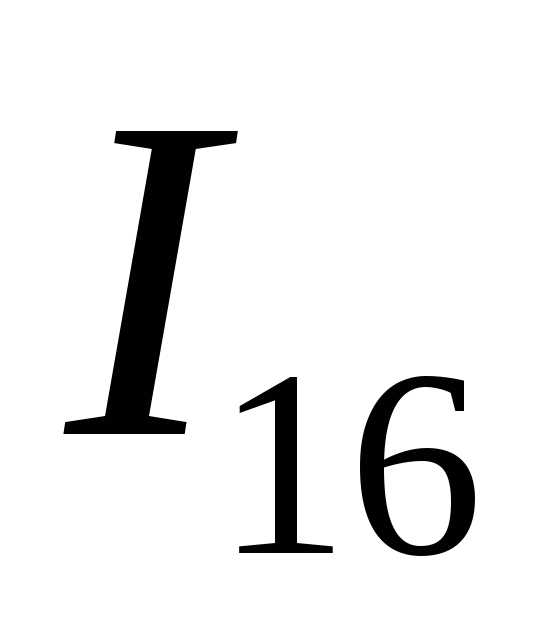 ,
,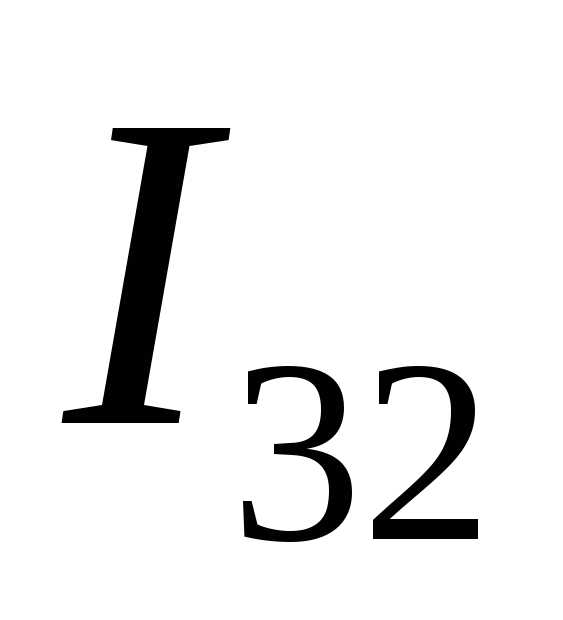 ,
… до тех пор, пока абсолютная величина
разности двух соседних членов этой
последовательности не станет
,
… до тех пор, пока абсолютная величина
разности двух соседних членов этой
последовательности не станет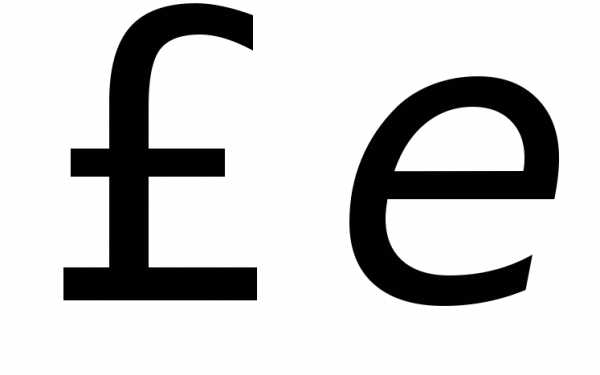 .
►
.
►
Задачи для самостоятельного решения
Вычислить интеграл

а) по определению как предел интегральных сумм,
б) приближенно методом прямоугольников с точностью 0,01 .
Указание. В пункте а) использовать равенство
.
Вычислить пределы
а) , б).
Указание. Записать эти пределы как пределы интегральных сумм. Соответствующие интегралы вычислить по формуле Ньютона-Лейбница (2.1).
studfiles.net
Свойства интегралов, формулы и примеры
1. Константу можно выносить за знак интеграла:
2. Интеграл суммы/разности равен сумме/разности интегралов от каждого из слагаемых:
3. Производная от интеграла равна подынтегральной функции:
4. Интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования:
5. Если , то
6. Интеграл от производной некоторой функции равен этой функции плюс константа интегрирования:
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
📝Что такое интеграл?
В переводе с латинского языка интеграл означает «целый». Это одно из наиболее важных и распространенных понятий в высшей математике, которое появилось из-за необходимости находить функции по их производным или измерять объёмы, площади, работу нескольких сил за конкретный промежуток времени, длины дуг и т.д. В соответствии с этими задачами принято выделять определённые и неопределенные интегралы.
Содержание статьи:
Обозначение
Первым символ для обозначения интегрирования придумал Ньютон. Он применял для этого небольшой квадрат. Однако данное обозначение не получило серьезного распространения. Сегодняшнее обозначение неопределенного интеграла было придумано в 1675 году Лейбницем:
Что касается обозначения определённого интеграла, где указаны пределы интегрирования, то его в 1819 году предложил Жан Батист Фурье.
Виды интегралов
Первообразная функции f(x) — функция F(x), производная которой при любом значении х равняется f(x). Добавляя постоянную к первообразной определенной функции, снова можно получить первообразную этой же функции. Соответственно, имея единственную первообразную F(x) функции f(x), можно получить единое выражение всех первообразных данной функции в виде F(x) + С. Подобное выражение первообразных принято называть неопределённым интегралом функции f(x):
Одно из главных правил интегрального исчисления определяет, что любая непрерывная функция f(x) имеет неопределённый интеграл.
Что касается определённого интеграл от функции f(x) с верхним пределом b и нижним пределом а, то он определяется в качестве разности:
где F(x) является первообразной функции f(x).
Определённый интеграл можно выразить посредством любой первообразной F(x). Верным является и обратное. Первообразную F(x) можно записать в следующем виде:
В этой формуле а – это произвольная константа. Таким образом, интеграл можно записать в виде:
История возникновения интеграла
Если углубиться в историю, то можно утверждать, что интегрирование зародилось в древнем Египте, приблизительно в 1800 году до нашей эры. Первой известной методикой вычисления интегралов считается способ исчерпывания Евдокса. Он предпринимал попытки найти объёмы и площади фигур, разрывая их на несколько частей, для которых уже известны площадь или объём. Через некоторое время данная методика была развита Архимедом. Он применял ее для вычислений площадей парабол и примерного расчёта площади круга. Подобные методы независимо разрабатывались в Китае в 3 столетии нашей эры Лю Хуэйем. Он использовал их с целью определения площади круга.
Следующий внушительный прогресс в исчислении интегралов произошел только в XVI веке. В работах с методом неделимых Кавальери, а также в научных трудах Ферма, были заложены основы сегодняшнего интегрального исчисления.
Последующие шаги были сделаны в середине XVII столетия Торричелли и Барроу, которые предоставили первые намеки на взаимосвязь между дифференцированием и интегрированием.
Зачем и кому нужны интегралы?
Ученые стремятся любые физические явления выражать в виде математических формул. Когда в руках есть определенная формула, то в дальнейшем уже можно с ее помощью посчитать все, что необходимо. А интеграл является одним из главных инструментов работы с любыми функциями.
К примеру, имея формулу круга, можно посредством интеграла вычислить его площадь. Если есть формула шара, то можно вычислить его объем. Посредством интегрирования можно найти работу, энергию, массу, давление, электрический заряд и прочие важные величины.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Интеграл — Циклопедия
Интеграл — это математический термин, обозначающий непрерывную сумму произведений значений подынтегральной функции на дифференциал аргумента.
[править] Интеграл от функции
Нахождение интеграла от функции называется интегрированием. При интегрировании подынтегральной функции находят первообразную функцию, производная от которой равна подынтегральной функции. Интеграл от функции может быть неопределённым, а может быть определённым.
Суть неопределённого интеграла это класс функций (первообразная плюс константа), отличающихся только константой, производная которых равна подынтегральной функции.
Суть определённого интеграла это некое число, равное непрерывной алгебраической сумме произведений значений подынтегральной функции на дифференциал аргумента. Для положительных подынтегральных функций определённый интеграл равен величине площади криволинейной трапеции, ограниченной графиком функции, осью абсцисс и пределами интегрирования.
[править] Неопределённый интеграл от функции
Неопределённый интеграл от функции определяется по формуле:
f(x) — подынтегральная функция,
F(x) — первообразная функция.
C — константа.
[править] Свойства неопределённых интегралов
Для функций u=f(x) и v=g(x) верны правила:
При f(x) и g(x)=C1 получаем:
При f(x)=C1 и g(x) получаем:
[править] Интегрирование по частям
Для функций u=f(x) и v=g(x) верно правило:
[править] Примеры неопределённых интегралов
[править] Определённый интеграл от функции
Определённый интеграл от функции определяется по формуле Ньютона-Лейбница:
f(x) — подынтегральная функция,
F(x) — первообразная функция.
[править] Примеры определённых интегралов
[править] Другие понятия:
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Участник:Logic-samara
cyclowiki.org
Интеграл произведения функций, формулы и примеры
ОПРЕДЕЛЕНИЕ Интеграл произведения функций в общем случае не равен произведению интегралов от каждого из сомножителей:
В зависимости от того, какие функции стоят под знаком интеграла, интеграл от произведения в некоторых случаях можно выразить через элементарные функции, а в некоторых определенный интеграл произведения функций можно оценить. Для этого используются теоремы про среднее.
Теоремы про среднее
ТЕОРЕМА Теорема 1. Пусть функции и являются интегрируемыми на отрезке причем и на Тогда
Следствие 1. Пусть функция интегрируема на отрезке и является ограниченной на этом отрезке: Тогда
ТЕОРЕМА Теорема 2. Пусть функция непрерывна на отрезке функция интегрируема на этом отрезке. Тогда существует такая точка что выполняется равенство:
Следствие 2. Пусть функция непрерывна на отрезке Тогда существует такое, что
Примеры решения задач по теме «Интеграл произведения»
ПРИМЕР 1| Задание | Оценить интеграл
|
| Решение | Подынтегральная функция задана на отрезке С помощью дифференциального исчисления можно показать, что на этом отрезке функция принимает свое наименьшее значение, равное и наименьшее Тогда, согласно следствию 1, можно записать:
или
|
| Ответ |
| Задание | Оценить интеграл
|
| Решение | Подынтегральная функция является убывающей на отрезке интегрирования следовательно, имеет место оценка:
Тогда, согласно следствию 1, имеем:
или
|
| Ответ |
Интеграл от натурального логарифма
Интегралы тригонометрических функций
Интеграл разности
Интеграл суммы
Интегралы от иррациональных функций
Интеграл от числа
ru.solverbook.com

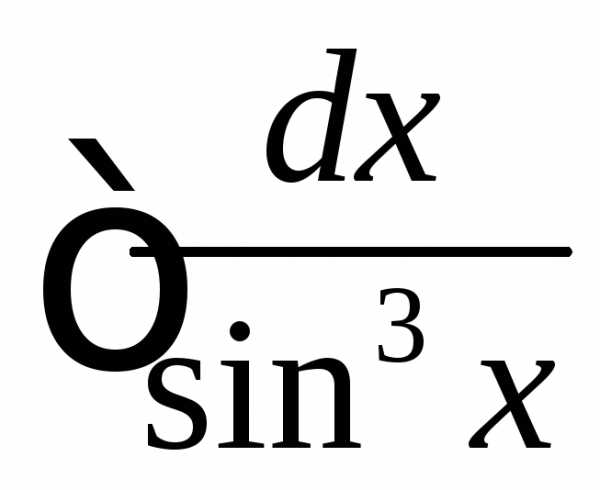 .
.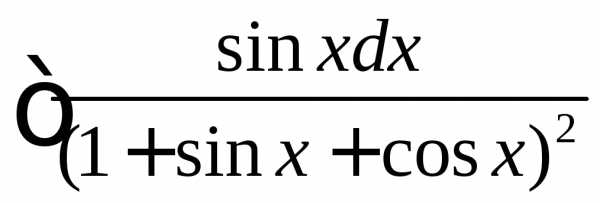 .
.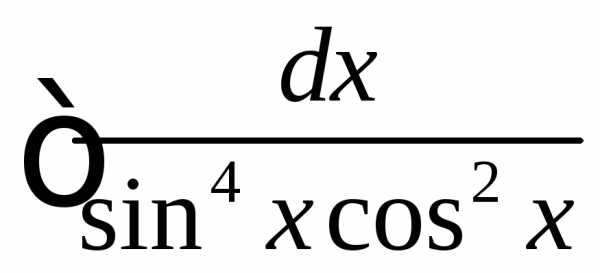 .
.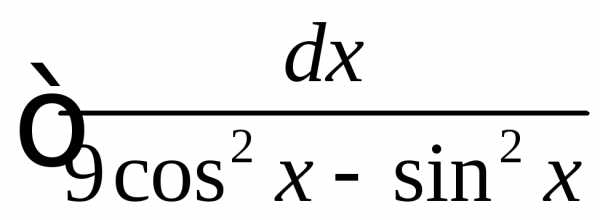 .
.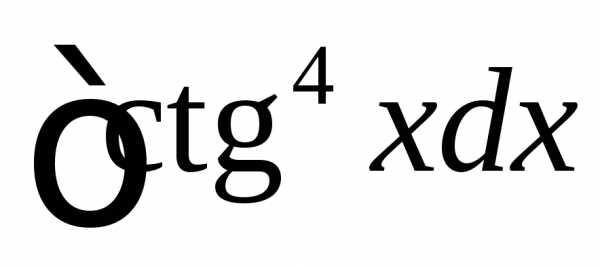 .
.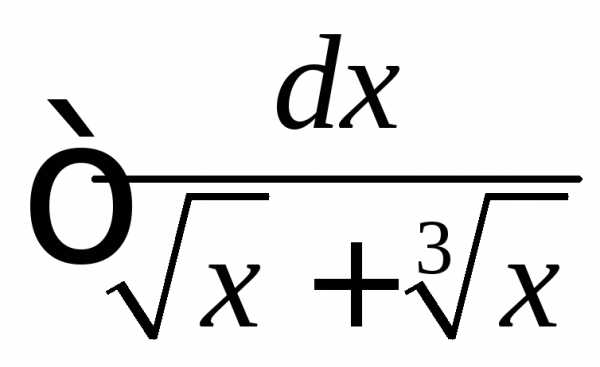 .
. .
.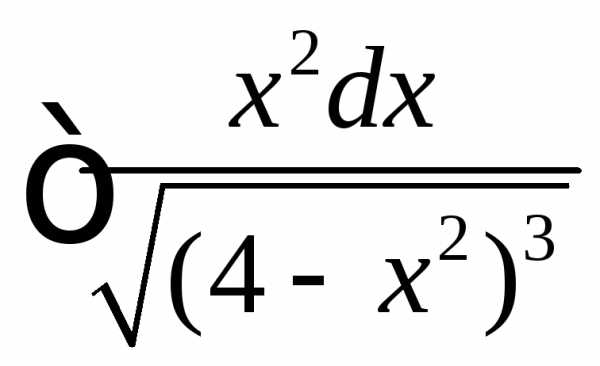 .
.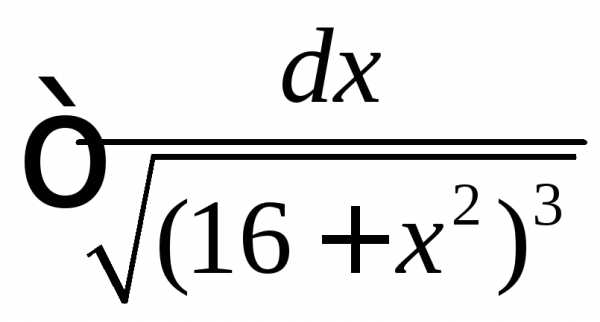
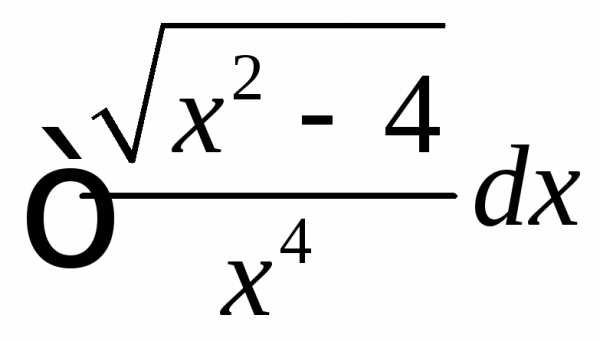 ,
,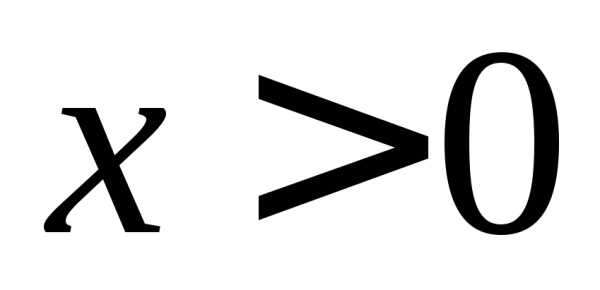 .
.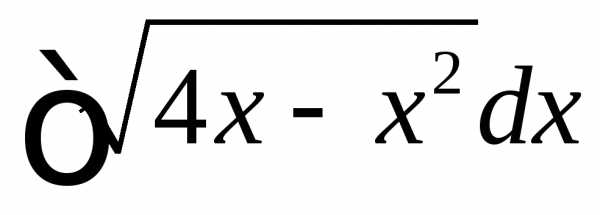 .
.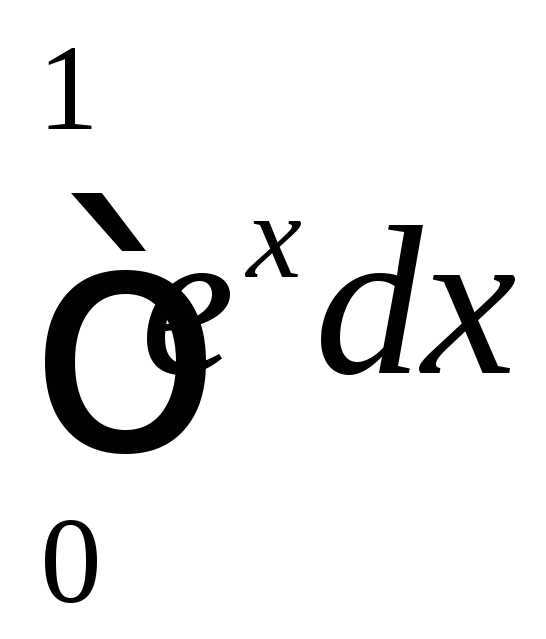 по определению, как предел интегральных
сумм.
по определению, как предел интегральных
сумм.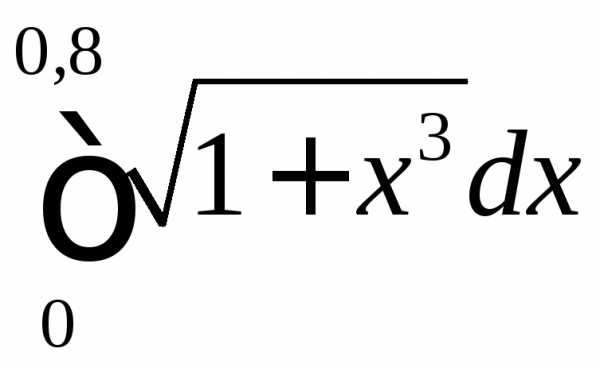 методом прямоугольников (методом
средних) с точностью до.
методом прямоугольников (методом
средних) с точностью до.