Калькулятор матрицы умножение онлайн – Онлайн калькулятор. Умножение матриц.

Содержание

Онлайн калькулятор умножения матриц

Решение

Даны две матрицы

A =	где,	a₁₁ = 4 a₁₂ = 1 a₂₁ = 0 a₂₂ = 5 a₃₁ = 2 a₃₂ = -3

B =	где,	b₁₁ = 0.45 b₁₂ = 12 b₁₃ = -9 b₂₁ = 3 b₂₂ = 1.4 b₂₃ = 0

Умножить две матрица можно только, если число столбцов матрицы А равно числу строк матрицы В

При умножении матрицы А размерности l × m на матрицу В размерности m × n получаем матрицу С размерности l × n

Элемент матрицы с индексом C_ij находится по формуле

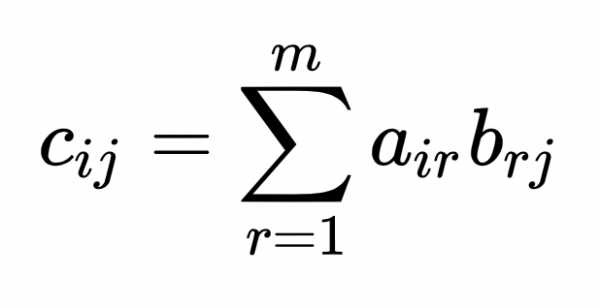
c₁₁ = a₁₁ ⋅ b₁₁ + a₁₂ ⋅ b₂₁ = 4 ⋅ 0.45 + 1 ⋅ 3 = 4.8

c₁₂ = a₁₁ ⋅ b₁₂ + a₁₂ ⋅ b₂₂ = 4 ⋅ 12 + 1 ⋅ 1.4 = 49.4

c₁₃ = a₁₁ ⋅ b₁₃ + a₁₂ ⋅ b₂₃ = 4 ⋅ (-9) + 1 ⋅ 0 = -36

c₂₁ = a₂₁ ⋅ b₁₁ + a₂₂ ⋅ b₂₁ = 0 ⋅ 0.45 + 5 ⋅ 3 = 15

c₂₂ = a₂₁ ⋅ b₁₂ + a₂₂ ⋅ b₂₂ = 0 ⋅ 12 + 5 ⋅ 1.4 = 7

c₂₃ = a₂₁ ⋅ b₁₃ + a₂₂ ⋅ b₂₃ = 0 ⋅ (-9) + 5 ⋅ 0 = 0

c₃₁ = a₃₁ ⋅ b₁₁ + a₃₂ ⋅ b₂₁ = 2 ⋅ 0.45 + (-3) ⋅ 3 = -8.1

c₃₂ = a₃₁ ⋅ b₁₂ + a₃₂ ⋅ b₂₂ = 2 ⋅ 12 + (-3) ⋅ 1.4 = 19.8

c₃₃ = a₃₁ ⋅ b₁₃ + a

32 ⋅ b₂₃ = 2 ⋅ (-9) + (-3) ⋅ 0 = -18

matematika-club.ru

Онлайн калькулятор — умножение матриц

Следующий калькулятор служит для перемножения двух матриц. Таким образом дополняем нашу коллекцию калькуляторов о матрицах:

Ну а данный калькулятор может умножать две матрицы:

Основным, пожалуй, правилом при умножении двух матриц есть то, что количество строк первой матрицы должно быть равно количеству столбцов во второй матрице.

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

hostciti.net

Умножение матрицы на число онлайн

Умножение матрицы на число

Операция умножения матрицы А на число k заключается в построении матрицы kA = [ka_ij]. Умножение матрицы на число допустимо для матриц любого размера, результатом умножения является матрица того же порядка, что и исходная матрица.

Таким образом, произведение матрицы А на число k – это результирующая матрица B = kA того же порядка, полученная умножением всех элементов

a_ij исходной матрицы на заданное число.

Математически умножение матрицы на число можно представить следующими выражениями:
А_m×n × k = В_m×n
a_ij × k = b_ij,
где i принимает значение от 1 до m, j имеет значения от 1 до n

Пример умножения матрицы на число.

Даны матрица А и число k:

Найти произведение матрицы и числа.
Решение:

Свойства умножения матрицы на число:

Единица является нейтральным числом умножения любой матрицы, результатом умножения на нейтральное число является исходная матрица.
1×А = А
Результатом умножения любой матрицы на ноль всегда является нулевая матрица, все элементы которой равняются нулю.
0×А = О
Для матриц одного порядка и действительного числа выполняется свойство дистрибутивности умножения относительно сложения.
k×(А+B) = k×A + k×B
Для любой матрицы и суммы действительных чисел выполняется свойство дистрибутивности. (k+n)×А = k×A + n×A
Для любой матрицы и произведения любых действительных чисел выполняется свойство ассоциативности умножения.
(k×n)×А = k×(n×A)

Вы также можете

в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x (например, в ячейку матрицы можно ввести 2x

, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.