Калькулятор возведения в степень – Онлайн калькулятор степеней. Возведение в степень онлайн.

Калькулятор степеней — возвести в степень онлайн

Калькулятор помогает быстро возвести число в степень онлайн. Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.

Что такое натуральная степень числа?

Число p называют n-ой степенью числа a, если p равно числу a, умноженному само на себя n раз: p = an = a·...·a
n — называется показателем степени, а число a — основанием степени.

Как возвести число в натуральную степень?

Чтобы понять, как возводить различные числа в натуральные степени, рассмотрим несколько примеров:

Пример 1. Возвести число три в четвёртую степень. То есть необходимо вычислить 3

4
Решение: как было сказано выше, 34 = 3·3·3·3 = 81.
Ответ: 34 = 81.

Пример 2. Возвести число пять в пятую степень. То есть необходимо вычислить 5⁵
Решение: аналогично, 55 = 5·5·5·5·5 = 3125.
Ответ: 55 = 3125.

Таким образом, чтобы возвести число в натуральную степень, достаточно всего лишь умножить его само на себя n раз.

Что такое отрицательная степень числа?

Отрицательная степень -n числа a — это единица, поделённая на a в степени n: a^-n = .

При этом отрицательная степень существует только для отличных от нуля чисел, так как в противном случае происходило бы деление на ноль.

Как возвести число в целую отрицательную степень?

Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.

Пример 1. Возвести число два в минус четвёртую степень. То есть необходимо вычислить 2^-4

Решение: как было сказано выше, 2-4 = = = 0.0625.

Ответ: 2-4 = 0.0625.

programforyou.ru

показатель и основание степени. Онлайн калькулятор

Степень с натуральным показателем

Произведение, в котором все множители одинаковые, можно записывать короче:

4 · 4 · 4 = 4³

Выражение 4³ (а также результат его вычисления) называется степенью.

Степень – это краткая запись произведения одинаковых сомножителей.

Число, показывающее количество одинаковых сомножителей, называют показателем степени. Возводимое в степень число называют основанием степени:

Запись 4³ читается так: четыре в степени три или четыре в третьей степени.

Степенью числа a с натуральным показателем n (где n > 1) называют произведение n множителей, каждый из которых равен a.

Пример 1. Вычислим 2⁴:

Пример 2. Вычислим 3⁷:

Если какое-нибудь число берётся сомножителем 2 раза, то произведение называется второй степенью этого числа, если какое-нибудь число берётся сомножителем 3 раза, то произведение называется третьей степенью этого числа и т. д. Например, произведение 16 из первого примера – это четвёртая степень числа 2.

Первой степенью числа называют само это число. Например, 2¹ = 2, 5¹ = 5, 100¹ = 100, т. е. первая степень любого числа равна самому числу:

a¹ = a

Вторую степень числа называют иначе квадратом числа. Например, запись 5² читают пять в квадрате. Третью степень числа называют иначе кубом числа. Например, запись 5³ читают пять в кубе. Эти названия заимствованы из геометрии.

Возведение в степень – это вычисление значения степени. Например, если стоит задача вычислить значение степени 3⁵, то её можно переформулировать так: возвести число 3 в пятую степень.

Пример: вычислить значение степени 3⁵.

Решение: данная степень равна произведению: 3 · 3 · 3 · 3 · 3. Перемножаем сомножители и получаем ответ: 243.

Ответ: 3⁵ = 243.

Степень часто используют для записи очень больших или очень малых чисел. Например, скорость света, которая примерно равна 300 000 000 (триста миллионов) метров в секунду удобнее записывать так: 3 · 10

8 м/с.

Степень можно использовать для представления разрядной единицы в виде степени:

399 = 3 · 100 + 9 · 10 + 9 · 1 = 3 · 10² + 9 · 10¹ + 9 · 1

Также степень часто используют в записи разложения числа на простые множители:

1000 = 2³ · 5³

Калькулятор возведения в степень

Данный калькулятор поможет вам выполнить возведение в степень. Просто введите основание с показателем степени и нажмите кнопку Вычислить.

naobumium.info

Калькулятор степеней онлайн: формула, примеры с решением

Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.

Основные действия со степенями

В первую очередь степень — это повторяющееся умножение. Число 13

4 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 13⁴ на 13², то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 13⁶. Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:

a^m × aⁿ = a^(m+n).

Если разделить 13⁴ на 13², то нам потребуется вычислить дробь вида:

(13 × 13 × 13 × 13) / (13 × 13).

Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 13². Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так:

a^m / aⁿ = a^(m – n).

Теперь давайте возведем 11⁴ в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так:

(a^m)ⁿ = a^(m × n).

Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 15⁰? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 15⁴ на 15⁴, что запишется как дробь:

15⁴ / 15⁴.

Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 15⁰. Следовательно:

15⁴ / 15⁴ = 15⁰ = 1.

Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так:

a⁰ = 1.

При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 8² на 8⁴ и запишем выражение в виде дроби.

(8 × 8) / (8 × 8 × 8 × 8).

Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8^-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:

a^-m = 1 / a^m

При этом для значения -1 правило трансформируется в элегантную формулу:

a^-1 = 1 / a.

И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7^(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка. Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат. Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как:

a^(m/n) есть корень n-ной степени из a^m.

Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.

Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.

Примеры из реальной жизни

Депозит в банке

Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:

Рост = a × e^(kt),

где a – начальное значение, e – константа, равная 2,718; k – коэффициент роста; t – время.

Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.

Школьная задача

Пусть в школьной задаче требуется построить график функции y = x^2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции. Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.

Заключение

Возведение в степень — арифметическая операция последовательного умножения. Степени имеют больше значение в прикладных науках, так как большинство реальных процессов описываются при помощи степенных функций. Используйте наш калькулятор для расчетов любых практических или школьных задач.

bbf.ru

Возведение в степень онлайн

Предлагаемый нами бесплатный калькулятор включает такую нужную для многих функцию, как калькулятор степеней. С его помощью выполнить возведение числа в степень проще простого, задайте выражение — получите результат. Калькулятор производит возведение в степень онлайн, как и любые другие функции, прямо на нашем сайте.

Как возвести число в степень в калькуляторе?

Возведение в степень — это действие умножения числа самого на себя n раз, где число x^y — степень, x — основание степени, y=n — показатель степени. Чтобы возвести в степень на калькуляторе, используйте соответствующие кнопки на панели управления. Если вам нужна более подробная информация по работе с цифровой панелью калькулятора, перейдите на страницу кнопки онлайн калькулятора.

Функция возведения в степень в калькуляторе представлена пятью кнопками: возведение в квадрат, возведение в куб, возведение в n степень произвольного числа, возведение в степень основания равного 10-ти и возведение в степень экспоненты.

Кнопки калькулятора, отвечающие за возведение в степень:

Возведение в квадрат и в куб

Первой степенью числа является само число. Любое число в нулевой степени равно 1. Возведение в квадрат — вторая степень, куб — третья. Квадрат числа всегда имеет положительное значение, за исключением квадрата комплексных чисел.

Эти кнопки калькулятора упрощают ввод операции: х² — возведение в квадрат, х³ — в куб. Одним нажатием в поле ввода вставляется запись вида ^2 или ^3.

Пример возведение в квадрат и куб:

Возведение в n степень

Используйте эту кнопку, когда нужно рассчитать какое-либо число в степени n. Кнопка x^y выводит в строке ввода выражения знак степени (циркумфлекс).

Наш онлайн калькулятор возведение в степень обозначает обычной «двухэтажной» записью на дисплее, а вот в поле ввода выражения нужно, конечно, использовать циркумфлекс.

Пример возведение чисел в степень:

Вычисление степени числа 10

Нажатие этой кнопки вставляет в поле ввода запись вида: 10^(), т.е. основанием степени записывается число 10. Удобно применять, когда нужно написать возведение в какую-нибудь степень именно числа 10.

Пример, как найти степень числа 10:

Экспонента в степени

Нажав на кнопку, увидите в строке запись exp(). Чтобы посчитать число е в степени, нужно возвести число Эйлера в степень e^x = exp(x). Кому интересно знать, чему равно число е: его значение 2.71828182845905.

Пример, как возвести е в степень:

Возведение в дробную степень

Допустим, нас интересует дробная степень числа x^y1/y2. Так как возведение в степень — действие, обратное к извлечению корня, расчёт сводится к нахождению корня степени y2 из числа x в степени y1. Если значение y2 чётное, то дробную степень можно вычислить только при положительном основании, так как корень отрицательного числа не существует и калькулятор в подобной ситуации выдаст вам ошибку!

При возведении в дробную степень не забывайте закрывать основание в скобки, иначе знаменатель дроби в показателе степени уйдет в знаменатель основания!

Этот пример показывает, как возвести в дробную степень на калькуляторе:

Наш онлайн калькулятор позволяет возвести как в положительную, так и в отрицательную степень. При отрицательном значении показателя, основание должно принять вид (1/x), другими словами, числитель и знаменатель основания степени должны поменяться местами и только после этого можно начинать возведение. Калькулятор позволяет возвести число в отрицательную степень автоматически, опуская все промежуточные преобразования и выдавая сразу окончательный ответ.

При возведении в отрицательную степень всевозможных функций, в том числе тригонометрических, онлайн калькулятор автоматически учитывает их четность/нечетность по правилу знаков.

Этот пример показывает, как возвести в отрицательную степень на калькуляторе:

Дробное число в степени калькулятор тоже рассчитает.

Возведение дроби в степень с помощью калькулятора:

В калькуляторе можно рассчитать и корень в степени.

Возведение корня в степень с помощью калькулятора:

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

Возведение в степень онлайн was last modified: Март 3rd, 2016 by Admin

compuzilla.ru

Возведение в степень и извлечение корня из числа онлайн.

Корень нечётной степени из положительного числа

В результате вычисления корня нечётной степени из положительного числа будет положительное число: .

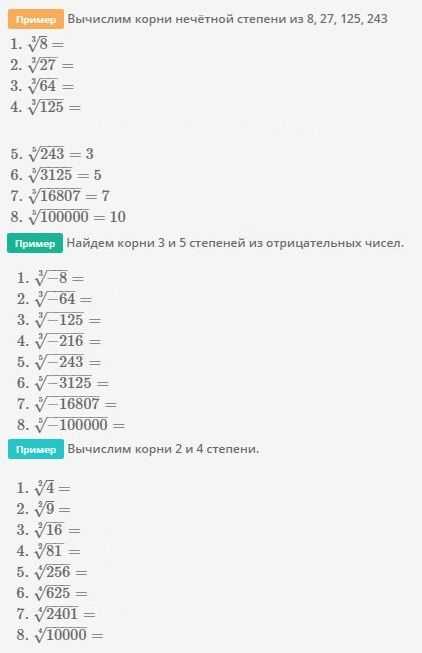
Пример Вычислим корни нечётной степени из 8, 27, 125, 243

Корни 3 степени также называют кубическими корнями.

В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.

Корень нечётной степени из отрицательного числа

В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .

Пример Найдем корни 3 и 5 степеней из отрицательных чисел.

Корень четной степени из положительного числа

Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .

Пример Вычислим корни 2 и 4 степени.

Корень 2-й степени называют квадратный корнем.

Корень четной степени из отрицательного числа

Корень четной степени из отрицательного числа не существует для вещественных чисел.

Корень любой степени из нуля

calcs.su

Возведение в степень — онлайн калькулятор, секретные примеры, игры

Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an = an.

Например, а=2, n=3: 2 * 2 * 2=2^3 = 8.

Вообще возведение в степень часто используется в различных формулах по математике и физике. Эта функция имеет более научное предназначение, чем четыре основные: Сложение, Вычитание, Умножение, Деление.

Возведение числа в степень

Возведение числа в степень – операция не сложная. Оно связано с умножением подобно связи умножения и сложения. Запись an – краткая запись n-ого количество чисел «а» умноженных друг на друга.

Рассмотри возведение в степень на самых простых примерах, переходя к сложным.

Например, 42. 42 = 4 * 4 = 16. Четыре в квадрате (во второй степени) равно шестнадцати. Если вам не понятно умножение 4 * 4, то читайте нашу стать об умножении.

Рассмотрим еще одни пример: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125. Пять в кубе (в третьей степени) равно ста двадцати пяти.

Еще один пример: 9^3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729. Девять в кубе равняется семи сотням двадцати девяти.

Формулы возведения в степень

Чтобы грамотно возводить в степень нужно помнить и знать формулы, указанные ниже. В этом нет ничего сверх естественного, главное понять суть и тогда они не только запомнятся, но и покажутся легкими.

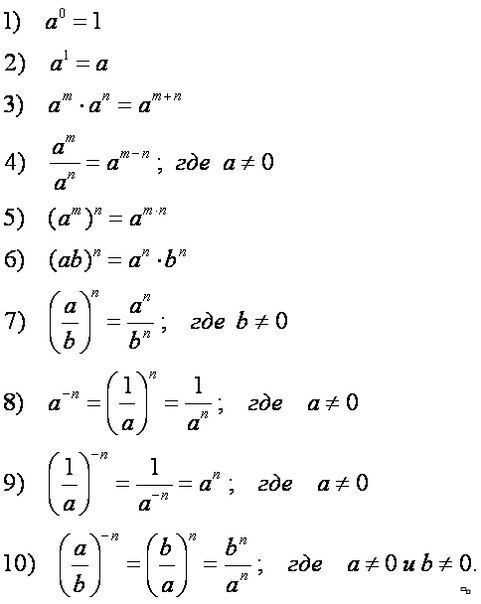
Возведение одночлена в степень

Что из себя представляет одночлен? Это произведение чисел и переменных в любом количестве. Например, двух – одночлен. И вот именно о возведении в степень таких одночленов данная статья.

Пользуясь формулами возведения в степень вычислить возведение одночлена в степень будет не трудно.

Например, (3x^2y^3)^2= 3^2 * x^2 * 2 * y^(3 * 2) = 9x^4y^6; Если возводить одночлен в степень, то в степень возводится каждая составная одночлена.

Возводя в степень переменную уже имеющую степень, то степени перемножаются. Например, (x^2)^3 = x^(2 * 3) = x^6;

Возведение в отрицательную степень

Отрицательная степень – обратное число. Что такое обратное число? Любому числу Х обратным будет 1/X. То есть Х-1=1/X. Это и есть суть отрицательной степени.

Рассмотрим пример (3Y)^-3:

(3Y)^-3 = 1/(27Y^3).

Почему так? Так как в степени имеется минус, то просто переносим в знаменатель данное выражение, а затем возводим в его в третью степень. Просто не так ли?

Возведение в дробную степень

Начнем рассмотрение вопрос на конкретном примере. 43/2. Что означает степень 3/2? 3 – числитель, означает возведение числа (в данном случае 4) в куб. Число 2 – знаменатель, это извлечение корня второй степени из числа (в данном случае 4).

Тогда получаем квадратный корень из 43 = 2^3 = 8. Ответ: 8.

Итак, знаменатель дробной степени может быть, как 3, так и 4 и до бесконечности любым числом и это число определяет степень квадратного корня, извлекаемого из заданного числа. Конечно же, знаменатель не может быть равным нулю.

Возведение корня в степень

Если корень возводится в степень, равной степени самого корня, то ответом будет подкоренное выражение. Например, (√х)2 = х. И так в любом случае равенства степени корня и степени возведения корня.

Если (√x)^4. То (√x)^4=x^2. Чтобы проверить решение переведем выражение в выражение с дробной степенью. Так как корень квадратный, то знаменатель равен 2. А если корень возводится в четвертую степень, то числитель 4. Получаем 4/2=2. Ответ: x = 2.

В любом случае лучший вариант просто перевести выражение в выражение с дробной степенью. Если не будет сокращаться дробь, значит такой ответ и будет, при условии, что корень из заданного числа не выделяется.

Возведение в степень комплексного числа

Что такое комплексное число? Комплексное число – выражение, имеющее формулу a + b * i; a, b – действительные числа. i – число, которое при возведение в квадрат дает число -1.

i^2=-1.

Рассмотрим пример. (2 + 3i)^2.

(2 + 3i)^2 = 22 +2 * 2 * 3i +(3i)^2 = 4+12i^-9=-5+12i.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

---

Возведение в степень онлайн

С помощью нашего калькулятора, Вы сможете посчитать возведение числа в степень:

Загрузка калькулятора…

Возведение в степень 7 класс

Возведение в степень начинают проходить школьники только в седьмом классе.

Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an=an.

Например, а=2, n=3: 2 * 2 * 2 = 2^3 = 8.

Примеры для решения:

Возведение в степень презентация

Презентация по возведению в степень, рассчитанную на семиклассников. Презентация может разъяснить некоторые непонятные моменты, но, вероятно, таких моментов не будет благодаря нашей статье.

Скачать презентацию

Итог

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

cepia.ru

Возведение в степень | Формулы с примерами

Формула возведения в степень

Степенью числа a с показателем n, называется произведение n сомножителей, каждый из которых равен a.
a — действительное число,
n — натуральное число.

Калькулятор возведения в степень онлайн

Правило возведения в степень

Степень показывает количество раз, которое некое число умножается на себя. Она обозначается малой цифрой (показателем степени) справа вверху от основного числа (основани степени).

Возведение в степень — действие нахождения степени:

Умножение числа на себя один раз называется возведением числа в квадрат.

Умножение числа на себя два раза называется возведением в куб.

Свойства возведения в степень

1. Если отрицательно число возвести в четную степень, то получим положительное число.

Пример

(-2)22 > 0; (-3)34 > 0; (-5)88 > 0.

2.Если отрицательное число возвести в нечетную степень, то получим отрицательное число.

! Возведение в степень — действие третьей ступени, его выполняют перед действиями второй ступени (умножением и делением) и первой ступени (сложением и вычитанем).

Возведение в степень примеры

1. x³ = x • x • x ;
a = x ;

2. k⁵ = k • k • k • k • k ;
a = k ;

3. 18¹ = 18 ;
a = 18;

4. 1¹⁸ = 1;
a = 1 ;

5. 0 ⁷ = 0;
a = 0;

6. 5³ = 5 • 5 • 5 = 125 ;
a = 5 ;

7. 7⁴ = 7 • 7 • 7 • 7 = 2 401 ;
a = 5 ;

formula-xyz.ru