Сумма модулей – Модуль числа — Youclever.org

Доказательства свойств модуля — Науколандия

Существуют следующие свойства модуля действительных чисел:

1) |a + b| ≤ |a| + |b|;

2) |ab| = |a| × |b|;

3) , a ≠ 0;

4) |a – b| ≥ |a| – |b|.

Проведем доказательства, рассматривая различные случаи значений a и b.

Доказательство 1) |a + b| ≤ |a| + |b|:

Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b. Из этого следует, что |a + b| = |a| + |b|.

Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a|. Выражение же |a| + |b| равно сумме абсолютных значений a и b, что больше, чем b – a. Поэтому |a + b| < |a| + |b|.

Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b|, что также меньше суммы модулей |a| + |b|.

Если a и b – отрицательные числа, то получим |–a – b|. Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b|). Но уже было доказано, что |a + b| = |a| + |b|, следовательно и |–a – b| = |a| + |b|.

Доказательство 2) |ab| = |a| × |b|:
Здесь, в отличие от сложения, рассматривать все случаи особо не требуется, т. к. абсолютное значение произведения любых чисел (положительных ли, отрицательных ли) не зависит от знаков множителей. В выражении |ab| мы сначала перемножаем числа, а потом «отбрасываем» знак (отрицательный, если он есть), в выражении |a| × |b| сначала избавляемся от знаков, а потом перемножаем. Но от того, в какой момент был взят модуль (до или после умножения), не зависит абсолютное значение произведения.

Доказательство 3) , a ≠ 0:

Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/a.

Если a – отрицательное число, то имеем . Взятие модуля в обоих выражениях приведет к делению единицы на абсолютное значение a. Значит эти выражения равны друг другу.

Доказательство 4) |a – b| ≥ |a| – |b|:

Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b|, потому что можно не брать модули вообще и тогда с двух сторон получим a – b.

Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b|, что больше, чем |a| – |b|.

Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b|, что больше, чем |a| – |b|.

scienceland.info

Уравнения и неравенства с модулем

Автор Сергей Валерьевич

Суббота, Август 18, 2012

Репетитору по математике часто приходится сталкиваться с отсутствием у старшеклассников навыков решения простейших уравнений и неравенств с модулем. Между тем среди заданий С3 или С5 из ЕГЭ по математике таковые могут встретиться. Даже если их не будет на экзамене в явном виде, в процессе выполнения некоторых задач из ЕГЭ вам, возможно, придется столкнуться с решением того или иного задания с модулем. Поэтому научиться решать 

уравнения и неравенства с модулем должен каждый выпускник средней школы. В данной статье рассмотрены некоторые способы их решения. Присутствует также видеоразбор решения одного уравнения, содержащего модуль.

Считается, что чем больше способов решения существует у задачи, тем она интереснее с математической точки зрения. Уравнения и неравенства с модулями можно поэтому смело назвать интересными. Рассмотрим пример.

Решите уравнение:

   

Решение. Постараемся найти как можно большее количество решений данного уравнения. Подробное объяснение решений смотрите в видеоуроке.

Способ №1. Решение возведением в квадрат.

Просто возводим обе части уравнения в квадрат. При этом не забываем, что подобное преобразование не является равносильным. Из-за этого могут появиться посторонние корни, поэтому полученные решения необходимо будет проверить прямой подстановкой в исходное уравнение.

   

   

   

Путем прямой подстановки полученных решений в исходное уравнение убеждаемся, что посторонних корней среди них нет. На самом деле в данном конкретном задании отсутствует необходимость проверки корней. Возведение обеих частей этого уравнения в квадрат не может привести к приобретению посторонних решений. Подумайте самостоятельно, почему это так.

Способ №2. Метод интервалов. Не совсем верное название, но мы его здесь употребим, поскольку в методической литературе оно встречается. Для решения нам потребуется найти значение переменной при котором подмодульное выражение обращается в ноль:  Наносим эту точку на числовую прямую и определяем знаки подмодульного выражения на полученных промежутках.

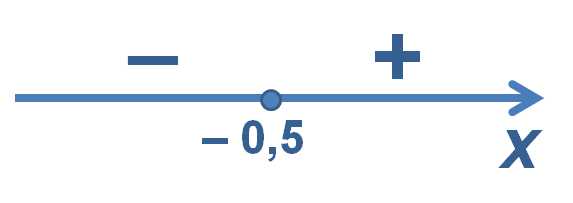
Числовая прямая

Далее на каждом промежутке раскрываем знак модуля в соответствии с полученными данными:

yourtutor.info

Модуль — сумма — Большая Энциклопедия Нефти и Газа, статья, страница 1

Модуль — сумма

Cтраница 1

Модуль суммы не может превзойти сумму модулей слагаемых.  [1]

Модуль суммы двух или нескольких комплексных чисел не превосходит суммы модулей этих чисел.  [2]

Модуль суммы двух или нескольких чисел меньше или равен сумме модулей этих чисел.  [3]

Модуль суммы индексов всех особых точек невырожденного векторного поля v степени т ( обозначается Ind v) не превосходит числа Петровского — — Олейник II ( т) и сравним по модулю 2 с числом и. Никаких других ограничений на Irul v не существует.  [4]

Заменим модуль суммы в правой части ( 20) суммой модулей и потребуем выполнения полученного неравенства. В этом случае ( 20) будет выполняться автоматически.  [5]

Докажите, что модуль суммы двух перемещений не превосходит суммы модулей составляющих перемещений. В каком случае модуль суммы равен сумме модулей слагаемых перемещений.  [6]

Известно, что модуль суммы меньше или равен сумме модулей слагаемых.  [7]

Доказать, что модуль суммы двух комплексных чисел не превосходит суммы модулей этих чисел.  [8]

Установим теперь свойства модуля суммы и разности двух комплексных чисел.  [9]

Теорема о том, что модуль суммы не больше суммы модулей слагаемых, легко распространяется на случай абсолютно сходящихся рядов.  [10]

Теорема о том, что модуль суммы не больше суммы модулей слагаемых, легко распространяется на случай абсолютно сходящихся рядов.  [11]

Поскольку разложить в ряд Фурье модуль суммы гармоник в общем виде нельзя, укажем, что при незначительных искажениях несущей выходной сигнал будет подобен детектированному.  [12]

Принципиальный интерес представляет способ выделения модуля суммы и разности входных — величин, предложенный в.  [13]

Установим теперь важные для дальнейшего свойства модуля суммы и разности двух комплексных чисел.  [14]

Такое отображение, фактически представляющее собой натягивание модуля суммы гауссовскнх полей на параболоиды в направлении внешней нормали, переведет гладкие параболоиды в некоторые случайные геометрические тела. Ограничивая эти фигуры снизу плоскостью z Л0, получим математическую модель кучевой облачности, в которой отдельные облака имеют случайную геометрию.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

Простейшие уравнения с модулем. Тест

Определение. Геометрический смысл

 

Модуль (или абсолютная величина)   числа   (обозначается как )— неотрицательное число, определение которого зависит от типа числа  

А именно:

Мы будем называть данное правило правилом раскрытия модуля.

Например, так как , попадаем в первую строку (ситуацию)

так как попадаем во вторую ситуацию.

С геометрической точки зрения,  – есть расстояние между числом   и началом координат.

Решением уравнения, например,  являются числа и , потому что расстояние от точки координатной прямой до нуля равно , и расстояние от точки   до нуля также равно 6.

|| с геометрической точки зрения означает расстояние между точками и .

 

Полезные примеры

 

1) Раскрыть модуль:

Так как больше, чем , то , а значит согласно правилу раскрытия модуля.

2) Раскрыть модуль:

Так как больше нуля при всех значениях , то согласно правилу раскрытия модуля.

3) Раскрыть модуль:

Так как , то , а значит, согласно правилу раскрытия модуля.

Решение уравнений

 

1) Решить уравнение .

Модуль – всегда неотрицательная величина, поэтому уравнение решений не имеет.

Ответ: { }

2) Решить уравнение: .

Модуль раскрывается таким образом в случае, когда  .

Ответ:

3) Решить уравнение:

Согласно геометрическому смыслу модуля левая и правая части равенства представляют из себя одно и то же.

Ответ:

4)  Решить уравнение:

Раскрываем модуль согласно правилу раскрытия модуля:

а)

Имеем: ,     

Откуда .

Поскольку мы находимся в ситуации , то подходит только корень .

б)

Имеем: ,    

Откуда или .

Поскольку мы находимся в ситуации , то ни один корень из найденных в пункте (б) нам не подходит.

Ответ: .

Коротко можно было бы решение оформить так:

5) Решить уравнение:

Раскрываем модуль согласно правилу раскрытия модуля:

a) Первый случай:

Что равносильно .

б) Второй случай:

Что равносильно

Ответ:

6) Решить уравнение:

Можно было бы действовать согласно правилу раскрытия модуля, но проще будет в данном случае рассуждать так:

Внутри модуля может «скрываться» как так и .

Поэтому или

или

Из первого уравнения или , а второе уравнение корней не имеет.

Ответ:

 

7) Решить уравнение:

Раскрываем модуль согласно правилу раскрытия модуля:

а) Первый случай:

Рассмотрим отдельно первую строку системы:

Рассмотрим уравнение из системы:

или

Разложим на множители левую часть уравнения способом группировки, предварительно разбив среднее слагаемое на два:

Откуда (трехчлен в скобках корней не имеет).

Данный корень удовлетворяет первой строке системы, он пойдет  в ответ.

б) Второй случай:

Решение неравенства системы:

Корень удовлетворяет решению неравенства системы.

Собираем решения.

Ответ:

 

Также, смотрите «Модуль. Простейшие неравенства с модулем» здесь.

Вы можете пройти тест  по теме «Модуль. Раскрытие модуля. Простешие уравнения с модулем»

egemaximum.ru

Внеклассный урок — Модуль числа

Модуль числа

Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.

Например, модулем числа 5 является 5, модулем числа –5 тоже является 5.

То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.

Обозначается так: |5|, |х|, |а| и т.д.

Правило:

|а| = а, если а ≥ 0.                                                                      |а| = –а, если а < 0.

 

Пояснение:

|5| = 5
Читается так: модулем числа 5 является 5.

|–5| = –(–5) = 5
Читается так: модулем числа –5 является 5.

|0| = 0
Читается так: модулем нуля является ноль.

 

Свойства модуля:

1) Модуль числа есть неотрицательное число: |а| ≥ 0 2) Модули противоположных чисел равны: |а| = |–а| 3) Квадрат модуля числа равен квадрату этого числа: |а|2 = a2 4) Модуль произведения чисел равен произведению модулей этих чисел: |а · b| = |а| · |b| 6) Модуль частного чисел равен отношению модулей этих чисел: |а : b| = |а| : |b| 7) Модуль суммы чисел меньше или равен сумме их модулей: |а + b| ≤ |а| + |b| 8) Модуль разности чисел меньше или равен сумме их модулей: |а – b| ≤ |а| + |b| 9) Модуль суммы/разности чисел больше или равен модулю разности их модулей: |а ± b| ≥ ||а| – |b|| 10) Постоянный положительный множитель можно вынести за знак модуля: |m · a| = m · |а|, m >0 11) Степень числа можно вынести за знак модуля: |аk| = |а|k, если аk существует 12) Если |а| = |b|, то a = ± b

 

Геометрический смысл модуля.

Модуль числа – это величина расстояния от нуля до этого числа.

Для примера возьмем снова число 5. Расстояние от 0 до 5 такое же, что и от 0 до –5 (рис.1). И когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Впрочем, не совсем верно: расстояние мы измеряем только положительными числами – или неотрицательными числами. Пусть цена деления нашей шкалы составляет 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до –5 тоже 5 см.

На практике часто расстояние отмеряется не только от нуля – точкой отсчета может быть любое число (рис.2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками а и b на числовой прямой.

 

Пример 1. Решить уравнение |х – 1| = 3.

Решение.

Смысл уравнения в том, что расстояние между точками х и 1 равно 3 (рис.2). Поэтому от точки 1 отсчитываем три деления влево и три деления вправо – и наглядно видим оба значения х:
х₁ = –2, х₂ = 4.

Можем и вычислить.

│х – 1 = 3
│х – 1 = –3

↕

│х = 3 + 1
│х = –3 + 1

↕

│х = 4
│ х = –2.

Ответ: х₁ = –2; х₂ = 4.

 

Пример 2. Найти модуль выражения:

3√5 – 10.

Решение.

Сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 – это довольно сложно. Поступим проще: возведем в корень 3 и 10. Затем сравним величину чисел, составляющих разность:

3 = √9. Следовательно, 3√5 = √9 · √5 = √45

10 = √100.

Мы видим, что первое число меньше второго. Значит, выражение отрицательное, то есть его ответ меньше нуля:

3√5 – 10 < 0.

Но согласно правилу, модулем отрицательного числа является это же число с противоположным знаком. У нас отрицательное выражение. Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:

–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.

Ответ:

|3√5 – 10| = 10 – 3√5.

 

raal100.narod.ru

Модуль числа и свойства модуля

Определение модуля

Определение: Модулем положительного числа называется само это число, модулем отрицательного числа называется число, ему противоположное, модуль нуля равняется нулю.

Примеры нахождения модуля

Геометрический смысл модуля

Задан отрезок .

Определение: На координатной прямой модуль — это расстояние от начала координат до точки, изображающей данное число.

Определение: Модуль разности двух чисел i — это расстояние между точками и на координатной прямой.

Свойства модуля

1. (Модуль любого числа — неотрицательное число)
2. (Модули противоположных чисел равны)
3. (Величина числа не превышает величина его модуля)
4. (Модуль произведения дорівнєю произведению модулей сомножителей)
5. (Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))
9. (Модуль суммы не превышает суммы модулей слагаемых)

cubens.com

Модуль — сумма — Большая Энциклопедия Нефти и Газа, статья, страница 2

Модуль — сумма

Cтраница 2

Для обнаружения такого переполнения, учитывая, что модуль суммы двух таких чисел всегда меньше двух, используют один дополнительный разряд. Код ( прямой, дополнительный, обратный), в котором имеется такой пополнительный разряд, азываются модифицированным. Правила пере-оса из разрядов знака остаются прежними в зависимости от того, в каком коде ( обратном или дополнительном) представлены числа. Q 2, указывает несовпадение цифр в знаковых разрядах. В этом случае комбинации 01 соответствует положительное, а 10 — отрицательное число.  [16]

При сложении двух рациональных чисел с разными знаками модуль суммы равен разности модулей слагаемых.  [17]

При записи правой части учтено, что квадрат модуля суммы двух комплексов равен сумме квадратов модулей этих комплексов плюс произведение первого комплекса на сопряженный комплекс второго и плюс произведение второго на сопряженный комплекс первого.  [18]

Неравенство Минковского очевидно при р 1, так как модуль суммы двух чисел не превосходит суммы их модулей. Кроме этого, оно заведомо выполняется, если хотя бы один из векторов х, у равен нулю.  [19]

Это сразу вытекает из определения абсолютной непрерывности и свойств модуля суммы и произведения.  [20]

Это сразу вытекает из определения абсолютной непрерывности и свойств модуля суммы и произведения.  [21]

Сумма двух отрицательных чисел есть число отрицательное; чтобы найти модуль суммы, надо сложить модули слагаемых.  [22]

Первый из них является од нополу пер йодным прецизионным формирователем модуля суммы с раздельными выходами для положительных и отрицательных полуволн напряжений, второй — сумматором, обеспечивающим двухполупериодное выпрямление рабочего сигнала, суммирование его с тормозным обратной полярности и устранение этой суммы.  [23]

Они позволяют оценивать сверху модули коэффициентов степенного ряда через максимум модуля суммы ряда на окружности z — z0 p и радиус этой окружности.  [24]

Напомним еще, что аналогичное неравенство имеет место и для сумм: модуль суммы не превосходит суммы модулей.  [25]

А — максимум модулей остальных коэффициентов, модуль старшего члена многочлена больше модуля суммы всех остальных членов, а поэтому никакое значение х, удовлетворяющее неравенству ( 1), не может служить корнем этого многочлена.  [26]

Поскольку количество центров облаков фиксировано, а их средние горизонтальные размеры при добавлении модуля суммы гауссовскнх полей увеличиваются, то реальный балл облачности N NO п определяется численно. Значение D2 рассчитывается, исходя из следующих соображений.  [27]

Сущность суммирования по модулю — mh заключается в том, что результат равен модулю суммы разрядов, если этот модуль меньше tnh. Если модуль суммы больше т то результат получают вычитанием mft из суммы.  [29]

Принцип действия ИПФ основан на сравнении модуля емкостного тока каждого из фазных вводов с модулем суммы комплексных амплитуд емкостных токов вводов двух других фаз.  [30]

Страницы:      1    2    3    4

www.ngpedia.ru