Как найти площадь геометрических фигур? – boeffblog.ru
Что такое площадь?
Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Как найти площадь треугольника?
1. Самая известная формула площади треугольника по стороне и высоте:
S = a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.
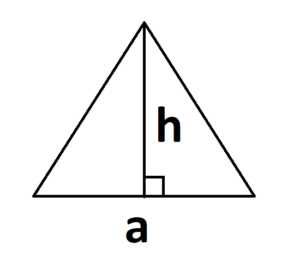
Причем, основание не обязательно должно находиться снизу. Так тоже сойдет. 
Если треугольник тупоугольный, то высота опускается на продолжение основания:

Если треугольник прямоугольный, то основанием и высотой являются его катеты:
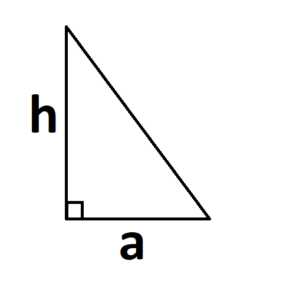
2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S = a · b · sinα
где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.
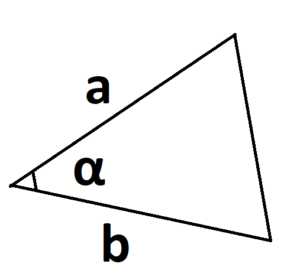
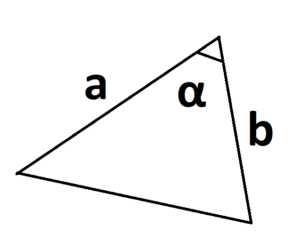
Главное условие – угол берется между двумя известными сторонами.
3. Формула площади по трем сторонам (формула Герона):
S =
где a, b и с – стороны треугольника, а р – полупериметр. p = (a + b + c)/2.
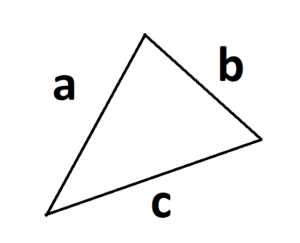
4. Формула площади треугольника через радиус описанной окружности:
S =
где a, b и с – стороны треугольника, а R – радиус описанной окружности.
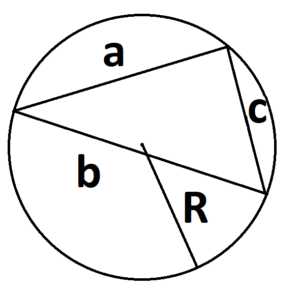
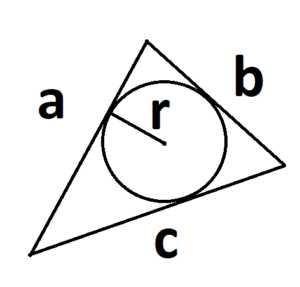
5. Формула площади треугольника через радиус вписанной окружности:
S =p · r
где р – полупериметр треугольника, а r – радиус вписанной окружности.
Как найти площадь прямоугольника?
1. Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
Как найти площадь квадрата?
1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a2
2. Также площадь квадрата можно найти через его диагональ:
S = d2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα
Как найти площадь ромба?
Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
2. Площадь ромба через угол между сторонами:
S = a · a sinα = a2 · sinα
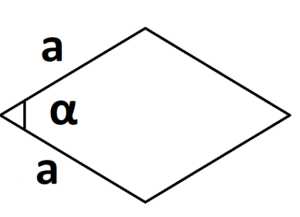
3. Площадь ромба через диагонали:
S = d1 · d2
Как найти площадь трапеции?
1. Площадь трапеции находится по следующей формуле:
S = · h
Как найти площадь круга?
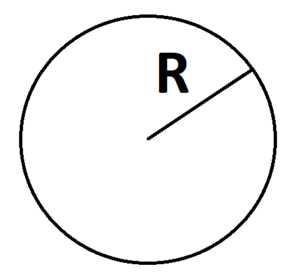
1. Площадь круга можно найти через радиус:
S = π r2
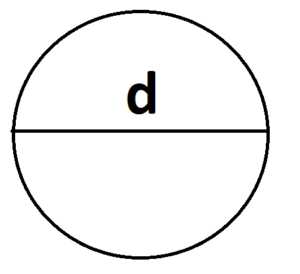
2. Площадь круга можно найти через диаметр:
S = πd2/4
boeffblog.ru
Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь фигуры. Все формулы
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.

Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Треугольник
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:

2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
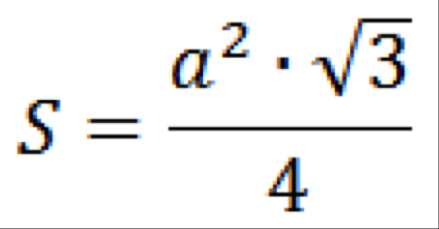
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
- Через радиус окружности r. Для площади круга вычисление можно сделать следующим образом:
- Через диаметр окружности d. Найти площадь круга можно так:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Похожие статьи
Рекомендуем почитать:
karate-ege.ru
Формула вычисления площади для всех геометрических фигур
Стандартное обозначение площади — S
Площадь
Пусть длина стороны квадрата равна a, тогда формул квадрата:
S = a ⋅ a = a2
Прямоугльник
Пусть длины сторон прямоугольника равны a и b
S = a ⋅ b
Параллелограмм
Пусть длины сторон параллелограмма равны a и b и
ha это высота на сторону a,
и hb это высота на сторону b
Формула площади параллелограмма:
S = a ⋅ ha = b ⋅ hb
Трапеция
Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами s h(the trapezoid altitude). Тогда формула площади:
$S = \frac{(a + b)\cdot h}{2}$
Площадь круга
$P = \pi\cdot r^2$
$\pi=3,14$
Площадь прямоугольного треугольника
$S=\frac{a \cdot b}{2}$
$S=\frac{c \cdot h_c}{2}$
Площадь треугольника — калькулятор
Стороны треугольника:Треугольник
ABC — треугольник
длина его сторон: a, b, c и длина его высот: ha, hb и hc.
S = ½(a ⋅ ha) = ½(b ⋅ hb) = ½(c ⋅ hc)S = ½(ab ⋅ sinC) = ½(ac ⋅ sinB) = ½(bc ⋅ sinA)
p = ½(a + b + c)
S = √p(p — a)(p — b)(p — c) — формула Герона
$S = R^2\sin(A) \cdot \sin(B) \cdot \sin(C) = \frac{abc}{4R}$
где R — радиус описанной окружностиПлощадь параллелограмма(ромба)
$S = AB\cdot DE = BC \cdot DF$
$S = AB \cdot AD \sin \alpha$
$S = \frac12 AC \cdot BD \sin \gamma$
Площадь выпуклого четырехугольника
$S = \frac12 AC \cdot BD \sin \varphi $
Площадь правильного многоугольника
$S = \frac14 n\cdot a^2\cdot \text{ctg}(\frac{\pi}{n})$
n — число ребер(вершин).
$\pi=3,14159265359$
www.math10.com
|
Треугольник |
|
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне. |
|
|
Треугольник |
|
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. |
|
|
Треугольник |
|
Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон. |
|
|
Треугольник |
|
Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла. |
|
|
Треугольник |
|
Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов. |
|
|
Треугольник |
|
Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника. |
|
|
Прямоугольный треугольник |
|
Площадь прямоугольного треугольника равна половине произведения его катетов. |
|
|
Равнобедренный треугольник |
|
Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания. |
|
|
Равносторонний треугольник |
|
Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх. |
|
|
Равносторонний треугольник |
|
Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх. |
|
|
Треугольник |
|
Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности. |
|
|
Треугольник |
|
Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов. |
|
|
Треугольник |
|
Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник). |
|
|
Треугольник |
|
Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника. |
|
|
Прямоугольник |
|
Площадь прямоугольника равна произведению двух соседних его сторон. |
|
|
Квадрат |
|
Площадь квадрата равна квадрату его стороны. |
|
|
Квадрат |
|
Площадь квадрата равна половине квадрата его диагонали. |
|
|
Параллелограмм |
|
Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне. |
|
|
Параллелограмм |
|
Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними. |
|
Ромб |
|
Площадь ромба равна произведению квадрата его стороны на синус одного из его углов. |
|
|
Ромб (дельтоид) |
|
Площадь ромба (как и дельтоида) равна половине произведения его диагоналей. |
|
|
Трапеция |
|
Площадь трапеции равна произведению полусуммы её оснований на высоту. |
|
|
Трапеция |
|
Площадь трапеции равна произведению её средней линии на высоту. |
|
|
Выпуклый четырёхугольник |
|
Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними. |
|
|
Вписанный четырёхугольник |
|
Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон. |
|
|
Круг |
|
Площадь круга равна произведению числа «пи» на квадрат радиуса. |
|
|
Круг |
|
Площадь круга равна четверти произведения числа «пи» на квадрат диаметра. |
|
|
Круговой сектор |
формулы для случаев градусной и радианной мер центральных углов |
Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору. |
|
|
Круговое кольцо |
|
Площадь кругового кольца равна произведению числа «пи» на разность квадратов внешнего и внутреннего радиусов. |
|
| Круговое кольцо |
|
Площадь кругового кольца равна четверти произведения числа «пи» на разность квадратов внешнего и внутреннего диаметров. |
|
| Круговое кольцо |
|
Площадь кругового кольца равна удвоенному произведению числа «пи», среднего радиуса кольца и его ширины. |
math4school.ru
Площадь фигуры — это… Что такое Площадь фигуры?
Пло́щадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Об определении
Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.
Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости, такая что:
- (положительность) площадь неотрицательна;
- (нормировка) квадрат со стороной единица имеет площадь 1;
- конгруэнтные фигуры имеют равную площадь;
- (аддитивность) площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
Определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
- Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:
Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура называется квадрируемой, если для любого существует пара многоугольников и , такие что и , где обозначает площадь .
Связанные определения
- Две фигуры называются равновеликими, если они имеют равную площадь.
Комментарии
На самом деле, есть довольно неестественный и неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. На множестве всех ограниченных подмножеств плоскости существуют различные функции площади, т. е. не равные функции, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур, на которых функционал площади определяется однозначно.
То же самое можно сделать для длины на прямой, но нельзя для объёма в евклидовом пространстве и также нельзя для площади на единичной сфере в евклидовом пространстве, (смотри соответственно парадокс Банаха — Тарского и парадокс Хаусдорфа).
Площади некоторых фигур
Формулы для нахождения площадей различных фигур
| Фигура | Формула | Комментарий |
|---|---|---|
| Правильный треугольник | — длина стороны треугольника. | |
| Треугольник | Формула Герона. — полупериметр, , и — длины сторон треугольника. | |
| Треугольник | и — две стороны треугольника, а — угол между ними. | |
| Треугольник | и — сторона треугольника и высота, проведённая к этой стороне. | |
| Квадрат | — длина стороны квадрата. | |
| Прямоугольник | и — длины сторон прямоугольника. | |
| Ромб | и — длины диагоналей ромба. | |
| Параллелограмм | — длина одной из сторон параллелограмма, а — высота, проведённая к этой стороне. | |
| Трапеция | и — длины параллельных сторон, а — расстояние между ними (высота). | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — длина стороны многоугольника, а — количество сторон многоугольника. | |
| — апофема (или радиус вписанной в многоугольник окружности), а — периметр многоугольника. | ||
| Круг | или | — радиус окружности, а — её диаметр. |
| Сектор круга | и — соответственно радиус и угол сектора (в радианах). | |
| Эллипс | и — большая и малая полуоси эллипса. | |
| Поверхность Цилиндра | и — радиус и высота цилиндра соответственно. | |
| Боковая поверхность цилиндра | и — радиус и высота цилиндра соответственно. | |
| Поверхность конуса | и — радиус и длина образующей соответственно. | |
| Боковая поверхность конуса | и — радиус и длина образующей соответственно. | |
| Поверхность сферы | и — радиус и диаметр соответственно. | |
| Поверхность эллипсоида | См. статью. |
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне:
- Площадь прямоугольника равна произведению его смежных сторон:
- Площадь произвольного четырехугольника ABCD равна половине произведения диагоналей и синуса угла между ними:
- ,
- где — угол между диагоналями.
- Площадь ромба ABCD равна половине произведения диагоналей:
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:
- Площадь трапеции равна произведению полусуммы оснований на высоту:
См. также
Ссылки
- В.Болтянский, О понятиях площади и объёма. Квант, № 5, 1977
- Б. П. Гейдман, Площади многоугольников, Библиотека «Математическое просвещение», выпуск 16, (2002).
- В. А. Рохлин, Площадь и объём, Энциклопедия элементарной математики, Книга 5, Геометрия, под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина.
dic.academic.ru
Нахождение площади различных фигур — Сегодня на уроке. — Каталог статей
 В этой статье мы разберемся, как вычислить площадь фигуры.
В этой статье мы разберемся, как вычислить площадь фигуры.
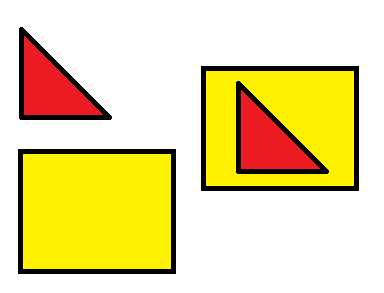
Сравнить площади разных фигур можно способом наложения. Посмотрите на рисунок. Мы видим две фигуры: треугольник и прямоугольник. Для того, чтобы их сравнить мы можем наложить меньшую фигуру на большую. Треугольник полностью поместился в прямоугольнике, это значит, что треугольник меньше прямоугольника.
Но не всегда можно сравнить площади фигур таким способом. Тогда можно разбить фигуру на равные квадраты и посчитать количество квадратов входящих в эту фигуру.
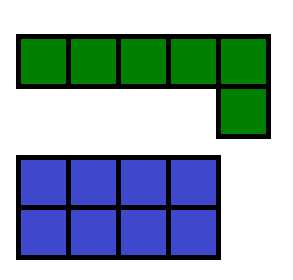 На
рисунке изображено две фигуры. Путем наложения эти фигуры сравнить
невозможно. Мы разбили эти фигуры на квадраты с одинаковой площадью.
Теперь можно посчитать количество квадратов входящих в эти фигуры. В
первую фигуру вписалось 6 квадратов, а во вторую 8. Значит площадь
первой фигуры меньше площади второй.
На
рисунке изображено две фигуры. Путем наложения эти фигуры сравнить
невозможно. Мы разбили эти фигуры на квадраты с одинаковой площадью.
Теперь можно посчитать количество квадратов входящих в эти фигуры. В
первую фигуру вписалось 6 квадратов, а во вторую 8. Значит площадь
первой фигуры меньше площади второй.
Площадь фигуры равна числу единичных квадратов, составляющих эту фигуру.
Если у квадрата сторона равна 1 см, то площадь такого квадрата равна 1 квадратному сантиметру (см2).
Площадь квадрата сторона которого равна 1 дециметр равна 1 квадратному дециметру (дм2) или 100 квадратным сантиметрам(см2).
Площадь фигуры обозначается заглавной латинской буквой S.
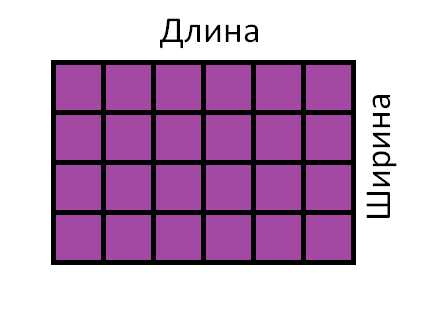 Допустим
нам надо найти площадь прямоугольника, длины сторон которого равны 6 и 4
см. Разделим прямоугольник на квадратные сантиметры и вычислим его
площадь.
Допустим
нам надо найти площадь прямоугольника, длины сторон которого равны 6 и 4
см. Разделим прямоугольник на квадратные сантиметры и вычислим его
площадь.
Итак, умножим длину прямоугольника на его ширину и получим площадь:
S = 6 × 4 = 24 см2
Чтобы вычислить площадь прямоугольника, надо измерить его длину и ширину в одинаковых единицах измерения и найти их произведение.
Если известна площадь прямоугольника и ширина, то найти длину просто, надо разделить площадь на известную длину.
Д = S ÷ Ш
или
Ш = S ÷ Д
Например, площадь прямоугольника равна 15 см2. Длина прямоугольника равна 5 см. Найдем его ширину:
Ш = 15 ÷ 5 = 3 см
Если фигура сложная, например, такая как на рисунке, то вычислить её площадь можно разбив фигуру на прямоугольники, вычислить их площадь, а затем сложить полученные площади.
Итак нашу фигуру мы можем разбить на два прямоугольника: первый площадью 2 см2, и второй площадью 8 см2:
S = 2 × 1 + 4 × 2 = 10 см2
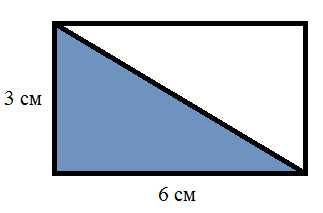 А как найти площадь прямоугольного треугольника. Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.
А как найти площадь прямоугольного треугольника. Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.
Теперь найдем площадь полученного прямоугольника и разделим её пополам:
S = (3 × 6) ÷ 2 = 9 см2
Кажется все просто, когда треугольник прямоугольный. Если у треугольника нет прямого угла, то вычислить его площадь можно следующим образом:
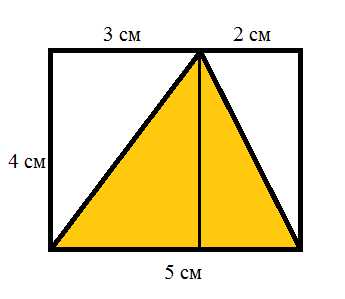 На
следующем рисунке мы видим треугольник, площадь которого нам надо
вычислить, он выделен желтым цветом. Впишем его в прямоугольник, так как
показано на рисунке. Длина полученного прямоугольна – 5 см. Ширина – 4
см. Вершина треугольника делит длину прямоугольника на части в 3 и 2 см.
На
следующем рисунке мы видим треугольник, площадь которого нам надо
вычислить, он выделен желтым цветом. Впишем его в прямоугольник, так как
показано на рисунке. Длина полученного прямоугольна – 5 см. Ширина – 4
см. Вершина треугольника делит длину прямоугольника на части в 3 и 2 см.
Теперь для того, чтобы найти площадь нашего треугольника, надо вычислить площади двух полученных прямоугольных треугольников и сложить их:
S1 = (3 × 4) ÷ 2 = 6 см2
S2 = (2 × 4) ÷ 2 = 4 см2
S = S1 + S2 = 6 + 4 = 10 см2
ludmilasorokina.3dn.ru


