8.2. Каноническое уравнение эллипса и его характеристики
Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек , называемых фокусами, есть величина постояннаяРасстояние между фокусами эллипсаназывается фокусным расстоянием и обозначается
Общее уравнение эллипса
где большая полуось,малая полуось,координаты центра эллипса.
Если центр эллипса находится в начале координат и фокусы эллипса находятся на оси на равных расстояниях от начала координат, то уравнение примет вид
причем,
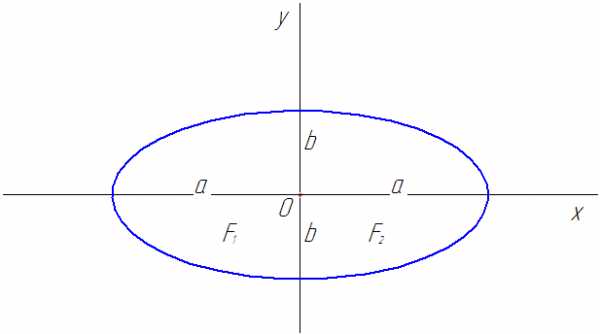
Рис. 13
Эллипс с центром в начале координат
Отношение фокусного расстояния к большой оси, т.е. называется
Эксцентриситет и коэффициент сжатия эллипсасвязаны соотношением
Директрисы эллипса.
Пусть дан эллипс
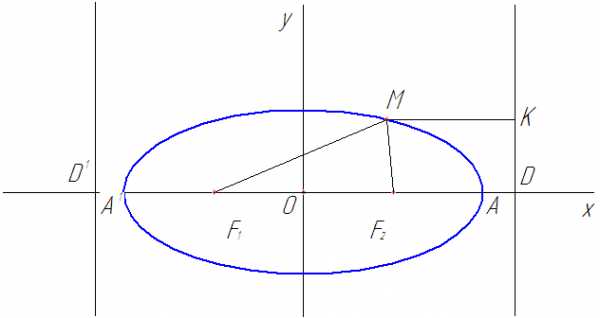
Рис. 14
Дирректрисы эллипса
с большой осью и эксцентриситетом
Отложим от центра эллипса на его большой оси отрезки
Прямые, проходящие через точки ипараллельно малой осиназываютсядиректрисами эллипса.
Для любой точки эллипса отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равно эксцентриситетут.е.
Рассмотрим пример. На эллипсе
найти точку, разность фокальных радиус-векторов которой равна 6,4.
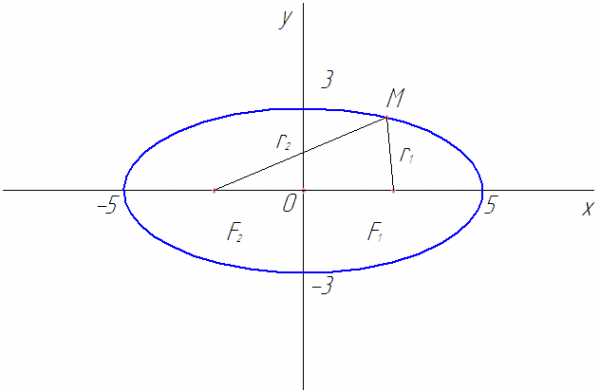
Рис. 15
Согласно уравнению эллипса определим расстояние от цента эллипса до фокусов
тогда
Кроме того,
Составим систему и решим ее
Получим
так как
Вывод: таких точек может быть две
8.3. Каноническое уравнение гиперболы и ее характеристики
Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная причем эта постоянная меньше расстояния между фокусами. Если поместить фокусы гиперболы в точкахто получается каноническое уравнение гиперболы
где Вершинами гиперболы являются точкитогдадействительная ось гиперболы,мнимая ось гиперболы.
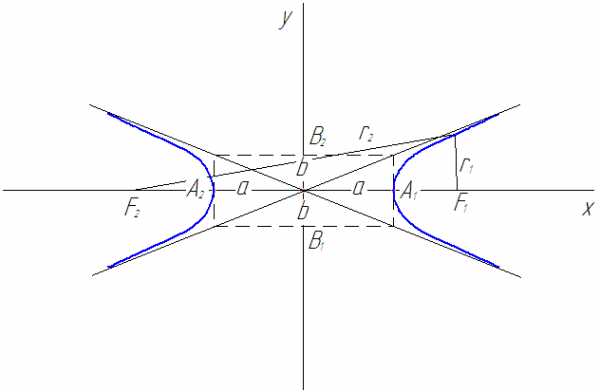
Рис. 16
Гипербола
Гипербола имеет две асимптоты
Эксцентриситет гиперболы
Фокальные радиус-векторы левой ветви гиперболы:
Фокальные радиус-векторы правой ветви гиперболы:
Рассмотрим пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллипса
Найдем координаты фокусов, в которых лежат вершины гиперболы
следовательно
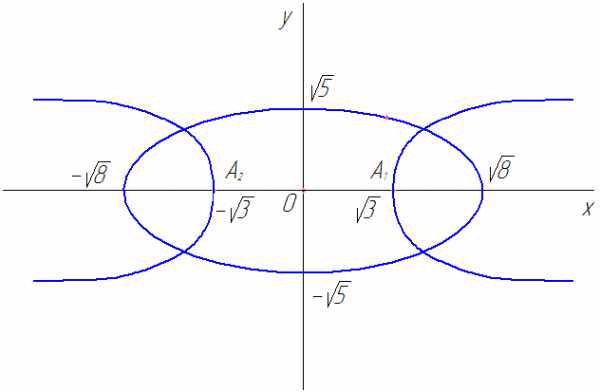
Рис. 17
Вершины гиперболы лежат в фокусах эллипса, следовательно
фокусы гиперболы, т.е.
Тогда
— уравнение гиперболы.
8.4. Каноническое уравнение параболы и ее характеристики
Парабола – это множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы является прямая а фокусом является точкато уравнение параболы имеет вид
Парабола симметрична относительно оси абсцисс
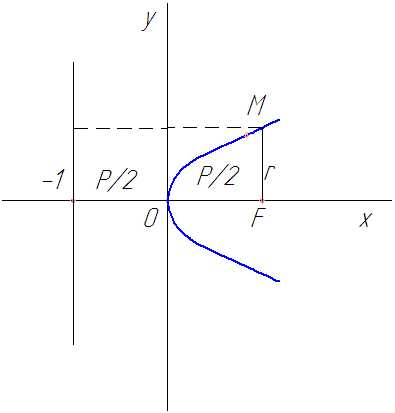
Рис. 18
Парабола
Рассмотрим пример. Составить простейшее уравнение параболы, если известно, что ее фокус находится в точке пересечения прямой и осью
В точке пересечения с осью координататогда
следовательно, фокус параболы.
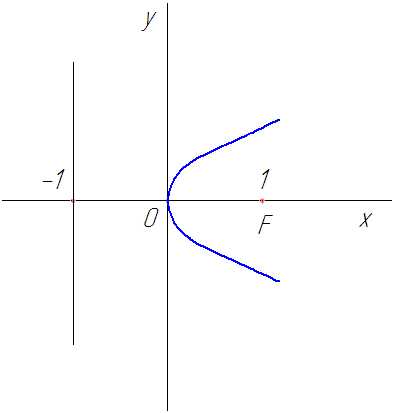
Рис. 19
Парабола
Парабола симметрична Так как
Тогда искомое уравнение параболы.
studfiles.net
Кривые второго порядка. Эллипс
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
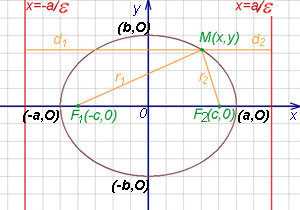
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b, то уравнение эллипса принимает вид . Это уравнение окружности радиуса a, а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a, если сжать её в a/b раз вдоль оси Oy.
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5, меньшая полуось — это b = 4. Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
Число
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения
эксцентриситета, бОльшая полуось эллипса a = 13.
Из уравнения эсцентриситета выражаем число
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
function-x.ru
(5) – Каноническое уравнение эллипса с центром в начале координат. Соответственно, уравнение
– Каноническое уравнение эллипса с центром в точке
Числа а и 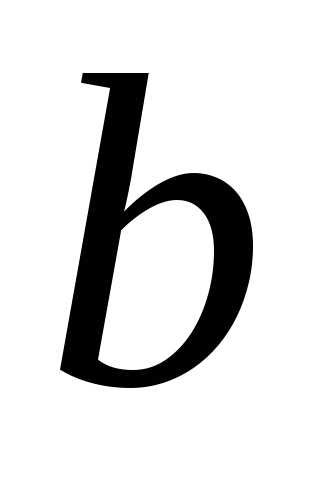 называются соответственнобольшой и малой
полуосями эллипса.
Заметим, что а >
называются соответственнобольшой и малой
полуосями эллипса.
Заметим, что а > 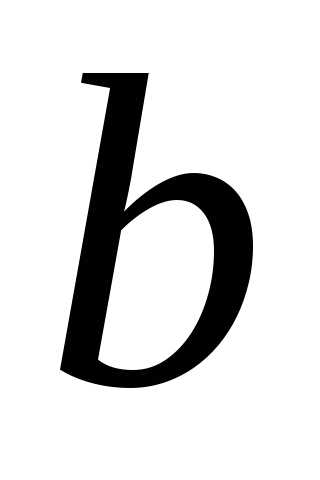 ,
еслиа <
,
еслиа < 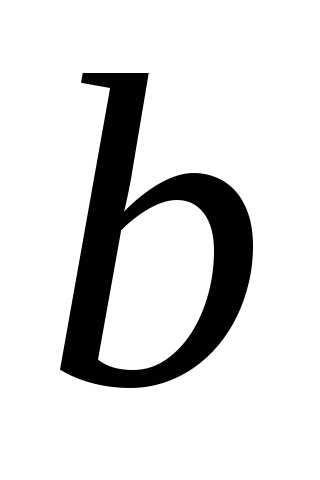 ,
то фокусы эллипса будут на осиОу,
если а =
,
то фокусы эллипса будут на осиОу,
если а = 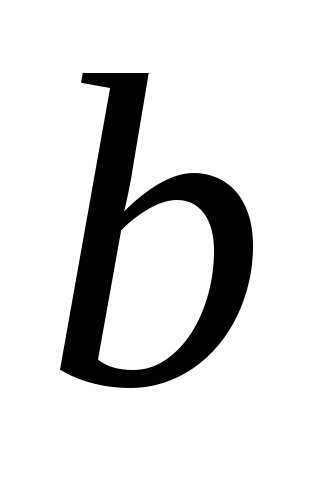 ,
то эллипс превращается в окружность.
,
то эллипс превращается в окружность.
Точки 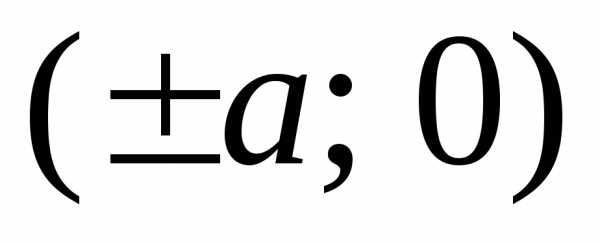 ,
,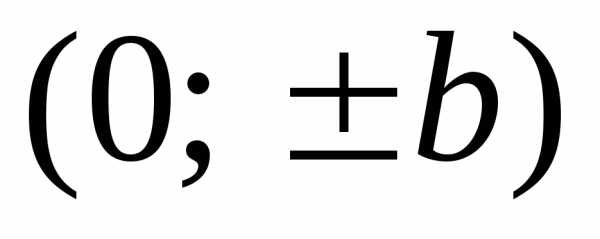 называютсявершинами
эллипса.
Отметим, что эллипс целиком расположен
внутри прямоугольника:
называютсявершинами
эллипса.
Отметим, что эллипс целиком расположен
внутри прямоугольника:
Так как
(6)
Эксцентриситетом эллипса называют отношение межфокусного расстояния 2с к длине большой оси 2а.
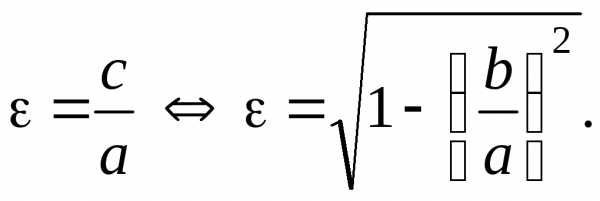 (7)
(7)
Следовательно,
причем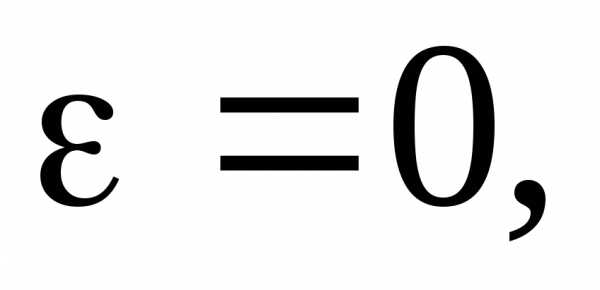 когда
когда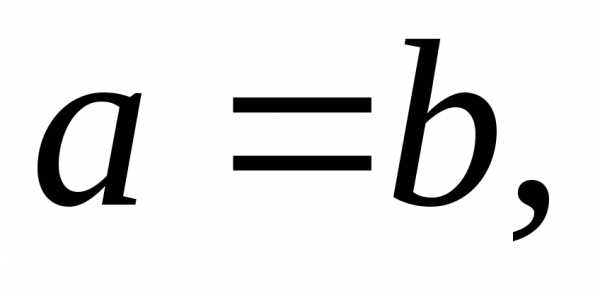 т. е. имеем окружность.
т. е. имеем окружность.
При  стремящемся к 1 эллипс становится более
вытянутым вдоль осиОх.
стремящемся к 1 эллипс становится более
вытянутым вдоль осиОх.
Выразим
фокальные радиусы точки 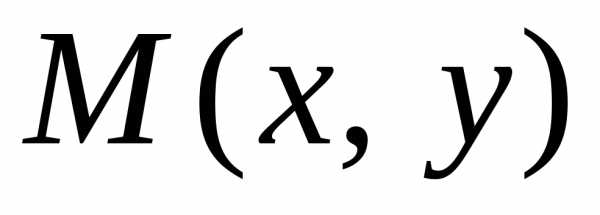 через эксцентриситет. Из (4):
через эксцентриситет. Из (4):
(8)
Из (3):
Значит,
подставив координаты точки 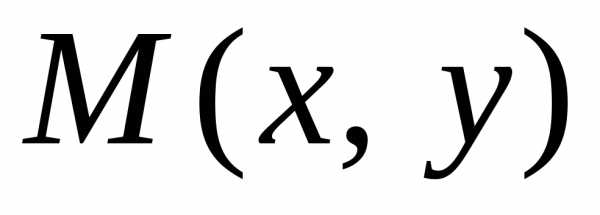 эллипса в уравнения (8), получаем фокальные
радиусы точкиМ.
эллипса в уравнения (8), получаем фокальные
радиусы точкиМ.
Прямые 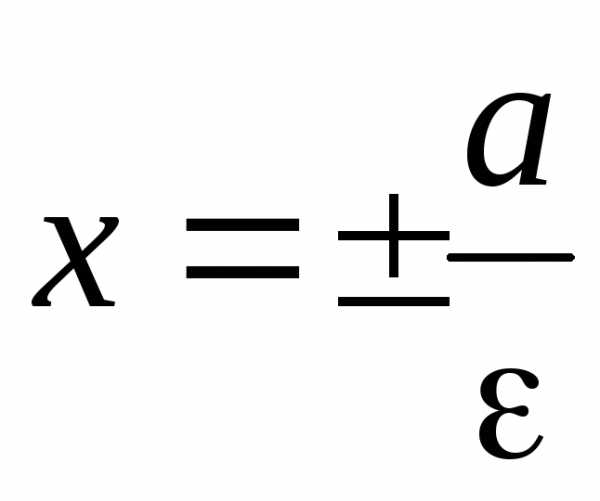 называютсядиректрисами
эллипса.
называютсядиректрисами
эллипса.
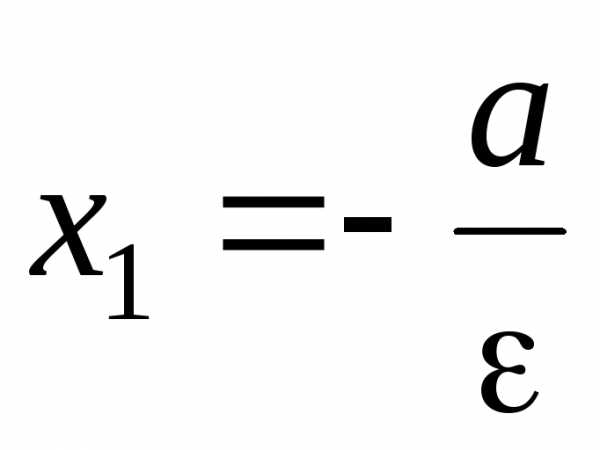 –левая
директриса,
–левая
директриса,
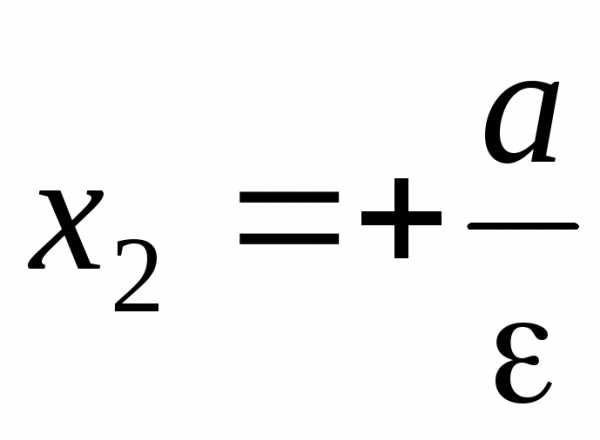 –правая
директриса.
–правая
директриса.
Заметим, что директрисы эллипса обладают следующим важным свойством:
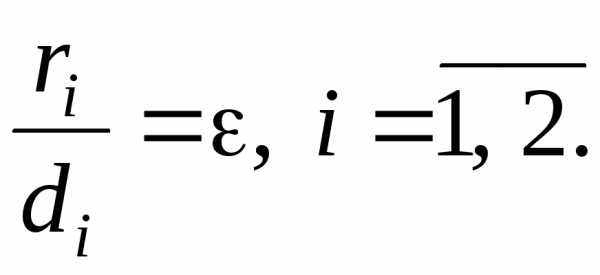 (9)
(9)
т. е. отношение расстояния ri от любой точки эллипса до фокуса к расстоянию di от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса.
2. Гипербола
Гиперболой называется множество точек плоскости,
для каждой из которых модуль разности
расстояний от которых до двух данных
точек 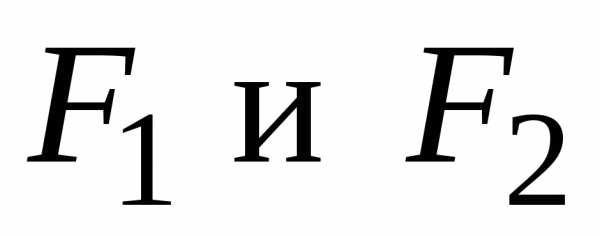 той же плоскости, называемых фокусами
гиперболы, есть заданная постоянная
величинаменьшая,
чем расстояние между фокусами
той же плоскости, называемых фокусами
гиперболы, есть заданная постоянная
величинаменьшая,
чем расстояние между фокусами
Пусть
фокусы гиперболы лежат на оси Ох,
причем
т. е.Заметим, что
Пусть 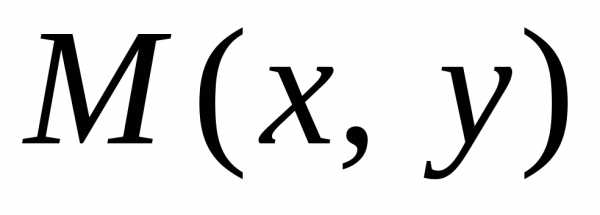 – произвольная точка гиперболы. Как и
ранее,–фокальные
радиусы точки М.
– произвольная точка гиперболы. Как и
ранее,–фокальные
радиусы точки М.
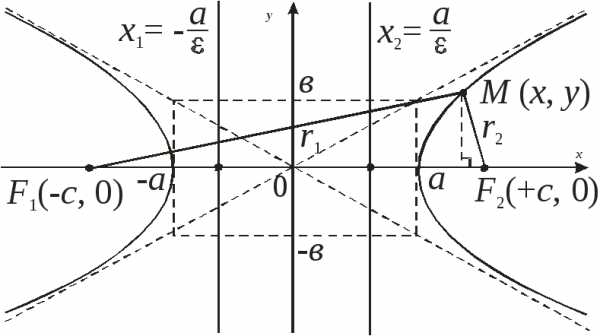
По определению гиперболы:
где
Следовательно,
(10)
Умножим (10) на
(11)
Сложим уравнения (10) и (11):
(12)
Возведем (12) в квадрат:
Пусть
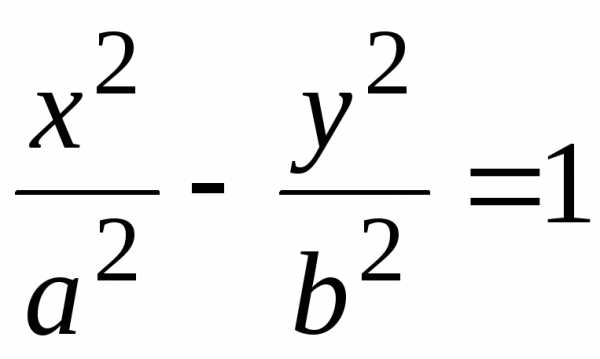
 (13)
(13)
(13) – каноническое уравнение гиперболы с центром в начале координат. Соответственно, уравнение
–
каноническое
уравнение гиперболы с центром в точке 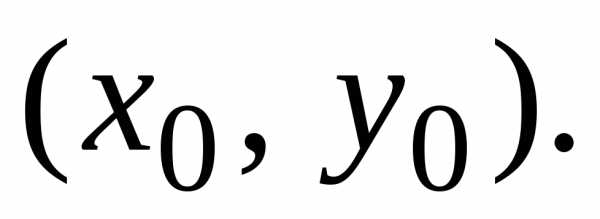
Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Гипербола с равными полуосями (a=b) называется равносторонней, ее каноническое уравнение имеет вид:
Точки 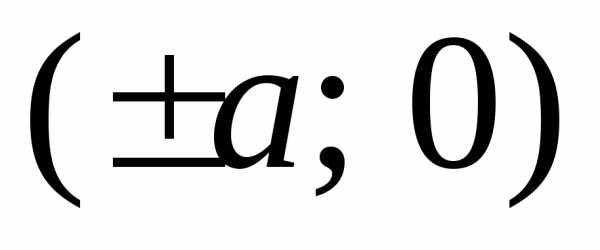 называются вершинами гиперболы.
называются вершинами гиперболы.
Заметим, что если уравнение гиперболы имеет вид
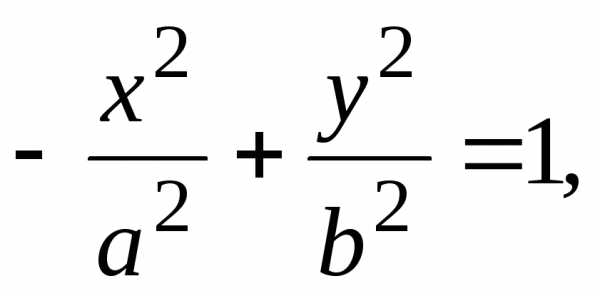 (14)
(14)
то фокусы гиперболы находятся на оси Оу, а ветви гиперболы будут направлены не влево и вправо, а вверх и вниз.
Так как , то(15)
Как
и в случае с эллипсом, эксцентриситетом гиперболы  называется отношение межфокусного
расстояния
называется отношение межфокусного
расстояния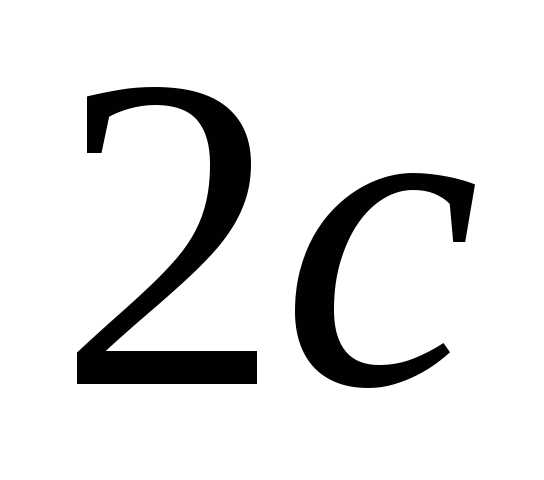 к длине действительной оси
к длине действительной оси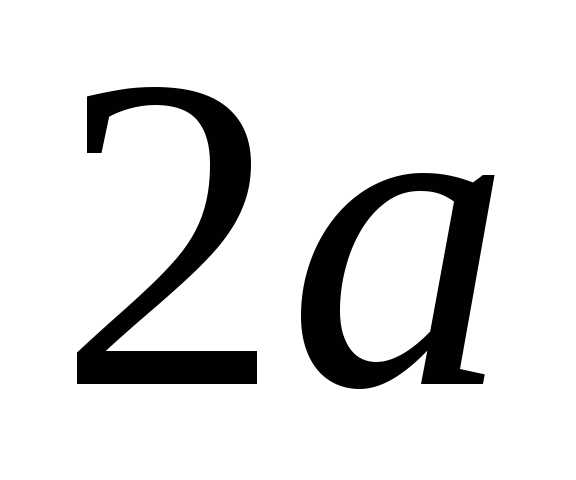 :
:
(16)
Следовательно, 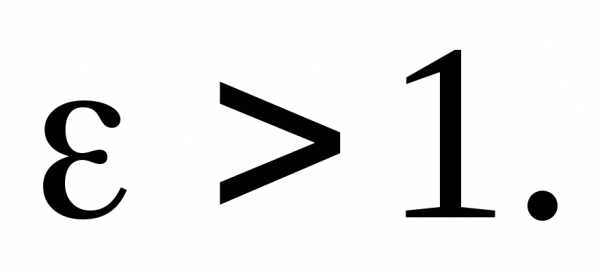
Выразим
фокальные радиусы точки 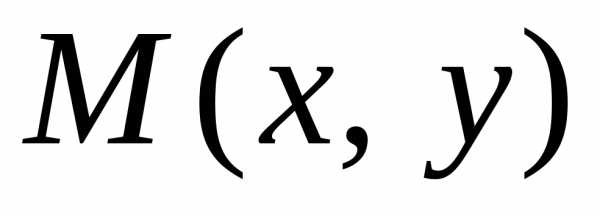 через эксцентриситет. Из (12)
через эксцентриситет. Из (12)
(17)
Прямые называются директрисами гиперболы. –левая директриса,
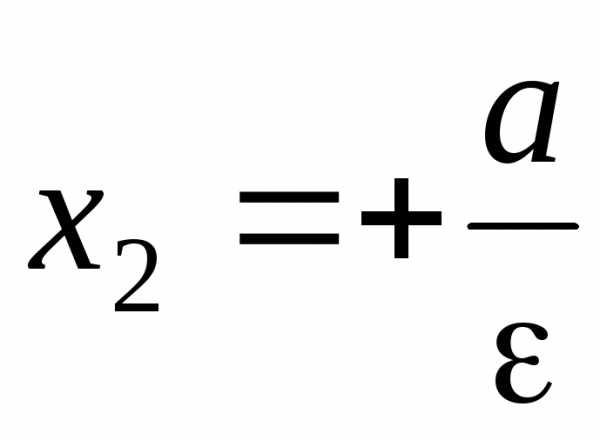 –правая
директриса.
–правая
директриса.
Директрисы гиперболы обладают тем же свойством, что и директрисы эллипса
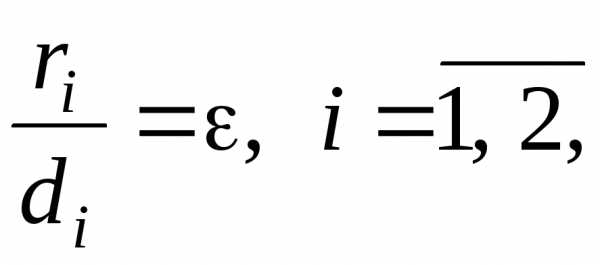 (18)
(18)
т.
е. отношение расстояния 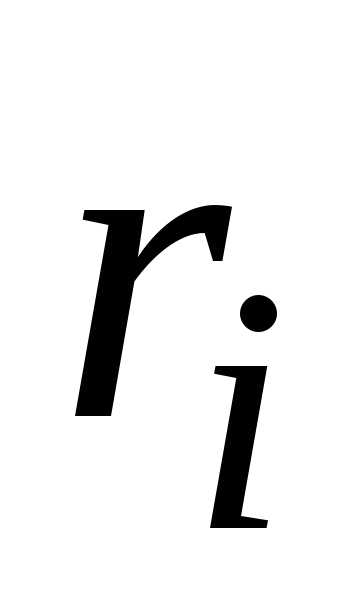 от любой точки гиперболы до фокуса к
расстоянию
от любой точки гиперболы до фокуса к
расстоянию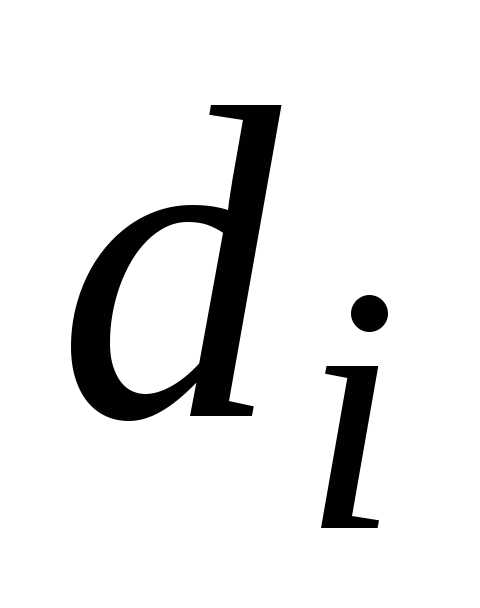 от нее до соответствующей директрисы
есть величина постоянная, равная
эксцентриситету гиперболы.
от нее до соответствующей директрисы
есть величина постоянная, равная
эксцентриситету гиперболы.
Для гиперболы важную роль играют также прямые
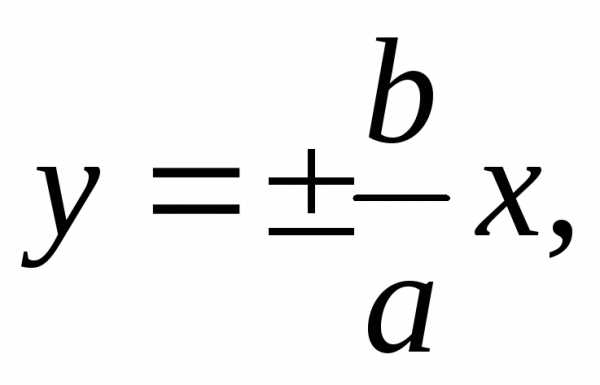 (19)
(19)
которые являются ее асимптотами, т. е. прямыми к которым график гиперболы неограниченно близко приближается, но не пересекает их. Заметим, что асимптоты гиперболы совпадают с диагоналями прямоугольника (если их продолжить)
Следует
отметить, что если уравнение гиперболы
имеет вид (14), т. е. ее фокусы находятся
на оси Оу,
то изменятся формулы для вычисления
фокальных радиусов, эксцентриситета,
директрис. Так 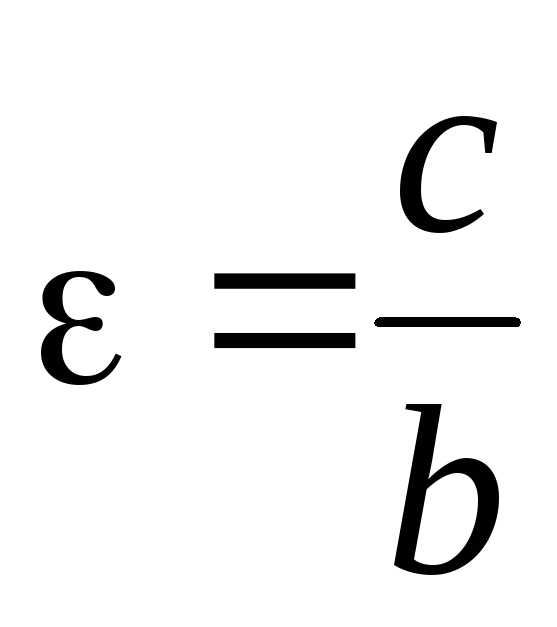 – эксцентриситет,
– эксцентриситет,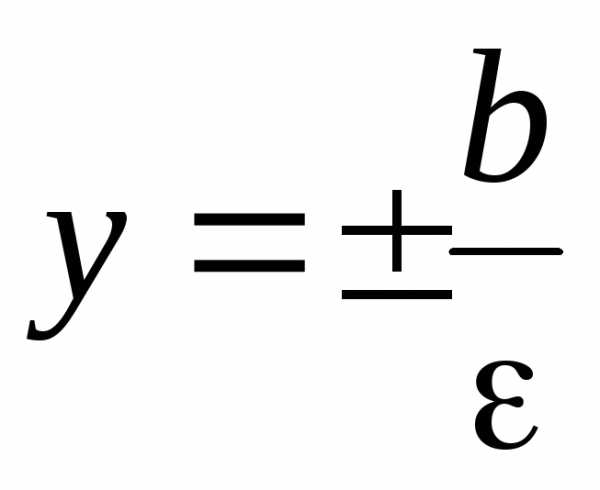 – уравнения директрис.
– уравнения директрис.
studfiles.net
42. Определение эллипса. Каноническое уравнение эллипса. Параметрические уравнения эллипса. Эксцентриситет эллипса.
Определение: Эллипсом называется множество точек на плоскости сумма расстояний от каждой из которых до двух заданных точек постоянна.
М – произвольная точка эллипса. О – середина F1F2. F1F2=2с. Сумма расстояний – 2a.Систему координат выберем таким образом чтобы Ох проходило через F1, F2 , а Оуделило пополам 2с.
F1M+ F2M=2a. — ур-е эллипса.
Преобразуем: ; 2a>2c, a>c,a2-c2=b2
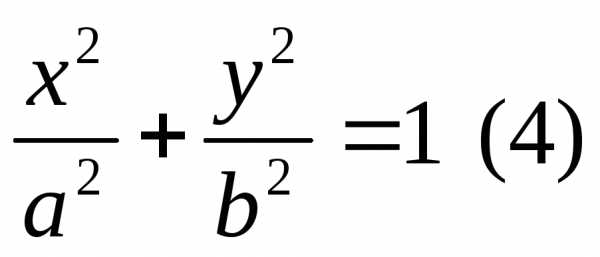
Очевидно
что каждая точка эллипса удовлетворяет
этому уравнению. Но т.к. в процессе
преобразований мы дважды возводили в
квадрат обе части то необходимо проверить
не получены ли лишние точки. Иначе говоря
нужно проверить что каждая точка
уравнения (4) принадлежит эллипсу.
Предварительно сделаем несколько
замечаний о форме линии, соответствующей
уравнению (4). 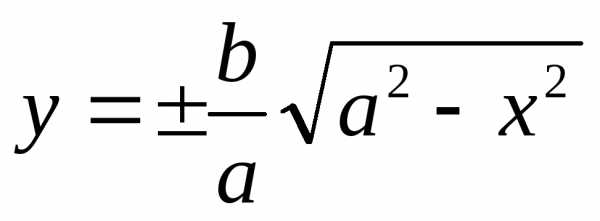 .
Из уравнений видно что прямая симметрична
относительно начала координат. С
возрастанием
.
Из уравнений видно что прямая симметрична
относительно начала координат. С
возрастанием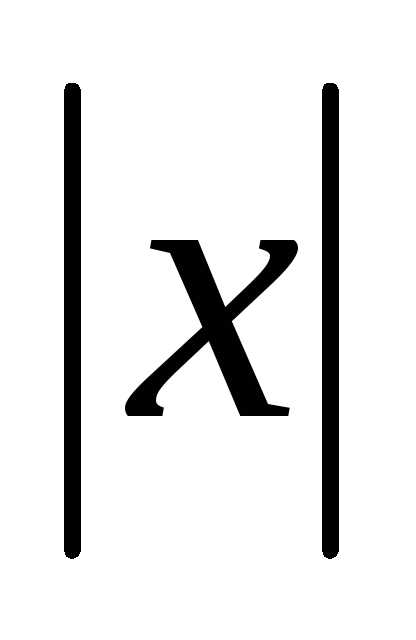 от 0 до а,
от 0 до а,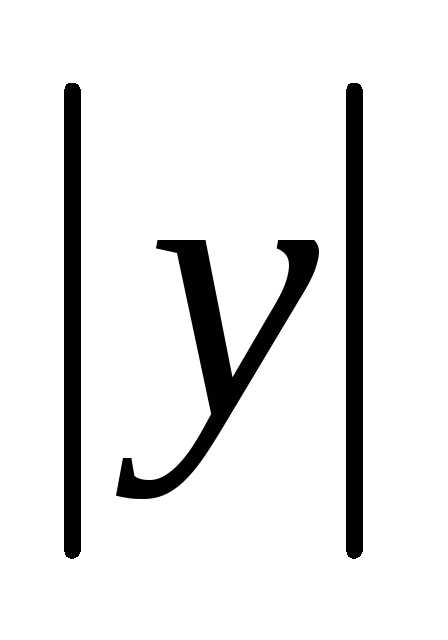 убывает
отb
до 0. Точки кривой лежат в прямоугольнике
убывает
отb
до 0. Точки кривой лежат в прямоугольнике
Проверим теперь что каждая точка линии определяемая полученным уравнением принадлежит эллипсу. Для этого надо показать что если координаты точки М(х0,у0) удовлетворяют (4) то F1M+ F2M=2a.
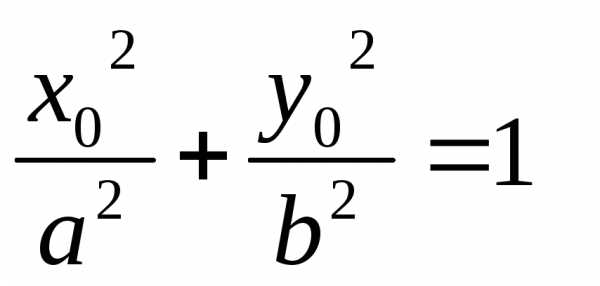
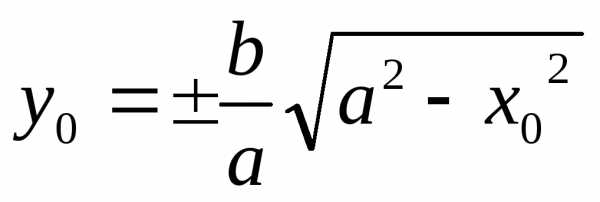
Таким образом лишних точекне появилось.
Числа  и
и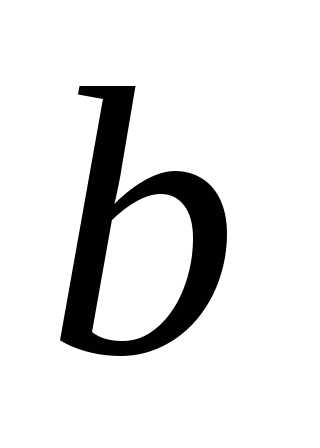 — большая и малая полуоси эллипса.F1, F2 – фокусы
эллипса.
— большая и малая полуоси эллипса.F1, F2 – фокусы
эллипса.
При 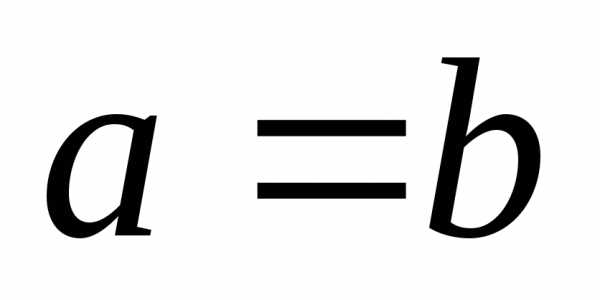 получаем- уравнение окружности.
получаем- уравнение окружности.
Параметрические
уравнения эллипса:
Построим две окружности радиусом  и
и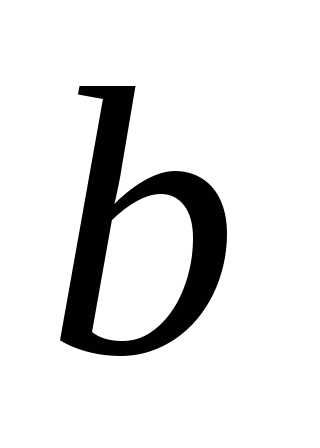 с центром в начале координат. Из точки
О проведем луч наклоненный к Ох под
угломt.
Проведем горизонтальную прямую через
В и вертикальную через А. Изменяя t
от 0 до 2 π точка М опишет эллипс.
с центром в начале координат. Из точки
О проведем луч наклоненный к Ох под
угломt.
Проведем горизонтальную прямую через
В и вертикальную через А. Изменяя t
от 0 до 2 π точка М опишет эллипс. 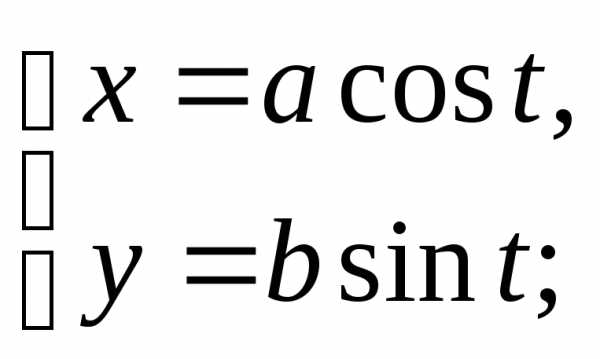 — парам-е уравнения эллипса. При а=b
получим
— парам-е уравнения эллипса. При а=b
получим 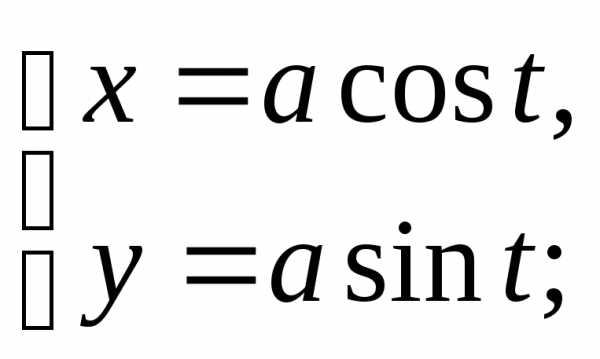 — параметрические уравнения окружности.
— параметрические уравнения окружности.
Определение. Эксцентриситет эллипса – отношение
половины расстояния между фокусами к
длине его большей оси: 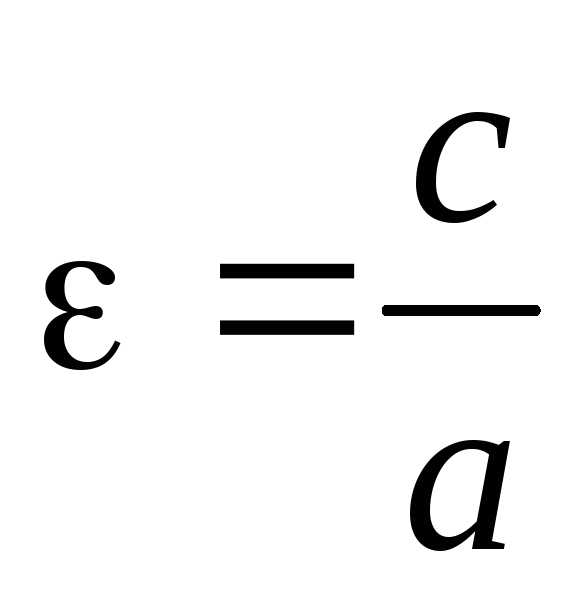 .
.
Так
как  ,
следовательно
,
следовательно < 1.,
следовательно,
< 1.,
следовательно,
Замечание: Эксцентриситет
эллипса можно рассматривать как меру
его вытянутости. Чем больше эксцентриситет
тем меньше отношение 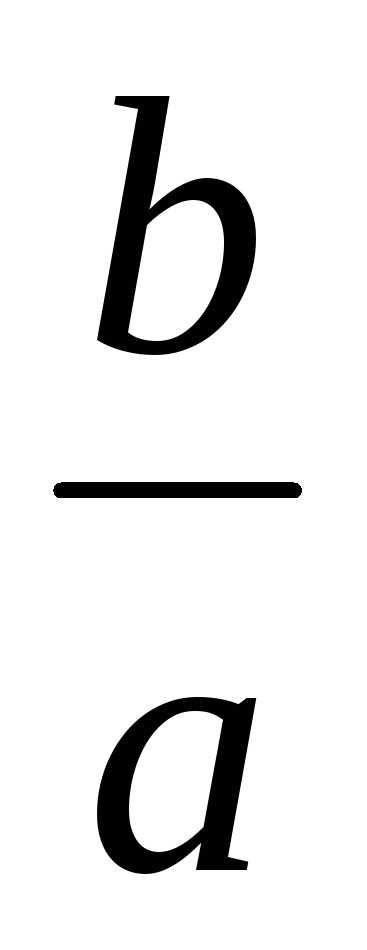 (малой
оси эллипса к его большой полуоси).
(малой
оси эллипса к его большой полуоси).
ксцентриситет гиперболы.
Определение: Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная и не равная 0.
Выберем опять оси координат и начало координат посередине отрезка F1F2. Расстояние F1F2 равно 2с. А разность расстояний обозначим через 2а.
Из определения имеем: . 2а<2c, а<c
Имеем:
возведем в квадрат.
еще раз в квадрат. После простых преобразований получим:
Поделив
обе части на 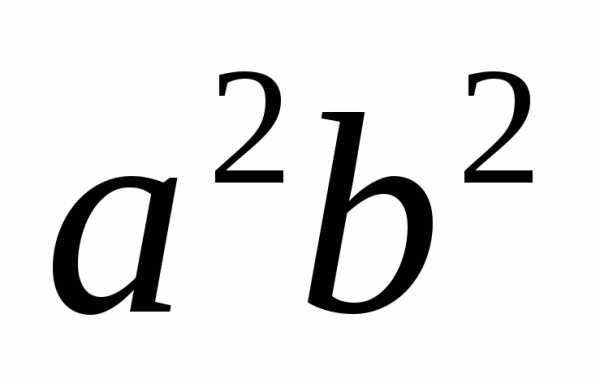 получим:
получим: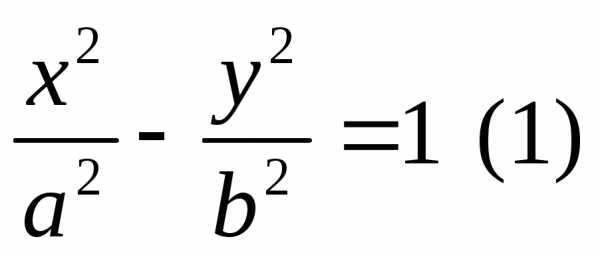 .
.
Как и в случае эллипса необходимо проверить что несмотря на двукратное возведение в квадрат мы не получим лишних точек. И следовательно уравнение (1) – уравнение гиперболы.
Предварительно
отметим некоторые свойства линии
определяемой уравнением (1). Из уравнения
(1) следует что 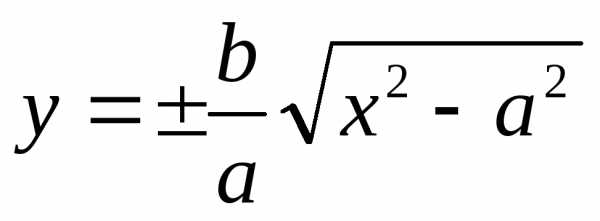 .
.
Линия
(1) симметрична относительно осей
координат и относительно начала
координат. Видно что 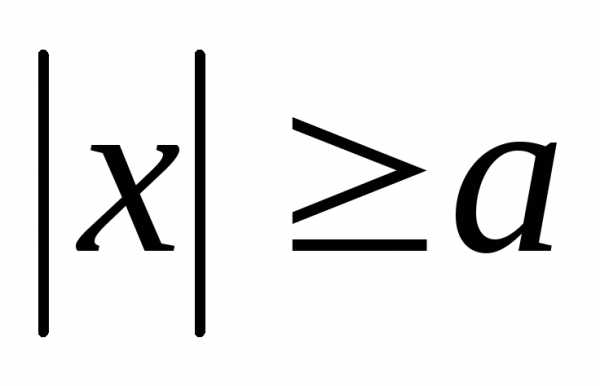 .
Значит в полосеточек кривой нет. Следовательно кривая
состоит из двух отдельных ветвей, одна
из которых расположена в полуплоскости
.
Значит в полосеточек кривой нет. Следовательно кривая
состоит из двух отдельных ветвей, одна
из которых расположена в полуплоскости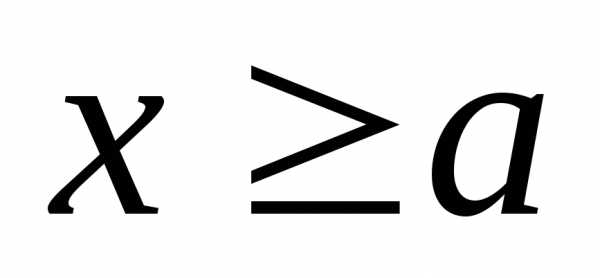 (правая
ветвь), а вторая – в полуплоскости —
(правая
ветвь), а вторая – в полуплоскости —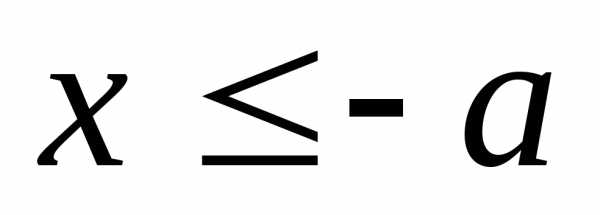 (левая
ветвь).
(левая
ветвь).
Пусть
М(х0,у0)
– произвольная точка линии, определяемая
уравнением (1). 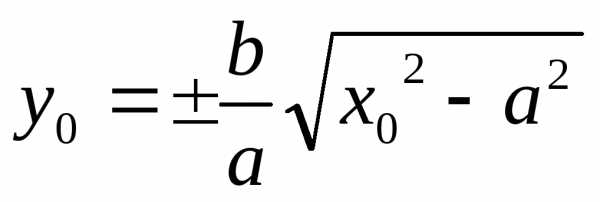 .
Если мы докажем что,
то тем самым мы докажем что уравнение
(1) является уравнением гиперболы.
.
Если мы докажем что,
то тем самым мы докажем что уравнение
(1) является уравнением гиперболы.
далее
в эту формулу подставляем у0, раскрываем
скобки, приводим подобные и учитывая
что
выделим под каждым корнем полные
квадраты. В результате получим:.
Пусть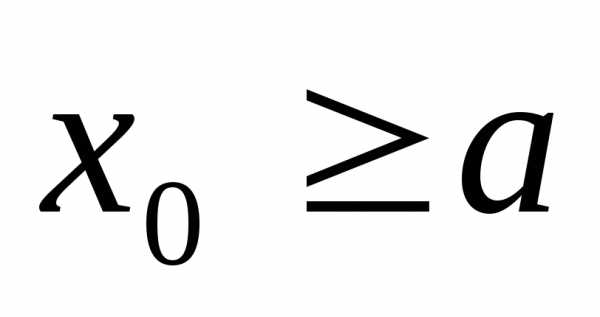 (для
точек правой ветви), тогда.
(для
точек правой ветви), тогда.
При 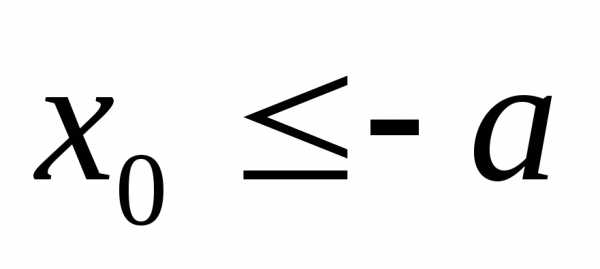 (для
точек левой ветви) тогда.
(для
точек левой ветви) тогда.
Таким образом . Получаем что. Значит уравнение (1) – это уравнение гиперболы. Лишних точек не получилось.
Число а называется вещественной полуосью гиперболы, число b – мнимой полуосью. Точки пересечения гиперболы с ее осью симметрии называются вершинами гиперболы. Точки F1 и F2 фокусы гиперболы.
О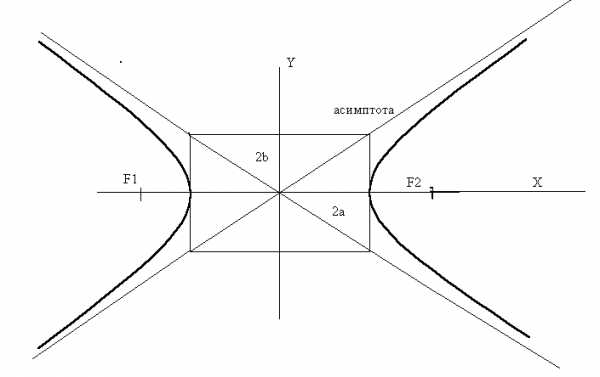 тметим
еще одну особенность формулы гиперболы.
Рассмотрим вместе с гиперболой пару
прямых
тметим
еще одну особенность формулы гиперболы.
Рассмотрим вместе с гиперболой пару
прямых 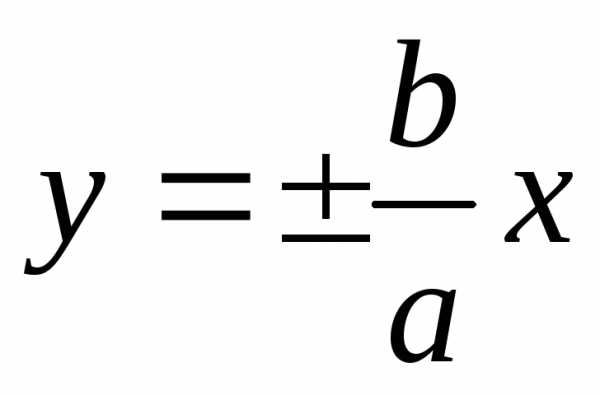 .
В первой четверти при одной и той же
абсциссе ординаты точек гиперболы
меньше соответствующих ординат
соответствующих точек прямой, т.к.
. ,
т.к.
.
Т.е. точки гиперболы при неограниченном
увеличении абсцисс как угодно близко
подходят к соответствующим точкам
прямой
.
В первой четверти при одной и той же
абсциссе ординаты точек гиперболы
меньше соответствующих ординат
соответствующих точек прямой, т.к.
. ,
т.к.
.
Т.е. точки гиперболы при неограниченном
увеличении абсцисс как угодно близко
подходят к соответствующим точкам
прямой 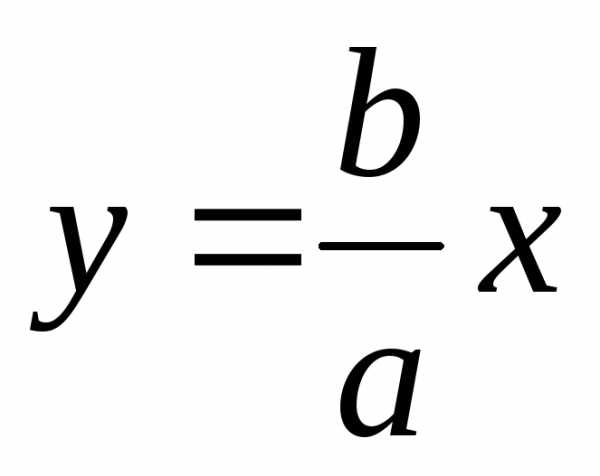 .
В силу симметрии точки гиперболы в
других четвертях неограниченно
приближаются к точкам прямых, когда
.
В силу симметрии точки гиперболы в
других четвертях неограниченно
приближаются к точкам прямых, когда 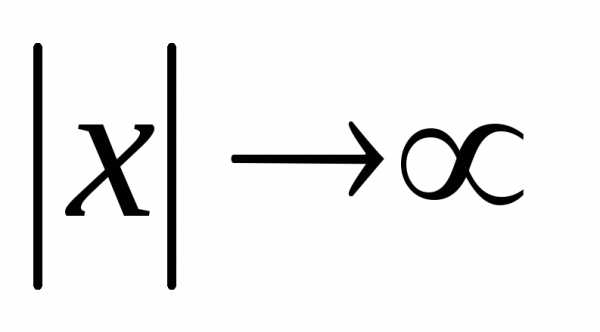 .
.
Прямые 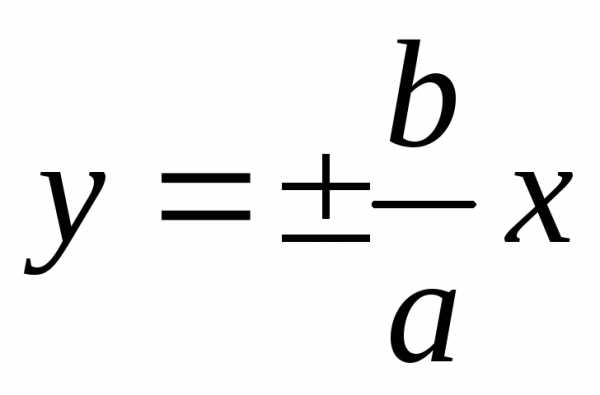 —
асимптоты гиперболы. Асимптоты гиперболы
направлены по диагоналям прямоугольника
со сторонами 2а и 2b,
расположенного симметрично относительно
осей симметрии гиперболы.
—
асимптоты гиперболы. Асимптоты гиперболы
направлены по диагоналям прямоугольника
со сторонами 2а и 2b,
расположенного симметрично относительно
осей симметрии гиперболы.
Если а=b то уравнение гиперболы принимает вид . Такая гипербола называется равнобочной.
Эксцентриситет гиперболы. Пусть с- половина расстояния между фокусами гиперболы, а – действительная полуось гиперболы.
Определение: Эксцентриситетом
гиперболы называется величина 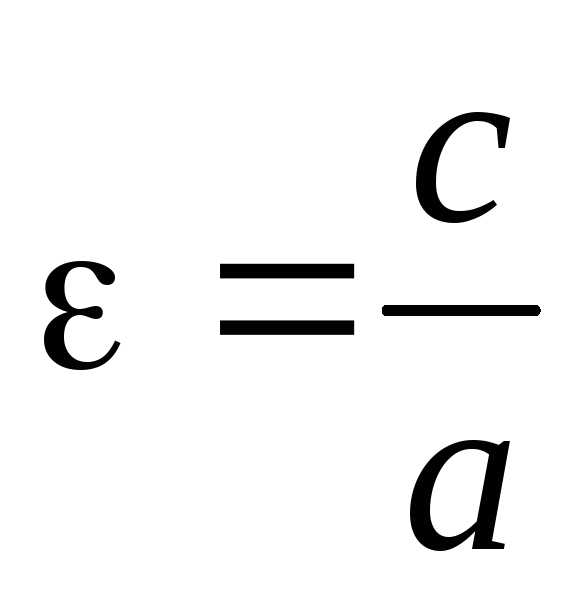 .
.
Учитывая связь между c,a,b получим: . Эксцентриситет гиперболы больше 1.
Замечание: Эксцентриситет
гиперболы можно рассматривать как
величину раствора угла между его
асимптотами, т.к. 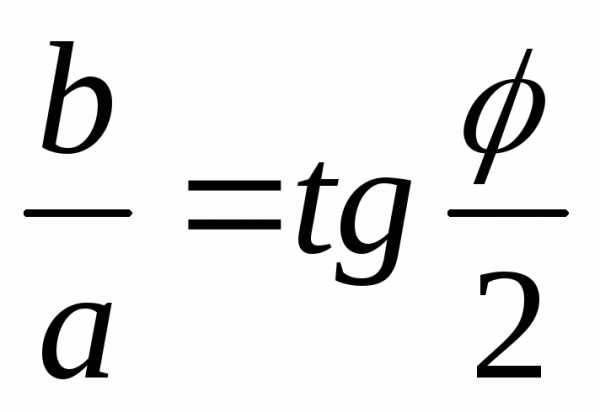 ,
где φ – величина угла между асимптотами
гиперболы.
,
где φ – величина угла между асимптотами
гиперболы.
studfiles.net
23. Каноническое уравнение эллипса.
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
. (4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любоерешение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и изопределения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.
1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
.
Воспользуемся формулой расстояния между двумя точками накоординатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
, , откуда получаем:
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
.
Сокращая, получаем:
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
.
Возводим в квадрат
.
Раскрываем скобки и сокращаем на :
,
откуда получаем:
.
Используя равенство (2), получаем:
.
Разделив последнее равенство на , получаем равенство (4), ч.т.д.
2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.
Тогда из (4) следует:
.
Подставляем это равенство в выражение для фокальных радиусов точки М:
.
Здесь мы воспользовались равенством (2) и (3).
Таким образом, . Аналогично, .
Теперь заметим, что из равенства (4) следует, что
или и т.к. , то отсюда следует неравенство:
.
Отсюда, в свою очередь, следует, что
или и
, . (5)
Из равенств (5) следует, что , т.е. точка М(х, у) является точкой эллипса, ч.т.д.
Теорема доказана.
24. Каноническое уравнение гиперболы.
Теорема. В канонической для гиперболы системе координат уравнение гиперболы имеет вид:
. (4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы
докажем, что координаты любой точки, лежащей на гиперболе, удовлетворяют
уравнению (4). На втором этапе мы докажем, что любое решение уравнения
(4) дает координаты точки, лежащей на гиперболе. Отсюда будет
следовать, что уравнению (4) удовлетворяют координаты тех и только тех
точек координатной плоскости, которые лежат на гиперболе. Отсюда и из
определения уравнения кривой будет следовать, что уравнение (4)
является уравнением гиперболы.
1) Пусть точка М(х, у) является точкой гиперболы, т.е. модуль разности ее фокальных радиусов равен 2а:
или
Воспользуемся
формулой расстояния между двумя точками на координатной плоскости и
найдем по этой формуле фокальные радиусы данной точки М:
, , откуда получаем:
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
.
Сокращая, получаем:
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
.
Возводим в квадрат
.
Раскрываем скобки и сокращаем на :
,
откуда получаем:
.
Используя равенство (2), получаем:
.
Разделив последнее равенство на , получаем равенство (4), ч.т.д.
2)
Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х,
у) – соответствующая точка на координатной плоскости Оху.
Тогда из (4) следует:
.
Подставляем это равенство в выражение для фокального радиуса точки М:
.
Здесь мы воспользовались равенством (2) и (3).
Таким образом,
.
Аналогично,
.
Теперь заметим, что из равенства (4) следует, что
или . Умножим неравенство
на :
,
.
Получаем:
или .
Отсюда следует, что числа х, и имеют одинаковые знаки, т.е. при и ,
а при и , а значит
и .
, т.е. , что означает принадлежность точки М(х, у) гиперболе, ч.т.д.
Теорема доказана.
studfiles.net
Лекция 2. Линии второго порядка, заданные каноническими уравнениями.
§ 102. Эллипс и его каноническое уравнение
Эллипсом называется геометрическое место точек, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2а, большее, чем расстояние 2с между фокусами.
Пусть М – произвольная точка эллипса, а  и
и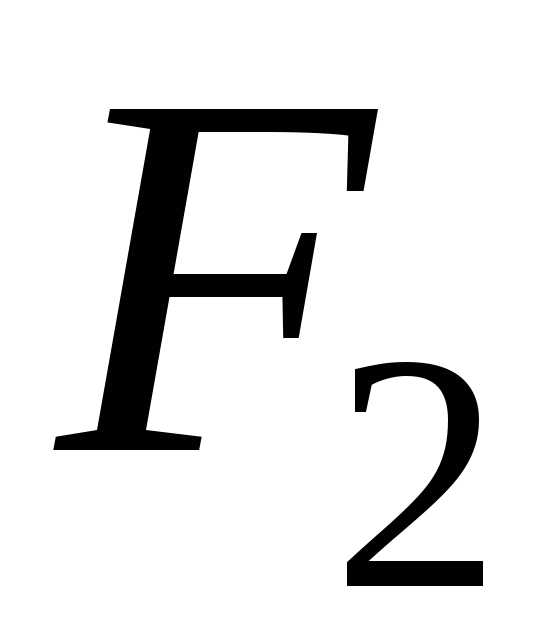 — его фокусы. Отрезки
— его фокусы. Отрезки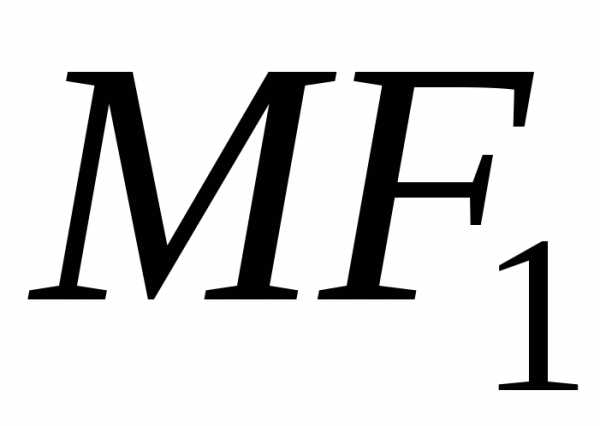 и
и так же, как и длины этих отрезков,
называются фокальными радиусами точкиМ эллипса. В силу данного определения
эллипса (см. рис.1)
так же, как и длины этих отрезков,
называются фокальными радиусами точкиМ эллипса. В силу данного определения
эллипса (см. рис.1)
(1)
Из
определения эллипса вытекает следующий
способ его вычерчивания. Воткнем в
чертежную доску две булавки и накинем
на них замкнутую нить, длина которой
равна
.
Натянем нить карандашом и будем
передвигать его, держа нить все время
натянутой. Карандаш опишет эллипс, так
как суммарасстояний от острияМ карандаша до точек  и,
в которые воткнуты булавки, во время
движения острия карандаша по бумаге не
будет изменяться, оставаясь равной
и,
в которые воткнуты булавки, во время
движения острия карандаша по бумаге не
будет изменяться, оставаясь равной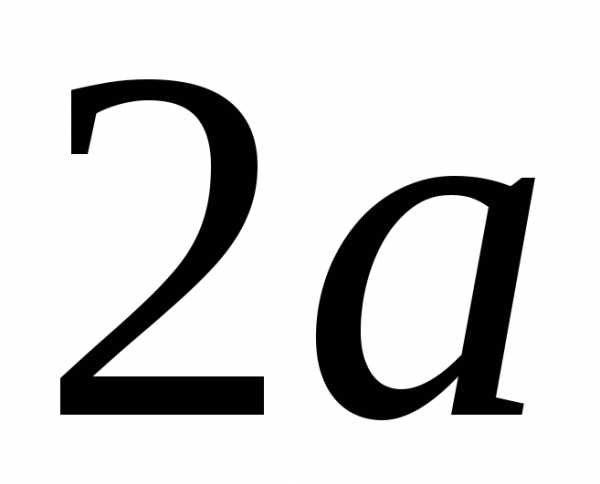 .
.
Введем
на плоскости прямоугольную систему
координат, принимая середину отрезка 
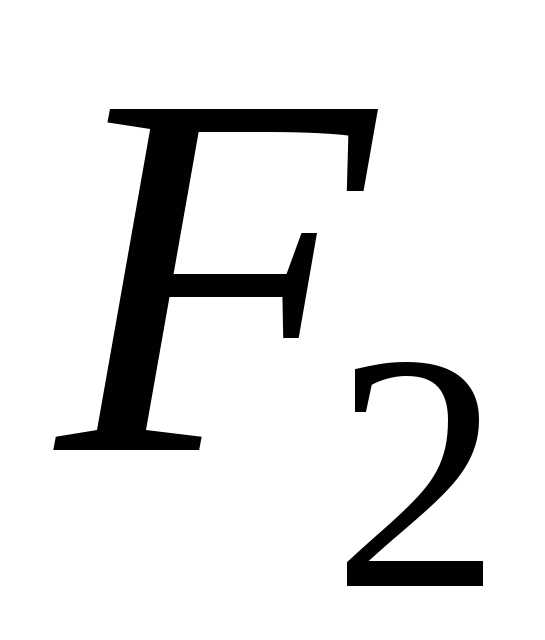 за начало координат, а за осьОх прямую
за начало координат, а за осьОх прямую 
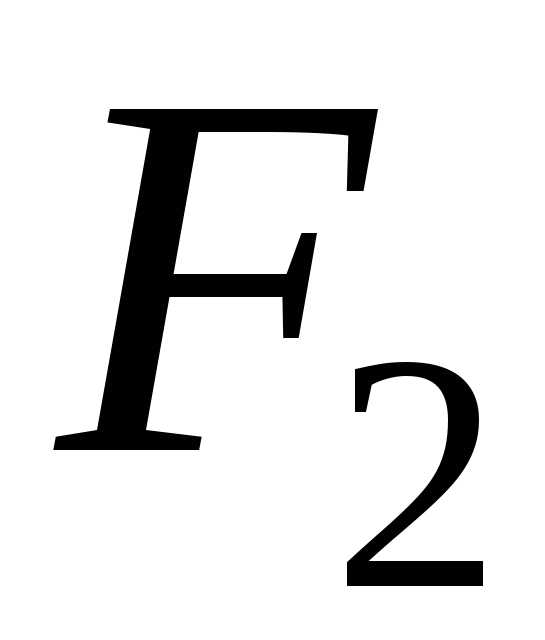 ,
ориентированную от точки
,
ориентированную от точки к точке
к точке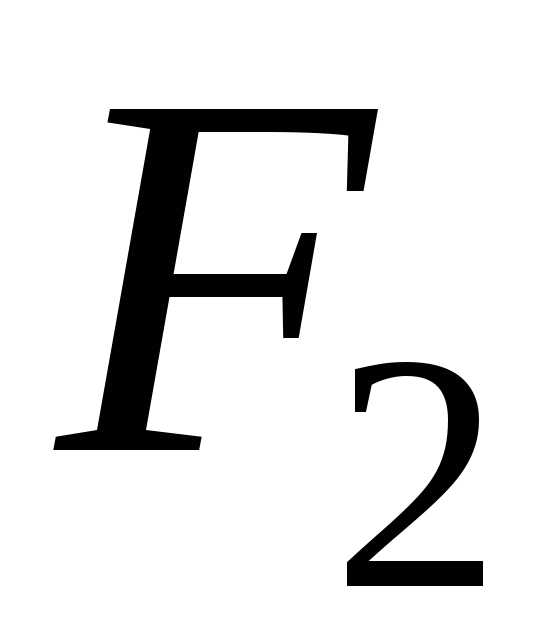 .
В выбранной системе координат фокус
.
В выбранной системе координат фокус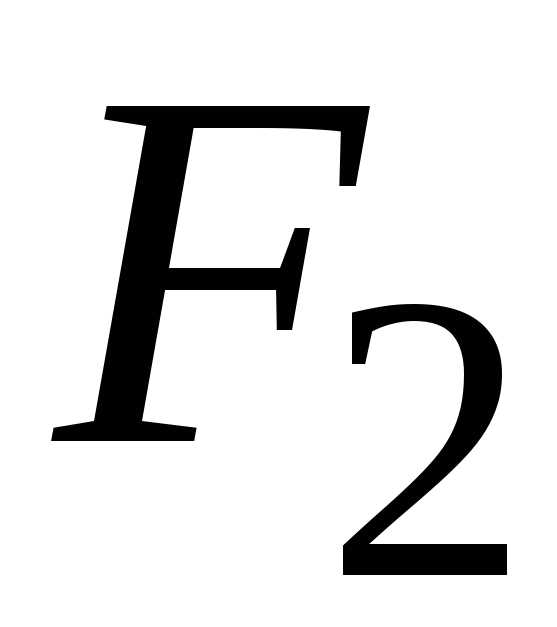 будет иметь координаты (с,
0), а фокус
будет иметь координаты (с,
0), а фокус  — координаты (-с,
0). Обозначая координаты точки М эллипса через х и у,
будем иметь
— координаты (-с,
0). Обозначая координаты точки М эллипса через х и у,
будем иметь
и соотношении (1) принимает вид:,
или . (2)
Возводя обе части (2) в квадрат, получим
или .
Возводя обе части этого уравнения в квадрат, получим
,
или .
Так как
по условию
,
то.
Обозначая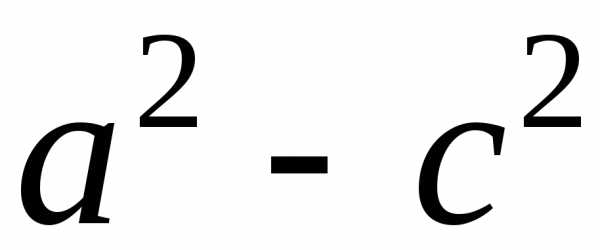 через
через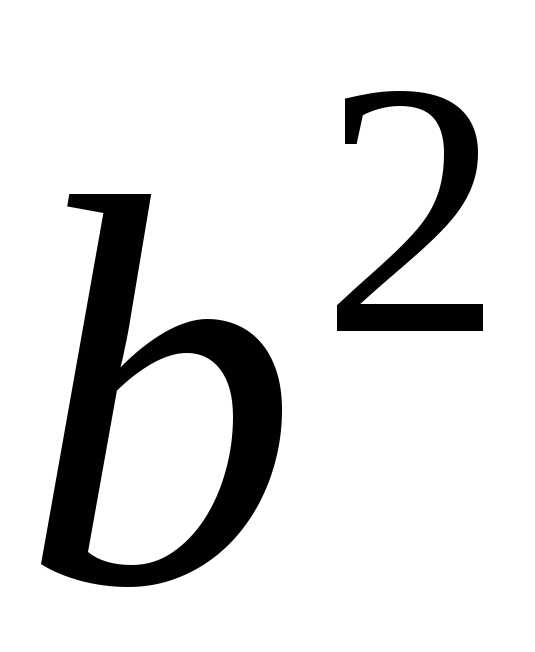
, (3)
получим
или 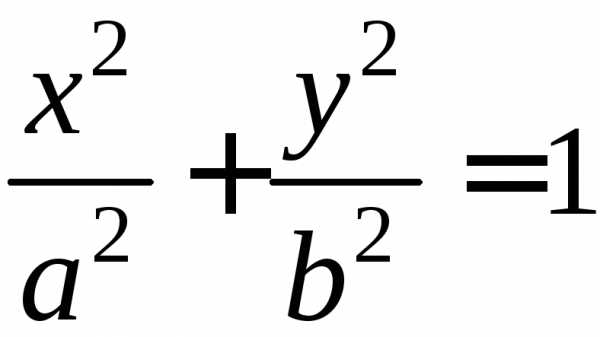 .
(4)
.
(4)
Мы доказали, что координаты любой токи М(х,у) эллипса удовлетворяют уравнению (4). Однако уравнение (4) еще нельзя назвать уравнением эллипса, так как не доказано обратное предложение, а именно: если числа х и у удовлетворяют уравнению (4), то точка М с координатами х и у удовлетворяет соотношению , т.е. лежит на эллипсе.
Докажем это. Пусть координаты точки М(х,у) удовлетворяют уравнению (4). Тогда
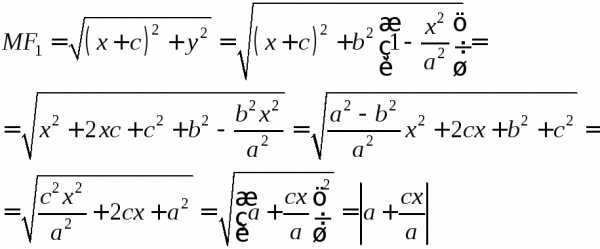 и,
аналогично,
и,
аналогично, 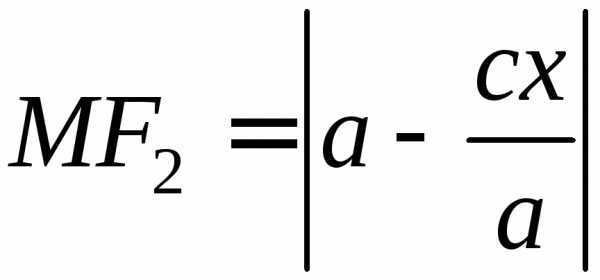 .
.
Далее,
поскольку 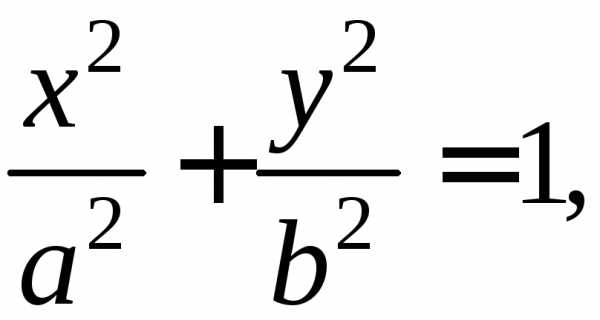
то 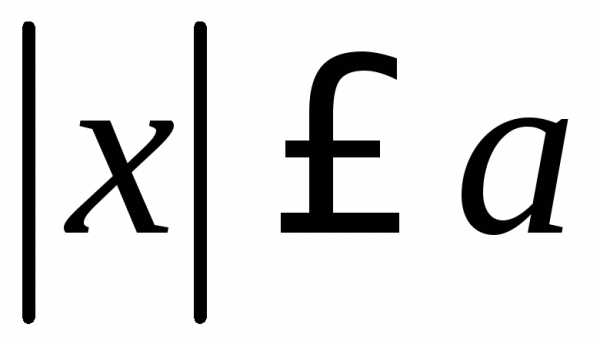 ,
а так както
,
а так както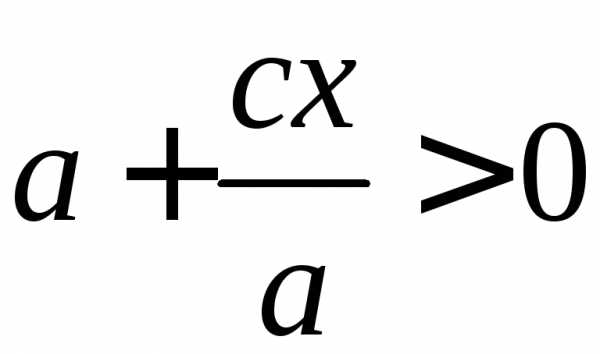 и
и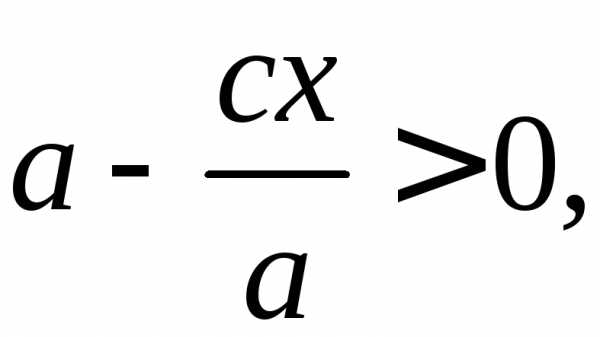 следовательно,
следовательно,
, (5)
откуда .
Таким образом, (4) есть уравнение эллипса, так как доказано, что координаты любой точки М эллипса, т. е. любой точки, для которой
,
удовлетворяют уравнению (4), и, обратно, если два числа х и у удовлетворяют уравнению (4), то точка М с этими координатами х и у удовлетворяет соотношению ,
т. е. лежит на эллипсе.
Уравнение 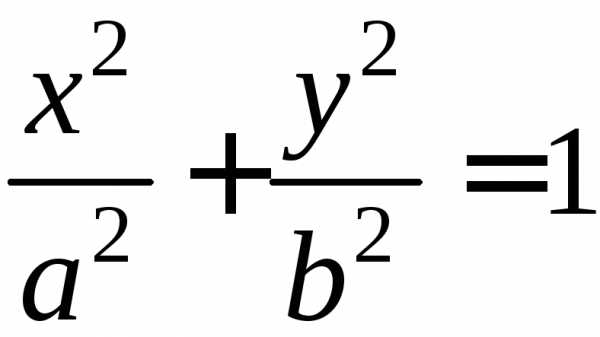
называется каноническим уравнение эллипса.
§ 103. Исследование формы эллипса
Так как в каноническое уравнение эллипса координаты х и у входят в четной степени (именно во второй), то если на эллипсе
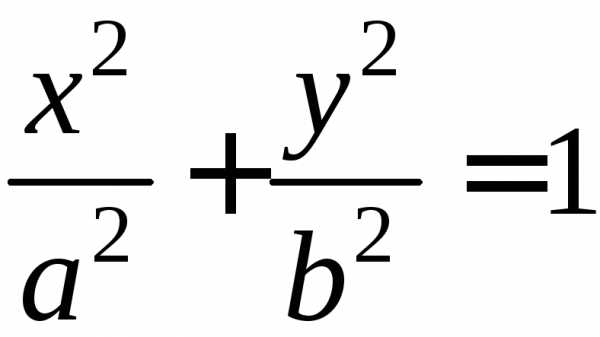 (1)
(1)
лежит точка М(х,у), т. е. координаты этой точки удовлетворяют уравнению (1), то на том же эллипсе лежат точки и, симметричные с точкойМ относительно осей Ох и Оу, и точка , симметричная с точкойМ относительно начала координат. Поэтому оси координат Ох и Оу для
э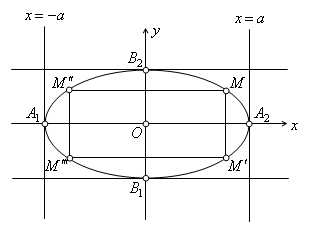 ллипса,
заданного каноническим уравнением (1)
являются осями симметрии, а начало
координат – центром симметрии. Из
уравнения эллипса
ллипса,
заданного каноническим уравнением (1)
являются осями симметрии, а начало
координат – центром симметрии. Из
уравнения эллипса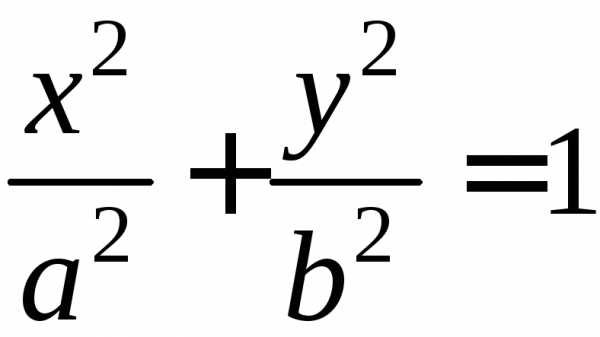 следует, что для координат любой его
точки имеют место соотношения
следует, что для координат любой его
точки имеют место соотношения
Геометрически это значит, что эллипс расположен внутри прямоугольника, сторонами которого являются прямые
Точки
пересечения эллипса с его осями симметрии
называются вершинами эллипса. Таким образом, эллипс (1) имеет 4 вершины:
,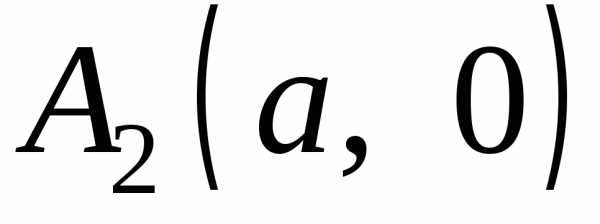 ,,
,,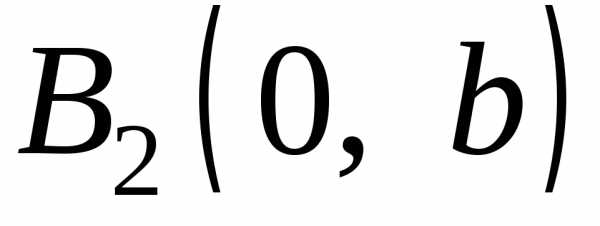 .
.
Полуосью эллипса называется отрезок (а также длина этого отрезка), одним концом которого является центр симметрии эллипса, а другим – одна из его вершин; а называется большей полуосью эллипса, а b – меньшей полуосью.
Отрезок 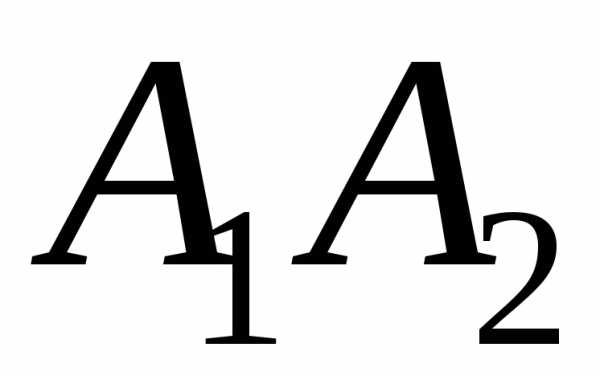 — большая ось эллипса.
— большая ось эллипса.
Отрезок 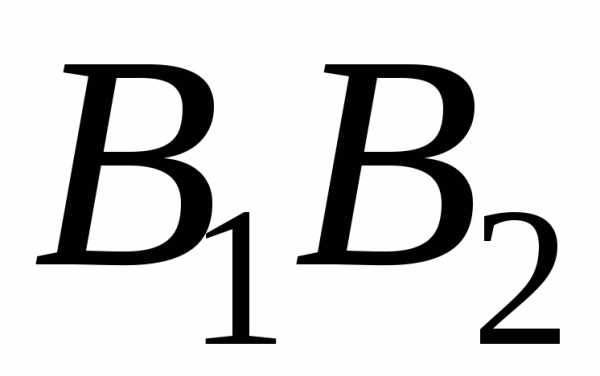 — меньшая ось эллипса.
— меньшая ось эллипса.
Замкнутая
линия является выпуклой, если любая
прямая пересекает ее не более чем в двух
точках. Эллипс есть выпуклая замкнутая линия,
так как, решая уравнение (1) эллипса
совместно с уравнением прямой
или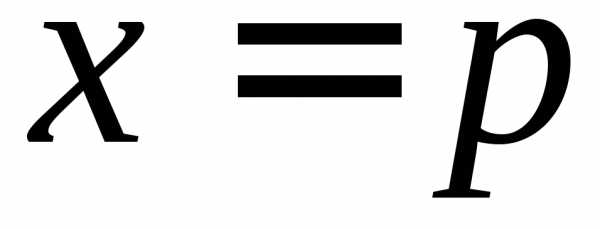 ,
получим уравнение второй степени
относительнох или у,
значит, любая прямая пересекает эллипс
не более чем в двух точках.
,
получим уравнение второй степени
относительнох или у,
значит, любая прямая пересекает эллипс
не более чем в двух точках.
Итак, эллипс – замкнутая выпуклая линия, имеющая центр симметрии и две (взаимно перпендикулярные) оси симметрии.
Условимся
уравнение 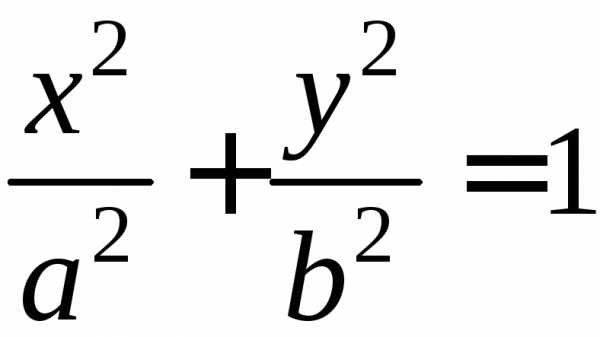 называть каноническим уравнением
эллипса и в том случае, когдаа = b и когда a < b.
называть каноническим уравнением
эллипса и в том случае, когдаа = b и когда a < b.
В случае а = b уравнение примет вид
,
т.е.
является уравнением окружности радиуса а с центром в начале координат. Таким
образом, мы рассматриваем окружность
как частный случай эллипса. Этот частный
случай соответствует совпадению фокусов  и
и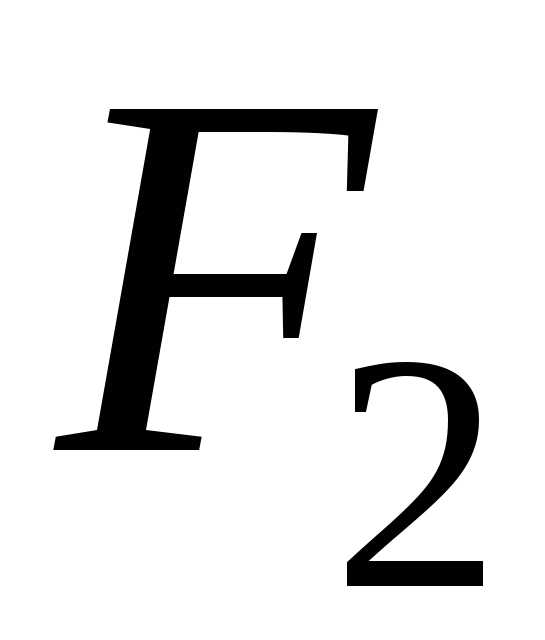 с центром окружности.
с центром окружности.
В случае а < b большей полуосью будет b,
а меньшей — а.
Фокусы будут расположены на оси Оу на расстоянии 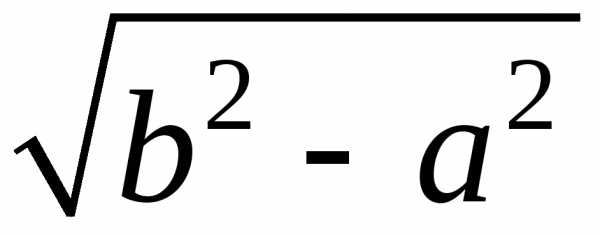 от центра эллипса.
от центра эллипса.
Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:
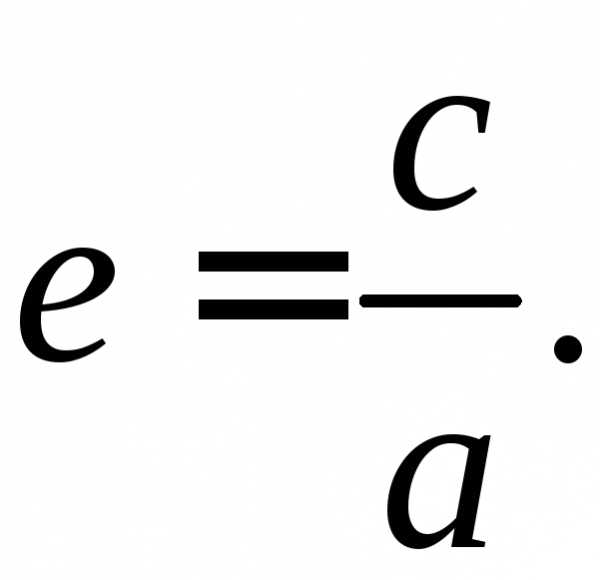
Так как тот. е. эксцентриситет эллипса есть неотрицательное число, меньшее единицы.
Отметим,
что 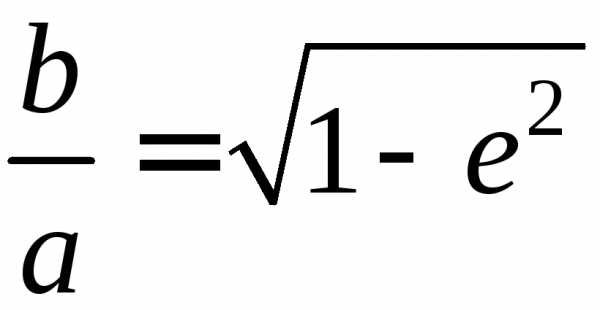 (поскольку).
(поскольку).
Следовательно, эксцентриситет определяется отношением полуосей эллипса, и, обратно, отношение полуосей эллипса определяет его эксцентриситет.
Если
эксцентриситет равен нулю е = 0, то а = b и эллипс является окружностью. Чем ближе
эксцентриситет е к 1, тем меньше 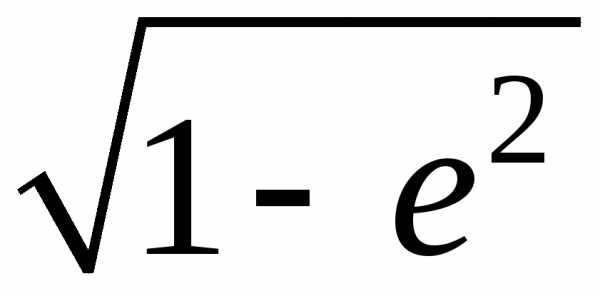 и, значит, тем меньше отношение меньшей
полуоси к большей. Таким образом,
эксцентриситет характеризует степень
«вытянутости» эллипса.
и, значит, тем меньше отношение меньшей
полуоси к большей. Таким образом,
эксцентриситет характеризует степень
«вытянутости» эллипса.
Вспоминая формулы:
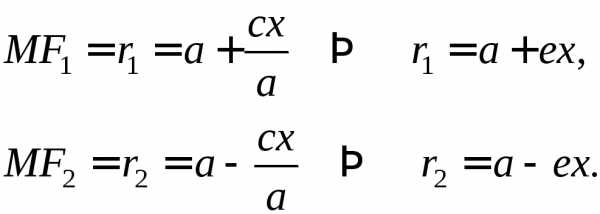
studfiles.net
Уравнение эллипса, формулы и примеры
Определение и уравнение эллипса
ОПРЕДЕЛЕНИЕ Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух данных точек и есть величина постоянная. Точки и называются фокусами эллипса.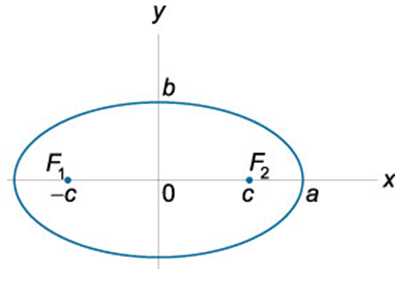
Каноническое (или простейшее) уравнение эллипса с центром в начале координат
Здесь — длина большей полуоси эллипса, — длина малой полуоси эллипса. Фокальным расстоянием называется расстояние между фокусами рассматриваемого эллипса.
Примеры решения задач
ПРИМЕР 1| Задание | Эллипс задан своим каноническим уравнением . Найти длины его большой и малой осей. |
| Решение | Из заданного канонического уравнения эллипса можно сделать вывод, что
Тогда . Следовательно, искомые длины большой и малой осей соответственно
|
| Ответ |
Величина
Величины и эллипса связаны соотношением:
Эксцентриситетом эллипса называется величина
Для эллипса
ПРИМЕР 2| Задание | Составить каноническое уравнение эллипса, если его полуоси |
| Решение | Каноническое уравнение эллипса имеет вид:
Подставляя в него заданные значения полуосей, получим:
|
| Ответ |
ru.solverbook.com
