Нормальные формы: ДНФ, КНФ, СДНФ, СКНФ
Нормальные формы формул алгебры высказываний бывают двух типов: дизъюктивные и конъюктивные, в каждом из этих типов выделен класс совершенных форм.
Алгоритм построения ДНФ:
1. Перейти к булевым операциям.
2. Перейти к формуле с тесными отрицаниями, т.е. к формуле, в которой отрицания находятся не выше, чем над переменными.
3. Раскрыть скобки.
4. Повторяющейся слагаемые взять по одному разу.
5. Применить законы поглощения и полупоглощения.
Пример.Найти ДНФ формулы
►
◄
Конъюнктивная нормальная форма (КНФ) – двойственное для ДНФ понятие, поэтому ее легко построить по схеме:
.
Пример.Найти КНФ формулы
► ~ ~
.◄
Совершенную дизъюнктивную нормальную форму СДНФ можно строить, используя следующий алгоритм:
1. = 1. алгоритма ДНФ
2. = 2. алгоритма ДНФ
3. = 3. алгоритма ДНФ
4. = 4. алгоритма ДНФ
5. Опустить тождественно ложные слагаемые, т. е. слагаемые вида
.
6. Пополнить оставшиеся слагаемые недостающими переменными
7. Повторить пункт 4.
Пример.Найти СДНФ формулы.
► ~
.◄
Для построения СКНФ можно пользоваться следующей схемой:
Пример.Найти СДНФ формулы.
► ~
.◄
Известно (теоремы 2.11, 2.12), что СДНФ и СКНФ определены формулой однозначно и, значит, их можно строить по таблице истинности формулы [1].
►Схема построения СДНФ и СКНФ по таблице истинности приведена ниже, для формулы ~ :
2.2. Задание.
2.2.1 Ниже приведены логические выражения. Максимально упростите выражения своего варианта, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните ваше упрощенное выражение с исходным.
2.2.2. Выяснить вопрос о равносильности f1 и f 2 путем сведения их к СДНФ (табл. 1).
2.2.3. Найти двойственную функцию для f3 по обобщенному и булевому принципу (табл.1). Сравнить полученные результаты.
2.3.1. Дайте определение высказывания.
2.3.2. Перечислите основные операции над высказыванием.
2.3.3. Что такое таблица истинности?
2.3.4. Составить таблицы истинности для следующих формул:
~ ~ ;
~ ;
~ ~ ~ ;
~ ~ ~ ~ .
2.3.5. Учитывая соглашения о порядке выполнения операций, опустить «лишние» скобки и знак « » в формулах:
;
;
;
;
~ .
2.3.6. Применяя равносильные преобразования, доказать тождественную истинность формул:
;
;
;
.
2.3.7.Найти двойственные формулы:
)
.
2.3.8. Привести к совершенной ДНФ (СДНФ) форме следующие формулы:
~
2.3.9. Привести к совершенной КНФ (СКНФ) форме следующие формулы:
~
~
Лабораторная работа № 3
Тема: «Минимизация булевых функций. Логические схемы»
Цель: Приобретение практических навыков работы с методами минимизации булевых функций.
3.1. Теоретические сведения [1].
Минимальные формы
Как было показано в [1], любая булева функция представима в совершенной нормальной форме (дизъюнктивной или конъюнктивной). Более того, такое представление является первым шагом перехода от табличного задания функции к ее аналитическому выражению. В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получается на основе принципа двойственности [1].
Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний). Такие формы называют минимальными. При каноническом синтезе предполагается, что на входы схемы подаются как сигналы , так и их инверсий .
Формула, представленная в дизъюнктивной нормальной форме, упрощается многократными применением операции склеивания и операции поглощения и (дуальные тождества для конъюнктивной нормальной формы имеют вид: и ). Здесь под и можно понимать любую формулу булевой алгебры. В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются уже невозможными, т.е. получаем тупиковую форму.
Среди тупиковых форм находится и минимальная дизъюнктивная форма, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма является минимальной, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.
Пусть, например, функция задана в совершенной нормальной дизъюнктивной форме:
.
Группируя члены и применяя операцию склеивания, имеем .
При другом способе группировки получим:
.
Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, так как ). В первом случае таким членом может быть . Тогда . Добавив член , получим: . Перебрав все возможные варианты, можно убедиться, что две последние формы являются минимальными.
Работа с формулами на таком уровне подобна блужданию в потемках. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать некоторые графические и аналитические представления и специально разработанную для этой цели символику.
Многомерный куб
Каждой вершине -мерного куба можно поставить в соответствие конституенту единицы. Следовательно, подмножество отмеченных вершин является отображением на -мерном кубе булевой функции от переменных в совершенной дизъюнктивной нормальной форме. На рис. 3.1 показано такое отображение для функции из п.3.7.

Рис.3.1 Отображение на трехмерном кубе функции, представленной в СДНФ
Для отображения функции от переменных, представленной в любой дизъюнктивной нормальной форме, необходимо установить соответствие между ее минитермами и элементами -мерного куба.
Минитерм ( -1)-го ранга можно рассматривать как результат склеивания двух минитермов -го ранга (конституент единицы), т.е. , На -мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координаты , соединяющим эти вершины, ребром (говорят, что ребро покрывает инцидентные ему вершины). Таким образом, минитермам ( -1)-го порядка соответствуют ребра -мерного куба. Аналогично устанавливается соответствие минитермов ( -2)-го порядка — граням -мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
Элементы -мерного куба, характеризующиеся измерениями, называют -кубами. Так, вершины являются 0-кубами, ребра – 1-кубами, грани – 2-кубами и т.д. Обобщая приведенные рассуждения, можно считать, что минитерм ( )-го ранга в дизъюнктивной нормальной форме для функции переменных отображается -кубом, причем каждый -куб покрывает все те -кубы низшей размерности, которые связаны с его вершинами. В качестве примера на рис. 3.2 дано отображение функции трех переменных. Здесь минитермы и соответствуют 1-кубам ( ), а минитерм отображается 2-кубом ( ).
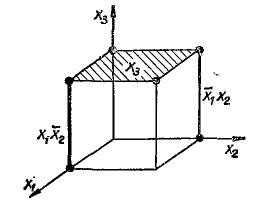
Рис.3.2 Покрытие функции
Итак, любая дизъюнктивная нормальная форма отображается на -мерном кубе совокупностью -кубов, которые покрывают все вершины, соответствующие конституентам единицы (0-кубы). Справедливо и обратное утверждение: если некоторая совокупность -кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим -кубам минитермов является выражение данной функции в дизъюнктивной нормальной форме. Говорят, что такая совокупность -кубов (или соответствующих им минитермов) образует покрытие функции.
Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число -кубов которого было бы поменьше, а их размерность — побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием. Например, для функции покрытие на рис. 3.3 соответствует минимальным формам и .
Рис. 3.3 Покрытия функции .
слева – ; справа –
 Отображение функции на -мерном кубе наглядно и просто при . Четырехмерный куб можно изобразить, как показано на рис. 3.4, где отображены функция четырех переменных и ее минимальное покрытие, соответствующее выражению . Использование этого метода при требует настолько сложных построений, что теряется все его преимущества.
Отображение функции на -мерном кубе наглядно и просто при . Четырехмерный куб можно изобразить, как показано на рис. 3.4, где отображены функция четырех переменных и ее минимальное покрытие, соответствующее выражению . Использование этого метода при требует настолько сложных построений, что теряется все его преимущества.
Рис. 3.4 Отображение функции на четырехмерном кубе
Карты Карно
В другом методе графического отображения булевых функций используются карты Карно, которые представляют собой специально организованные таблицы соответствия. Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством. На рис. 3.5 показаны карты Карно для двух, трех, четырех переменных.
Рис. 3.5 Карты Карно для двух, трех и четырех переменных
Как и в обычных таблицах истинности, клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки). Например, на рис. 3.6, а показана карта Карно для функции, отображение которой на четырехмерном кубе дано на рис. 3.4. Для упрощения строки и столбцы, соответствующие значениям 1 для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
 | |||
 | |||
а б
Рис. 3.6 Отображение на карте Карно функции четырех переменных
(а) и ее минимального покрытия (б)
Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно s-кубу соответствует совокупность 2 соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике (с учетом соседства противоположных краев карты). Поэтому все положения, изложенные в выше (см. п. многомерный куб), справедливы для карт Карно. Так, на рис. 3.6, б показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме рассматриваемой функции.
Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие s-куб, дают минитер (n–s)-го ранга, в который входят те (n–s) переменные, которые сохраняют одинаковые значения на этом s-кубе, причем значении 1 соответствуют сами переменные, а значениям 0 – их отрицания. Переменные, которые не сохраняют свои значения на s-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в дизъюнктивной нормальной форме (крайняя правая является минимальной) (рис. 3.7).
Рис. 3.7 Способы считывания с карты Карно дизъюнктивной нормальной формы булевой функции (слева направо: ; ;
Пример.Получить минимальные формы для функции
Пример.Получить минимальную форму для функции, заданной на карте.
Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае четырех переменных. Для отображения функций пяти переменных используется две карты Карно на четыре переменные, а для функции шести переменных – четыре таких карты. При дальнейшем увеличении числа переменных карты Карно становятся практически непригодными.
Известные в литературе карты Вейча отличаются только другим порядком следования наборов значений переменных и обладают теми же свойствами, что и карты Карно.
Комплекс кубов
Несостоятельность графических методов при большом числе переменных компенсируется различными аналитическими методами представления булевых функций. Одним из таких представлений является комплекс кубов, использующий терминологию многомерного логического пространства в сочетании со специально разработанной символикой.
Комплекс кубов К(у) функции определяется как объединение множеств Кs(у) всех ее s-кубов (s=0.1,…,n), т. е. , причем некоторые из Кs(у) могут быть пустыми. Для записи s-кубов и минитермов функции от n переменных используются слова длины n, буквы которых соответствуют всем n переменным. Входящие в минитерм переменные называются связанными и представляются значениями, при которых минитерм равен единице (1 для и 0 для ). Не входящие в минитерм переменные являются свободными и обозначаются через . Например, 2-куб функции пяти переменных, соответствующий минитерму запишем как ( ). 0-кубы, соответствующие конституентам единицы, представляются наборами значений переменных, на которых функция равна единице. Очевидно, в записи s-куба всегда имеется s свободных переменных. Если все n переменных свободны, что соответствует n-кубу, то это означает тождественность единице рассматриваемой функции. Таким образом, для функций, не равных тождественно единице Ø.
Множество всех s-кубов записывается как совокупность слов, соответствующих каждому s-кубу. Для удобства будем располагать слова s-кубов в столбцы, а их совокупность заключать в фигурные скобки. Например, комплекс кубов, соответствующий представлению функции на трехмерном кубе (рис. 3,10а), выражается как , где
; ; .
Для сравнения на рис. 3.8 изображен комплекс кубов в принятых обозначениях.
Рис. 3.8 Комплекс кубов функции трех переменных (а) и его символическое представление (б)
Комплекс кубов образует максимальное покрытие функции. Исключая из него все те s-кубы, которые покрываются кубами высшей размерности, получаем покрытия, соответствующие тупиковым формам. Так, для рассматриваемого примера (рис. 3.8) имеем тупиковое покрытие
,
которое соответствует функции . В данном случае это покрытие является и минимальным.
Для двух булевых функций операция дизъюнкции соответствует объединению их комплексов кубов , а операция конъюнкции — пересечению комплексов кубов . Отрицанию функции соответствует дополнение комплекса кубов, т. е. , причем определяется всеми вершинами, на которых функция принимает значение 0. Таким образом, имеет место взаимно-однозначное соответствие (изоморфизм) между алгеброй булевых функций и булевых множеств, представляющих комплексы кубов.
Представление функции в виде комплексов кубов менее наглядно, однако его важнейшие достоинства состоят в том, что снимаются ограничения по числу переменных и облегчается кодирование информации при использовании вычислительных машин.
Минимизация булевых функций
Постановка задачи. Минимизация схемы в булевом базисе сводится к поиску минимальной дизъюнктивной формы, которой соответствует минимальное покрытие. Общее число букв, входящих в нормальную форму, выражается ценой покрытия , где — число — кубов, образующих покрытие данной функции от п переменных. Минимальное покрытие характеризуется наименьшим значением его цены.
Обычно задача минимизации решается в два шага. Сначала ищут сокращенное покрытие, которое включает все -кубы максимальной размерности, но не содержит ни одного куба, покрывающегося каким-либо кубом этого покрытия. Соответствующею дизъюнктивную нормальную форму называют сокращенной, а ее минитермы — простыми импликантами. Для данной функции сокращенное покрытие является единственным, но оно может быть избыточным вследствие того, что некоторые из кубов покрываются совокупностями других кубов.
На втором шаге осуществляется переход от сокращенной к тупиковым дизъюнктивным нормальным формам, из которых выбираются минимальные формы. Тупиковые формы образуются путем исключения из сокращенного покрытия всех избыточных кубов, без которых оставшаяся совокупность кубов еще образует покрытие данной функции, но при дальнейшем исключении любого из кубов она уже не покрывает множества всех вершин, соответствующих единичным значениям функции, т. е. перестает быть покрытием.
Куб сокращенного покрытия, который покрывает вершины данной функции, не покрываемые никакими другими кубами, не может оказаться избыточным и всегда войдет в минимальное покрытие. Такой куб, как и соответствующая ему импликанта, называют экстремалью (существенной импликантой), а покрываемые им вершины — отмененными вершинами. Множество экстремалей образует ядро покрытия, ясно, что при переходе от сокращенного покрытия к минимальному прежде всего следует выделить все экстремали. Если множество экстремалей не образует покрытия, то оно дополняется до покрытия кубами из сокращенного покрытия.
Приведенные определения иллюстрируются на рис. 3.9, где сокращенное покрытие (см. рис. 3.9а,) и минимальные покрытия (рис. 3.9б) и (см. рис. 3.9, б) выражаются следующим образом:

Рис. 3.9 Сокращенное ( ) и минимальные покрытия ( , ) функции (а – сокращенное, б, в — минимальные)
Сокращенная форма представляет собой дизъюнкцию четырех простых импликант, т. е. Экстремалями являются простые импликанты и ,которым соответствуют 1-кубы (
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Алгоритм построения днф
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
A→B= ךAvB A⇔B=(A^B)v(ךAvךB)
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
ך(AvB)= ךA^ךB ך(A^B)= ךAvךB
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример построения днф
Приведем к ДНФ формулу :F=((X→Y)↓ ך(Y→Z))
Выразим логические операции → и ↓ через :v ^ ך
F=(( ךXvY)↓ ך(ךYvZ))= ך ((ךXvY)v ך (ךYvZ))
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
F= ך ((ךXvY)v ך (ךYvZ))=( ך ךX^ ךY)^( ךYvZ)=(X^ ךY)^( ךYvZ)
Используя закон дистрибутивности, приводим формулу к ДНФ:
F=(X^ ךY^ ךY)v(X^ ךY^Z)
Конъюнктивная нормальная форма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкцийлитералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ. Для этого можно использовать: Закон двойного отрицания, Закон де Моргана, Дистрибутивность.
Примеры и контр примеры
Формулы в КНФ:
ך A^(BvC) (AvB)^( ך BvCv ך D)^(Dv ך E)A^B
Формулы не в КНФ:
ך (BvC) (A^B)vC A^(Bv(D^E))
Но эти 3 формулы не в КНФ эквивалентны следующим формулам в КНФ:
ך B^ ך C (AvC)^(BvC) A^(BvD)^(BvE)
Построение КНФ
Алгоритм построения КНФ
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
A→B= ך AvB A↔B=(A^B)v(ך A^ ך B)
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
ך (AvB)= ך A^ ך B ך (A^B)= ך Av ך B
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример построения КНФ
Приведем к КНФ формулу
F=(X→Y)^(( ך Y→Z) → ך X)
Преобразуем формулу F к формуле не содержащей → :
F=( ך XvY)^( ך (ך Y→Z)v ך X)=( ך XvY)^( ך (ך ך YvZ)v ך X)
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
F=( ך XvY)^(( ך Y^ ך Zv ך X)=( ך XvY)^(( ך Y^ ך Z)v ך X)
По закону дистрибутивности получим КНФ:
F=( ך XvY)^( ך Xv ך Y)^( ך Xv ך Z)
k-конъюнктивной нормальной формой называют конъюнктивную нормальную форму, в которой каждая дизъюнкция содержит ровно kлитералов.
Например, следующая формула записана в 2-КНФ:
(AvB)^( ך BvC)^(Bv ך C)
Переход от КНФ к СКНФ
Если в простой дизъюнкции не хватает какой-то переменной (например, z), то добавляем в нее выражение : (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:
(XvY)^(Xv ך Yv ך Z)=(XvYv(Z^ ך Z))^(Xv ך Yv ך Z)=(XvYvZ)^(XvY vך Z)^(Xv ךYv ךZ)
Таким образом, из КНФ получена СКНФ.
Переход от КНФ к СКНФ
Если в простой дизъюнкции не хватает какой-то переменной (например, z), то добавляем в нее выражение :Z^ ך Z=0 (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:
(XvY)^(Xv ךY ךZ)=(XvYv(Zv ךZ))^(Xv ךYv ךZ)=(XvYvZ)^(XvYv ךZ)^(Xv ךYv ךZ) Таким образом, из КНФ получена СКНФ.
25. Совершенные дизъюнктивные и конъюнктивные нормальные формы и алгоритмы приведения к ним. Примеры.
Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая конъюнктивная нормальная форма, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных дизъюнкций
в каждой дизъюнкции нет одинаковых пропозициональных переменных
каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
k-конъюнктивной нормальной формой называют конъюнктивную нормальную форму, в которой каждая дизъюнкция содержит ровно k литералов.
Например, следующая формула записана в 2-КНФ:
Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных букв
каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.
Для любой функции алгебры логики существует своя СДНФ, причём единственная.
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности:
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
Совершенная ДНФэтой функции:
studfiles.net
Учебник по дискретной математике ДНФ, СДНФ, КНФ, СКНФ
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например, является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том жепорядке.
Например, выражение является ДНФ, но не СДНФ. Выражение является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение – простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение – КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые , то ко всей дизъюнкции добавляем слагаемое К1К2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
или
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
www.mini-soft.ru
Построение СКНФ и СДНФ по таблице истинности
Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $\left(A\vee \overline{B}\vee C\right)\wedge \left(A\vee C\right)$;
дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $\left(A\wedge \overline{B}\wedge C\right)\vee \left(B\wedge C\right)$.
СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:
не содержит одинаковых элементарных дизъюнкций;
ни одна из дизъюнкций не содержит одинаковых переменных;
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:
не содержит одинаковых элементарных конъюнкций;
ни одна из конъюнкций не содержит одинаковых переменных;
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
Пример 1
Записать логическую функцию по ее таблице истинности:
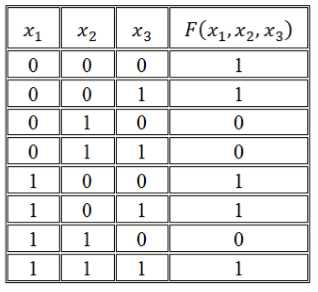
Рисунок 1.
Решение:
Воспользуемся правилом построения СДНФ:
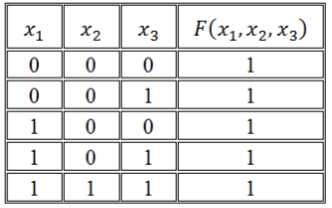
Рисунок 2.
Получим СДНФ:
\[F\left(x_1,\ x_2,\ x_3\right)=\left(\overline{x_1}\wedge \overline{x_2}\wedge \overline{x_3}\right)\vee \left(\overline{x_1}\wedge \overline{x_2}\wedge x_3\right)\vee \left(x_1\wedge \overline{x_2}\wedge \overline{x_3}\right)\vee \left(x_1\wedge \overline{x_2}\wedge x_3\right)\vee \left(x_1\wedge x_2\wedge x_3\right)\]Воспользуемся правилом построения СКНФ:
Рисунок 3.
Получим СКНФ:
\[F\left(x_1,\ x_2,\ x_3\right)=\left(x_1\vee \overline{x_2}\vee x_3\right)\wedge \left(x_1\vee \overline{x_2}\vee \overline{x_3}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\right)\]Пример 2
Функция задана таблицей истинности:
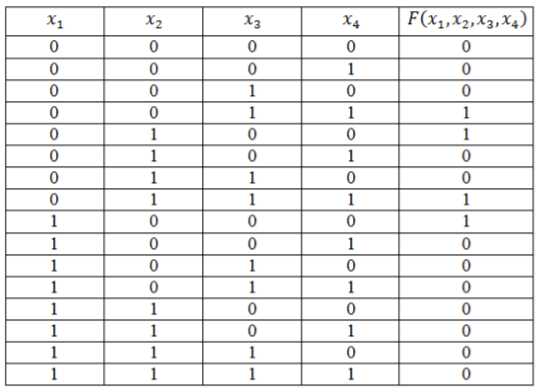
Рисунок 4.
Представить эту функцию в виде СДНФ и СКНФ.
Решение:
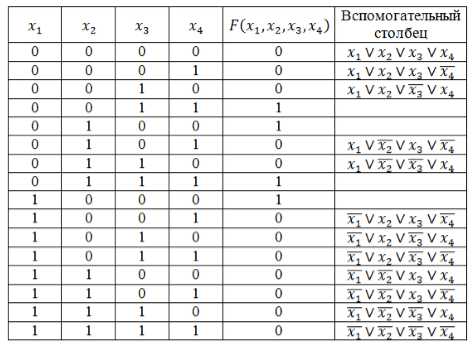
Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.
Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.

Рисунок 5.
Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:
\[F\left(x_1,x_2,x_3,x_4\right)=\left(\overline{x}\wedge \overline{y}\wedge z\wedge f\right)\vee \left(\overline{x_1}\wedge x_2\wedge \overline{x_3}\wedge \overline{x_4}\right)\vee \left(\overline{x_1}\wedge x_2\wedge x_3\wedge x_4\right)\vee \left(x_1\wedge \overline{x_2}\wedge \overline{x_3}\wedge \overline{x_4}\right).\]Запишем логическую функцию в СКНФ.
Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.

Рисунок 6.
Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:
\[F\left(x_1,x_2,x_3,x_4\right)=\left(x_1\vee x_2\vee x_3\vee x_4\right)\wedge \left(x_1\vee x_2\vee x_3\vee \overline{x_4}\right)\wedge \left(x_1\vee x_2\vee \overline{x_3}\vee x_4\right)\wedge \left(x_1\vee \overline{x_2}\vee x_3\vee \overline{x_4}\right)\wedge \left(x_1\vee \overline{x_2}\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee x_2\vee x_3\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee x_2\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee x_2\vee \overline{x_3}\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\vee x_4\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee \overline{x_3}\vee \overline{x_4}\right).\]
spravochnick.ru
32. Минимальные , кратчайшие и тупиковые днф.
Элементарную конъюнкцию К будем называть импликантой функции f , если для ∀ã , K(ã)=1 влечет за собой выполнение условия f(ã)=1.
Импликант К –простой, если выражение получающееся из его выбрасывания любых их множителей не является импликантой f.
ДНФ называют минимальной, если она содержит наименьшее число литералов, среди всех ДНФ, эквивалентных ей.
Длиной ДНФ называют число входящих в нее элементарных конъюнкций.
ДНФ называют кратчайшей, если она имеет наименьшую длину среди всех эквивалентных ей ДНФ.
Заметим, что кратчайшая ДНФ не обязана быть в то же время минимальной среди всех ДНФ, эквивалентных исходной функции. Но поиск минимальных ДНФ проводится среди кратчайших ДНФ.
Тупиковой ДНФ функции f(n) называется такая ДНФ её простых импликант из которой нельзя выбросить ни одного импликанта не изменив функцию f.
Следовательно для получения минимальной ДНФ необходимо построить все её тупиковые ДНФ и выбрать те из них которые содержат наименьшее количество переменных.
Алгоритм построения тупиковой ДНФ:
Пусть f(n) – функция алгебры логики (булевая).
1)находим табличные значения функции f(n)=(101…01)
2)по табличным значениям строим СДНФ
3)строим СДНФ функции f в виде: f=K1˅ K2˅….˅Km , где Ki – простые импликанты.
4)строим матрицу покрытий простых импликант функции f
5)для каждого столбца j (1jK) находим множество Ej номеров строк для которых aj=1.
Cоставляем множество Ejтаких элементов, Ej= (ej1 ,ej2 ,…, eji), где eji– импликанты соответствующие значению 1.
Полученное выражение A=˅(j=1,k)Ej– называется решёточным покрытием ДНФ функции f.
Удаляя все дублирующиеся символы получаем тупиковую ДНФ.
33. Сокращённые днф. Построение сокращённых днф булевых функций методом Блейка.Пример.
Элементарную конъюнкцию К будем называть импликантой функции f , если для ∀ ã, K(ã)=1 влечет за собой выполнение условия f(ã)=1.
Импликант К –простой, если выражение получающееся из его выбрасывания любых их множителей не является импликантой f.
Теорема: Всякая функция реализуется дизъюнкцией своих простых импликант. Сокращённая –дизъюнкция всех простых импликант функции f.
Любая функция f реализуется своей СДНФ.
Для преобразования ДНФ в СДНФ:
(полное склеивание)
(неполное склеивание)
(обобщенное склеивание)
A˅A*B=A (поглощение)
A˅A=A ; A&A=A (удаление дублирующих членов)
Метод Блейка: получение СДНФ состоит в применении правил обобщенного склеивания и поглощения, причем правила применяются слева направо.
На первом этапе производится операция обобщенного склеивания, до тех пор пока это возможно. На втором этапе операция поглощения.
Пример: D=x*y˅⌐x*z˅⌐y*z;
D1=x*y˅⌐x*z˅⌐y*z˅y*z˅x*z˅z=x*y˅z˅z˅z=x*y˅z
34. Построение сокращённых днф булевых функций методом Квайна.Пример.
Теорема Квайна: Если в ДНФ функции f провести все операции неполного склеивания, после чего все операции поглощения и удаления дублирующих членов, то в результате получится СДНФ функции f.
Пример:f( 4)=(0101101001101001) ;
ДНФ=⌐x1⌐ x2⌐ x3 x4 ˅⌐x1⌐x2 x3 x4 ˅⌐x1 x2⌐x3 ⌐ x4 ˅⌐x1 x2 x3 x4 ˅x1⌐x2⌐ x3 x4 ˅x1⌐x2 x3 ⌐ x4 ˅x1 x2⌐x3 ⌐ x4 ˅x1 x2 x3 x4
X1 | X2 | X3 | X4 | f |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 1 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 | 1 |
x4 | x3 x4 | x2 x4 | x2 x3 | x1 x4 | x1 x3 | x1 x2 | x1 x2 x3 x4 | |
x4 | x4 | x4 | x4 | |||||
x3 x4 | x4 | |||||||
x2 x4 | x4 | |||||||
x2 x3 | ||||||||
x1 x4 | x4 | |||||||
x1 x3 | ||||||||
x1 x2 | ||||||||
x1 x2 x3 x4 |
⌐x1⌐ x2⌐ x3 x4 | ⌐x1⌐x2 x3 x4 | ⌐ x1 x2⌐x3 x4 | ⌐x1 x2 x3 ⌐x4 | x1⌐x2⌐ x3 x4 | x1⌐x2 x3 ⌐ x4 | x1 x2⌐x3 ⌐ x4 | x1 x2 x3 x4 | |
⌐x1⌐x2 x4 | Ӿ | Ӿ | ||||||
⌐x1⌐x3 x4 | Ӿ | Ӿ | ||||||
⌐x2⌐ x3 x4 | Ӿ | Ӿ |
⌐x1⌐x2x4 ˅⌐x1x2⌐x3 x4 ˅x1⌐x2⌐x3 x4
studfiles.net
П. 2.2. Дизъюнктивная и конъюнктивная нормальная форма. ?????
Определение 2.2. Формула, в которую входят только операции конъюнкции, дизъюнкции и отрицания, причем операция отрицания относится непосредственно к высказывательным переменным, называетсяприведенной.
Пример:
1) — является приведенной;
2) — не является приведенной, так как содержит операцию импликации;
3) 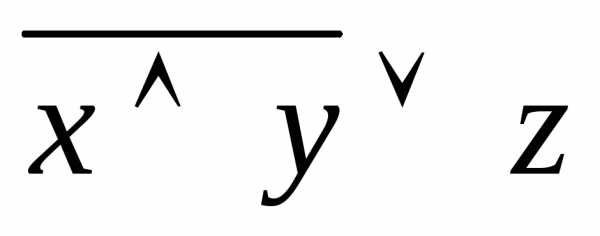 — не является приведенной, так как
операция отрицания отнесена к формуле
— не является приведенной, так как
операция отрицания отнесена к формуле ,
а не к высказывательной переменной.
,
а не к высказывательной переменной.
Для любой формулы алгебры высказываний путем равносильных преобразований можно получить приведенную формулу, например, .
Пусть задана система высказывательных
переменных 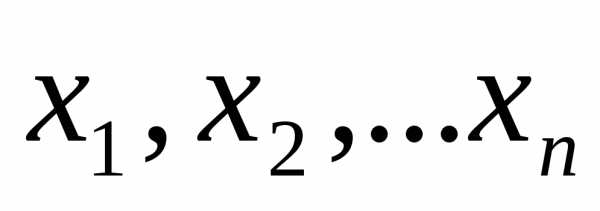 (1).
(1).
Определение 2.3. Элементарной дизъюнкциейвысказывательных переменных из системы (1) называется дизъюнкция некоторых переменных этой системы или их отрицаний.
Определение 2.4. Элементарной конъюнкциейназывается конъюнкция некоторых переменных этой системы или их отрицаний.
Например:
1) Пусть задана система 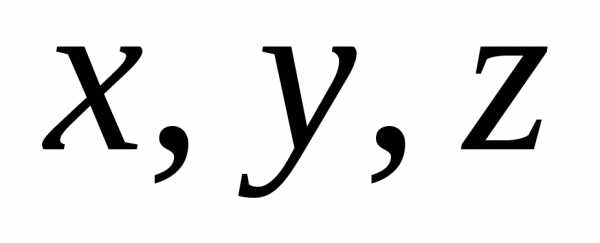 .
Формулыявляются элементарными дизъюнкциями;
первые две из них – одночленными.
.
Формулыявляются элементарными дизъюнкциями;
первые две из них – одночленными.
2) – элементарными конъюнкциями.
Теорема 2.1. Элементарная дизъюнкция
(элементарная конъюнкция) является
тождественно истинной (тождественно
явной) тогда и только тогда, когда она
наряду с некоторой высказывательной
переменной содержит отрицание этой переменной
содержит отрицание этой переменной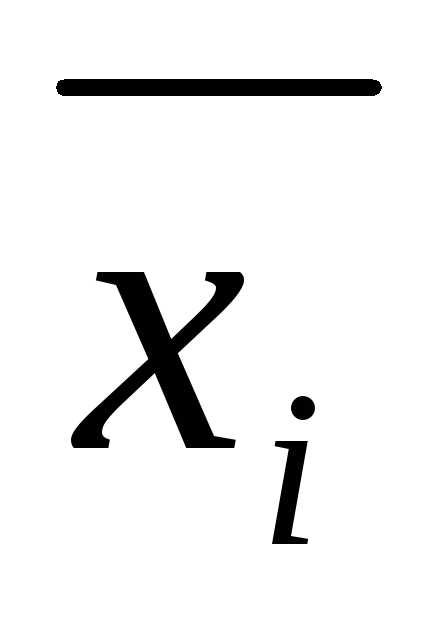 .
.
Доказательство.(э. стр. 37).
Определение 2.5.Формула называетсядизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией некоторого числа элементарных конъюнкций.
ДНФ можно записать в виде
,
где каждое — элементарная дизъюнкция.
— элементарная дизъюнкция.
Например: ;– являются ДНФ.
Определение 2.6.Формула называетсяконъюнктивной нормальной формой (КНФ), если она является конъюнкцией некоторого числа элементарных дизъюнкций.
Например: – является КНФ.
Теорема 2.2. КНФ (ДНФ) является
тождественно истинной (тождественно
ложной) тогда и только тогда, когда
каждая составляющая её элементарная
дизъюнкция (элементарная конъюнкция)
содержит некоторую высказывательную
переменную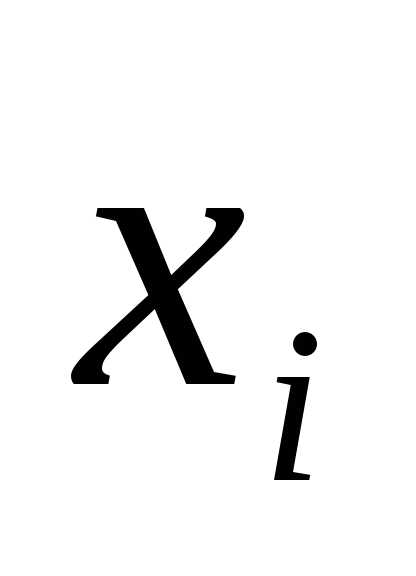 вместе с ее отрицанием
вместе с ее отрицанием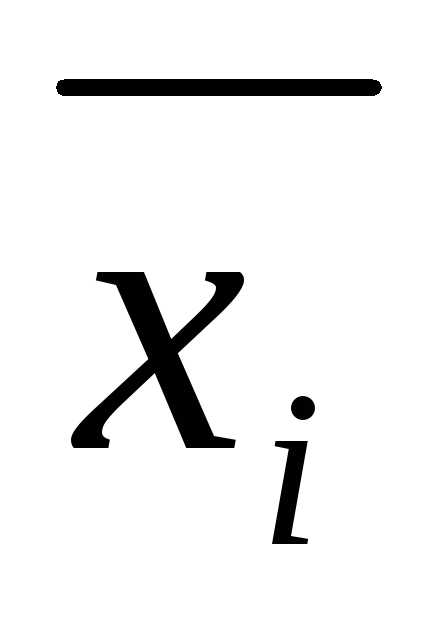 .
.
Доказательствовытекает из Т. 2.1.
Теорема 2.3. Для любой формулы алгебры высказываний существует эквивалентная ей КНФ (ДНФ).
Доказательствопроведем для случая КНФ. Пусть задана формула А. Вначале получим для данной формулы А эквивалентную ей приведенную формулу В. Применяя к В дистрибутивный закон, получим КНФ.
Схема приведения формулы к КНФ и ДНФ:
Для облегчения процедуры раскрытия
скобок (дистрибутивный закон) можно
воспользоваться формальной заменой
логических операций на арифметические.
Если формула приводится к КНФ, то 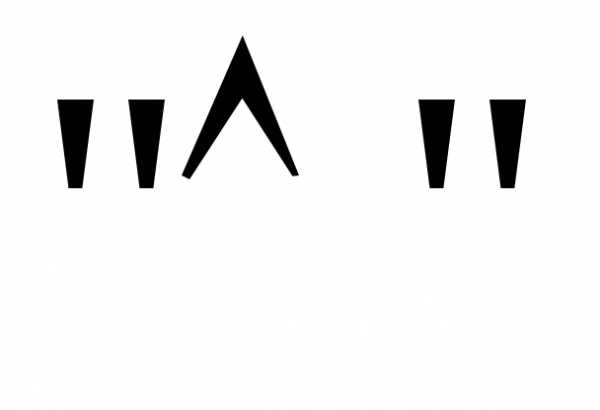 меняется
на
меняется
на ,
а
,
а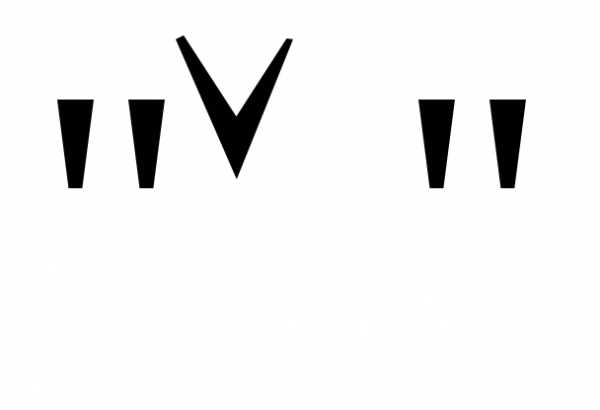 на
на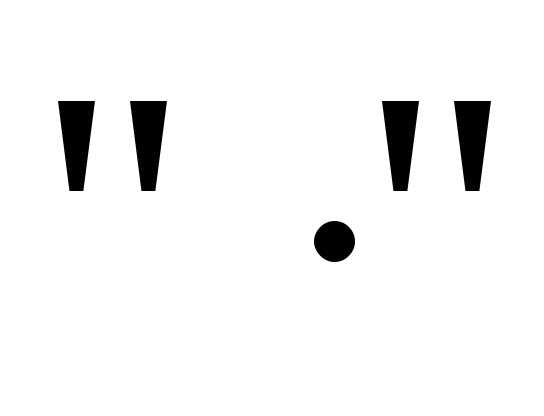 ,
к ДНФ –
,
к ДНФ –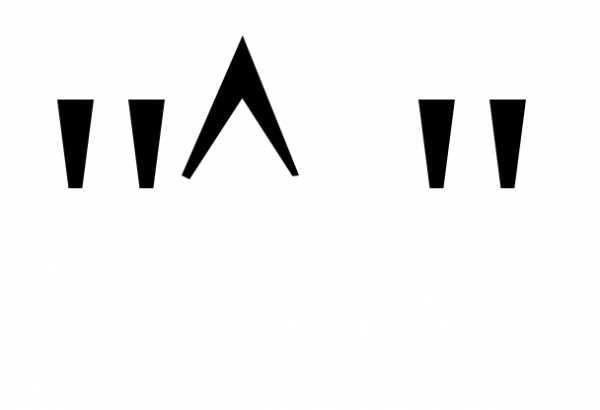 –
–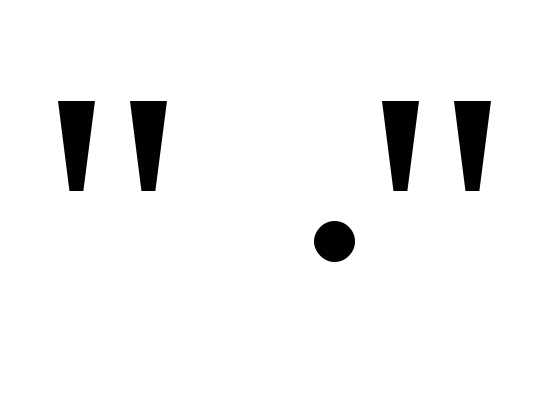 ,
и
,
и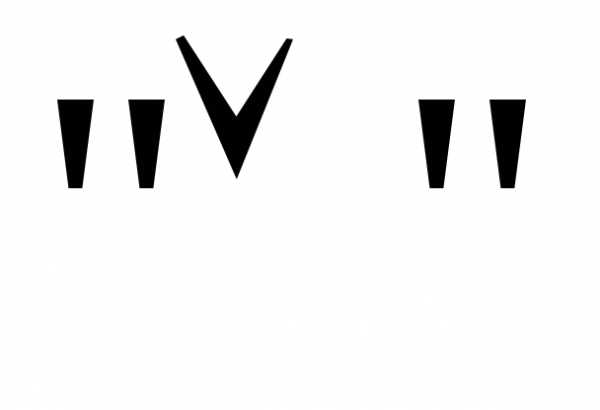 –
–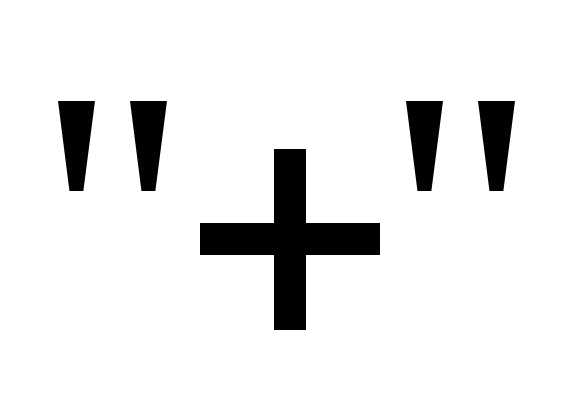 .
На последнем шаге нужно совершить
обратную замену.
.
На последнем шаге нужно совершить
обратную замену.
Например:
1) Приведите к конъюнктивной нормальной форме (КНФ) .
Решение:
.
Заменим в приве-денной формуле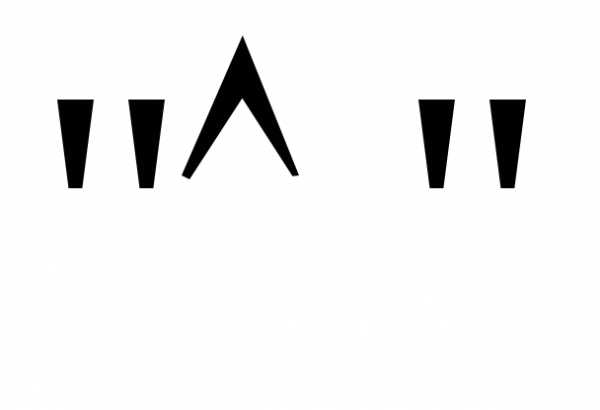 на
на ,
,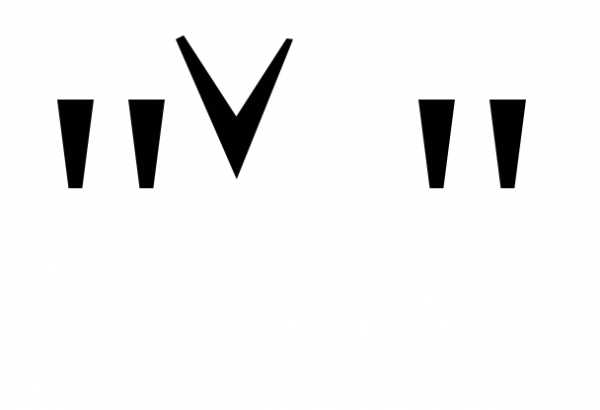 на
на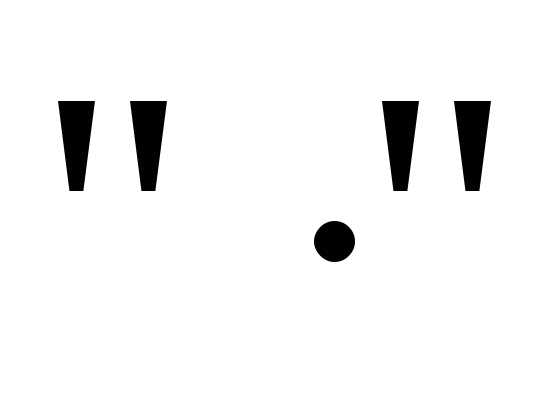 и раскроем скобки:.
и раскроем скобки:.
Сделав обратную замену, получим КНФ формулы А:
.
2) Привести к ДНФ формулу .
Решение:
– приведенная формула.
Заменим в приведенной формуле  на
на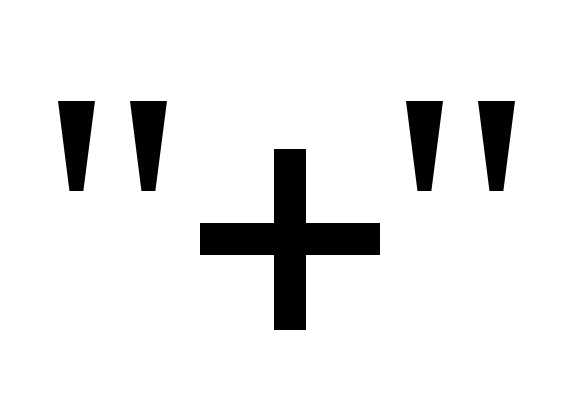 ,
,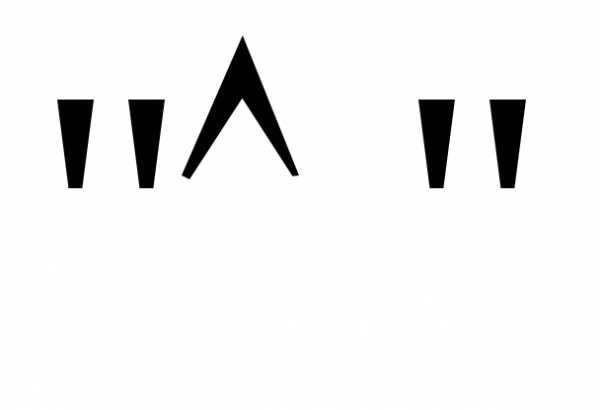 на
на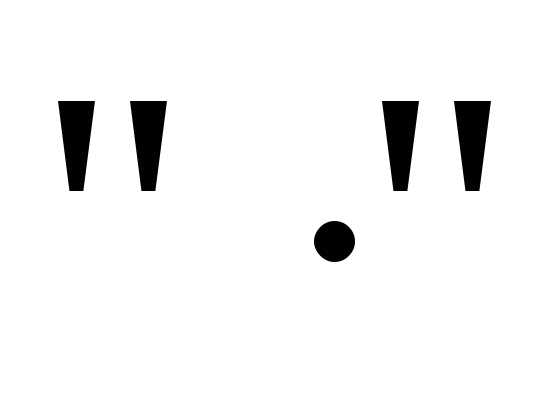 и раскроем скобки:
и раскроем скобки:
.
Сделав обратную замену, получим ДНФ формулы А:.
Определение 2.7.Элементарная конъюнкция (дизъюнкция) называется полной, если каждая переменная входит в нее один и только один раз.
Например:
Пусть задана система переменных .,являются, а,– полными элементарными конъюнкциями.
Определение 2.8.Совершенной конъюнктивной нормальной формой (СКНФ) называется конъюнкция различных полных элементарных дизъюнкций.
Определение 2.9.Совершенной дизъюнктивной нормальной формой (СДНФ) называется дизъюнкция различных полных элементарных конъюнкций.
Например:
Пусть задана система переменных .
Формула – СКНФ, а– СДНФ.
Теорема 2.4. Для любой не тождественно истинной (тождественно ложной) формулы алгебры высказываний существует эквивалентная ей СКНФ (СДНФ).
Доказательство: (э. стр.40).
Алгоритм получения СДНФ:
1. Для формулы Аполучаем любую ДНФ.
2. Если в ДНФ есть слагаемое, не содержащее  ,
то заменяем.
,
то заменяем.
3. Если в ДНФ два одинаковых слагаемых В, то лишнее можно отбросить, так как.
4. Если в некоторое слагаемое ВДНФА входит дважды, то лишнюю
входит дважды, то лишнюю можно отбросить, так как.
можно отбросить, так как.
5. Если слагаемое Вв ДНФАсодержит
конъюнкцию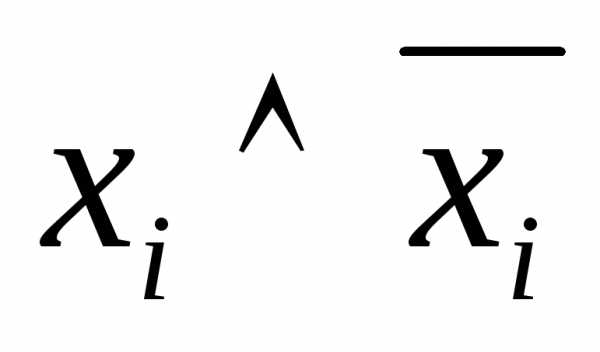 ,
то
,
то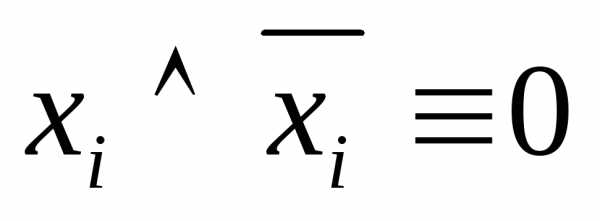 и
и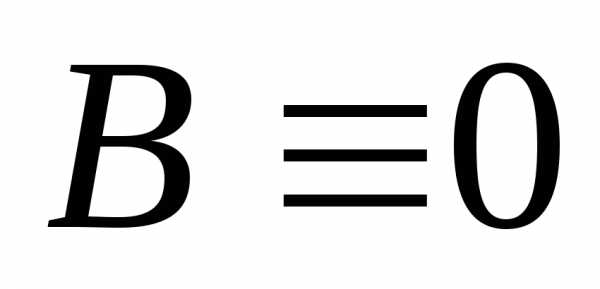 ,
и это слагаемое можно отбросить.
,
и это слагаемое можно отбросить.
Например: привести к СДНФ формулу .
Решение:
Алгоритм получения СКНФ путем равносильных преобразований похож на алгоритм получения СДНФ:
1. Для формулы Аполучаем любую КНФ.
2. Если элементарная дизъюнкция В,
входящая в КНФ, не содержит ,
то.
,
то.
3. если в некоторую элементарную дизъюнкцию Ввходит дважды, то лишнюю переменную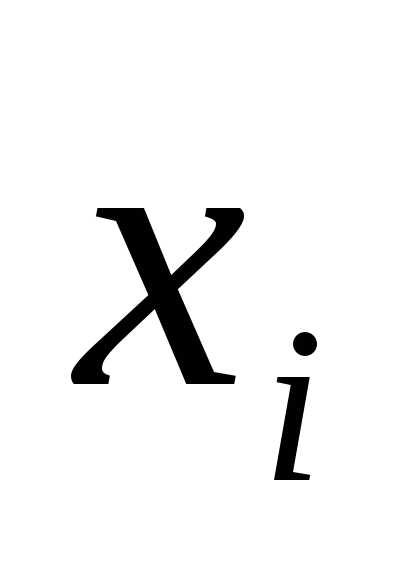 можно отбросить, так как.
можно отбросить, так как.
4. Если КНФ содержит два одинаковых сомножителя В, то лишнюю элементарную дизъюнкцию можно отбросить, так как.
5. Если в элементарную дизъюнкцию Ввходит пара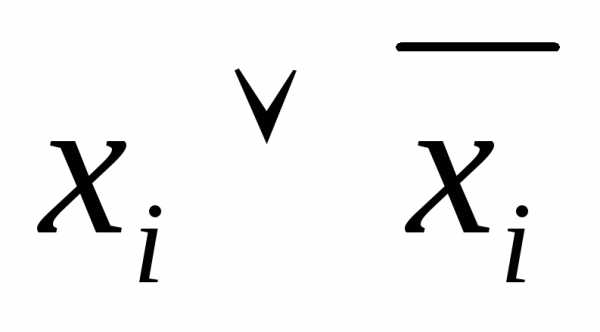 ,
то ее можно отбросить, так как
,
то ее можно отбросить, так как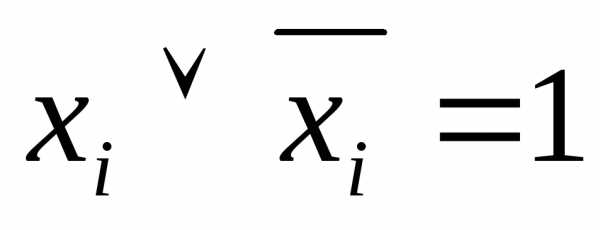 ,
а.
,
а.
Например: привести к СКНФ .
Если же будет задана таблица истинности формулы, то алгоритм построения СДНФ следующий:
1. В таблице истинности отмечаем наборы переменных, для которых значение формулы равно 1.
2. Записываем для каждого отмеченного
набора конъюнкцию всех переменных
следующим образом: если 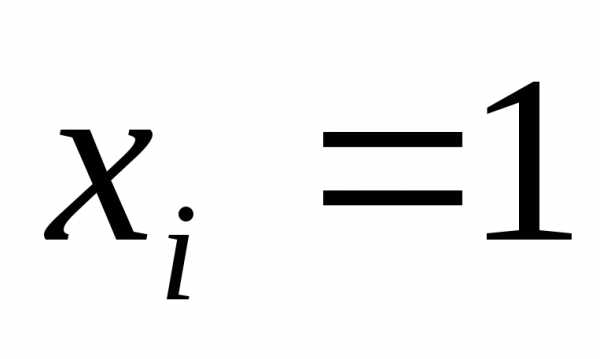 ,
то конъюнкция включает саму переменную,
а противном случае – ее отрицание.
,
то конъюнкция включает саму переменную,
а противном случае – ее отрицание.
3. Все полученные конъюнкции связываем операциями дизъюнкции. Получив СДНФ можно восстановить формулы алгебры высказываний.
Например: Задана таблица истинности
функции  .
.
x | y | z |
|
1 | 1 | 1 | 1 |
1 | 1 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 0 | 0 | 0 |
0 | 1 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 0 | 0 | 1 |
Эту формулу можно упростить. Для удобства
обозначим  –
–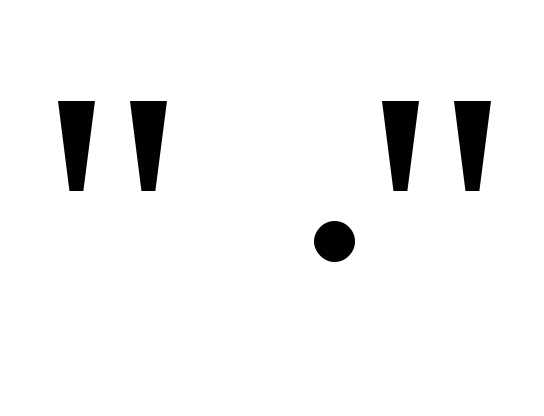 .
.
Алгоритм получения СКНФ по таблице истинности:
1. В таблице истинности отмечаем наборы переменных, для которых значение формулы равно 0.
2. Записываем для каждого отмеченного набора дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в дизъюнкцию включаем саму переменную, а противном случае – ее отрицание.
3. Все полученные дизъюнкции связываем операциями конъюнкции.
Например: Построить формулу по данной таблице истинности
x | y | z | А |
1 | 1 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 0 | 1 | 0 |
1 | 0 | 0 | 1 |
0 | 1 | 1 | 0 |
0 | 1 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 0 | 0 | 1 |
.
studfiles.net
6.2. Сокращённая днф. Метод Квайна.
Определение 1. Элементарным произведением называется конъюнкт, в который любая переменная входит не более одного раза. Формула (х1, х2, … хп) называется импликантой формулы (х1, х2, … хп), если элементарное произведение и для соответствующих формулам и функций f и f справедливо неравенство ff. Формула (х1, х2, … хп) называется импликантой функции f, если импликанта совершенной ДНФ, представляющей функцию f. Импликанта (х1, х2, … хп)=формулы называется простой, если после отбрасывания любой литеры из не получается формула, являющаяся импликантой формулы . Дизъюнкция всех простых импликант данной формулы (функции) называется сокращённой ДНФ.
Пример
6.1. Найдем все импликанты, простые
импликанты и сокращённую ДНФ функции ху.
Всевозможные элементарные произведения
от переменных х и у
это в точности следующие: х, у,  ,
, ,ху,
,ху,  у, х
у, х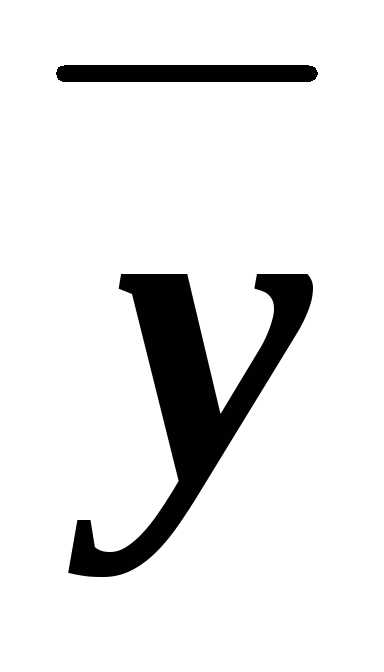 ,
,
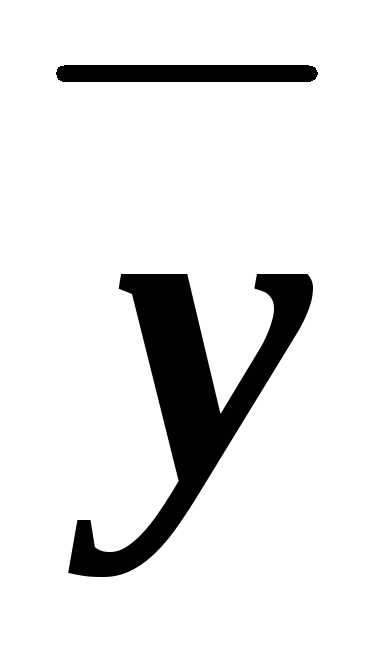 .
Построим для самой функции и для этих
элементарных произведений таблицу
истинности:
.
Построим для самой функции и для этих
элементарных произведений таблицу
истинности:
х | у | ху | х | у |
|
| ху |
| х |
|
0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Сравнивая значения
элементарных произведений со значениями
функции ху,
заключаем, что импликантами этой функции
являются в точности х, у, ху,  у, х
у, х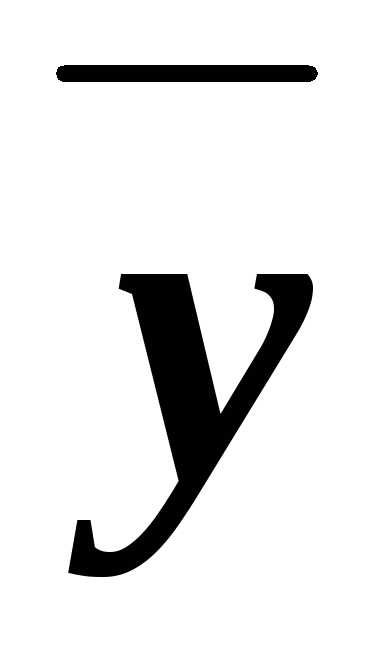 ,
так как для всех них выполнено условиехуf,
где f
одна из х, у, ху,
,
так как для всех них выполнено условиехуf,
где f
одна из х, у, ху,  у, х
у, х (например,хух
(например,хух ).
Из этих импликант простыми являются
толькох и у.
Действительно, удаление одной из литеры
в импликантах ху,
).
Из этих импликант простыми являются
толькох и у.
Действительно, удаление одной из литеры
в импликантах ху,  у, х
у, х ведёт к получению других, а именно х или у.
Таким образом, сокращённой ДНФ функции
является ху (что, впрочем, следует из определения
самой функции).
ведёт к получению других, а именно х или у.
Таким образом, сокращённой ДНФ функции
является ху (что, впрочем, следует из определения
самой функции).
В качестве другого
примера отметим, что всевозможными
импликантами функции ху являются  у, х
у, х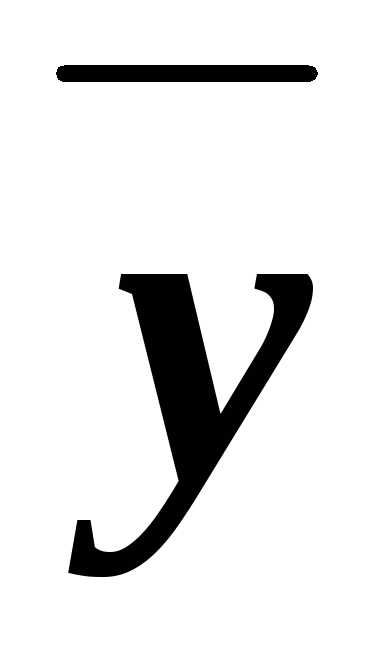 ,
из которых все являются простыми, и,
следовательно, сокращённой ДНФ является
,
из которых все являются простыми, и,
следовательно, сокращённой ДНФ является ух
ух .
.
Ясно, что с помощью таблицы истинности при большом числе переменных построение сокращённой ДНФ становится проблематичной. Существуют специальные методы, позволяющие избегать работы с таблицами истинности. Они основаны на следующих операциях замены подформул, формул, выражающих функции, им эквивалентными подформулами:
АхА А операция
полного склеивания;
А операция
полного склеивания;
АхА ААхА
ААхА операция
неполного склеивания;
операция
неполного склеивания;
АхАА операция элементарного поглощения (0, 1)
Упражнение 6.1.Найти сокращённые ДНФ функций из упражнения 5.1.
Решение. а) Применим к СДНФ функции сначала операцию неполного склеивания, а затемэлементарного поглощения:

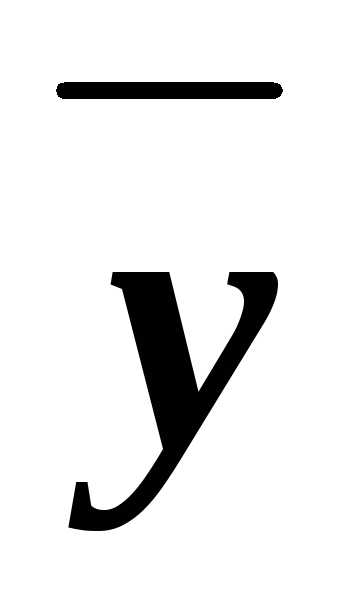 z
z y
y x
x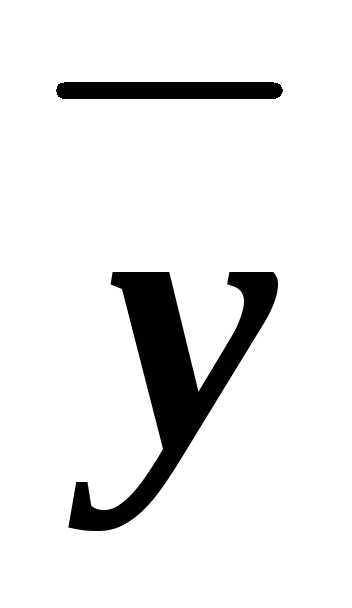 z
z
 z
z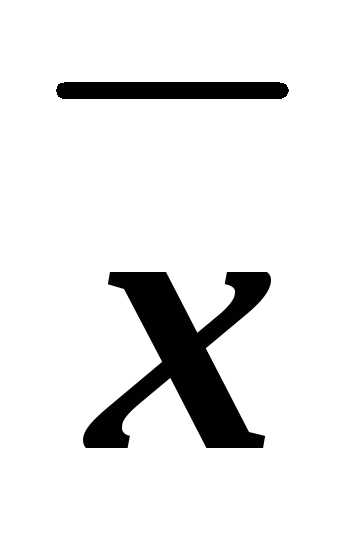
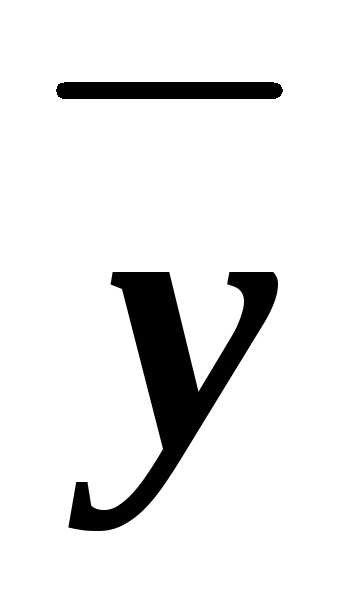 z
z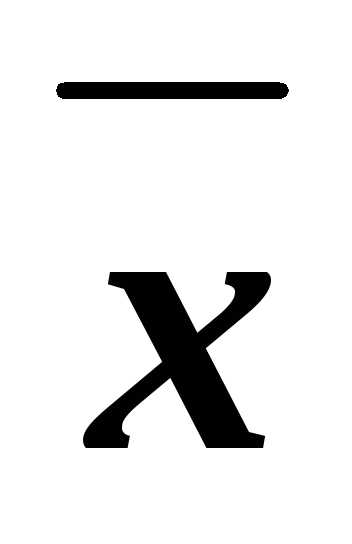 y
y x
x z
z
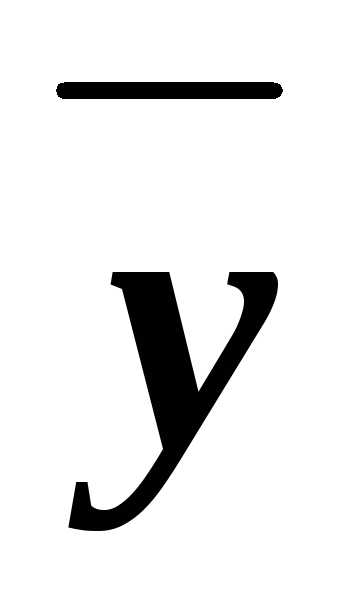 z
z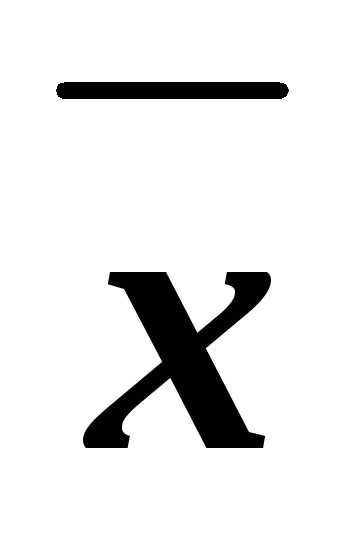 y
y .
.
В результате получили сокращённую ДНФ функции.
(1) К паре конъюнктов 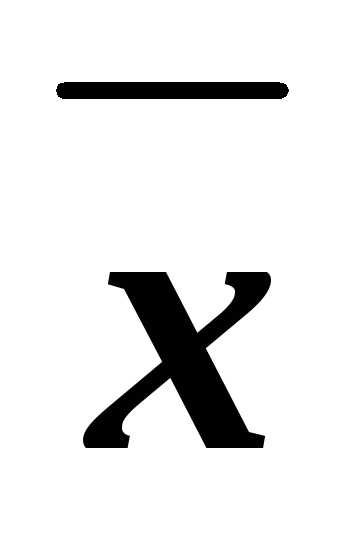
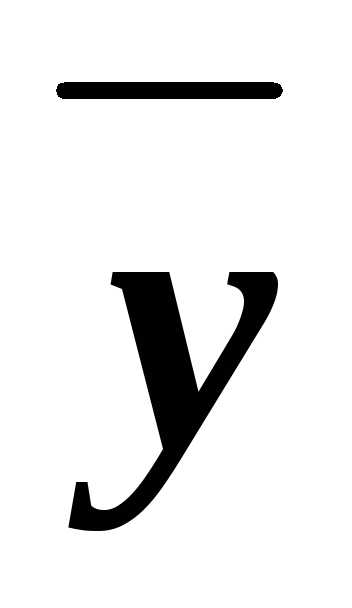 zиx
zиx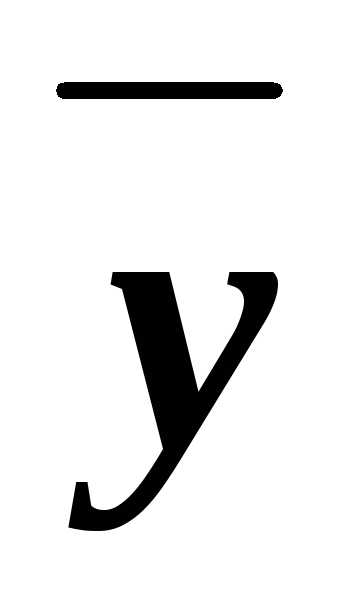 z(точнее, к их дизъюнкции) применили
операцию неполного склеивания:
z(точнее, к их дизъюнкции) применили
операцию неполного склеивания:
 zx
zx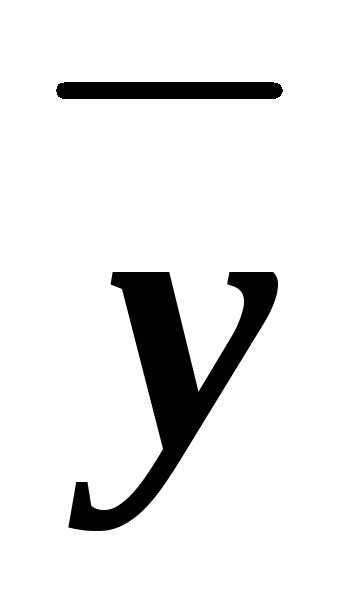 z
z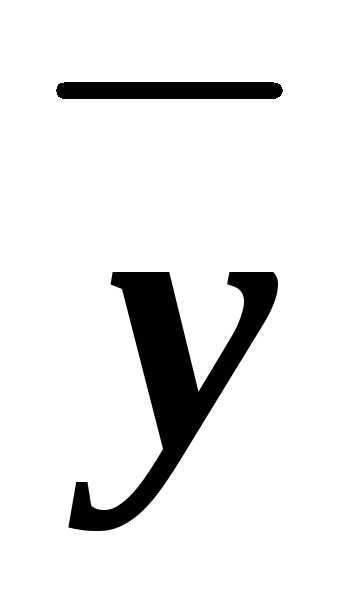 z.
Больше пар, к которым можно применить
эту операцию, нет.
z.
Больше пар, к которым можно применить
эту операцию, нет.
(2) К парам ( z,
z,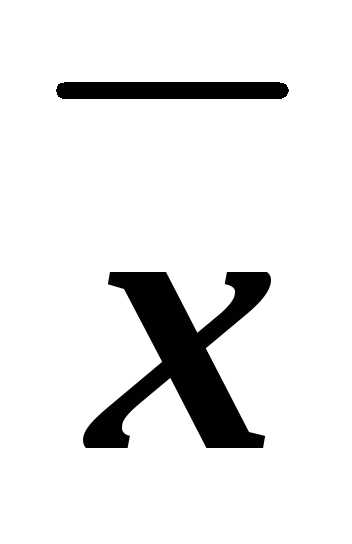
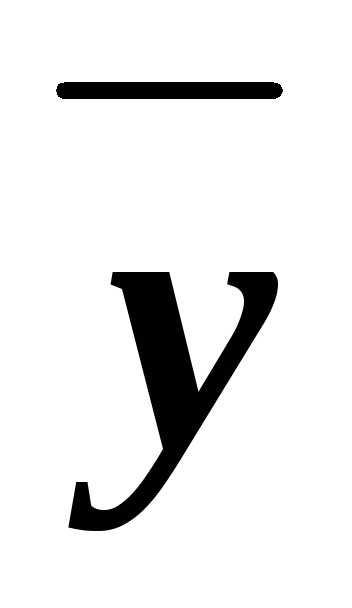 z)
и (
z)
и (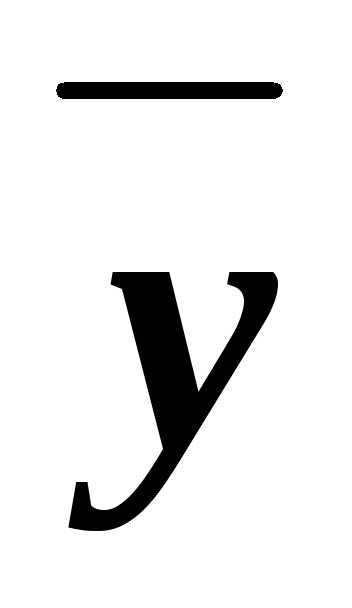 z,x
z,x z)
применили операцию элементарного
поглощения:
z)
применили операцию элементарного
поглощения: 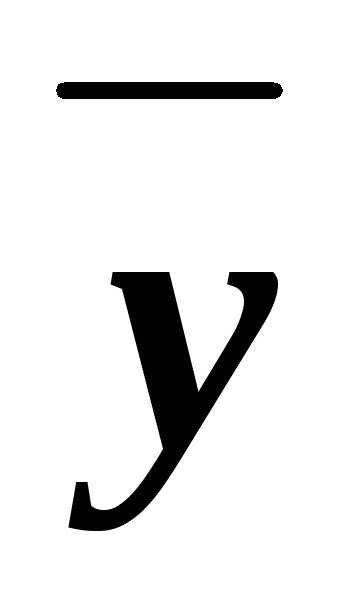 z
z
 z
z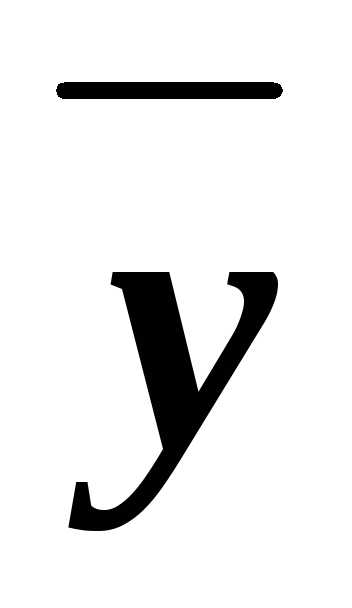 zи
zи 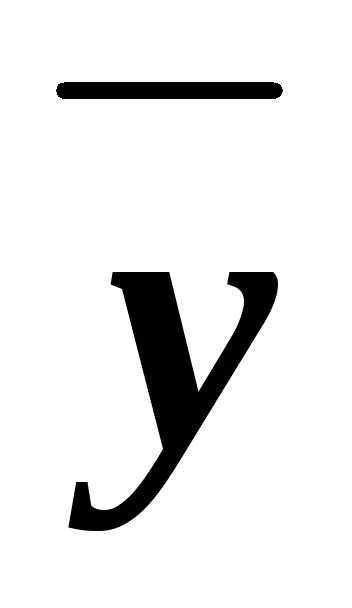 zx
zx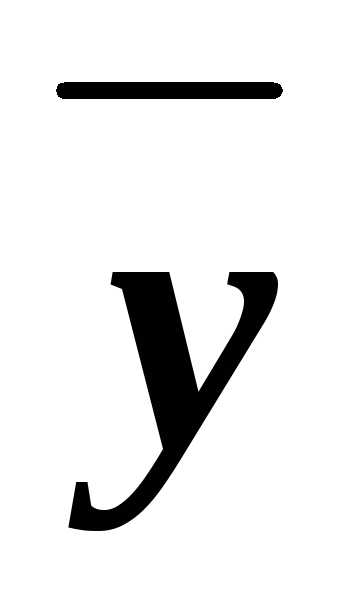 z
z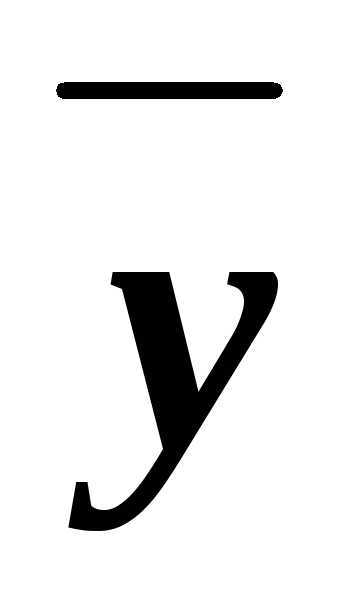 z..
z..
Ответ:  z
z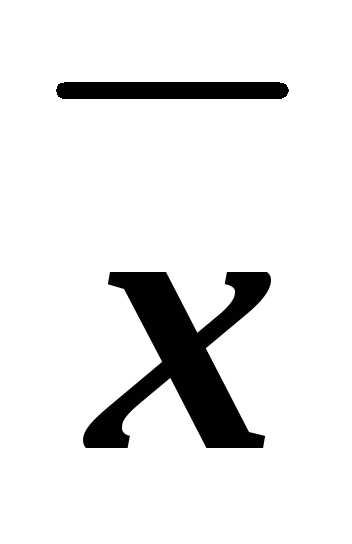 y
y .
.
6.3. Минимальная ДНФ. Таблица Квайна. Рассмотрим ещё
Пример
6.2. Пусть функция f(x, y, z)
задана совершенной ДНФ f(x, y, z)=
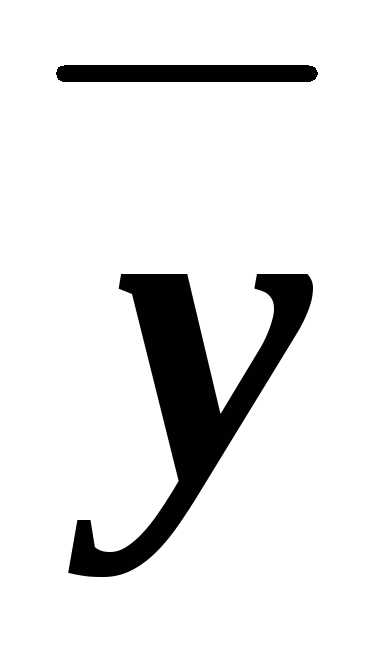


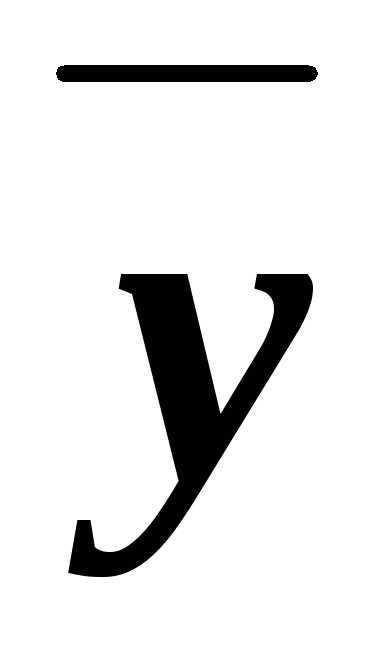 zx
zx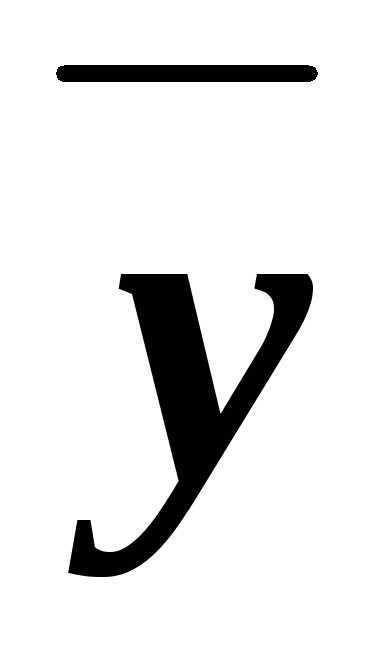
 xy
xy .
Производя над ней операции склеивания
и элементарного поглощения, получаем
её сокращённую ДНФf(x, y, z)=
.
Производя над ней операции склеивания
и элементарного поглощения, получаем
её сокращённую ДНФf(x, y, z)=

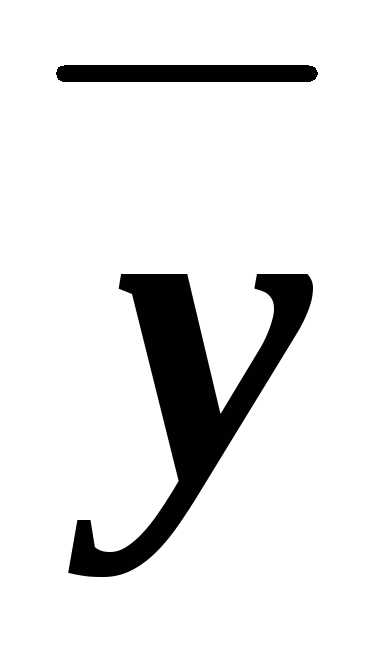
 x
x .
Построив её таблицу истинности, можно
убедиться, что импликанту
.
Построив её таблицу истинности, можно
убедиться, что импликанту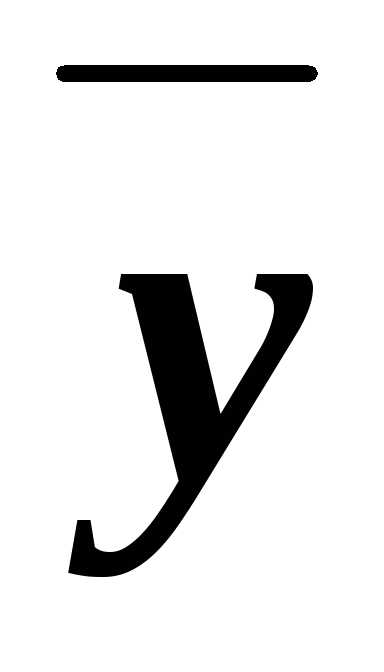
 можно удалить, то естьf(x, y, z)=
можно удалить, то естьf(x, y, z)=
 x
x ,
и сокращённую ДНФ функции можно упрощать
дальше, удаляя лишние импликанты.
,
и сокращённую ДНФ функции можно упрощать
дальше, удаляя лишние импликанты.
Определение 2. Тупиковой ДНФ называется ДНФ, которая получается из сокращённой ДНФ удалением всех лишних импликант, не меняя таблицу истинности. Минимальной ДНФ функции называется её тупиковая ДНФ с наименьшим числом вхождений переменных.
Одним из способов получения минимальной ДНФ из сокращённой ДНФ является использование так называемой таблицы Квайна (ТК). Заголовками столбцов ТК являются конституенты единицы СДНФ, а заголовками строк простые импликанты из сокращённой ДНФ. Таблица заполняется знаками «+» на пересечениях тех строк и столбцов, для которых конъюнкт, стоящий в заголовке строки, входит в конституенту единицы, являющейся заголовком столбца. В тупиковую ДНФ выбирается минимальное число тех простых импликант, знаки «+» при которых охватывают все столбцы ТК.
ТК для функции примера 6.2 имеет вид
Минимальное число
простых импликант, знаки «+» при которых
охватывают все столбцы, образуют
импликанты первой и третьей строки, то
есть 
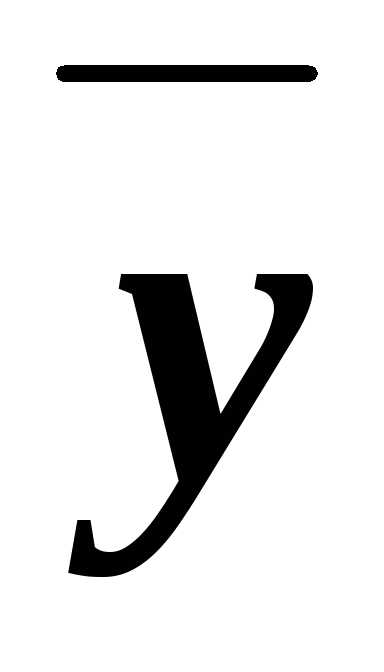 иx
иx .
Поэтому
.
Поэтому
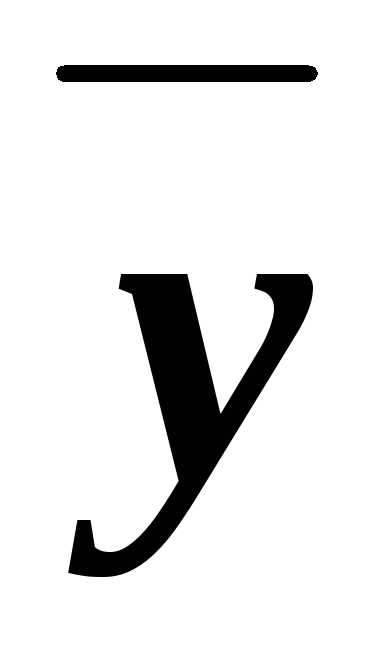 x
x является МДНФ функции.
является МДНФ функции.
Упражнение 6.2.Найти все тупиковые и минимальные ДНФ функций упражнения 5.1.
6.4. Метод Квайна-Мак-Класки. При больших п (порядка 4) метод Квайна становится громоздким. Существует ряд модификаций метода, позволяющих технически упростить данный метод. Опишем один из методов, называемых методом Квайна-Мак-Класки.
Сначала заметим, что при операции склеивания склеиваются элементарные произведения, отличающиеся только одной литерой. Это и положено в основу модификации. Алгоритм метода следующий:
1. Представим каждую конституенту булевой функции в виде двоичного набора длины п.
2. Сгруппируем наборы так, чтобы в каждую группу попали те и только те наборы, которые имеют одинаковое число единиц, располагая их в порядке возрастания числа единиц.
3. Сравнивая наборы из соседних групп, выделяем пары, отличающиеся только в одной позиции (тем самым выделяем конституенты, отличающиеся только одной литерой).
4. В обоих выделенных наборах пар заменяем отличающиеся символы (0 и 1) на «-» (тем самым из двух различных наборов получаем один и тот же набор из 0, 1 и «-», что соответствует тому, что два одинаковых элементарных произведения склеили по отличающейся литере, при этом знак «-» соответствует тому, что соответствующая литера в полученном элементарном произведении будет отсутствовать).
Если в результате склеивания получается уже имеющийся набор, то результат склеивания (то есть полученный набор) опускается (это соответствует тому, что согласно закона идемпотентности одинаковые элементарные произведения сливаются в одну). Если в результате склеивания получаются наборы, отличающиеся только в одной позиции, причём в соответствующей позиции одного стоит знак «-» (у других 0 или 1), то остальные опускаются (что соответствует элементарному поглощению)
5. После всевозможных склеиваний на очередном этапе, переходим к пункту 2.
Процесс продолжается до тех пор, пока склеивать будет нечего. Простыми импликантами являются те элементарные произведения, которые не участвовали в процессе склейки на очередном шаге.
Пример 6.3. Проиллюстируем метод на примере функции, имеющей систему равенств f(0, 1, 0)=f(0, 1, 1)=f(1, 0, 1)=f(1, 1, 0)=f(1, 1, 1)=1 примера 6.2. Располагать группы и результаты всех шагов удобно в таблице. Кроме того, наборы, участвующие при склейке на очередном шаге, будем как-то помечать, например, знаком «*». Тогда после конечного шага все наборы, не участвовавшие при склейке на очередном шаге, останутся непомеченными.
В
I шаг | II шаг | |
010* | 01-* -10* | -1- |
011* 101* 110* | -11* 1-1 11-* | |
111* |
Заметим, что для удобства в таблице Квайна при обозначении элементарных произведений также удобно использование наборов из 0 и 1. Так, таблица Квайна для нашего примера выглядит следующим образом:
010
011
101
110
111
-1-
+
+
+
+
1-1
+
+
Из таблицы видим, что полученная сокращённая ДНФ является минимальной, и даже тупиковой.
Упражнение 6.3.Найти все тупиковые и минимальные ДНФ функций упражнения 5.2.
Решение. б) Применяя модификацию метода Квайна, находим сокращённую ДНФ.
Iшаг
IIшаг
0000*
-000
000-
0001*
1000*
10-0*
1-00*
1—0
0110*
1010*
1100*
011-*
-110*
1-10*
11-0*
-11-
0111*
1110*
-111*
111-*
1111*
Она же оказыется тупиковой и минимальной, в чем легко убедиться, построив таблицу Квайна:
0000 | 0001 | 0110 | 0111 | 1000 | 1010 | 1100 | 1110 | 1111 | |
1—0 | + | + | + | + | |||||
-11- | + | + | + | + | |||||
-000 | + | + | |||||||
0001 | + |
studfiles.net

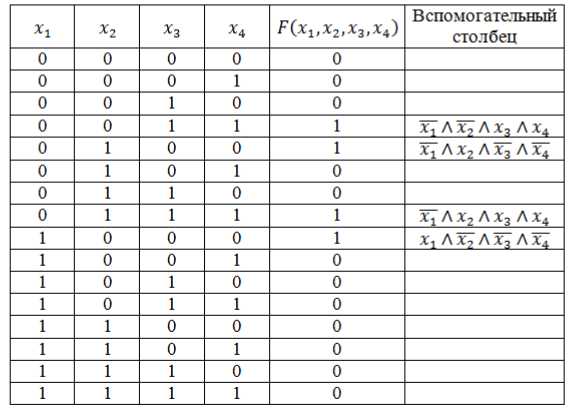
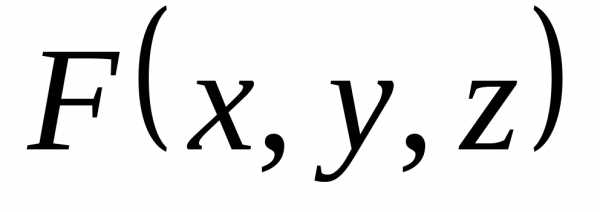

 у
у

