Координаты середины отрезка формула – Середина отрезка. Координаты середины отрезка

Формула нахождения координаты середины отрезка

Начальные геометрические сведения

Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.

Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.

Начнём с определений.

Определение 1

Отрезок — часть прямой, ограниченная двумя точками (концами).

Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.

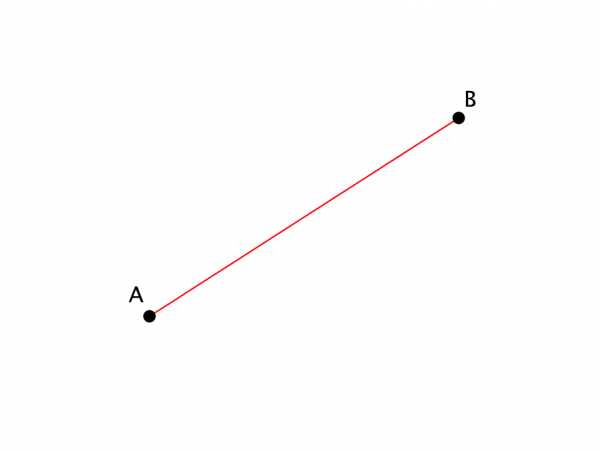
Рисунок 1. Отрезок. Автор24 — интернет-биржа студенческих работ

Определение 2

Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.

Если это точка $C$, то $AC=CB$.

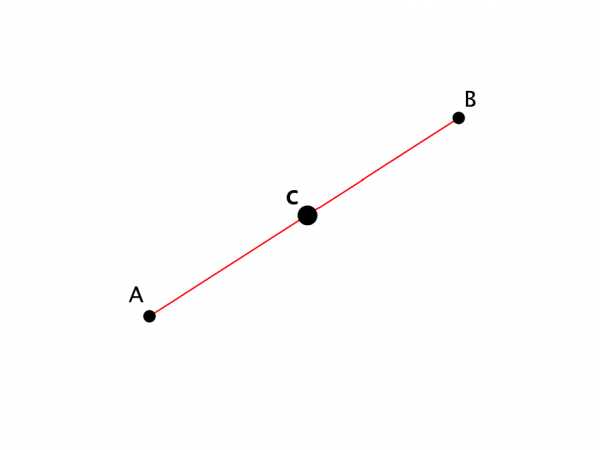
Рисунок 2. Середина отрезка. Автор24 — интернет-биржа студенческих работ

Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.

Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.

Формула нахождения координаты середины отрезка

Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.

Дадим определение координатам.

Определение 3

Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.

В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.

Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ

Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.

Таким образом, оси определяют плоскость $XOY$.

Координаты точек в такой системе определяются двумя числами.

Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.

Перейдём сразу к формуле координаты середины отрезка.

Определение 4

Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:

Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ

Практическая часть

Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.

Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.

Пример 1

Имеем рисунок:

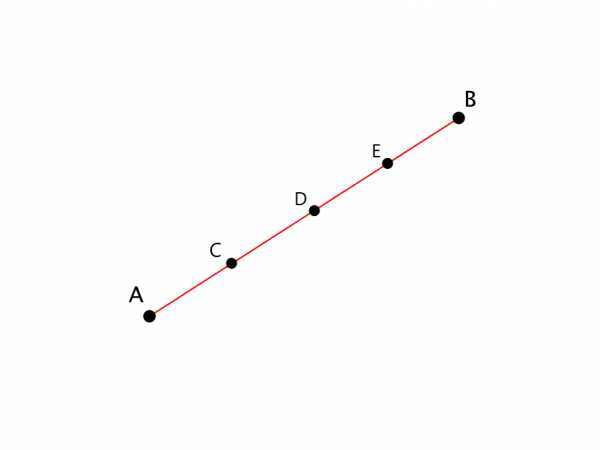
Рисунок 5. Отрезки на плоскости. Автор24 — интернет-биржа студенческих работ

На рисунке отрезки $AC, CD, DE, EB$ равны.

1. Серединой каких отрезков является точка $D$?
2. Какая точка является серединой отрезка $DB$?

Ответы:

1. точка $D$ является серединой отрезков $AB$ и $CE$;
2. точка $E$.

Рассмотрим другой простой пример, в котором нужно вычислить длину.

Пример 2

Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?

Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.

Ответ: 18 см.

Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.

Пример 3

Точка $B$ — середина отрезка $AC$. $AC = 8,4$ см. Какая длина $AB$?

Так как т. $B$ делит $AC$ пополам, то $AB = \frac{8,4}{2}$ см. Значит, $AB = 4,2$ см.

Ответ: 4,2 см.

Если в очередной задаче возникают трудности с пониманием её решения (например, нетипичные случаи с несколькими отрезками, образующими углами и прочими усложнениями), то лучше рассмотреть задачу, сделав по её условию рисунок. Наглядность способствует лучшему пониманию и более скорому нахождению решения.

Теперь решим задачи по аналитической геометрии.

Пример 4

Даны точки $T_1(7,11)$ и $T_2(1,23)$. Требуется найти координаты середины отрезка $T_1T_2$.

Абсцисса середины отрезка: $x=\frac{7+1}{2}=4$. Ордината: $y=\frac{11+23}{2}=17$.

Ответ: $(4,17)$.

Пример 5

Даны точки $T(6,-1)$ и $S(-4,-8)$. Точка $S$ — середина $TK$. Найти координаты $K$.

Подставим значения и получим уравнения:

$-4=\frac{6+x_2}{2}, -8=\frac{-1+y_2}{2}.$

Найдём координаты:

$-2=6+x_2, -4=-1+y_2; x_2=-8, y_2=-3$.

Ответ: $K(-8,-3)$.

spravochnick.ru

Координаты середины отрезка

Координаты середины отрезка через координаты его концов не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:

   

Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.

Задача.
Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.

Решение.
Используем рассмотренную выше формулу:

   

Ответ. М (5; 14).

С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.

Задача.
Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.

Решение.
Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:

   

Подставим известные координаты и вычислим отдельные координаты:

   

   

   

   

   

   

   

   

Получили координаты конца отрезка .

Ответ. .

ru.solverbook.com

Как найти координаты середины отрезка

Как найти координаты середины отрезка
Для начала разберемся, что такое середина отрезка.
Серединой отрезка считают точку, которая принадлежит данному отрезку и отстоит на одинаковое расстояние от его концов.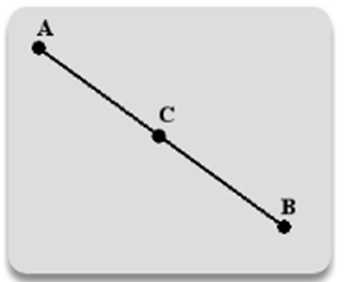

Координаты такой точки несложно найти, если известны координаты концов этого отрезка. В таком случае координаты середины отрезка будут равны половине суммы соответствующих координат концов отрезка.

Координаты середины отрезка часто находят, решая задачи на медиану, среднюю линию и т.п.
Рассмотрим вычисление координат середины отрезка для двух случаев: когда отрезок задан на плоскости и задан в пространстве.
Пусть отрезок на плоскости задан двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:

   

   

Пусть отрезок задан в пространстве двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:

   

   

   

 
Пример.
Найти координаты точки К — середины МО, если М (—1; 6) и О (8; 5).
 
Решение.
Поскольку точки имеют две координаты, значит, отрезок задан на плоскости. Используем соответствующие формулы:

   

   

Следовательно, середина МО будет иметь координаты К (3,5; 5,5).
 
Ответ. К (3,5; 5,5).

ru.solverbook.com

Нахождение координат середины отрезка. Нахождение координат точки, делящей отрезок в данном отношении.

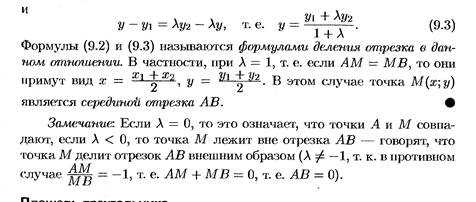
Координаты середины отрезка в пространстве

 

Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2). Тогда серединой отрезка A1A2 будет точка С с координатами x, y, z, где

 

 

26) Каноническое уравнение прямой (вывод). Параметрическое задание прямой. Уравнение прямой через две точки (вывод).

Каноническое уравнение прямой

в пространстве:

где — координаты некоторой фиксированной точки M₀, лежащей на прямой; — координаты вектора, коллинеарного этой прямой.

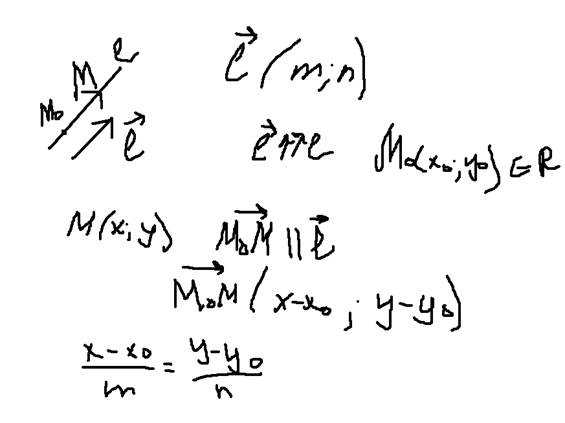
Параметрическое уравнение прямой в пространстве:

27)

Общее уравнение прямой и его частные случаи. Условия параллельности и перпендикулярности прямых заданных в общем виде. Направляющий и нормальный вектор прямой. Нахождение их координат из общего уравнения прямой.

Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

(9)

Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0.

Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.

Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

 

Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

 

1 * A + (-1) * B = 0, т.е. А = В.

28) Уравнение прямой в отрезках (вывод) Уравнение прямой с угловым коэфицентом. Геометрический смысл углового коэффицента прямой.

Уравнение прямой через точку с данным угловым коэффициентом. Условия параллельности и перпендикулярности прямых, заданных с угловым коэффициентом.

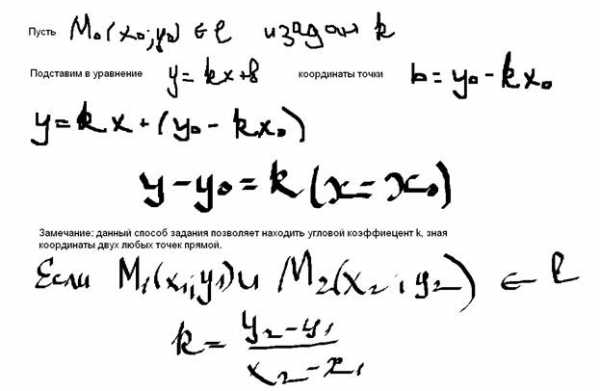
Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂

В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

Уравнение прямой в полярной системе координат. Уравнение прямой через точку с данным нормальным вектором.

Нормальное уравнение прямой. Приведение общего уравнения прямой к нормальному виду. Расстояние от точки до прямой. Расстояние между двумя параллельными прямыми.

Расстоянием между параллельными прямыми называется часть перпендикуляра к этим параллельным прямым заключенная между ними

Определение и каноническое уравнение эллипса. Свойства эллипса.

Свойства:

Точки пересечения эллипса с осями,называются вершинами.

(большая ось- фокальная и малая ось)

Из канонического уравнения следует что

Эллипс лежит внутри прямоугольника со сторонами 2a и 2b.

Т.к. уравнение эллипса содержит только квадраты переменных то, если точка с координатами (x;y) принадл. Э, то точка с коорд. (-x;y) и (x;-y) и(-x;-y) принадлежат Э. след. Эллипс симметричен относительно Ox, Oy, начала координат.

Эксцентриситет эллипса.

Это отношение фокусного расстояния к длине большой оси

Этот показатель характеризует форму эллипса

Чем меньше Е тем Эллипс больше приближается к окружности.

Если Е=0 эллипс превращается в окружность x^2+y^2=a^2

Директрисы эллипса.

Это прямые которые перпендикулярны фокальной оси и находятся на расстоянии a/E от ее центра x= +/- a/E

R1+R2=2a

R1,R2- фокальные радиусы

Для фокальных радиусов имеют место формулы

Основное свойство.

Отношение расстояния от произвольной точки эллипса до фокуса к расстоянию до соответствующей директрисы есть величина постоянная равная ексцентриситету.

Определение и каноническое уравнение гиперболы. Свойства гиперболы. Асимптоты гиперболы.

Свойства :

Гипербола лежит вне прямоугольника со сторонами 2a и 2b.

Эксцентриситет гиперболы.

E=c/a E>1

B^2=c^2-a^2

Чем меньше E тем меньше отношение е полуосей,тем больше вытягивается прямоугольник, ветви приближаются к осям,сжаты.

5.

Директрисы

Основное свойство.

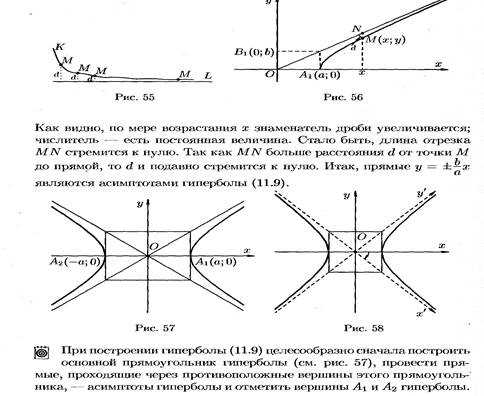
Определение и каноническое уравнение параболы. Свойства параболы.



infopedia.su