Таблица вероятностей лапласа – Таблица значений функции Лапласа онлайн. Задачи с решением по теории вероятностей и математической статистике

alexxlab / / Школьная жизнь

Таблица значений функции Лапласа онлайн. Задачи с решением по теории вероятностей и математической статистике

 

В таблице даны значения функции  для положительных значений  и для ; для  пользуются той же таблицей, так как функция  нечетна, то есть . В таблице приведены значения интеграла лишь до , так как для  можно принять . Эту функцию называют функцией Лапласа.

Таблица значений функции Лапласа в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:

Цветом в таблице подсвечены аргументы функции Лапласа, рядом, в соседнем столбце — значения функции Лапласа.

x Ф(x)
x 		Ф(x) x Ф(x) x Ф(x)
0,00 0,0000 0,32 0,1255 0,64 0,2389 0,96 0,3315
0,01 0,0040 0,33 0,1293 0,65 0,2422 0,97 0,3340
0,02 0,0080 0,34 0,1331 0,66 0,2454 0,98 0,3365
0,03 0,0120 0,35 0,1368 0,67 0,2486 0,99 0,3389
0,04 0,0160 0,36 0,1406 0,68 0,2517 1,00 0,3413
0,05 0,0199 0,37 0,1443 0,69 0,2549 1,01 0,3438
0,06 0,0239 0,38 0,1480 0,70 0,2580 1,02 0,3461
0,07 0,0279 0,39 0,1517 0,71 0,2611 1,03 0,3485
0,08 0,0319 0,40 0,1554 0,72 0,2642 1,04 0,3508
0,09 0,0359 0,41 0,1591 0,73 0,2673 1,05 0,3531
0,10 0,0398 0,42 0,1628 0,74 0,2703 1,06 0,3554
0,11 0,0438 0,43 0,1664 0,75 0,2734 1,07 0,3577
0,12 		0,0478 0,44 0,1700 0,76 0,2764 1,08 0,3599
0,13 0,0517 0,45 0,1736 0,77 0,2794 1,09 0,3621
0,14 0,0557 0,46 0,1772 0,78
0,2823 		1,10 0,3643
0,15 0,0596 0,47 0,1808 0,79 0,2852 1,11 0,3665
0,16 0,0636 0,48 0,1844 0,80 0,2881 1,12 0,3686
0,17 0,0675 0,49 0,1879 0,81 0,2910 1,13 0,3708
0,18 0,0714 0,50 0,1915 0,82 0,2939 1,14 0,3729
0,19 0,0753 0,51 0,1950 0,83 0,2967 1,15 0,3749
0,20 0,0793 0,52 0,1985 0,84 0,2995 1,16 0,3770
0,21 0,0832 0,53 0,2019 0,85 0,3023 1,17 0,3790
0,22 0,0871 0,54 0,2054 0,86 0,3051 1,18 0,3810
0,23 0,0910 0,55 0,2088 0,87 0,3078 1,19 0,3830
0,24 0,0948 0,56 0,2123 0,88 0,3106 1,20 0,3849
0,25 		0,0987 0,57 0,2157 0,89 0,3133 1,21 0,3869
0,26 0,1026 0,58 0,2190 0,90 0,3159 1,22 0,3883
0,27 0,1064 0,59 0,2224 0,91 0,3186 1,23 0,3907
0,28 0,1103 0,60 0,2257 0,92 0,3212 1,24 0,3925
0,29 0,1141 0,61 0,2291 0,93 0,3238 1,25 0,3944
0,30 0,1179 0,62 0,2324 0,94 0,3264
0,31 0,1217 0,63 0,2357 0,95 0,3289

 

 

Продолжение таблицы

x Ф(x) x Ф(x) x Ф(x) x Ф(x)
1,26 0,3962 1,59 0,4441 1,92 0,4726 2,50 0,4938
1,27 0,3980 1,60 0,4452 1,93 0,4732 2,52 0,4941
1,28 0,3997 1,61 0,4463 1,94 0,4738 2,54 0,4945
1,29 0,4015 1,62 0,4474 1,95 0,4744 2,56 0,4948
1,30 0,4032 1,63 0,4484 1,96 0,4750 2,58 0,4951
1,31 0,4049 1,64 0,4495 1,97 0,4756 2,60 0,4953
1,32 0,4066 1,65 0,4505 1,98 0,4761 2,62 0,4956
1,33 0,4082 1,66 0,4515 1,99 0,4767 2,64 0,4959
1,34 0,4099 1,67 0,4525 2,00 0,4772 2,66 0,4961
1,35 0,4115 1,68 0,4535 2,02 0,4783 2,68 0,4963
1,36 0,4131 1,69 0,4545 2,04 0,4793 2,70 0,4965
1,37 0,4147 1,70 0,4554 2,06 0,4803 2,72 0,4967
1,38 0,4162 1,71 0,4564 2,08 0,4812 -2,74 0,4969
1,39 0,4177 1,72 0,4573 2,10 0,4821 2,76 0,4971
1,40 0,4192 1,73 0,4582 2,12 0,4830 2,78 0,4973
1,41 0,4207 1,74 0,4591 2,14 0,4838 2,80 0,4974
1,42 0,4222 1,75 0,4599 2,16 0,4846 2,82 0,4976
1,43 0,4236 1,76 0,4608 2,18 0,4854 2,84 0,4977
1,44 0,4251 1,77 0,4616 2,20 0,4861 2,86 0,4979
1,45 0,4265 1,78 0,4625 2,22 0,4868 2,88 0,4980
1,46 0,4279 1,79 0,4633 2,24 0,4875 2,90 0,4981
1,47 0,4292 1,80 0,4641 2,26 0,4881 2,92 0,4982
1,48 0,4306 1,81 0,4649 2,28 0,4887 2,94 0,4984
1,49 0,4319 1,82 0,4656 2,30 0,4893 2,96 0,4985
1,50 0,4332 1,83 0,4664 2,32 0,4898 2,98 0,4986
1,51 0,4345 1,84 0,4671 2,34 0,4904 3,00 0,49865
1,52 0,4357 1,85 0,4678 2,36 0,4909 3,20 0,49931
1,53 0,4370 1,86 0,4686 2,38 0,4913 3,40 0,49966
1,54 0,4382 1,87 0,4693 2,40 0,4918 3,60 0,499841
1,55 0,4394 1,88 0,4699 2,42 0,4922 3,80 0,499928
1,56 0,4406 1,89 0,4706 2,44 0,4927 4,00 0,499968
1,57 0,4418 1,90 0,4713 2,46 0,4931 4,50 0,499997
1,58 0,4429 1,91 0,4719 2,48 0,4934 5,00 0,499997

100task.ru

Таблица значений функции Лапласа

Таблица значений функции Лапласа используется в теории вероятности довольно часто. В данном разделе описываюся случаи, в которых необходимо использовать значения таблицы. Разбираются примеры и прикладывается сама таблица значений. 

 

Таблица значений:

x Ф(x) x Ф(x) x Ф(x) x Ф(x) x Ф(x) x Ф(x)
0 0 0,5 0,19146 1 0,34134 1,5 0,43319 2 0,47725 3 0,49865
0,01 0,00399 0,51 0,19497 1,01 0,34375 1,51 0,43448 2,02 0,47831 3,05 0,49886
0,02 0,00798 0,52 0,19847 1,02 0,34614 1,52 0,43574 2,04 0,47932 3,1 0,49903
0,03 0,01197 0,53 0,20194 1,03 0,34849 1,53 0,43699 2,06 0,4803 3,15 0,49918
0,04 0,01595 0,54 0,2054 1,04 0,35083 1,54 0,43822 2,08 0,48124 3,2 0,49931
0,05 0,01994 0,55 0,20884 1,05 0,35314 1,55 0,43943 2,1 0,48214 3,25 0,49942
0,06 0,02392 0,56 0,21226 1,06 0,35543 1,56 0,44062 2,12 0,483 3,3 0,49952
0,07 0,0279 0,57 0,21566 1,07 0,35769 1,57 0,44179 2,14 0,48382 3,35 0,4996
0,08 0,03188 0,58 0,21904 1,08 0,35993 1,58 0,44295 2,16 0,48461 3,4 0,49966
0,09 0,03586 0,59 0,2224 1,09 0,36214 1,59 0,44408 2,18 0,48537 3,45 0,49972
0,1 0,03983 0,6 0,22575 1,1 0,36433 1,6 0,4452 2,2 0,4861 3,5 0,49977
0,11 0,0438 0,61 0,22907 1,11 0,3665 1,61 0,4463 2,22 0,48679 3,55 0,49981
0,12 0,04776 0,62 0,23237 1,12 0,36864 1,62 0,44738 2,24 0,48745 3,6 0,49984
0,13 0,05172 0,63 0,23565 1,13 0,37076 1,63 0,44845 2,26 0,48809 3,65 0,49987
0,14 0,05567 0,64 0,23891 1,14 0,37286 1,64 0,4495 2,28 0,4887 3,7 0,49989
0,15 0,05962 0,65 0,24215 1,15 0,37493 1,65 0,45053 2,3 0,48928 3,75 0,49991
0,16 0,06356 0,66 0,24537 1,16 0,37698 1,66 0,45154 2,32 0,48983 3,8 0,49993
0,17 0,06749 0,67 0,24857 1,17 0,379 1,67 0,45254 2,34 0,49036 3,85 0,49994
0,18 0,07142 0,68 0,25175 1,18 0,381 1,68 0,45352 2,36 0,49086 3,9 0,49995
0,19 0,07535 0,69 0,2549 1,19 0,38298 1,69 0,45449 2,38 0,49134 3,95 0,49996
0,2 0,07926 0,7 0,25804 1,2 0,38493 1,7 0,45543 2,4 0,4918 4 0,49997
0,21 0,08317 0,71 0,26115 1,21 0,38686 1,71 0,45637 2,42 0,49224 4,05 0,49997
0,22 0,08706 0,72 0,26424 1,22 0,38877 1,72 0,45728 2,44 0,49266 4,1 0,49998
0,23 0,09095 0,73 0,2673 1,23 0,39065 1,73 0,45818 2,46 0,49305 4,15 0,49998
0,24 0,09483 0,74 0,27035 1,24 0,39251 1,74 0,45907 2,48 0,49343 4,2 0,49999
0,25 0,09871 0,75 0,27337 1,25 0,39435 1,75 0,45994 2,5 0,49379 4,25 0,49999
0,26 0,10257 0,76 0,27637 1,26 0,39617 1,76 0,4608 2,52 0,49413 4,3 0,49999
0,27 0,10642 0,77 0,27935 1,27 0,39796 1,77 0,46164 2,54 0,49446 4,35 0,49999
0,28 0,11026 0,78 0,2823 1,28 0,39973 1,78 0,46246 2,56 0,49477 4,4 0,49999
0,29 0,11409 0,79 0,28524 1,29 0,40147 1,79 0,46327 2,58 0,49506 4,45 0,5
0,3 0,11791 0,8 0,28814 1,3 0,4032 1,8 0,46407 2,6 0,49534 4,5 0,5
0,31 0,12172 0,81 0,29103 1,31 0,4049 1,81 0,46485 2,62 0,4956 4,55 0,5
0,32 0,12552 0,82 0,29389 1,32 0,40658 1,82 0,46562 2,64 0,49585 4,6 0,5
0,33 0,1293 0,83 0,29673 1,33 0,40824 1,83 0,46638 2,66 0,49609 4,65 0,5
0,34 0,13307 0,84 0,29955 1,34 0,40988 1,84 0,46712 2,68 0,49632 4,7 0,5
0,35 0,13683 0,85 0,30234 1,35 0,41149 1,85 0,46784 2,7 0,49653 4,75 0,5
0,36 0,14058 0,86 0,30511 1,36 0,41309 1,86 0,46856 2,72 0,49674 4,8 0,5
0,37 0,14431 0,87 0,30785 1,37 0,41466 1,87 0,46926 2,74 0,49693 4,85 0,5
0,38 0,14803 0,88 0,31057 1,38 0,41621 1,88 0,46995 2,76 0,49711 4,9 0,5
0,39 0,15173 0,89 0,31327 1,39 0,41774 1,89 0,47062 2,78 0,49728 4,95 0,5
0,4 0,15542 0,9 0,31594 1,4 0,41924 1,9 0,47128 2,8 0,49744 5 0,5
0,41 0,1591 0,91 0,31859 1,41 0,42073 1,91 0,47193 2,82 0,4976    
0,42 0,16276 0,92 0,32121 1,42 0,4222 1,92 0,47257 2,84 0,49774    
0,43 0,1664 0,93 0,32381 1,43 0,42364 1,93 0,4732 2,86 0,49788    
0,44 0,17003 0,94 0,32639 1,44 0,42507 1,94 0,47381 2,88 0,49801    
0,45 0,17364 0,95 0,32894 1,45 0,42647 1,95 0,47441 2,9 0,49813    
0,46 0,17724 0,96 0,33147 1,46 0,42785 1,96 0,475 2,92 0,49825    
0,47 0,18082 0,97 0,33398 1,47 0,42922 1,97 0,47558 2,94 0,49836    
0,48 0,18439 0,98 0,33646 1,48 0,43056 1,98 0,47615 2,96 0,49846    
0,49 0,18793 0,99 0,33891 1,49 0,43189 1,99 0,4767 2,98 0,49856    

 

Рассмотрим примеры применения данной таблицы на конкретных примерах:

 

 

matecos.ru

Таблица значений интегральной функции Лапласа

Стандартное нормальное распределение используется при проверке различных гипотез, в том числе о среднем значении,  различии между двумя средними и о пропорциональности значений. Оно имеет среднее 0 и стандартное отклонение 1. Значения, приведенные в таблице, представляют собой величину площади под  стандартной нормальной (гауссовой) кривой от 0 до соответствующего z-значения. Например, величина этой площади между значениями 0 и  2.34 составляет 0.49036. Значение площади между 0 и отрицательным значением соответствуют абсолютному значению заданной величины. Например, площадь под кривой от  -1.3 до 0 равна площади под кривой между  1.3 и 0 и составляет 0.4032.

   

Z

Ф(z)

Z

Ф(z)

Z

Ф(z)

Z

Ф(z)

Z

Ф(z)

Z

Ф(z)

0,00

0,00000

0,50

0,19146

1,00

0,34134

1,50

0,43319

2,00

0,47725

3,00

0,49865

0,01

0,00399

0,51

0,19497

1,01

0,34375

1,51

0,43448

2,02

0,47831

3,05

0,49886

0,02

0,00798

0,52

0,19847

1,02

0,34614

1,52

0,43574

2,04

0,47932

3,10

0,49903

0,03

0,01197

0,53

0,20194

1,03

0,34849

1,53

0,43699

2,06

0,48030

3,15

0,49918

0,04

0,01595

0,54

0,20540

1,04

0,35083

1,54

0,43822

2,08

0,48124

3,20

0,49931

0,05

0,01994

0,55

0,20884

1,05

0,35314

1,55

0,43943

2,10

0,48214

3,25

0,49942

0,06

0,02392

0,56

0,21226

1,06

0,35543

1,56

0,44062

2,12

0,48300

3,30

0,49952

0,07

0,02790

0,57

0,21566

1,07

0,35769

1,57

0,44179

2,14

0,48382

3,35

0,49960

0,08

0,03188

0,58

0,21904

1,08

0,35993

1,58

0,44295

2,16

0,48461

3,40

0,49966

0,09

0,03586

0,59

0,22240

1,09

0,36214

1,59

0,44408

2,18

0,48537

3,45

0,49972

0,10

0,03983

0,60

0,22575

1,10

0,36433

1,60

0,44520

2,20

0,48610

3,50

0,49977

0,11

0,04380

0,61

0,22907

1,11

0,36650

1,61

0,44630

2,22

0,48679

3,55

0,49981

0,12

0,04776

0,62

0,23237

1,12

0,36864

1,62

0,44738

2,24

0,48745

3,60

0,49984

0,13

0,05172

0,63

0,23565

1,13

0,37076

1,63

0,44845

2,26

0,48809

3,65

0,49987

0,14

0,05567

0,64

0,23891

1,14

0,37286

1,64

0,44950

2,28

0,48870

3,70

0,49989

0,15

0,05962

0,65

0,24215

1,15

0,37493

1,65

0,45053

2,30

0,48928

3,75

0,49991

0,16

0,06356

0,66

0,24537

1,16

0,37698

1,66

0,45154

2,32

0,48983

3,80

0,49993

0,17

0,06749

0,67

0,24857

1,17

0,37900

1,67

0,45254

2,34

0,49036

3,85

0,49994

0,18

0,07142

0,68

0,25175

1,18

0,38100

1,68

0,45352

2,36

0,49086

3,90

0,49995

0,19

0,07535

0,69

0,25490

1,19

0,38298

1,69

0,45449

2,38

0,49134

3,95

0,49996

0,20

0,07926

0,70

0,25804

1,20

0,38493

1,70

0,45543

2,40

0,49180

4,00

0,49997

0,21

0,08317

0,71

0,26115

1,21

0,38686

1,71

0,45637

2,42

0,49224

4,05

0,49997

0,22

0,08706

0,72

0,26424

1,22

0,38877

1,72

0,45728

2,44

0,49266

4,10

0,49998

0,23

0,09095

0,73

0,26730

1,23

0,39065

1,73

0,45818

2,46

0,49305

4,15

0,49998

0,24

0,09483

0,74

0,27035

1,24

0,39251

1,74

0,45907

2,48

0,49343

4,20

0,49999

0,25

0,09871

0,75

0,27337

1,25

0,39435

1,75

0,45994

2,50

0,49379

4,25

0,49999

0,26

0,10257

0,76

0,27637

1,26

0,39617

1,76

0,46080

2,52

0,49413

4,30

0,49999

0,27

0,10642

0,77

0,27935

1,27

0,39796

1,77

0,46164

2,54

0,49446

4,35

0,49999

0,28

0,11026

0,78

0,28230

1,28

0,39973

1,78

0,46246

2,56

0,49477

4,40

0,49999

0,29

0,11409

0,79

0,28524

1,29

0,40147

1,79

0,46327

2,58

0,49506

4,45

0,50000

0,30

0,11791

0,80

0,28814

1,30

0,40320

1,80

0,46407

2,60

0,49534

4,50

0,50000

0,31

0,12172

0,81

0,29103

1,31

0,40490

1,81

0,46485

2,62

0,49560

4,55

0,50000

0,32

0,12552

0,82

0,29389

1,32

0,40658

1,82

0,46562

2,64

0,49585

4,60

0,50000

0,33

0,12930

0,83

0,29673

1,33

0,40824

1,83

0,46638

2,66

0,49609

4,65

0,50000

0,34

0,13307

0,84

0,29955

1,34

0,40988

1,84

0,46712

2,68

0,49632

4,70

0,50000

0,35

0,13683

0,85

0,30234

1,35

0,41149

1,85

0,46784

2,70

0,49653

4,75

0,50000

0,36

0,14058

0,86

0,30511

1,36

0,41309

1,86

0,46856

2,72

0,49674

4,80

0,50000

0,37

0,14431

0,87

0,30785

1,37

0,41466

1,87

0,46926

2,74

0,49693

4,85

0,50000

0,38

0,14803

0,88

0,31057

1,38

0,41621

1,88

0,46995

2,76

0,49711

4,90

0,50000

0,39

0,15173

0,89

0,31327

1,39

0,41774

1,89

0,47062

2,78

0,49728

4,95

0,50000

0,40

0,15542

0,90

0,31594

1,40

0,41924

1,90

0,47128

2,80

0,49744

5,00

0,50000

0,41

0,15910

0,91

0,31859

1,41

0,42073

1,91

0,47193

2,82

0,49760

 

 

0,42

0,16276

0,92

0,32121

1,42

0,42220

1,92

0,47257

2,84

0,49774

 

 

0,43

0,16640

0,93

0,32381

1,43

0,42364

1,93

0,47320

2,86

0,49788

 

 

0,44

0,17003

0,94

0,32639

1,44

0,42507

1,94

0,47381

2,88

0,49801

 

 

0,45

0,17364

0,95

0,32894

1,45

0,42647

1,95

0,47441

2,90

0,49813

 

 

0,46

0,17724

0,96

0,33147

1,46

0,42785

1,96

0,47500

2,92

0,49825

 

 

0,47

0,18082

0,97

0,33398

1,47

0,42922

1,97

0,47558

2,94

0,49836

 

 

0,48

0,18439

0,98

0,33646

1,48

0,43056

1,98

0,47615

2,96

0,49846

 

 

0,49

0,18793

0,99

0,33891

1,49

0,43189

1,99

0,47670

2,98

0,49856

 

 

 

Вернуться Статистические таблицы

helpstat.ru

Таблица значений функции Лапласа |

Значения функции Лапласа

     

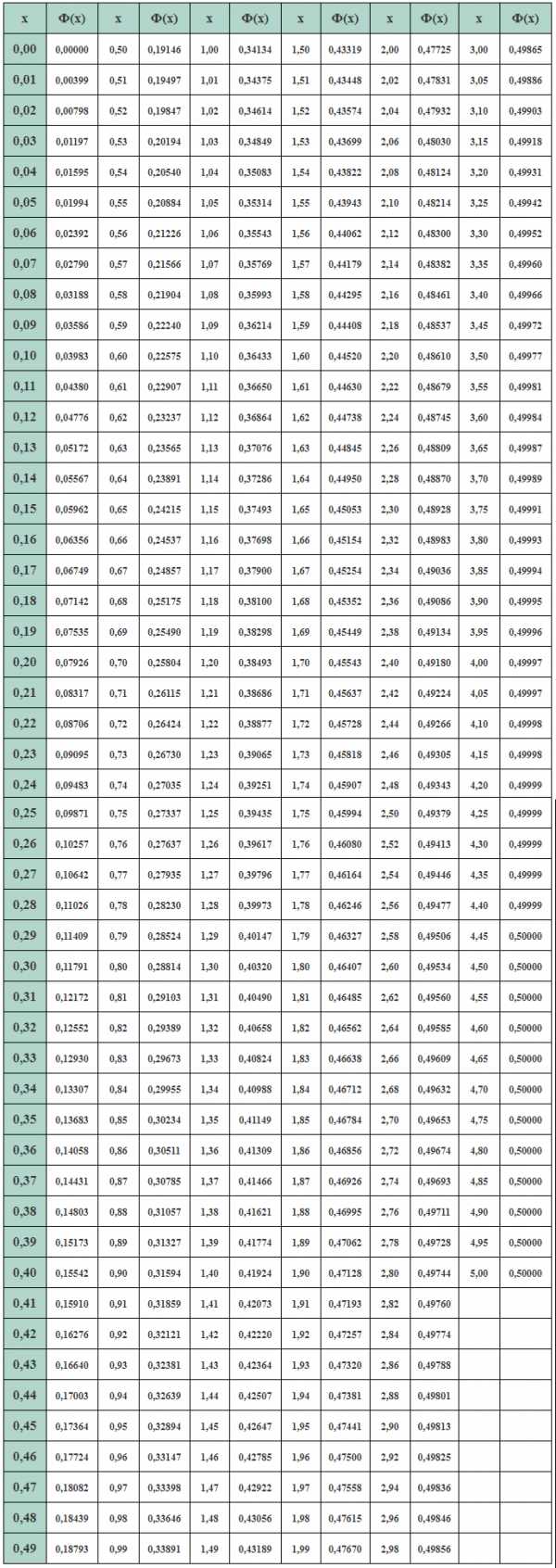
xФ(x)xФ(x)xФ(x)xФ(x)xФ(x)xФ(x)
0,000,000000,500,191461,000,341341,500,433192,000,477253,000,49865
0,010,003990,510,194971,010,343751,510,434482,020,478313,050,49886
0,020,007980,520,198471,020,346141,520,435742,040,479323,100,49903
0,030,011970,530,201941,030,348491,530,436992,060,480303,150,49918
0,040,015950,540,205401,040,350831,540,438222,080,481243,200,49931
0,050,019940,550,208841,050,353141,550,439432,100,482143,250,49942
0,060,023920,560,212261,060,355431,560,440622,120,483003,300,49952
0,070,027900,570,215661,070,357691,570,441792,140,483823,350,49960
0,080,031880,580,219041,080,359931,580,442952,160,484613,400,49966
0,090,035860,590,222401,090,362141,590,444082,180,485373,450,49972
0,100,039830,600,225751,100,364331,600,445202,200,486103,500,49977
0,110,043800,610,229071,110,366501,610,446302,220,486793,550,49981
0,120,047760,620,232371,120,368641,620,447382,240,487453,600,49984
0,130,051720,630,235651,130,370761,630,448452,260,488093,650,49987
0,140,055670,640,238911,140,372861,640,449502,280,488703,700,49989
0,150,059620,650,242151,150,374931,650,450532,300,489283,750,49991
0,160,063560,660,245371,160,376981,660,451542,320,489833,800,49993
0,170,067490,670,248571,170,379001,670,452542,340,490363,850,49994
0,180,071420,680,251751,180,381001,680,453522,360,490863,900,49995
0,190,075350,690,254901,190,382981,690,454492,380,491343,950,49996
0,200,079260,700,258041,200,384931,700,455432,400,491804,000,49997
0,210,083170,710,261151,210,386861,710,456372,420,492244,050,49997
0,220,087060,720,264241,220,388771,720,457282,440,492664,100,49998
0,230,090950,730,267301,230,390651,730,458182,460,493054,150,49998
0,240,094830,740,270351,240,392511,740,459072,480,493434,200,49999
0,250,098710,750,273371,250,394351,750,459942,500,493794,250,49999
0,260,102570,760,276371,260,396171,760,460802,520,494134,300,49999
0,270,106420,770,279351,270,397961,770,461642,540,494464,350,49999
0,280,110260,780,282301,280,399731,780,462462,560,494774,400,49999
0,290,114090,790,285241,290,401471,790,463272,580,495064,450,50000
0,300,117910,800,288141,300,403201,800,464072,600,495344,500,50000
0,310,121720,810,291031,310,404901,810,464852,620,495604,550,50000
0,320,125520,820,293891,320,406581,820,465622,640,495854,600,50000
0,330,129300,830,296731,330,408241,830,466382,660,496094,650,50000
0,340,133070,840,299551,340,409881,840,467122,680,496324,700,50000
0,350,136830,850,302341,350,411491,850,467842,700,496534,750,50000
0,360,140580,860,305111,360,413091,860,468562,720,496744,800,50000
0,370,144310,870,307851,370,414661,870,469262,740,496934,850,50000
0,380,148030,880,310571,380,416211,880,469952,760,497114,900,50000
0,390,151730,890,313271,390,417741,890,470622,780,497284,950,50000
0,400,155420,900,315941,400,419241,900,471282,800,497445,000,50000
0,410,159100,910,318591,410,420731,910,471932,820,49760
0,420,162760,920,321211,420,422201,920,472572,840,49774
0,430,166400,930,323811,430,423641,930,473202,860,49788
0,440,170030,940,326391,440,425071,940,473812,880,49801
0,450,173640,950,328941,450,426471,950,474412,900,49813
0,460,177240,960,331471,460,427851,960,475002,920,49825
0,470,180820,970,333981,470,429221,970,475582,940,49836
0,480,184390,980,336461,480,430561,980,476152,960,49846
0,490,187930,990,338911,490,431891,990,476702,980,49856

www.matematicus.ru

Таблица. Нормированный интеграл вероятностей (нормированная функция Лапласа). Таблица значений нормированной функции Лапласа. Она же нормированная функция ошибок.





 Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Теория вероятностей. Математическая статистика. Комбинаторика.  / / Таблица. Нормированный интеграл вероятностей (нормированная функция Лапласа). Таблица значений нормированной функции Лапласа. Она же нормированная функция ошибок.

Таблица. Нормированный интеграл вероятностей (нормированная функция Лапласа). Таблица значений нормированной функции Лапласа. Она же нормированная функция ошибок.

*

U

0

1

2

3

4

5

6

7

8

9
0,0 0,0000 00399 00798 01197 01595 01994 02892 02790 03188 03586
0,1 03983 04380 04776 05172 05567 05962 06356 06749 07142 07535
0,2 07926 08317 08706 09095 09483 09871 10257 10642 11026 11409
0,3 11791 12172 12552 12930 13307 13683 14058 14431 14803 15173
0,4 15542 15910 16276 16640 17003 17364 17724 18082 18439 18793
0,5 19146 19497 19847 20194 20540 20884 21226 21566 21904 22240
0,6 22575 22907 23237 23565 23891 24215 24537 24857 25175 25490
0,7 25804 26115 26424 26730 27035 27337 27637 27935 28230 28524
0,8 28814 29103 29389 29673 29955 30234 30511 30785 31057 31327
0,9 31594 31859 32121 32381 32639 32894 33147 33398 33646 33891
1,0 34134 34375 34614 34850 35083 35314 35543 35769 35993 36214
1,1 36433 36650 36864 37076 37286 37493 37698 37900 38100 38298
1,2 38493 38686 38877 39065 39251 89435 39617 39796 39973 40147
1,3 40320 40490 40658 40824 40988 41149 41308 41466 41621 41774
1,4 41924 42073 42220 42364 42507 42647 42786 42922 43056 43189
1,5 43319 43448 43574 43699 43822 43943 44062 44179 44295 44408
1,6 44520 44630 44738 44845 44950 45053 45154 45254 45352

dpva.ru

Функция Лапласа(таблица значений)

x

Φ(x)

x

Φ(x)

x

Φ(x)

x

Φ(x)

0

0

0,65

0,2422

1,3

0,4032

1,95

0,4744

0,01

0,004

0,66

0,2454

1,31

0,4049

1,96

0,475

0,02

0,008

0,67

0,2486

1,32

0,4066

1,97

0,4756

0,03

0,012

0,68

0,2517

1,33

0,4082

1,98

0,4761

0,04

0,016

0,69

0,2549

1,34

0,4099

1,99

0,4767

0,05

0,0199

0,7

0,258

1,35

0,4115

2

0,4772

0,06

0,0239

0,71

0,2611

1,36

0,4131

2,02

0,4783

0,07

0,0279

0,72

0,2642

1,37

0,4147

2,04

0,4793

0,08

0,0319

0,73

0,2673

1,38

0,4162

2,06

0,4803

0,09

0,0359

0,74

0.2703

1,39

0,4177

2,08

0,4812

0,1

0,0398

0,75

0,2734

1,4

0,4192

2,1

0,4821

0,11

0,0438

0,76

0,2764

1,41

0,4207

2,12

0,483

0,12

0,0478

0,77

0,2794

1,42

0,4222

2,14

0,4838

0,13

0,0517

0,78

0,2823

1,43

0,4236

2,16

0,4846

0,14

0,0557

0,79

0,2852

1,44

0,4251

2,18

4854

0,15

0,0596

0,8

0,2881

1,45

0,4265

2,2

0,4861

0,16

0,0636

0,81

0,291

1,46

0,4279

2,22

0,4868

0,17

0,0675

0,82

0,2939

1,47

0,4292

2,24

0,4875

0,18

0,0714

0,83

0,2967

1,48

0,4306

2,26

0,4881

0,19

0,0753

0.84

0,2995

1,49

0,4319

2,28

0,4887

0,2

0,0793

0,85

0,3023

1,5

0,4332

2,3

0,4893

0,21

0,0832

0,86

0,3051

1,51

0,4345

2,32

0,4898

0,22

0,0871

0,87

0,3078

1,52

0,4357

2,34

0,4904

0,23

0,091

0,88

0,3106

1,53

0,437

2,36

0,4908

0,24

0,0948

0,89

0,3133

1,54

0,4382

2,38

0,4913

0,25

0,0987

0,9

0,3159

1,55

0,4394

2,4

0,4918

0,26

0,1026

0,91

0,3186

1,56

0,4406

2,42

0,4922

0,27

0,1064

0,92

0,3112

1,57

0,4418

2,44

0,4927

0,28

0,1103

0,93

0,3238

1,58

0,4429

2,46

0,4931

0,29

0,1141

0,94

0,3264

1,59

0,4441

2,48

0,4934

0,3

0,1179

0,95

0,3289

1,6

0,4452

2,5

0,4938

0,31

0,1217

0,96

0,3315

1,61

0,4463

2,52

0,4941

0,32

0,1255

0,97

0,334

1,62

0,4474

2,54

0,4945

0,33

0,1293

0,98

0,3365

1,63

0,4484

2,56

0,4948

0,34

0,1331

0,99

0,3389

1,64

0,4495

2,58

0,4951

0,35

0,1368

1

0,3413

1,65

0,4505

2,6

0,4953

0,36

0,1406

1,01

0,3438

1,66

0,4515

2,62

0,4956

0,37

0,1443

1,02

0,3461

1,67

0,4525

2,64

0,4959

0,38

0,148

1,03

0,3485

1,68

0,4535

2,66

0,4961

0,39

0,1517

1,04

0,3508

1,69

0,4545

2,68

0,4963

0,4

0,1554

1,05

0,3531

1,7

0,4554

2,7

0,4965

0,41

0,1591

1,06

0,3554

1,71

0,4564

2,72

0,4967

0,42

0,1628

1,07

0,3577

1,72

0,4573

2,74

0,4969

0,43

0,1664

1,08

0,3599

1,73

0,4582

2,76

0,4971

0,44

0,17

1,09

0,3621

1,74

0,4591

2,78

0,4973

0,45

0,1736

1,1

0,3643

1,75

0,4599

2,8

0,4974

0,46

0,1772

1,11

0,3665

1,76

0,4608

2,82

0,4976

0,47

0,1808

1,12

0,3686

1,77

0,4616

2,84

0,4977

0,48

0,1844

1,13

0,3708

1,78

0,4625

2,86

0,4979

0,49

0,1879

1,14

0,3729

1,79

0,4633

2,88

0,498

0,5

0,1915

1,15

0,3749

1,8

0,4641

2,9

0,4981

0,51

0,195

1,16

0,377

1,81

0,4649

2,92

0,4982

0,52

0,1985

1,17

0,379

1,82

0,4656

2,94

0,4984

0,53

0,2019

1,18

0,381

1,83

0,4664

2,96

0,4985

0,54

0,2054

1,19

0,383

1,84

0,4671

2,98

0,4986

0,55

0,2088

1,2

0,3849

1,85

0,4678

3

0,49865

0,56

0,2123

1,21

0,3869

1,86

0,4686

3,2

0,49931

0,57

0,2157

1,22

0,3888

1,87

0,4693

3,4

0,49966

0,58

0,219

1,23

0,3907

1,88

0,4699

3,6

0,499841

0,59

0,2224

1,24

0,3925

1,89

0,4706

3,8

0,499928

0,6

0,2257

1,25

0,3914

1,9

0,4713

4

0,499968

0,61

0,2291

1,26

0,3962

1,91

0,4719

4,5

0,499997

0,62

0,2324

1,27

0,398

1,92

0,4726

5

0,5

0,63

0,2357

1,28

0,3997

1,93

0,4732

0,64

0,2389

1,29

0,4015

1,94

0,4738

http://lab4students.narod.ru/din.html

Напомним смысл знака “!” (факториал): 0! = 1.

Подчеркнем, что здесь неравенство а ≤ -300 – нестрогое, т.е. F(-300) = 0.

Отметим, что в этой формуле не важно, как написать: х < a или х ≤ а, — так как вероятность отдельного значения непрерывной случайной величины все равно нулевая.

studfiles.net

Таблица значений интегральной функции лапласа

Интегральная теорема Лапласа

Вновь предположим, что производится писпытаний, в каждом из которых вероятность появления события Апостоянна и равна р(0рРп (k1 , k2)того, что событие А появится в писпытаниях не менее k1и не более k2раз (для краткости будем говорить «от k1до k2раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже, опустив доказательство.

Теорема. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рп (k1 , k2) того, что событие А появится в п испытаниях от k1 до k2 раз, приближенно равна определенному интегралу

(*)

где

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл

не выражается через элементарные функции.

Таблица для интеграла

приведена в приложении 2.

В таблице даны значения функции Ф(х) для положительных значений хи для х = 0; для х.

В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5. Функцию Ф (х) часто называют функцией Лапласа.

Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразуем соотношение (*) так:

Итак, вероятность того, что событие А появится в п независимых испытаниях от k1 до k2 раз, вычисляется по формуле:

Пример 4. Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение. По условию, р=0,2; q=0,8; n=400; k1=70; k2=100. Воспользуемся интегральной теоремой Лапласа:

Вычислим нижний и верхний пределы интегрирования:

Таким образом, имеем

Р400(70, 100) = Ф(2,5) – Ф(–1,25) = Ф(2,5) + Ф(1,25).

По таблице приложения 2 находим:

Ф (2,5) = 0,4938; Ф (1,25)=0,3944.

Искомая вероятность равна:

Р400 (70, 100) = 0,4938 + 0,3944 = 0,8882.

Задачи

1. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент:

а) включено 4 мотора; б) включены все моторы; в) выключены все моторы.

Отв. а) Р6(4)=0,246; б) Р6(6)=0,26; в) Р6(0) = 0,000064.

2. Найти вероятность того, что событие А появится в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна 0,3.

Отв. Р = 1 – [Р5(0) + Р5(1)] = 0,472.

3. Событие В появится в случае, если событие А появится не менее двух раз. Найти вероятность того, что наступит событие В, если будет произведено 6 независимых испытаний, в каждом из которых вероятность появления события А равна 0,4.

Отв. Р = 1 – [Р6(0) + Р6(1)] = 0,767.

4. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, что событие А появится хотя бы 2 раза.

Отв. Р = 1 – [Р8(0) + Р8(1)] = 0,19.

5. Монету бросают 6 раз. Найти вероятность того, что герб выпадет:

а) менее двух раз; б) не менее двух раз.

Отв. а) Р = Р6(0) + Р6(1) = 7/64; б)Q = l – [Р6(0) + Р6(1)]=57/64.

6. Вероятность попадания в цель при одном выстреле из орудия р=0,9. Вероятность поражения цели при k попаданиях (k≥1) равна 1-qk. Найти вероятность того, что цель будет поражена, если сделано два выстрела.

Указание. Воспользоваться формулами Бернулли и полной вероятности.

Отв. 0,9639.

7. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.

Отв. Р400 (104) = 0,0006.

8. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти ве

zna4enie.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *