Корни уравнения третьей степени – Кубическое уравнение | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Содержание

Исследовательская работа по математике » Кубическое уравнение и методы его решения»

МБОУ « Мордовско-Паевская средняя общеобразовательная школа»

Районная научно—практическая конференция

« Первые шаги в науку-2016»

Секция «Точные науки. Математика»

Выполнил: ученик 11 класса МБОУ

« Мордовско—Паевская СОШ»

Ерочкин Иван

Руководитель: учитель математики

Кадышкина Н.В.

г. Инсар, 2016 г.

Оглавление

Введение

Основная часть

Кубическое уравнение и корни кубического уравнения …………………3
Методы решения…………………………………………………………….3

2.1.Простейшие кубические уравнения……………………………………….4

2.2. Способ разложения левой части уравнения на множители…………… 5

2.3. Способ понижения степени уравнения…………………………………..5

2.4.Теорема Виета для кубического уравнения………………………………6

2.5.Формула Кардано …………………………………………………………….7

2.6. Метод неопределенных коэффициентов…………………………………..12

2.7. Использование монотонности функции……………… ………………….13

2.8. Графический способ…………………………………………………………14

Решение кубических уравнений и некоторые выводы о рациональности

способов решения……………………………………………………………… 14

Заключение………………………………………………… ……………………. 15

Литература……………………………………………………………………… 16

Введение

Увлечение математикой начинается с размышления над какой-то интересной задачей или проблемой. Любому завороженному математическими тайнами человеку интересно знать историю математических открытий, разные способы решения задач, уметь использовать математические теоремы для решения сложных задач. Заинтересовался методами решения уравнений третьей степени c произвольными действительными коэффициентами. Так как в учебниках, да и в других книгах по математике, большинство рассуждений и доказательств проводится не на конкретных примерах, а в общем виде, то я решил искать частные примеры, подтверждающие ли опровергающие мою мысль. Рассмотрев немало практических примеров, мне удалось в результате исследования сделать выводы о рациональных способах решения кубических уравнений. В моей работе я рассмотрел кубические уравнения и способы их решения, которые не изучаются в школьной программе.

Однако моей главной задачей в ходе работы было нахождение более рационального способа для решения уравнений третьей степени.

Цель работы: узнать о кубических уравнениях больше, чем позволяет школьная программа, найти наиболее простой и наглядный способ решения кубического уравнения, выявить наиболее рациональные способы решения.

Для достижения поставленной цели необходимо выполнить задачи:

Подобрать необходимую литературу.
Отобрать материал для исследования, выбрать главную, интересную, понятную информацию.
Проанализировать и систематизировать полученную информацию.
Найти различные методы и приёмы решений уравнений третьей степени.
Создать электронную презентацию работы.

Актуальность: Практически все, что окружает современного человека – все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, в том числе и кубических, которые необходимо научиться решать.

Объект: кубическое уравнение и способы его решения.

Предмет исследования — различные способы решения кубических уравнений.

Гипотеза — предположение о том, что существует связь между коэффициентами кубического уравнения и его корнями, при решении таких уравнений можно применять разнообразные способы.

В процессе выполнения работы применялись такие методы исследования: — сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации.

Основная часть

I. Кубическое уравне́ние — алгебраическое уравнение третьей степени, общий вид которого следующий:

ax ³+ b x ²+ cx + d =0, аǂ (1) где x-переменная, a,b,c,d, — некоторые числа. Если а=1,то уравнение называют приведенным кубическим уравнением: х³+bх²+cx+d=0 (2).

Корни уравнения Согласно основной теореме алгебры, кубическое уравнение может иметь три корня (с учетом кратности). Из справочной литературы я узнал, что для кубических уравнений тоже существует дискриминант, как и для квадратных уравнений, с помощью которого различаются три случая существования корней кубического уравнения (1), о котором речь пойдёт ниже.

Пока я не нашёл ответ на вопрос, существуют ли общие формулы для корней кубических уравнений, рассмотрим частные случаи.

I I. Методы решения

2.1.Начнем с простейшего случая, когда свободный член d =0, в этом случае, то есть уравнение имеет вид. Решается вынесением х за скобки. В скобках останется квадратный трехчлен, корни которого легко найти через дискриминант.

Пример. Найти действительные корни уравнения.

Решение. ,x=0 или. меньше нуля, то действительных корней трехчлен не имеет.

Ответ: х=0.

Если в кубическом уравнении(1) b=c=0, то оно имеет достаточно простой вид: ax³+d=0. В этом случае . Пример. Найти действительные корни кубического уравнения

Решение:

2.2. Способ разложения левой части уравнения на множители

Симметрические или возвратные уравнения.

Уравнение вида ах³ + bx² + bх + a = 0 называется возвратным или симметрическими, если его коэффициенты, стоящие на симметричных относительно середины позициях, равны.

Левую часть уравнения можно разложить на множители:

Такое уравнение обязательно имеет корень х = -1, корни квадратного уравнения легко находятся через дискриминант

Пример:, — корень уравнения, , , D=36-4=32,

Ответ: ,

Пример: Решить уравнение: х³ + 2x² + 2х + 1 = 0.

Решение.

У исходного уравнения обязательно есть корень х = -1, поэтому разделим х³ + 2x² + 2х + 1 на (х + 1) по схеме Горнера:

х³ + 2x² + 2х + 1 = (х + 1)(x² + х + 1) = 0. Квадратное уравнение x² + х + 1 = 0 не имеет корней.

Ответ: -1.

Пример. Решить кубическое уравнение .

Решение. Это уравнение возвратное. Проведем группировку:

Очевидно, x = -1 является корнем уравнения. Находим корни квадратного трехчлена .

Ответ:

Кососимметрические уравнения

Уравнение вида называется кососимметрическим кубическим уравнением. Такое уравнение обязательно имеет корень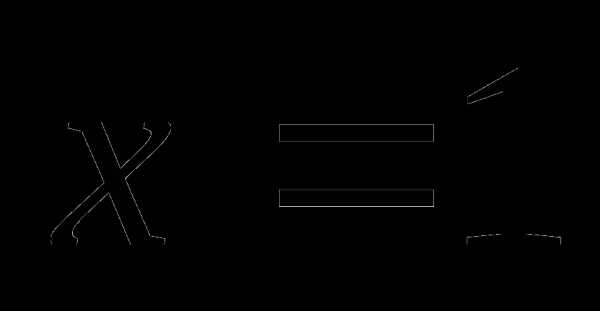 и сводится к квадратному.

Например: .

Используя корень , сводим уравнение к квадратному , которое не имеет действительных корней.

Ответ: .

Рассмотрим решение уравнения в комплексных числах

или , D = 1 – 36 = — 35, D < 0

Ответ: ,

Для разложения многочлена на множители можно использовать различные способы: вынесение за скобки общего множителя, способ группировки, деление многочлена на многочлен, метод неопределенных коэффициентов, разложение по формулам сокращенного умножения и т.д.

2.3. Способ понижения степени уравнения.

Способ основан на теореме Безу и делении многочленов. Алгоритм его выполнения сводится к нижеследующему:

Первоначально подберем один из корней уравнения, использовав свойство, что у кубического уравнения неизменно присутствует, по крайней мере, один действительный корень, причем целый корень кубического уравнения с целыми коэффициентами будет делителем свободного члена d.

И, соответственно, требуется обнаружить корень среди этих чисел и проверить его путём подстановки в уравнение. Примем данный корень за x ₁.

На следующем этапе разделим многочлен ax ³+ b x ²+ cx + d на двучлен x – x ₁.

Применим теореме Безу (деление многочлена на линейный двучлен), согласно которой это деление без остатка возможно, и по итогу вычислений получаем многочлен второй степени, который равен нулю. Решая полученное квадратное уравнение, мы найдём (или нет!) два других корня.

Пример: x ³ – 3x² – 13x + 15 = 0.

Делители свободного члена: 0, ± 1, ± 2, ± 3. Получаем, что 1 является корнем. Далее разделим левую часть этого уравнения на двучлен x- 1, и получим: x² – 2x – 15.

infourok.ru

Степенные уравнения | LAMPA — онлайн-учебник, который каждый может улучшить

Кубическое уравнение

Уравнение вида ax3+bx2+cx+d=0ax^3+bx^2+cx+d=0ax3+bx2+cx+d=0 называется кубическим уравнением.

В ЕГЭ, как правило, встречаются кубические уравнения вида (kx+b)3=c(kx+b)^3=c(kx+b)3=c.

Приведите уравнение к виду (kx+b)3=c(kx+b)^3=c(kx+b)3=c (к этому виду можно привести почти все кубические уравнения в ЕГЭ).
Извлеките кубический корень из обеих частей уравнения. Так как функция y=x3y=x^3y=x3, это эквивалентное преобразование. Тогда уравнение примет вид kx+b=c3.kx+b=\sqrt[3]{c}.kx+b=3c. Кубический корень из ccc можно .
Решите получившееся линейное уравнение: x=c3−bk.x=\frac{\sqrt[3]{c}-b}{k}{.}x=k3c−b.

Решим уравнение 4(x+1)3=5004(x+1)^3=5004(x+1)3=500.

Приведем уравнение к виду (kx+b)3=c(kx+b)^3=c(kx+b)3=c (важно, чтобы вся левая часть уравнения представляла собой некоторое выражение в 3-й степени): 4(x+1)3=500⇔(x+1)3=125.4(x+1)^3=500\,\,\,\,\Leftrightarrow \,\,\,\,(x+1)^3=125.4(x+1)3=500⇔(x+1)3=125.
Извлечем кубический корень из обеих частей уравнения: (x+1)3=125⇔x+1=1253=5.(x+1)^3=125\,\,\,\,\Leftrightarrow \,\,\,\,x+1=\sqrt[3]{125}=5.(x+1)3=125⇔x+1=3125=5. Отсюда получаем x=5−1=4.x=5-1=4{.}x=5−1=4.

Уравнения 4-й степени и более высоких степеней

Уравнение, левая часть которого представляет собой , называется уравнением nnn-й степени.
Уравнение nnn-й степени имеет вид cnxn+cn−1xn−1+…+c1x+c0=0c_n x^n + c_{n-1}x^{n-1}+…+c_1 x+c_0=0cnxn+cn−1xn−1+…+c1x+c0=0.
В частности, уравнение вида ax4+bx3+cx2+dx+e=0ax^4+bx^3+cx^2+dx+e=0ax4+bx3+cx2+dx+e=0 называется уравнением 4-й степени.

В ЕГЭ, как правило, встречаются уравнения вида (kx+b)n=c(kx+b)^n=c(kx+b)n=c, где nnn — .

Приведите уравнение к виду (kx+b)n=c(kx+b)^n=c(kx+b)n=c (в ЕГЭ к этому виду можно привести почти все уравнения степени 333 и выше).
Извлеките корень nnn-й степени из обеих частей уравнения.
- Если nnn — нечетное число, то уравнение примет вид kx+b=cn.kx+b=\sqrt[n]{c}.kx+b=nc.
- Если nnn — четное число, то при c≥0c\ge 0c≥0 уравнение эквивалентно объединению [kx+b=cn,kx+b=−cn,\left[\begin{array}{lr} kx+b=\sqrt[n]{c},\\ kx+b=-\sqrt[n]{c},\end{array}\right.[kx+b=nc,kx+b=−nc, где квадратная скобка [[[ обозначает «или».
Решите получившееся линейное уравнение:
- для нечетных nnn получаем один корень уравнения x=cn−bkx=\frac{\sqrt[n]{c}-b}{k}x=knc−b
- для четных nnn при c≥0c\ge 0c≥0 получаем два корня [x=cn−bk,x=−cn−bk.\left[\begin{array}{lr} x=\frac{\sqrt[n]{c}-b}{k},\\x=\frac{-\sqrt[n]{c}-b}{k}{.}\end{array}\right.[x=knc−b,x=k−nc−b.

Решим уравнение 4(x+1)4=3244(x+1)^4=3244(x+1)4=324.

Приведем уравнение к виду (kx+b)4=c(kx+b)^4=c(kx+b)4=c (важно, чтобы вся левая часть уравнения представляла собой некоторое выражение в 4-й степени): 4(x+1)4=324⇔(x+1)4=81.4(x+1)^4=324\,\,\,\,\Leftrightarrow \,\,\,\,(x+1)^4=81.4(x+1)4=324⇔(x+1)4=81.
Извлечем корень 4-й степени из обеих частей уравнения: (x+1)4=81⇔[x+1=814,x+1=−814(x+1)^4=81\,\,\,\,\Leftrightarrow \,\,\,\,\left[\begin{array}{lr} x+1=\sqrt[4]{81},\\x+1=-\sqrt[4]{81}\end{array}\right.(x+1)4=81⇔[x+1=481,x+1=−481⇔[x+1=3,x+1=−3.\,\,\,\,\Leftrightarrow \,\,\,\,\left[\begin{array}{lr}x+1=3,\\x+1=-3{.}\end{array}\right.⇔[x+1=3,x+1=−3. Отсюда получаем два корня: x1=3−1=2x_1=3-1=2×1=3−1=2, x2=−3−1=−4x_2=-3-1=-4×2=−3−1=−4.

lampa.io

Уравнение третьей степени Википедия

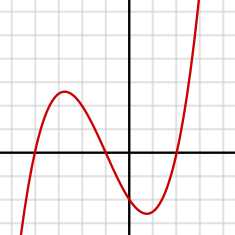График кубической функции y=(x3+3×2−6x−8)/4{\displaystyle y=(x^{3}+3x^{2}-6x-8)/4}, у которой 3 действительных корня (в месте пересечения горизонтальной оси, где у = 0). Имеются 2 критические точки Уравнение 8×3+7×2−4x+1{\displaystyle 8x^{3}+7x^{2}-4x+1} имеет один действительный и два мнимых корня.

Куби́ческое уравне́ние — алгебраическое уравнение третьей степени, общий вид которого следующий:

ax3+bx2+cx+d=0,a≠0.{\displaystyle ax^{3}+bx^{2}+cx+d=0,\;a\neq 0.}

Для графического анализа кубического уравнения в декартовой системе координат используется кубическая парабола.

Кубическое уравнение общего вида может быть приведено к каноническому виду путём деления на a{\displaystyle a} и замены переменной x=y−b3a,{\displaystyle x=y-{\tfrac {b}{3a}},} приводящей уравнение к виду:

y3+py+q=0,{\displaystyle y^{3}+py+q=0,}

где

q=2b327a3−bc3a2+da=2b3−9abc+27a2d27a3,{\displaystyle q={\frac {2b^{3}}{27a^{3}}}-{\frac {bc}{3a^{2}}}+{\frac {d}{a}}={\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}},}

p=ca−b23a2=3ac−b23a2.{\displaystyle p={\frac {c}{a}}-{\frac {b^{2}}{3a^{2}}}={\frac {3ac-b^{2}}{3a^{2}}}.}

История[

ru-wiki.ru