Сектор окружности – Сектор окружности формулы, описание и рисунки

Содержание

Площадь сектора круга

Площадь сектора круга и площадь сегмента учить не нужно! Дорогие друзья! Вы, наверное, не раз просматривали справочник с математическими формулами, и, наверняка, возникала мысль: «Да разве возможно их все выучить?». Скажу вам, что возможно, но зачем? Зачем забивать голову массой формул, постоянно повторять их, ужасаться тому, что какую-то забыл и снова повторять? Не надо!

На самом деле достаточно запомнить треть всех формул, базовых формул или ещё меньше. Далее вы поймёте о чём идёт речь. Все остальные формулы можно быстро вывести, зная основу, применяя логику, и запомнив принципы, которым нужно следовать.

Приведу пример, существует 32 формулы приведения, учить их – это бессмысленное занятие. Как быстро вспомнить любую из них — изложено в статье «Формулы приведения», посмотрите.

В этой статье мы рассмотрим, как быстро восстановить в памяти формулы площади сектора круга, площади его сегмента, длину дуги окружности. Именно эти формулы понадобятся для решения ряда по планиметрии, которые разберем в следующей статье. Итак, «базовые» формулы, их нужно выучить и знать!

Площади круга (формула):

Формула длины окружности:

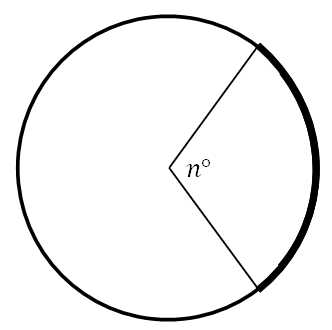
Изобразим сектор, соответствующий определённому центральному углу n:

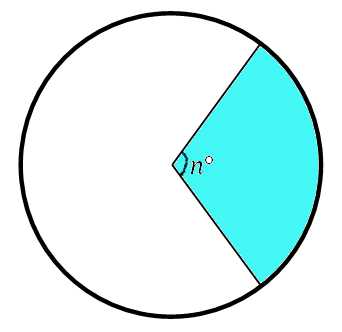
Рассуждаем логически: если площадь круга равна S=ПR², то площадь соответствующая сектору в один градус будет равна 1/360 от площади круга (мы знаем, что вся окружность — это угол в 360 градусов), то есть

Далее понятно, что площадь сектора, соответствующая центральному углу в n градусов равна произведению одной тристашестидесятой площади круга и центрального угла n (соответствующего сектору), то есть

Вот вам и формула площади сектора.

Или можно выстроить рассуждение следующим образом:

Сектор в 1 градус — это 1/360 часть круга, соответственно сектор в n градусов — это n/360 часть круга. То есть площадь сектора будет равна произведению площади круга и этой части:

Далее найдём площадь сегмента.

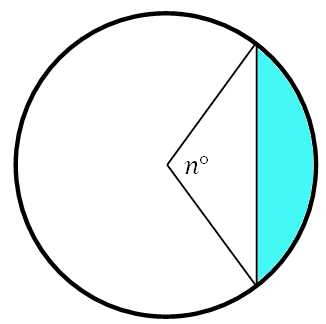
Всё просто. Необходимо из площади сектора вычесть площадь треугольника (он обозначен жёлтым цветом). Площадь треугольника, как мы знаем, равна половине произведения соседних сторон на синус угла между ними (эту формулу нужно знать, она не сложная). В данном случае это:

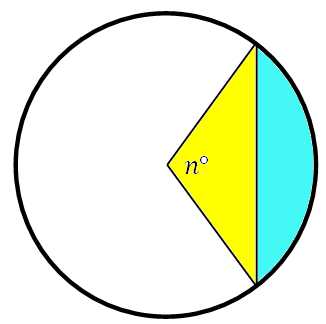
Значит,

Вот вам и площадь сегмента!

Площадь сегмента, где центральный угол больше 180 градусов находится просто:

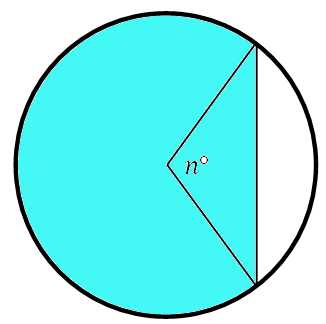
Из площади круга вычитаем площадь полученного нами сегмента:

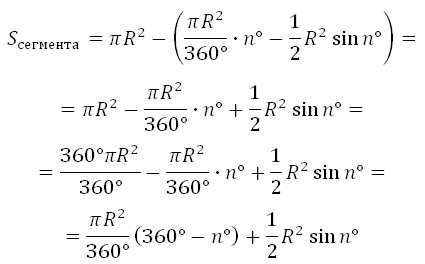
Угол 360 – n градусов это угол, который соответствует изображённому сектору (жёлтый цвет):

То есть, другими словами, к его площади мы прибавляем площадь треугольника и получаем площадь оговоренного сегмента.

Аналогичным образом определяем длину дуги окружности. Как уже сказано, длина окружности равна:

Значит, длина дуги окружности соответствующая одному градусу будет равна одной тристашестидесятой от 2πR, то есть

Далее понятно, что длина дуги, соответствующая центральному углу в n градусов равна произведению одной тристашестидесятой длины окружности и соответствующему углу, то есть

Получили длину дуги окружности. Конечно, данную информацию учителя дают ученикам, и ничего такого секретного вы не узнали. Но, уверен, статья принесёт вам пользу.

Повторюсь, что самое главное — знать формулы площади круга и длины окружности, а далее работает только логика.

Предлагаю посмотреть дополнительный урок Дмирия Тарасова на эту тему. Рассматриваются формулы длины дуги окружности и площади сектора, где центральный угол задан в радианной мере.

На этом всё. Успехов Вам!!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Формула нахождения площади сектора круга онлайн

Площадь сектора круга является лишь частью площади всей плоской фигуры, которая ограничена окружностью с радиусом r. Если на окружности разместить две точки A и B, из которых к центру круга прочертить два радиуса, в результате получим сектор круга, который ограничивается дугой AB на окружности и двумя радиусами. Радиусы делят S круга на два сектора. Если между радиусами угол будет равен 180 градусов, то получится два равных сектора. Мы знаем, что S круга равна квалрату радиуса умноженному на «пи» — число постоянное, равное 3,1415. Площадь сектора можно определить по нескольким формам.
1. Через радиус и длину дуги:

здесь r — радиус сектора;
p — величина дуги сектора.

Расчет площади сектора круга через длину дуги и радиус

2. Через радиус и угол сектора, выраженный в градусах:

здесь r — радиус сектора;
n — показанный в градусах угол сектора.

Расчет площади сектора круга через радиус и угол

3. Через радиус и угол дуги сектора, показанный в радианах:

здесь r — радиус сектора;
α — показанный в радианах угол сектора.
С помощью онлайн калькуляторы вы легко вычислите S сектора круга, подставив исходные данные в нужную форму для расчета.

Расчет площади сектора круга через угол сектора в радианах

infofaq.ru

Площадь сектора круга — формула, пример расчета

Сектор круга – это плоская фигура, ограниченная дугой и радиусами, соединяющими концы дуги с центром круга.

Существует две формулы площади сектора круга. Расчеты могут производиться как через длину дуги, так и через угол между радиусами. Если известна длина дуги, то применяется такая формула:

Когда дан угол между ограничивающими сектор радиусами, расчет площади представляет собой произведение площади круга на соотношение угла между радиусами к углу полной окружности, т.е. 360°.

Рассмотрим пример расчета площади сектора круга по обеим формулам.

Пусть дан сектор, в котором l = 5 см, r = 3 см, α = 95°. Найдем площадь по всем формулам:

Площадь сектора кольца

Сектор кольца – это плоская фигура, которая располагается в окружности и ограничивается двумя дугами разного радиуса и линиями, проведенными от центра к большей дуге.
Формула площади сектора кольца представляет собой разность площадей большего и меньшего сектора круга.

Если дан угол α, то площадь сектора кольца можно найти по следующей формуле:

Рассмотрим пример расчета площади сектора кольца.

Пусть дана окружность с радиусом 5 см. Сектор кольца ограничен углом α = 45°, а радиус меньшего сектора равен r = 3 см. Найдем площадь.
Из условий задачи мы понимаем, что больший радиус равен радиусу окружности, то есть R = 5 см. Подставим данные в формулу:

Расчет площади шарового сектора

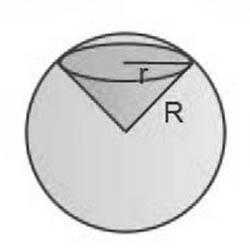
Шаровым сектором называют часть шара, которая ограничивается кривой поверхностью шарового сегмента и конической фигурой, вершиной которой является центр шара, а основанием – шаровой сегмент.
Чтобы вывести формулу площади шарового сектора, потребуется найти высоты конуса и сегмента. Она легко вычисляется по теореме Пифагора. Для этого необходимо знать радиус шара и радиус основания конуса. Обозначим радиус шара как R, а радиус сегмента – r. Тогда

Площадь сектора – это сумма площадей конуса и сегмента. Подставим выведенные формулы в общую:

Рассмотрим пример расчета площади поверхности шарового сектора.

Пусть дан шар с радиусом R = 4 см, в котором выделен сектор с радиусом основания r = 1,5 см. Найдем площадь.
Подставляем все данные в формулу и производим расчеты:

2mb.ru

что такое сектор круга? помогите пожалуйста! (по научному)

Кусок круглого пирога.

ограничено двумя радиусами.

Определения. Все приводимые определения эквивалентны: Сектор круга — это пересечение круга и некоторого его центрального угла. Сектор круга — это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром. Сектор круга — это часть угла, включающая точки удаленные от вершины угла не более чем на некоторое расстояние (радиус сектора). Параметры сектора. Форму и размеры сектора полностью определяют два параметра: угол θ, радиус R. Критерий конгруэнтности. Сектора, у которых совпадают оба параметры параметра R и θ, — конгруэнтны. Критерий подобия. Сектора, у которых совпадают параметры θ, — подобны. Площадь сектора: S = θR2/2, если угол θ выражен в радианах, S = (θ/360°)·πR2, если угол θ выражен в градусах. Периметр сектора: P = (2 + θ)·R, если угол θ выражен в радианах, P = (2 + πθ/180°)·R, если угол θ выражен в градусах, а π — постоянная пи. Частные случаи секторов: При θ = 0 получается вырожденный сектор, совпадающий с отрезком длиной R. У сектора с углом θ = 1 радиан (≈57°) длины всех сторон равны R, а периметр — 3R. Сектор с углом θ = 90° называется квадрантом; особенность квадранта: все три его угла имеют величину 90°. У сектора с углом θ = 2 радиана (≈114°) площадь равна квадрату радиуса R2. Сектор с углом θ = 180° представляет собой половину окружности; особенность: такой сектор имеет только 2 угла величиной 90°. При θ > 180° сектор становится невыпуклой фигурой. При θ = 360° сектор вырождается в полную окружность. Дополнительные сектора. Любые два радиуса разбивают круг на пару секторов. Такие сектора называются взаимно дополнительными, их сумма углов составляет 360°. Круговые диаграммы. Два или более радиусов разбивают круг на такое же число секторов, сумма углов которых составляет 360°. Это свойство используется при построении так называемых секторных (круговых) диаграмм, в которых вся окружность принимается за 100% некоторого ресурса, а отдельные сектора отражают его разделение по долям. Развертка конуса. Любой невырожденный сектор представляет собой развертку конуса (без основания). Высоту h этого конуса можно найти по формуле: h = R√(1 — θ2/4π2), если угол θ выражен в радианах, h = R√(1 — (θ/360°)2), если угол θ выражен в градусах.

touch.otvet.mail.ru

Площадь сектора круга — Циклопедия

Задача B3: площадь сектора [3:01] Сектор круга с α Сектор круга с α>π/2

Площадь сектора Задание 3 ЕГЭ // Математика и мы [24:22]

Площадь сектора круга — это число, характеризующее сектор круга в единицах измерения площади.

Сектор круга — это часть круга, заключённая между двумя радиусами.

Введём обозначения:

R — радиус круга;

a — полуоснование сегмента;

h — высота сегмента;

R-h — отклонение основания сегмента от центра круга;

α — угол между осью симметрии сектора и радиусом в крайней точке сектора;

S_сект — площадь сектора круга.

[править] 1-й способ

[править] 2-й способ

[править] Другие формулы

cyclowiki.org

🎓 сектор окружности ⚗ с английского на русский 🧬

сектор — а, м. secteur m.,&LT; лат. sector. 1. мат. Сектор или пропорциональный циркуль; есть орудие из двух пальмового дерева или кости, медных, либо серебреных линеек, двумя концами своими соединенных имеет шарньером, и свободно около цилиндрического… … Исторический словарь галлицизмов русского языка

СЕКТОР

— (лат. sector, от secare отделять, рассекать). В геометрии: часть круга, заключающаяся между двумя радиусами и дугою. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. СЕКТОР в геометрии: часть круга, ограниченная… … Словарь иностранных слов русского языка

сектор — 3.26 сектор: Конкретная область промышленности или технологии, в которой используются специализированные методы неразрушающего контроля, требующие знаний о конкретном изделии, оборудовании или специальной подготовки. Примечание Сектор можно… … Словарь-справочник терминов нормативно-технической документации

сектор обзорности A — 3.3.3 сектор обзорности A (sector of vision А): Сегмент обзорности перед машиной на измерительной площадке с хордой длиной 9,5 м в окружности радиусом 12 м, которая делится пополам продольной плоскостью, проходящей через центральную точку… … Словарь-справочник терминов нормативно-технической документации

СЕКТОР — (лат. sector, букв. рассекающий, отделяющий, от seco разрезаю, разделяю) 1) плоский С. часть площади криволинейной фигуры, огранич. двумя прямыми, исходящими из одной точки внутри фигуры, и дугой между ними. 2) Круговой С. часть круга, огранич.… … Большой энциклопедический политехнический словарь

Дуга окружности — Дуга одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки A и B окружности разбивают ее на две части; каждая из этих частей называется дугой. Если A и B – концы диаметра (т … Википедия

Купол — У этого термина существуют и другие значения, см. Купол (значения). Разрез купола Купол (итал. cupola … Википедия

Крюк (деталь) — У этого термина существуют и другие значения, см. Крюк. Крюк деталь, которая обычно применяется для закрепления и поднятия груза с помощью подъемных средств типа подъёмного крана, троса или цепи, к которой прикрепляется сам крюк. В общем… … Википедия

Часы прибор для измерения времени — Содержание: 1) Исторический очерк развития часовых механизмов: а) солнечные Ч., b) водяные Ч., с) песочные Ч., d) колесные Ч. 2) Общие сведения. 3) Описание астрономических Ч. 4.) Маятник, его компенсация. 5) Конструкции спусков Ч. 6) Хронометры … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Часы — Содержание. 1) Исторический очерк развития часовых механизмов: а) солнечные Ч., b) водяные Ч., с) песочные Ч., d) колесные Ч. 2) Общие сведения. 3) Описание астрономических Ч. 4.) Маятник, его компенсация. 5) Конструкции спусков Ч. 6) Хронометры … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Национальный банк Казахстана — (National Bank of Kazakhstan) Сведения о национальном банке республики Казахстан, функции и задачи Национальноо банка Сведения о национальном банке республики Казахстан, функции и задачи Национальноо банка, история создания банка Содержание… … Энциклопедия инвестора

translate.academic.ru

Сектор — круг — Большая Энциклопедия Нефти и Газа, статья, страница 1

Сектор — круг

Cтраница 1

Секторы круга обозначают долю того или иного объекта. При помощи таких диаграмм удобно показывать различные зависимости. Другими словами, на круговой диаграмме удобно отображать процессы и явления, допускающие членение по какому-либо признаку при условии, что части членения будут соизмеримы друг с другом. [1]

Сектор круга ( рис. 112) АСВ рассекается хордой АВ на две части, сегмент А ЕВ и треугольник АСВ, из которых первый меньше второго, когда угол АСВ очень мал, и больше второго, когда угол АСВ является очень тупым углом. Таким образом, существует положение, при котором сектор АСВ делится хордой АВ на две равные части. [2]

Сектор круга закрашивается от StAngle до EndAngle. Рисуется текущим цветом и заполняется текущим видом заполнения. [3]

Найти сектор круга АСВ, который делится хордой АВ на две равные части, так что треугольник АСВ оказывается равным сегменту А ЕВ. [5]

В сектор круга радиуса R с центральным углом в 150Э вписан круг. [6]

В сектор АОВ круга радиуса R с центральным углом а вписан правильный треугольник, одна из вершин которого лежит в середине дуги АВ, а две другие — на радиусах ОА и ОВ. [7]

Радиус сектора круга равен г, а хорда его дуги равна а. [8]

Из сектора круга радиуса R свертывается коническая воронка. При каком центральном угле она имеет наибольший объем. [9]

Чтобы найти секторы круга, в которых tg2x0, нужно вначале построить радиусы, соответствующие углам, для котэрых tg 2х — О и tg 2x не существует. [10]

Дана площадь S сектора круга. Найти значение центрального угла, при котором периметр сектора является наименьшим. [11]

Пластинка, имеющая форму сектора круга, шарнирно оперта по контуру; нагрузка равномерно распределена по всей поверхности. [12]

Пластинка, имеющая форму сектора круга, защемлена по дуге контура и шарнирно оперта по прямолинейным краям; нагрузка равномерно распределена по всей поверхности. [13]

Качалка, имеющая форму сектора круга радиуса R, качается на горизонтальном столе. По какой траектории движется ее вершина. [14]

Решение первой краевой задачи для сектора круга дается формулой из разд. [15]

Страницы: 1 2 3 4