Как найти объем пирамиды по векторам: Объем пирамиды, построенной на векторах онлайн

Как определить объем пирамиды

• Альфашкола
• Статьи
• Как определить объем пирамиды

Пирамида (др.-греч. πυραμίς, πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.

 

Лемма

Две пирамиды, имеющие равные высоты и равновеликие основания, имеют равные объемы.

 

Теорема

Объем пирамиды равен одной трети произведения площади основания на высоту: \(V={1\over3}S*H\) , где S – площадь основания, H – высота пирамиды.

 

Теорема 

Объем V усеченной пирамиды может быть найден по формуле \(V={1\over3}H(S1+{{\sqrt {S1S2}}}+S2)\), где H – высота усеченной пирамиды, S1 и S2 – площади ее оснований.

 

Часто даны координаты вершин пирамиды ABCD и требуется найти ее объем. Даная задача может быть решена методами аналитической геометрии. Покажем ее решение на примере.

 

Пусть даны координаты вершин пирамиды ABCD и требуется найти ее объем: A(10;6;6), B(-2;8;2), C(6;8;9), D(7;10;3).

Решение

 

Объем пирамиды равен \(1\over6\) объема параллелепипеда, построенного на векторах AB, AC, AD. Найдем координаты этих векторов, для этого из соответствующей координаты конца вектора вычтем координату его начала:

AB=(-12;2;-4), AC=(-4;2:3), AD=(-3;4;-3).

 

Тогда объем параллелепипеда равен значению детерминанта (определителя) матрицы, составленной из координат векторов (строка матрицы – координаты вектора). Определитель третьего порядка находим по правилу треугольников.

 

 

Автор — Дмитрий Айстраханов

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Мария Евгеньевна Эминова

Репетитор по математике

Стаж (лет)

Образование:

Удмуртский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Елена Александровна Дворянинова

Репетитор по математике

Стаж (лет)

Образование:

Северо-Казахстанский Государственный Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Маргарита Руслановна Мередова

Репетитор по математике

Стаж (лет)

Образование:

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Физика
• Химия
• Русский язык
• Английский язык
• Обществознание
• История России
• Биология
• География
• Информатика

Похожие статьи

• Как легко разделить на 0,125
• РУДН: Нефтегазовое дело (вступительные испытания, отзывы)
• Уравнения с параметром.
  Задание №18 в ЕГЭ
• Рациональные уравнения
• Как найти точку пересечения плоскости и прямой
• Задачи на оптимизацию. Задание №17 из ЕГЭ
• Решаем олимпиадные задачи для 5 класса
• Летние идеи для занятия спортом

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Даны координаты вершин пирамиды. решение задачи Аналитическая геометрия с ответом

Пример 1

Даны координаты вершин пирамиды А₁А₂А₃А₄ . Найти:

1) длину ребра А₁А₂;

2) угол между рёбрами А₁А₂  и А₁А₄ ;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃;

Сделать чертёж.

А₁(3; 5; 4),        А₂(8; 7; 4),            А₃(5; 10; 4),          А₄(4; 7; 8).

Пример 2

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

1. А₁ (7; 7; 3), А₂ (6; 5; 8), А₃ (3; 5; 8), А₄ (8; 4; 1).

Пример 3

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Пример 4

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти:

1) координаты и модули векторов А₁ А₂и А₁ А₄;  

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) площадь грани А₁ А₂ А₃;         

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂ А₃;

7) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3.

Сделать чертеж.

А₁ (0; 4; -4), А₂ (5; 1; -1), А₃ (-1; -1; 3), А₄ (0; -3; 7).

Пример 5

Пример 6

Пример 7

Пример 8

Пример 9

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

векторных пространств — объем пирамиды линейной алгебры

спросил 8 лет, 9 месяцев назад

Изменено 7 лет, 11 месяцев назад

Просмотрено 10 тысяч раз

$\begingroup$

Найдите объем пирамиды с треугольным основанием, ограниченной векторами (1,-1, 2) и (1, 1, 1) и вершина, расположенная в (3, 2, 5).

Не знаю, как решить эту проблему. Я знаю, что объем пирамиды: 1/3 (основание * высота), но с заданными векторами я не уверен, как это решить.

Надеюсь, кто-нибудь сможет мне помочь, буду очень признателен.

Спасибо.

• линейная алгебра
• векторные пространства
• объем

$\endgroup$

1

$\begingroup$

Подсказка 1: Для двух произвольных векторов $v_1$ и $v_2$ $\|v_1 \times v_2\| = \|v_1\| \|v_2\|\sin(\theta)$. Вы должны быть в состоянии найти площадь основания, используя этот факт.

Подсказка 2: $v_1 \times v_2 $ даст вам вектор, перпендикулярный основанию.

Подсказка 3: Пусть $u = \frac {v_1 \times v_2}{\|v_1 \times v_2\| }$, то $u \cdot v_3$ даст вам высоту пирамиды, где $v_3$ — вектор к вершине из угла в начале координат.

Подсказка 4 (бонус): Тройное произведение векторов $|v_3 \cdot (v_1 \times v_2)|$ дает объем параллелепипеда, заданного тремя векторами. Сколько пирамид поместится в параллелепипеде?

$\endgroup$

$\begingroup$

Я предполагаю, что поскольку вам даны только два вектора $\vec{a}, \vec{b}$ по основанию, третий находится путем соединения головок. В этом случае площадь основания равна

$$A_{база} = \frac{1}{2}|\vec{a} \times \vec{b}| = \frac{1}{2}|-3\шляпа{x} + \шляпа{y} + 2 \шляпа{z}| = \sqrt{14}/2.$$

Перекрестное произведение также определяет нормаль к плоскости, содержащей $\vec{a}, \vec{b}$. Уравнение этой плоскости $-3x + y + 2z = 0$, так как начало координат содержится в плоскости.

Расстояние до плоскости, являющейся высотой пирамиды, равно

$$h = \frac{-3(3) + 1(2) + 2(5)}{\sqrt{14}} = \frac{3}{\sqrt{14}}.$$

Тогда ваш объем равен

$$V = \frac{1}{3}A_{base}h = \frac{1}{3} \frac{\sqrt{14}}{2} \frac{3}{\sqrt{14 }} = \frac{1}{2}. $$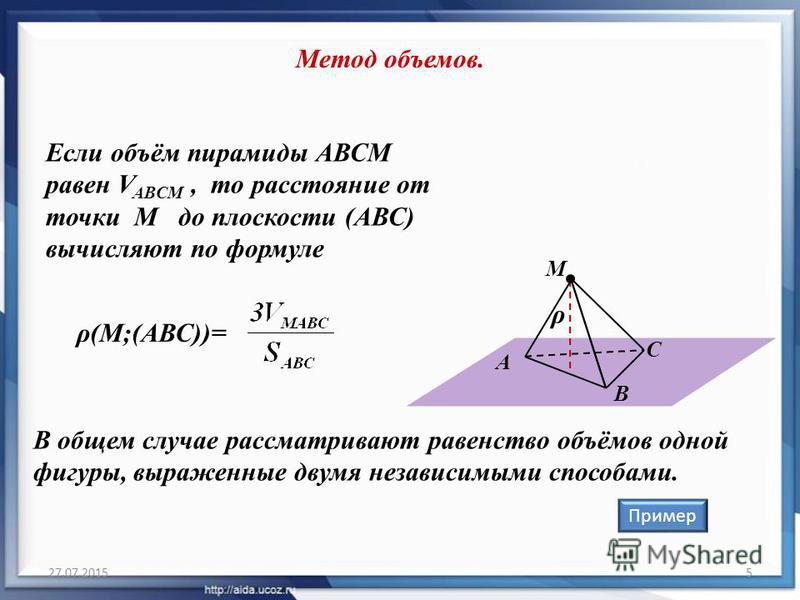

$\endgroup$

4

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

линейная алгебра — Объем пирамиды как определитель?

Задавать вопрос

спросил 10 лет, 1 месяц назад

Изменено 10 лет, 1 месяц назад

Просмотрено 3к раз

$\begingroup$

У меня есть три заданные точки A, B и C, каждая из которых является углом пирамиды. Другой угол находится в ориго.

Задача состоит в том, чтобы составить определитель, описывающий объем пирамиды.

К сожалению, моя книга и Википедия не согласны, как это сделать, поэтому я спрашиваю вас, ребята.

ПС. Следующий вопрос заключается в том, будет ли объем каким-либо другим, если векторы положения ( a , b и c ) а ориго все где расположены в одной плоскости?

Любая помощь будет очень признательна!

• линейная алгебра
• определитель

$\endgroup$

3

$\begingroup$

Параллелепипед, натянутый на $\mathbf a, \mathbf b, \mathbf c$, имеет (ориентированный) объем $(\mathbf a\times \mathbf b)\cdot \mathbf c$ (или с любой их перестановкой). Пирамида имеет $\frac16$ этого объема. Выражение также можно записать в виде $$V = \frac16 \det(\mathbf a, \mathbf b, \mathbf c)$$ т.