Вычисление объемов тел с помощью интеграла
Прежде чем мы перейдём к нашей теме, давайте ненадолго вернёмся в алгебру и вспомним формулу Ньютона-Лейбница, которая позволяет нам вычислить определённый интеграл, повторим основные свойства интеграла.
Если функция непрерывна на отрезке , то справедлива формула:
– первообразная для .
− геометрический смысл определённого интеграла.
Изучая алгебру, мы говорили, что с помощью определённого интеграла можно вычислять площадь плоских фигур.
Сегодня на уроке мы попробуем применить определённый интеграл к вычислению объёмов тел.
Заключим тело , объём которого нужно найти между двумя параллельными плоскостями и .
Введём систему координат так, чтобы ось , абсциссы точек пересечения оси с плоскостями и обозначим буквами и . Пусть .
Пересечём наше тело произвольной плоскостью, перпендикулярной к оси . Фигура – полученная в сечении тела плоскостью является либо кругом либо многоугольником для любого из отрезка . В граничных точках сечение может вырождаться в точку, как, например, в нашем случае при .
Обозначим площадь фигуры за . Предположим, что – это непрерывная функция на числовом отрезке .
Разобьём числовой отрезок на равных отрезков.
Длина каждого отрезка равна .
Через точки с абсциссами проведём плоскости, перпендикулярные к оси . Тогда наше тело разобьётся на тел , , …, .
Высота каждого из этих тел равна .
Если фигура – круг, то объём тела приближённо равен объёму цилиндра, с основанием и высотой .
Если же в сечении – многоугольник, то объём тела приближённо равен объёму прямой призмы с основанием и высотой .
Каждый из этих объёмов равен произведению площади основания на высоту . Тогда объём всего тела равен сумме этих объёмов . Чем больше , тем точнее приближённое значение объёма всего тела и меньше .
Без доказательства примем, что объём тела равен .
С другой стороны, сумма является интегральной суммой для непрерывной функции на числовом отрезке , поэтому можно записать, что предел .
Тогда получим, что объем тела равен .
Эта формула называется основной формулой для вычисления объёмов тел.
Давайте теперь попробуем найти с помощью определённого интеграла объёмы пространственных тел.
Начнём с прямоугольного параллелепипеда, высота которого равна , а площадь основания – .
Площадь сечения прямоугольного параллелепипеда не изменяется в любой точке отрезка от до и равна площади основания. Тогда получим, что объём прямоугольного параллелепипеда равен . Вынесем за знак интеграла и получим, что объём прямоугольного параллелепипеда равен .
Теперь попробуем с помощью интеграла вычислить объём прямой призмы.
Пусть дана прямая -угольная призма с площадью основания и высотой .
Как и в случае прямоугольного параллелепипеда, площадь сечения прямой призмы не изменяется в любой точке отрезка от до и равна площади основания. Тогда получим, что объём прямой призмы равен . Вынесем за знак интеграла и получим, что объём прямой призмы равен .
Теперь рассмотрим цилиндр с высотой и площадью основания .
Как и в случае прямоугольного параллелепипеда и прямой призмы, площадь сечения цилиндра не изменяется в любой точке отрезка от до и равна площади основания. Тогда получим, что объём цилиндра равен . Вынесем за знак интеграла и получим, что объём цилиндра равен .
Решим несколько задач.
Задача: сечение тела плоскостью, перпендикулярной к оси и проходящей через точку с абсциссой , является квадратом, сторона которого равна . Найти объем этого тела.
Решение: воспользуемся только что доказанной формулой.
По рисунку видно, что пределами интегрирования будут числа . Поскольку сечение плоскости – квадрат, значит, площадь сечения равна .
Тогда получим, что объём этой фигуры равен .
Задача: найти объём тела, полученного вращением данной кривой вокруг оси .
Решение: очевидно, что границами интегрирования будут числа .
В сечении полученного тела плоскостью, перпендикулярной оси будет круг, радиус которого равен ординате точки с абсциссой , то есть радиусом этого круга будет .
Площадь такого круга равна . Поскольку принимает только неотрицательные значения, то можно записать, что площадь сечения равна .
Вычислим объём полученного тела как . Применив формулу Ньютона-Лейбница, получим, что объём данного тела равен .
Задача: найти объём тела, полученного вращением данной кривой вокруг оси .
Решение: давайте внимательно посмотрим на получившееся тело.
Его можно получить из цилиндра, который получится при вращении прямоугольника вокруг своей стороны. Для этого надо из данного цилиндра «вынуть» фигуру, которую мы получили в предыдущей задаче.
Объём такой фигуры будет равен разности объёмов .
Радиусом основания цилиндра будет ордината точки с абсциссой равной 1. То есть радиус основания цилиндра равен . Высота цилиндра тоже равна . Тогда получим, что объём цилиндра равен .
Тогда объём искомой фигуры равен .
Итоги:
Сегодня на уроке мы показали, что объём геометрического тела можно найти с помощью определённого интеграла. Определили объёмы известных нам тел через интегралы. Рассмотрели несколько задач.
videouroki.net
«Вычисление объемов тел вращения с помощью определенного интеграла»
Тема: «Вычисление объемов тел вращения с помощью определенного интеграла»
Тип урока: комбинированный.
Цель урока: научиться вычислять объемы тел вращения с помощью интегралов.
Задачи:
закрепить умение выделять криволинейные трапеции из ряда геометрических фигур и отработать навык вычислений площадей криволинейных трапеций;
познакомиться с понятием объемной фигуры;
научиться вычислять объемы тел вращения;
способствовать развитию логического мышления, грамотной математической речи, аккуратности при построении чертежей;
воспитывать интерес к предмету, к оперированию математическими понятиями и образами, воспитать волю, самостоятельность, настойчивость при достижении конечного результата.
Ход урока
I. Организационный момент.
Приветствие группы. Сообщение учащимся целей урока.
– Сегодняшний урок мне бы хотелось начать с притчи. “Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: “Скажет живая – я ее у мертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: “Все в твоих руках”.
– Поэтому давайте сегодня плодотворно поработаем, приобретем новый багаж знаний, и полученные умения и навыки будем применять в дальнейшей жизни и в практической деятельности. “Все в Ваших руках”.
II. Повторение ранее изученного материала.
– Давайте вспомним основные моменты ранее изученного материала. Для этого выполним задание “Исключите лишнее слово”.
(Студенты говорят лишнее слово.)
– Правильно “Дифференциал”. Попробуйте оставшиеся слова назвать одним общим словом. (Интегральное исчисление.)
– Давайте вспомним основные этапы и понятия связанные с интегральным исчислением..
Задание. Восстановите пропуски. (Студент выходит и вписывает маркером необходимые слова.)
Работа в тетрадях.
– Формулу Ньютона-Лейбница вывели английский физик Исаака Ньютона (1643–1727) и немецкий философ Готфрида Лейбница (1646–1716). И это не удивительно, ведь математика – язык, на котором говорит сама природа.
– Рассмотрим, как при решении практических заданий используется эта формула.
Пример 1: Вычислить площадь фигуры, ограниченной линиями
Решение: Построим на координатной плоскости графики функций . Выделим площадь фигуры, которую надо найти.
III. Изучение нового материала.
– Обратите внимание на экран. Что изображено на первом рисунке? (На рисунке представлена плоская фигура.)

– Что изображено на втором рисунке? Является ли эта фигура плоской? (На рисунке представлена объемная фигура.)
– В космосе, на земле и в повседневной жизни мы встречаемся не только с плоскими фигурами, но и объемными, а как же вычислить объем таких тел? Например: объем планеты, кометы, метеорита, и т.д.
– Об объеме задумываются и строя дома, и переливая воду из одного сосуда в другой. Правила и приёмы вычисления объёмов должны были возникать, другое дело, насколько они были точны и обоснованы.
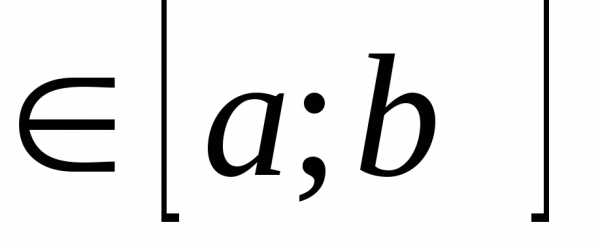
1612 год был для жителей австрийского города Линц, где жил тогда известный астроном Иоганн Кеплер очень урожайным, особенно на виноград. Люди заготовляли винные бочки и хотели знать, как практически определить их объёмы.
– Таким образом, рассмотренные работы Кеплера положили начало целому потоку исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И. Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика переменных величии заняла с этого времени ведущее место в системе математических знаний.
– Вот сегодня мы с вами и займемся такой практической деятельностью, следовательно,
Тема нашего урока: “Вычисление объемов тел вращения с помощью определенного интеграла”.
– Определение тела вращения вы узнаете, выполнив следующее задание.
“Лабиринт”.
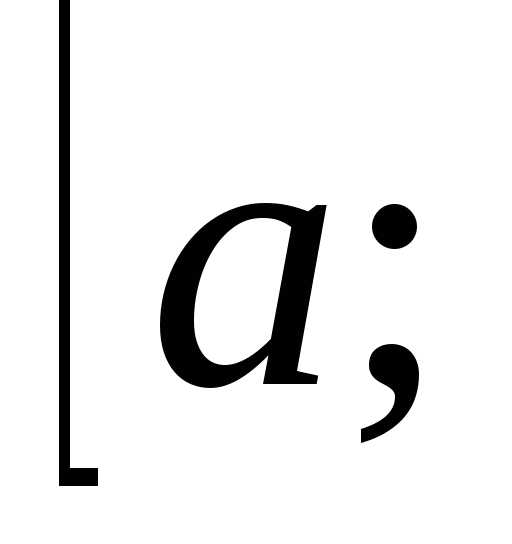
Задание. Найдите выход из запутанного положения и запишите определение.
IV Вычисление объемов.
При помощи определенного интеграла можно вычислить объем того или иного тела, в частности, тела вращения.
Телом вращения называется тело, полученное вращением криволинейной трапеции вокруг ее основания (рис. 1, 2)
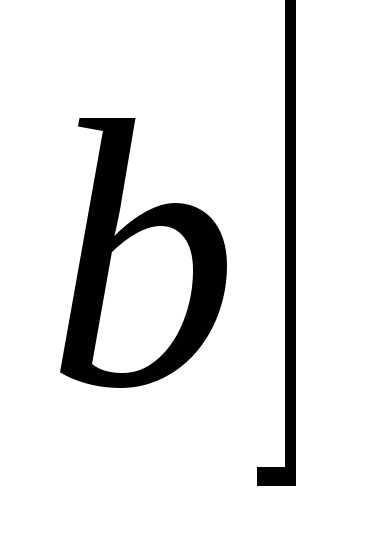
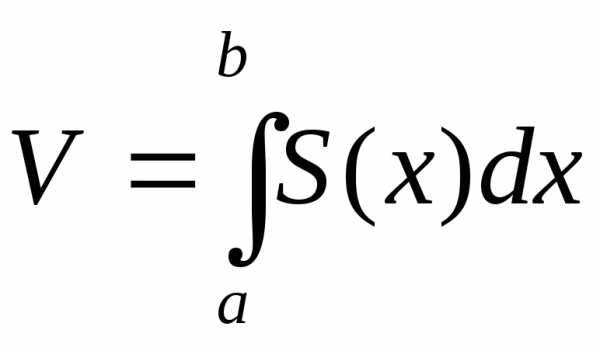
Объем тела вращения вычисляется по одной из формул:
1., если вращение криволинейной трапеции вокруг оси ОХ.
2. , если вращение криволинейной трапеции вокруг оси ОУ.
Студенты записывают основные формулы в тетрадь..
– Преподаватель объясняет решение примеров на доске.
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной трапеции, ограниченной линиями: x2 + y2 = 64, y = -5, y = 5, x = 0.
Решение.
Ответ : 1163 cm3.
2. Найти объем тела, получаемого вращением параболической трапеции, вокруг оси абсцисс y = , x = 4, y = 0.
Решение .
V. Математический тренажер.
2. Совокупность всех первообразных от данной функции называется
А) неопределенным интегралом,
Б) функцией,
В) дифференциацией.
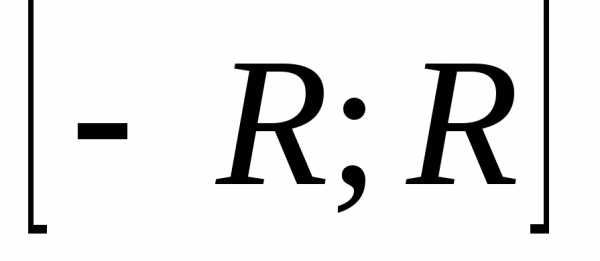
7. Найти объем тела, получаемого вращением вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:

Д/З. Закрепление нового материала
Вычислить объем тела, образованного вращением лепестка, вокруг оси абсцисс y = x2, y2 = x.
Решение:
Построим графики функции. y = x2, y2 = x. График y2 = x преобразуем к виду y = .
Имеем V = V1 – V2 Вычислим объем каждой функции:
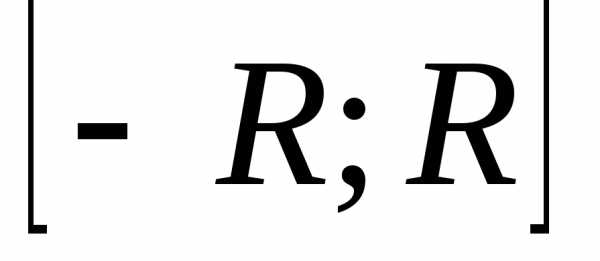
Вывод:
Определенный интеграл – это некоторый фундамент для изучения математики, которая вносит незаменимый вклад в решение задач практического содержания.
Тема “Интеграл” ярко демонстрирует связь математики с физикой, биологией, экономикой и техникой.
Развитие современной науки немыслимо без использования интеграла. В связи с этим, начинать его изучение необходимо в рамках средне специального образования!
VI. Выставление оценок. (С комментированием.)
Великий Омар Хайям – математик, поэт, философ. Он призывает быть хозяевами своей судьбы. Слушаем отрывок из его произведения:
Ты скажешь, эта жизнь – одно мгновенье.
Её цени, в ней черпай вдохновенье.
Как проведёшь её, так и пройдёт.
Не забывай: она – твоё творенье.
infourok.ru
интеграл в деле
Как вычислить объем тела вращения с помощью определенного интеграла?
Помимо нахождения площади плоской фигуры с помощью определенного интегралаважнейшим приложением темы является вычисление объема тела вращения. Материал простой, но читатель должен быть подготовленным: необходимо уметь решатьнеопределенные интегралы средней сложности и применять формулу Ньютона-Лейбница в определенном интеграле. Как и для задачи нахождения площади, нужны уверенные навыки построения чертежей – это чуть ли не самое важное (поскольку интегралы сами по себе чаще будут лёгкими). Освоить грамотную и быструю технику построения графиков можно с помощью методического материала Графики и свойства Элементарных функций. Но, собственно, о важности чертежей я уже неоднократно говорил на уроке Определенный интеграл. Как вычислить площадь фигуры.
Вообще в интегральном исчислении очень много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения, длину дуги, площадь поверхности тела и многое другое. Поэтому будет весело, пожалуйста, настройтесь на оптимистичный лад!
Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … Интересно, кто что представил… =))) Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг оси абсцисс ; – вокруг оси ординат .
В данной статье будут разобраны оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс. В качестве бонуса я вернусь кзадаче нахождения площади фигуры, и расскажу вам, как находить площадь вторым способом – по оси . Даже не столько бонус, сколько материал удачно вписывается в тему.
Начнем с наиболее популярной разновидности вращения.
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями ,вокруг оси.
Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости необходимо построить фигуру, ограниченную линиями,, при этом не забываем, что уравнениезадаёт ось. Как рациональнее и быстрее выполнить чертёж, можно узнать на страницахГрафики и свойства Элементарных функций и Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.
Чертёж здесь довольно прост:
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси . В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси. На самом деле у тела есть математическое название, но в справочнике что-то лень смотреть, поэтому едем дальше.
Как вычислить объем тела вращения?
Объем тела вращения можно вычислить по формуле:
В формуле перед интегралом обязательно присутствует число . Так повелось – всё, что в жизни крутится, связано с этой константой.
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболысверху. Это и есть та функция, которая подразумевается в формуле.
В практических заданиях плоская фигура иногда может располагаться и ниже оси . Это ничего не меняет – функция в формуле возводится в квадрат:, таким образомобъем тела вращения всегда неотрицателен, что весьма логично.
Вычислим объем тела вращения, используя данную формулу:
Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.
Ответ:
В ответе нужно обязательно указать размерность – кубические единицы . То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубическиеединицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.
Пример 2
Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями,,
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Рассмотрим две более сложные задачи, которые тоже часто встречаются на практике.
Пример 3
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями ,,и
Решение: Изобразим на чертеже плоскую фигуру, ограниченную линиями ,,,, не забывая при этом, что уравнениезадает ось:
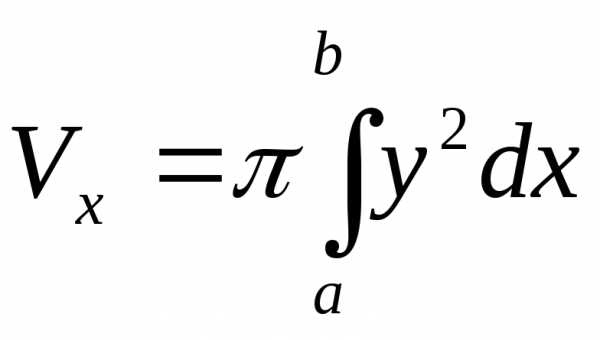
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси получается такой сюрреалистический бублик с четырьмя углами.
Объем тела вращения вычислим как разность объемов тел.
Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси получается усеченный конус. Обозначим объем этого усеченного конуса через.
Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси , то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через.
И, очевидно, разность объемов – в точности объем нашего «бублика».
Используем стандартную формулу для нахождения объема тела вращения:
1) Фигура, обведенная красным цветом ограничена сверху прямой , поэтому:
2) Фигура, обведенная зеленым цветом ограничена сверху прямой , поэтому:
3) Объем искомого тела вращения:
Ответ:
Любопытно, что в данном случае решение можно проверить, используя школьную формулу для вычисления объема усеченного конуса.
Само решение чаще оформляют короче, примерно в таком духе:
Теперь немного отдохнем, и расскажу о геометрических иллюзиях.
У людей часто возникают иллюзии, связанная с объемами, которую подметил еще Перельман (не тот) в книге Занимательная геометрия. Посмотрите на плоскую фигуру в прорешанной задаче – она вроде бы невелика по площади, а объем тела вращения составляет чуть более 50 кубических единиц, что кажется слишком большим. Кстати, среднестатистический человек за всю свою жизнь выпивает жидкость объемом с комнату площадью 18 квадратных метров, что, наоборот, кажется слишком маленьким объемом.
Вообще, система образования в СССР действительно была самой лучшей. Та же книга Перельмана, написанная им еще в 1950 году, очень хорошо развивает, как сказал юморист, соображаловку и учит искать оригинальные нестандартные решения проблем. Недавно с большим интересом перечитал некоторые главы, рекомендую, доступно даже для гуманитариев. Нет, не нужно улыбаться, что я предложил беспонтовое времяпровождение, эрудиция и широкий кругозор в общении – отличная штука.
После лирического отступления как раз уместно решить творческое задание:
Пример 4
Вычислить объем тела, образованного вращением относительно оси плоской фигуры, ограниченной линиями,, где.
Это пример для самостоятельного решения. Обратите внимание, что все дела происходят в полосе , иными словами, даны практически готовые пределы интегрирования. Также постарайтесь правильно начертить графики тригонометрических функций, если аргумент делится на два:, то графики растягиваются по осив два раза. Попробуйте найти хотя бы 3-4 точкипо тригонометрическим таблицам и точнее выполнить чертеж. Полное решение и ответ в конце урока. Кстати, задание можно решить рационально и не очень рационально.
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Второй параграф будет еще интереснее, чем первый. Задание на вычисление объема тела вращения вокруг оси ординат – тоже достаточно частый гость в контрольных работах. Попутно будет рассмотрена задача о нахождении площади фигуры вторым способом – интегрированием по оси , это позволит вам не только улучшить свои навыки, но и научит находить наиболее выгодный путь решения. В этом есть и практический жизненный смысл! Как с улыбкой вспоминала мой преподаватель по методике преподавания математики, многие выпускники благодарили её словами: «Нам очень помог Ваш предмет, теперь мы эффективные менеджеры и оптимально руководим персоналом». Пользуясь случаем, я тоже выражаю ей свою большую благодарность, тем более, что использую полученные знания по прямому назначению =).
Рекомендую для прочтения всем, даже полным чайникам. Более того, усвоенный материал второго параграфа окажет неоценимую помощь при вычислении двойных интегралов.
Пример 5
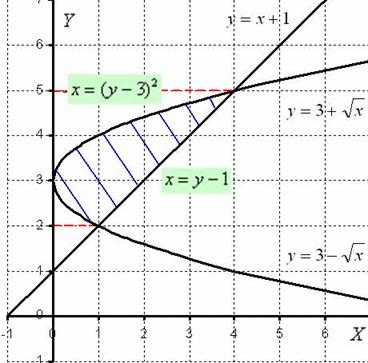
Дана плоская фигура, ограниченная линиями ,,.
1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси .
Внимание! Даже если вы хотите ознакомиться только со вторым пунктом, сначалаобязательно прочитайте первый!
Решение: Задача состоит из двух частей. Начнем с площади.
1) Выполним чертёж:
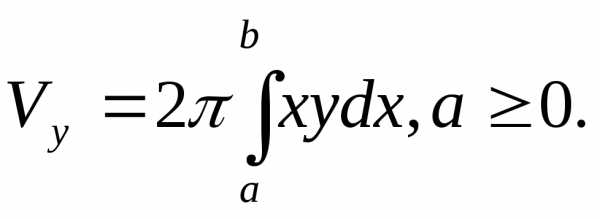
Легко заметить, что функция задает верхнюю ветку параболы, а функция– нижнюю ветку параболы. Перед нами тривиальная парабола, которая «лежит на боку».
Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом.
Как найти площадь фигуры? Её можно найти «обычным» способом, который рассматривался на уроке Определенный интеграл. Как вычислить площадь фигуры. Причем, площадь фигуры находится как сумма площадей: – на отрезке ; – на отрезке.
Поэтому:
Чем в данном случае плох обычный путь решения? Во-первых, получилось два интеграла. Во-вторых, под интегралами корни, а корни в интегралах – не подарок, к тому же можно запутаться в подстановке пределов интегрирования. На самом деле, интегралы, конечно, не убийственные, но на практике всё бывает значительно печальнее, просто я подобрал для задачи функции «получше».
Есть более рациональный путь решения: он состоит в переходе к обратным функциям и интегрированию по оси .
Как перейти к обратным функциям? Грубо говоря, нужно выразить «икс» через «игрек». Сначала разберемся с параболой:
Этого достаточно, но убедимся, что такую же функцию можно вывести из нижней ветки:
Для самопроверки рекомендую устно или на черновике подставить координаты 2-3-х точек параболы в уравнение , они обязательно должны удовлетворять данному уравнению.
С прямой всё проще:
Теперь смотрим на ось : пожалуйста, периодически наклоняйте голову вправо на 90 градусов по ходу объяснений (это не прикол!). Нужная нам фигура лежит на отрезке, который обозначен красным пунктиром. При этом на отрезкепрямаярасположена выше параболы, а значит, площадь фигуры следует найти по уже знакомой вам формуле:. Что поменялось в формуле? Только буква, и не более того.
! Примечание: Пределы интегрирования по оси следует расставлятьстрого снизу вверх!
Находим площадь:
На отрезке , поэтому:
Обратите внимание, как я осуществил интегрирование, это самый рациональный способ, и в следующем пункте задания будет понятно – почему.
Для читателей, сомневающихся в корректности интегрирования, найду производные:
Получена исходная подынтегральная функция, значит интегрирование выполнено правильно.
Ответ:
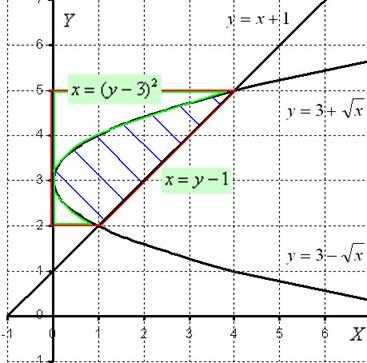
2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси .
Перерисую чертеж немного в другом оформлении:
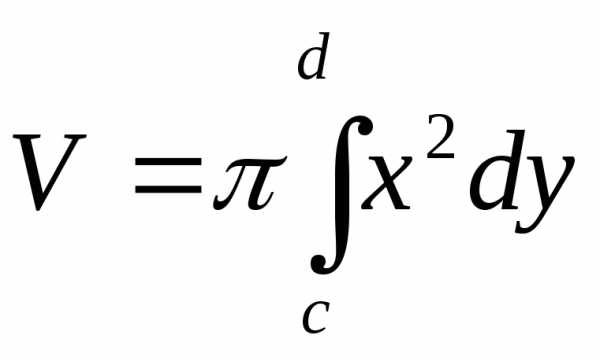
Итак, фигура, заштрихованная синим цветом, вращается вокруг оси . В результате получается «зависшая бабочка», которая вертится вокруг своей оси.
Для нахождения объема тела вращения будем интегрировать по оси . Сначала нужно перейти к обратным функциям. Это уже сделано и подробно расписано в предыдущем пункте.
Теперь снова наклоняем голову вправо и изучаем нашу фигуру. Очевидно, что объем тела вращения, следует найти как разность объемов.
Вращаем фигуру, обведенную красным цветом, вокруг оси , в результате получается усеченный конус. Обозначим этот объем через.
Вращаем фигуру, обведенную зеленым цветом, вокруг оси и обозначаем черезобъем полученного тела вращения.
Объем нашей бабочки равен разности объемов .
Используем формулу для нахождения объема тела вращения:
В чем отличие от формулы предыдущего параграфа? Только в букве.
А вот и преимущество интегрирования, о котором я недавно говорил, гораздо легче найти , чем предварительно возводить подынтегральную функцию в 4-ую степень.
Ответ:
Однако нехилая бабочка.
Заметьте, что если эту же плоскую фигуру вращать вокруг оси , то получится совершенно другое тело вращения, другого, естественно, объема.
Пример 6
Дана плоская фигура, ограниченная линиями ,и осью.
1) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной . 2) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси.
Это пример для самостоятельного решения. Желающие также могут найти площадь фигуры «обычным» способом, выполнив тем самым проверку пункта 1). А вот если, повторюсь, будете вращать плоскую фигуру вокруг оси , то получится совершенно другое тело вращения с другим объемом, кстати, правильный ответ(тоже для любителей порешать).
Полное же решение двух предложенных пунктов задания в конце урока.
Да, и не забывайте наклонять голову направо, чтобы разобраться в телах вращения и в пределах интегрирования!
Хотел, было уже, закончить статью, но сегодня принесли интересный пример как раз на нахождение объема тела вращения вокруг оси ординат. Свежачок:
Пример 7
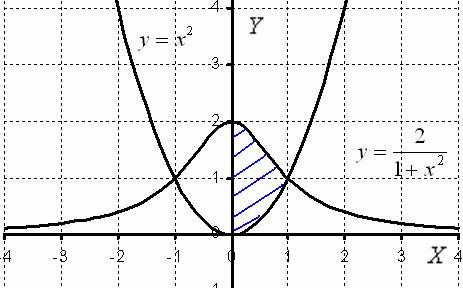
Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной кривымии.
Решение: Выполним чертеж:
Попутно знакомимся с графиками некоторых других функций. Такой вот интересный график чётной функции ….
Для цели нахождения объема тела вращения достаточно использовать правую половину фигуры, которую я заштриховал синим цветом. Обе функции являются четными, их графики симметричны относительно оси , симметрична и наша фигура. Таким образом, заштрихованная правая часть, вращаясь вокруг оси, непременно совпадёт с левой нештрихованной частью.
Перейдем к обратным функциям, то есть, выразим «иксы» через «игреки»: Обратите внимание, что правой ветке параболысоответствует обратная функция. Левой неиспользуемой ветке параболы соответствует обратная функция. В таких случаях нередко возникают сомнения, какую же функцию выбрать? Сомнения легко, развеиваются, возьмите любую точку правой ветки и подставьте ее координаты в функцию. Координаты подошли, значит, функциязадает именно правую ветку, а не левую.
К слову, та же история и с функций . Чайнику, не всегда бывает сразу понятно, какую обратную функцию выбрать:или. В действительности я и сам всегда страхуюсь, подставляя в найденную обратную функцию пару точек графика.
Теперь наклоняем голову вправо и замечаем следующую вещь:
– на отрезке над осьюрасположен график функции; – на отрезкенад осьюрасположен график функции;
Логично предположить, что объем тела вращения нужно искать уже как сумму объемов тел вращений!
Используем формулу:
В данном случае:
Ответ:
В задаче нахождения площади фигуры суммирование площадей используется часто, а суммирование объемов тел вращения, видимо, редкость, раз такая разновидность чуть было не выпала из моего поля зрения. Все-таки хорошо, что своевременно подвернулся рассмотренный пример – удалось вытащить немало полезного.
Успешной раскрутки фигур!
studfiles.net
Вычисление площадей и объемов с помощью определенного интеграла
Площадь криволинейной трапеции
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на отрезке функции, осью и прямыми и равен
Пример.Вычислить площадь фигуры, ограниченной линиями
Изображая эти линии, получаем криволинейную трапецию
Площадь фигуры ограниченной графиками двух функций и прямыми и
Если на заданном отрезке непрерывные функции и имеют то свойство, что для всех то
Пример.Вычислить площадь фигуры, ограниченной линиями
Изобразим заданные линии и абсциссы их точек пересечения.
Абсциссы точек пересечения:
Тогда по формуле
Объемы тел
В общем случае
Если тело заключено между двумя перпендикулярными к оси плоскостями, проходящими через точки и то
где — площадь сечения тела плоскостью, которая проходит через точку и перпендикулярна к оси
Для тела вращения
Если тело получено в результате вращения вокруг оси криволинейной трапеции, которая ограничена графиком непрерывной и невідємної функции на отрезке и прямыми и то
cubens.com
Урок «Вычисление объемов тел вращения с помощью определенного интеграла»
Тема: «Вычисление объемов тел вращения с помощью определенного интеграла»
Тип урока: комбинированный.
Цель урока: научиться вычислять объемы тел вращения с помощью интегралов.
Задачи:
закрепить умение выделять криволинейные трапеции из ряда геометрических фигур и отработать навык вычислений площадей криволинейных трапеций;
познакомиться с понятием объемной фигуры;
научиться вычислять объемы тел вращения;
способствовать развитию логического мышления, грамотной математической речи, аккуратности при построении чертежей;
воспитывать интерес к предмету, к оперированию математическими понятиями и образами, воспитать волю, самостоятельность, настойчивость при достижении конечного результата.
Ход урока
I. Организационный момент.
Приветствие группы. Сообщение учащимся целей урока.
– Сегодняшний урок мне бы хотелось начать с притчи. “Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: “Скажет живая – я ее у мертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: “Все в твоих руках”.
– Поэтому давайте сегодня плодотворно поработаем, приобретем новый багаж знаний, и полученные умения и навыки будем применять в дальнейшей жизни и в практической деятельности. “Все в Ваших руках”.
II. Повторение ранее изученного материала.
– Давайте вспомним основные моменты ранее изученного материала. Для этого выполним задание “Исключите лишнее слово”.
(Студенты говорят лишнее слово.)
– Правильно “Дифференциал”. Попробуйте оставшиеся слова назвать одним общим словом. (Интегральное исчисление.)
– Давайте вспомним основные этапы и понятия связанные с интегральным исчислением..
Задание. Восстановите пропуски. (Студент выходит и вписывает маркером необходимые слова.)
Работа в тетрадях.
– Формулу Ньютона-Лейбница вывели английский физик Исаака Ньютона (1643–1727) и немецкий философ Готфрида Лейбница (1646–1716). И это не удивительно, ведь математика – язык, на котором говорит сама природа.
– Рассмотрим, как при решении практических заданий используется эта формула.
Пример 1: Вычислить площадь фигуры, ограниченной линиями
Решение: Построим на координатной плоскости графики функций . Выделим площадь фигуры, которую надо найти.
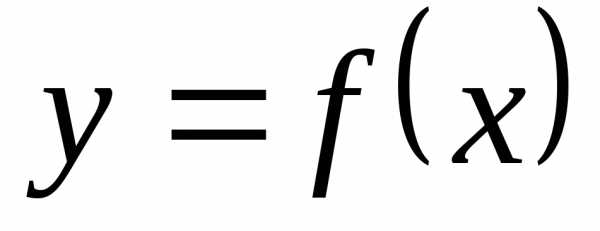
III. Изучение нового материала.
– Обратите внимание на экран. Что изображено на первом рисунке? (На рисунке представлена плоская фигура.)
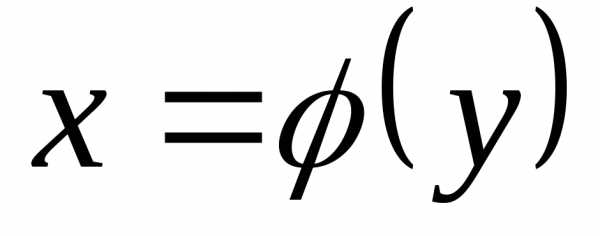
– Что изображено на втором рисунке? Является ли эта фигура плоской? (На рисунке представлена объемная фигура.)
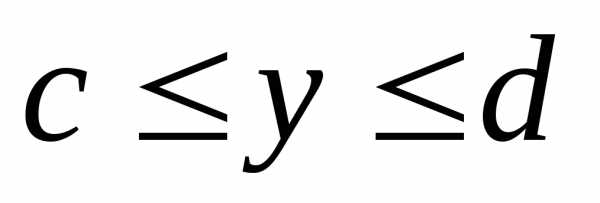
– В космосе, на земле и в повседневной жизни мы встречаемся не только с плоскими фигурами, но и объемными, а как же вычислить объем таких тел? Например: объем планеты, кометы, метеорита, и т.д.
– Об объеме задумываются и строя дома, и переливая воду из одного сосуда в другой. Правила и приёмы вычисления объёмов должны были возникать, другое дело, насколько они были точны и обоснованы.
1612 год был для жителей австрийского города Линц, где жил тогда известный астроном Иоганн Кеплер очень урожайным, особенно на виноград. Люди заготовляли винные бочки и хотели знать, как практически определить их объёмы.
– Таким образом, рассмотренные работы Кеплера положили начало целому потоку исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И. Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика переменных величии заняла с этого времени ведущее место в системе математических знаний.
– Вот сегодня мы с вами и займемся такой практической деятельностью, следовательно,
Тема нашего урока: “Вычисление объемов тел вращения с помощью определенного интеграла”.
– Определение тела вращения вы узнаете, выполнив следующее задание.
“Лабиринт”.
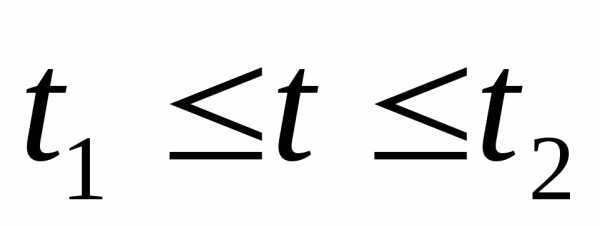
Задание. Найдите выход из запутанного положения и запишите определение.
IV Вычисление объемов.
При помощи определенного интеграла можно вычислить объем того или иного тела, в частности, тела вращения.
Телом вращения называется тело, полученное вращением криволинейной трапеции вокруг ее основания (рис. 1, 2)
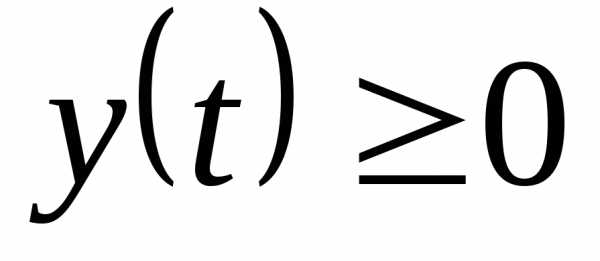
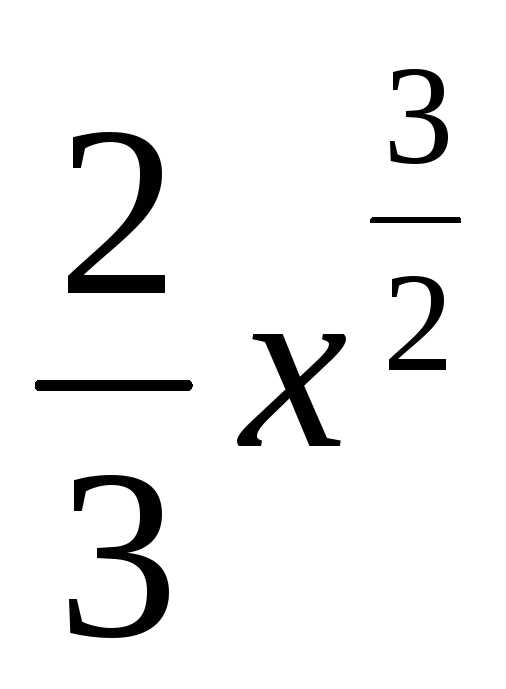
Объем тела вращения вычисляется по одной из формул:
1., если вращение криволинейной трапеции вокруг оси ОХ.
2. , если вращение криволинейной трапеции вокруг оси ОУ.
Студенты записывают основные формулы в тетрадь..
– Преподаватель объясняет решение примеров на доске.
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной трапеции, ограниченной линиями: x2 + y2 = 64, y = -5, y = 5, x = 0.
Решение.
Ответ : 1163 cm3.
2. Найти объем тела, получаемого вращением параболической трапеции, вокруг оси абсцисс y = , x = 4, y = 0.
Решение .
V. Математический тренажер.
2. Совокупность всех первообразных от данной функции называется
А) неопределенным интегралом,
Б) функцией,
В) дифференциацией.
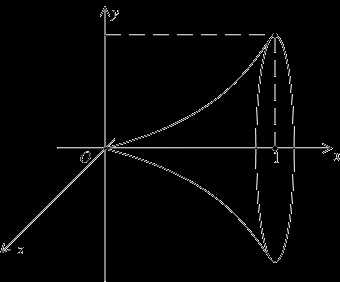
7. Найти объем тела, получаемого вращением вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
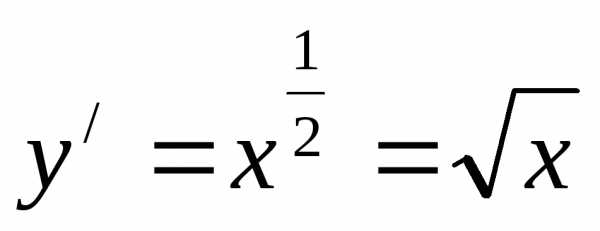
Д/З. Закрепление нового материала
Вычислить объем тела, образованного вращением лепестка, вокруг оси абсцисс y = x2, y2 = x.
Решение:
Построим графики функции. y = x2, y2 = x. График y2 = x преобразуем к виду y = .
Имеем V = V1 – V2 Вычислим объем каждой функции:
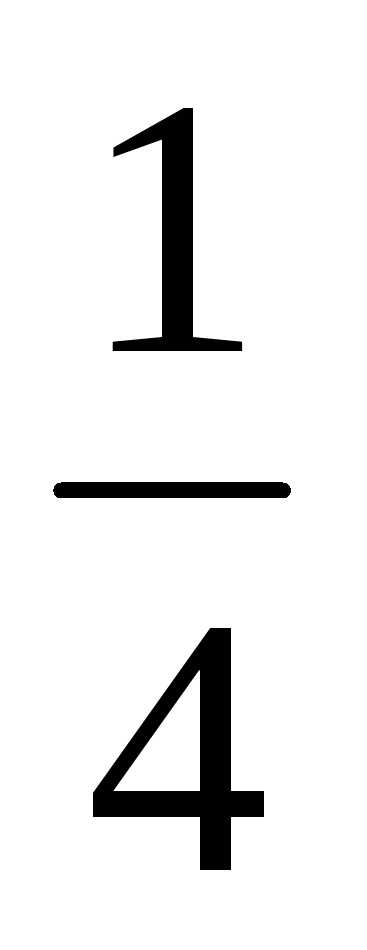
Вывод:
Определенный интеграл – это некоторый фундамент для изучения математики, которая вносит незаменимый вклад в решение задач практического содержания.
Тема “Интеграл” ярко демонстрирует связь математики с физикой, биологией, экономикой и техникой.
Развитие современной науки немыслимо без использования интеграла. В связи с этим, начинать его изучение необходимо в рамках средне специального образования!
VI. Выставление оценок. (С комментированием.)
Великий Омар Хайям – математик, поэт, философ. Он призывает быть хозяевами своей судьбы. Слушаем отрывок из его произведения:
Ты скажешь, эта жизнь – одно мгновенье.
Её цени, в ней черпай вдохновенье.
Как проведёшь её, так и пройдёт.
Не забывай: она – твоё творенье.
Ссылка на источник: http://festival.1september.ru
xn--j1ahfl.xn--p1ai
Вычисление объемов тел с помощью определенного интеграла
Тема: «Вычисление объемов тел вращения с помощью определенного интеграла.
Тип урока: комбинированный.
Цель урока: научиться вычислять объемы тел вращения с помощью интегралов.
Задачи:
закрепить умение выделять криволинейные трапеции из ряда геометрических фигур и отработать навык вычислений площадей криволинейных трапеций;
познакомиться с понятием объемной фигуры;
научиться вычислять объемы тел вращения;
способствовать развитию логического мышления, грамотной математической речи, аккуратности при построении чертежей;
воспитывать интерес к предмету, к оперированию математическими понятиями и образами, воспитать волю, самостоятельность, настойчивость при достижении конечного результата.
Ход урока
I. Организационный момент.
Приветствие группы. Сообщение учащимся целей урока.
– Сегодняшний урок мне бы хотелось начать с притчи. “Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: “Скажет живая – я ее у мертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: “Все в твоих руках”. (Презентация. Слайд)
– Поэтому давайте сегодня плодотворно поработаем, приобретем новый багаж знаний, и полученные умения и навыки будем применять в дальнейшей жизни и в практической деятельности. “Все в Ваших руках”.
II. Повторение ранее изученного материала.
– Давайте вспомним основные моменты ранее изученного материала. Для этого выполним задание “Исключите лишнее слово”. (Слайд.)

(Студенты говорят лишнее слово.)
– Правильно “Дифференциал”. Попробуйте оставшиеся слова назвать одним общим словом. (Интегральное исчисление.)
– Давайте вспомним основные этапы и понятия связанные с интегральным исчислением..
“Математическая гроздь”.
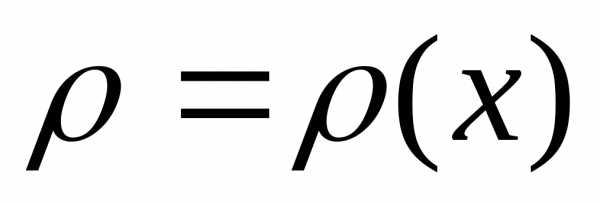
Задание. Восстановите пропуски. (Студент выходит и вписывает маркером необходимые слова.)
Работа в тетрадях.
– Формулу Ньютона-Лейбница вывели английский физик Исаака Ньютона (1643–1727) и немецкий философ Готфрида Лейбница (1646–1716). И это не удивительно, ведь математика – язык, на котором говорит сама природа.
– Рассмотрим, как при решении практических заданий используется эта формула.
Пример 1: Вычислить площадь фигуры, ограниченной линиями
Решение: Построим на координатной плоскости графики функций . Выделим площадь фигуры, которую надо найти.
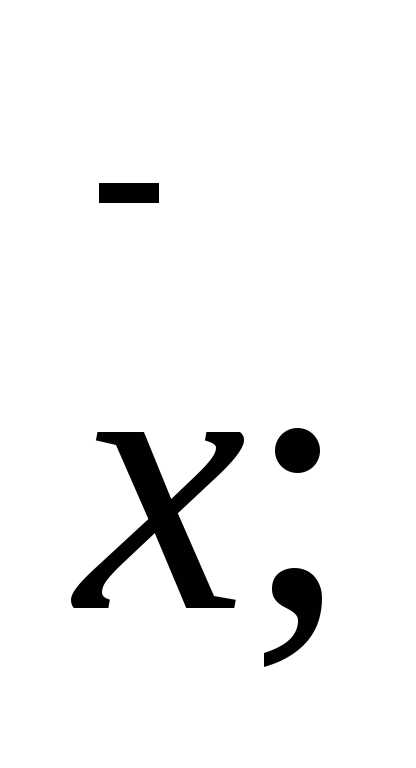
III. Изучение нового материала.
– Обратите внимание на экран. Что изображено на первом рисунке? (Слайд) (На рисунке представлена плоская фигура.)
Б 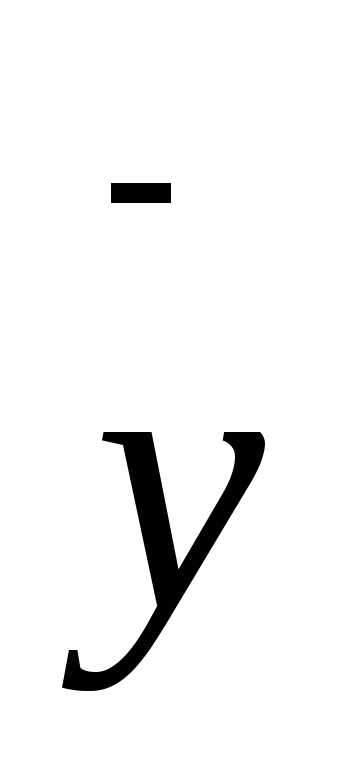
– Что изображено на втором рисунке? Является ли эта фигура плоской? (Слайд) (На рисунке представлена объемная фигура.)
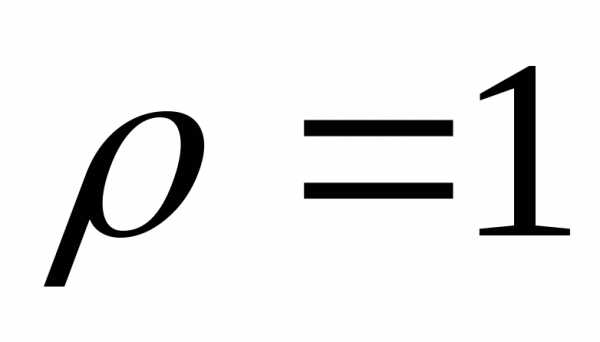
– В космосе, на земле и в повседневной жизни мы встречаемся не только с плоскими фигурами, но и объемными, а как же вычислить объем таких тел? Например: объем планеты, кометы, метеорита, и т.д.
– Об объеме задумываются и строя дома, и переливая воду из одного сосуда в другой. Правила и приёмы вычисления объёмов должны были возникать, другое дело, насколько они были точны и обоснованы.

1612 год был для жителей австрийского города Линц, где жил тогда известный астроном Иоганн Кеплер очень урожайным, особенно на виноград. Люди заготовляли винные бочки и хотели знать, как практически определить их объёмы. (Слайд 2)
– Таким образом, рассмотренные работы Кеплера положили начало целому потоку исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И. Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика переменных величии заняла с этого времени ведущее место в системе математических знаний.
– Вот сегодня мы с вами и займемся такой практической деятельностью, следовательно,
Тема нашего урока: “Вычисление объемов тел вращения с помощью определенного интеграла”.(Слайд)
– Определение тела вращения вы узнаете, выполнив следующее задание.
“Лабиринт”.
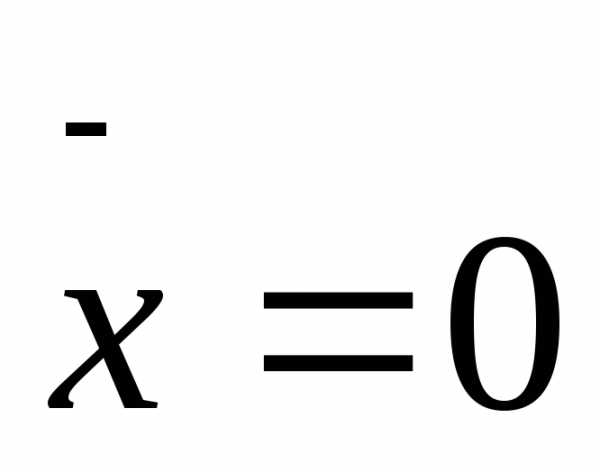
Задание. Найдите выход из запутанного положения и запишите определение.
Слайд. “Карта инструктаж” Вычисление объемов.
При помощи определенного интеграла можно вычислить объем того или иного тела, в частности, тела вращения.
Телом вращения называется тело, полученное вращением криволинейной трапеции вокруг ее основания (рис. 1, 2)
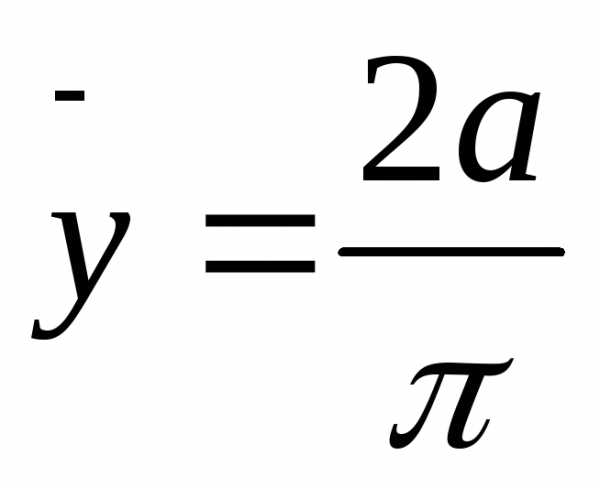
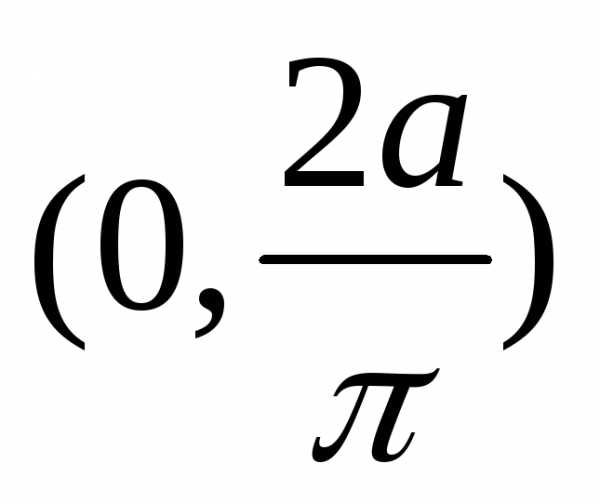
Объем тела вращения вычисляется по одной из формул:
1., если вращение криволинейной трапеции вокруг оси ОХ.
2. , если вращение криволинейной трапеции вокруг оси ОУ.
Карту инструктаж получает каждый студент. Преподаватель подчеркивает основные моменты.
– Преподаватель объясняет решение примеров на доске.
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной трапеции, ограниченной линиями: x2 + y2 = 64, y = -5, y = 5, x = 0.
Решение.
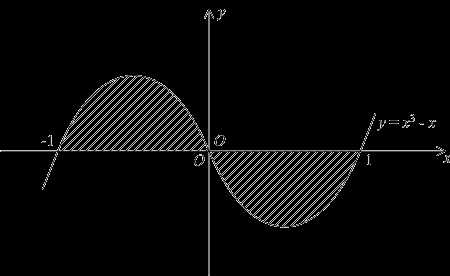
Ответ : 1163 cm3.
Найти объем тела, получаемого вращением параболической трапеции, вокруг оси абсцисс y = , x = 4, y = 0.
Решение .
IV. Закрепление нового материала
Пример 2. Вычислить объем тела, образованного вращением лепестка, вокруг оси абсцисс y = x2, y2 = x.
Решение .
Построим графики функции. y = x2, y2 = x. График y2 = x преобразуем к виду y = .
Имеем V = V1 – V2 Вычислим объем каждой функции
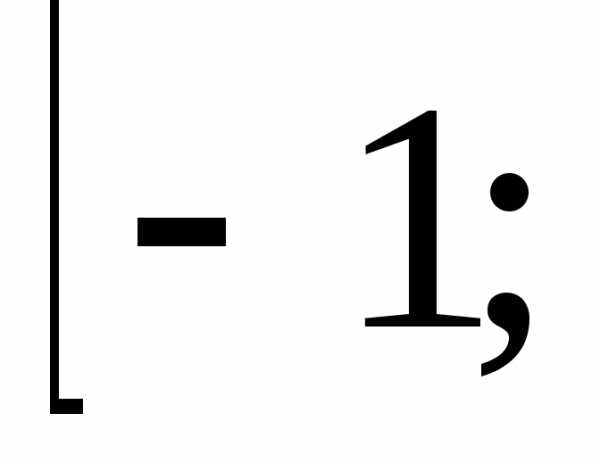
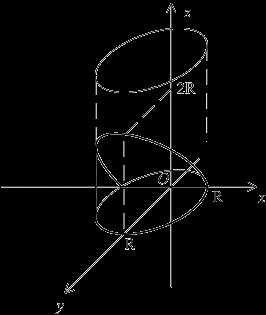
– Теперь, давайте, рассмотрим башню для радиостанции в Москве на Шаболовке, построенной по проекту замечательного русского инженера, почётного академика В. Г. Шухова. Она состоит из частей – гиперболоидов вращения. Причём, каждый из них изготовлен из прямолинейных металлических стержней, соединяющих соседние окружности (рис.8, 9).
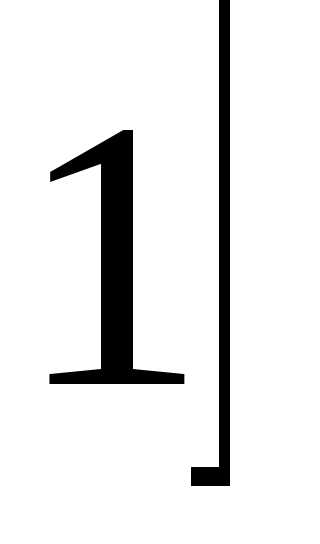
– Рассмотрим задачу.
Найти объем тела, получаемого вращением дуг гиперболы вокруг ее мнимой оси, как показано на рис. 8, где
Решение.
куб. ед.
Математический тренажер.
2. Совокупность всех первообразных от данной функции называется
А) неопределенным интегралом,
Б) функцией,
В) дифференциацией.
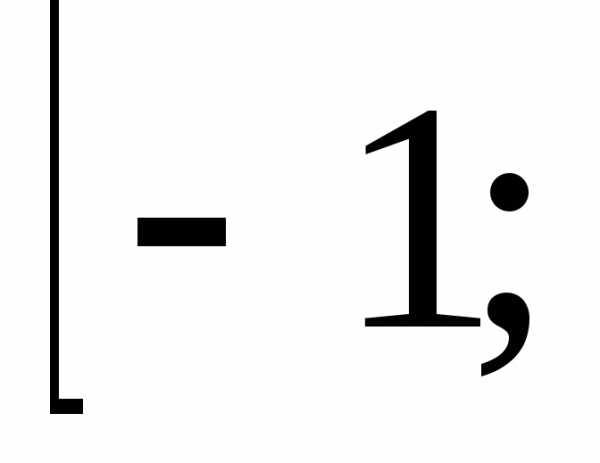
7. Найти объем тела, получаемого вращением вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
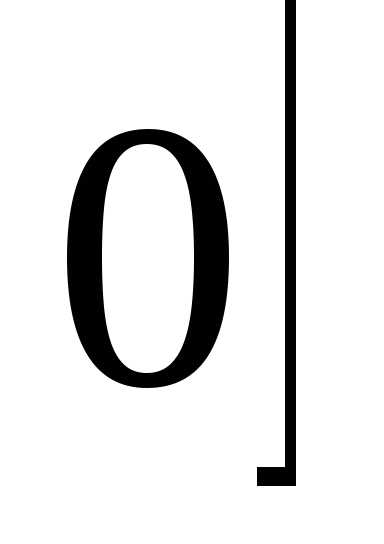
Д/З. Вычислить объем тела полученный вращением вокруг оси абсцисс.
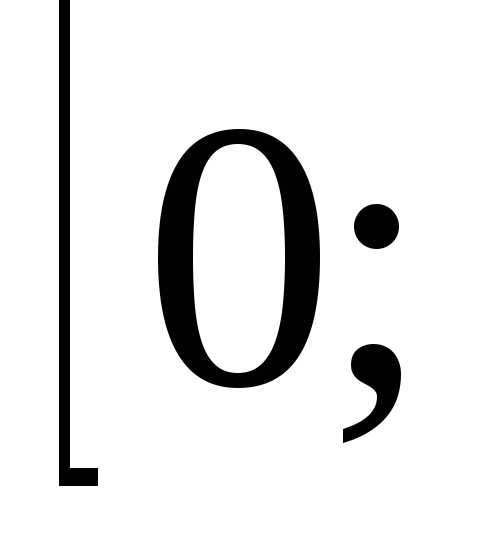
Вывод (слайд).
Определенный интеграл – это некоторый фундамент для изучения математики, которая вносит незаменимый вклад в решение задач практического содержания.
Тема “Интеграл” ярко демонстрирует связь математики с физикой, биологией, экономикой и техникой.
Развитие современной науки немыслимо без использования интеграла. В связи с этим, начинать его изучение необходимо в рамках средне специального образования!
Выставление оценок. (С комментированием.)
Великий Омар Хайям – математик, поэт, философ. Он призывает быть хозяевами своей судьбы. Слушаем отрывок из его произведения:
Ты скажешь, эта жизнь – одно мгновенье.
Её цени, в ней черпай вдохновенье.
Как проведёшь её, так и пройдёт.
Не забывай: она – твоё творенье.
multiurok.ru
Вычисление объёмов тел вращения с помощью определённого интеграла
Объём тела, полученного от вращения вокруг оси Ох криволинейной трапеции, ограниченной непрерывной кривой, определяемой уравнением y=f(x)0, осью Ох и прямымиx=aиx=b, вычисляется по формуле
b
V=y2 dx (1)
a
Объём тела, полученного от вращения вокруг оси Оу криволинейной трапеции, ограниченной непрерывной кривой, определяемой уравнением х=(у)0, осью Оу и прямыми у=с иx=d, вычисляется по формуле
d
V=x2 dy (2)
c
Пример Вычислить объём тела, образованного вращением фигуры, ограниченной линиямиy2= 4x,x=3, вокруг оси Ох.
Решение:Построим параболу у2=4х и прямую х=3.
УПределы интегрирования а=0,b=3.
A Объём тела, полученного при вращении фигуры
ОАВ вокруг оси Ох найдём по формуле (1):
X=33 3
0Х V=4xdx=4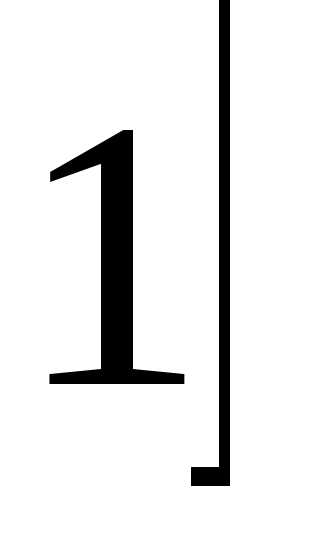 =18(куб.ед.)
=18(куб.ед.)
0 0
By2= 4x
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Несобственными интеграламипервого рода называют интегралы от ограниченных функций с одним или двумя бесконечными пределами. Несобственный интеграл от функцииf(x) в пределах отaдо +определяется равенством
b
f(x) dx = lim f(x) dx
a b a
b b
f(x) dx = lim f(x) dx
a a
b
и f(x) dx = lim f(x) dx
a a
b
Если предел в правой части равенства существует и конечен, то несобственный интеграл называется сходящимся, если же предел не существует или бесконечен— расходящимся.
Несобственные интегралы второго родаэто интегралы на конечном отрезке от функций, котрые терпят бесконечный разрыв.
Если функция f(x) имеет бесконечный разрыв в точкесотрезка [a,b] и непрерывна приaxcиcxb, то по определению полагают
b c- b
f(x) dx = lim f(x) dx + lim f(x) dx
a a c+
Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры.
1. Вычислить 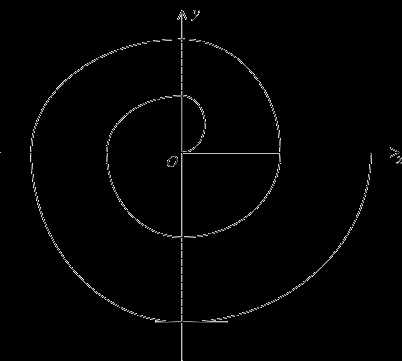 dx
dx
1bb
По определению  dx=lim
dx=lim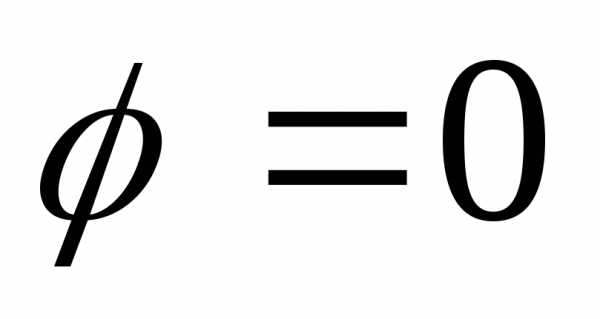 dx=lim(-
dx=lim(- )
=lim(-
)
=lim(- +1)=1,
+1)=1,
1 b 1 b 1 b
т.е. искомый несобственный интеграл равен 1.
Используя формулу Ньютона-Лейбница, можно убедиться, что
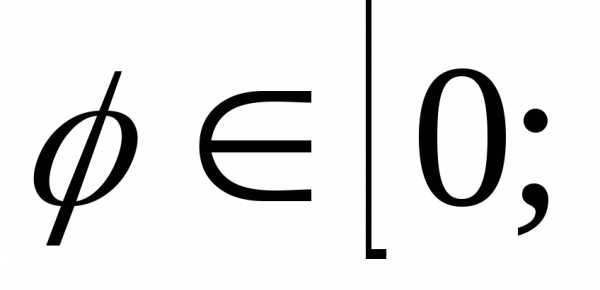 dx
dx
1
является
сходящимся к  еслиm>1 и расходящимся,
еслиm1.
еслиm>1 и расходящимся,
еслиm1.
Геометрический смысл этого результата
состоит в том, что среди всех кривых
вида y=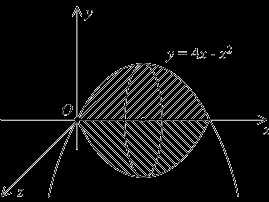 гиперболаy=
гиперболаy= 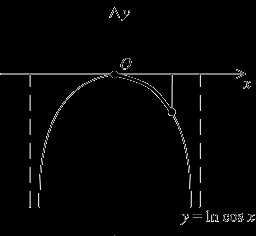 является своеобразным “порогом”.
является своеобразным “порогом”.
y
y=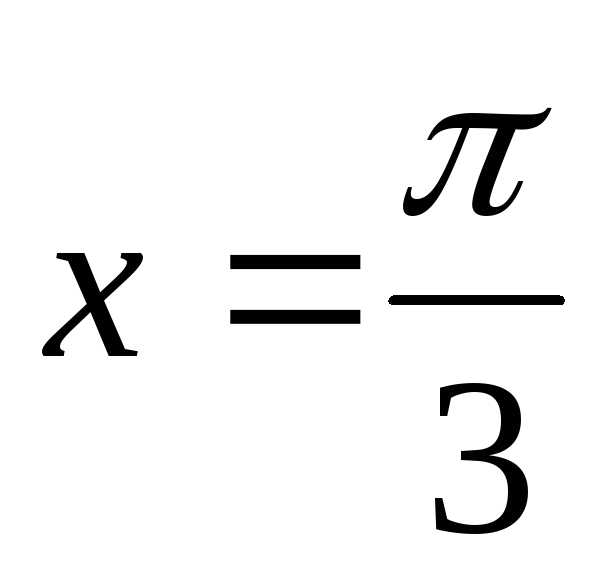 (m1)
(m1)
1
y=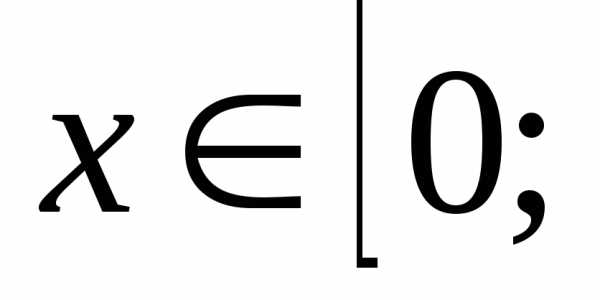
1 x
2. Вычислить (или установить расходимость)cosxdx
0
По определению имеем
bb
cosx dx = lim cosx dx = lim (sinx)= lim (sinb-sin0)=lim sinb,
0 b 0 b 0 b b
Последний предел не существует. Следовательно, несобственный интеграл расходится.
3. Найти 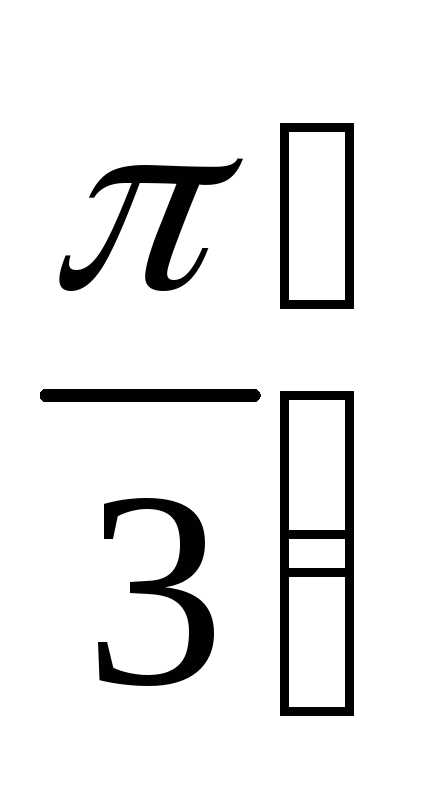 dx
dx
Подынтегральная функция четная, поэтому 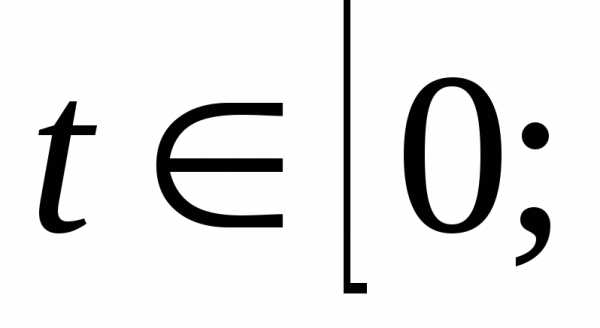 dx=2
dx=2 dx
dx
+bb 0
Тогда 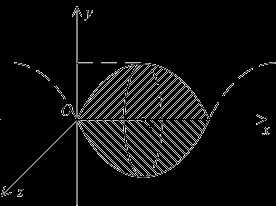 dx=
lim 1/(1+x2)
dx= lim arctg x
= lim arctg b=
dx=
lim 1/(1+x2)
dx= lim arctg x
= lim arctg b=
0 b 0 b 0 b
Т.о., 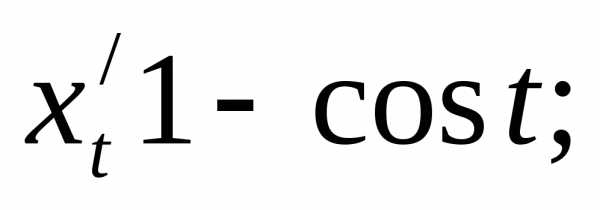 dx=
сходится.
dx=
сходится.
4. Найти xexdx.
0 b b
Имеем
xexdx=lim[-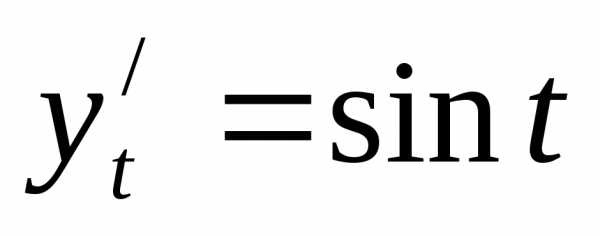 exd(-x2)]=lim[
exd(-x2)]=lim[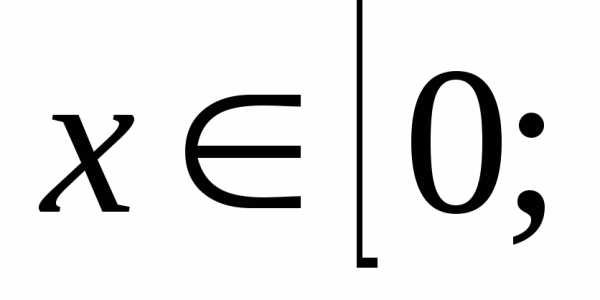 e-x]=
lim[-
e-x]=
lim[- e-b+
e-b+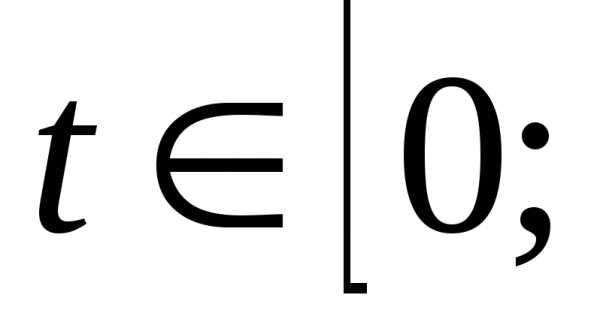 ]=
]= ,
,
0 b 0 0 b
1
5. Найти 1/x dx.
0
Подынтегральная функция f(x)=1/x в точкеx=0 неограничена. Поэтому:
1 1 1
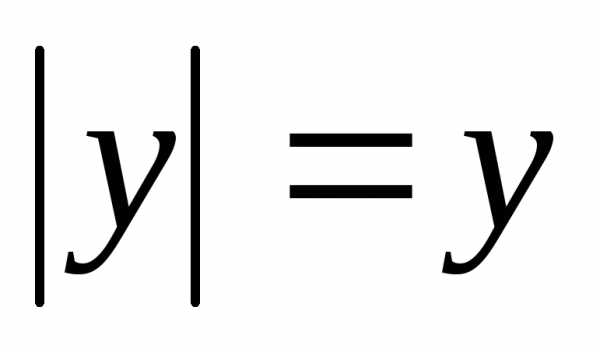 dx= lim
dx= lim 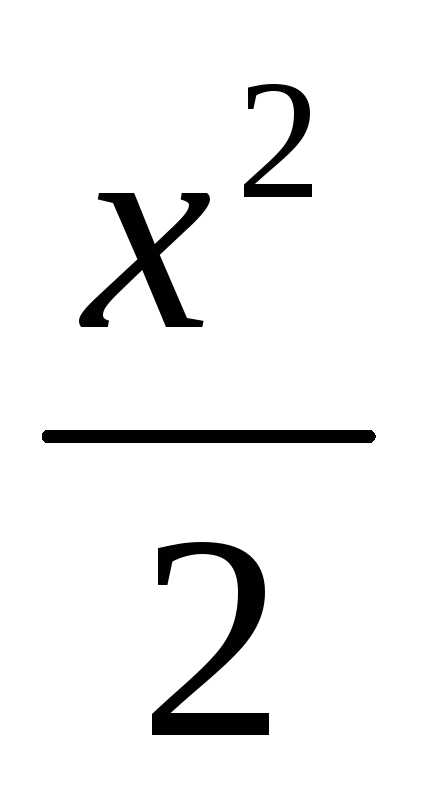 dx= lim(lnx)=lim(ln(1)-ln(a))=+
dx= lim(lnx)=lim(ln(1)-ln(a))=+
0 a0 a a0 a
Несобственный интеграл расходится.
studfiles.net
