Знаки объединения и пересечения множеств – Пересечение и объединение множеств

элементы и подмножества. Пересечение и объединение множеств

Множество – совокупность любых объектов. Множества обозначают большими буквами латинского алфавита – от A до Z.

Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:

N – множество натуральных чисел

Z – множество целых чисел

Элемент множества – это любой объект, входящий в состав множества. Принадлежность объекта к множеству обозначается с помощью знака ∈. Запись

5∈Z

читается так: 5 принадлежит множеству Z или 5 – элемент множества Z.

Множества делятся на конечные и бесконечные. Конечное множество – множество, содержащее определённое (конечное) количество элементов. Бесконечное множество – множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.

Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись

L = {2, 4, 6, 8}

означает, что множество L состоит из четырёх чётных чисел.

Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.

Подмножество

Подмножество – это множество, все элементы которого, являются частью другого множества.

Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера – это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае множеств.

Рассмотрим два множества:

L = {2, 4, 6, 8}   и  

M = {2, 4, 6, 8, 10, 12}

Каждый элемент множества L принадлежит и множеству M, значит множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂:

L⊂M

Запись L⊂M читается так: множество L является подмножеством множества M.

Множества состоящие из одних и тех же элементов, независимо от их порядка, называются равными и обозначаются знаком =.

Рассмотрим два множества:

L = {2, 4, 6}   и   M = {4, 6, 2}

так как оба множества состоят из одних и тех же элементов, то L = M.

Пересечение и объединение множеств

Пересечение двух множеств – это совокупность элементов, принадлежащих каждому из этих множеств, то есть их общая часть. Пересечение обозначается знаком

∩.

Например, если

L = {1, 3, 7, 11}   и   M = {3, 11, 17, 19}, то   L∩M = {3, 11}.

Запись L∩M читается так: пересечение множеств L и M.

Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.

Объединением двух множеств называется множество, содержащее все элементы исходных множеств в единственном экземпляре, то есть если один и тот же элемент встречается в обоих множествах, то в новое множество этот элемент будет включён только один раз. Объединение обозначается знаком ∪.

Например, если

L = {1, 3, 7, 11}   и   M = {3, 11, 17, 19},

то   L∪M = {1, 3, 7, 11, 17, 19}.

Запись

L∪M читается так: объединение множеств L и M.

При объединении равных множеств, объединение будет равно любому из данным множеств:

если L = M,   то   L∪M = L   и   L∪M = M.

naobumium.info

Лекция 4. Объединение множеств.

Лекция 4.  Объединение множеств. Свойства объединения множеств.

Определение. Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.

Объединение множеств А и В обозначают А∪ В. Таким образом, по определению,    А ∪ В = { х | х ∈А или х∈В}.

Например, если А = { a , c , k , m , n } и       В   =   { 

a , b , c , d , e }, 

  то  А ∪ В   =   { a , c , k , m , n , b , d , e }.

Если изобразить А и В при помощи кругов Эйлера-Венна, то объединением данных множеств является заштрихованная область           (рис. 4).

           

Для объединения множеств выполняются следующие свойства.

1)    Переместительное или коммутативное свойство: А ∪ В = В ∪ А.

2)    Сочетательное или ассоциативное свойство:(А ∪ В)∪ С = А ∪ (В ∪ С).

3)    А ∪ ∅= А (пустое множество является нейтральным элементом).

4)    А ∪ U = U (универсальное множество является поглощающим  элементом).

5)   Если В ⊂А, то А∪В = В

Операции объединения и пересечения множеств связаны законами дистрибутивности или иначе распределительными свойствами:

(А ∪ В) ∩С = (А∩С) ∪ (В∩С)  и  (А∩В) ∪ С = (А ∪ С) ∩(В ∪ С).

       

П р и м е р  1. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.

        Р е ш е н и е.  Запишем множества А и В, перечислив их элементы: А = { м, а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }. Буквы м, т, е, и принадлежат и множеству А, и множеству В, поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е, и }. В объединение этих множеств войдут все элементы множества А и несовпадающие с ними элементы из множества В: А ∪ В = { м, а, т, е, и, к, с, р, о, я }.

       

П р и м е р  2 . В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? Только немецкий язык?

          Р е ш е н и е.  Через А обозначим множество школьников, изучающих английский язык, через В – множество школьников,         изучающих немецкий язык. Изобразим эту ситуацию с помощью диаграммы. Два языка изучают 18 школьников, поставим это число в пересечение множеств А и В. Английский язык изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит, только английский язык изучают 7 человек, укажем это число на диаграмме. Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9 человек. Поместим и это число на диаграмму.  Теперь известно количество элементов в каждой части множеств, изображенных на диаграмме. Чтобы  ответить  на главный вопрос задачи, нужно сложить все числа: 7 + 18 + 9 = 34. Ответ: 34 человека в классе изучают иностранные языки.

Задания для самостоятельной работы по теме:

1.Найдите объединение множеств А и В, если:

а) А = {26,39,5,58,17,81}, В = {17, 26, 58}.

б) А = {26,39,5,58, 17,81}, В = {17, 26, 58, 5, 39, 81}.

2. Из каких элементов состоит объединение множества букв в слове «математика» и множества букв в слове «геометрия»?

3. М — множество однозначных чисел, Р — множество нечетных натуральных чисел. Из каких чисел состоит объединение данных множеств? Содержатся ли в нем числа -7 и 9?

4. Используя координатную прямую, найдите объединение множеств решений неравенств, в которых х — действительное число:

а) х > -2 и х > 0; в) х > 5 и х < -7,5;

б) х > -3,7 и х < 4; г) -2 < х < 4 и х > -1;

д) -7<х<5 и -6<х<2.

infourok.ru

1.3.2 Объединение множеств

Вновь возьмём множества Х = {0, 1, 3, 5} и Y = {1, 2, 3, 4} и наряду с ними рассмотрим множество {0, 1, 2, 3, 4, 5}. Это множество содержит все элементы множества Х и все элементы множества Y и не содержит никаких других элементов.

Множество, состоящее из всех элементов, принадлежащих или множеству А или множеству В, называется объединением множеств А и В, обозначается А U В. А U В = { х А или х

В }

Итак, {0, 1, 3, 5} {1, 2, 3, 4} = {0, 1, 2, 3, 4, 5}.

Если изобразить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью.

А U В

Если множества не имеют общих элементов, то их объединение выглядит так:

А U В

Если одно из множеств является подмножеством другого, то их объединение будет выглядеть так:

А U В

Часто приходится рассматривать объединение и пересечение трёх и более множеств. Объединение множеств А, В и С есть множество, каждый элемент которого принадлежит хотя бы одному из множеств А, В или С; пересечение множеств А, В и С есть множество всех элементов, принадлежащих и множеству А, и множеству В, и множеству С.

А U В U С А ∩ В ∩ С

Например, объединение множеств остроугольных, тупоугольных и прямоугольных треугольников есть множество всех треугольников.

Еще операции над множествами можно показать с помощью детского анекдота: Однажды лев, царь зверей, собрал зверей на поляне и повелел им разделиться на умных и красивых. После того, как пыль улеглась, лев увидел на поляне две большие группы зверей и мартышку, прыгающую между ними. На вопрос: почему она прыгает туда, сюда, мартышка ответила: «Что мне, разорваться, что ли?». Так вот, мартышка из анекдота – это пример пересечения умных зверей и красивых. А объединением умных и красивых зверей является все множество зверей.

Объединение и пересечение множеств обладают многими свойствами, аналогичными свойствам суммы и произведения чисел:

№ п/п	Свойство операций над множествами	Свойство арифметических операций	Название свойства
1		a + b = b + a	Коммутативность
2
3		(а+b)+c = a+(b+c)	Ассоциативность
4
5			Дистрибутивность

Однако эта аналогия не всегда имеет место. Например, для множеств справедливы равенства:

6. (А U С) ∩ (В U С) = (A ∩ B) U С.

7. А U А = А.

8. А ∩ А = А.

Соответствующие равенства для чисел верны не всегда.

Заметим, что, если в выражении есть знаки пересечения и объединения множеств, и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.

1.3.3 Вычитание множеств

Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.

Разностью множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В, обозначается А \ В. А \ В = {х А и х В}.

Х \ Y = {0, 1, 3, 5} \ {1, 2, 3, 4} = {0, 5}. Если мы найдем разность множеств Y и Х, то результат будет выглядеть так: Y \ X = {2; 4}. Таким образом, разность множеств не обладает переместительным (коммутативным) свойством.

Если изобразить множестваА и В при помощи кругов Эйлера, то разность данных множеств изобразится заштрихованной областью.

А \ В

Если множества не имеют общих элементов, то их разность будет изображаться так:

В

А

А \ В

Если одно из множеств является подмножеством другого, то их разность будет изображаться так:

А

В

\ В

Пересечение – более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в выражении А \ В ∩ С такой: сначала находят пересечение множеств В и С, а затем полученное множество вычитают из множества А. Что касается объединения и вычитания множеств, то их считают равноправными. Например, в выражении А \ В U С надо сначала выполнить вычитание (из А вычесть В), а затем полученное множество объединить с множеством С.

Вычитание множеств обладает рядом свойств:

1. (А \ В) \ С = (А \ С) \ В.

2. (А U В) \ С = (А \ С) U (В \ С).

3. (А \ В) ∩ С = (А ∩ С) \ (В ∩С).

4. А \ (В U С) = (А \ В) ∩ (А \ С).

5. А \ (В ∩ С) = (А \ В) U (А \ С).

studfiles.net

Законы пересечения и объединения множеств — Мегаобучалка

1. Переместительный (коммутативный) закон пересечения и объединения множеств.

Из определений пересечения и объединения множеств вытекает:

Определение. Для любых множеств А и В справедливо равенство: АÇ B = B Ç A и A È B = B È A.

2. Сочетательный (ассоциативный) закон пересечения и объединения множеств.

Определение. Для любых множеств А, В и С выполняются равенства: ( А Ç B ) Ç С = A Ç ( ВÇ С), ( A È B ) È С = A È ( B È С).

Свойство ассоциативности для пересечения и объединения множеств не столь очевидно, как свойство коммутативности, и поэтому нуждается в доказательстве. Но прежде всего можно эти свойства проиллюстрировать при помощи кругов Эйлера. Рассмотрим, например, ассоциативное свойство пересечения множеств. Изобразим множества А, В и С в виде трех попарно пересекающихся кругов. (См. рис.3)

Р Рис. 3

3. Закон пересечения множеств: ( А Ç B ) Ç С = A Ç ( ВÇ С)

В выражении ( А Ç B ) Ç С скобки определяют следующий порядок действий: сначала выполняется пересечение множеств А и В – оно показано на рисунке вертикальной штриховкой, а затем находят пересечение полученного множества и множества С. Если выделить множество С горизонтальной штриховкой, то область, заштрихованная дважды, будет изображать множество ( А Ç B ) Ç С.

Представим теперь наглядно множество A Ç ( ВÇ С).(См. рис.4) В соответствии с указанным порядком действий сначала надо найти пересечение множеств В и С – на рисунке оно показано вертикальной штриховкой, а затем выполнить пересечение множества А с полученным множеством. Если отметить множество А горизонтальной штриховкой, то область, заштрихованная дважды, и будет изображать множество A Ç ( ВÇ С). Видим, что области, представляющие на рисунке множества ( А Ç B ) Ç СиA Ç ( В Ç С ), одинаковы, что и подтверждает справедливость свойства ассоциативности для пересечения множеств. Рис. 4.

Аналогично можно проиллюстрировать свойство ассоциативности и для объединения множеств.

Замечание. Важность ассоциативного свойства пересечения и объединения множеств состоит в следующем:

1) можно находить пересечение и объединение трех множеств, зная, как это делается для двух;

2) на основании этого свойства в выражениях ( А Ç B ) Ç С, A Ç ( ВÇ С),( A È B ) È С , A È ( B È С) можно опускать скобки и писать А Ç B Ç С или A È B È С, что облегчает запись.

Рассмотрим строгое доказательство свойства ассоциативности одной из операций над множествами, например объединения, т.е. докажем, что для любых множеств А, В и С справедливо равенство ( A È B ) È С = A È ( B È С).

Доказательство. Чтобы доказать равенство двух множеств, надо убедится в том, что каждый элемент множества ( A È B ) È С содержится в множестве A È ( B È С), и наоборот.

1. Пусть х – любой элемент множества ( A È B ) È С. Тогда, по определению объединения, х Î A È B или хÎС.

Если х Î A È B, то, по определению объединения, х Î А или х Î В. В том случае, когда х ÎА, то, также по определению объединения, х Î A È ( B È С).

Если х Î В, то имеем, что х Î B È С, а значит, х Î A È ( B È С). Случай, когда х Î А и х Î В, сводится к рассмотренным. Таким образом, из того, что х Î A È B, следует, что х Î A È ( B È С).

Если х Î С, то, по определению объединения, х Î В È С, и следовательно, х Î A È ( B È С).

Случай, когда х Î A È B и х Î С, сводится к рассмотренным выше.

Итак, мы показали, что каждый элемент множества ( A È B ) È С содержится и в множестве A È ( B È С), т.е. ( A È B ) È С Ì A È ( B È С).

2. Пусть у — любой элемент множества A È ( B È С). Тогда, по определению объединения, уÎА или уÎ B È С.

Если у Î А, то, по определению объединения, у ÎA È ( B È С).

Если у Î B È С, то у Î B или уÎ С. В том случае, когда у Î B, то уÎ A È B и, значит, уÎ ( A È B ) È С. Когда же у Î С, то у Î ( A È B ) È С. Случай, когда у Î В и у Î С, сводится к уже рассмотренным.

Итак, мы показали, что каждый элемент множества A È (B È С) содержится и в множестве (A È B) È С, т.е. A È (B È С) Ì (A È B) È С.

Согласно определению равных множеств заключаем, что ( A È B ) È С = A È ( B È С), что и требовалось доказать.

Аналогично доказывается и ассоциативное свойство пересечения множеств.

Замечание. Взаимосвязь пересечения и объединения множеств отражается в распределительных, или дистрибутивных, свойствах этих операций. Таких свойств два:

1. Пересечение дистрибутивно относительно объединения множеств, т.е. для любых множеств А, В и С выполняется равенство (А È B ) Ç С = (А Ç С) È ( ВÇ С).

2. Объединение дистрибутивно относительно пересечения множеств, т.е. для любых множеств А, В и С выполняется равенство (А Ç B ) È С = (А È С) Ç ( В È С ).

Замечание. Если в выражении есть знаки пересечения и объединения множеств и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.

megaobuchalka.ru

Пересечение и объединение множеств Что значит объединение

Пересечение и объединение множеств

Что значит объединение? Объединением двух множеств называется множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств. Обозначают A U B и читают «объединение A и B». Операции объединения и пересечения множеств обладают многими свойствами сложения и умножения чисел, например переместительным, сочетательным и распределительным свойствами. Пусть А – множество простых двузначных чисел, В – множество двузначных чисел, оканчивающихся цифрой 1. Рассмотрим теперь мн-во К, которому принадлежат все элементы множества А и все элементы мн-ва В. Мн-во К составлено из всез двузначных чисел, которые являются простыми или оканчиваются цифрой 1, т. е. К = {11, 13, 17, 19, 21, …, 83, 89, 91, 97} Говорят, что мн-во К является объединением множеств А и В

Что значит пересечение? Пересечением двух множеств называется множество, состоящее из всех общих элементов этих множеств. Обозначают A∩B и читают «пересечение A и B». Понятия объединения и пересечения множеств дос

present5.com

3. Законы пересечения и объединения множеств

1. Переместительный (коммутативный) закон пересечения и объединения множеств.

Из определений пересечения и объединения множеств вытекает:

Определение. Для любых множеств А и В справедливо равенство: А       и       .

2. Сочетательный (ассоциативный) закон пересечения и объединения множеств.

Определение. Для любых множеств а, в и с выполняются равенства:

(А    С     В С,       С       С.

Свойство ассоциативности для пересечения и объединения множеств не столь очевидно, как свойство коммутативности, и поэтому нуждается в доказательстве. Но прежде всего можно эти свойства проиллюстрировать при помощи кругов Эйлера. Рассмотрим, например, ассоциативное свойство пересечения множеств. Изобразим множества А, В и С в виде трех попарно пересекающихся кругов. (См. рис.3)

3. Закон пересечения множеств: ( А     С     В С

В выражении ( А     С скобки определяют следующий порядок действий: сначала выполняется пересечение множеств А и В – оно показано на рисунке вертикальной штриховкой, а затем находят пересечение полученного множества и множества С. Если выделить множество С горизонтальной штриховкой, то область, заштрихованная дважды, будет изображать множество ( А     С.

Представим теперь наглядно множество   В  С. (См. рис.4) В соответствии с указанным порядком действий сначала надо найти пересечение множеств В и С – на рисунке оно показано вертикальной штриховкой, а затем выполнить пересечение множества А с полученным множеством. Если отметить множество А горизонтальной штриховкой, то область, заштрихованная дважды, и будет изображать множество    В С. Видим, что области, представляющие на рисунке множества ( А     С и    В  С ), одинаковы, что и подтверждает справедливость свойства ассоциативности для пересечения множеств. Рис. 4.

Аналогично можно проиллюстрировать свойство ассоциативности и для объединения множеств.

Замечание. Важность ассоциативного свойства пересечения и объединения множеств состоит в следующем:

1. можно находить пересечение и объединение трех множеств, зная, как это делается для двух;

2. на основании этого свойства в выражениях ( А     С,    В С,      С ,      С можно опускать скобки и писать А    С или     С, что облегчает запись.

Рассмотрим строгое доказательство свойства ассоциативности одной из операций над множествами, например объединения, т.е. докажем, что для любых множеств А, В и С справедливо равенство       С       С.

Доказательство. Чтобы доказать равенство двух множеств, надо убедится в том, что каждый элемент множества       С содержится в множестве      С, и наоборот.

1. Пусть х – любой элемент множества       С. Тогда, по определению объединения, х     или хС.

Если х    , то, по определению объединения, х  А или х  В. В том случае, когда х А, то, также по определению объединения, х       С.

Если х  В, то имеем, что х    С, а значит, х       С. Случай, когда х  А и х  В, сводится к рассмотренным. Таким образом, из того, что х    , следует, что х       С.

Если х  С, то, по определению объединения, х  В  С, и следовательно, х       С.

Случай, когда х     и х  С, сводится к рассмотренным выше.

Итак, мы показали, что каждый элемент множества       С содержится и в множестве      С, т.е.       С       С.

2. Пусть у — любой элемент множества      С. Тогда, по определению объединения, уА или у   С.

Если у  А, то, по определению объединения, у      С.

Если у    С, то у   или у С. В том случае, когда у  , то у  и, значит, у       С. Когда же у  С, то у        С. Случай, когда у  В и у  С, сводится к уже рассмотренным.

Итак, мы показали, что каждый элемент множества   (  С) содержится и в множестве (  )  С, т.е.   (  С)  (  )  С.

Согласно определению равных множеств заключаем, что       С       С, что и требовалось доказать.

Аналогично доказывается и ассоциативное свойство пересечения множеств.

Замечание. Взаимосвязь пересечения и объединения множеств отражается в распределительных, или дистрибутивных, свойствах этих операций. Таких свойств два:

1. Пересечение дистрибутивно относительно объединения множеств, т.е. для любых множеств А, В и С выполняется равенство (А     С = (А  С)  ( В С).

2. Объединение дистрибутивно относительно пересечения множеств, т.е. для любых множеств А, В и С выполняется равенство (А     С = (А  С)  ( В  С ).

Замечание. Если в выражении есть знаки пересечения и объединения множеств и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.

studfiles.net

Свойства пересечения и объединения множеств

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Из школьного курса математики известно, что операция, при помощи которой находят сумму чисел, называется сложе­нием. Над числами выполняют и другие операции, например умножение, вычитание, деление; при этом результат умноже­ния чисел называют произведением, деления — частным, т.е. для операций над числами и результатов этих операций суще­ствуют разные термины. Для рассмотренных операций над множествами ситуация иная: операции, при помощи которых находят пересечение и объединение множеств, называются соответственно пересечением и объединением.

Из школьного курса математики нам также известно, что операции над числами обладают рядом свойств. Например, сложение действительных чисел обладает переместительным и сочетательным свойствами: для любых действительных чисел а и Ь справедливо равенство а + b = b + а, а для любых чисел a, b и с — равенство (а + b)+ с = а + b+ с).

Аналогичными свойствами обладает умножение действи­тельных чисел. Кроме того, для сложения и умножения выпол­няется распределительное свойство: для любых действительных чисел а, b и с справедливо равенство: (а+b) · с = а · с + b ·с.

Выясним, обладают ли «похожими» свойствами пересече­ние и объединение множеств.

Если обратиться к определениям пересечения и объедине­ния множеств, то можно увидеть, что в них не фиксируется порядок оперирования множествами. Например, выполняя объединение, можно к элементам одного множества присоединить элементы другого, а можно поступить наоборот: к элементам второго множества присоединить элементы перво­го. (При этом надо только помнить, что в новом множестве не должно быть повторяющихся элементов.) Аналогичная си­туация и в случае, когда выполняется пересечение множеств. Это означает, что пересечение и объединение множеств обла­дают переместительным, или, как говорят в математике, ком­мутативным свойством: для любых множеств А и В выпол­няются равенства: А В = В A и A B = B A.

Пересечение и объединение множеств обладают также со­четательным, или ассоциативным, свойством: для любых множеств А, В и С выполняются равенства:

(А В) С = А (В С и (А В) С = А (В С).

Заметим, что назначение скобок в этих записях то же, что и в записях операций над числами.

Свойство ассоциативности для пересечения и объединения множеств не столь очевидно, как свойство коммутативности, и поэтому нуждается в доказательстве. Но прежде можно эти свойства проиллюстрировать при помощи кругов Эйлера. Рассмотрим, например, ассоциативное свойство пересечения множеств. Изобразим множества А, В и С в виде трех попарно пересекающихся кругов (рис. 9).

В выражении (А В) С скобки определяют следующий порядок действий: сначала выполняется пересечение множеств А и В — оно показано на рисунке 9а вертикальной штрихов­кой, а затем находят пересечение полученного множества и множества С. Если выделить множество С горизонтальной штриховкой, то область, заштрихованная дважды, будет изо­бражать множество (А В) С.

Представим теперь наглядно множество А (В С). В соответствии с указанным порядком действий сначала

 

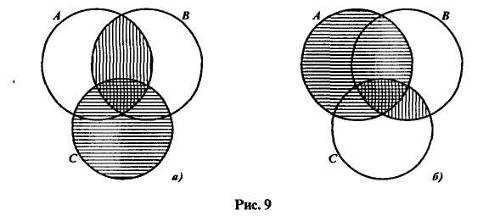
надо найти пересечение множеств В и С — на рисунке 96 оно показано вертикальной штриховкой, а затем выполнить пересечение множества А с полученным множеством. Если отметить множество А горизонтальной штриховкой, то область, заштрихованная дважды, и будет изображать множество А (В С).

Видим, что области, представляющие на рисунке 9 множества (А В) С и А (В С), одинаковы, что и подтверждает справедливость свойства ассоциативности для пересечения множеств.

Аналогично можно проиллюстрировать свойство ассоциативности и для объединения множеств.

В чем важность ассоциативного свойства пересечения и объединения множеств? Во-первых, можно находить пересечение и объединение трех множеств, зная, как это делать для двух. Во-вторых, на основании этого свойства в выражениях А (В С), (А В) С, А (В С), (А В) С можно опускать скобки и писать А В С или А В С, что облегчает запись.

Рассмотрим строгое доказательство свойства ассоциативности одной из операций над множествами, например объединения, т.е. докажем, что для любых множеств А,В и С справедливо равенство (А B) C = А (B С).

Чтобы доказать равенство двух множеств, надо убедиться в том, что каждый элемент множества (А В) С содержится в множестве А (В С), и наоборот.

1. Пусть х — любой элемент множества (А В) С. Тогда, по определению объединения, х А В или х С.

Если х А В, то, по определению объединения, х А или х В. В том случае, когда х А, то, также по определению объединения, х А (В С).

Если х В, то имеем, что х В С, а значит, х А (В С). Случай, когда х А и х В, сводится к рассмотренным. Таким образом, из того, что х А В, следует, что х А (В С).

Если х С, то, по определению объединения, х В С, и следовательно, х А (В С).

Случай, когда х А В и х С, сводится к рассмотренным выше.

Итак, мы показали, что каждый элемент множества (А В) С содержится и в множестве А (В С), т.е. (А В) С А (В С).

2. Пусть y — любой элемент множества А (В С). Тогда, по определению объединения, у А или у В С.

Если y А, то, по определению объединения, у А В и, следовательно, у А и (В С).

Если y В С, то у В или у C. B том случае, когда у В, то у А В и, значит, у (А В) и С. Когда же у С, то у (А B) C. Случай, когда у В и у С, сводится к уже рассмотренным.

Итак, мы показали, что каждый элемент множества А (B С) содержится в множестве (A В) С, т.е. А (В С) (А В) С.

Согласно определению равных множеств заключаем, что (А В) С = А (В С), что и требовалось доказать.

Аналогично доказывается и ассоциативное свойство пересечения множеств.

Взаимосвязь пересечения и объединения множеств отражается в распределительных, или дистрибутивных, свойствах этих операций. Таких свойств два:

1. Пересечение дистрибутивно относительно объединения множеств, т.е. для любых множеств А, В к С выполняется равенство

(А В) С = (А С) (В С).

2. Объединение дистрибутивно относительно пересечения множеств, т.е. для любых множеств А, В и С выполняется равенство

(А В) С = (А С) (В С).

Заметим, что если в выражении есть знаки пересечения и объединения множеств и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение. В связи со сказанным запись дистрибутивного свойства пересечения относительно объединения можно упростить, опустив скобки в правой части равенства.

Убедиться в справедливости сформулированных свойств можно путем доказательства, которое аналогично доказательству свойства ассоциативности объединения.

Проиллюстрировать свойства дистрибутивности можно, используя круги Эйлера.

Если провести аналогию с действиями над числами, то можно увидеть, что дистрибутивное свойство пересечения относительно объединения сопоставимо с распределительным свойством умножения относительно сложения, при условии, что в качестве операции, аналогичной пересечению, рассматривать умножение, а для объединения — сложение.

Но для дистрибутивного свойства объединения множеств относительно пересечения аналогичного свойства над числами нет.

Действительно, наличие такого свойства означало бы, что для всех чисел выполняется равенство а • b + с = (а + с) • (b + с), что невозможно. Подмеченное отличие говорит о том, что наряду с тем, что пересечение и объединение множеств обладают рядом свойств, аналогичных свойствам сложения и умножения чисел, операции над множествами обладают свойствами, которых нет у операций над числами.

Завершая рассмотрение свойств пересечения и объединения множеств, отметим еще следующее.

Понятие пересечения и объединения множеств можно обобщить на любое конечное число множеств:

А₁ А₂ … А_n = {х | х А₁ и х А₂ и… и х А_n},

А₁ А₂ … А_n = {х | х А₁ или х А₂ или … или х А_n},

Аналогично можно поступить и по отношению к рассмотренным свойствам данных операций.

 

Рекомендуемые страницы:

lektsia.com

No related posts.