Кто автор названия тригонометрических функций – ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ | Энциклопедия Кругосвет

Тригонометрические функции — это… Что такое Тригонометрические функции?

Рис. 1
Графики тригонометрических функций:      синуса      косинуса      тангенса      котангенса      секанса      косеканса

Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.

К тригонометрическим функциям относятся:

прямые тригонометрические функции

• синус (sin x)
• косинус (cos x)

производные тригонометрические функции

• тангенс (tg  x)
• котангенс (ctg x)

другие тригонометрические функции

• секанс (sec x)
• косеканс (cosec x)

В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x.

Кроме этих шести, существуют также некоторые редко используемые тригонометрические функции (версинус и т.д.), а также обратные тригонометрические функции (арксинус, арккосинус и т. д.), рассматриваемые в отдельных статьях.

Синус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми вещественнозначными функциями. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и неограниченно дифференцируемые на области определения, но не непрерывные. Тангенс и секанс имеют разрывы второго рода в точках ±πn + π/2, а котангенс и косеканс — в точках ±πn.

Способы определения

Геометрическое определение

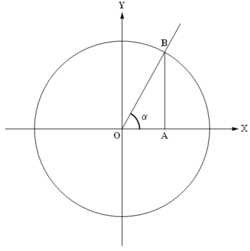Рис. 2
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим x_B, ординату обозначим y_B (см. рисунок).

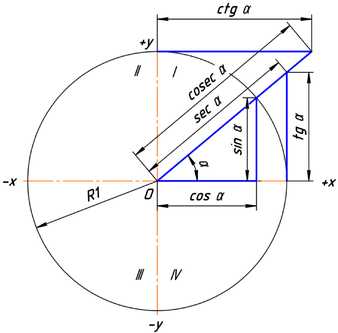Рис. 3
Численные значения тригонометрических функций угла в тригонометрической окружности с радиусом, равным единице

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате

y_B, а косинус — абсциссе x_B. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.

Определение тригонометрических функций для острых углов

Рис. 4
Тригонометрические функции острого угла

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:

• Синусом угла α называется отношение AB/OB (отношение противолежащего катета к гипотенузе).
• Косинусом угла α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе).
• Тангенсом угла α называется отношение AB/OA (отношение противолежащего катета к прилежащему).
• Котангенсом угла α называется отношение ОА/AB (отношение прилежащего катета к противолежащему).
• Секансом угла α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету).
• Косекансом угла α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету).

Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.

Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см.: Теорема синусов, Теорема косинусов).

Определение тригонометрических функций как решений дифференциальных уравнений

Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения

с начальными условиями , то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:

Определение тригонометрических функций как решений функциональных уравнений

Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:

Определение тригонометрических функций через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:

Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:

где

 — числа Бернулли,

 — числа Эйлера.

Значения тригонометрических функций для некоторых углов

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).

Значения косинуса и синуса на окружности.

Значения тригонометрических функций нестандартных углов

Значения тригонометрических функций прочих углов  

Свойства тригонометрических функций

Простейшие тождества

Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Это соотношение называется основным тригонометрическим тождеством.

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Непрерывность

Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва котангенс и косеканс —

Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Периодичность

Функции  — периодические с периодом 2π, функции и  — c периодом π.

Формулы приведения

Формулами приведения называются формулы следующего вида:

Здесь f — любая тригонометрическая функция, g — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:

Некоторые формулы приведения:

Формулы сложения

Значения тригонометрических функций суммы и разности двух углов:

Аналогичные формулы для суммы трёх углов:

Формулы для кратных углов

Формулы двойного угла:

Формулы тройного угла:

Прочие формулы для кратных углов:

следует из формулы дополнения и формулы Гаусса для Гамма-функции

Формулы половинного угла:

Произведения

Формулы для произведений функций двух углов:

Аналогичные формулы для произведений синусов и косинусов трёх углов:

Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.

Степени

Суммы

Для функций от аргумента существует представление:

где угол находится из соотношений:

Однопараметрическое представление

Все тригонометрические функции можно выразить через тангенс половинного угла.

Производные и интегралы

Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:

Тригонометрические функции комплексного аргумента

Определение

Формула Эйлера:

позволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:

где

Соответственно, для вещественного x,

Комплексные синус и косинус тесно связаны с гиперболическими функциями:

Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:

• комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
• все нули комплексных синуса и косинуса лежат на вещественной оси.

Комплексные графики

На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.

История названий

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современные краткие обозначения sin и cos введены Уильямом Отредом и закреплены в трудах Эйлера.

Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583).

Сам термин тригонометрические функции введён Клюгелем в 1770 году.

См. также

Литература

• Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
• Г. Б. Двайт Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.

Ссылки

dic.academic.ru

Применение тригонометрических функций

История тригонометрических функций

Самой первой тригонометрической функцией была хорда, соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы (II в. до н. э.), нужные для астрономии.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды они назвали “архиджива”, что означало “половина тетивы лука”. Кроме sin x, индийцы рассматривали также величину 1 – cos x, которую они называли “комаджива”, и величину cos x – “котиджива”.
Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин “секанс”. В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название “косинус” и “котангенс”, причем приставка “ко” (co) обозначает дополнение (complementum).
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру. Последний пришел к выводу, что эти обозначения весьма удобны, и стал употреблять их в своих математических работах. Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x: tang x, cot x, sec x, cosec x. Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга. Эйлер установил современную точку зрения на тригонометрические как функции числового аргумента.
В1770 г. появилось и удерживается до наших дней название Тригонометрические функции. Его ввел Г. С. Клюгель в работе “Аналитическая тригонометрия”.

 Определение и графики тригонометрических функций

Величины углов (аргументы функций): α, x  Тригонометрические функции: sinα, cosα, tanα, cotα, secα, cscα Множество действительных чисел: R  Координаты точки окружности: x, y

Радиус круга: r  Целые числа: k

1. Тригонометрические функциипредставляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
2. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс,котангенс, секанси косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
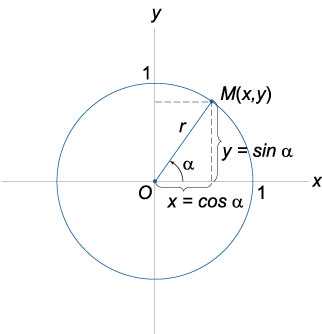
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OMи положительным направлением оси Ox равен α.

   Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: 
   sinα=y/r. 
   Поскольку r=1, то синус равен ординате точки M(x,y).

   Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: 
   cosα=x/r 

   Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: 
   tanα=y/x,x≠0 

   Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: 
   cotα=x/y,y≠0 

   Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): 
   secα=r/x=1/x,x≠0 

   Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): 
   cscα=r/y=1/y,y≠0 

   В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: 
   Синусом угла α называется отношение противолежащего катета к гипотенузе. 
   Косинусом угла α называется отношение прилежащего катета к гипотенузе. 
   Тангенсом угла α называется противолежащего катета к прилежащему. 
   Котангенсом угла α называется прилежащего катета к противолежащему. 
   Секанс угла α представляет собой отношение гипотенузы к прилежащему катету. 
   Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету. 

   График функции синус 
   y=sinx, область определения: x∈R, область значений: −1≤sinx≤1 

   График функции косинус 
   y=cosx, область определения: x∈R, область значений: −1≤cosx≤1

4.  

ya-znau.ru

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — это… Что такое ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ?

класс элементарных функций: синус, косинус, тангенс, котангенс, секанс, косеканс. Обозначаются соответственно: sin x,cos x, tg x,ctg x, sec x,cosec x.
Тригонометрические функции действительного аргумента. Пусть А — точка окружности с центром в начале координат и радиусом, равным единице, — угол между осью абсцисс и вектором ОА, отсчитываемый от положительного направления оси абсцисс (рис. 1). При этом если отсчет ведется против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке — отрицательной, т. е. — полярный угол точки А.

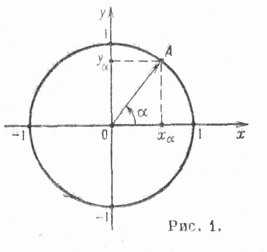
Если — прямоугольные декартовы координаты точки А, то Т. ф. синус и косинус определяются формулами

Остальные Т. ф. могут быть определены формулами

Все Т. ф.- периодические функции. Графики Т. ф. даны на рис. 2.

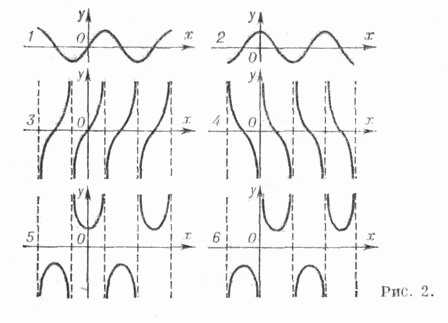Основные свойства Т. ф.: область определения, множество значений, четность и участки монотонности приведены в табл.

Функция	Область определения	Множество значений	Четность	Участки монотонности
sinx		[-1, +1]	нечетная	возрастает при …. … убывает при
cosx		[-1, +1]	четная	возрастает при убывает при
tg x			нечетная	возрастает при
ctg x			нечетная	убывает при
sec x			четная	возрастает при убывает при
соsес x			нечетная	возрастает при убывает при

Каждая Т. ф. в каждой точке своей ооласти определения непрерывна и бесконечно дифференцируема; производные Т. ф.:

Интегралы от Т. ф.:

Все Т. ф. допускают разложение в степенные ряды:

при

при

при 0 < |х|< (B_n — числа Бернулли).
Функция y=sinx, являющаяся обратной по отношению к функции z=sin у, определяет . как многозначную функцию от х’, она обозначается y=Arcsin x. Аналогично определяются функции, обратные по отношению к другим Т. ф.; все они наз. обратными тригонометрическими функциями.
Тригонометрические функции комплексного переменного. Т. ф. для комплексных значений переменного z=x+iy определяются как аналитические продолжения соответствующих Т. ф. действительного переменного в комплексную плоскость.
Так, sinz и cosz можно определить с помощью рядов для sinxи cos х. Эти ряды сходятся во всей плоскости, поэтому sinz и cosz- целые функции.
Т. ф. тангенс и котангенс определяются формулами

Т. ф. tg z и ctg z — мероморфнае функции. Полюсы tg zпростые (1-го порядка) и находятся в точках полюсы ctg z также простые и находятся в точках
Все формулы, справедливые для Т. ф. действительного аргумента, остаются справедливыми и для комплексного аргумента.
В отличие от Т. ф. действительного переменного, функции sin zи cos z принимают все комплексные значения: уравнения sin z=a и cos z=a имеют решения для любого комплексного а:

Т. ф. tg z и ctg z принимают все комплексные значения, кроме уравнения tg z=o, ctg z=a имеют решения для любого комплексного числа

Т. ф. можно выразить через показательную функцию:

и гиперболические функции:sin z=-.sh iz, cos z=chiz, tg z =- i th iz.

В. И. Битюцков.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

dic.academic.ru

10 секретных тригонометрических функций, о которых вам никогда не рассказывали

Существует 10 секретных тригонометрических функций, о которых вы никогда не слышали, и у них восхитительные названия, такие как гаверсинус и эксеканс.

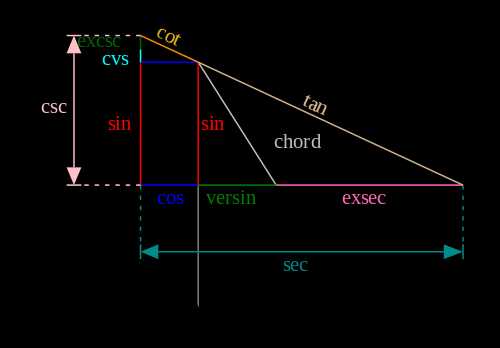
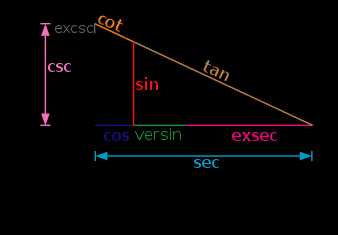
Рис. 1. Здесь изображена единичная окружность и более чем изобилие тригонометрических функций. (Известны максимум 8 тригонометрических функций). Знакомые синус, косинус и тангенс отмечены синим, красным, и желтовато-коричневым, соответственно. Версинус отмечен зеленым рядом с косинусом и розовым эксекансом справа от версинуса. Экскосеканс и синус-коверсус также имеются на рисунке. Не обозначены веркосинус, косинус-коверсус и все, что с гавер.

Если вы хотите помучить студентов этим и ввернуть интересные слова в разговор, чтобы показаться эрудированным и/или невыносимым, вот определения всех “забытых тригонометрических функций’’:

версинус: ,
веркосинус: ,
синус-коверсус: ,
косинус-коверсус: ,
гаверсинус: ,
гаверкосинус: ;
когаверсинус: ,
когаверкосинус: ,
эксеканс: ,
экскосеканс: .

Нужно признаться, что испытываешь некоторое разочарование, когда видишь это. Эти функции — простые комбинации добрых старых синуса и косинуса. Почему же они получили собственные названия?! Для того времени и места, где я могу сидя на диване найти синус любого угла с точностью до 100 десятичных знаков почти мгновенно с помощью онлайн калькулятора, версинус не нужен. Но эти кажущиеся избыточными функции были необходимы в докалькуляторном мире.

В темные докалькуляторные дни люди использовали логарифмы для умножения больших чисел. Сначала давайте вспомним, что такое логарифмы. Равенство означает, что . Например, , так что . Применение логарифмов удобно, поскольку . Другими словами, логарифмы переводят умножение в сложение. Если вы хотите перемножить два числа с помощью таблицы логарифмов, вы найдете в ней логарифмы обоих чисел и затем их сложите. Тогда по таблице логарифмов вы найдете число, которое имеет полученный логарифм, и это будет ответ. Это сейчас кажется громоздким, но умножение вручную требует гораздо больше операций. Когда каждая операция занимает некоторое количество времени (и дает некоторую ошибку), процедура, которая конвертирует умножение в сложение, экономит время и может помочь увеличить точность вычислений.

Секретные тригонометрические функции, подобно логарифмам, упрощали расчеты. Версинус и гаверсинус использовались чаще всего. Если угол близок к нулю, его косинус очень близок к . Если в вычислениях имеется , то ответ может быть неправильным, если в вашей таблице косинусов не хватает значащих цифр. Для примера, косинус равен , а . Разность . Если у вас в таблице косинусов три значащих цифры, вы получите только одну значащую цифру в вашем результате, из-за нулей в разности. И таблица только с тремя значащими цифрами не покажет различия между углами и . Во многих случаях это не имеет значения, но это может быть проблемой, если ошибка появляется в процессе вычислений.

Дополнительные тригонометрических функции также имеют то преимущество, что они всегда неотрицательны. Версинус принимает значения от до , так что если вы используете для умножения таблицы логарифмов с версинусом, вам не придется беспокоиться о том, что для отрицательных чисел логарифм не определен. (Он не определена и для , но с этим случаем легко справиться). Еще одно преимущество версинуса и гаверсинуса состоит в том, что они могут избавить от необходимости возводить в квадрат. Немного тригонометрической мудрости (типа запоминания одной тригонометрической формулы из их бесконечного списка, который вы изучали в школе) показывает, что . Таким образом, гаверсинус — это всего лишь . Аналогично, гаверкосинус — это . Если в ваших вычислениях есть квадраты синуса или косинуса, вы можете использовать таблицы гаверсинуса или гаверкосинуса, и вам не придется возводить в квадрат или извлекать квадратные корни.

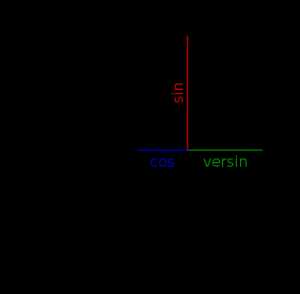
Рис. 2. На рисунке показаны синус, косинус и версинус угла.

Версинус определяется довольно очевидным образом и, кажется, использовался еще в 400 г. н.э. в Индии. Но гаверсинус, возможно, играл более важную роль в новейшей истории, когда его применяли в навигации. Формула гаверсинуса дает очень точный способ вычисления расстояния между двумя точками на поверхности сферы, у которых известны широта и долгота. Формула гаверсинуса является переформулировкой сферической теоремы косинусов, но именно эта формулировка более полезна для малых углов и расстояний. (С другой стороны, формула гаверсинуса дает плохой результат для углов, близких к , для которых хорошо работает сферическая теорема косинусов). Формула гаверсинуса может дать точные результаты, не требуя больших вычислительных затрат на операции возведения в квадрат и извлечения квадратных корней. Совсем недавно, в 1984 году, любительский астрономический журнал Sky & Telescope пел хвалу формуле гаверсинуса, которая полезна не только для наземной навигации, но и для астрономических расчетов. Более подробно об этой формуле и вычислении расстояний на сфере читайте здесь.

Об истории других тригонометрических функций из приведенного списка информации меньше. Они помогали делать более точными расчеты вблизи определенных углов, но некоторые из них широко использовались, а другие были названы по аналогии с ними, но применялись редко. Может быть, кто-то из вас знает об этом больше. Пишите.

В таблице секретных тригонометрических функций , “ha’’, очевидно, означает половину (от английского слова half), например, гаверсинус составляет половину версинуса. “Co’’ означает те же функции, но от дополнительного угла. (Дополнительный угол — это угол, в сумме с данным дающий . В прямоугольном треугольнике два острых угла являются дополнительными друг для друга). Например, косинус угла является синусом дополнительного угла. Аналогично синус-коверсус является версинусом дополнительного угла. Он обозначен светло-голубым над одним из красных синусов на рис. 1.

Вот только немного смущает веркосинус. Если “co’’ означает дополнительный угол, то веркосинус будет таким же, как коверсинус, а это не так. Вместо этого веркосинус является версинусом смежного угла (сумма смежных углов равна ), а не дополнительного. В дополнение к определениям через и версинус и веркосинус могут быть определены как и . В случае версинуса, возможно, определение с участием старше, чем определение с участием квадрата синуса. Возможно, кто-то из вас знает об этом больше.

В любом случае, таблица сверхсекретных дополнительных тригонометрических функций является веселым упражнением для выяснения, что значат префиксы.

Источник: http://blogs.scientificamerican.com/roots-of-unity/2013/09/12/10-trig-functions-youve-never-heard-of/

hijos.ru

Тригонометрия — это… Что такое Тригонометрия?

Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии^[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

В Школе СССР имела статус учебного предмета.

Определение тригонометрических функций

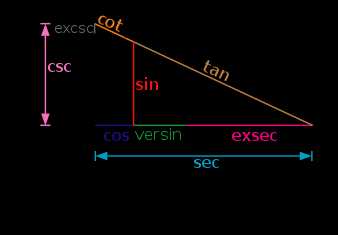
Тригонометрические функции угла θ внутри единичной окружности

Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).

• Синус — отношение противолежащего катета к гипотенузе.
• Косинус — отношение прилежащего катета к гипотенузе.
• Тангенс — отношение противолежащего катета к прилежащему.
• Котангенс — отношение прилежащего катета к противолежащему.
• Секанс — отношение гипотенузы к прилежащему катету.
• Косеканс — отношение гипотенузы к противолежащему катету.

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:

Для острых углов новые определения совпадают с прежними.

Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.

История

Древняя Греция

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.

Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sin α/ sin β < α/β < tan α/ tan β, где 0° < β < α < 90°, совместно с другими теоремами.

Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд. Возможно Гиппарх взял идею такого деления у Гипсикла, который ранее разделил день на 360 частей, хотя такое деление дня могли предложить и вавилонские астрономы.

Менелай Александрийский (100 н. э.) написал «Сферику» в трёх книгах. В первой книге он представил основы для сферических треугольников, аналогично I книге «Начал» Евклида о плоских треугольниках. Он представил теорему, для которой нет аналога у Евклида, о том, что два сферических треугольника конгруэнтны, если соответствующие углы равны, но он не делал различия между конгруэнтными и симметричными сферическими треугольниками. Другая его теорема гласит о том, что сумма углов сферического треугольника всегда больше 180°. Вторая книга «Сферики» применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».

Позднее Клавдий Птолемей (90 — 168 г. н. э.) в «Альмагесте» расширил Гиппарховы «Хорды в окружности». Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. Теорема, которая была центральной в вычислении хорд Птолемея, также известна сегодня как теорема Птолемея, которая говорит о том, что сумма произведений противоположных сторон выпуклого вписанного четырёхугольника равна произведению диагоналей. Отдельный случай теоремы Птолемея появился как 93 предложение «Данных» Евклида.

Теорема Птолемея влечёт за собой эквивалентность четырёх формул суммы и разности для синуса и косинуса. Позднее Птолемей вывел формулу половинного угла. Птолемей использовал эти результаты для создания своих тригонометрических таблиц, хотя, возможно, эти таблицы были выведены из работ Гиппарха. Ни таблицы Гиппарха, ни Птолемея не сохранились до настоящего дня, хотя свидетельства других древних авторов снимают сомнения об их существовании.

Средневековая Индия

Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как

Индийцы также знали формулы для кратных углов , , где .

Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.

Южноиндийские математики в 16 веке добивались больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.

В 8 в. учёные стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки.

См. также

Примечания

1. ↑ Советский энциклопедический словарь. М.: Советская энциклопедия, 1982.

dic.academic.ru

Тригонометрия — Википедия

Тригономе́трия (от греч. τρίγωνον (треугольник) и греч. μέτρεο (меряю), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии^[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и форму Земли).

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

Древняя Греция[править]

Первые тригонометрические таблицы видимо были составлены Гиппархом, который сейчас известен как «отец тригонометрии»^[2].

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме. Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sinα/sinβ < α/β < tgα/tgβ, где 0° < β < α < 90°, совместно с другими теоремами.

Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд. Возможно Гиппарх взял идею такого деления у Гипсикла, который ранее разделил день на 360 частей, хотя такое деление дня могли предложить и вавилонские астрономы.

Менелай Александрийский (100 н. э.) написал «Сферику» в трёх книгах. В первой книге он представил основы для сферических треугольников, аналогично I книге «Начал» Евклида о плоских треугольниках. Он представил теорему, для которой нет аналога у Евклида, о том, что два сферических треугольника конгруэнтны, если соответствующие углы равны, но он не делал различия между конгруэнтными и симметричными сферическими треугольниками. Другая его теорема гласит о том, что сумма углов сферического треугольника всегда больше 180°. Вторая книга «Сферики» применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».

Позднее Клавдий Птолемей (90 — 168 г. н. э.) в «Альмагесте» расширил Гиппарховы «Хорды в окружности». Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. Теорема, которая была центральной в вычислении хорд Птолемея, также известна сегодня как теорема Птолемея, которая говорит о том, что сумма произведений противоположных сторон выпуклого вписанного четырёхугольника равна произведению диагоналей. Отдельный случай теоремы Птолемея появился как 93-е предложение «Данных» Евклида.

Теорема Птолемея влечёт за собой эквивалентность четырёх формул суммы и разности для синуса и косинуса. Позднее Птолемей вывел формулу половинного угла. Птолемей использовал эти результаты для создания своих тригонометрических таблиц, хотя, возможно, эти таблицы были выведены из работ Гиппарха. Ни таблицы Гиппарха, ни Птолемея не сохранились до настоящего дня, хотя свидетельства других древних авторов снимают сомнения в их существовании.

Средневековая Индия[править]

Замена хорд синусами стала главным достижением средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как

Индийцы также знали формулы для кратных углов где

Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.

Южноиндийские математики в XVI веке добились больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.

С VIII века учёные стран Ближнего и Среднего Востока развили тригонометрию своих предшественников. В середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки.

Определение тригонометрических функций[править]

Тригонометрические функции угла θ внутри единичной окружности

Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).

• Синус — отношение противолежащего катета к гипотенузе.
• Косинус — отношение прилежащего катета к гипотенузе.
• Тангенс — отношение противолежащего катета к прилежащему.
• Котангенс — отношение прилежащего катета к противолежащему.
• Секанс — отношение гипотенузы к прилежащему катету.
• Косеканс — отношение гипотенузы к противолежащему катету.

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:

Для острых углов новые определения совпадают с прежними.

Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.

Свойства функции синус[править]

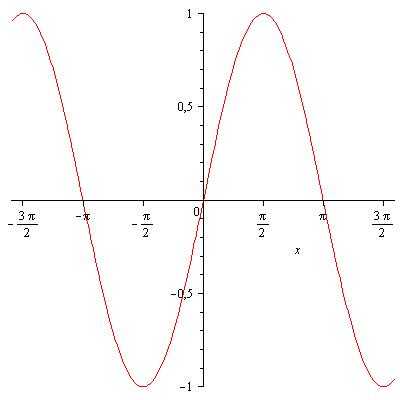
1. Область определения функции — множество всех действительных чисел: .
2. Множество значений — промежуток [−1; 1]: = [−1;1].
3. Функция является нечётной: .
4. Функция периодическая, наименьший положительный период равен : .
5. График функции пересекает ось Ох при .
6. Промежутки знакопостоянства: при и при .
7. Функция непрерывна и имеет производную при любом значении аргумента:
8. Функция возрастает при , и убывает при .
9. Функция имеет минимум при и максимум при .

Свойства функции косинус[править]

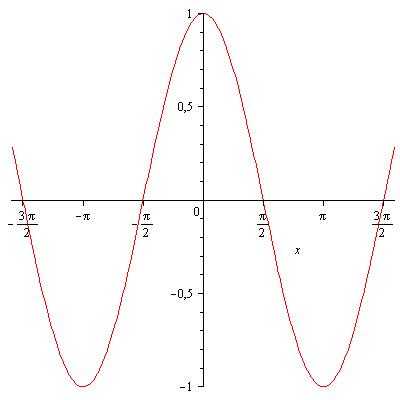
1. Область определения функции — множество всех действительных чисел: .
2. Множество значений — промежуток [−1; 1]: = [−1;1].
3. Функция является чётной: .
4. Функция периодическая, наименьший положительный период равен : .
5. График функции пересекает ось Ох при .
6. Промежутки знакопостоянства: при и при
7. Функция непрерывна и имеет производную при любом значении аргумента:
8. Функция возрастает при и убывает при
9. Функция имеет минимум при и максимум при

Свойства функции тангенс[править]

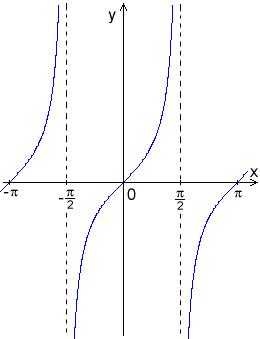
1. Область определения функции — множество всех действительных чисел: , кроме чисел
2. Множество значений — множество всех действительных чисел:
3. Функция является нечётной: .
4. Функция периодическая, наименьший положительный период равен : .
5. График функции пересекает ось Ох при .
6. Промежутки знакопостоянства: при и при .
7. Функция непрерывна и имеет производную при любом значении аргумента из области определения:
8. Функция возрастает при .

Свойства функции котангенс[править]

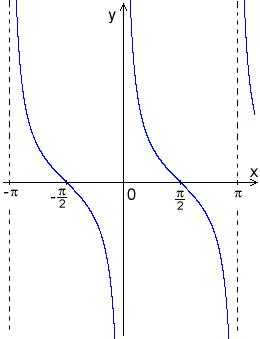
1. Область определения функции — множество всех действительных чисел: кроме чисел
2. Множество значений — множество всех действительных чисел:
3. Функция является нечётной:
4. Функция периодическая, наименьший положительный период равен :
5. График функции пересекает ось Ох при
6. Промежутки знакопостоянства: при и при
7. Функция непрерывна и имеет производную при любом значении аргумента из области определения:
8. Функция убывает при

Применение тригонометрии[править]

Секстант — навигационный измерительный инструмент, используемый для измерения высоты светила над горизонтом с целью определения географических координат той местности, в которой производится измерение.

Существует множество областей, в которых применяются тригонометрия и тригонометрические функции. Например, метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, в географии для измерения расстояний между объектами, а также в спутниковых навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн.

Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в аптеках, в химии, в теории чисел (следовательно, и в криптологии), в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

Стандартные тождества[править]

Тождества — это равенства, справедливые при любых значениях входящих в них переменных.

Формулы преобразования суммы углов[править]

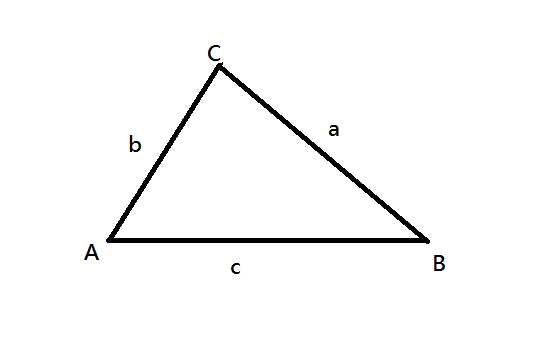Треугольник со сторонами a, b, c и соответственно противоположными углами A, B, C

В следующих тождествах, A, B и C являются углами треугольника; a, b, c — длины сторон треугольника, лежащие напротив соответствующих углов.

Теорема синусов[править]

Стороны треугольника пропорциональны синусам противолежащих углов. Для произвольного треугольника

где  — радиус окружности, описанной вокруг треугольника.

Теорема косинусов[править]

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Для плоского треугольника со сторонами и углом , противолежащим стороне ,

или:

Теорема тангенсов[править]

Формула Эйлера[править]

Формула Эйлера утверждает, что для любого действительного числа выполнено следующее равенство:

где  — основание натурального логарифма,  — мнимая единица. Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:

Вышеуказанные уравнения могут быть получены путем сложения или вычитания формул Эйлера:

с последующим решением относительно синуса или косинуса.

Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:

Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения результат выражения остается вещественным. Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением.

Решение простых тригонометрических уравнений[править]

Если  — вещественных решений нет.

Если  — решением является число вида

Если  — вещественных решений нет.

Если  — решением является число вида

Решением является число вида

Решением является число вида

Сферическая тригонометрия[править]

Важным частным разделом тригонометрии, используемым в астрономии, геодезии, навигации и других отраслях, является сферическая тригонометрия, рассматривающая свойства углов между большими кругами на сфере и дуг этих больших кругов. Геометрия сферы существенно отличается от евклидовой планиметрии; так, сумма углов сферического треугольника, вообще говоря, отличается от 180°, треугольник может состоять из трёх прямых углов. В сферической тригонометрии длины сторон треугольника (дуги больших кругов сферы) выражаются посредством центральных углов, соответствующих этим дугам. Поэтому, например, сферическая теорема синусов выражается в виде

и существуют две теоремы косинусов, двойственные друг другу.

1. ↑ Советский энциклопедический словарь. М.: Советская энциклопедия, 1982.
2. ↑ Boyer. Greek Trigonometry and Mensuration // . — 1991. — P. 162.

английская

• Boyer Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — ISBN 0-471-54397-7.
• Christopher M. Linton (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy . Cambridge University Press.
• Weisstein, Eric W. «Trigonometric Addition Formulas». Wolfram MathWorld. Weiner.

www.wiki-wiki.ru