Разложение в ряд Фурье онлайн
Разложение некоторой функции f(x) в тригонометрический ряд Фурье на отрезке [-k, k] имеет вид:
a02∞n1ancosnπxkbnsinnπxk
где
an1kkkfxcosnπxkdx для (n = 0, 1, 2, 3,…)
bn1kkkfxsinnπxkdx для (n = 1, 2, 3,…)
В качестве примера, разложим в ряд Фурье функцию f(x)=x на отрезке [-1, 1]. В этом случае коэффициенты an и bn определяются по формулам:
an11xcosnπxdx0
bn11xsinnπxdx21nnπ
Таким образом, разложение функции f(x)=x в ряд Фурье на отрезке [-1, 1] имеет вид:
∞n121nnπsinnπx
На рисунке ниже приведено два графика: f(x)=x (желтым цветом) и yx25n121nnπsinnπx , (синим цветом) для которого мы взяли порядок разложения функции в ряд Фурье равным 25.

Стоит отметить, что в приведенном выше примере, коэффициенты an равны нулю не случайно. Дело в том, что функция f(x)=x является нечетной на интервале [-1, 1]. Функция cosnπx — напротив является чётной. Произведение чётной функции на нечетную является нечётной функцией, поэтому согласно свойствам , интеграл от нечётной функции на симметричном интервале равен нулю.
В случае, если бы мы раскладывали в ряд Фурье на симметричном интервале какую-нибудь чётную функцию, например x2 , коэффициенты bn равнялись бы нулю, поскольку в этом случае, подинтегральное выражение x2sinnπx — являлось бы нечётной функцией.
Исходя из приведённых выше рассуждений можно сделать следующие выводы:
- Разложение в ряд Фурье нечётной функции на симметричном интервале будет содержить только слагаемые с синусами.
- Разложение в ряд Фурье чётной функции на симметричном интервале будет содержить только слагаемые с косинусами.
- Если нам необходимо получить разложение в ряд Фурье некоторой произвольной функции на интервале [0, b] , то у нас есть две возможности. Мы можем продолжить эту функцию на интервал [-b, 0] нечётным образом и тогда в разложении получим только синусы. Или же мы можем продолжить её в указанный интервал чётным образом и тогда получим в разложении только косинусы.
Стоит также отметить, что используя приведённые выше формулы и соответствующую замену переменной, можно получить формулы для коэффициентов разложения функции в ряд Фурье на произвольном интервале [p, q]:
an1kqpfxcosnπxkdx
bn1kqpfxsinnπxkdx
здесь kqp2 .
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha раскладывает произвольную функцию в ряд Фурье на интервале [-π π]. В принципе, это не накладывает существенных ограничений, поскольку, используя соответствующую замену переменной, мы можем получить разложение на произвольном интервале [p, q].
Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.
Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов. Вариант для печати.
Ряд Фурье периодических функций с периодом 2π.
Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.
Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):
Стандартная (=обычная) запись через сумму sinx и cosx
f(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2sin2x+b3sin3x+…,
где ao, a1,a2,…,b1,b2,.. — действительные константы, т.е.
(1)
Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:
Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,
Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)
f(x)=ao+c1sin(x+α1)+c2sin(2x+α2)+…+cn sin(nx+αn)
Где ao — константа, с 1=(a12+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен an=arctg an/bn.
Для ряда (1) член (a1cosx+b1sinx) или c1sin(x+α1) называется первой или основной гармоникой, (a2cos2x+b2sin2x) или c2sin(2x+α2) называется второй гармоникой и так далее.
Для точног
Как разложить функцию в ряд Фурье
Разложение функций в ряды Фурье используется достаточно часто, поскольку в таком виде их удобно дифференцировать, интегрировать, использовать сдвиг функции по аргументу, а также свёртку функций. Несмотря на то, что процедура разложения функции в ряд Фурье даже в самом простом случае может быть достаточно трудоёмкой, система Вольфрам Альфа, как правило, легко справляется с этой задачей.Ряды Фурье представляются в тригонометрической и экспоненциальной (комплексной) форме:
В первом варианте в качестве базиса разложения используется система синусов и косинусов. Но при работе с рядами Фурье вместо них бывает удобнее использовать экспоненты мнимого аргумента. Видимо поэтому, Вольфрам Альфа отдает предпочтение второму варианту.
Самый простой способ разложить функцию в ряд Фурье — отправить в Вольфрам Альфа запрос вида Fourier series [функция, аргумент, количество членов ряда]. Например,
В полученном результате, как и требуется, представлены члены разложения до 5-го номера включительно; коэффициенты при сопряженных степенях экспоненты являются комплексно-сопряженными числами.
Одновременно Вольфрам Альфа дает графическое представление аппроксимации заданной функции рядом Фурье (здесь центральная часть графика аппроксимирует заданную параболу):
Еще более отчетливо особенности Фурье-аппроксимации можно видеть в результатах следующего запроса (где ряд Фурье аппроксимирует прямую):
Представление заданной функции рядом Фурье в тригонометрической форме выводится в самой нижней части выдачи (здесь — для второго примера):
Кстати, несмотря на то, что выше в выдаче системы было: «Wolfram|Alpha doesn’t understand your query. Showing instead result for query: Fourier», — что означает «Система не понимает ваш запрос. Показан результат, соответствующий запросу: Fourier», не ведитесь на это 😉 По запросу «Fourier», который предлагает использовать система, будут выведены либо биографические сведения об ученом-математике Jean-Baptiste-Joseph Fourier (mathematician), либо преобразование Фурье данной функции Fourier[t^2+t]; зависит от того, поставите ли вы между словом «Fourier» и скобкой пробел или нет.
Если в запросе Fourier series не указывать явно количество членов разложения n, то система Вольфрам Альфа по умолчанию выводит четыре варианта для значений n от 0 до 3, и только для комплексной формы ряда Фурье:
Дополнительные варианты разложения для n больше 3 можно получить тут же с помощью кнопки «More». Но это относится только к графическому представлению результатов:
Таким образом, чтобы получить разложение функции в тригонометрический ряд Фурье, нужно в запросе Fourier series явно указывать количество членов разложения.
Что делать, если стоит задача найти не разложение в ряд Фурье, а коэффициенты ряда Фурье?
Прежде всего, можно использовать запрос FourierCoefficient[выражение, аргумент, n], по которому система Вольфрам Альфа выводит n-й коэффициент разложения выражения в комплексный ряд Фурье.
Например, 5-й коэффициент разложения выражения (t^2+t) в ряд Фурье можно получить так:
FourierCoefficient[t^2+t, t, 5]
Если же при не указывать явно n, то данный запрос выведет общее выражение для n-го коэффициента ряда Фурье данного выражения:
FourierCoefficient[t^2+t, t, n]
Кроме этого, Вольфрам Альфа тут же выводит также таблицу коэффициентов комплексного ряда Фурье (до 15-го члена включительно, если нажать «More»):
В этом кратком обзоре я не упомянул, как разложить функцию в ряд Фурье по синусам и косинусам или как использовать калькулятор рядов Фурье системы Вольфрам Альфа, а также ничего не сказал о двумерных рядах Фурье. Все это — темы моих будущих постов. Следите за блогом.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Разложение функции у=1-х в ряды фурье по синусам и косинусам
Типовой расчёт (вар. 4)
Задача 5.
А) Разложить функцию , заданную па полупериоде , в ряд Фурье по косинусам. Построить графики второй, третьей частичных сумм. Записать равенство Парсеваля для полученного ряда
Б) Разложить функцию , заданную на полупериоде , в ряд Фурье по синусам. Построить графики второй, третьей частичных сумм.
В) Разложить функцию в ряд Фурье, продолжая ее па полупериод функцией, равной 0. Построить графики второй, четвертой частичных сумм.
Решение
а) Доопределим функцию на промежутке чётным образом и продолжим её на всю числовую ось как периодическую с периодом, равным 8. — чётная функция. Тригонометрический ряд Фурье содержит только косинусы. Вычислим коэффициенты Фурье этой функции.
, следовательно
Так как рассматриваемая функция непрерывна всюду, то сумма её ряда Фурье равна данной функции при всех х и
.
Равенство Парсеваля:
, так как , то
Б) Доопределим функцию на промежутке нечётным образом, а значение в т : и продолжим её на всю числовую ось как периодическую с периодом, равным 8. Согласно теореме Дирихле тригонометрический ряд Фурье такой функции будет сходиться к этой функции во всех точках непрерывности. Вычислим коэффициенты Фурье этой функции.
Так как рассматриваемая функция непрерывна всюду, то сумма её ряда Фурье равна данной функции при всех х и .
В) Разложим в ряд Фурье функцию
Т=8
Вычислим коэффициенты Фурье этой функции
, следовательно
Ряд Фурье имеет вид:
| < Предыдущая | Следующая > |
|---|
Ряды Фурье — Студопедия
Функция 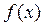 , определённая при всех значениях x называется периодической, если существует такое число T (T≠ 0), что при любом значении x выполняется равенство f(x + T) = f(x). Число T в этом случае является периодом функции.
, определённая при всех значениях x называется периодической, если существует такое число T (T≠ 0), что при любом значении x выполняется равенство f(x + T) = f(x). Число T в этом случае является периодом функции.
Свойства периодических функций:
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т.
2) Если функция f(x) имеет период Т,то функция f(ax) имеет период 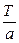
В самом деле, для любого аргумента х:

(умножение аргумента на число означает сжатие или растяжение графика этой функции вдоль оси ОХ)
Например, функция 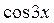 имеет период
имеет период 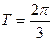 , периодом функции
, периодом функции 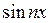 является
является 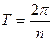
3) Если f(x) периодическая функция периода Т, то равны любые два интеграла от этой функции, взятые по промежутку длины Т (при этом предполагается, что эти интегралы существуют).

Ряд Фурье для функции с периодом T= 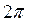 .
.
Тригонометрическим рядом называется ряд вида:
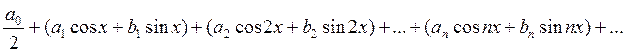
или, короче,
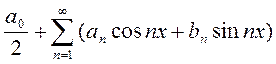 , где
, где 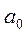 ,
, 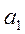 ,
, 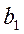 ,
, 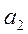 ,
,  , … ,
, … , 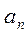 ,
, 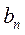 , … — действительные числа, называемые коэффициентами ряда.
, … — действительные числа, называемые коэффициентами ряда.
Каждое слагаемое 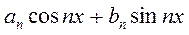
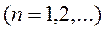 тригонометрического ряда является периодической функцией периода
тригонометрического ряда является периодической функцией периода 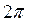 (т.к.
(т.к. 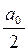 — имеет любой
— имеет любой
период, а период ( 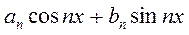 ) равен
) равен 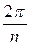 , а значит, и
, а значит, и 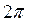 ). Каждое слагаемое (
). Каждое слагаемое ( 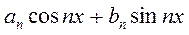 ), при n=1,2,3… является аналитическим выражением простого гармонического колебания
), при n=1,2,3… является аналитическим выражением простого гармонического колебания 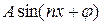 , где A — амплитуда,
, где A — амплитуда,
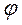 — начальная фаза. Учитывая сказанное, получаем: если тригонометрический ряд сходится на отрезке длины периода
— начальная фаза. Учитывая сказанное, получаем: если тригонометрический ряд сходится на отрезке длины периода 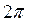 , то он сходится на всей числовой оси и его сумма
, то он сходится на всей числовой оси и его сумма 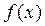 является периодической функцией периода
является периодической функцией периода 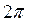 .
.
Пусть тригонометрический ряд равномерно сходится на отрезке 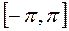 (следовательно, и на любом отрезке) и его сумма равна
(следовательно, и на любом отрезке) и его сумма равна 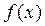 . Для определения коэффициентов этого ряда воспользуемся следующими равенствами:
. Для определения коэффициентов этого ряда воспользуемся следующими равенствами:
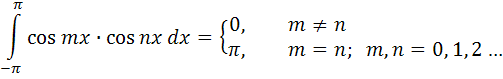
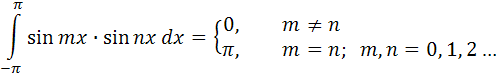 (4.1)
(4.1)
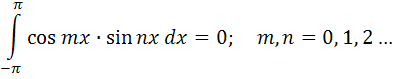
А так же воспользуемся следующими свойствами.
1) Как известно, сумма равномерно сходящегося на некотором отрезке 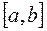 ряда, составленного из непрерывных функций, сама является непрерывной функцией на этом отрезке. Учитывая это, получим, что сумма равномерно сходящегося на отрезке
ряда, составленного из непрерывных функций, сама является непрерывной функцией на этом отрезке. Учитывая это, получим, что сумма равномерно сходящегося на отрезке 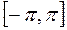 тригонометрического ряда – непрерывная функция на всей числовой оси.
тригонометрического ряда – непрерывная функция на всей числовой оси.
2) Равномерная сходимость ряда 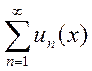 на отрезке
на отрезке 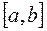 не нарушится, если все члены ряда умножить на функцию
не нарушится, если все члены ряда умножить на функцию 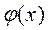 , непрерывную на этом отрезке.
, непрерывную на этом отрезке.
В частности, равномерная сходимость на отрезке 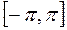 данного тригонометрического ряда не нарушится, если все члены ряда умножить на
данного тригонометрического ряда не нарушится, если все члены ряда умножить на 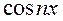
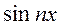 .
.По условию
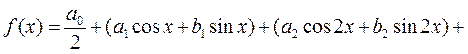
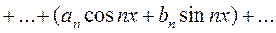 (4.2)
(4.2)
В результате почленного интегрирования равномерно сходящегося ряда (4.2) и учитывая вышеприведенные равенства (4.1) (ортогональность тригонометрических функций), получим:

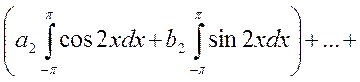
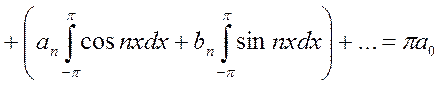
Следовательно, коэффициент 
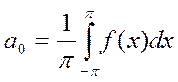 .
.
Умножая равенство (4.2) на 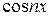 , интегрируя это равенство в пределах от
, интегрируя это равенство в пределах от 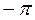 до
до 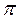 и, учитывая вышеприведенные выражения (4.1), получим:
и, учитывая вышеприведенные выражения (4.1), получим: 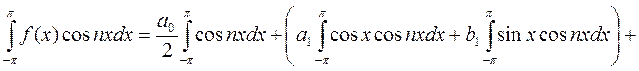
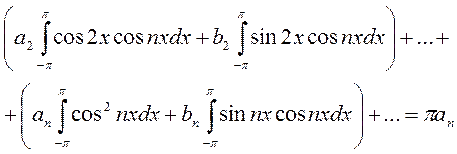
Следовательно, коэффициент
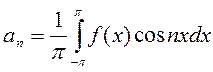
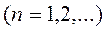
Аналогично, умножая равенство (4.2) на 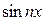 и интегрируя его в пределах от
и интегрируя его в пределах от 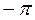 до
до 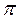 , с учетом равенств (4.1) имеем:
, с учетом равенств (4.1) имеем:
 , следовательно, коэффициент
, следовательно, коэффициент
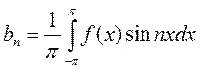 .
.
Таким образом, получены следующие выражения для коэффициентов ряда Фурье:
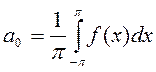
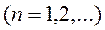
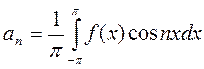
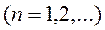
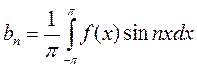 (4.3)
(4.3)
Достаточные признаки разложимости функции в ряд Фурье. Напомним, что точку xo разрыва функции f(x) называют точкой разрыва первого рода, если существуют конечные пределы справа и слева функции f(x) в окрестности точки.
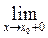
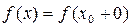 -предел справа,
-предел справа,
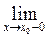
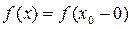 -предел слева.
-предел слева.
Теорема (Дирихле). Если функция f(x) имеет период 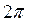 и на отрезке
и на отрезке 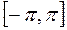 непрерывна или имеет конечное число точек разрыва первого рода и, кроме того, отрезок
непрерывна или имеет конечное число точек разрыва первого рода и, кроме того, отрезок 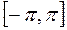 можно разбить на конечное число отрезков так, что внутри каждого из них f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях x. Причём в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва функции f(x) его сумма равна
можно разбить на конечное число отрезков так, что внутри каждого из них f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях x. Причём в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва функции f(x) его сумма равна  , т.е. среднему арифметическому предельных значений слева и справа. Кроме того, ряд Фурье для функции f(x) сходится равномерно на любом отрезке, который вместе со своими концами принадлежит интервалу непрерывности функции f(x).
, т.е. среднему арифметическому предельных значений слева и справа. Кроме того, ряд Фурье для функции f(x) сходится равномерно на любом отрезке, который вместе со своими концами принадлежит интервалу непрерывности функции f(x).
Пример: разложить в ряд Фурье функцию

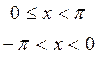
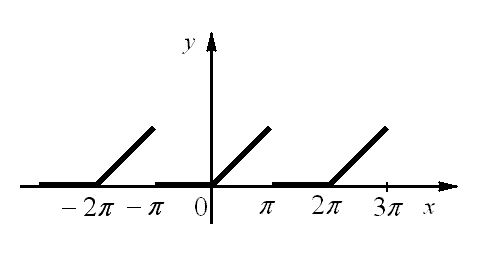 удовлетворяющую условию
удовлетворяющую условию 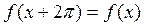 .
.
Рис.4.1.
Решение. Функция f(x) удовлетворяет условиям разложимости в ряд Фурье, поэтому можно записать:

В соответствии с формулами (4.3) , можно получить следующие значения коэффициентов ряда Фурье:
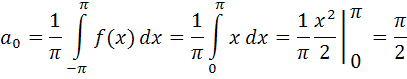
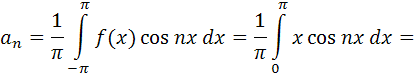
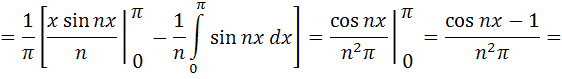
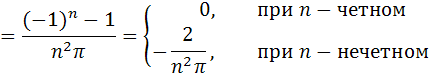
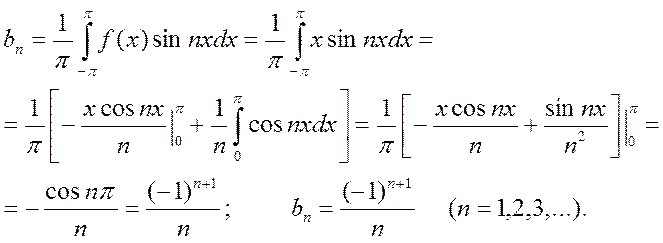 При вычислении коэффициентов ряда Фурье использовалась формула «интегрирования по частям».
При вычислении коэффициентов ряда Фурье использовалась формула «интегрирования по частям».
И, следовательно,
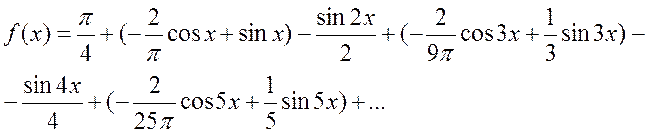
Ряды Фурье для чётных и нечётных функций с периодом T = 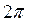 .
.
Используем следующее свойство интеграла по симметричному относительно x=0 промежутку:
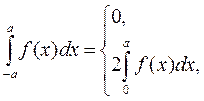 если f(x) – нечётная функция,
если f(x) – нечётная функция,
если f(x) – чётная функция.
Заметим, что произведение двух чётных или двух нечётных функций – чётная функция, а произведение чётной функции на нечётную функцию – нечётная функция. Пусть теперь f(x) – чётная периодическая функция с периодом 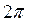 ,удовлетворяющая условиям разложимости в ряд Фурье. Тогда, используя вышеуказанное свойство интегралов, получим:
,удовлетворяющая условиям разложимости в ряд Фурье. Тогда, используя вышеуказанное свойство интегралов, получим:
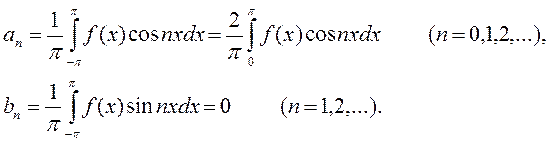
Таким образом, ряд Фурье для чётной функции содержит только чётные функции – косинусы и записывается так:
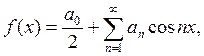 (4.4)
(4.4)
при этом
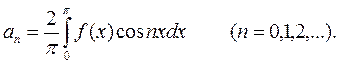 (4.5)
(4.5)
а коэффициенты bn = 0.
Рассуждая аналогично, получаем, что если f(x) – нечётная периодическая 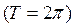 функция, удовлетворяющая условиям разложимости в ряд Фурье, то, следовательно, ряд Фурье для функции нечётной содержит только нечётные функции – синусы и записывается следующим образом:
функция, удовлетворяющая условиям разложимости в ряд Фурье, то, следовательно, ряд Фурье для функции нечётной содержит только нечётные функции – синусы и записывается следующим образом:
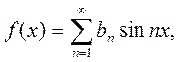 (4.6)
(4.6)
при этом an =0 при n= 0, 1,…
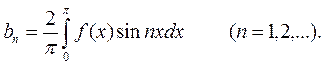 (4.7)
(4.7)
Пример: разложить в ряд Фурье периодическую 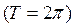 функцию
функцию
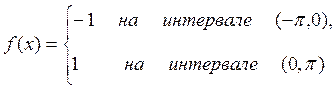
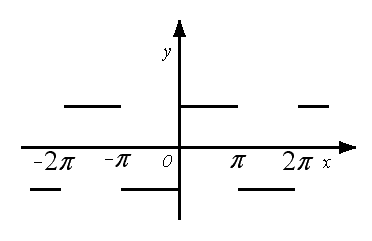
Рис. 4.2.
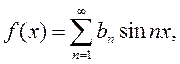 Так как заданная нечетная функция f(x) удовлетворяет условиям разложимости в ряд Фурье, то
Так как заданная нечетная функция f(x) удовлетворяет условиям разложимости в ряд Фурье, то
при этом
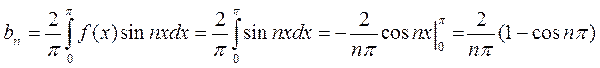
или, что то же,
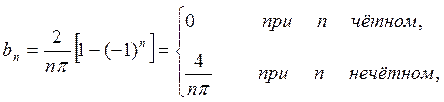
И ряд Фурье для данной функции f(x) можнозаписать так:
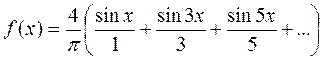
Ряды Фурье для функций любого периода T=2l.
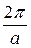 Пусть f(x) – периодическая функция любого периода T=2l (l-полупериод), кусочно-гладкая или кусочно-монотонная на отрезке [-l, l]. Полагая x=at, получим функцию f(at) аргумента t, период которой равен . Подберём а так, чтобы период функции f(at) был равен
Пусть f(x) – периодическая функция любого периода T=2l (l-полупериод), кусочно-гладкая или кусочно-монотонная на отрезке [-l, l]. Полагая x=at, получим функцию f(at) аргумента t, период которой равен . Подберём а так, чтобы период функции f(at) был равен 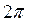 , т.е.
, т.е.
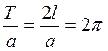 , откуда
, откуда 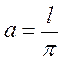
Тогда подстановка 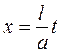 (сжатие или растяжение по оси ОХ) приводит к
(сжатие или растяжение по оси ОХ) приводит к
функции 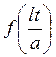 периода
периода 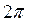 . Это функция удовлетворяет условиям разложимости в ряд Фурье, т.к. она кусочно-гладкая или кусочно-монотонная на отрезке
. Это функция удовлетворяет условиям разложимости в ряд Фурье, т.к. она кусочно-гладкая или кусочно-монотонная на отрезке 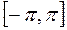 .
.
Так как 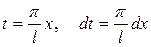 , а пределам интегрирования по t
, а пределам интегрирования по t 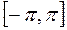 соответствуют пределы интегрирования по x
соответствуют пределы интегрирования по x 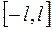 , то ряд Фурье функции f(x) периода T=2l запишется в виде:
, то ряд Фурье функции f(x) периода T=2l запишется в виде:
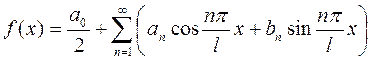 , (4.8)
, (4.8)
при этом
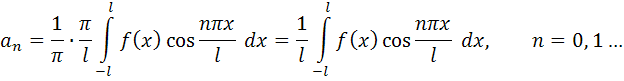
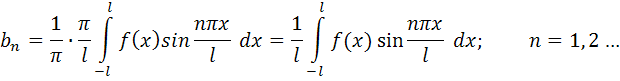 (4.9)
(4.9)
Ряд Фурье для чётной или нечётной функции любого периода T=2l.
Пусть f(x) – чётная, кусочно-монотонная или кусочно-гладкая функция на отрезке [-l, l], тогда её можно разложить на этом отрезке в ряд Фурье. По свойству интеграла по симметричному относительно x=0 интервалу получим 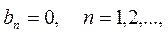
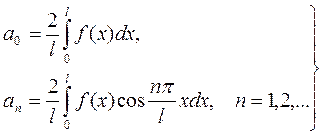 (4.10)
(4.10)
Таким образом, ряд Фурье чётной функции f(x) с периодом T=2l запишется в виде:
 (4.11)
(4.11)
при этом коэффициенты ряда определяются равенствами (4.10).
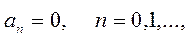 Если f(x) – нечётная функция, кусочно-монотонная или кусочно-гладкая на отрезке [-l, l ], то
Если f(x) – нечётная функция, кусочно-монотонная или кусочно-гладкая на отрезке [-l, l ], то
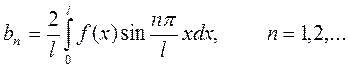 (4.12)
(4.12)
Ряд Фурье для нечётной периодической функции с периодом T = 2l имеет вид:
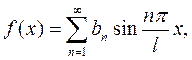 (4.13)
(4.13)
При этом коэффициенты ряда определяются формулами (4.12). Следует заметить, что все сделанные раньше замечания относительно разложения в ряд Фурье функции f(x), заданной на отрезке 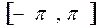 [интервале
[интервале  ], остаются справедливыми и для функции f(x), заданной на отрезке
], остаются справедливыми и для функции f(x), заданной на отрезке 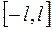 [интервале (-l, l)]. Аналогично всё сказанное о разложении функции на отрезке
[интервале (-l, l)]. Аналогично всё сказанное о разложении функции на отрезке 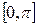 [интервале
[интервале 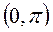 ], переносится на отрезок
], переносится на отрезок 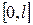 [интервале
[интервале 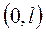 ].
].
Пример:разложить функцию f(x)=x, -1<x<1, периода T=2 в ряд Фурье (рис 4.3).
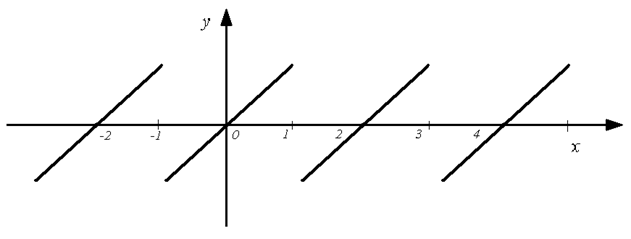
Рис 4.3.
Решение. Функция f(x) – нечётная, удовлетворяющая условиям разложимости в ряд Фурье, поэтому на основании формул (4.12) и (4.13) имеем:

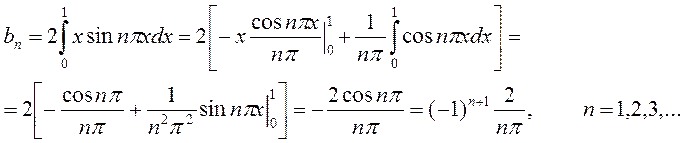
(при вычислении интеграла использовали формулу «интегрирования по частям»).
Ряд Фурье на полупериоде — Студопедия
Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.
Если требуется получить разложение Фурье на полупериоде по косинусамфункции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье ao и an
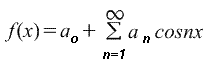
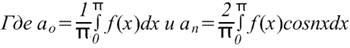
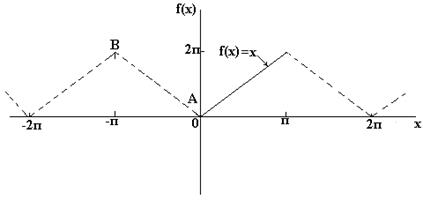
Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

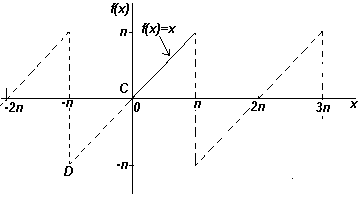
лекция№60
Лекция №60
6.21. Ряды Фурье для чётных и нечётных функций.
Теорема: Для любой чётной функции её ряд Фурье состоит только из косинусов.

Для любой нечётной
функции: 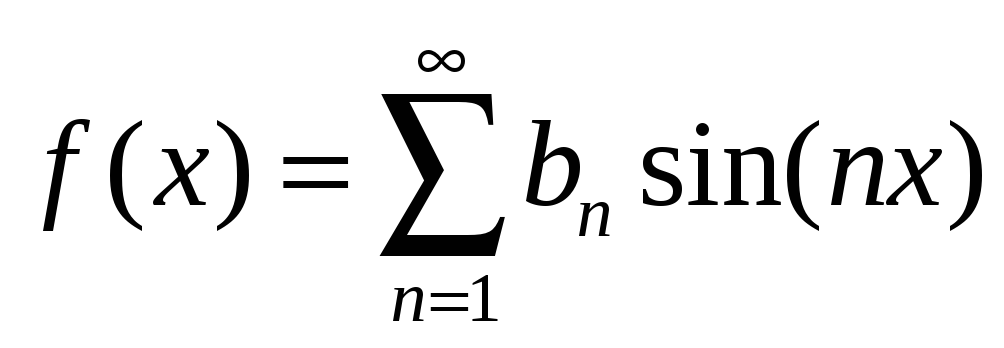 .
.
Доказательство: Из определения четной и нечетной функции следует, что если ψ(x) – четная функция, то
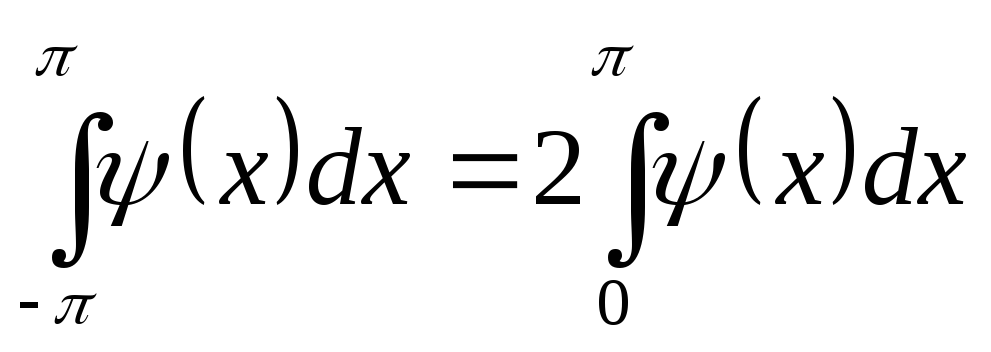 .
.
Действительно,
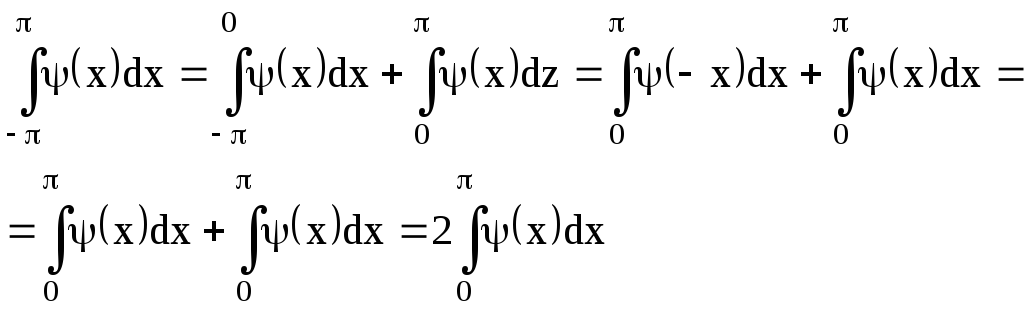
так как по определению четной функции ψ(- x) = ψ(x).
Аналогично можно доказать, что если ψ(x) – нечетная функция, то
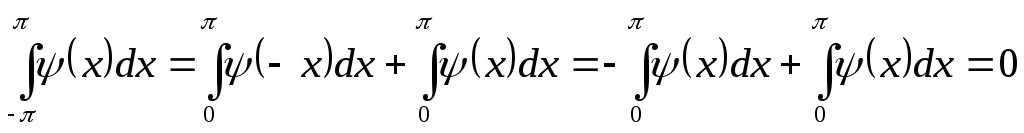
Если в ряд Фурье разлагается нечетная функция ƒ(x), то произведение ƒ(x) ·coskx есть функция также нечетная, а ƒ(x) · sinkx – четная; следовательно,
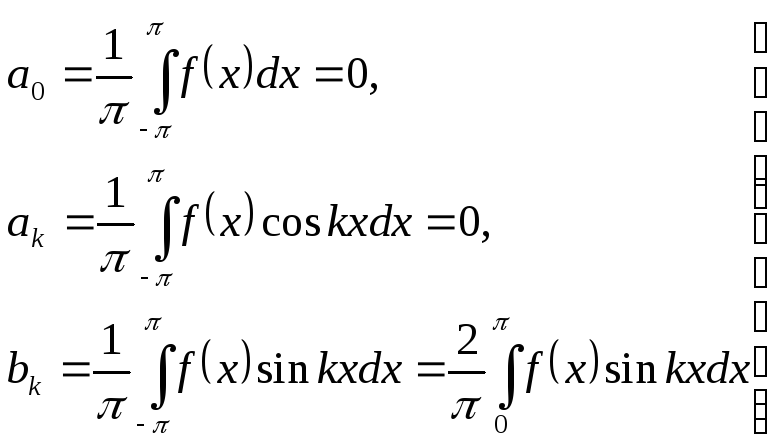 (21)
(21)
т. е. ряд Фурье нечетной функции содержит «только синусы».
Если в ряд Фурье разлагается четная функция, то произведение ƒ(x)·sinkx есть функция нечетная, а ƒ(x) · coskx – четная, то:
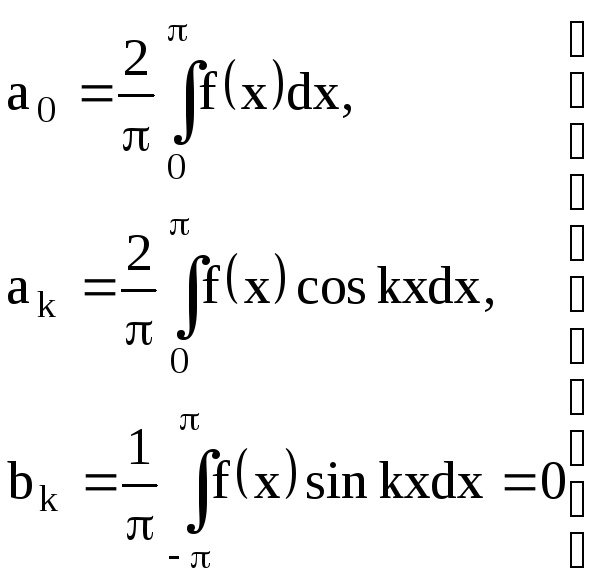 (22)
(22)
т. е. ряд Фурье четной функции содержит «только косинусы».
Полученные формулы
позволяют упрощать вычисления при
разыскании коэффициентов Фурье в тех
случаях, когда заданная функция является
четной или нечетной, а также получать разложение в ряд Фурье функции,
заданной на части промежутка 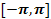 .
.
Во многих задачах
функция 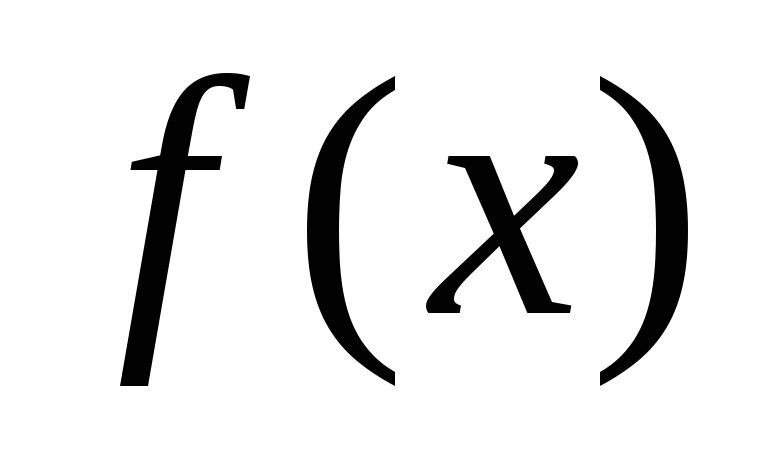 задается в интервале
задается в интервале 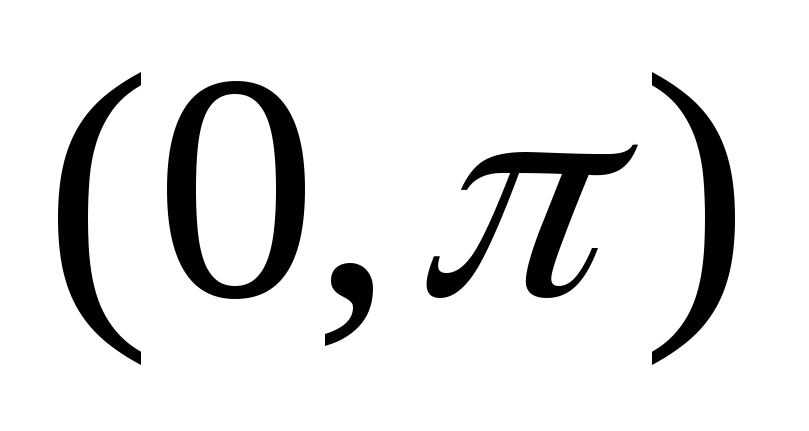 .
Требуется представить данную функцию
в виде бесконечной суммы синусов и
косинусов углов, кратных числам
натурального ряда, т.е. необходимо
произвести разложение функции в ряд
Фурье. Обычно в таких случаях поступают
следующим образом.
.
Требуется представить данную функцию
в виде бесконечной суммы синусов и
косинусов углов, кратных числам
натурального ряда, т.е. необходимо
произвести разложение функции в ряд
Фурье. Обычно в таких случаях поступают
следующим образом.
Чтобы разложить
заданную функцию по косинусам, функцию 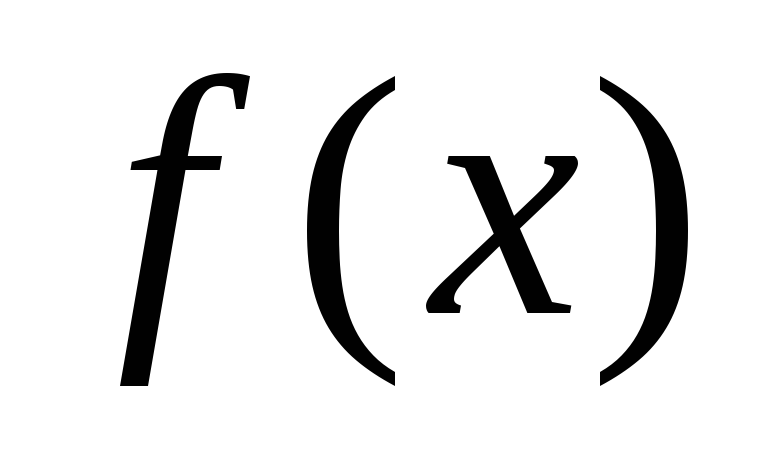 доопределяют в интервале
доопределяют в интервале 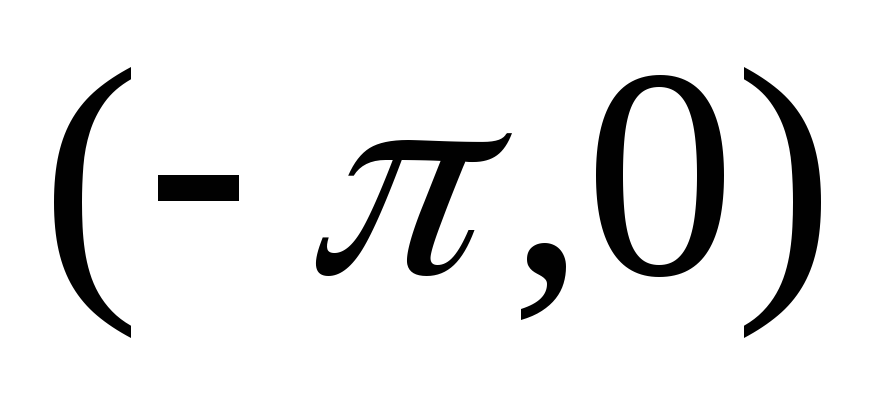 четным образом, т.е. так, что в интервале
четным образом, т.е. так, что в интервале 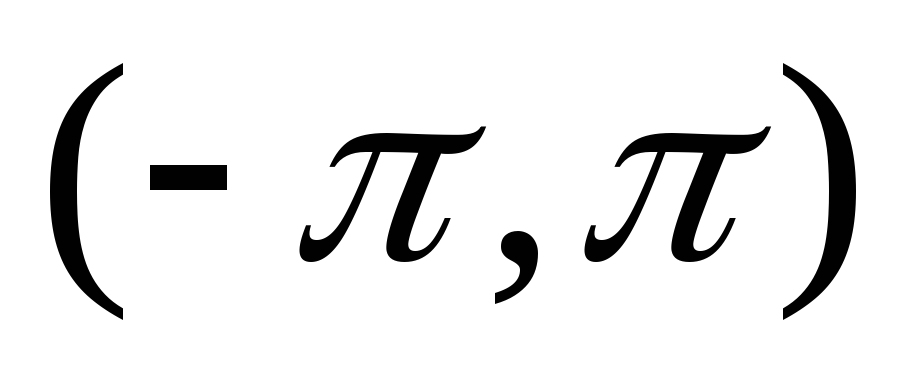
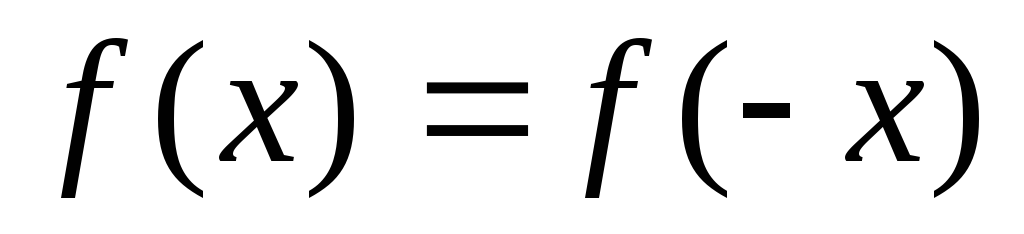 .
Тогда для «продолженной» четной функции
справедливы все рассуждения предыдущего
параграфа, и, следовательно, коэффициенты
ряда Фурье определяются по формулам
.
Тогда для «продолженной» четной функции
справедливы все рассуждения предыдущего
параграфа, и, следовательно, коэффициенты
ряда Фурье определяются по формулам
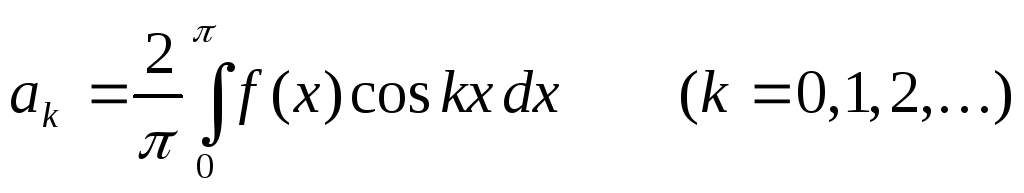 ,
,
 .
.
В этих формулах,
как видим, фигурируют значения функции 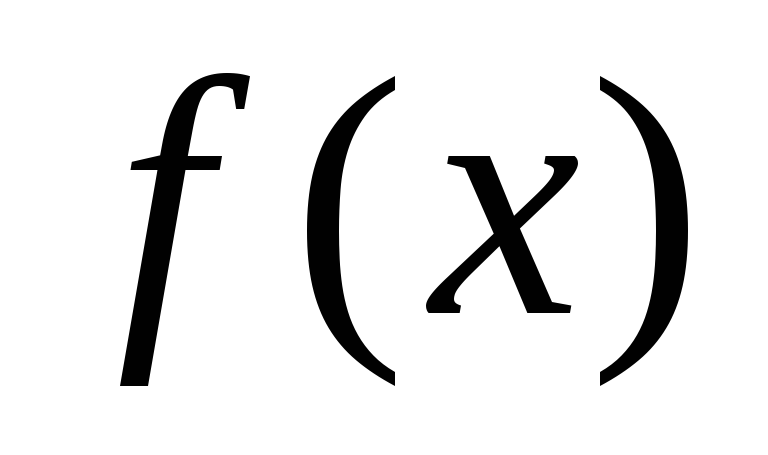 ,
лишь заданные в интервале
,
лишь заданные в интервале 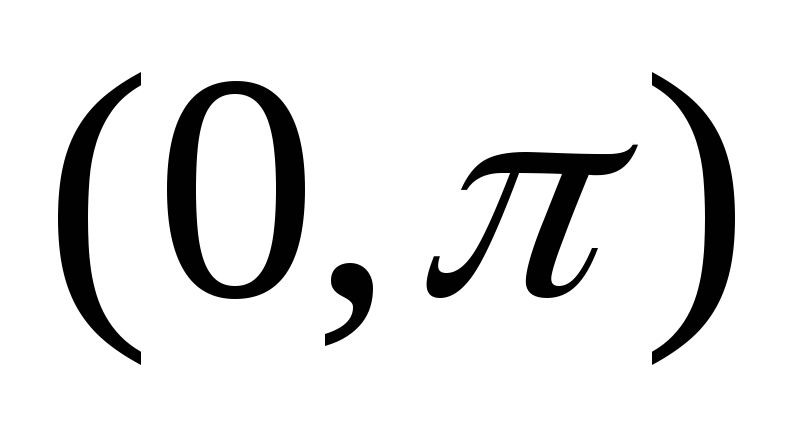 .
Чтобы разложить функцию
.
Чтобы разложить функцию 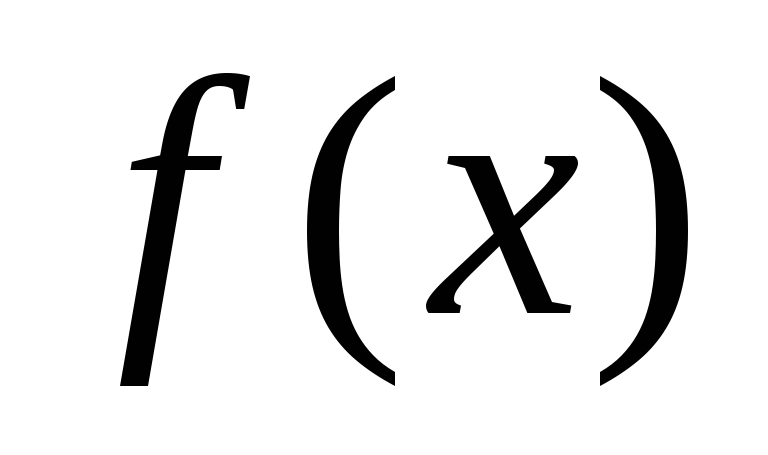 ,
заданную в интервале
,
заданную в интервале 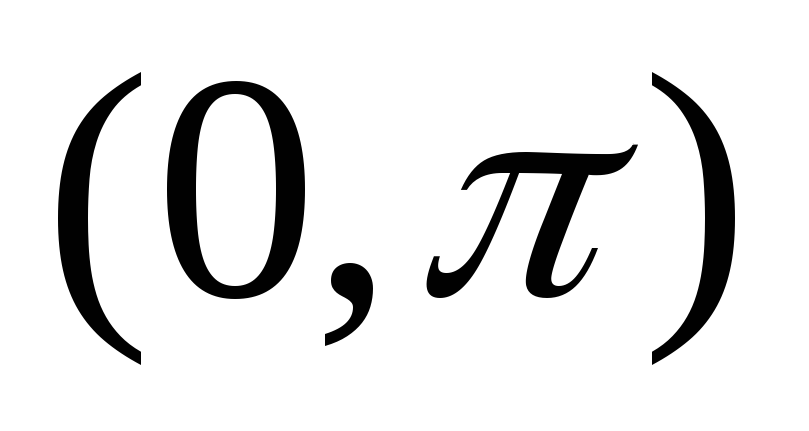 ,
по синусам, необходимо доопределить
эту функцию в интервале
,
по синусам, необходимо доопределить
эту функцию в интервале 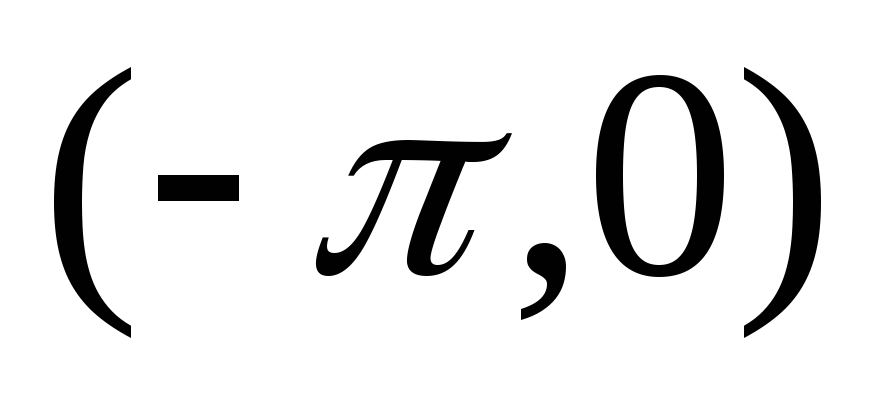 нечетным образом, т.е. так, что в интервале
нечетным образом, т.е. так, что в интервале 
 .
.
Тогда вычисление коэффициентов ряда Фурье нужно вести по формулам
 ,
,
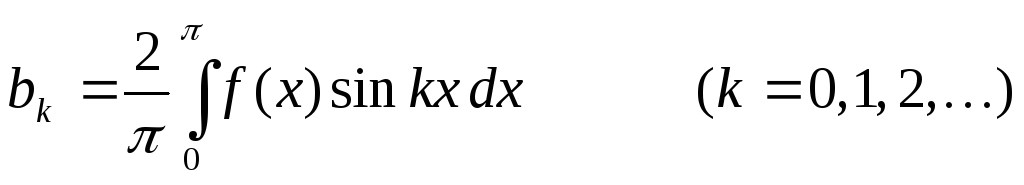 .
.
Теорема 1. Функцию заданную на промежутке 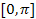 можно бесконечным числом способов
разложить в тригонометрический ряд
Фурье, в частности по cos или по sin.
можно бесконечным числом способов
разложить в тригонометрический ряд
Фурье, в частности по cos или по sin.
Замечание. Функция 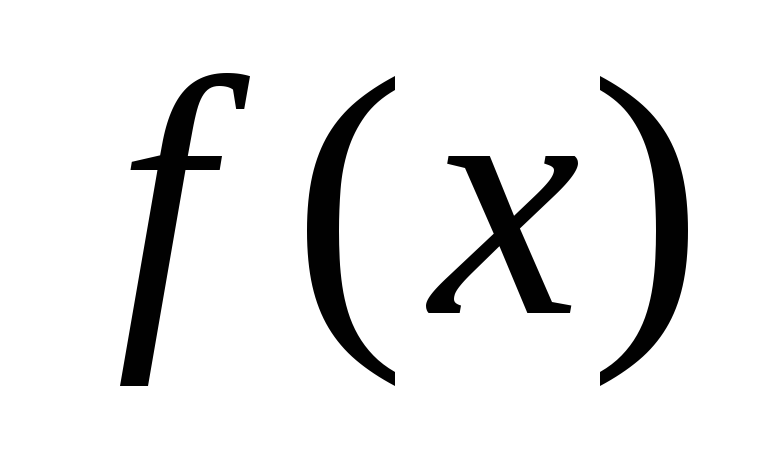 ,
заданная в интервале
,
заданная в интервале 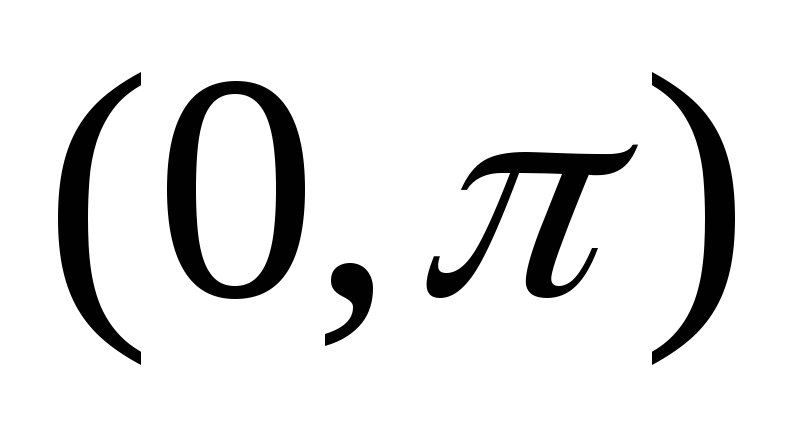 может быть доопределена в интервале
может быть доопределена в интервале 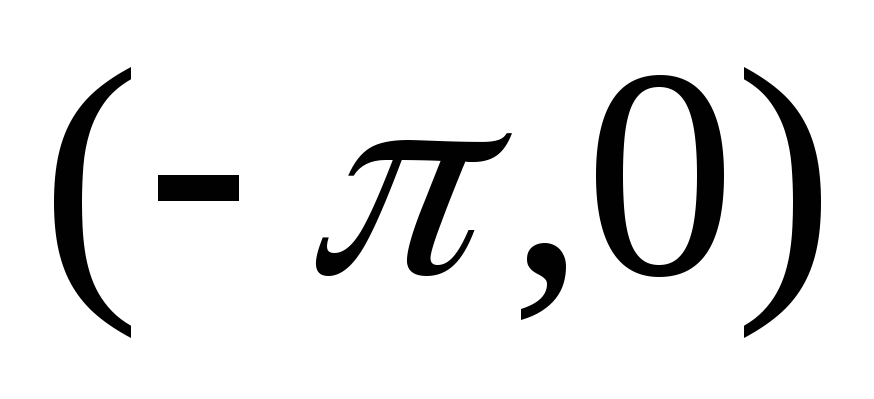 любым образом, а не только так, как было
сделано выше. Но при произвольном
доопределении функции разложение в ряд
Фурье будет более сложным, чем то, которое
получается при разложении по синусам
или косинусам.
любым образом, а не только так, как было
сделано выше. Но при произвольном
доопределении функции разложение в ряд
Фурье будет более сложным, чем то, которое
получается при разложении по синусам
или косинусам.
Пример. Разложить в ряд Фурье по косинусам
функцию 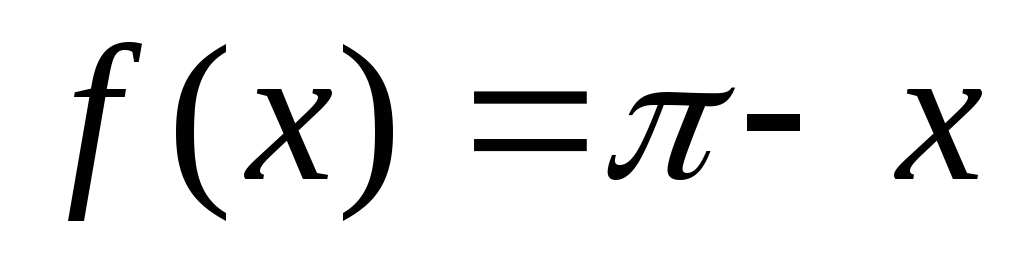 ,
заданную в интервале
,
заданную в интервале 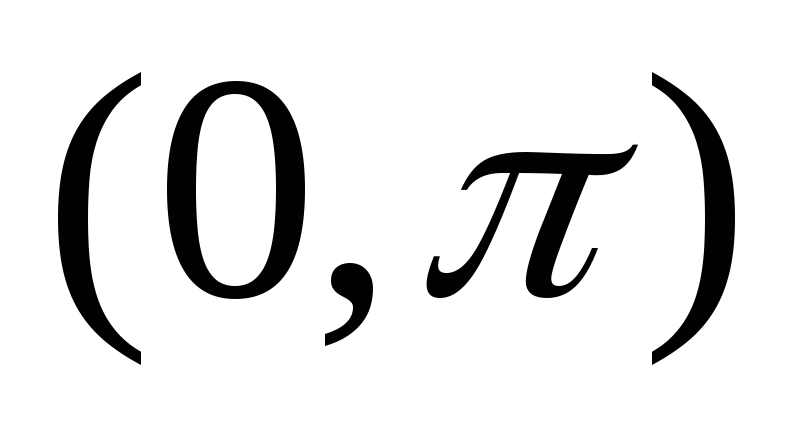 (рис.2а).
(рис.2а).
Решение. Доопределим функцию 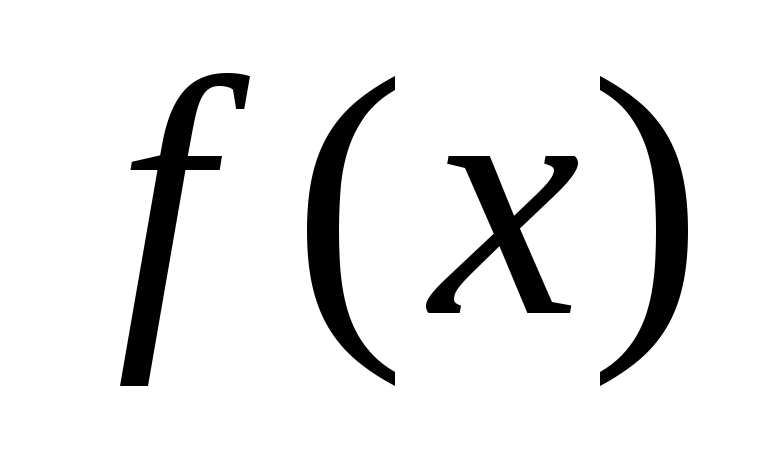 в интервале
в интервале 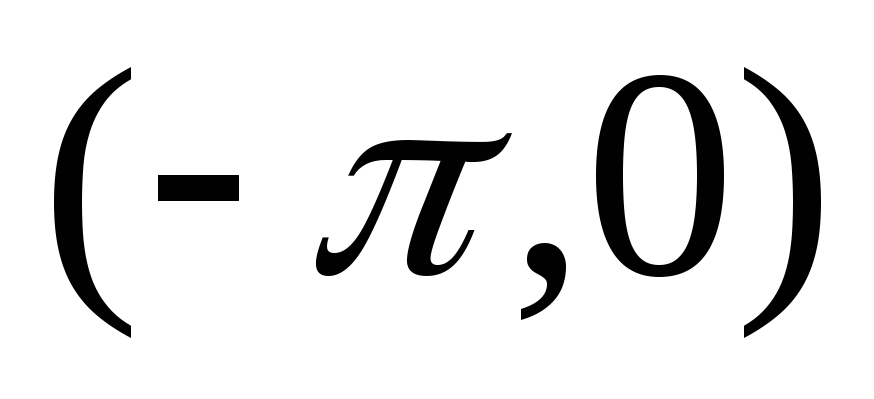 четным образом (график симметричен
относительно оси
четным образом (график симметричен
относительно оси 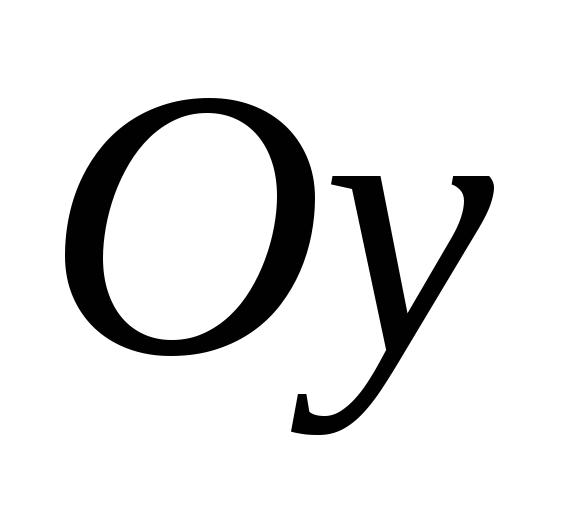 )
)
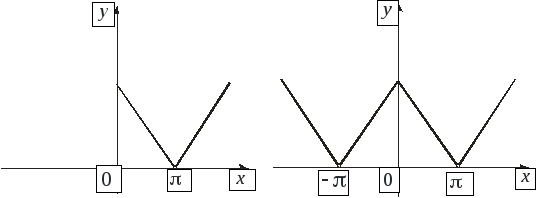
а б
Рис.2
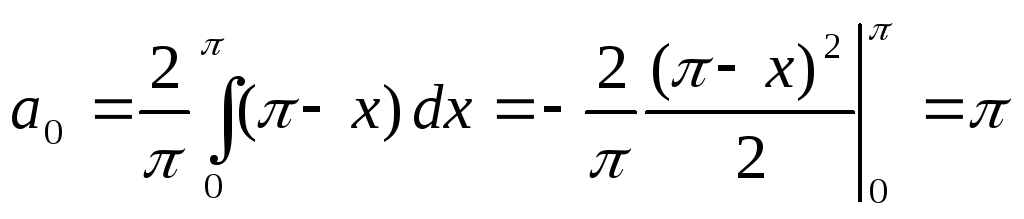 ,
,

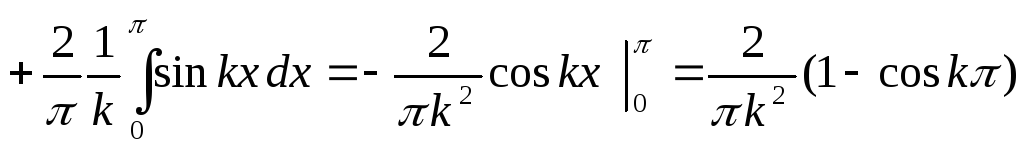 .
.
Так как 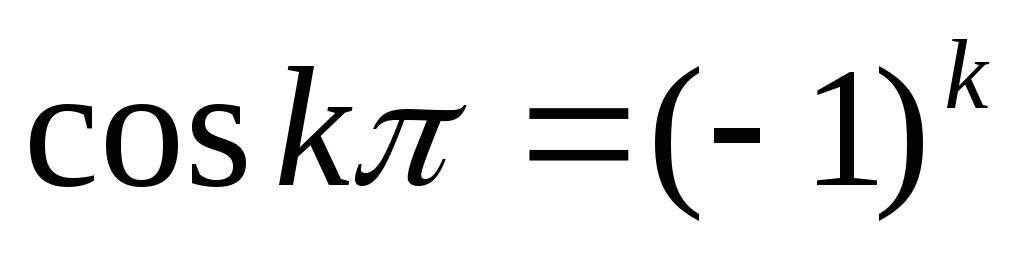 ,
то
,
то
при 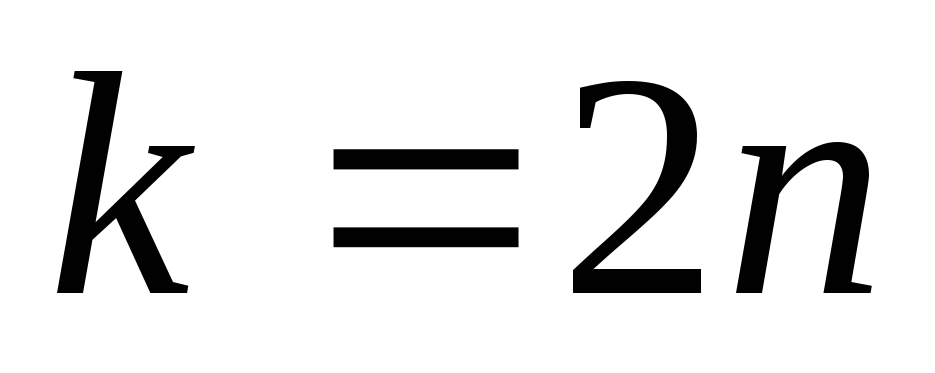
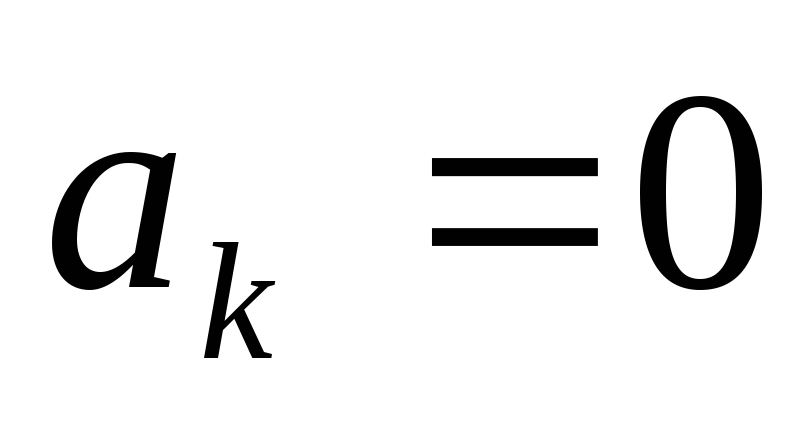 ,
,
при 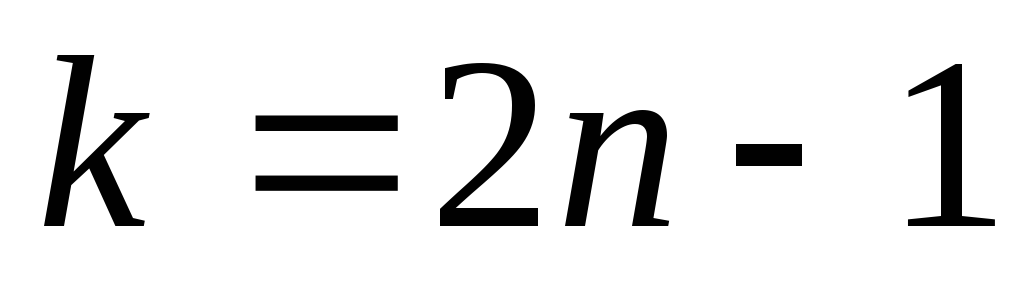
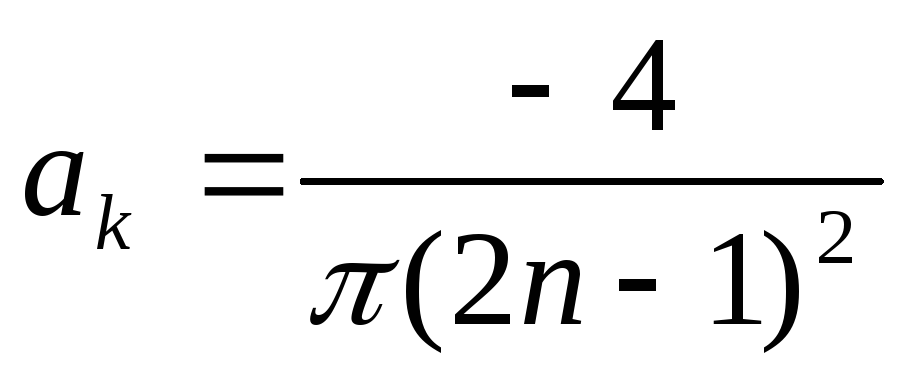
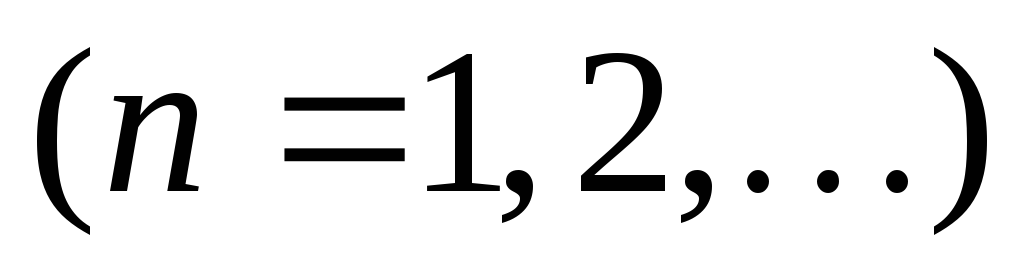
и

6.22. Ряд Фурье для функции, заданной на произвольном промежутке
До
сих пор мы рассматривали функцию,
заданную в интервале 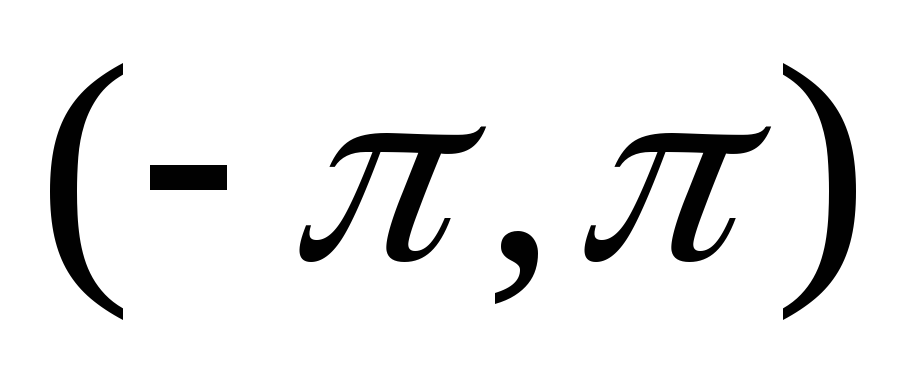 ,
считая ее вне этого интервала периодической,
с периодом
,
считая ее вне этого интервала периодической,
с периодом  .
.
Рассмотрим
теперь функцию 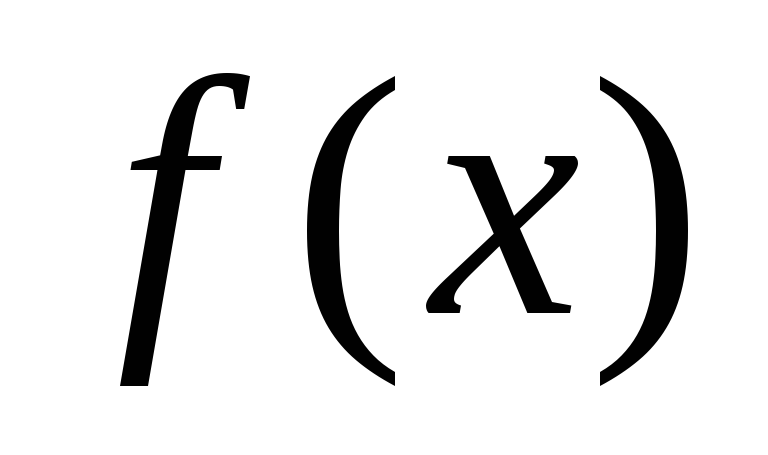 ,
период которой равен 2l,
т.е.
,
период которой равен 2l,
т.е. 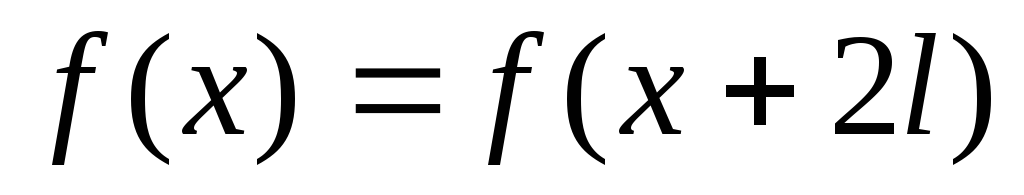 на интервале
на интервале 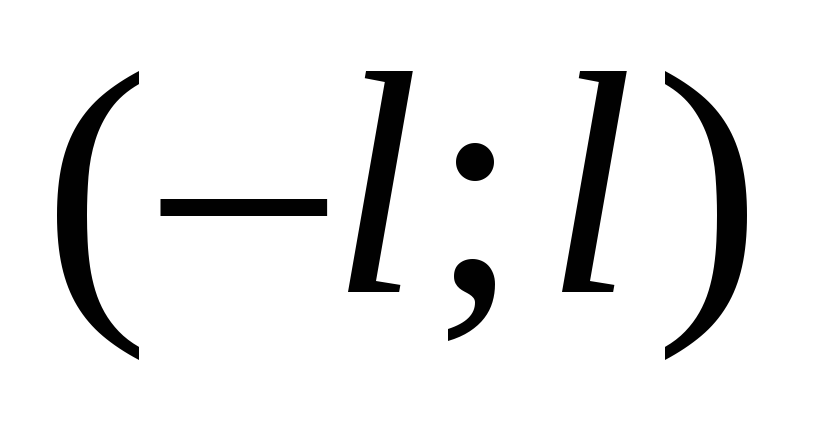 ,
и покажем, что в этом случае функция
,
и покажем, что в этом случае функция 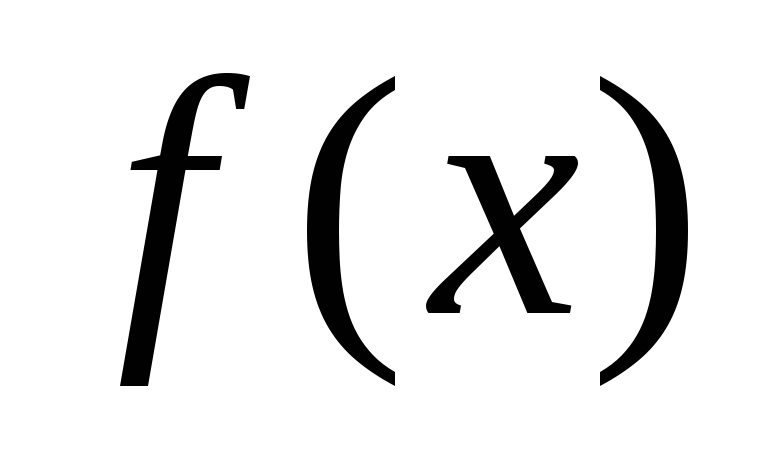 может быть разложена в ряд Фурье.
может быть разложена в ряд Фурье.
Положим 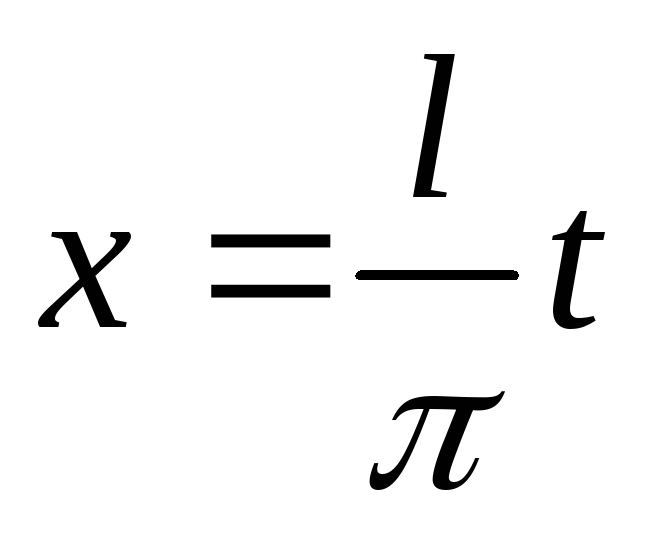 ,
или
,
или 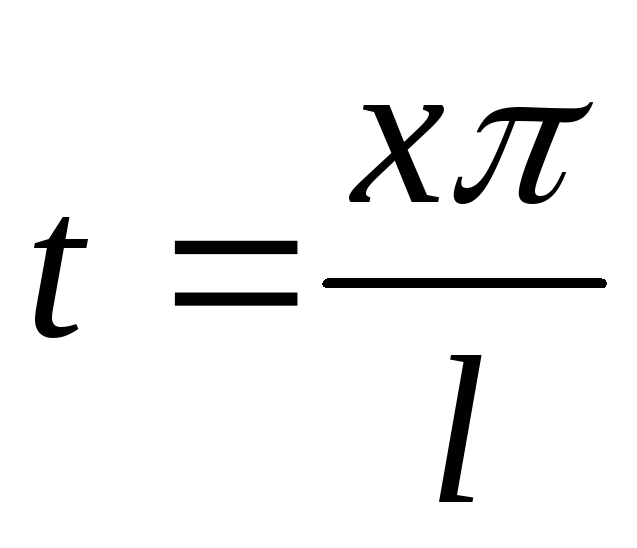 .
Тогда при изменении
.
Тогда при изменении 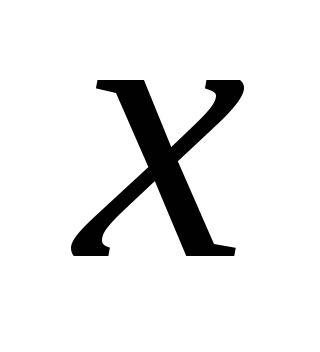 от –l до l новая переменная
от –l до l новая переменная 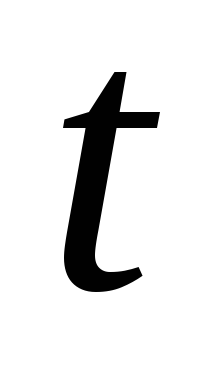 изменяется от
изменяется от 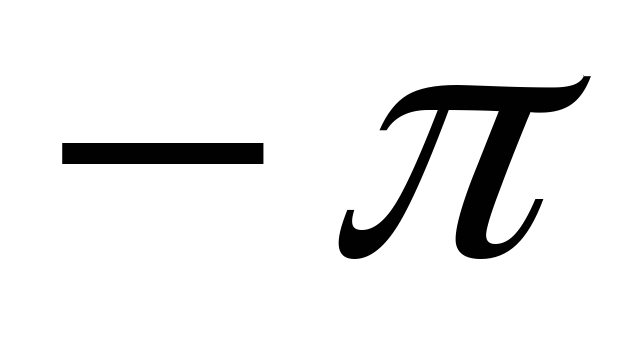 до
до  и, следовательно, функцию
и, следовательно, функцию 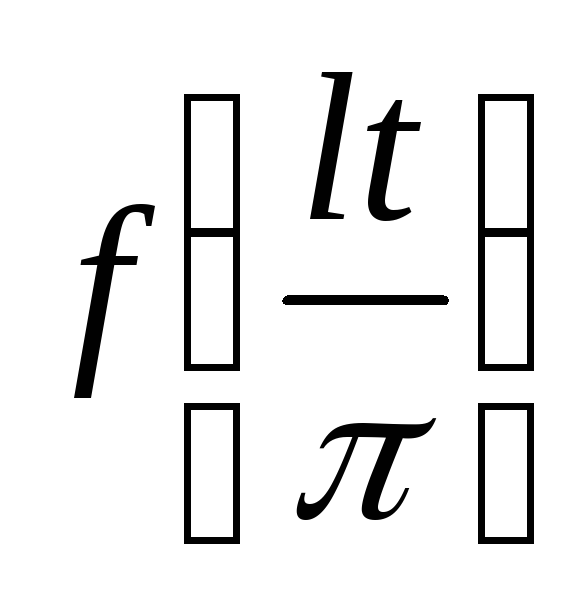 можно рассматривать как функцию, заданную
в интервале от
можно рассматривать как функцию, заданную
в интервале от 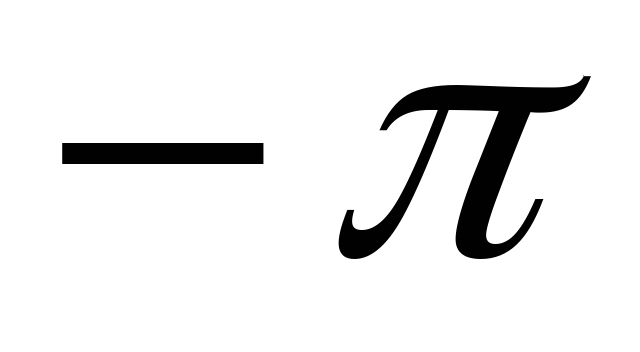 до
до  и периодическую вне этого промежутка,
с периодом
и периодическую вне этого промежутка,
с периодом  .
.
Итак, 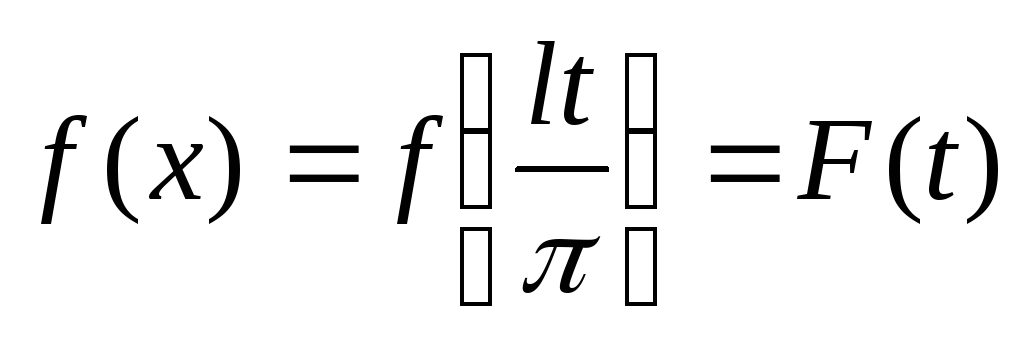 .
.
Разложив 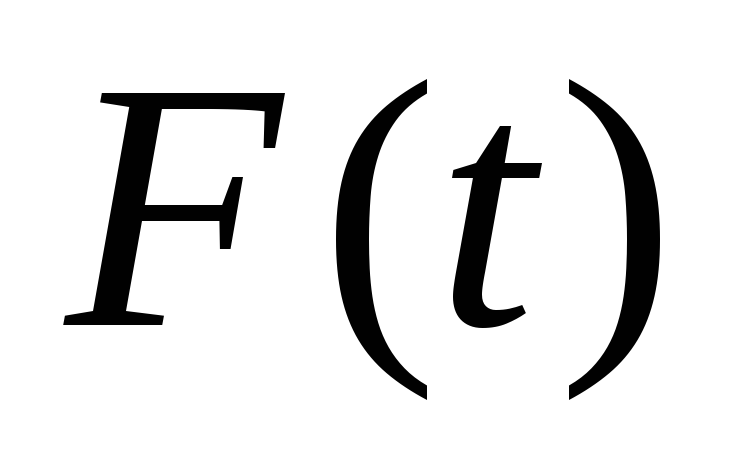 в ряд Фурье, получим
в ряд Фурье, получим
 ,
,
где

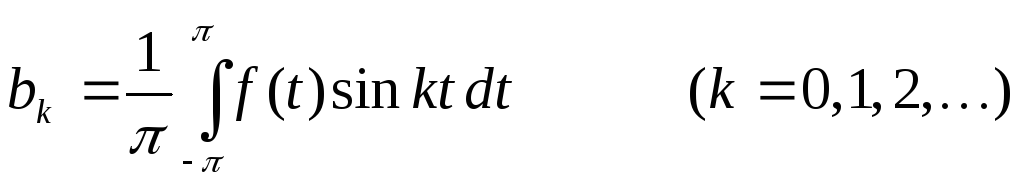 .
.
Переходя
к старым переменным, т.е. полагая 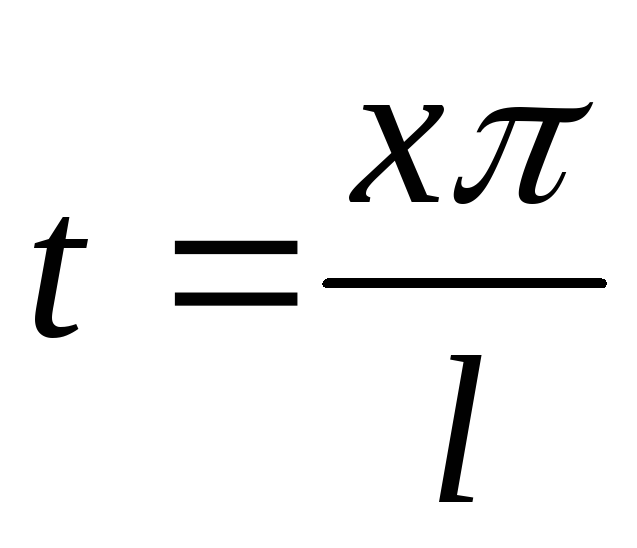
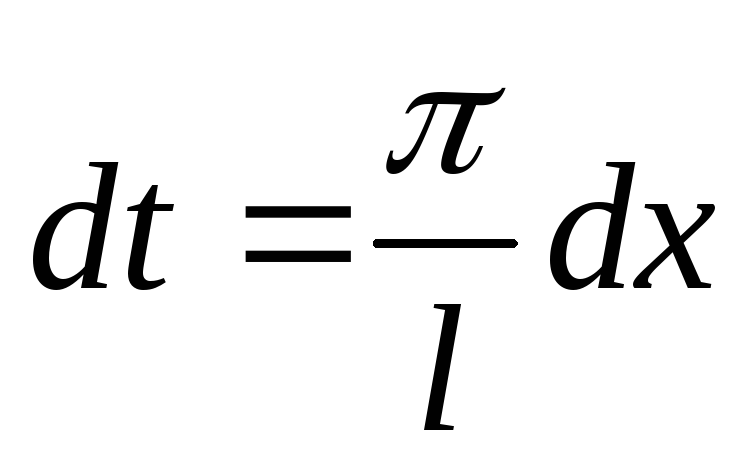 ,
получим
,
получим  ,
, 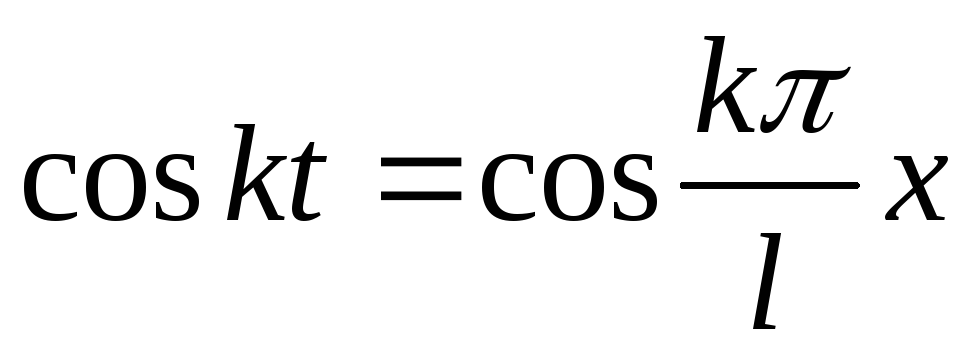 и
и 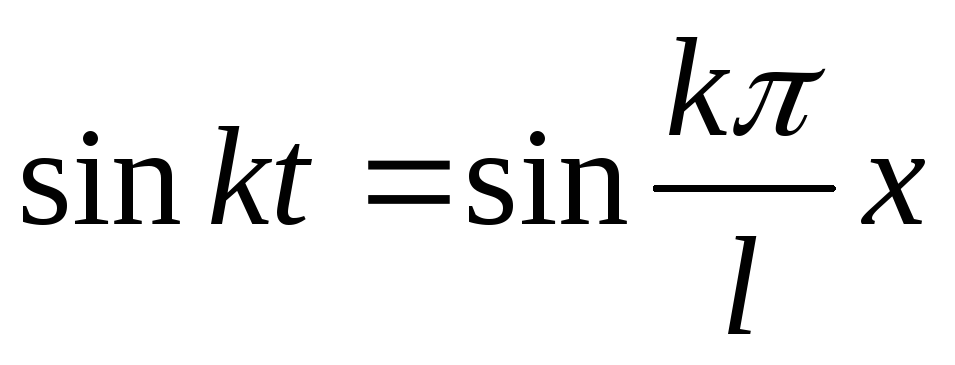 .
.
То
есть ряд Фурье для функции 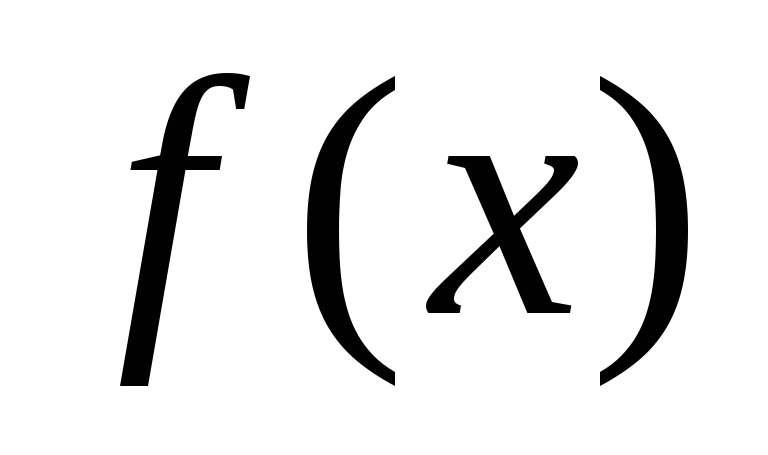 ,
заданной в интервале
,
заданной в интервале 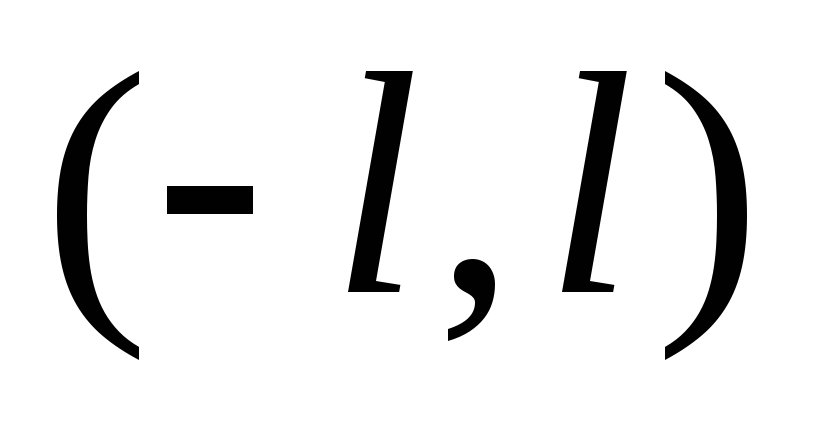 ,
будет иметь вид:
,
будет иметь вид:
 ,
,
где
 ,
,
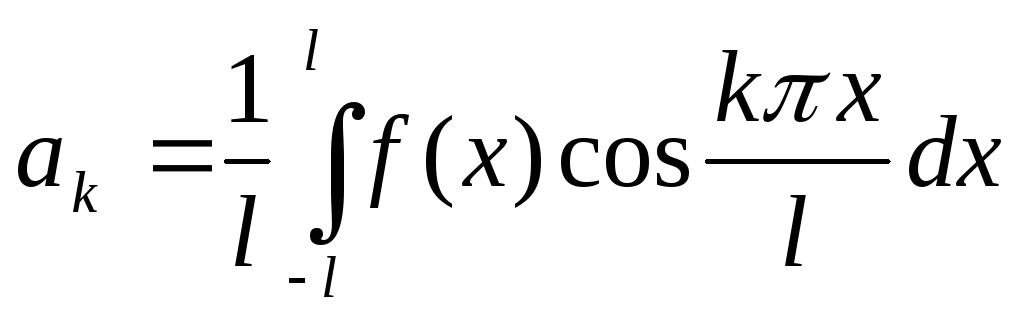 ,
,
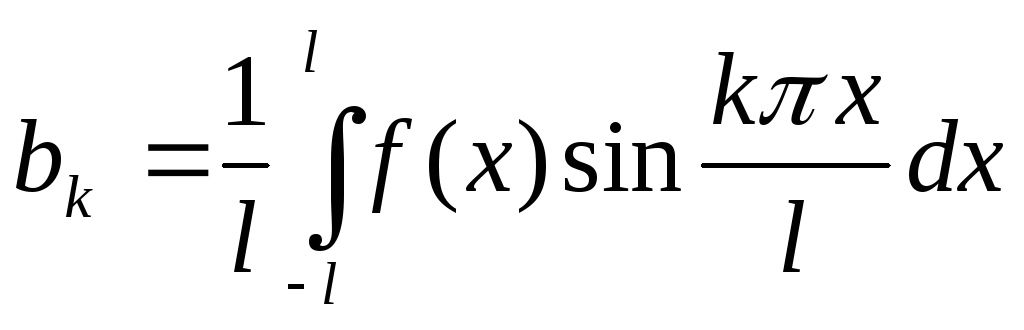
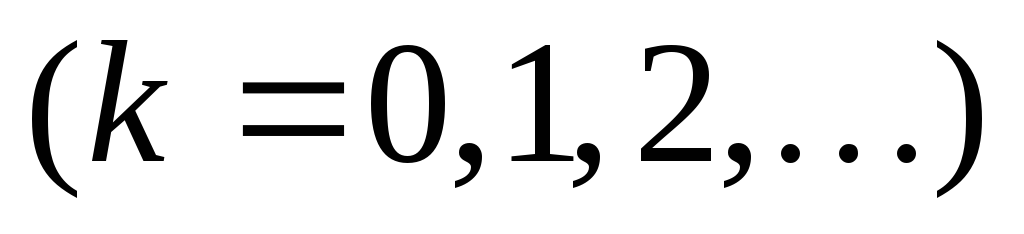 .
.
Если
функция 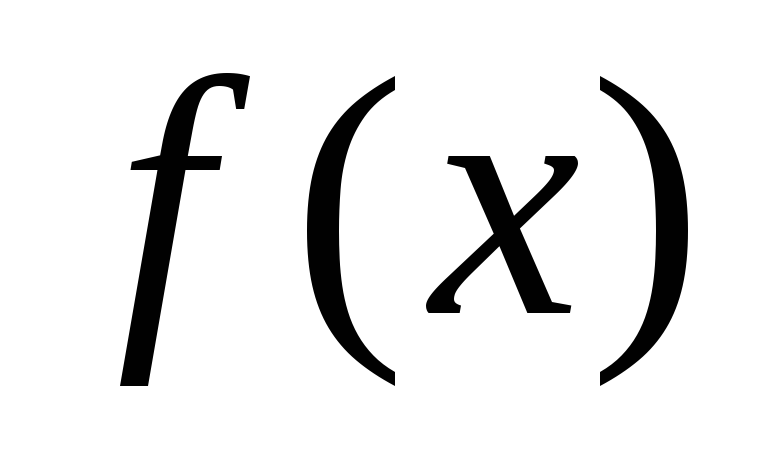 четная, то формулы для определения
коэффициентов ряда Фурье упрощаются:
четная, то формулы для определения
коэффициентов ряда Фурье упрощаются:
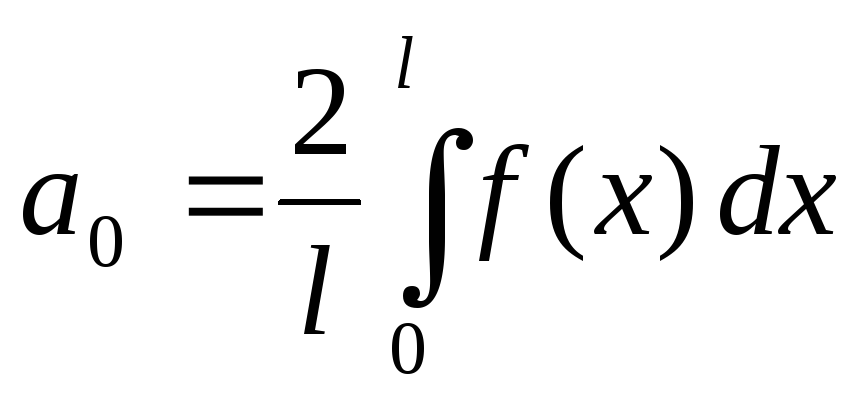 ,
,
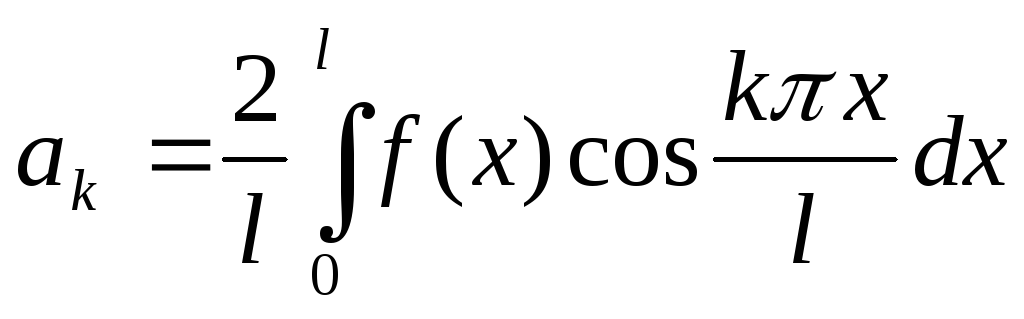 ,
,
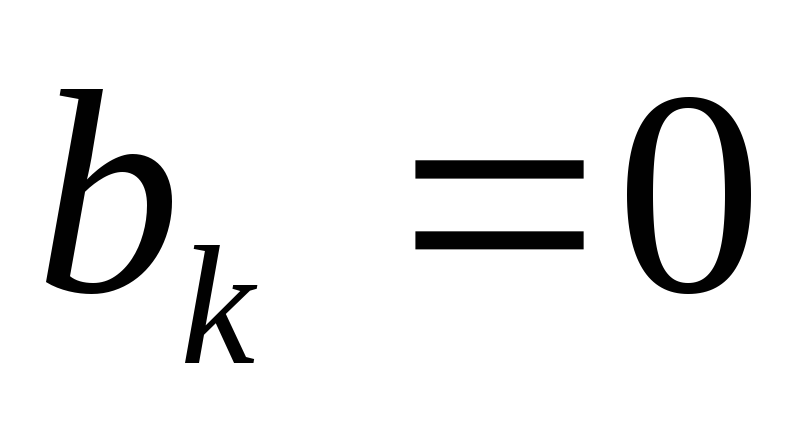
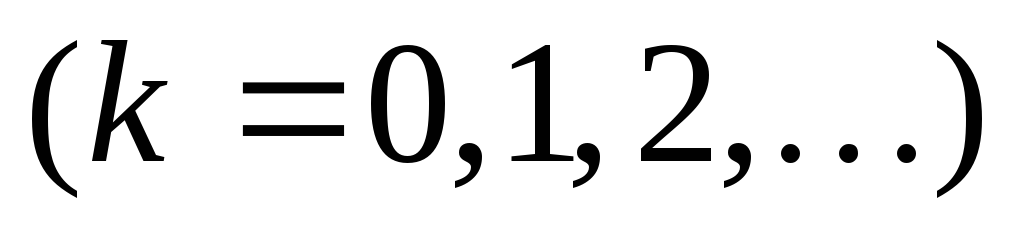 .
.
В
случае, если функция 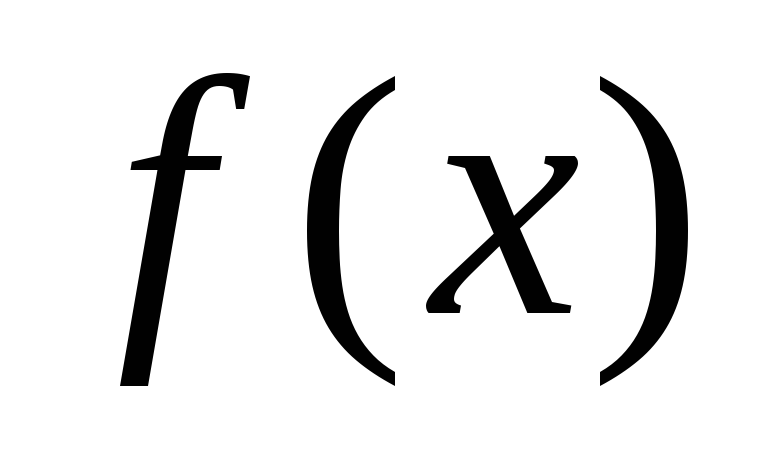 нечетная:
нечетная:
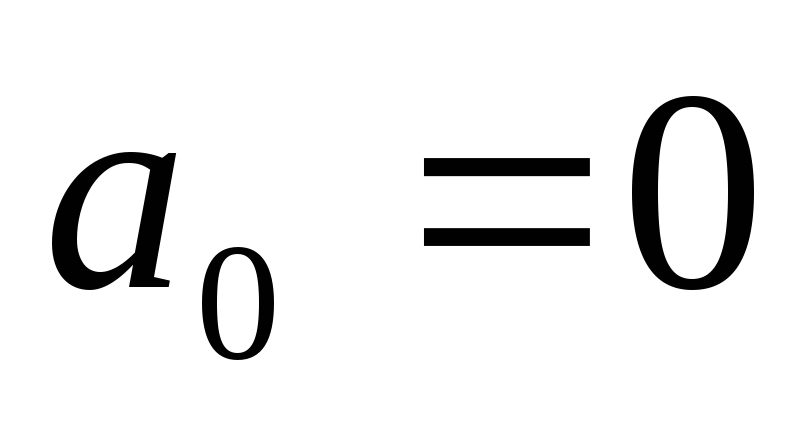 ,
,
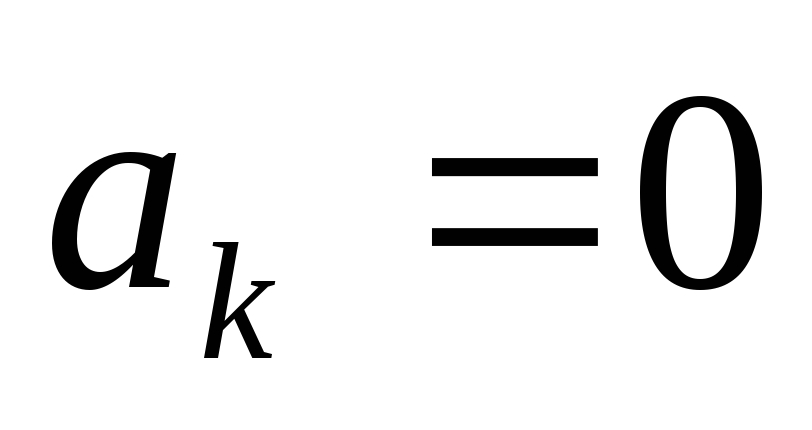 ,
,
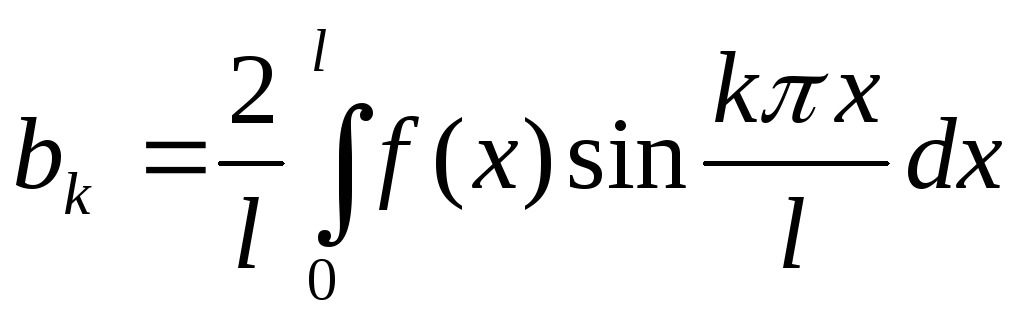
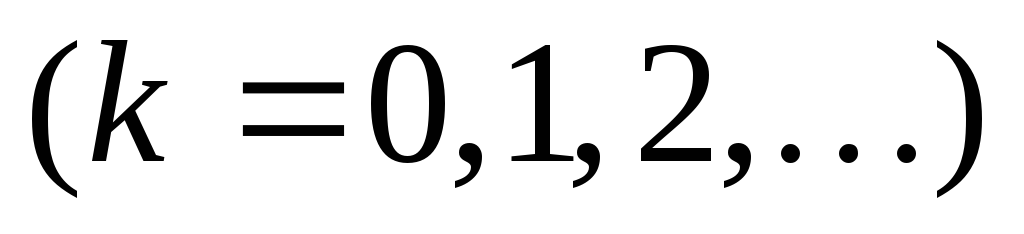 .
.
Если
функция  задана в интервале
задана в интервале 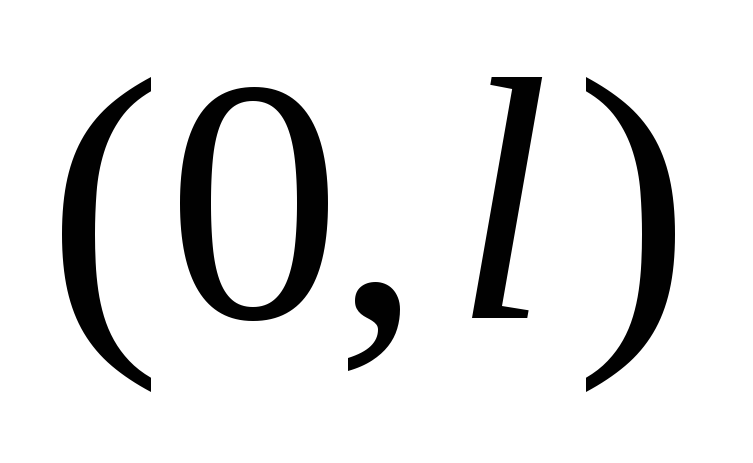 ,
то ее можно продолжить в интервале
,
то ее можно продолжить в интервале 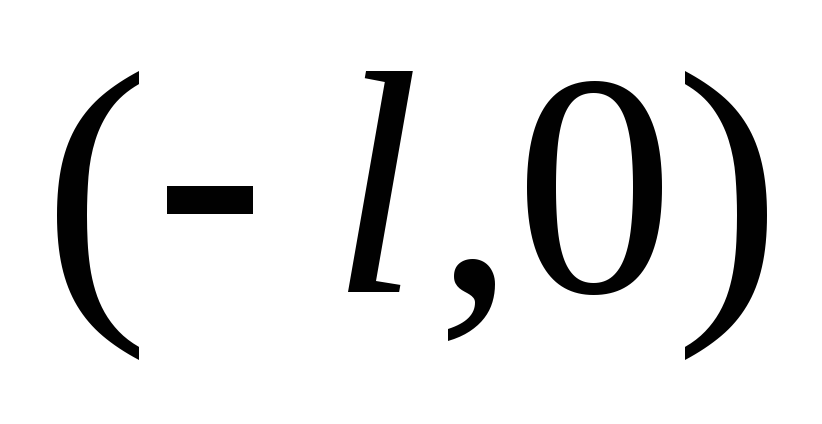 либо четным, либо нечетным образом. В
случае четного продолжения функции в
интервале
либо четным, либо нечетным образом. В
случае четного продолжения функции в
интервале 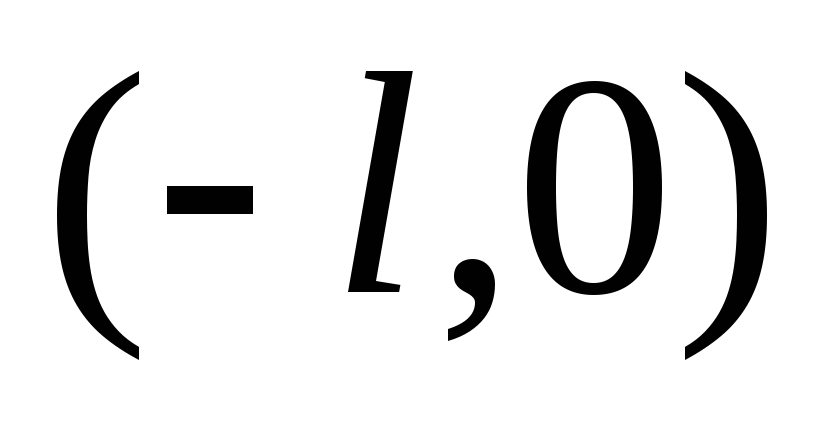 коэффициенты ряда Фурье находятся по
формулам
коэффициенты ряда Фурье находятся по
формулам
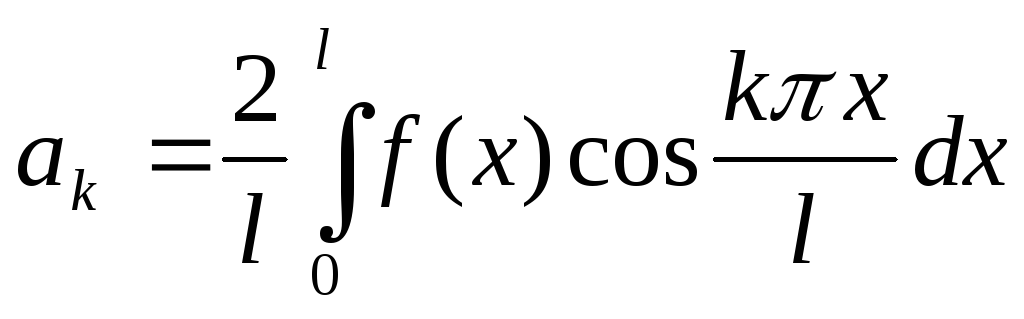 ,
, 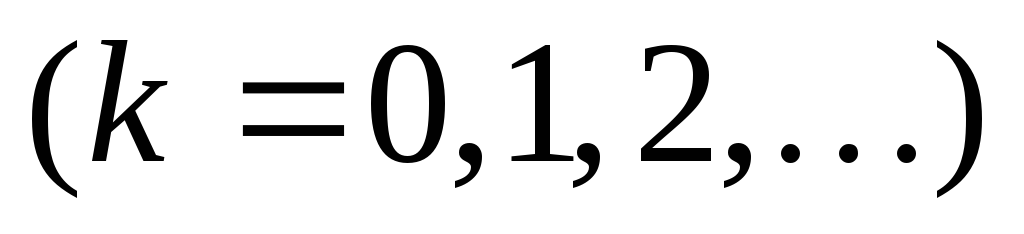
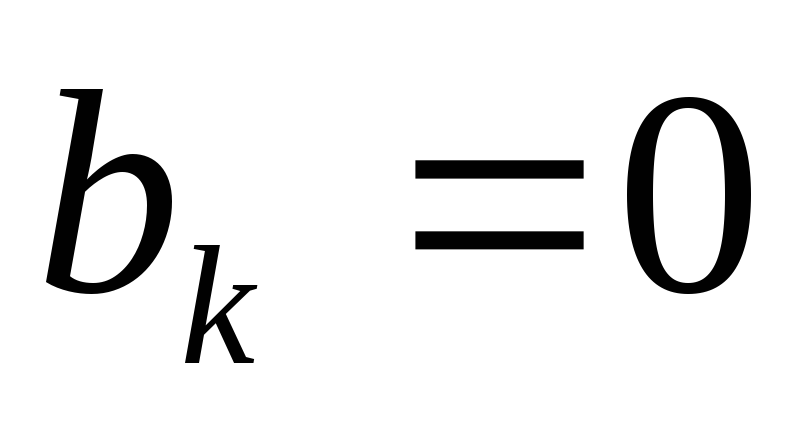 .
.
В
случае нечетного доопределения функции
в интервале 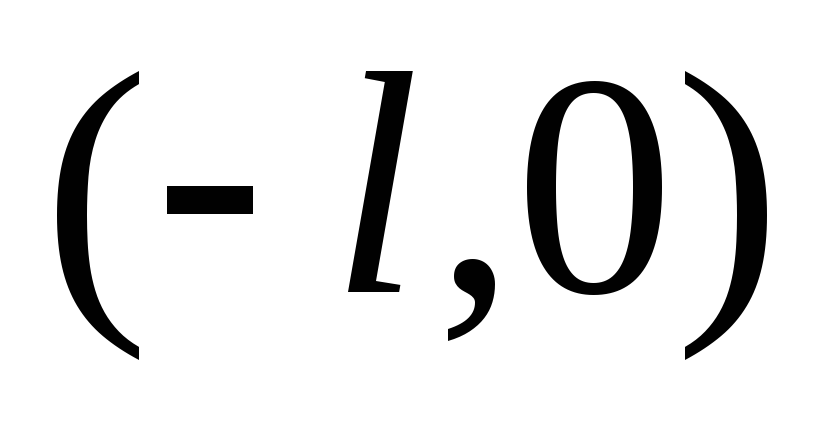 коэффициенты ряда Фурье находятся по
формулам
коэффициенты ряда Фурье находятся по
формулам
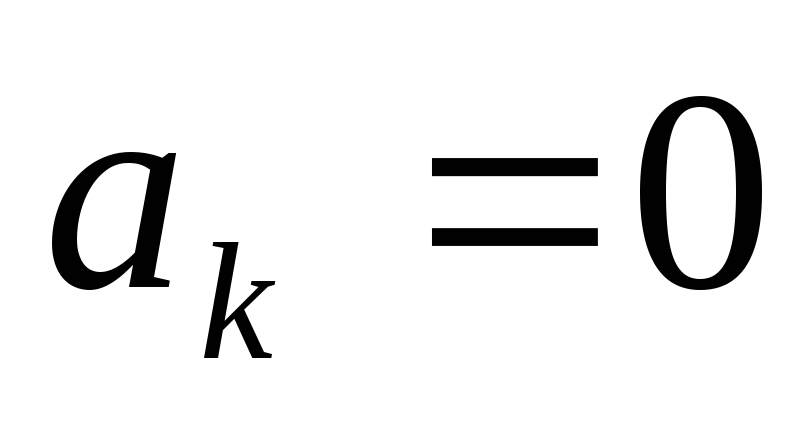 ,
,
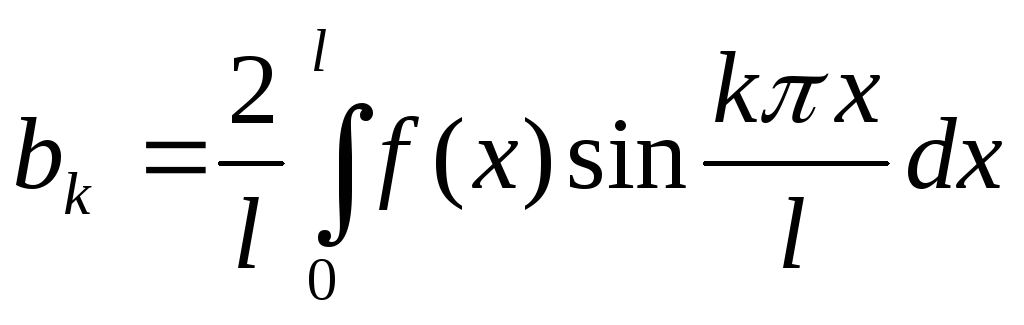
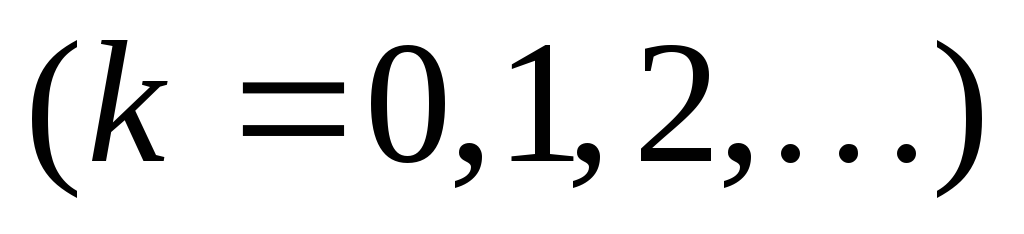 .
.
Пример. Разложить в ряд Фурье функцию

по синусам кратных дуг.
Решение. График заданной функции представлен на рис.3. Продолжим функцию нечетным образом (рис.4), т.е. будем вести разложение по синусам.
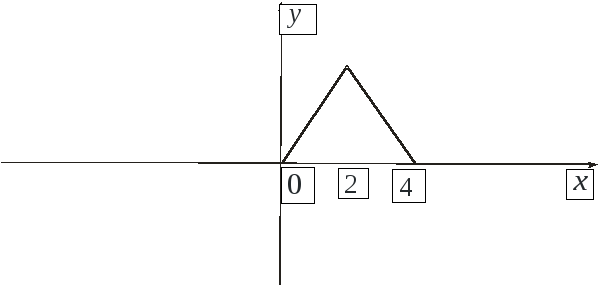
Рис.3
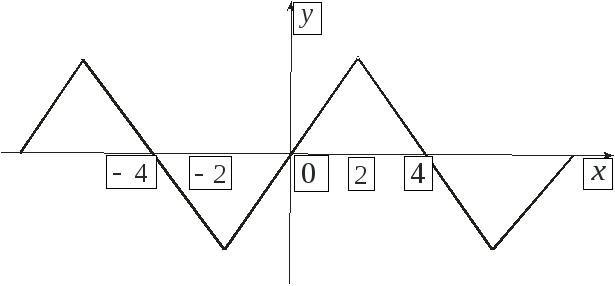
Рис.4
Все
коэффициенты 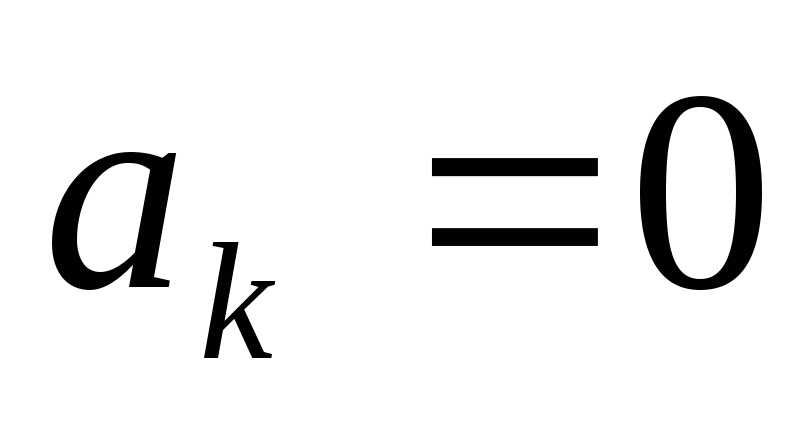
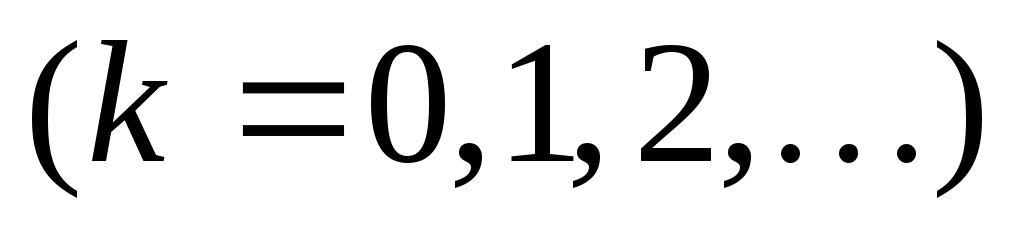 ,
,
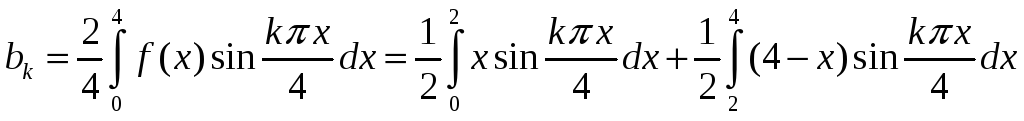
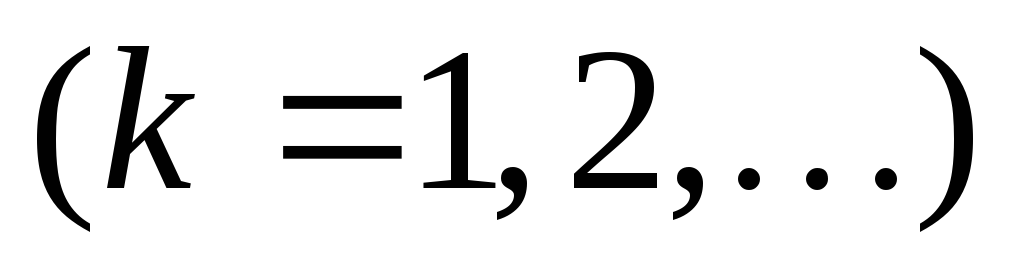
Введем
замену  .
Тогда при
.
Тогда при 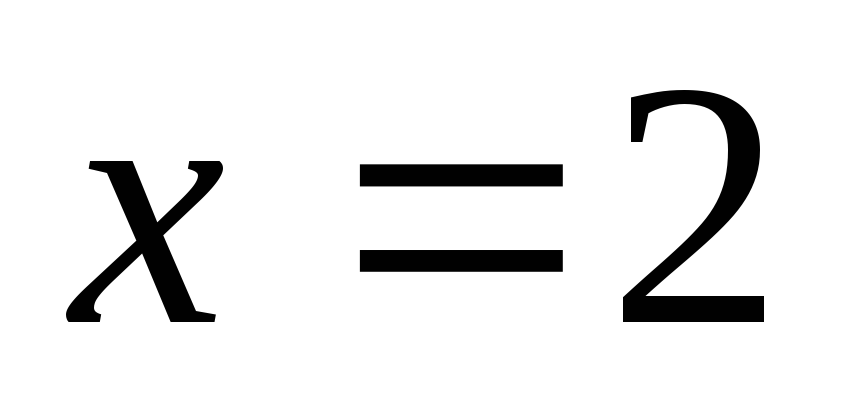 получим
получим 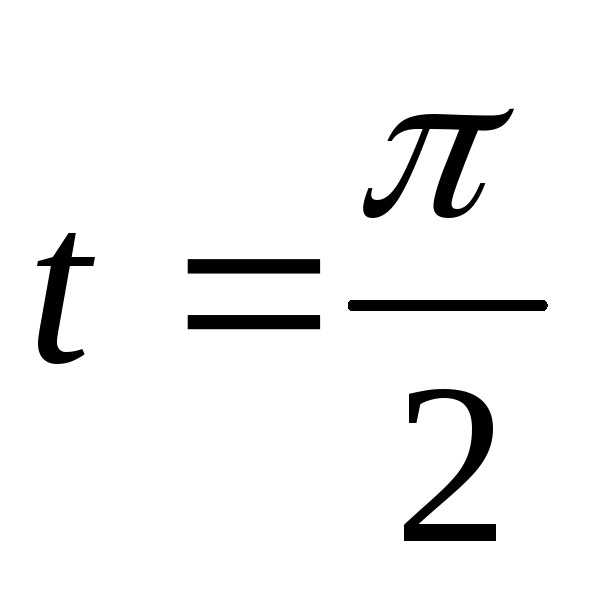 ,
при
,
при 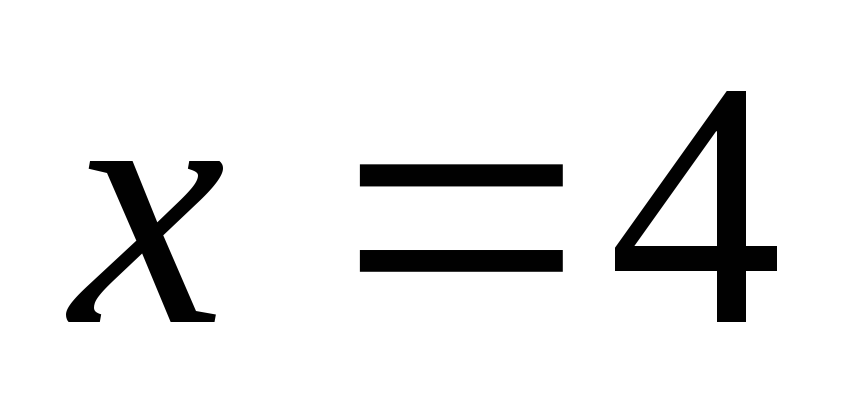 имеем
имеем 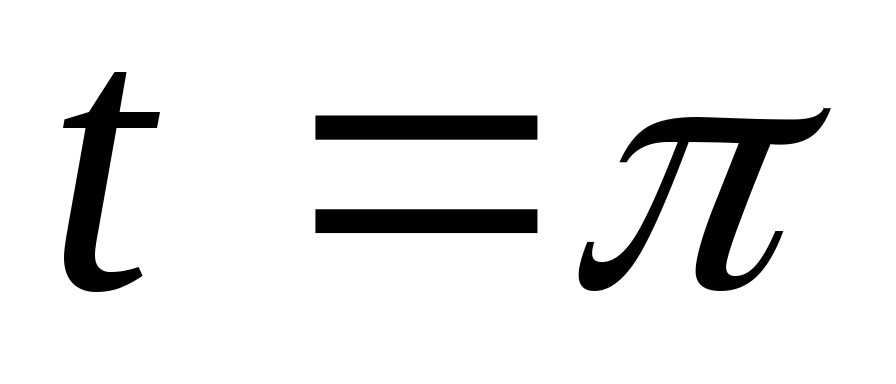 .
.

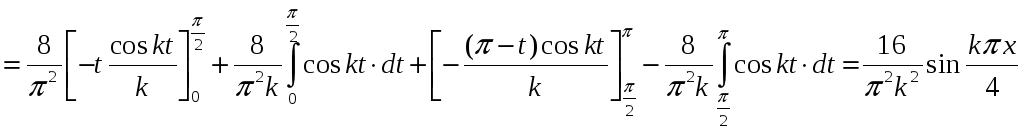
Таким образом
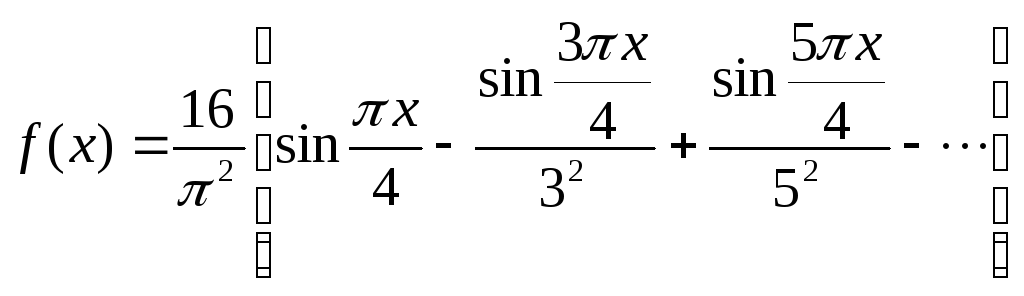 .
.
6.23..Понятие о разложении в ряд Фурье непериодических функций
Функцию, заданную в основной области (-ℓ, ℓ), можно периодически продолжить за основную область с помощью функционального соотношения ƒ(x+2 ℓ) = ƒ(x).
Для непериодической функции ƒ(x) (-∞ < x < +∞) можно выделить участок (-ℓ < x < ℓ), а затем взять периодическую функцию φ(x) с периодом Т=2 ℓ, которая в промежутке (-ℓ, ℓ) равна ƒ(x). Периодическую функцию φ(x) можно разложить в ряд Фурье
φ(x)=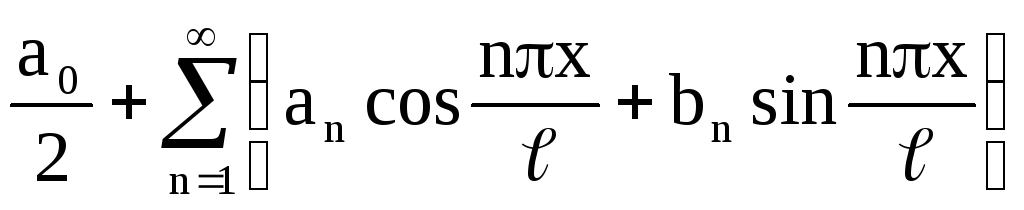 (2.18)
(2.18)
Формула (2.18) будет верна на всей оси -∞ < x < ∞ . Можно написать подобное разложение для функции
ƒ(x)=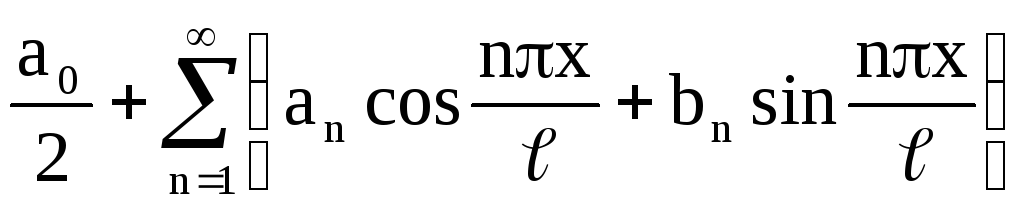 (2.19)
(2.19)
Формула (2.19) будет верна только на конечном промежутке (-ℓ, ℓ), так как на этом промежутке ƒ(x) и φ(x) совпадают.
Таким образом, непериодическую функцию можно разложить в ряд Фурье на конечном промежутке.
Дифференциальные уравнения — Серия косинусов Фурье
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Задачи практики и задания еще не написаны.Пока позволяет время, я работаю над ними, однако у меня нет того количества свободного времени, которое я имел раньше, поэтому пройдет некоторое время, прежде чем здесь что-нибудь появится.
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Серия синуса Фурье
- Серия Фурье
- Разделы
- Дифференциальные уравнения высшего порядка
- Уравнения в частных производных
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Проблем пока не написано.
- Проблемы с назначением Загрузок
- Проблем пока не написано.
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Прямые, окружности и кусочные функции
- Параболы
- Эллипсы
- Гиперболы
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- Полиномиальные функции
- Делительные многочлены
- Нули / корни многочленов
- Графические полиномы
- Нахождение нулей многочленов
- Частичные дроби
- Экспоненциальные и логарифмические функции
- Экспоненциальные функции
- Логарифмических функций
- Решение экспоненциальных уравнений
- Решение логарифмических уравнений
- Приложения
- Системы уравнений
- Линейные системы с двумя переменными
- Линейные системы с тремя переменными
- Расширенные матрицы
- Отборочные
Серия синусов Фурье и косинусов
Синус Фурье и ряды косинусов Напомним, что ряд Фурье f ( x ) определяется как
где
У нас есть следующий результат:
Теорема. Пусть f ( x ) будет функцией, определенной и интегрируемой на интервале .
- (1)
- Если f ( x ) четное, то имеем
и
- (2)
- Если f ( x ) нечетное, то имеем
и
Эта теорема помогает определить ряд Фурье для функций, определенных только на интервале.Основная идея — распространить эти функции на интервал а затем воспользуйтесь определением ряда Фурье.
Пусть f ( x ) — функция, определенная и интегрируемая на.
Устанавливать
и
Тогда f 1 нечетное, а f 2 четное. Легко проверить, что эти две функции определены и интегрируемы на и равны f ( x ) on. Функция f 1 называется нечетным расширением из f ( x ),
, а f 2 называется его четным расширением .
Определение. Пусть f ( x ), f 1 ( x ) и f 2 ( x ) будут такими, как определено выше.
- (1)
- Ряд Фурье f 1 ( x ) называется серией синуса Фурье функции f ( x ) и определяется как
где
- (2)
- Ряд Фурье f 2 ( x ) называется серией косинусов Фурье функции f ( x ) и определяется как
где
Пример. Найдите ряд косинусов Фурье f ( x ) = x для .
Ответ. У нас есть
и
Следовательно, мы имеем
Пример. Найдите ряд синуса Фурье функции f ( x ) = 1 для .
Ответ. У нас есть
Следовательно
Пример. Найти ряд Фурье-синус функции для .
Ответ. У нас есть
что дает b 1 = 0 и для n > 1 получаем
Следовательно
Особый случай 2 L -периодических функций.
Как и для -периодических функций, мы можем определить ряды синуса и косинуса Фурье для функций, определенных на интервале [- L , L ].Сначала вспомним ряд Фурье f ( x )
где
для .
- 1.
- Если f ( x ) четное, то b n = 0, для.
Кроме того, у нас есть
и
Наконец, у нас есть
- 2.
- Если f ( x ) нечетное, то a n = 0, для всех,
и
Наконец, у нас есть
Аналогичным образом можно расширить определения синуса Фурье и косинуса.
[Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра]S.O.S MATH: Домашняя страница
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор : М.А.Хамси
Авторское право 1999-2020 MathMedics, LLC. Все права защищены.Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час .
Дифференциальные уравнения — Серия синуса Фурье
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Задачи практики и задания еще не написаны.Пока позволяет время, я работаю над ними, однако у меня нет того количества свободного времени, которое я имел раньше, поэтому пройдет некоторое время, прежде чем здесь что-нибудь появится.
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Периодические функции и ортогональные функции
- Серия косинусов Фурье
- Разделы
- Дифференциальные уравнения высшего порядка
- Уравнения в частных производных
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Проблем пока не написано.
- Проблемы с назначением Загрузок
- Проблем пока не написано.
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Прямые, окружности и кусочные функции
- Параболы
- Эллипсы
- Гиперболы
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- Полиномиальные функции
- Делительные многочлены
- Нули / корни многочленов
- Графические полиномы
- Нахождение нулей многочленов
- Частичные дроби
- Экспоненциальные и логарифмические функции
- Экспоненциальные функции
- Логарифмических функций
- Решение экспоненциальных уравнений
- Решение логарифмических уравнений
- Приложения
- Системы уравнений
- Линейные системы с двумя переменными
- Линейные системы с тремя переменными
- Расширенные матрицы
- Отборочные
Дифференциальные уравнения — сходимость рядов Фурье
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Задачи практики и задания еще не написаны.Пока позволяет время, я работаю над ними, однако у меня нет того количества свободного времени, которое я имел раньше, поэтому пройдет некоторое время, прежде чем здесь что-нибудь появится.
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Серия Фурье
- Введение в дифференциальные уравнения в частных производных
- Разделы
- Дифференциальные уравнения высшего порядка
- Уравнения в частных производных
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Проблем пока не написано.
- Проблемы с назначением Загрузок
- Проблем пока не написано.
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Прямые, окружности и кусочные функции
- Параболы
- Эллипсы
- Гиперболы
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- Полиномиальные функции
- Делительные многочлены
- Нули / корни многочленов
- Графические полиномы
- Нахождение нулей многочленов
- Частичные дроби
- Экспоненциальные и логарифмические функции
- Экспоненциальные функции
- Логарифмических функций
- Решение экспоненциальных уравнений
- Решение логарифмических уравнений
- Приложения
- Системы уравнений
- Линейные системы с двумя переменными
- Линейные системы с тремя переменными
- Отборочные
