Формула площади цилиндра через диаметр: Онлайн калькулятор площади цилиндра. Как узнать площадь цилиндра.

Площадь поверхности цилиндра: расчет боковой, полной поверхности цилиндра, формула нахождения

Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.

Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.

Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.

Площадь поверхности цилиндра онлайн калькулятор

Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.

Площадь боковой поверхности цилиндра

Сначала нужно представить, как выглядит развертка в двухмерном пространстве.

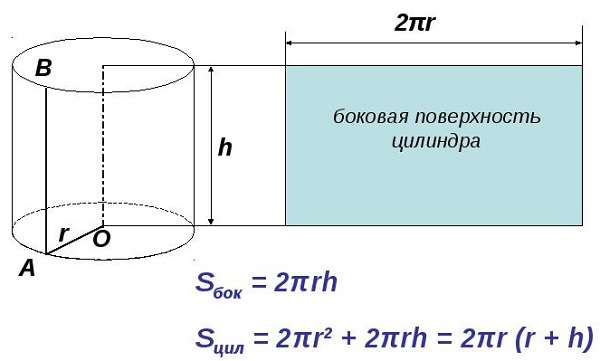
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r, где r — радиус окружности. Другая сторона прямоугольника равна высоте h. Найти искомое не составит труда.

Sбок = 2π * r * h,

где число π = 3.14.

Площадь полной поверхности цилиндра

Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.

Конечная формула выглядит следующим образом:

Sпол = 2π * r2 + 2π * r * h.

Площадь цилиндра формула через диаметр

Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

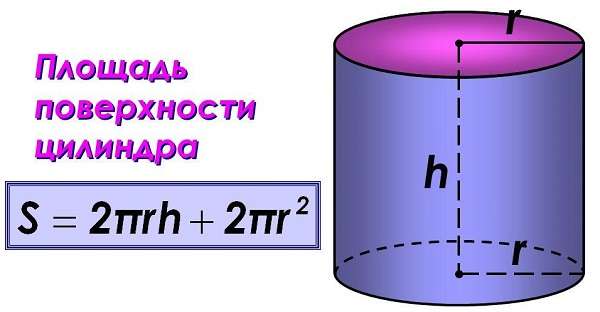
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.

Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,

Вместо r в полную формулу нужно вставить значение r = d/2.

Примеры расчета площади цилиндра

Вооружившись знаниями, приступаем к практике.

Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.

Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:

Sпол = 2 * 3.14 * 242 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм2).

Переводим в привычные м2 и получаем 0,01868928, приблизительно 0.02 м2.

Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.

Данные следующие: диаметр 0,2 м, высота 2 м. Используем формулу через диаметр:

Sпол = 3.14 * 0.22/2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м2.

Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.

Один момент, есть формула:

Sбок = 2 * 3.14 * 1 * 1 = 6.28 м2.

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.

Цилиндр. Формулы и свойства

Определение.

Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями (основами цилиндра).

Цилиндрическая поверхность — поверхность, получаемая при движении прямой (образующей L) параллельно самой себе, вдоль плоской кривой направляющей.

Основания цилиндра — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.

Круговой цилиндр

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность, а основания

перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Прямой круговой цилиндр можно описать, как объёмного фигуру, образующуюся вращением прямоугольника вокруг своей стороны на 360°.

Определение. Радиус цилиндра r — это радиус основания цилиндра.

Определение. Диаметр цилиндра d — это диаметр основания цилиндра.

Определение. Высота цилиндра h — это расстояние между основаниями цилиндра.

Определение. Ось цилиндра — это прямая O₁O₂, которая проходит через центры оснований цилиндра.

Определение. Поверхность цилиндра состоит из цилиндрической поверхности и оснований цилиндра.

Определение. Осевое сечение цилиндра — это сечение цилиндра плоскостью, проходящей через ось цилиндра.

Определение. Касательная плоскость к цилиндру — это плоскость, которая проходит через образующую цилиндра и перпендикулярно к осевому сечении цилиндра.

Формула. Объём цилиндра:

V = πr2h = π	d2	h ,
	4

где r — радиус основы, h — высота цилиндра, d — диаметр основы. Формула. Площадь ,боковой поверхности цилиндра:

S_b = 2πrh = πdh

Формула. Полная площадь поверхности цилиндра:

S = 2πr(h + r)

Косой цилиндр — цилиндр, основы которого не параллельны (Рис.2)

Наклонный цилиндр — цилиндр, у которого образующие не перпендикулярно основам цилиндра (Рис.3 — наклонный круговой цилиндр).

Площадь поверхности цилиндра — формулы, пример расчета

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.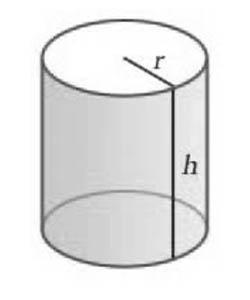

Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:

Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить формулу площади круга:
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.

Площадь боковой поверхности цилиндра

Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:

А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h = 4 см, r = 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:

Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
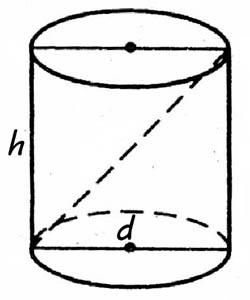
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.

Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника:

Рассмотрим пример расчета площади осевого сечения цилиндра. Для этого возьмем условия из задачи, указанной выше. Чтобы найти величину нам потребуется диаметр. Мы знаем, что он равен двойному радиусу: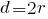

Подставим данные:

Как найти площадь поверхности цилиндра: боковую, основания, полную

В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.

Формула вычисления площади цилиндра

1. Боковая поверхность

Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.

Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:

S = 2 π R h

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:

S = π R²

Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:

S = π (d/2)²

3. Полная площадь

Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:

S = 2 π R h + 2 π R² или S = 2 π R (h + R)

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см².

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см)  = 326,56 см².

Объем полого цилиндра

Объем полого цилиндра, формулы для вычисления объема и площадей правильного полого цилиндра.

Формула вычисления объема полого цилиндра часто применяются при расчете массы полой круглой трубы. Для вычисления массы трубы, необходимо вычисленный объем трубы (полого цилиндра) умножить на плотность материала из которого изготовлена труба (цилиндр).

Расчет площади поверхностей цилиндра, иногда необходим для определения расхода материала для нанесения защитного покрытия трубы (полого цилиндра).

Объем полого цилиндра, вычисленный через внутренний и наружный радиусы

r₁ — внешний радиус

r₂ — внутренний радиус

h — высота цилиндра

… вычисление …

Площадь основания

… вычисление …

Площадь внутренней и внешней боковой поверхности

… вычисление …

Общая площадь

… вычисление …

---

Объем полого цилиндра по толщине стенки и наружному диаметру

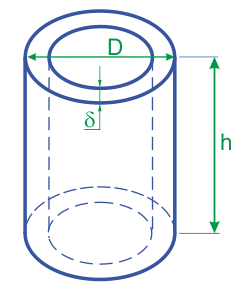
D — внешний диаметр

δ — толщина стенки

h — высота цилиндра

… вычисление …

Площадь основания

… вычисление …

Площадь внутренней и внешней боковой поверхности

… вычисление …

Общая площадь поверностей

… вычисление …

---

Объем полого цилиндра, вычисляемый по внутреннему диаметру и толщине стенки

d — внутренний диаметр

δ — толщина стенки

h — высота цилиндра

… вычисление …

Упрощение формулы:

Площадь основания

… вычисление …

Площадь внутренней и внешней боковой поверхности

… вычисление …

Упрощение формулы:

Общая площадь поверностей

… вычисление …

---

Различия между разными видами цилиндров, а также со свойствами правильного цилиндра, можно ознакомиться в статье «Объем цилиндра» в разделе« Теория».

Объем и площадь других видов цилиндров рассмотрен в статьях:

Объем цилиндра

Объем части цилиндра

Объем части полого цилиндра

---

Вы можете скачать формулы объема и площади поверхностей правильного полого цилиндра в виде картинки.

скачать скачать скачать скачать скачать скачать

Объём цилиндра. Калькулятор объёма цилиндра онлайн

Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.

Высота цилиндра — это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.

Объем прямого цилиндра

Цилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».

Объем цилиндра через радиус основания и высоту цилиндра

Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)

\[ \LARGE V = \pi \cdot R^{2} \cdot H \]

где:
V — объем цилиндра
π — число пи (3.1415)
R — радиус основания
H — высота цилиндра

Объем цилиндра через площадь основания и высоту цилиндра

Объем цилиндра равен произведению площади основания цилиндра на его высоту.

\[ \LARGE V = S \cdot H \]

где:
V — объем цилиндра
H — высота цилиндра
S — площадь цилиндра

Объем цилиндра через диаметр основания и высоту цилиндра

Объем цилиндра равен произведению диаметра основания и числа пи (3.1415) делённое на четыре высоты цилиндра

\[ \LARGE V = \frac {\pi \cdot D^{2} }{4 \cdot H} \]

где:
V — объем цилиндра
π — число пи (3.1415)
D — диаметр основания
H — высота цилиндра

Калькулятор объёма цилиндра

Входные данные

 

Радиус цилиндра r:

 

Высота цилиндра h:

 

Количество знаков после запятой в результате вычислений

1 2 3 4 5 6 7

Результат

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Объем цилиндра

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Объем правильного цилиндра через радиус и высоту цилиндра

— Вычисления   (показано)   (скрыто)

— примечания   (показано)   (скрыто)

r — радиус основания цилиндра

h — высота цилиндра

… вычисление …

Площадь основания цилиндра

… вычисление …

Площадь боковой поверхности

… вычисление …

Общая площадь

… вычисление …

Упрощение формулы:

---

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

S — площадь основания цилиндра

h — высота цилиндра

… вычисление …

Площадь боковой поверхности

… вычисление …

Общая площадь

… вычисление …

---

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

d — диаметр основания цилиндра

h — высота цилиндра

… вычисление …

Площадь основания цилиндра

… вычисление …

Площадь боковой поверхности

… вычисление …

Общая площадь

… вычисление …

---

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

---

Теория

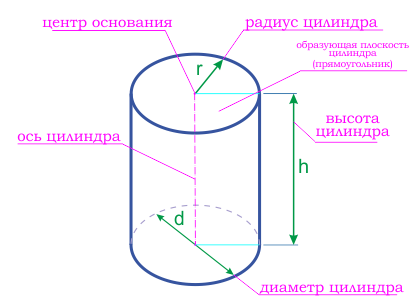
Цилиндр может быть правильным или наклонным.

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

---

Поверхности цилиндра

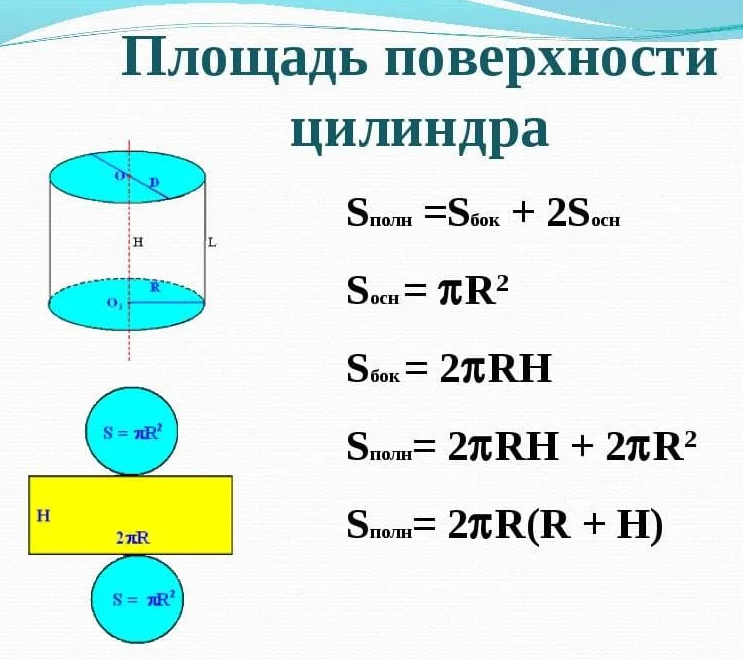
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

---

Сечения цилиндра

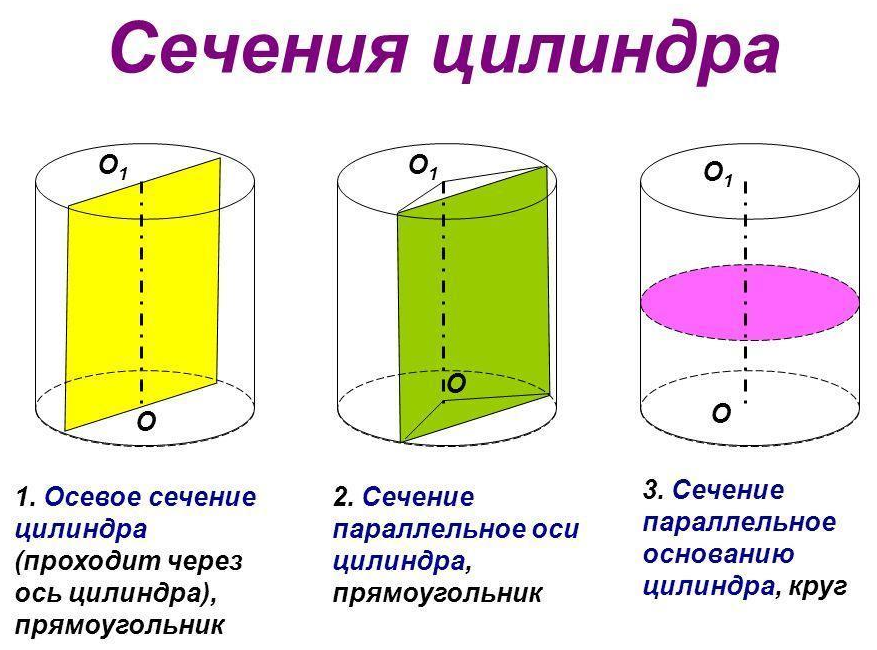
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура.

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг.

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс.

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса.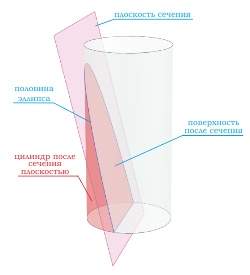

---

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм³, см³, мл³.

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

---

Объем и площадь других видов цилиндров рассмотрен в статьях:

Объем полого цилиндра

Объем части цилиндра

Объем части полого цилиндра

---

Вы можете скачать формулы объема и площади поверхностей правильного цилиндра в виде картинки

Площадь цилиндра с вычислителем

Площадь поверхности цилиндра с калькулятором — Math Open Reference

Определение: Количество квадратных единиц, необходимое для точного покрытия поверхности цилиндра. Дается формулой:

где:
π — Пи, приблизительно 3,142
r — радиус цилиндра
h высота цилиндра

Попробуй это Перетащите оранжевую точку, чтобы изменить размер цилиндра, обратите внимание, как рассчитывается площадь.

Площадь цилиндра можно определить, разбив его на три части:

• Два круга, составляющие концы цилиндра.
• Сторона цилиндра, которая в развернутом состоянии представляет собой прямоугольник

Объединяя эти части, мы получаем формулу: где:
π — Pi, приблизительно 3,142
r — радиус цилиндра
h высота цилиндра

Подробнее о том, как выводится эта формула, см. Определение площади поверхности цилиндра.

шт.

Помните, что радиус и высота должны быть в одних и тех же единицах — при необходимости преобразуйте их. Результирующая площадь будет в этих квадратных единицах. Так, например, если высота и радиус указаны в сантиметрах, то площадь будет в квадратных сантиметрах.

Калькулятор

Используйте калькулятор выше, чтобы рассчитать высоту, радиус или площадь поверхности цилиндра.

Введите любые два значения, и будет вычислено недостающее.Например: введите радиус и высоту и нажмите «Рассчитать». Площадь поверхности будет рассчитана.

Точно так же, если вы введете высоту и площадь, будет рассчитан радиус, необходимый для получения этой площади.

Что попробовать

1. На рисунке выше отрегулируйте высоту и диаметр цилиндра и обратите внимание, как рассчитывается площадь поверхности.
2. Нажмите «сбросить» и «скрыть детали». Отрегулируйте цилиндр до нового размера и рассчитайте площадь поверхности.Нажмите «показать подробности», чтобы проверить свой ответ.
3. Нажмите «сбросить». Посчитайте, что произойдет, если вы удвоите высоту — удвоится ли и площадь поверхности?
4. Нажмите «сбросить». Посчитайте, что произойдет, если вы удвоите диаметр — удвоится ли и площадь поверхности?

Связанные темы

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.

Цилиндр. Формулы и свойства цилиндра

Цилиндрическая поверхность — это поверхность, полученная путем перемещения прямой (образующей) параллельно самой себе по плоской кривой.

Основания цилиндров представляют собой плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.

Определение. Образующая цилиндра г представляет собой комбинацию всех параллельных сегментов (AB), которые соединяют основания цилиндров.

Цилиндр круговой правый

Обычно слово цилиндр понимается как относящееся к конечному сечению правого кругового цилиндра конечной высоты с круговыми концами, перпендикулярными оси.

Правый круговой цилиндр описывается как трехмерная форма, которая образуется путем вращения прямоугольника на своей стороне на 360 °. В этом случае образуется правильный круговой цилиндр с кругом в основании цилиндра.

Определение. Радиус цилиндра r цилиндра — это радиус баз.

Определение. Диаметр цилиндра d — диаметр оснований.

Определение. Высота цилиндра h — расстояние между основаниями цилиндра.

Определение. Ось — это линия, проходящая через центры оснований цилиндров.

Определение. Площадь поверхности , состоящая из боковой части (боковой части), верхней части и нижней части.

Определение. Осевое сечение — это сечение плоскости цилиндра, проходящее через ось цилиндра.

Определение. Касательная плоскость к цилиндру — это плоскость, проходящая через образующую цилиндра и перпендикулярная осевому сечению цилиндра.

Формула. Объем цилиндра :

V = πr 2 h = π	d 2	h,
	4

где r — радиус основания, h — высота цилиндра, d — диаметр основания. Формула. Боковое сечение (A _l ) по радиусу и высоте:

A _l = 2πrh = πdh

Формула. Площадь поверхности (A _s ) по радиусу и высоте:

A _с = 2πr (h + r)

Если основания (верхняя и нижняя поверхности) не параллельны, цилиндр называется наклонным (рис.2).

Если основания не перпендикулярны высоте, цилиндр называется наклонным (рис. 3).

.

Math Made Easy! Как найти площадь поверхности цилиндра

Учебное пособие по геометрии

Общая площадь поверхности цилиндра

Для старшеклассников геометрии, которые на самом деле не «фанаты» геометрического предмета, такие проблемы, как определение площади поверхности цилиндра, часто заставляют детей закрывать учебники и бросать или находить репетитора по геометрии.

Но пока не паникуйте. Геометрию, как и многие другие виды математики, часто намного легче понять, если разбить ее на небольшие части.Этот учебник по геометрии сделает именно это — разбивает уравнение для определения площади поверхности цилиндра на простые для понимания части.

Обязательно ознакомьтесь с проблемами площади поверхности цилиндра и решениями в разделе Geometry Help Online ниже, а также попробуйте Math Made Easy! викторина .

Уравнение для общей площади цилиндра

S.A. = 2 π r ² + 2 π rh

Где: r — радиус цилиндра, а h — высота цилиндра.

Перед началом убедитесь, что вы понимаете следующие уроки геометрии:

Math Made Easy! Совет

По общему признанию, формула для площади поверхности цилиндра не слишком хороша. Итак, попробуем разбить формулу на понятные части. Хороший математический совет — попытаться визуализировать геометрическую форму с помощью объекта, с которым вы уже знакомы.

Какие предметы в вашем доме представляют собой цилиндры? Я знаю, что у меня в кладовой много цилиндров, более известных как консервы.

Рассмотрим банку. Банка состоит из верхней и нижней части и изогнутой стороны. Если бы вы могли развернуть край банки, это был бы прямоугольник. Хотя я не собираюсь разворачивать банку, я могу легко развернуть этикетку вокруг нее и увидеть, что это прямоугольник.

Теперь вы можете визуализировать общую площадь цилиндра (банки):

• банка имеет 2 круга, а
• банка 1 прямоугольник

Другими словами, уравнение общей площади цилиндра можно представить как:

С.A. = (2) (площадь круга) + (площадь прямоугольника)

Следовательно, чтобы вычислить площадь поверхности цилиндра, необходимо вычислить площадь круга (дважды) и площадь прямоугольника (один раз).

Давайте снова посмотрим на общую площадь поверхности уравнения цилиндра и разобьем его на простые для понимания части.

Площадь цилиндра = 2 π r ² (часть 1) + 2 π правая (часть 2)

• Порция 1: Первая часть уравнения цилиндра имеет отношение к площади двух кругов (верха и низа банки).Поскольку мы знаем, что площадь одного круга равна πr ² , то площадь двух кругов равна 2πr ² . Итак, первая часть уравнения цилиндра дает нам площадь двух окружностей.
• Часть 2: Вторая часть уравнения дает нам площадь прямоугольника, изгибающегося вокруг банки (развернутая этикетка в нашем хорошем примере консервов). Мы знаем, что площадь прямоугольника — это просто его ширина (w) умноженное на его высоту (h). Так почему же ширина во второй части уравнения ( 2 π r) (h ) записывается как (2 π r)? Снова изобразите этикетку.Обратите внимание, что ширина прямоугольника, когда он скатывается вокруг банки, точно такая же, как и ее окружность. А уравнение для окружности равно 2πr. Умножьте (2πr) на (h), и вы получите площадь прямоугольной части цилиндра.

Справка по геометрии в Интернете: Площадь поверхности цилиндра

Ознакомьтесь с тремя распространенными типами геометрических задач для определения площади поверхности цилиндра при различных измерениях.

# 1 Найти площадь поверхности цилиндра по радиусу и высоте

Задача: Найдите общую площадь поверхности цилиндра с радиусом 5 см.и высотой 12 см.

Решение: Поскольку мы знаем, что r = 5 и h = 12, замените 5 на r и 12 на h в уравнении площади поверхности цилиндра и решите.

• S.A. = (2) π (5) ² + (2) π (5) (12)
• S.A. = (2) (3,14) (25) + (2) (3,14) (5) (12)
• S.A. = 157 + 376,8
• S.A. = 533,8

Ответ: Площадь поверхности цилиндра радиусом 5 см. и высотой 12 см. это 533.8 см. в квадрате.

# 2 Найдите площадь поверхности цилиндра по диаметру и высоте

Задача: Какова общая площадь поверхности цилиндра диаметром 4 дюйма и высотой 10 дюймов?

Решение: Поскольку диаметр равен 4 дюймам, мы знаем, что радиус равен 2 дюймам, так как радиус всегда равен 1/2 диаметра. Подставьте 2 для r и 10 для h в уравнение для площади поверхности цилиндра и решите:

• С.A. = 2π (2) ² + 2π (2) (10)
• S.A. = (2) (3,14) (4) + (2) (3,14) (2) (10)
• S.A. = 25,12 + 125,6
• S.A. = 150,72

Ответ: Площадь поверхности цилиндра диаметром 4 дюйма и высотой 10 дюймов составляет 150,72 дюйма в квадрате.

# 3 Найдите площадь поверхности цилиндра с учетом площади одного конца и высоты

Задача: Площадь одного конца цилиндра составляет 28,26 кв. Футов, а его высота — 10 футов.Какова общая площадь цилиндра?

Решение: Мы знаем, что площадь круга равна πr ² , и мы знаем, что в нашем примере площадь одного конца цилиндра (который представляет собой круг) составляет 28,26 кв. Фута. Поэтому замените 28,26 на πr ² в формуле для площади цилиндра. Вы также можете заменить 10 на h, так как это дано.

S.A. = (2) (28,26) + 2πr (10)

Эта проблема все еще не может быть решена, так как мы не знаем радиуса r.Чтобы решить для r, мы можем использовать уравнение площади круга. Мы знаем, что площадь круга в этой задаче составляет 28,26 фута, поэтому мы можем заменить это на A в формуле для площади круга, а затем решить для r:

• Площадь круга (решить для r):
• 28,26 = πr ²
• 9 = r ² (разделите обе части уравнения на 3,14)
• r = 3 (извлеките квадратный корень из обеих частей уравнения)

Теперь, когда мы знаем r = 3, мы можем подставить его в формулу цилиндра вместе с другими заменами, как показано ниже:

• С.А. = (2) (28,26) + 2π (3) (10)
• S.A. = (2) (28,26) + (2) (3,14) (3) (10)
• S.A. = 56,52 + 188,4
• S.A. = 244.92

Ответ: Общая площадь цилиндра, у которого площадь конца 28,26 кв. Футов и высота 10 составляет 244,92 кв. Фута .

Вам нужна дополнительная помощь по геометрии?

Если у вас есть другая конкретная проблема, с которой вам нужна помощь, связанная с общей площадью поверхности цилиндра , пожалуйста, спросите в разделе комментариев ниже.Я буду рад помочь и, возможно, даже включу вашу проблему в раздел проблемы / решения выше.

.

Площадь цилиндра

Вы сталкиваетесь с цилиндрами в повседневных делах, например, когда пьете банку газировки, открываете металлическую банку с едой или бьете своих друзей цилиндрической лапшой для бассейна. Математически цилиндр — это трехмерный объект, пара конгруэнтных окружностей, разделенных изогнутой поверхностью.

Содержание

1. Определение цилиндра
2. Площадь цилиндра
3. Площадь цилиндра Формула
4. Площадь боковой поверхности цилиндра
5. Формула площади боковой поверхности
6. Как найти площадь поверхности цилиндра

Определение цилиндра

Цилиндр имеет две грани, две изогнутые кромки, где изогнутая стенка встречается с концевыми окружностями, и изогнутая поверхность, проходящая между двумя круглыми концами.

Цилиндр — это трехмерное твердое тело, имеющее высоту (h), ширину (w) или диаметр (D) и длину (l). Поскольку он трехмерный, он имеет площадь поверхности вместо простой площади (площадь обычно ассоциируется только с двумерными формами, такими как круг или прямоугольник).

Цилиндры обычно имеют перпендикулярные стороны к концам, что делает их правыми цилиндрами . Цилиндры тоже могут быть наклонными. Их два круглых конца могут не совпадать, поэтому стена или изогнутая поверхность наклонены, как наклонный цилиндр знаменитой Пизанской башни.

Площадь поверхности цилиндра

Когда мы говорим о площади поверхности цилиндра, мы действительно имеем в виду две площади поверхности: площадь боковой поверхности , и общую площадь поверхности , . Общая площадь поверхности обычно называется площадью поверхности.

Если вас попросят определить площадь поверхности цилиндра, вы захотите найти площади двух концов и изогнутой поверхности.

Убедитесь, что вы понимаете связь между радиусом, диаметром и π, поскольку все они играют роль в определении площади поверхности правильного цилиндра.

Диаметр и радиус цилиндра выходят из двух окружностей, которые обычно считаются основаниями , или верхом и низом цилиндра, хотя математической причины для того, чтобы цилиндр встал, не существует. Представьте себе цистерны в поезде; они представляют собой цилиндры «по бокам», их основания с обоих концов.

Все, что вы делаете при вычислении площади поверхности, — это измеряете площадь двух окружностей, высоту h цилиндра и используете π, чтобы связать их.

Площадь поверхности цилиндра формулы

Формула площади поверхности цилиндра:

В этой формуле a — общая площадь поверхности, r — радиус окружностей на обоих концах, h — высота, а π — иррациональное число, которое мы упрощаем и сокращаем до 3.141595, или даже короче 3.14.

Формула площади на самом деле является формулой для изогнутой поверхности (то есть части 2πrh), добавленной к площади обоих концов (то есть части 2πr2). Если вы видите фразу «площадь основания цилиндра», автор имеет в виду верхний и нижний концы, а не изогнутую поверхность между ними.

Площадь всегда будет выражаться в квадратных единицах , вытекающих из линейных единиц в задаче, так как любые две линейные единицы, умноженные друг на друга, дают квадратные единицы.

Площадь боковой поверхности цилиндра

Как упоминалось выше, существует также площадь боковой поверхности объекта. Боковая поверхность объекта определяется как площадь всех сторон объекта, за исключением области его основания и вершины. Для цилиндра боковая поверхность — изогнутая поверхность, соединяющая основание и верх.

Формула площади боковой поверхности

Формула для вычисления площади боковой поверхности аналогична приведенной выше формуле площади поверхности, но, поскольку мы не включаем верхнюю часть или основание, мы должны удалить эту часть формулы.Формула площади боковой поверхности:

Как найти площадь поверхности цилиндра

Вот цилиндр из сердцевины рулона бумажных полотенец:

[чертеж картонной трубки диаметром 1,7 дюйма, длиной 11 дюймов]

Представьте, что мы храним внутри что-то чудесное, например, персонализированные палочки для еды или шашлык из шашлыка ручной работы. Нам нужно закрыть оба конца. Зная, что картонная трубка имеет ширину 1,7 дюйма и длину 11 дюймов, если бы мы закрыли концы, какова была бы ее площадь поверхности?

Здесь не было радиуса r; нам сказали диаметр, но вспоминая соотношение между частями окружностей, мы вспоминаем:

Диаметр (D) = 2 × Радиус (r)

1.7 = 2r

85 = г

Подставьте значения r и h в формулу, используя 3,14 для π:

А = 2πrh + 2πr2

А = 2π * 0,85 * 11 + 2π * 0,852

А = (6,283185 * 9,352) + (6,283185 * 0,72252)

А = 63,287382

В трубке для бумажных полотенец используется картон размером чуть более 0,4 квадратных футов!

Вот типичная банка содовой. По вашим оценкам, сколько алюминия необходимо для его изготовления?

[вставить рисунок карикатуры с этикетками 4.83 дюйма в высоту, 2,60 дюйма в диаметре в самой широкой части тела]

Да, сода может немного вмятин с обоих концов, но нам просто нужна оценка. Во-первых, нам нужен радиус, поэтому берем половину диаметра банки:

.