Квадратичная функция ее свойства и график видеоурок – Квадратичная функция. Видеоурок. Алгебра 8 Класс

Квадратичная функция. Видеоурок. Алгебра 8 Класс

Вспомним определение: квадратичной называется функция вида

y = , где .

Здесь  – независимая переменная, или аргумент;  – зависимая переменная, или функция;  – конкретные числа, параметры, коэффициенты. Тройка этих конкретных чисел задает конкретную квадратичную функцию. Частным случаем такой функции является функция .

Напомним важнейший результат: график функции (1) и график функции (2) есть одна и та же парабола, но расположенная в разных местах координатной плоскости.

Чтобы получить этот результат и понять, каким образом преобразовываются графики функций, вспомнить правила преобразования графиков функций, рассмотрим несколько примеров, а именно:

(1) , где

(2) , где

(3) , где

Вспомним, каким образом влияет на график функции этот коэффициент. Для этого расположим все три графика в одной координатной плоскости.

Сразу рассмотрим первую функцию . Она проходит через точку с координатами . Это известная нам парабола, свойства ее тоже нам известны. Как поведет себя функция ? Там, где аргумент был равен , функция тоже будет равна , то есть точка  лежит на графике этой функции. При  первая функция была равна , а вторая функция будет равна . А третья функция будет равна . Схематически проведем вторую функцию  – она пойдет более круто. Это означает, что если функция   возрастала, то функция  возрастает еще круче. если функция   

interneturok.ru

Функция y=k/х, ее свойства и график (продолжение 1). Видеоурок. Алгебра 8 Класс

Тема: Квадратичная функция. Функция

Урок: Функция , её свойства и график (продолжение 1)

На этом уроке мы продолжим изучение функции , её графика и свойств, а также научимся решать типовые задачи.

Напомним, как выглядит график данной функции.

В случае, если , то ветви гиперболы расположены в ,  координатных четвертях, а если , то – , . (Рис. 1,2 соответственно).

Рис. 1.    

Рис. 2.

Перечислим теперь основные свойства функции :

1) Область определения: .

2) Монотонность на промежутках  и .

3) Асимптоты: координатные оси .

4) Центр симметрии .

Вспомним также о влиянии коэффициента :  – чтобы получить из первого графика второй, необходимо растянуть его в 2 раза от оси .

Рис. 3.

Повторив все основные свойства гиперболы, перейдём к решению типовых задач.

Задача 1

Гипербола  проходит через точку

interneturok.ru

Квадратичная функция, её график и свойства

Материалы

к урокам алгебры

9 класс

Учитель Козина Н.А.

Функция y = ax 2 , её график и свойства.

Урок № 9

Квадратичная функция. Определение.

Квадратичной функцией называется функция, которую можно задать формулой вида

y = ax 2 + bx + c,

где x – независимая переменная, a, b и c – некоторые числа, причем a  0.

Квадратичная функция.

Примеры.

• Зависимость пути от времени при равноускоренном движении.

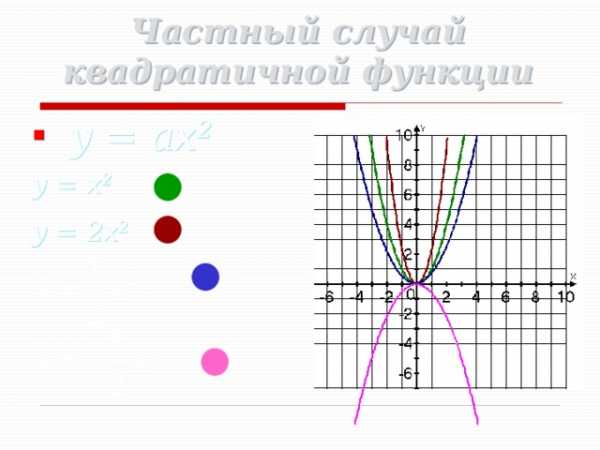
Частный случай квадратичной функции

y = x 2

y = 2x 2

0. 1) Если x=0, то y=0. График функции проходит через начало координат. 2) Если x  0, то y0. График функции расположен в верхней полуплоскости. «

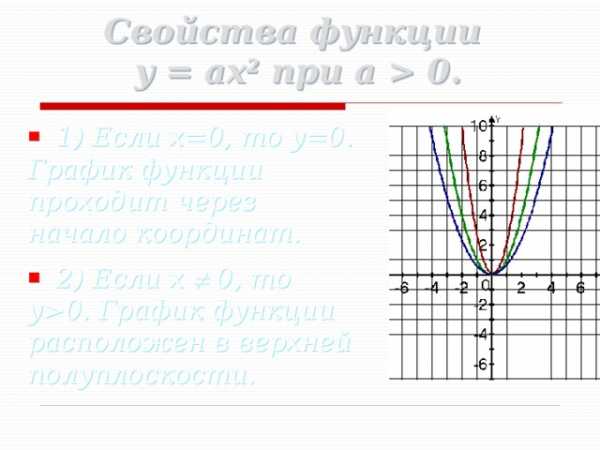
Свойства функции y = ax 2 при a 0.

• 1) Если x=0, то y=0. График функции проходит через начало координат.
• 2) Если x  0, то y0. График функции расположен в верхней полуплоскости.

0. 3) Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси y. «

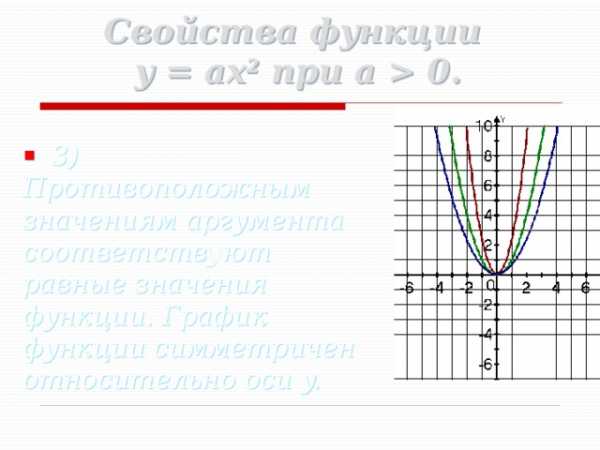
Свойства функции y = ax 2 при a 0.

• 3) Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси y.

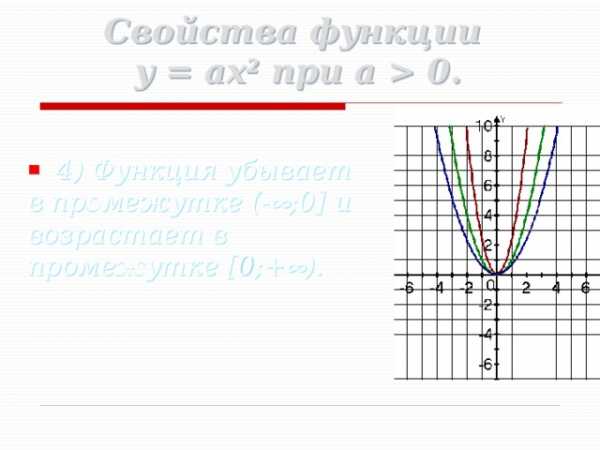0. 4) Функция убывает в промежутке (-  ;0] и возрастает в промежутке [0;+  ). «

Свойства функции y = ax 2 при a 0.

• 4) Функция убывает в промежутке (-  ;0] и возрастает в промежутке [0;+  ).

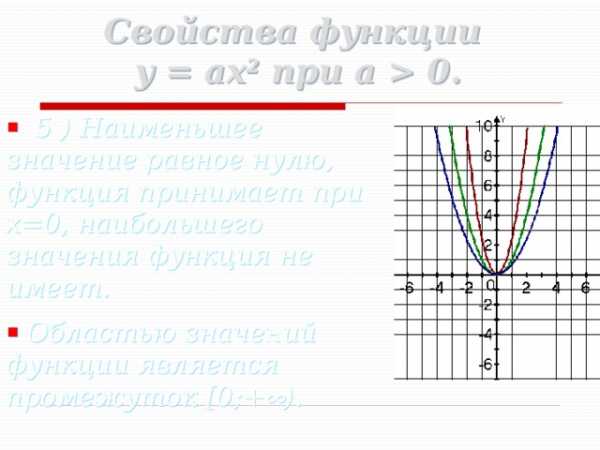0. 5 ) Наименьшее значение равное нулю, функция принимает при x=0, наибольшего значения функция не имеет. Областью значений функции является промежуток [0;+  ). «

Свойства функции y = ax 2 при a 0.

• 5 ) Наименьшее значение равное нулю, функция принимает при x=0, наибольшего значения функция не имеет.
• Областью значений функции является промежуток [0;+  ).

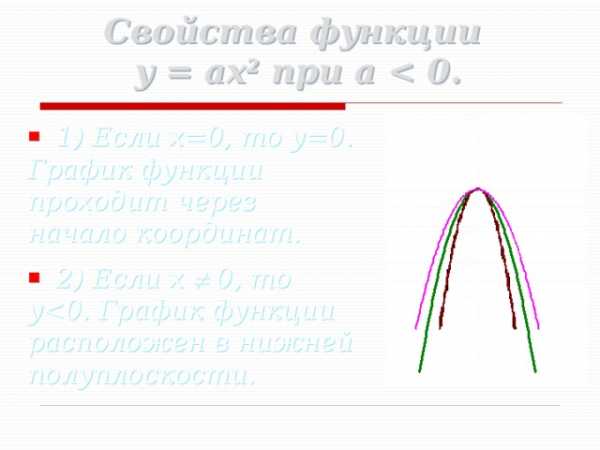
Свойства функции y = ax 2 при a

• 1) Если x=0, то y=0. График функции проходит через начало координат.
• 2) Если x  0, то y

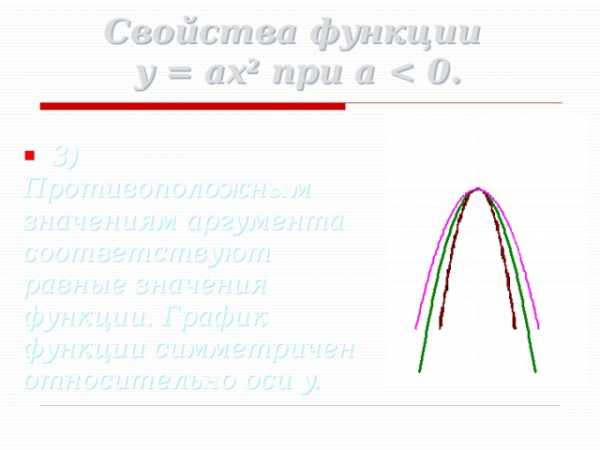
Свойства функции y = ax 2 при a

• 3) Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси y.

Свойства функции y = ax 2 при a

• 4) Функция убывает в промежутке [0;+  ) и возрастает в промежутке (-  ;0].

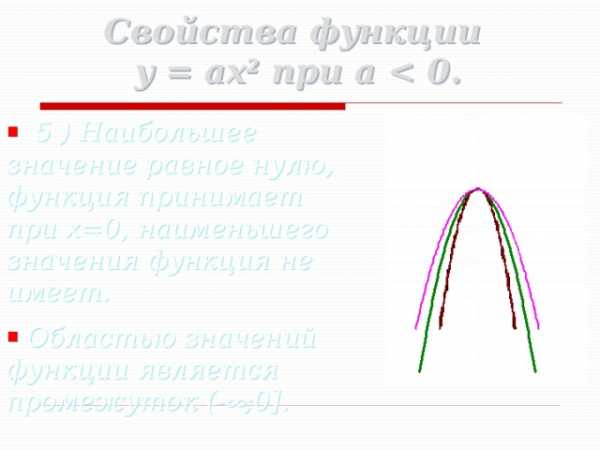
Свойства функции y = ax 2 при a

• 5 ) Наибольшее значение равное нулю, функция принимает при x=0, наименьшего значения функция не имеет.
• Областью значений функции является промежуток (-  ;0].

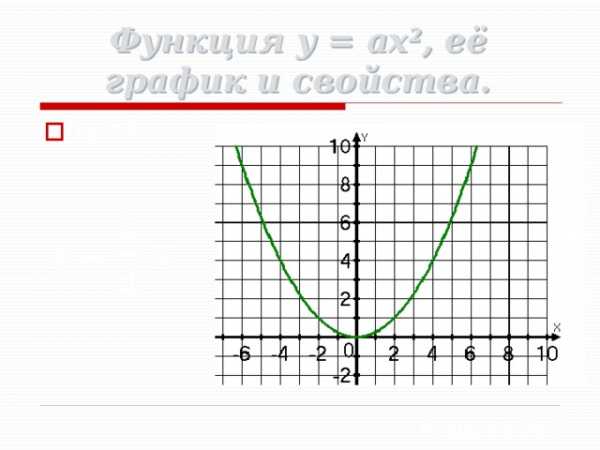
Функция y = ax

2 , её график и свойства.

К уроку № 9

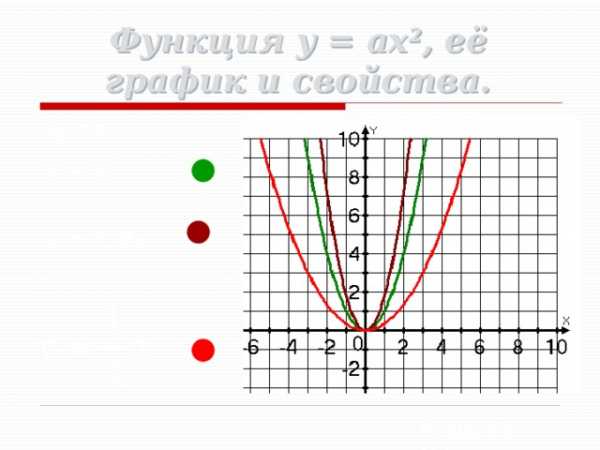
Функция y = ax 2 , её график и свойства.

№ 75

y = x 2

y = 1,8x 2

К уроку №9

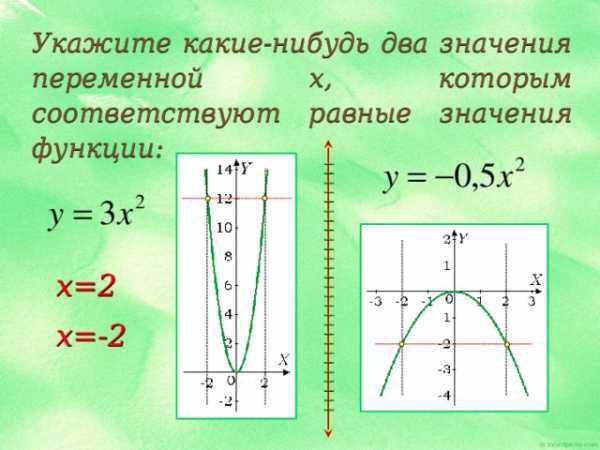
Укажите какие-нибудь два значения переменной x, которым соответствуют равные значения функции:

x=2

x=-2

Не выполняя вычислений, сравните значения выражений:

=

Известно, что график функции проходит через точку (-8;-16).

Определите знак коэффициента а;

“ -”

Укажите координаты еще одной точки графика этой функции.

(8; -16)

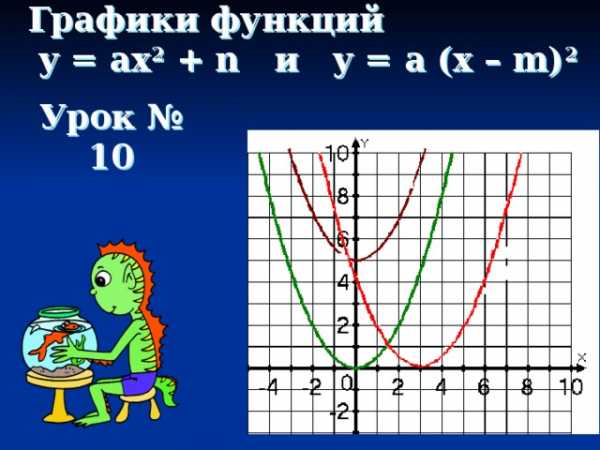
Графики функций y = ax 2 + n и y = a (x – m) 2

Урок № 10

0, или на –n единиц вниз, если n «

Графики функций y = ax 2 + n и y = a (x – m) 2

Правило.

График функции y = ax 2 + n является параболой, которую можно получить из графика функции y = ax 2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n 0, или на –n единиц вниз, если n

0, или на –m единиц влево, если m «

Графики функций y = ax 2 + n и y = a (x – m) 2

Правило.

График функции y = a (x – m) 2 является параболой, которую можно получить из графика функции y = ax 2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m 0, или на –m единиц влево, если m

0, или на –m единиц влево, если m 0, или на –n единиц вниз, если n «

График функции y = a (x – m) 2 + n

Правило.

График функции y = a (x – m) 2 + n является параболой, которую можно получить из графика функции y = ax 2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m 0, или на –m единиц влево, если m 0, или на –n единиц вниз, если n

График функции y = a (x – m) 2 + n

Правило.

Производить параллельные переносы можно в любом порядке.

График функции y = f (x – m) + n можно получить из графика y = f (x) с помощью двух соответствующих параллельных переносов.

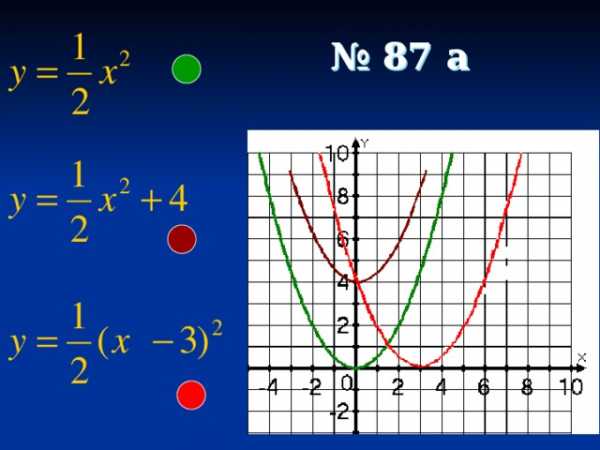
№ 87 а

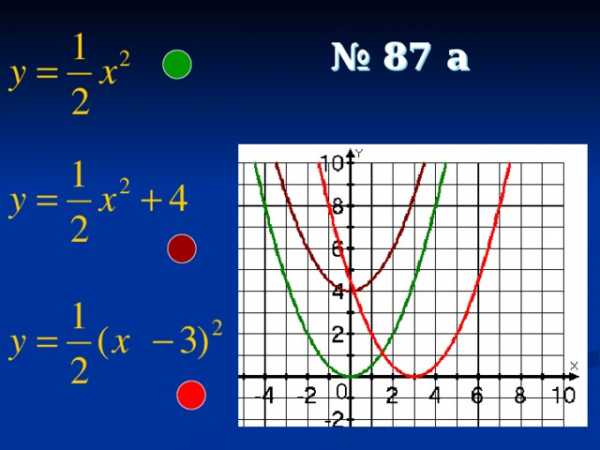
№ 87 а

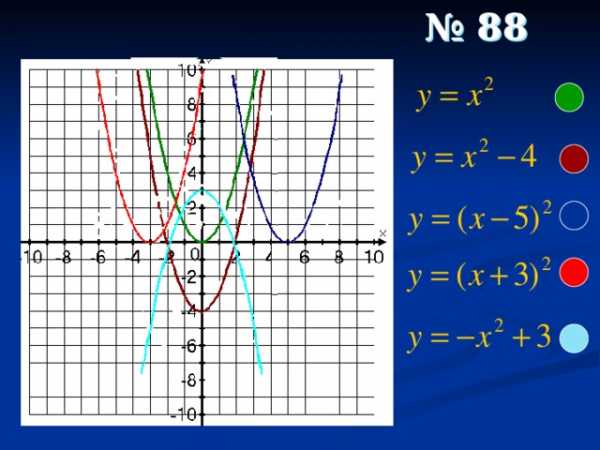
№ 88

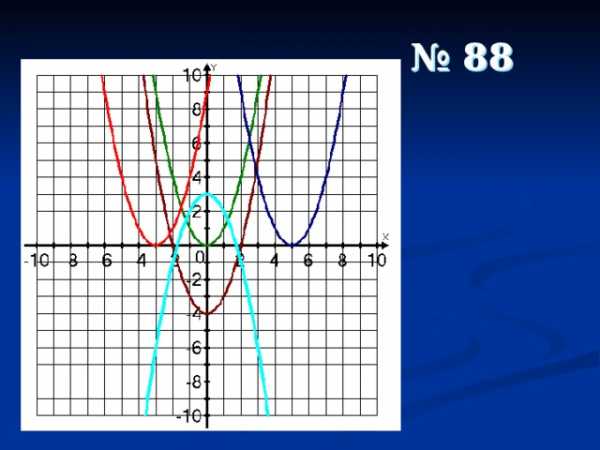
№ 88

К уроку № 10

Построение графика квадратичной функции.

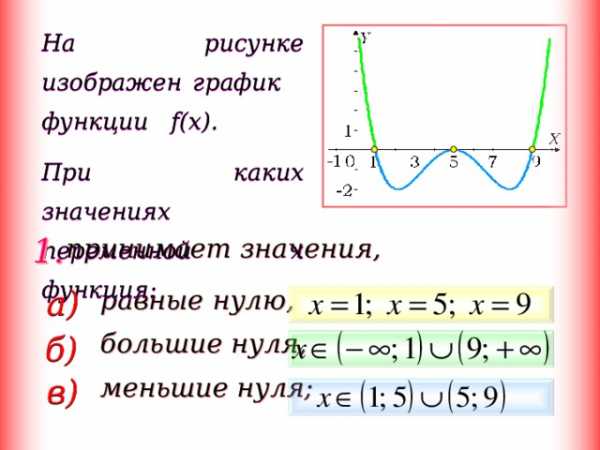
На рисунке изображен график функции f(x).

При каких значениях переменной x функция:

1.

принимает значения,

равные нулю,

большие нуля,

меньшие нуля;

а)

б)

в)

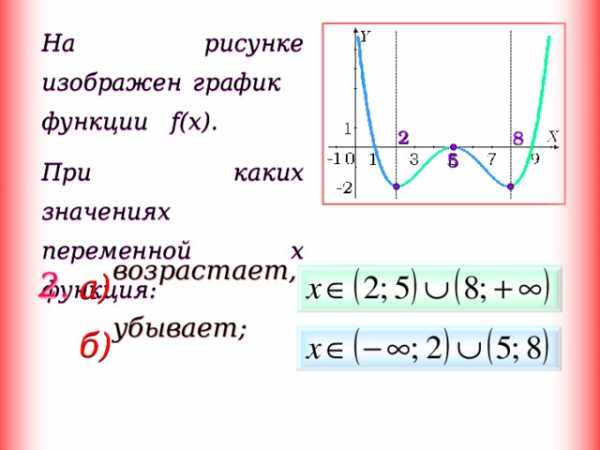
На рисунке изображен график функции f(x).

При каких значениях переменной x функция:

2

8

5

возрастает,

убывает;

2.

а)

б)

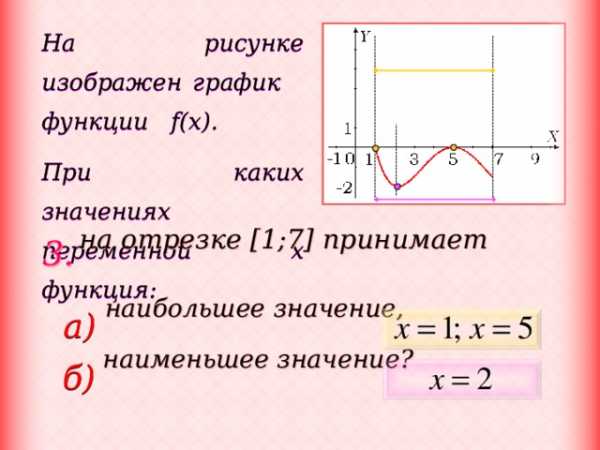
На рисунке изображен график функции f(x).

При каких значениях переменной x функция:

на отрезке [1;7] принимает

наибольшее значение,

наименьшее значение?

3.

а)

б)

Решите уравнения:

videouroki.net

Урок алгебры в 9-м классе «Квадратичная функция. Ее свойства и график»

Разделы: Математика

---

Цели – обобщить и систематизировать знания учащихся о квадратичной функции: повторить изученные приемы исследования свойств функции, методы построения графиков; закрепить и упрочить умения и навыки учащихся по данной теме, показать ее прикладной характер, ориентировать на использование полученных знаний при дальнейшем изучении математики.
 
План урока:

1. Разминка.
2. Фронтальная работа по построению графика квадратичной функции и исследованию ее свойств.
3. Работа в группах по построению графика квадратичной функции с модулем.
4. Решение задачи, носящей прикладной характер, с применением свойств квадратичной функции.
5. Тест, контролирующий знания учащихся по теме.

Ход урока

Учитель: Ребята, сегодня мы с вами продолжаем вести разговор об одном из важных разделов математики – функциональной зависимости. Прежде всего вспомним определение функции.

Ученик: Функция – это такая зависимость переменной у от переменной х, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Учитель: Какую функцию называют квадратичной? Что является ее графиком?

Ученик: Квадратичной функцией называется функция. которую можнозадать формулой вида y = ax² + bx + c, где x – независимая переменная, a, b и с – некоторые числа, причем а 0. График – парабола.

Учитель: С какими способами построения графиков квадратичной функции мы познакомились?

Ученик:

1. способ выделения полного квадрата и дальнейшего построения с использованием искусственных преобразований;
2. построение графика на основании специального исследования квадратного трехчлена.

Учитель: Повторим некоторые этапы построения графиков квадратичной функции при выполнении теста – разминки.

I. Разминка (ученики устно отвечают на вопросы теста, подготовленного на карточки или слайды). В это время предложить трем ученикам самостоятельно решить на доске задачи.

Тест:

1. Какому графику соответствует функция, заданная формулой y = x² – 2? (Рисунок 1)

Рисунок 1

2. На каком из рисунков изображен график функции  (Рисунок 2)

Рисунок 2

3. Функция задана формулой . На каком из рисунков изображен ее график? (Рисунок 3)

Рисунок 3

4. Функция задана формулой . Каковы координаты вершины параболы?
   a (2; – 7).
   b (– 2; 24).
   c (2; 25).
5. Каково наибольшее значение функции, заданной формулой ?
   a 5.
   b 7.
   c –7.

Ответы: 1b; 2c; 3b; 4a; 5b.

Индивидуальные задания на доске:

1. Параболу у = 2х² сдвинули влево на 3 единицы и вниз на 5 единиц. Задайте формулой функцию, график которой получился в результате таких преобразований.

Решение: у = 2(х + 3)² – 5.

2. Найдите область значений функции у = х² – 2х.

Решение:Функция ограничена снизу, у₀ ===1, E(f) = (2; +)

3. Постройте график функции у = (3 – x)(х+ 1).

Решение: у = — х² + 2х +3. Нули функции: х₁ = – 1 ; х₂ = 3.  =

(3 – 1)(1 + 1) = 4. (1; 4) – вершина параболы, ветви вниз.

II. Фронтальная работа.

Задание классу (ученик у доски):

Постройте график функции у = — х²+ 6х – 5.

По графику проведите исследование свойств функции.

Индивидуальные задания на карточках:

1. Определите, при каких значениях с наименьшее значение функции у = 2х² + 16х + с равно 2.

Решение:

; ; .

2. Определите, при каких значениях b и c вершиной параболы у = х² + bx + c является точка А(–2; –1).

Решение: ; –2 = ; b = 4. ; ; ; .

III. Работа в группах.

Задание группам:

Построить график функции y = |x² – 4x + 3|. Какие виды преобразований необходимо выполнить, чтобы получить данный график из графика функции y = x².

Решение:

Виды преобразований:

• смещение вправо на 2 единицы;
• смещение вниз на 1 единицу;
• симметрия относительно оси Ох отрицательной части графика.

Дополнительно: Построить график функции у = 3х² + 6|х| + 6.

Индивидуальные задания на карточках (ученики выполняют на доске, объясняют решение классу после работы по группам):

1. Найти наибольшее значение функции у = — 1,5(х – 1)²на отрезке [0; 2]

Решение: х₀ = 1 [0; 2], функция ограничена сверху, у_наиб = у(1) = 0.

2. Найти наименьшее значение функции у = 2(х +3)² на отрезке [– 4; 1]

Решение: х₀ = -3  [– 4; 1], Функция ограничена снизу, у_наим = у(-3) = 0.

3. По графику у = ах² + bx + c определите знаки чисел a, b, c. (рисунок 4)

Решение:

• ветви вниз  a < 0
•  > 0, a < 0 b > 0
• при x = 0 y = c > 0

Рисунок 4

IV. Решение задачи с практическим содержанием на применение свойств квадратичной функции. (Ученик у доски)

Требуется оградить прямоугольную площадку, примыкающую к стене. Забор должен иметь длину 60 м. Какой должна быть длина и ширина площадки, чтобы площадь ее была бы наибольшей?

Решение:

Пусть х м – ширина площадки, тогда длина ее будет равна (60 – 2х) м, а площадь составит у = х(60 – 2х) м² .Выделим полный квадрат:

у = -2(х² – 30х) = -2(х² – 30х + 225 – 225)= -2(х – 15)² + 450.

При х = 15 у_наиб = 450. Ширина – 15 м, длина – 30 м.

V. Тест.

Вариант I

1. Какая линия является графиком функции у = – (х – 3)² + 2?
   А. Прямая, проходящая через начало координат.
   Б. Прямая, не проходящая через начало координат.
   В. Парабола.
   Г. Гипербола.
2. График функции у = 2(х + 2)²получается из графика функции у =2х²сдвигом на две единицы:
   А. Вправо.
   Б. Влево.
   В. Вверх.
   Г. Вниз.
3. Найдите наименьшее значение функции у = 3(х – 2)²на отрезке [–2; 5].
   А. 0.
   Б. –12.
   В. 12.
   Г. 27.
4. Какая из перечисленных функций является ограниченной сверху?
   А. у = 2х² – 5х + 3.
   Б. у = 3х² – 1.
   В. у = -3х² + х + 1.
   Г. у = .
5. Уравнение оси симметрии параболы у = –3х² + 5х + 1 имеет вид:
   А. .
   Б. .
   В. .
   Г. .

Вариант II

1. Какая линия является графиком функции у = – (х + 2)² — 4?
   А. Прямая, проходящая через начало координат.
   Б. Прямая, не проходящая через начало координат.
   В. Парабола.
   Г. Гипербола.
2. График функции у = 3х² – 2 получается из графика функции у =3х²сдвигом на две единицы:
   А. Вправо.
   Б. Влево.
   В. Вверх.
   Г. Вниз.
3. Найдите наименьшее значение функции у = 3(х + 2)²на отрезке [–2; 1].
   А. 0.
   Б. –12.
   В. 12.
   Г. 27.
4. Какая из перечисленных функций является ограниченной снизу?
   А. у = –2х² – 5х + 3.
   Б. у = 3х² – 1.
   В. у = -3х² + х + 1.
   Г. у = .
5. Уравнение оси симметрии параболы у = 2х² – 7х + 1 имеет вид:
   А. .
   Б. .
   В. .
   Г. .

Ответы:

• Вариант I: Г Б Г Б В
• Вариант II: Б А А В В

VI. Итоги урока.

VII. Домашнее задание.

Домашняя контрольная работа

Вариант I

1. Разложите на множители квадратные трехчлены:
   а) х² – 12х + 35;
   б) 7у²+ 19у — 6
2. Постройте график функции у = х² – 6х + 5. Найдите с помощью графика:
   а) нули функции;
   б) промежутки знакопостоянства;
   в) промежуток, в котором функция возрастает.
3. Найдите наименьшее значение квадратного трехчлена х² – 8х + 7
4. Сократите дробь:
5. Найдите промежутки монотонности функции y = x² – 5|x| +4.

Вариант II

1. Разложите на множители квадратные трехчлены:
   а) х² – 18х + 45;
   б) 9у²+ 25у — 6
2. Постройте график функции у = х² – 8х + 13. Найдите с помощью графика:
   а) нули функции;
   б) промежутки знакопостоянства;
   в) промежуток, в котором функция убывает.
3. Найдите наименьшее значение квадратного трехчлена –х² + 6х — 4
4. Сократите дробь:
5. Найдите промежутки монотонности функции y = x² – 6|x| +5.

21.07.2010

urok.1sept.ru

Квадратичная функция, ее свойства и график. 9-й класс

Разделы: Математика

---

Тип урока: закрепление и обобщение изученного материала.

Цели урока:

1. Повторить свойства квадратичной функции.
2. Закрепить их знание при построении графиков квадратичной функции.
3. Подготовка к государственной (итоговой) аттестации.
4. Показать связь квадратичной функции и её графика с реальным миром

Учебно-воспитательные задачи:

Образовательные:

1. Закрепить представления о квадратичной функции, умение описывать ее свойства;
2. Закрепить умения строить график квадратичной функции;
3. Обобщить и систематизировать умения выполнять преобразования графиков квадратичной функции;

Развивающие:

1. Развивать графические навыки учащихся, навыки чтения графиков;
2. Развивать мышление, сообразительность.
3. Развить представления учащихся об особенностях заданий по данной теме, предлагаемых на экзамене по математике в новой форме в 9-м классе.

Воспитательные:

1. Воспитывать такие качества личности, как познавательная активность, самостоятельность.
2. Воспитывать умение слушать, анализировать, соблюдать единые требования к оформлению решений.
3. Воспитывать интерес к предмету.

Оборудование: мультимедийный проектор, экран, раздаточный материал (текст теста)

Структура урока:

I. Мотивационная беседа с последующей постановкой цели урока.
II. Актуализация знаний.
III. Выполнение упражнений.
IV. Защита проекта учащегося.
V. Домашнее задание.
VI. Подведение итогов урока.

Ход урока

I. Мотивационная беседа с последующей постановкой цели.

Есть хорошая поговорка: “Повторение – мать учения”. Математика – не исключение, и чтобы её хорошо усваивать, необходимо повторять и приводить в систему уже изученное.

А что мы изучали на предыдущих уроках? (изучали квадратичную функцию, её свойства, строили график квадратичной функции).

Как вы считаете, мы выполнили поставленную задачу? Если кто-то ответит “Да”, то вы молодцы. Это можно будет сегодня продемонстрировать. Если кто-то подумал “Не совсем”, то у вас есть возможность восполнить пробелы. Потому что сегодня на уроке мы должны: (слайд 2)

1. Повторить теоретический материал по теме “Квадратичная функция”;
2. Выполнить задания на построение и преобразование графиков, а также по графику описать свойства данной функции.

II. Актуализация знаний.

Устная работа.

1. Что называется квадратичной функцией? Приведите примеры.
2. Что представляет собой график квадратичной функции?
3. На экране график функции. (Cлайд 3)

Перечислить общие свойства функции. (Область определения и область значений функции, нули функции, промежутки знакопостоянства функции, промежутки возрастания и убывания функции, наибольшее или наименьшее значения функции).

III. Выполнение упражнений.

1. Найти координаты вершины параболы (слайд 4)

У = х² – 4х – 5

У = -5х² + 3

2. Построить график функции у = 3х² – 12х + 9 и описать её свойства. (слайд 5)

3. Используя шаблон параболы у = х² построить графики следующих функций: (слайд 6)

1. у = -(х – 1)² – 1
2. у = (х + 1)² – 1
3. у = -2х² + 8
4. у = -(х – 3)²
5. у = х² + 1

4. Какой формулой задаётся парабола, изображённая на рисунке. (а = 1) (слайд 7)

5. Мною неоднократно упоминалось о том, что тема “Квадратичная функция” широко представлена на экзамене по математике в 9-ом классе. (Слайд 9, 10, 11)

IV. Защита проекта.

Сейчас мы посмотрим проект, подготовленный ученицей нашего класса на тему “Связь с реальным миром”. (Презентация 2)

V. Самостоятельная работа в форме теста с заданиями с выбором одного верного ответа из трёх предложенных вариантов.

Проверка осуществляется по предложенной таблице с ответами, учащиеся самостоятельно оценивают свою тестовую работу. (Слайд 12)

(Текст теста – см. Приложение.)

V. Домашнее задание.

Сборник для подготовки к экзаменам. Автор Л. В. Кузнецова.

№ 923; № 192(1).

VI. Итог урока.

Дать оценку успешности достижения цели; самооценка учащимися реальных результатов изучения темы.

Задаются вопросы:

Какие вопросы темы мы с вами сегодня повторили?

Что нового вы узнали на этом уроке?

Что на уроке вам понравилось?

Объявляются оценки.

Литература.

1. Алгебра: учебник для 9 классов общеобразовательных учреждений. Макарычев Ю.Н., Н.Г. Миндюк и др. Под редакцией  С.А. Теляковского. М.: Просвещение, 2009
2. Алгебра 9 класс. Поурочные планы по учебнику “Алгебра 9 класс” / Ю.Н. Макарычев/ Под редакцией С.А. Теляковского . М.: Просвещение, 2002. /Сост. Д.Ф. Айвазян.– Волгоград – АСТ, 2008
3. ГИА-9. Математика. Учебно-тренировочные тесты под ред.Ф. Ф. Лысенко.
4. Сайты Интернета.

Приложение

Презентация 1

Презентация 2

Презентация 3

25.03.2012

Поделиться страницей:

urok.1sept.ru

Урок по теме «Квадратичная функция и ее график»

Разделы: Математика

---

Цели урока:

Образовательные:

• повторить понятие квадратичной функции;
• повторить алгоритм построения графика квадратичной функции;
• повторить свойства данной функции;
• закрепить умение определять свойства квадратичной функции по графику;
• закрепить навыки построения квадратичной функции;
• систематизировать знания по теме;

Воспитательные:

• учить работать самостоятельно;
• воспитание внимания;
• воспитание на уроке воли и упорства для достижения цели;
• воспитание, уважительного отношения друг к другу;

Развивающие:

• Развить навыки самоконтроля;
• развивать математическую речь;
• развить устойчивое внимание;
• развить умение переключать внимание.

Тип урока: урок обобщения и систематизации знаний.

Оборудование урока:

• Компьютер;
• мультимедийный проектор;
• карточки с заданиями.

План урока:

1. Организационный момент.
2. Сообщение темы и цели урока.
3. Повторить основные свойства квадратичной функции (устная работа).
4. Применение знаний, умений и навыков учащихся при построении графиков квадратичной функции.
5. Самостоятельная работа (Тест).
6. Рефлексия (“Что знаю?”, “Чего не знаю?”, “Что получилось?”, “Что нет?”).
7. Подведение итогов урока.

Ход урока

I. Организационный момент.

II. Сообщение темы и цели урока.

III. Устная работа.

для того чтобы достичь целей урока вспомним теоретический материал по теме «Квадратичная функция».

• Функцию какого вида называют квадратичной? (слайд 2)
• Что является графиком квадратичной функции? (слайд 3)
• Как зависит направление ветвей параболы от коэффициента а? (слайд 4)
• Как определить координаты вершины параболы? (слайд 5)
• Каков алгоритм построения квадратичной функции? (слайд 6)
• Для каждой из функций укажите координаты вершины параболы, направление ее ветвей, уравнение оси симметрии.

1. у = х² – 1;
2. у =  + 5;
3. у = ;
4. у = ;

IV. Применение знаний, умений и навыков учащихся при построении графиков квадратичной функции.

V. Тест.

Вариант 1.

• Для неравенства х² > 4  найдите верную запись:
  а) х > 2;
  б) х > 2 или x > –2;
  в) –2 < x < 2;
  г) х < –2 или x > 2.

• На рисунке 1 показан график некоторой функции у = ах² + bx + c Укажите верную комбинацию:
  а) а > 0; D > 0;
  б) а < 0; D > 0;
  в) а > 0; D < 0;
  г) а < 0; D < 0.
  
  Рис. 1.

• На рисунке 2 показан график некоторой функции у = ах² + bx + c Найдите формулу, задающую эту функцию
  а) у = – х² + 4х +2;
  б) у = х² – 4х +2;
  в) у = – х² – 4х +2;
  г) у = х² – 4х – 2.
  
  Рис. 2.

Вариант 2.

• Для неравенства х² < 9 найдите верную запись:
  а) х < 3;
  б) х < 3 или x < –3;
  в) –3 < x < 3;
  г) х < –3 или x > 3.
  

• На рисунке 3 показан график некоторой функции у = ах² + bx + c Укажите верную комбинацию:
  а) а > 0; D > 0;
  б) а < 0; D > 0;
  в) а > 0; D < 0;
  г) а < 0; D < 0.
  
  Рис. 3.

• На рисунке 4 показан график некоторой функции у = ах² + bx + c Найдите формулу, задающую эту функцию
  а) у = – х² + 6х +9;
  б) у = х² – 6х +9;
  в) у = – х² – 6х – 9;
  г) у = х² – 6х – 9.
  
  Рис 4.

Взаимопроверка результатов теста.

Дети меняются тетрадями и проверяют работу.

VI. Рефлексия.

Ответьте на вопросы:

1. Какие знания понадобились тебе на уроке?
2. Что понравилось на уроке больше всего?
3. Где во время урока у тебя всё получалось хорошо?
4. Какими словами можешь выразить своё настроение как результат работы на уроке?

VII. Подведение итогов урока.

Используемый материал:

1. Алгебра 9 класс. Авторы: Ю.Н. Макарычев и др.
2. Алгебра 8 класс. Авторы: Ю.Н. Макарычев и др.
3. Алгебра 7 класс. Авторы: Ю.Н. Макарычев и др.
4. Тесты по алгебре. Автор: П.И. Алтынов.
5. gimn7matem.narod.ru
6. fgraphiks.narod.ru
7. findmapplaces.com

Презентация.

23.12.2011

Поделиться страницей:

urok.1sept.ru

Методический комплект «Квадратичная функция, ее свойства и график»

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (1,1 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

…Математические сведения могут применяться умело и с пользой только в том случае,
если они усвоены творчески, так, что учащийся видит сам, как можно было бы прийти к ним самостоятельно.

  А.Н. Колмогоров.

Методический комплект “Квадратичная функция, ее свойства и график” может быть использован как при обобщении знаний по данной теме, так и при объяснении нового материала (выборочно), а также для обобщающего повторения при подготовке к ГИА.

Описание составляющих методического комплекта:

1. Мультимедийная составляющая работы представляет собой презентацию, основная задача которой носит иллюстративный характер. Презентация состоит из 11 слайдов, которые описаны следующим образом:

№ слайда	Комментарии
Слайд 1	Титульный
Слайд 2	Визуальное распределение информации (определение, построение и свойства квадратичной функции). По гиперссылкам можно перейти к слайду 3(определение квадратичной функции), к слайду 5 (алгоритм построения графика квадратичной функции) и к слайду 8 (свойства квадратичной функции).
Слайд 3	Определение квадратичной функции.
Слайд 4	Задание на распознавание формулы квадратичной функции, по стрелке можно вернуться к схеме на слайде 2.
Слайды 5,6	Алгоритм построения графика квадратичной функции
Слайд 7	Рассмотрен конкретный пример построения графика квадратичной функции, по стрелке можно вернуться к схеме на слайде 2.
Слайд 8	Свойства квадратичной функции представлены в виде таблицы (для случая а>0), для случая а<0, учащимся предлагается заполнить таблицу самостоятельно.
Слайд 9	Рассмотрены свойства квадратичной функции на конкретном примере, по стрелке можно вернуться к схеме на слайде 2.
Слайд 10	Практическое задание для фронтального опроса. По графику квадратичной функции назвать ее свойства.
Слайд 11	Наглядный пример квадратичной функции в жизни.

• Приложение 1. Включает в себя индивидуальные тестовые задания по распознаванию графика квадратичной функции, полученной путем сдвига функции у = х², а также заготовки таблиц для заполнения свойств квадратичной функции) раздаются ученикам для экономии времени.
• Приложение 2. Тестовые задания состоят из двух частей, первая часть – это демонстрационный вариант с решениями и с заданиями для самопроверки ученика. Учитель может использовать это задание в подготовке к контрольной работе по данной теме или в качестве домашней работы при подготовке к ГИА на уроках итогового повторения.

Вторая часть – это 6 вариантов обобщающих тестов. Каждый тест состоит из 16 заданий. Задания расположены по возрастанию уровня сложности.
Первые 12 заданий направлены на проверку уровня обязательной подготовки учащихся, остальные 4 задания расширяют знания свойств квадратичной функции
и направлены на подготовку к ГИА в 9 классе для повышенного уровня (соответствуют содержанию 2 части экзаменационной работы).

• Буклет представляет собой справочное пособие по теме “Квадратичная функция, ее свойства и график” и может быть распечатан каждому ученику в качестве памятки.

Урок алгебры в 9 классе
“Квадратичная функция, ее свойства и график”.
(2 урока)

Тип урока: систематизации и обобщения знаний.

Цели:

1. Обеспечить повторение, обобщение и систематизацию материала темы, повторить приемы исследования квадратичной функции, алгоритм построения графика квадратичной функции, создать условия контроля (самоконтроля) знаний и умений;
2. Способствовать развитию логического мышления, умению выделять главное;
3. Содействовать воспитанию интереса к математике, умению общаться, умению оценивать и рецензировать ответы учеников.

Оснащение: мультимедийный проектор, демонстрационный материал (презентация) раздаточный материал (приложение 1, приложение 2), буклеты.

Ход урока

№	Этапы урока	Деятельность учителя	Деятельность ученика	Средства	Время
1.	Организационный	Сообщение темы и целей урока	Слушают учителя, записывают тему урока в тетрадь	Слайд 1	3 мин.
2.	Актуализация знаний	1. Объявляет работу в парах (рассказать соседу по парте): а) определение квадратичной функции; б) алгоритм построения графика квадратичной функции. 2. Вызывает одного из учеников озвучить ответы на заданные вопросы, одновременно высвечивая ответы на экране.	1.Работа в парах. 2.Слушают учителя и ответ у доски	Слайд 2 Слайды 3,4,5,6	7 мин.
3.	Применение знаний, умений и навыков при отработке алгоритма построения графика квадратичной функции	1а) Учитель дает задание самостоятельно в тетрадях построить график функции у = х2 – 4х +3. 1б). Демонстрирует построение графика функций с помощью презентации. 1в). Вызывает к доске ученика и на ранее заготовленном шаблоне графика функции у = х2 ученик рассказывает и показывает как построить графики функций: у = х2; у = -х2; у =( х-6)2; у = х2+5; у = (х-6)2+2	1. Работают в тетрадях. 2. Проверяют самостоятельно, следя за комментариями учителя. 3. Слушают, задают вопросы (что не понятно)	Слайд 7	30 мин. (15 мин) (5 мин) (10 мин)
4.	Тест	Раздает тест (каждому индивидуальный вариант)	Выполняют тест, сдают учителю.	Тест (приложение 1)	7 мин.
5.	Применение знаний, умений и навыков при отработке свойств квадратичной функции	Фронтальная работа: перечислить свойства квадратичной функции

xn--i1abbnckbmcl9fb.xn--p1ai

No related posts.