2.3. Квантовые числа
Волновая функция, являющаяся решением уравнения Шредингера, называется орбиталью. Для решения этого уравнения вводятся три квантовых числа (n, l и ml )
Главное квантовое число n. оно определяет энергию электрона и размеры электронных облаков. Энергия электрона главным образом зависит от расстояния электрона от ядра: чем ближе к ядру находится электрон, тем меньше его энергия. Поэтому можно сказать, что главное квантовое число n определя-
ет расположение электрона на том или ином энергетическом уровне. Главное квантовое число имеет значения ряда целых чисел от 1 до ∞. При значении главного квантового числа, равного 1 (n = 1), электрон находится на первом энергетическом уровне, расположенном на минимально возможном расстоянии от ядра. Общая энергия такого электрона наименьшая.
Электрон, находящийся на наиболее удаленном от ядра энергетическом уровне, обладает максимальной энергий. Поэтому при переходе электрона с более удаленного энергетического уровня на более близкий выделяется энергия. Энергетические уровни обозначают прописными буквами согласно схеме:
Значение n …. 1 2 3 4 5
Обозначение K L M N Q
Орбитальное квантовое число l. Согласно квантово-механическим расчетам электронные облака отличаются не только размерами, но и формой. Форму электронного облака характеризует орбитальное или побочное квантовое число. Различная форма электронных облаков обусловливает изменение энергии электрона в пределах одного энергетического уровня, т.е. ее расщепления на энергетические подуровни. Каждой форме электронного облака соответствует определенное значение механического момента движения электрона
, определяемого орбитальным квантовым числом: 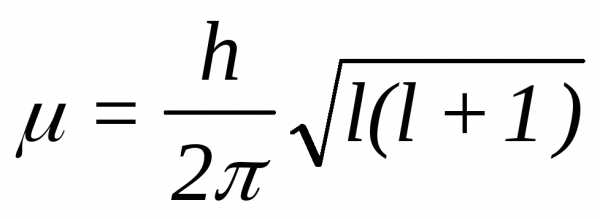

Определенной форме электронного облака соответствует вполне определенное значение орбитального момента количества движения электрона . Так как может принимать только дискретные значения, задаваемые квантовым числом l, то и формы электронных облаков не могут быть произвольными: каждому возможному значению l соответствует вполне определенная форма электронного облака.
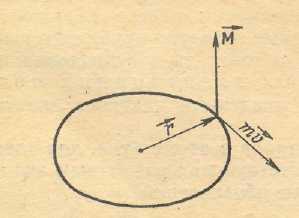
Рис.
5. Графическая интерпретация момента
движения электрона, где μ — орбитальный момент количества
μ — орбитальный момент количества
Орбитальное квантовое число может иметь значения от 0 до n — 1, всего n – значений.
Энергетические подуровни обозначены буквами:
Значение l 0 1 2 3 4
Обозначение s p d f g
Магнитное квантовое число ml. Из решения уравнения Шредингера следует, что электронные облака ориентированы определенным образом в пространстве. Пространственная ориентация электронных облаков характеризуется магнитным квантовым числом.
Магнитное квантовое число может принимать любые целочисленные значения как положительные, так и отрицательные в пределах от –l до +l, а всего это число может принимать (2l+1) значений для данного l, включая нулевое. Например, если l = 1, то возможны три значения
m (–1,0,+1) орбитальный момент , есть вектор, величина которого квантована и определяется значением l. Из уравнения Шредингера следует, что не только величина µ, но и направление этого вектора, характеризующее пространственную ориентацию электронного облака, квантовано. Каждому направлению вектора заданнойдлины соответствует определенное значение его проекции на ось z, характеризующее некоторое направление внешнего магнитного поля. Значение этой проекции характеризует ml.
Спин электрона. Изучение атомных спектров показало, что три квантовых числа n, l и ml не являются полной характеристикой поведения электронов в атомах. С развитием спектральных методов исследований и повышением разрешающей способности спектральных приборов была обнаружена тонкая структура спектров. Оказалось, что линии спектров расщепляются. Для объяснения этого явления было введено четвертое квантовое число, связанное с поведением самого электрона. Это квантовое число было названо
Наличие спина у электрона было доказано экспериментально в 1921 г., В. Герлахом и О. Штерном, которые сумели разделить пучок атомов водорода на две части, соответствующие ориентации электронного спина. Схема их эксперимента показана на рис. 6. Когда атомы водорода пролетают через область сильного магнитного поля, электрон каждого атома взаимодействует с магнитным полем, и это заставляет атом отклоняться от исходной прямолинейной траектории, Направление, в котором отклоняется атом, зависит от ориентации спина его электрона. Спин у электрона не зависит от внешних условий и не может быть уничтожен или изменен.
Таким образом, было окончательно установлено, что полностью состояние электрона в атоме характеризуется четырьмя квантовыми числами n, l, ml. и ms,
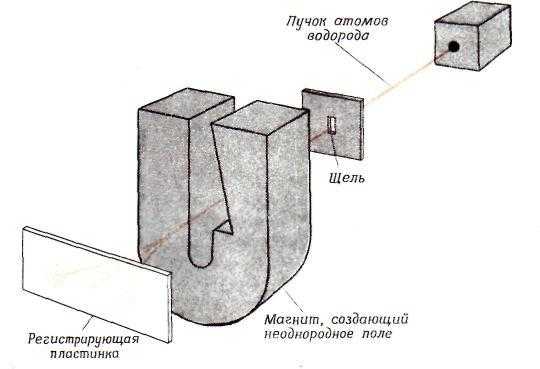
Рис. 6. Схема эксперимента Штерна — Герлаха
studfiles.net
Квантовые числа электрона в атоме
(6.87а)
n – главное квантовое число определяет энергию электрона
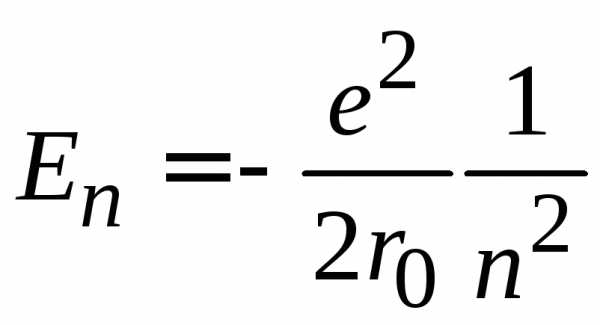 ,
,
где возможные значения
следуют из (6.87а) и .
l – орбитальное квантовое число, определяет модуль момента импульса электрона
.
При заданном значении n возможные значения
.
Максимальное
значение 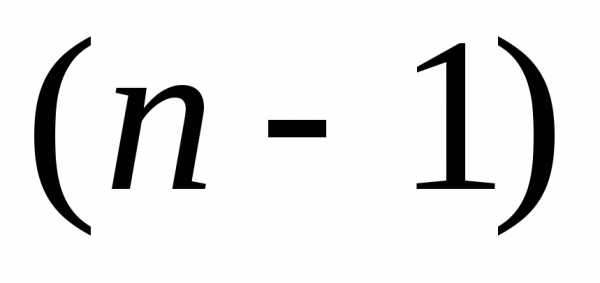 следует из (6.87а)при
следует из (6.87а)при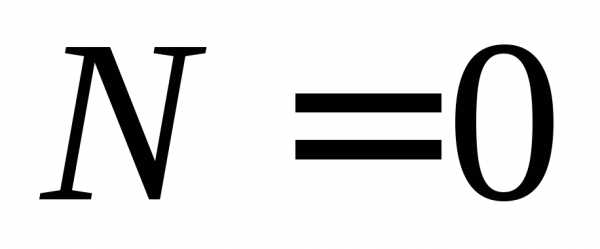 .
.
–число проекций орбитального момента на ось
z при заданном значении l. Нечетность числа проекцийследует из симметрии проекций при замене знака и из наличия нулевой проекции.
Решения для низших значений квантовых чисел
Наиболее устойчивым является состояние электрона с наименьшей энергией, называемое основным состоянием. Состояния с большей энергией называются возбужденными. За счет электромагнитных флуктуаций электрон самопроизвольно переходит в состояние с меньшей энергией, испуская избыток энергии в виде кванта – фотона.
Основное состояние
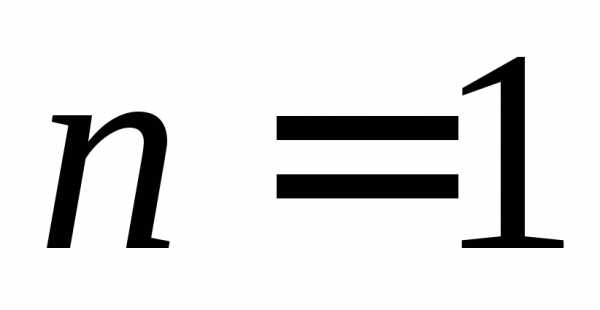 ,
, 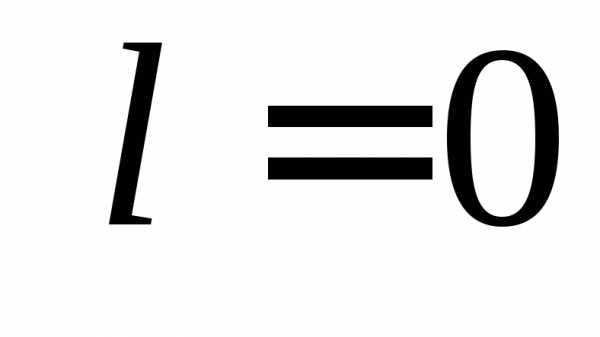 ,
,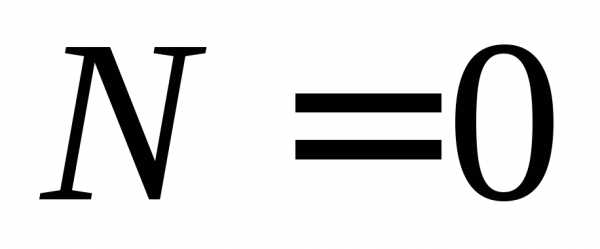 ,
,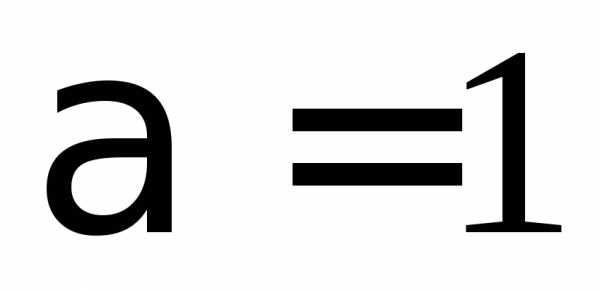 ,
,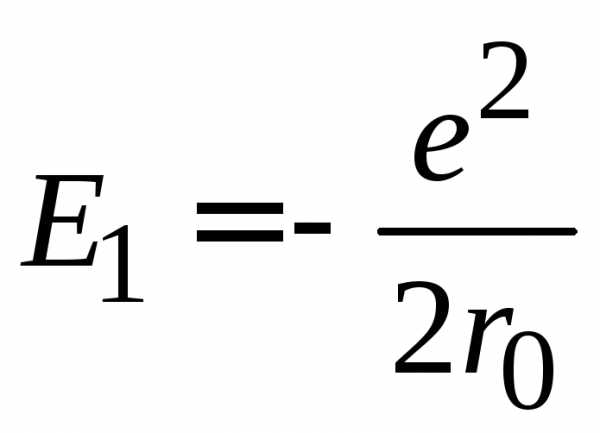 .
.
с учетом
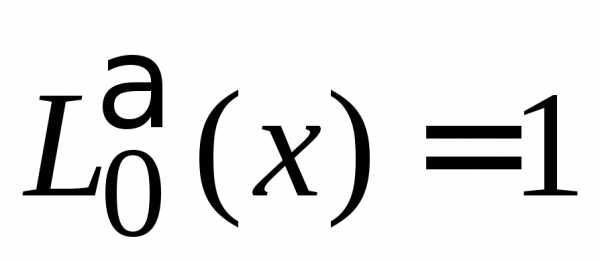 ,
, 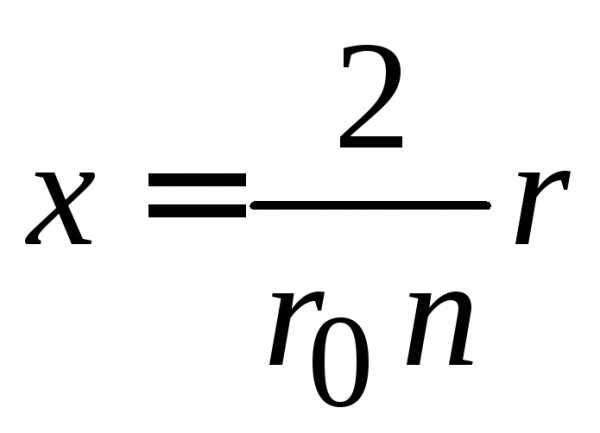 ,
,
получаем функцию основного состояния
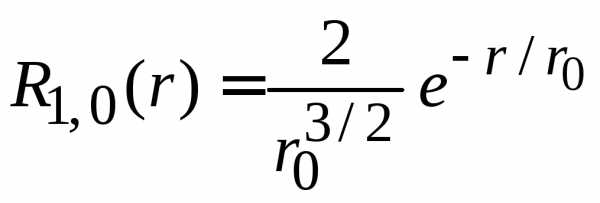 .
.
Первое возбужденное состояние
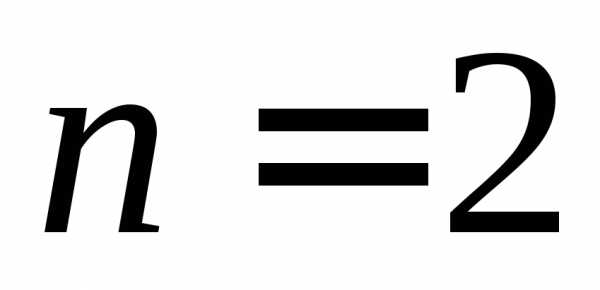 ,
, 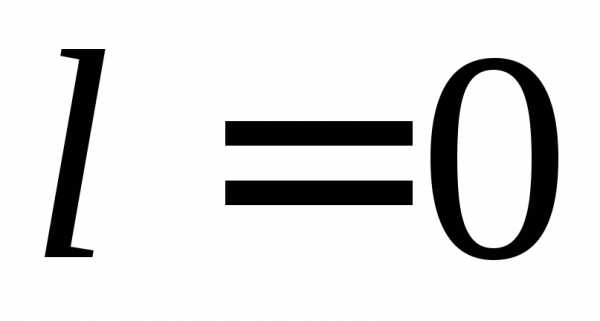 ,
,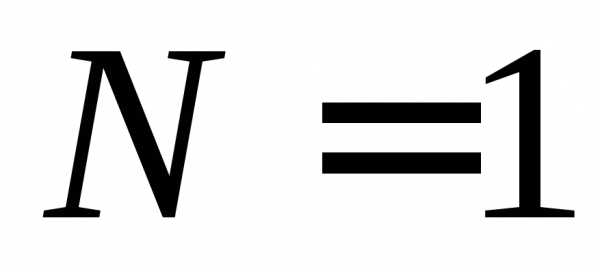 ,
,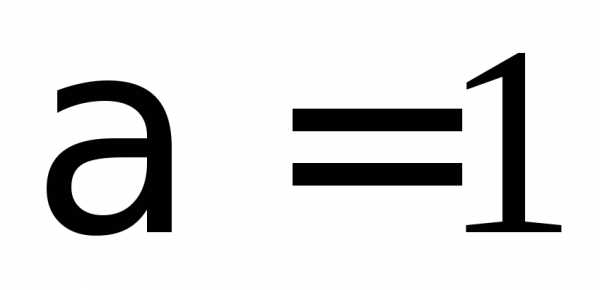 ,
,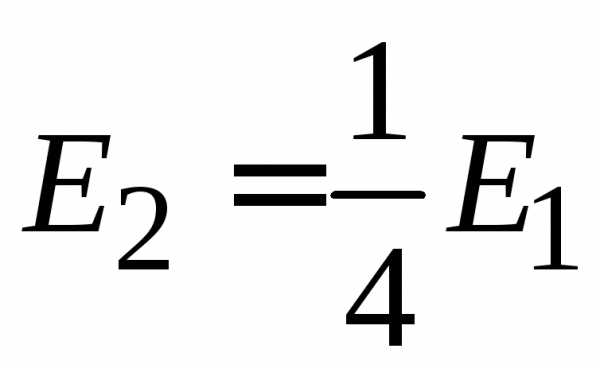 .
.
С учетом
, 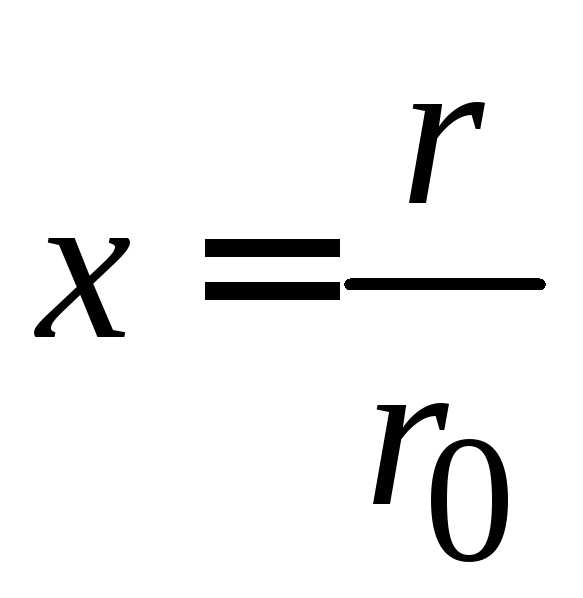 ,
,
находим
,Первое возбужденное состояние вырождено, т. е. энергия одинакова для разных l и равных n и, а функции состояний отличаются. Например, для
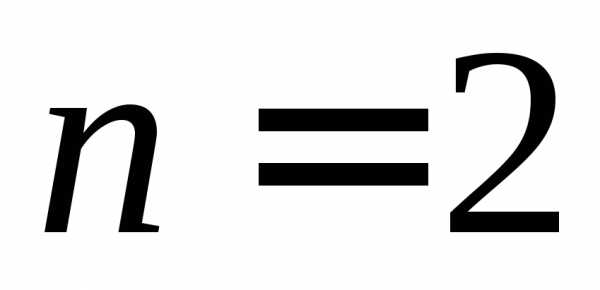 ,
, 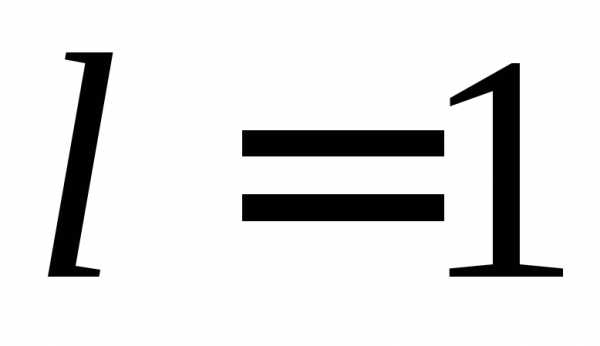 ,
,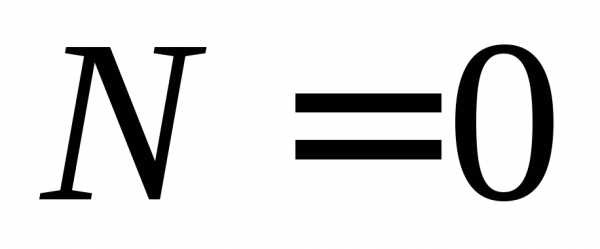 ,
,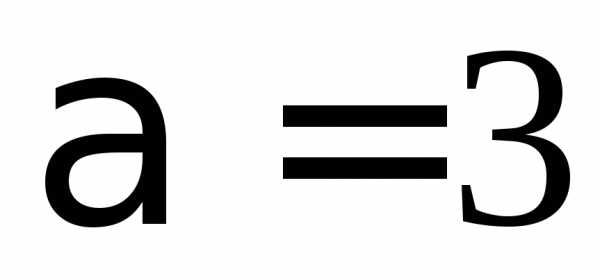 ,
,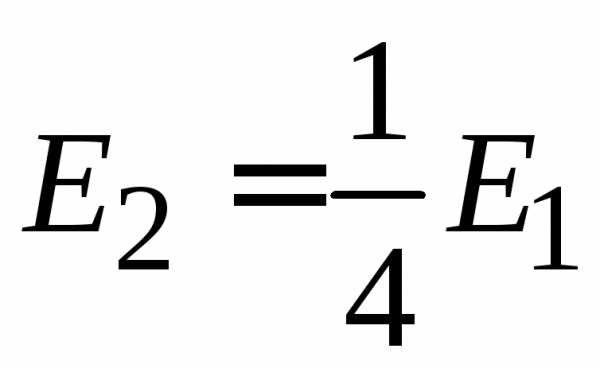
с учетом
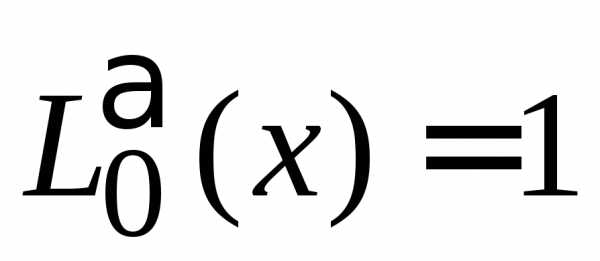 ,
, 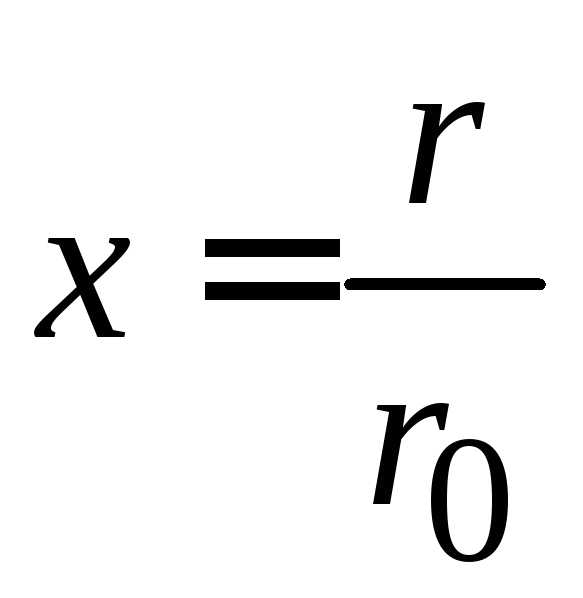 ,
,
находим
.
На рисунке показаны графики функций
.
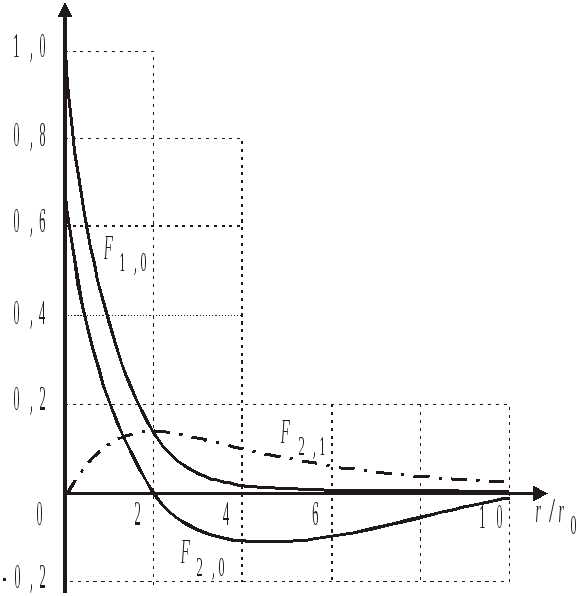
Нормировка вероятности
Вероятность обнаружения электрона в шаровом слое радиусом r единичной толщины равна
.
Вероятность найти электрон во всем пространстве равна единице, это дает условие нормировки радиальной функции с учетом радиального объема в сферических координатах
, 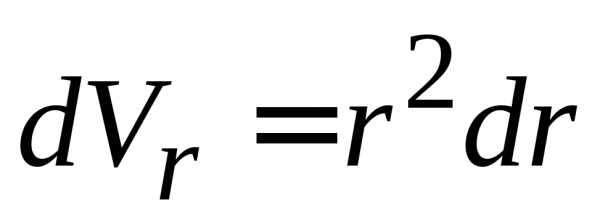 ,
,
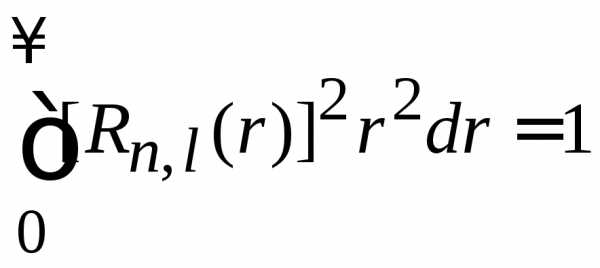 .
.
Для
безразмерной 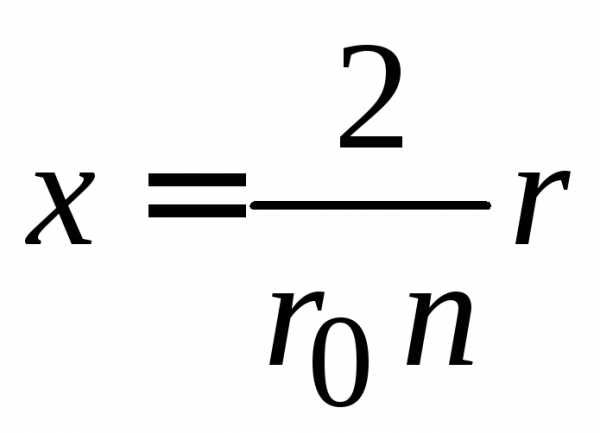 получаем
получаем
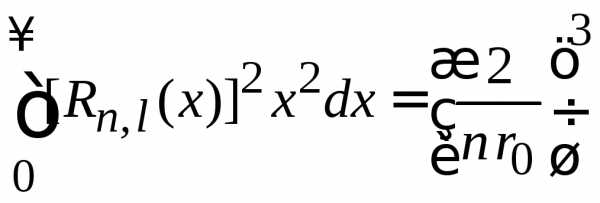 .
(6.88)
.
(6.88)
Докажем, что решение (6.87)
удовлетворяет (6.88). С учетом левая сторона (6.88) равна
. (6.88а)
Вычисляем интеграл, используя (6.76):
при
, .
Находим
.
Подстановка результата в (6.88а) дает (6.88).
Рекуррентные соотношения
1. Рекуррентное соотношение (6.58) для полиномов Лагерра с одинаковыми порядками α
умножаем на
.
С учетом (6.87)
,
, ,
получаем соотношение между функциями с одинаковым орбитальным числом l
– . (6.89)
2. Используя (6.59)
,
находим
,
.
Результаты подставляем в исходное равенство
.
Заменяем
, ,
получаем
.
Умножаем слагаемые на
,
и сравниваем с (6.87)
,
приходим к соотношению, где индекс l у функции, стоящей слева, на единицу меньше, чем у функций, стоящих справа:
–. (6.90)
3. Рекуррентное соотношение (6.57)
умножаем на x и используем (6.61)
,
находим
.
Выражаем 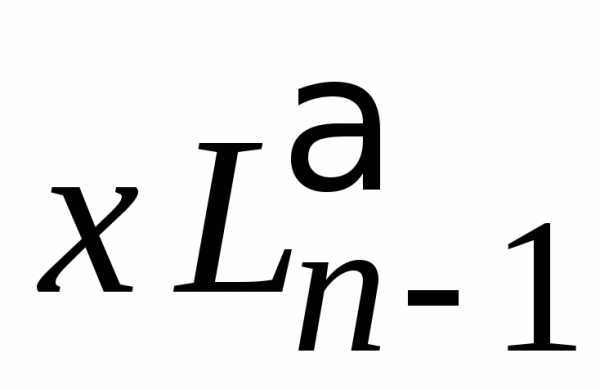 с помощью (6.58)
с помощью (6.58)
,
заменяем и получаем
.
Полагаем ,, умножаем слагаемые на
,
находим соотношение, где индекс l у функции, стоящей слева, на единицу больше, чем у функций, стоящих справа:
. (6.91)
4. Дифференцируем (6.87)
,
используем (6.54)
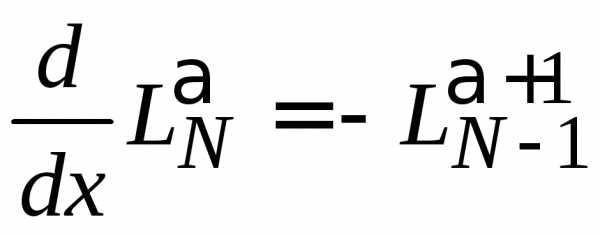 ,
,
получаем
.
Используем рекуррентные соотношения (6.58)
и (6.61)
,
которые убирают множитель x из круглой скобки и выравнивают верхний индекс:
.
В результате получаем
– . (6.92)
Вычисление матричных элементов
Матричный
элемент оператора  между состояниями
между состояниями 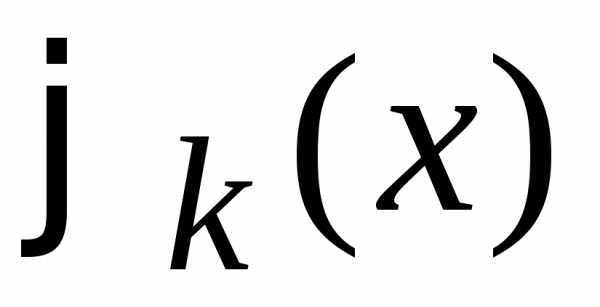 и
и 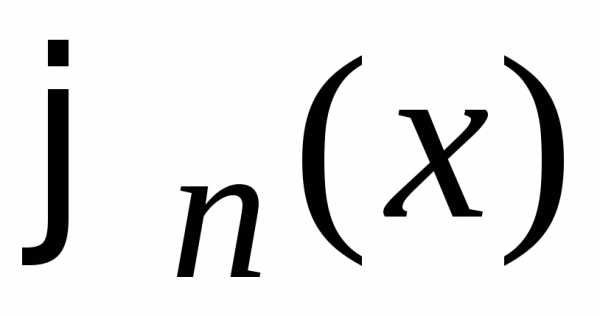 определяется в виде
определяется в виде
, (1)
Для
электрона в атоме водорода функции 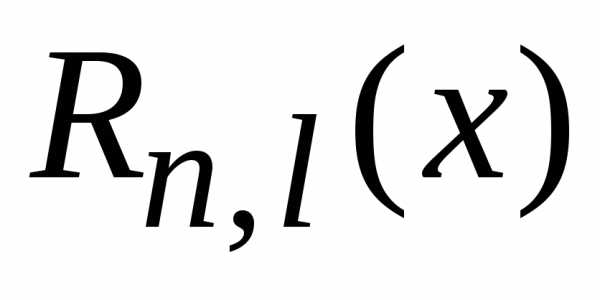 вещественные.Диагональный
матричный элемент является средним
значением величины F,
описываемой оператором
вещественные.Диагональный
матричный элемент является средним
значением величины F,
описываемой оператором  :
:
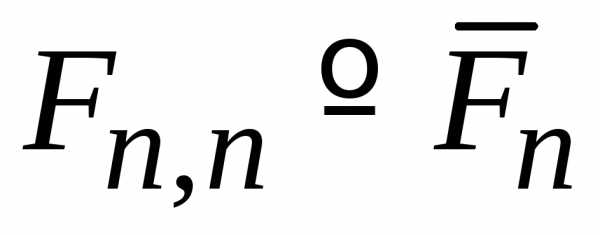 .
.
ПРИМЕРЫ
1.
Найдем среднее расстояние электрона
от ядра  в состоянии
в состоянии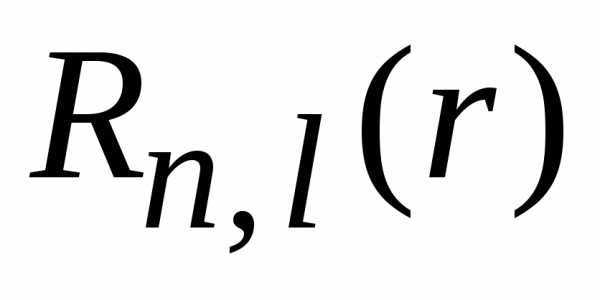 с квантовыми числами
с квантовыми числами 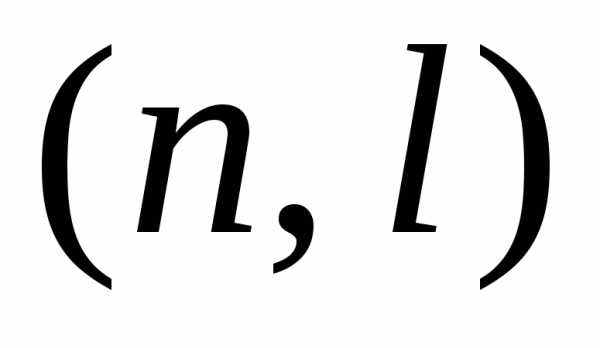 .
.
С
учетом оператора радиуса 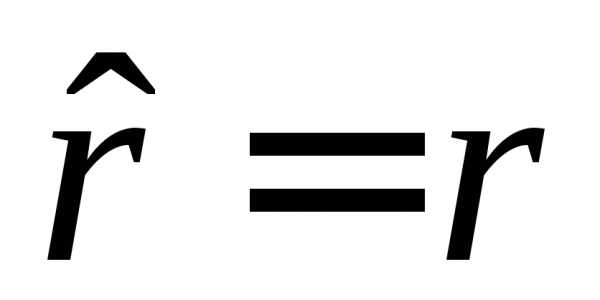 и радиального
объема
и радиального
объема 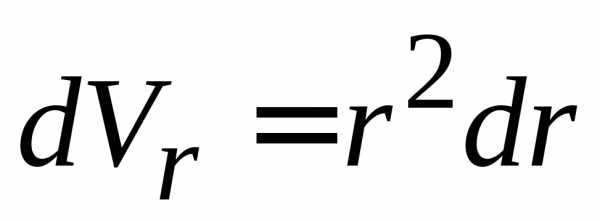 ,
находим
,
находим
,
где сделана замена
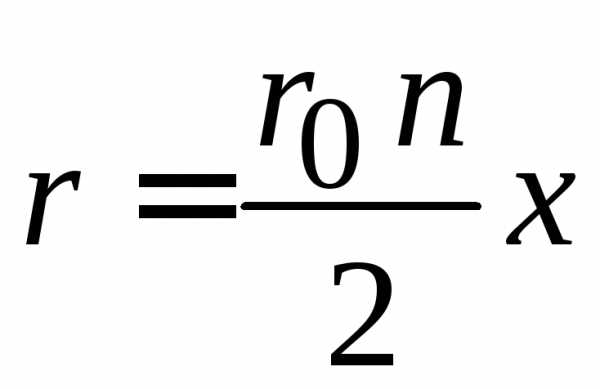 .
.
Вычисляем интеграл с помощью рекуррентного соотношения (6.89), устраняющего x под интегралом:
– ,
и условия ортонормированности (6.86)
.
При
возведении в квадрат рекуррентного
соотношения и интегрировании, условие
ортогональности зануляет перекрестные
произведения благодаря символу Кронекера 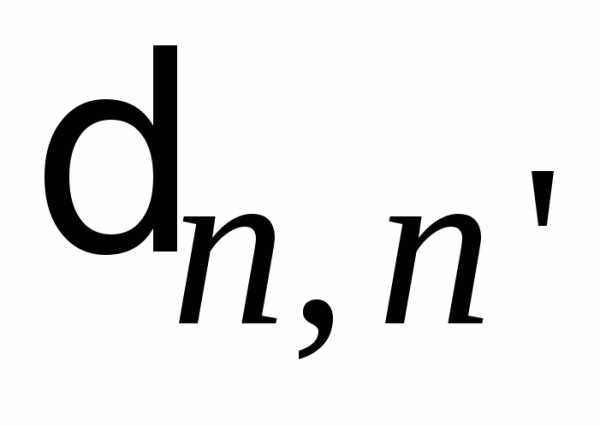 .
Остается сумма квадратов слагаемых
.
Остается сумма квадратов слагаемых
.
С учетом (6.86)
получаем
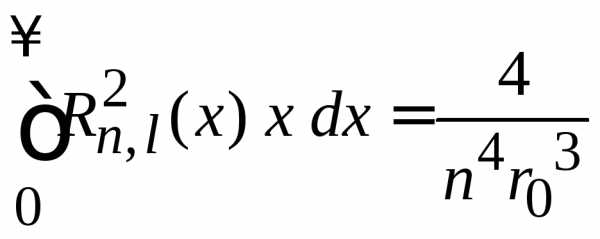 ,
,
,
.
Для
находим
.
Приведение
подобных дает среднее
расстояние электрона от ядра в состоянии 
. (П.5.8)
При
увеличении энергии электрона растет
главного числа n и увеличивается  .
При увеличении орбитального момента
возрастает орбитальное числоl,
и эксцентриситет эллиптической орбиты,
в результате среднее расстояние до ядра
уменьшается.
.
При увеличении орбитального момента
возрастает орбитальное числоl,
и эксцентриситет эллиптической орбиты,
в результате среднее расстояние до ядра
уменьшается.
2. Рекуррентное соотношение Крамерса связывает средние расстояния электрона от ядра в разных степенях
, (П.5.10)
где
; .
Доказательство
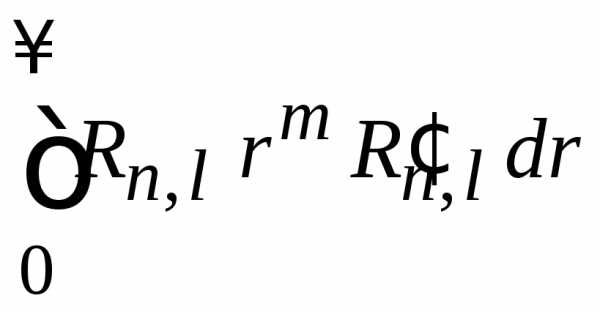
по частям, где
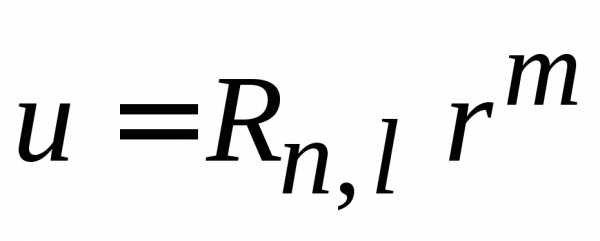 ,
.
,
.
Свободное слагаемое обращается в нуль с учетом (6.87)
.
Получаем 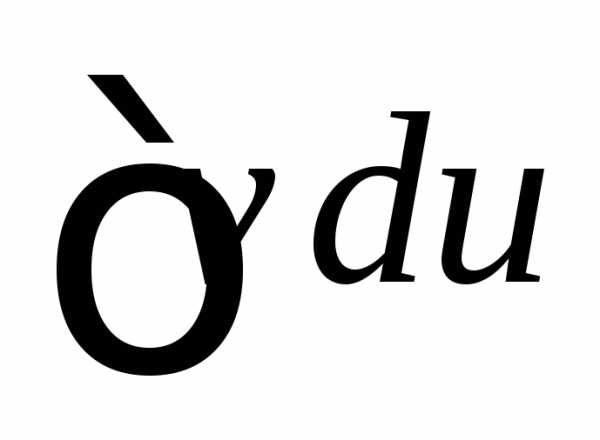 в виде
в виде
,
тогда
.
В результате
.
,
,
где
.
.
Умножаем
уравнение на 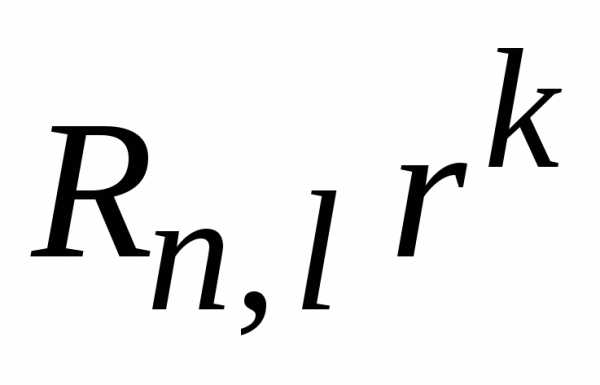 ,
интегрируем, используем полученные
ранее соотношения
,
интегрируем, используем полученные
ранее соотношения
,
,
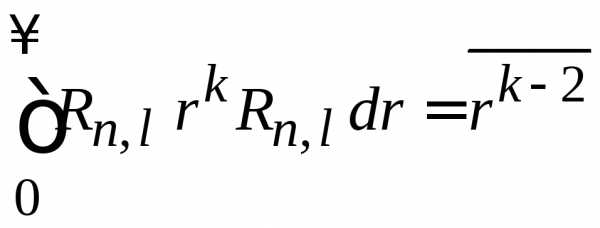 ,
,
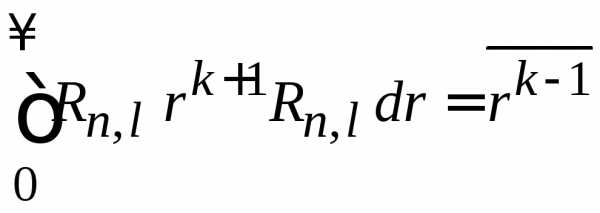 ,
,
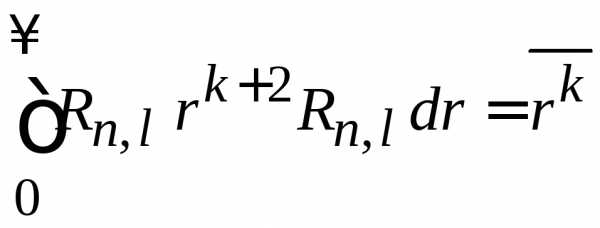 ,
,
и находим
.
Умножаем
уравнение Шредингера
(П.5.11) на 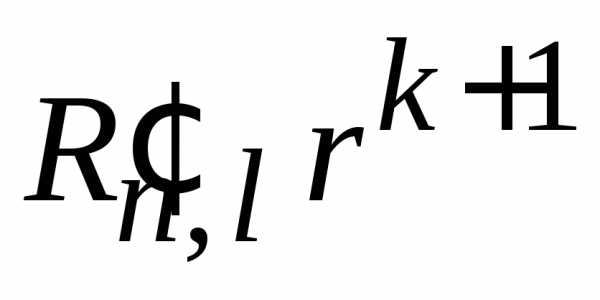 ,
интегрируем и аналогично получаем
,
интегрируем и аналогично получаем
.
studfiles.net
Квантовые числа электронов — HimHelp.ru
Главное квантовое число n определяет общую энергию электрона на данной орбитали. Оно может принимать любые целые значения, начиная с единицы (n = 1,2,3, …). Под главным квантовым числом, равным ∞, подразумевают, что электрону сообщена энергия, достаточная для его полного отделения от ядра (ионизация атома).
Кроме того, оказывается, что в пределах определенных уровней энергии электроны могут отличаться своими энергетическими подуровнями. Существование различий в энергетическом состоянии электронов, принадлежащих к различным подуровням данного энергетического уровня, отражается побочным (иногда его называют орбитальным) квантовым числом l. Это квантовое число может принимать целочисленные значения от 0 до n — 1 (l = 0,1, …, n — 1). Обычно численные значения l принято обозначать следующими буквенными символами:
Значение l 0 1 2 3 4
Буквенное обозначение s p d f g
В этом случае говорят о s-, р-, d-, f-, g-состояниях электронов, или о s-, р-, d-, f-, g-орбиталях.
Орбиталь — совокупность положений электрона в атоме, т.е. область пространства, в которой наиболее вероятно нахождение электрона.
Побочное (орбитальное) квантовое число l характеризует различное энергетическое состояние электронов на данном уровне, определяет форму электронного облака, а также орбитальный момент р — момент импульса электрона при его вращении вокруг ядра (отсюда и второе название этого квантового числа — орбитальное)
Таким образом, электрон, обладая свойствами частицы и волны, с наибольшей вероятностью движется вокруг ядра, образуя электронное облако, форма которого в s-, р-, d-, f-, g-состояниях различна.
Подчеркнем, что форма электронного облака зависит от значения побочного квантового числа l. Так, если l = 0 (s-орбиталь), то электронное облако имеет шаровидную форму (сферическую симметрию) и не обладает направленностью в пространстве
При l = 1 (р-орбиталь) электронное облако имеет форму гантели, т.е. форму тела вращения, полученного из «восьмерки» . Формы электронных облаков d-, f— и g-электронов намного сложнее.
Движение электрона по замкнутой орбите вызывает появление магнитного поля. Состояние электрона, обусловленное орбитальным магнитным моментом электрона (в результате его движения по орбите), характеризуется третьим квантовым числом — магнитным m1. Это квантовое число характеризует ориентацию орбитали в пространстве, выражая проекцию орбитального момента импульса на направление магнитного поля.
Соответственно ориентации орбитали относительно направления вектора напряженности внешнего магнитного поля, магнитное квантовое число m1 может принимать значения любых целых чисел, как положительных, так и отрицательных, от –l до +l, включая 0, т.е. всего (2l + 1) значений.
Таким образом, m1 характеризует величину проекции вектора орбитального момента количества движения на выделенное направление. Например, р-орбиталь («гантель») в магнитном поле может ориентироваться в пространстве в трех различных положениях, так как в случае l = 1 магнитное квантовое число может иметь три значения: -1, 0, +1. Поэтому электронные облака вытянуты по осям х, y и z, причем ось каждого из них перпендикулярна двум другим .
Для объяснения всех свойств атома в 1925 г. была выдвинута гипотеза о наличии у электрона так называемого спина (сначала — для наглядности — считалось, что это явление аналогично вращению Земли вокруг своей оси при движении ее по орбите вокруг Солнца). На самом деле, спин — это чисто квантовое свойство электрона, не имеющее классических аналогов. Строго говоря, спин — это собственный момент импульса электрона, не связанный с движением в пространстве. Для всех электронов абсолютное значение спина всегда равно s = 1/2. Проекция спина на ось = (магнитное спиновое число ms) может иметь лишь два значения: ms = 1/2 или ms = -1/2 .
Поскольку спин электрона s является величиной постоянной, его обычно не включают в набор квантовых чисел, характеризующих движение электрона в атоме, и говорят о четырех квантовых числах.
www.himhelp.ru
Химия для студентов: Квантовые числа
Состояние электрона в атоме описывается уравнением Шредингера. Решения уравнения Шредингера для одноэлектронного атома нумеруются тремя целочисленными параметрами, называемыми квантовыми числами, которые описывают всю совокупность сложных движений электрона в атоме. Квантовые числа изменяются дискретно (на единицу). Их всего четыре: главное (n), орбитальное (l), магнитное (ml) и спиновое (ms). Первые три характеризуют движение электрона в пространстве, а четвертое – вокруг собственной оси.Главное квантовое число (n). Определяет энергетический уровень электрона, его удаленность от ядра, размер электронного облака. Принимает целые значения (n = 1, 2, 3 …) и соответствует номеру периода. Из периодической системы для любого элемента по номеру периода можно определить число энергетических уровней атома и какой энергетический уровень является внешним. Электроны, обладающие близкими значениями энергии, образуют энергетический уровень. Он содержит строго определенное число электронов – максимально 2n2. Энергетические уровни подразделяются на s-, p-, d— и f— подуровни; их число равно номеру уровня.
Орбитальное квантовое число (l) характеризует геометрическую форму орбитали. Принимает значение целых чисел от 0 до (n — 1). Независимо от номера энергетического уровня каждому значению орбитального квантового числа соответствует орбиталь особой формы. Набор орбиталей с одинаковыми значениями n называется энергетическим уровнем, c одинаковыми n и
l — подуровнем.
На первом энергетическом уровне (n = 1) орбитальное квантовое число l принимает единственное значение l = (n — 1) = 0. Форма обитали — сферическая; на первом энергетическом только один подуровень — 1s. Для второго энергетического уровня (n = 2) орбитальное квантовое число может принимать два значения: l = 0, s— орбиталь – сфера большего размера, чем на первом энергетическом уровне; l = 1, p— орбиталь – гантель. Таким образом, на втором энергетическом уровне имеются два подуровня – 2s и 2p. Для третьего энергетического уровня (n = 3) орбитальное квантовое число l принимает три значения: l = 0, s— орбиталь – сфера большего размера, чем на втором энергетическом уровне; l = 1, p — орбиталь – гантель большего размера, чем на втором энергетическом уровне; l = 2, d— орбиталь сложной формы.
Таким образом, на третьем энергетическом уровне могут быть три энергетических подуровня – 3s, 3p и 3d.
Магнитное квантовое число (ml) характеризует положение электронной орбитали в пространстве и принимает целочисленные значения от -l до +l, включая 0. Это означает, что для каждой формы орбитали существует (2l + 1) энергетически равноценных ориентации в пространстве.
Для s— орбитали (l = 0) такое положение одно и соответствует m = 0. Сфера не может иметь разные ориентации в пространстве.
Для p— орбитали (l = 1) – три равноценные ориентации в пространстве
(2l + 1 = 3): m = -1, 0, +1.
Для d- орбитали (l = 2) – пять равноценных ориентаций в пространстве
(2l + 1 = 5): m = -2, -1, 0, +1, +2.
Таким образом, на s— подуровне – одна орбиталь,
на p- подуровне – три орбиталей,
на d- подуровне – пять орбиталей,
на f— подуровне – 7 орбиталей.
Спиновое квантовое число (ms) характеризует магнитный момент, возникающий при вращении электрона вокруг своей оси. Принимает только два значения +1/2 и –1/2, соответствующие противоположным направлениям вращения. На одной орбитали располагаются два электрона с противоположным спином, таким образом суммарный спин заполненной орбитали равен нулю. Например, p-подуровень имеет три орбитали, которые заполняются последовательно каждая одним электроном и только четвертый электрон заполняет первую орбиталь с уже имеющимся электроном.
Для рассмотрения электронной формулы атома перейдем на сайт:
chemistryostu.blogspot.com
Квантовые числа
Квантовые числа. Введение
Состояние каждого электрона в атоме описывается с помощью четырех квантовых чисел, три из которых соответствуют возможностям движения электрона в направлениях осей координат, а четвертое — характеризует движение электрона вокруг собственной оси. Эти квантовые числа следующие:
•Главное квантовое число (п)
•Орбитальное квантовое число (/)
Магнитное квантовое число (т)
Спиновое квантовое число (s)
Главное квантовое число
Главное квантовое число (п) — характеризует энергетический уровень электрона и удаленность этого уровня от ядра, а также размер электронного облака.
Принимает ряд целочисленных значений от 1 до : и=1,2,3,…7…и т.д. до бесконечности.
В периодической системе элементов п соответствует номеру периода.
При п= I электрон обладает самым низким уровнем энергии, самым малым размером электронного облака. Для каждого атома по номеру периода его расположения в периодической системе элементов можно узнать:
— сколько энергетических уровней имеет атом,
какой энергетический уровень будет внешним.
Орбитальное квантовое число
Орбитальное квантовое число (У) — определяет геометрическую форму электронного облака (орбитали). Принимает целочисленные значения от 0 до (п -1) 1 = 0, 1,2,… (л-1).
Каждому значению орбитального квантового числа (независимо от номера энергетического уровня) соответствует орбиталь особой формы, которая в атоме носит название энергетический подуровень
Для / = 0 s-подуровень, л’-орбиталь, орбиталь-сфера; / = 1 р-подуровень, р-орбиталь, орбиталь-гантель; 1 = 2 ^/-подуровень, с/-орбиталь, орбиталь сложной формы; / = 3 /^подуровень, /:орбиталь, орбиталь более сложной формы.
Магнитное квантовое число
Магнитное квантовое число (т) — характеризует положение электродной орбитали в пространстве. Магнитное квантовое число принимает целочисленные значения, но не произвольным образом, а скачком в зависимости or значения / (т.е. от формы орбитали), изменяясь от — / до +/, включая 0: т=-1, …-1,0, +1,… т/.
Это означает, что для каждой формы орбитали существует (2/+1) энергетически равн’оцеллых ориентации в пространстве (рис. 1.2).
Для л’-орбитали (/ — 0) такое положение одно и соответствует т = 0. Сфера не может иметь разные ориентации в пространстве.
Для /?-орбитали (/ — 1) — три равноценные ориентации в пространстве: т = -1, т = О, т = +1 (если / 1, то 2/ + 1 = 3).
Для rf-орбитали (/ = 2) — пять равноценных ориентации в пространстве: т = -2, т = -1, т = 0, т = +1, т = +2.
Упрощая, говорят: на л-подуровне одна орбиталь, нар-подуровне три орбитали, на (/-подуровне пять орбиталей, на/-подуровне семь орбиталей.
Спиновое квантовое число
Спиновое квантовое число (s)- характеризует магнитный момент, возникающий при вращении электрона вокруг собственной оси — спин. Может принимать только два значения: + 1/2 и -1/2, соответствующие двум противоположным направлениям вращения: по часовой и против часовой стрелки .
Состояние электронов в многоэлектронных атомах всегда отве^ чает квантовомеханическому закону, сформулированному Паули (принцип Паули). Согласно этому принципу в атомной или молекулярной . сист.еме не может бы.ть двух электронов, у которых все «четыре квантовых числа были бы од и н а ко в ы м и. Принцип (запрет) Паули/-ограничивает число электронов в атоме, обладающих определен-/ ными значениями п, I, nil, ms (может быть только ограниченное \ число не повторяющих друг друга комбинаций этих величин). Максимальное число электронов в атоме, обладающих данным n, равно2n кв .
При заполнении оболочки электроны сначала располагаются ,по ячейкам, отвечающим различным значениям магнитного квантового числа, и только после того как все ячейки в оболочке заполнены при дальнейшем прибавлении электронов в ячейках появляется по два электрона с противоположно направленными спинами. Иным и словами, заполнение электронных оболочек про* \ исходит таким образом, чтобы суммарны и спин I был максимальным***. Это важное положение носит назва- I ние правила Хунда.
studfiles.net
