Математические уравнения – Решение простейших линейных уравнений

Уравнение

Цели урока:

1) Обучающая: формировать представления об уравнении, корне уравнения, решении уравнений; организовать деятельность, направленную на выполнение учебных заданий, связанных с решением уравнений вида: х + а = b, x — a = b, a — x = b и приводимых к ним; создать условия для расширения знаний математических понятий и формирования новых знаний.

2) Развивающая: содействовать развитию и обогащению словарного запаса.

3) Воспитывающая: содействовать расширению кругозора.

Тип урока: изучение нового материала с первичным закреплением.

План урока:

1. Организационный этап.

2. Актуализация опорных знаний.

3. Этап получения новых знаний.

4. Этап обобщения и закрепления нового материала.

5. Рефлексия.

6. Заключительный этап.

Форма урока: Видеоматериал с элементами практикума.

Ход урока:

1. Организационный этап.

Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы узнать, ваше настроение и как вы настроены к работе на уроке.

2. Актуализация опорных знаний:

На предыдущих уроках мы с вами решали задачи способом моделирования условия задачи отрезками, и в ходе решения составляли выражения для нахождения неизвестного числа.

3. Этап получения знаний:

Скачать видеоурок «Уравнение»

Тема нашего урока «Уравнение». На этом уроке мы узнаем такие понятия как уравнение, корень уравнения. А также научимся составлять и решать уравнения.

В математике принято и очень удобно обозначать неизвестное число буквой, затем составлять равенство и решать это равенство. Рассмотрим

задачу: Лере задали прочитать рассказ. Она прочитала этот рассказ за два дня. В первый день Лера прочитала 40 страниц. Сколько страниц прочитала Лера за второй день, если известно, что весь рассказ состоял из 65 страниц?

Решение: Для наглядности внесем известные нам данные в таблицу. Мы знаем, что за первый день Лера прочитала 40 страниц, и знаем, что всего 65 страниц в рассказе. Обозначим буквой х неизвестное количество страниц, которые Лера прочитала за второй день. Составим равенство по известным нам данным. Мы к страницам, прочитанным за первый день (40), прибавим количество прочитанных страниц за второй день (х), и это будет равно количеству всех страниц в рассказе (65). Получили равенство: 40 + х = 65. Нам надо найти такое значение х, при котором будет выполняться это равенство. По смыслу вычитания, чтобы найти неизвестное слагаемое мы должны от известной суммы отнять известное слагаемое. Т. е. получаем х = 65 — 40. Вычислим правую часть получившегося равенства, получим х = 25. Значит, Лера прочитала 25 страниц рассказа за второй день. Ответом задачи будет: Лера прочитала 25 страниц за второй день.

Равенство 40 + х = 65 называют уравнением.

Уравнение — это равенство, содержащее букву, значение которой надо найти.

Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения.

Например, корнем уравнения 40 + х = 65 является число 25.

Если в равенство входит буква, то оно может быть верным при одних значениях этой буквы и неверным при других ее значениях. Например, уравнение 40 + х = 65 при х = 25 — верно, подставим вместо х значение 25, видим, что равенство выполняется верно. А при х = 15 — это равенство будет уже неверным, т.к. при замене х на число 15 равенство 40 + 15 никак не может быть равно 65.

Иногда надо узнать, является ли данное число корнем уравнения или нет. Тогда его не надо решать, нужно просто подставить предлагающиеся числа вместо неизвестного числа. Если получится верное равенство, то это данное число и есть корень уравнения, если равенство неверно — число не является корнем. Например, выполним задание: какое из чисел 3, 5 или 7, является корнем уравнения х + 7 = 12? Подставим по очереди каждое данное нам число. При х = 3 получаем равенство 3+7 равно оно 10, что в свою очередь не равно 12. При х = 5, получаем 5+7=12. При х = 7, получаем 7+7=14 и ≠12. При подстановке чисел мы убедились, что только число 5 дает в сумме с числом 7 верное равенство.

Решить уравнение — значит найти все его корни, или убедиться, что уравнение не имеет корней.

Запишите полезные правила для решения некоторых уравнений:

1. Нахождение неизвестного слагаемого:

a + x = b, где a и b — любые натуральные числа. Если нам неизвестно второе слагаемое, то мы должны из суммы вычесть первое слагаемое, т. е. x = b — a.

x + a = b. Если нам неизвестно первое слагаемое, то мы должны от суммы отнять второе слагаемое, т. е. x = b — a.

2. Нахождение неизвестного уменьшаемого:

x — a = b. Если нам неизвестно уменьшаемое, то мы должны к разности прибавить вычитаемое, т. е. x = b + a.

3. Нахождение неизвестного вычитаемого:

a — x = b. Если нам неизвестно вычитаемое, то мы должны от уменьшаемого отнять разность, т. е. x = а — b.

4. Этап обобщения и закрепления нового материала.

Итак, сделаем основные выводы: на этом уроке мы узнали, что такое уравнение, корень уравнения. Научились составлять уравнения и решать их.

Для закрепления материала ответьте на вопросы:

— Какое равенство называют уравнением?

— Какое число называют корнем уравнения?

— Что означает требование Решить уравнение?

— Как проверить, является ли определенное число корнем данного уравнения?

— Как найти неизвестное слагаемое (уменьшаемое, вычитаемое)?

5. Рефлексия.

Были ли трудности при работе на уроке? Если да, то какие?

videouroki.net

Предложения со словосочетанием МАТЕМАТИЧЕСКИЕ УРАВНЕНИЯ

Это безусловно справедливо в отношении математического уравнения, описывающего динамическую систему. Так в свои четыре года, я решал сложные математические уравнения, знал наизусть почти весь молитвослов и прошёл десятки психологических тестов. Майнинг — это решение сложных

математических уравнений с целью получения вознаграждения. Мы уже установили, что законы физики, как и математические уравнения, описывающие их, представляют собой определённую степень приближения к законам природы. Магниты на холодильник с цифрами и математическими символами позволяют вроде бы случайно ввести в свой дом математические уравнения и задачи.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Когда-нибудь я тоже научусь различать смыслы слов.

В каком смысле употребляется прилагательное здоровый в отрывке:

Я чувствовал приятную усталость и предвкушал здоровый сон в удобной кровати.

В прямом
смысле

В переносном
смысле

Это устойчивое
выражение

Это другое
прилагательное

А математик так стукнулся головой, что в ней перемешались все математические уравнения. Шахтёры — добровольцы, использующие специальное программное обеспечение для проверки транзакции путём решения сложного математического уравнения. В любом случае большинству людей, получающих выгоду от блокады, не нужно будет разбираться в горных или сложных

математических уравнениях. Спустя три нескончаемых часа русского языка, литературы и химии я начал задыхаться прямо у доски, на которой писал математическое уравнение. Постараемся обойтись без математических уравнений, химических формул, сложных терминов. Любое когда-либо существовавшее математическое уравнение получено с помощью аналитического ума. Одна из возможных форм предпосылки похожа на математическое уравнение: поведение X ведёт к последствиям Y. Казалось, что он записывает решение математических уравнений. Нынешний кризис — первый спланированный и рассчитанный как математическое уравнение. Даже обратимость физических процессов, вроде бы раскрываемая математическими уравнениями, не подрывает этого качества переживания времени. Эмоции индивидуальны; ни одно математическое уравнение не предскажет вам с точностью, как отреагирует другая сторона. Бессознательное приобретает своё значение, подобно неизвестному в математическом уравнении. Сможем ли мы решить математические уравнения турбулентности? Наверняка нужно всего лишь применить правильные законы физики и решить соответствующие математические уравнения. Я объясню, каким образом математические уравнения оказываются лучшими гадалками. Более того, оно чуть ли не полностью состояло из математических уравнений. Он уже понял, что счастье — вовсе не абстрактное понятие, а математическое уравнение, слагаемые в котором каждый для себя выбирает сам. Модель может быть выражена каким-то математическим уравнением — модель «затраты-выпуск». Математические уравнения всегда вызывали у него чувство сравнимое с ужасом пещерных людей перед непознаваемыми силами природы. Они были исписаны математическими уравнениями, странными символами и схемами. Проблемы бывают самые разные: что приготовить на ужин, как вывести новый товар на рынок, как решить математическое уравнение, как спасти брак и т. Вальрас впервые предпринял попытку описать экономическую теорию в виде математических уравнений. Несмотря на то что ей пришлось задержаться в школе, разбирая с учителем новые методы решений математических уравнений, она не стала торопиться. Из взаимное влияние объясняется не через чувства и намерения, а с помощью математических уравнений, описывающих законы природы. Математическое уравнение спирали можно охарактеризовать как возрастающую положительную функцию, отражающую криволинейную область, а в ней восходящее движение. Примерно с такой же скоростью я решаю в уме сложные математические уравнения. — Разве я не говорил вам, что размещение клиентов в ресторане похоже на математическое уравнение? Ещё спустя некоторое время вся вселенная была представлена в виде математических уравнений и подготовлена к преобразованию или составлению. Свести человеческое тело к простому математическому уравнению не так-то просто. Приглядевшись, я увидел цепочки сложных математических уравнений, которые так быстро преследовали друг друга слева направо, что я ничего не мог в них разобрать. Но самое изощрённое числовое творение по существу ничем не отличалось от математического уравнения. Люди и события не подчиняются законам логики, они куда менее предсказуемы и управляемы, чем математические уравнения. Так как же в принципе математические уравнения могут вывести само познание? Метод математического моделирования представляет собой процесс построения моделей происходящих физических процессов с использованием математических уравнений. Они были густо исписаны сложными математическими уравнениями. Временами фигуры и звуки математических уравнений казались неправильными. Вот только я не книгу читал, а пытался вывести математические уравнения, которые, как я знал, могут привести меня к ответу. Физика описывает законы природы через математические уравнения. Физика решает эту проблему, используя символы, и законы природы она представляет в виде математических уравнений. Как уже говорилось, физик описывает законы природы на языке математики, через математические уравнения.

kartaslov.ru

Уравнение — Математическая энциклопедия

Аналитическая запись задачи о разыскании значений аргументов, при к-рых значения двух данных функций равны. Аргументы, от к-рых зависят эти функции, наз. обычно неизвестными, а значения неизвестных, при к-рых значения функций равны,- решениями, или корнями, У.; о таких значениях неизвестных говорят, что они удовлетворяют данному У. Совокупность решений данного У. зависит от области Мзначений, допускаемых для неизвестных. У. может не иметь решений в М, тогда оно наз. неразрешимым в области М. Если У. разрешимо, то оно может иметь одно или несколько, или даже бесконечное множество решений. Напр., У. х 4-4 = 0 неразрешимо в области рациональных чисел, но имеет два решения: в области действительных чисел и четыре решения: — в области комплексных чисел. У. sin x = 0 имеет бесконечное множество решений: в области действительных чисел. Если У. имеет решениями все числа области М, то оно наз. тождеством в области М. Совокупность У., для к-рых требуется найти значения неизвестных, удовлетворяющие одновременно всем этим У., наз. системой У.; совокупность значений неизвестных, удовлетворяющих одновременно всем У. системы, наз. решением системы. Две системы У. (или два У.) наз. равносильными, если каждое решение одной системы (одного У.) является решением другой системы (другого У.), и наоборот, причем обе системы (оба У.) рассматриваются в одной и той же области. Процесс разыскания решений У. заключается обычно н замене У. равносильным. В нек-рых случаях приходится заменять данное У. другим, для к-poro совокупность корней шире, чем у данного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних корней, то все полученные корни преобразованного У. проверяют подстановкой в исходное У. Наиболее полно изучены алгебраические уравнения;их решение было одной из важнейших задач алгебры в 16-17 вв. Если f(x) — трансцендентная функция, то У. f(x)=0 наз. трансцендентным, причем в зависимости от вида f(x)оно наз. тригонометрическим У., логарифмическим У., показательным У. При практич. решении У. обычно применяются различные приближенные методы (см., напр., Линейная алгебра;численные методы). Среди систем У. простейшими являются системы линейных уравнений. Решение системы У. (не обязательно линейных) сводится, вообще говоря, к решению одного У. при помощи т. н. исключения неизвестных (см. Исключения теория). В теории чисел рассматриваются т. н. неопределенные У., изучение решений к-рых составляет предмет теории диофантовых уравнений. В общем случае У. является записью задачи о разыскании таких элементов анек-рого множества А, что F(а)=Ф(а), где Fи Ф — заданные отображения множества Аво множество В. Если Аи В — множества чисел, то возникают У. рассмотренного выше вида. Если Аи В — множества точек в многомерных пространствах, то получаются системы У. Если Аи В- множества функций, то в зависимости от характера отображения могут получаться дифференциальные уравнения обыкновенные, дифференциальные уравнения с частными производными, интегральные уравнения и др. виды У. По материалам одноименной статьи из БСЭ-3.

Источник: Математическая энциклопедия на Gufo.me

gufo.me

Решаем математические уравнения с помощью PhotoMath

Сколько бы ни было приложений в App Store, как бы ни варьировалось их качество, время от времени там появляются совсем неординарные проекты. Вспомнить хотя бы переводчик с дополненной реальностью Word Lens или CamFind, которая распознает предметы на фото. На днях в магазине приложений Apple появилась еще одна интересная разработка: PhotoMath — приложение, которое решает математические задачи, используя камеру вашего смартфона.

Принцип работы приложения предельно прост: вы берете в руки смартфон с запущенным PhotoMath, наводите камеру на какую-либо математическую формулу, а затем смотрите результат вычислений на дисплее. Эх, такую бы штуку мне, когда я в школе учился…

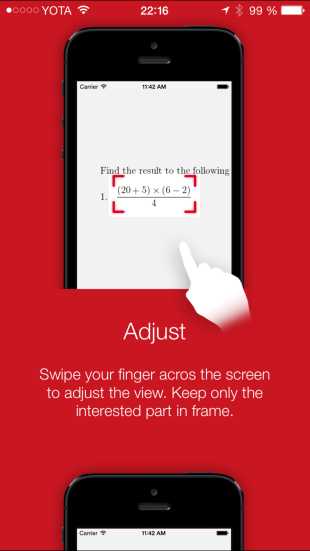
Однако приложение пригодится не только тем, кто не хочет думать и решать самостоятельно. Помимо полученного результата, PhotoMath также распишет весь процесс решения уравнения по шагам. Это может помочь не только ученику, но и, например, родителям, которые решат проверить его домашнее задание.

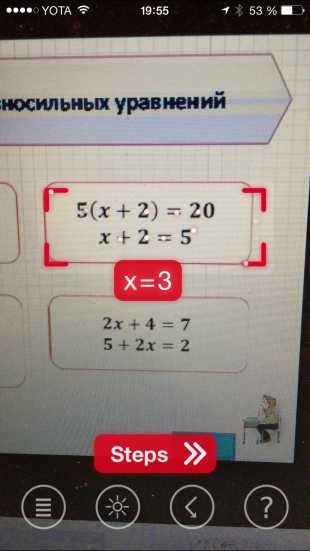
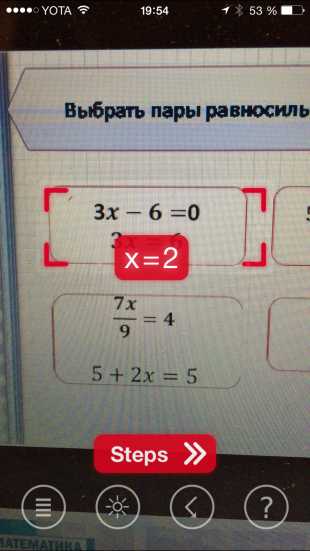
На данный момент в приложении конечно же есть и свои ограничения: так, к примеру, PhotoMath умеет решать только не сложные дроби, десятичные числа, линейные уравнения и стандартную арифметику. Тем не менее разработчики обещают улучшать приложение и дальше, что в теории позволит совершать сложные расчеты всего за несколько секунд. К сожалению, распознавание текста (в данном случае формул) тоже нельзя назвать идеальным, но очень хорошим — запросто. PhotoMath умеет распознавать лишь печатный текст, написанные уравнения “от руки” ему даются крайне тяжело (конечно, если они не написаны типографским шрифтом). Но и этот недостаток разработчики обещают довести до рабочего состояния.

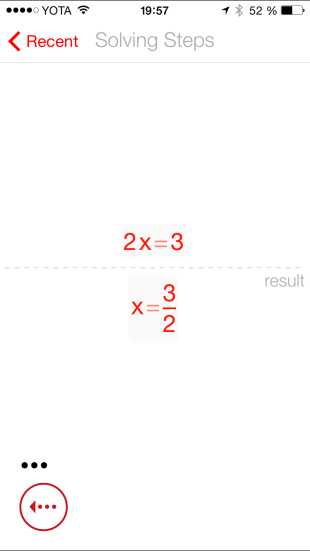
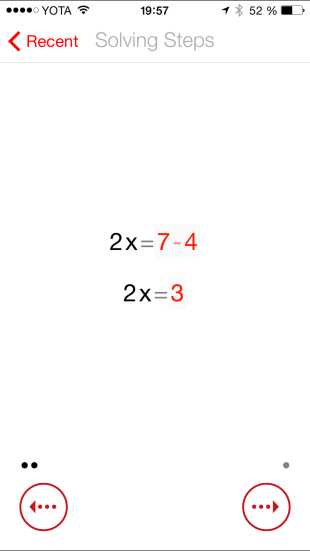
На данный момент приложение абсолютно бесплатно и доступно для смартфонов на iOS, а также Windows Phone. Версия для Android обещает появиться в скором будущем. Как заверяют разработчики, приложение было создано все же не в образовательных целях, а как пример доступности технологии. Поэтому пока еще рано совсем “отключать” мозг и решать все с помощью смартфона. Тем не менее демонстрация, я считаю, получилась хорошей. Остается только пожелать разработчикам удачи в их нелегком деле.

А как вам подобное решение? Пригодилось бы такое приложение, когда вы еще учились в школе? Делитесь мнением в комментариях!

Цена: Бесплатно

lifehacker.ru

НЕЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ — это… Что такое НЕЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ?

— ур-ния, не обладающие свойством линейности; применяются в физике как матем. модели нелинейных явлений в разл. сплошных средах. Н. у. м. ф.- важная часть матем. аппарата, используемого в фундам. физ. теориях: теории тяготения и квантовой теории поля.

Строго говоря, все сплошные среды описываются нелинейными ур-ниями. Выбор для описания среды линейных или нелинейных ур-ний зависит от роли, к-рую играют нелинейные эффекты, и определяется конкретной физ. ситуацией. Напр., при описании распространения лазерных импульсов необходимо учитывать зависимость показателя преломления среды от интенсивности эл.-магн. поля. Возникающие при этом Н. у. м. ф. являются основой матем. аппарата нелинейной оптики.

Линейные ур-ния, используемые в физике, являются результатом линеаризации более точных Н. у. м. ф. на фоне их простейших (фоновых) решений. Исторически первым примером Н. у. м. ф. были найденные в 18 в. Эйлера уравнения для идеальной жидкости:

Здесь r, Р,u — плотность, давление и скорость жидкости. Для баротропной жидкости, когда Р= Р(r), ур-ния Эйлера можно линеаризовать на фоне тривиального решения r = r₀, u₀ =0 в предположении потенциальности поля скоростей: u =j. Полагая r = r₀ + dr, dr << r₀, получаем из (1) волновое уравнение для звуковых волн. Однако при рассмотрении вихревых движений жидкости, когда её можно считать несжимаемой, r = r₀, div u = 0, ур-ния Эйлера (1) становятся существенно нелинейными. Их линеаризация на фоне решения u₀.= 0 приводит к тривиальному ур-нию дu/дt =0.

Т. о., линеаризация Н. у. м. ф. не всегда ведёт к содержат. результату. Может оказаться, что линеаризация имеет смысл, но линейные ур-ния сохраняют применимость лишь конечное время. Эта ситуация типична, если фоновое решение неустойчиво, но может иметь место и при устойчивом фоновом решении. Так, одномерные ур-ния Эйлера

при произвольном нач. условии r r₀, u.0 при х. описывают образование ударных волн. При этом за достаточно большое время теряют применимость не только линейное приближение, но и сами ур-ния (2), решения к-рых при tстановятся неоднозначными.

Даже если линеаризация Н. у. м. ф. возможна, с точки зрения физики исключительно важны «существенно нелинейные» решения, качественно отличающиеся от решений линейных ур-ний. Такими могут быть стационарные решения солитонного типа, локализованные в одном или неск. измерениях (см. Солитон), или решения типа волновых коллапсов, описывающие самопроизвольную концентрацию энергии в небольших областях пространства (см. также Самофокусировка света). Существенно нелинейными являются и стационарные решения ур-ний гидродинамики. Весьма важен вопрос об устойчивости существенно нелинейных решений, в т. ч. гидродинамич. течений и солитонов, к-рый решается либо при помощи линеаризации Н. у. на фоне изучаемых решений, либо при помощи вариац. оценок.

Решения Н. у. м. ф. во мн. случаях обнаруживают тенденцию к стохастизации. В этом случае они требуют статистич. описания, что составляет предмет теории турбулентности. Турбулентность часто развивается как результат неустойчивости фонового состояния. Если уровень нелинейности решения остаётся малым, то говорят о слабой турбулентности, в противном случае — о сильной турбулентности. Сильная турбулентность может сопровождаться волновыми коллапсами, целиком или частично состоять из взаимодействующих солитонов.

Нелинейные уравнения в физике. Н. у. м. ф., встречающиеся в физике, отличаются большим разнообразием. Их значит. часть представляет собой обобщения гидродинамич. ур-ний Эйлера, напр. Навье — Стокса уравнения для описания движений вязкой несжимаемой жидкости. Описываемая ими гидродинамич. турбулентность является предельно сильной.

В метеорологии были выведены ур-ния Буссинеска, описывающие движения несжимаемой жидкости в поле тяжести и сил Кориолиса и используемые в океанологии и физике атмосферы. Ур-ния магнитной гидродинамики описывают движение проводящей жидкости в магн. поле и применяются в астрофизике и физике плазмы.

Классич. примером Н. у. м. ф. являются уравнения теории упругости. Развитие микроскопической теории кристаллов дополнило их уравнениями равновесия и динамики дислокаций, также существенно нелинейными.

Многие Н. у. м. ф. возникли в физике в связи с развитием теории конденсиров. сред, они описывают мак-роскопич. проявления квантовомеханич. эффектов; неизвестной ф-цией в них является плотность параметра порядка (см. Фазовый переход). Если параметр порядка скалярный, это двухжидкостные ур-ния гидродинамики сверхтекучего гелия (см. Сверхтекучесть), ур-ния Гинзбурга — Ландау и их обобщения, описывающие магнетостатику и электродинамику сверхпроводников (см. Сверхпроводимость). Если параметр порядка векторный или тензорный, это ур-ния Ландау — Лифшица, описывающие ферромагнетики и антиферромагнетики, ур-ния обобщённой гидродинамики сверхтекучего гелия, макроскопич. модели жидких кристаллов. Для всех этих ур-ний наиб. интерес представляют их существенно нелинейные решения, часто описывающие локализованные (хотя бы частично) объекты: вихри в жидком гелии и в сверхпроводниках, доменные стенки в ферромагнетиках и антиферромагнетиках, дисклинации в жидких кристаллах и солитоны, к-рые в том или ином виде существуют во всех упомянутых средах.

Н. у. м. ф. возникают также как результат применения приближения Хартри — Фока к многочастичным квантовомеханич. системам и имеют в этом качестве применения в атомной и ядерной физике. Ещё одним источником Н. у. м. ф. является хим. физика. Это- Н. у. диффузии, описывающие волны горения и детонации, а также колебат. хим. реакции (см. Автоволны). К ним примыкают возникшие в биофизике ур-ния, описывающие распространение импульса по нервному волокну. Ур-ния этих типов возникают в задачах о самоорганизации (см. Синергетика )и диссипативных структурах.

Н. у. м. ф. играют важную роль и в фундам. физике, напр. ур-ния Эйнштейна для гравитац. поля (см. Тяготение). Ур-ния Эйнштейна в вакууме имеют ясный геом. смысл, описывая римановы пространства, Риччи тензор к-рых равен нулю. Геом. интерпретацию имеют и мн. Н. у. в квантовой теории поля, в частности Ян-га — Миллса поля.

Локализов. решения Н. у. м. ф. в квантовой теории поля можно рассматривать как точки стационарной фазы при квазиклассич. вычислении функциональных интегралов, для Грина функций, содержащих информацию о спектре масс и сечениях взаимодействия элементарных частиц. Если точкам стационарной фазы соответствуют траектории подбарьерных переходов между топологически неэквивалентными вырожденными состояниями вакуума, классич. Н. у. м. ф. следует рассматривать в мнимом времени, т. е. не в пространстве Минковского, а в четырёхмерном евклидовом пространстве. Локализов. решения таких ур-ний — четырёхмерные солитоны — получили назв. инстантонов. Ур-ния Янга — Миллса описывают частицы, обладающие асимптотической свободой. В двумерном пространстве-времени этим же свойством обладает ур-ние n -поля:

(здесь x = х+ t,h= x — t —«конусные» переменные). Это ур-ние является частным случаем более общего ур-ния «главного кирального поля»

(здесь g — элемент нек-рой группы Ли). Инстантон-ные решения этого ур-ния можно использовать для описания солитонных конфигураций в жидком гелии.

Универсальные модели. В этих моделях проявляется одна из характерных черт теории Н. у. м. ф.: среди огромного их многообразия можно выделить небольшое число ур-ний сравнительно простого вида, к-рые можно использовать как матем. модели различных по своей природе физ. ситуаций. Эти ур-ния играют, в известном смысле, ту же роль, что и классич. ур-ния в частных производных (ур-ние Лапласа, ур-ние диффузии, волновое ур-ние).

К числу таких универсальных моделей относятся Кортевега — де Фриса уравнение, Шрёдингера уравнение нелинейное, синус-Гордона уравнение, Кадомцева — Петвиашвили уравнение, Вюргерса уравнение, Хохло-ва — Заболотской уравнение и др. Необходимо отметить еще систему ур-ний «трёх волн»:

являющуюся универсальной моделью для описания па-раметрич. взаимодействий волн в нелинейных средах. Система (5) допускает многочисл. обобщения.

Большое разнообразие встречающихся в физике Н. у. и. ф. затрудняет развитие общих матем. методов их исследования. Лишь для сравнительно немногих Н. у. м. ф. доказаны теоремы существования и единственности, к таким относятся ур-ния Янга — Миллса, ур-ния Навье — Стокса в двумерном случае, ур-ния газовой динамики. Для ур-ний Навье — Стокса в трёхмерном случае теорема единственности решения задачи Коши до сих пор не доказана. Затруднена даже проблема классификации Н. у. м. ф. Часть их попадает под классич. разделение на эллиптич., гиперболич. и параболич. ур-ния, но значит. число важных Н. у. м. ф. (среди них Кортевега — де Фриса ур-ние, Кадомцева — Петвиашвили ур-ние) не могут быть отнесены ни к одному из этих типов. Нек-рую классификацию Н. у. м. ф. можно осуществить на основе физ. соображений. Прежде всего это разделение на стационарные и эволюц. ур-ния. Большинство стационарных ур-ний относится к эллиптич. типу. Среди эволюц. ур-ний, явно содержащих производные по времени, можно выделить консервативные Н. у. м. ф., сохраняющие интеграл энергии, и диссипативные Н. у. м. ф., описывающие «открытые системы», обменивающиеся энергией с «внешним миром». Одним из интересных достижений теории Н. у. м. ф. было обнаружение того факта, что консервативные Н. у. м. ф., как правило, являются га-мильтоновыми системами, хотя явное введение кано-нич. переменных зачастую оказывается трудной задачей. Установлена гамильтонова природа большинства консервативных обобщений ур-ний Эйлера и даже системы ур-ний Власова, описывающих плазму без столкновений. Для гамильтоновых систем, близких к линейным, развиты методы теории возмущений, позволяющие учитывать нелинейные эффекты и производить статистич. описание решений.

Все перечисленные выше универсальные Н. у. м. ф., за исключением Бюргерса ур-ния и Хохлова — Заболотской ур-ния, являются гамильтоновыми. Точные решения. Для физики важно знать как можно больше точных решений Н. у. м. ф., особенно существенно нелинейных. Простейшие из таких решений можно находить, используя очевидные свойства симметрии Н. у. м. ф., а также отыскивая всевозможные автомодельные подстановки (см. Автомодельностъ). Более тонкие способы вычисления точных решений используют методы теории групп Ли. Пусть Н. у. м. ф. для ф-ции двух переменных u(x,t )имеет вид

Ф-ция наз. симметрией уравнения (6), если оно совместно с ур-нием u_t = = , где t — новая переменная. Симметрии образуют алгебру Ли относительно скобки Пуассона

По алгебре симметрии Н. у. м. ф. восстанавливают группу Ли — Беклунда непрерывных преобразований, оставляющих Н. у. м. ф. инвариантным. Точные решения Н. у. м. ф. находят как решения, остающиеся инвариантными при действии к.-л. подгруппы группы Ли — Беклунда. Группа Ли — Беклунда и алгебра симметрии существуют у каждого Н. у. м. ф. В большинстве случаев группа Ли — Беклунда является конечномерной. Существуют, однако, случаи, когда эта группа бесконечномерна, как у всех перечисленных выше универсальных Н. у. м. ф.

Если преобразование из группы Ли — Беклунда оставляет инвариантным функционал действия гамиль-тонова Н. у. м. ф., то оно имеет интеграл движения — функционал, не зависящий от времени. Интегралы движения образуют алгебру Ли относительно скобок Пуассона, изоморфную нек-рой подалгебре алгебры симметрии.

Перечисленные выше универсальные гамильтоновы Н. у. м. ф. обладают бесконечными наборами независимых интегралов движения. Ур-ния, обладающие этим свойством, несколько условно наз. интегрируемыми, хотя интегрируемость (см. Гамильтонова система )доказана лишь для немногих из них. Интегрируемыми являются, в частности, одномерные ур-ния Эйлера (2).

Обширный класс интегрируемых Н. у. м. ф. составляют ур-ния, к к-рым применим обратной задачи рассеяния метод. Для этих ур-ний, к к-рым относятся, в частности, перечисленные выше универсальные гамильтоновы системы, возможно явное вычисление большого кол-ва точных решений, в т. ч. описывающих солитоны и их взаимодействия. При помощи метода обратной задачи удаётся вычислять инстантонные решения ур-ний Ян-га — Миллса, а также найти многочисленные точные решения ур-ний Эйнштейна.

Если Н. у. м. ф. не обладает бесконечной группой Ли — Беклунда, возможности его аналитич. исследования сильно ограничены. В ряде случаев можно, используя разложение по набору заданных ф-ций (метод Галеркина), свести его к системе обыкновенных диф-ференц. ур-ний, к-рую можно изучать качеств. методами, а также интегрировать при помощи ЭВМ. Таким способом удаётся моделировать не слишком развитую турбулентность, в т. ч. изучать странные аттракторы. Наконец, если число независимых переменных, входящих в Н. у. м. ф., не превышает три, оказывается достаточно эффективным их прямое численное решение на ЭВМ.

Лит.: Уизем Д ж., Линейные и нелинейные волны, пер. с англ., М., 1977; Теория солитонов. Метод обратной задачи, М., 1980; Ablowitz М. J., Segur H., Solitons and the inverse scattering transform, Phil., 1981;Ибрагимов Н.

В. Е. Захаров.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

dic.academic.ru

Уравнения математической физики — это… Что такое Уравнения математической физики?

        дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории У. м. ф. характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг У. м. ф. с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У. м. ф. уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование (см. Математическая физика).

         Классификация уравнений математической физики. Значительная часть У. м. ф. составляют линейные уравнения с частными производными 2-го порядка общего вида:

        

        , (1)

         где все коэффициенты a_ij (a_ij = a_ij), b_i, с и правая часть f представляют собой заданные функции независимых переменных x₁, x₂,…, х_п (n ≥ 2), а u – искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно λ) уравнения

        

         = 0, (2)

         и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все n корней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных n – 1 корней, – к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты a_ij постоянны, то уравнение (1) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от x₁,…, х_п, то и корни уравнения (2) зависят от x₁,…, х_п, а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими).

         Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.

         Основные примеры уравнений математической физики.

                  – простейшее уравнение гиперболического типа, а также соответствующие неоднородные уравнения (в правой части которых добавлены известные функции) – Телеграфное уравнение и т.д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболического типа во многом аналогичны свойствам приведённых простейших таких уравнений.                   – простейшее уравнение эллиптического типа и соответствующее неоднородное уравнение – Пуассона уравнение. Уравнения и системы эллиптического типа появляются обычно при анализе стационарных состояний. Теплопроводности уравнение:         

         – простейший пример уравнения параболического типа. Уравнения и системы параболического типа появляются обычно при анализе процессов выравнивания.

         Первым примером уравнений смешанного типа явилось т. н. уравнение Трикоми:

                  Для этого уравнения полуплоскость у у = 0 – зоной параболичности.          Ряд задач математической физики приводит к интегральным уравнениям (См. Интегральные уравнения) различных типов. Так, например, интегральные уравнения Вольтерра возникают в тех задачах физики, в которых существует предпочтительное направление изменения независимого переменного (например, времени, энергии и т.д.). В задаче о крутильных колебаниях возникает некоторое интегро-дифференциальное уравнение (См. Интегро-дифференциальные уравнения).          Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У. м. ф. много усилий было затрачено на отыскание их общего решения. Уже Ж. Д’Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л. Эйлером (1770), П. Лаплас предложил (1773) «каскадный метод», дающий общее решение некоторых др. линейных однородных гиперболических уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значительного класса уравнений, для которых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось что при анализе физических процессов У. м. ф. обычно появляются вместе с дополнительными условиями, характер которых коренным образом влияет на направление исследования решения (см. Краевые задачи, Коши задача).          Широкое распространение получили методы приближённого решения краевых задач, в которых задача сводится к решению системы алгебраических (обычно линейных) уравнений (см. Ритца и Галёркина методы. Сеток метод). При этом за счёт увеличения числа неизвестных в системе можно достичь любой степени точности приближения.

         Лит.: Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; Годунове. К., Уравнения математической физики, М., 1971; Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.

dic.academic.ru

Проект по математике «Уравнения и их решения»

Слайд 1

Щитова Я.К.

Слайд 3

Где зародилось искусство решать уравнения. Алгебра как искусство решать уравнения зародились очень давно в связи с потребностью практики, в результате поиска общих приёмов решения однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приёмы решения линейных уравнений. Слово «алгебра» возникло после появления тракта «Китаб аль-джебр валь-мукабала» хорезмского математика и астронома Мухаммеда Бен Мусса аль Хорезми. Термин «аль-джебр», взятый из названия книги, в дальнейшем стал употребляться как алгебра. Кто ввел в математику знак равенства? Знак равенства ввел в 1556 году английский математик Рекорд, который объяснил это так, что ничто не может быть более равным, чем два параллельных отрезка.

Слайд 4

Кто является создателем современной буквенной символики? Франсуа Виет (1540 — 13 декабря 1603) — выдающийся французский математик, один из основоположников алгебры . Создателем современной буквенной символики является французский математик Франсуа Виет (1540 – 1603). До XVI в. изложение алгебры велось в основном словесно. Буквенные обозначения и математические знаки появлялись постепенно. Знаки + — впервые встречаются у немецких алгебраистов XVI в. Несколько позже вводится знак * для умножения. Знак деления (:) был введён лишь в XVII в. Решительный шаг в использовании алгебраической символики был сделан в XVI в., когда французский математик Франсуа Виет (1540-1603) и его современники стали применять буквы для обозначения не только неизвестных (что делалось и ранее), но и любых чисел. Однако эта символика ещё отличалась от современной. Так, Виет для обозначения неизвестного числа применял букву N (Numerus-число), для квадрата и куба неизвестного буквы Q (Quadratus — квадрат) и C (Cubus — куб). Например, запись уравнения X в кубе, минус 8X в квадрате, плюс 16X, равно 40 у Виета выглядела бы так: 1C-8Q+16N aequ 40 (aequali — равно).

Слайд 5

Виет делит изложение на две части: общие законы и их конкретно-числовые реализации. То есть он, сначала решает задачи в общем виде, и только потом приводит числовые примеры. В общей части он обозначает буквами не только неизвестные, что уже встречалось ранее, но и все прочие параметры, для которых он придумал термин «коэффициенты». Виет использовал для этого только заглавные буквы — гласные для неизвестных, согласные для коэффициентов. Виет свободно применяет разнообразные алгебраические преобразование — например, замену переменных или смену знака выражения при переносе его в другую часть уравнения. Новая система позволила просто, ясно и компактно описать общие законы арифметики и алгоритмы. Символика Виета была сразу же оценена учёными разных стран, которые приступили к её совершенствованию. Диофант – единственный известный нам древнегреческий математик, который занимался алгеброй. Он решал различные уравнения, особое внимание уделял неопределенным уравнениям, теория которых называется теперь «диофантовым анализом». У Диофанта была попытка ввести буквенную символику. В верхней строке записано уравнение: Первая книга предварена обширным введением, в котором описаны используемые Диофантом обозначения. Предусмотрены специальные знаки для следующих степеней неизвестного, вплоть до шестой, называемой куб- кубом, и для противоположных им степеней. Знака сложения у Диофанта нет: он просто пишет рядом положительные члены, причём в каждом члене сначала записывается степень неизвестного, а затем численный коэффициент.

Слайд 6

Назовите гениального французского математика и революционера создавшего основы общей теории уравнений? Нильс Хенрик Абель (1802 – 1829) внес важный вклад в теорию уравнений. В 1824 году он опубликовал доказательство неразрешимости в радикалах общего буквенного выражения пятой степени. «Абель оставил математикам столь богатое наследие, что им будет чем заниматься в ближайшие 150 лет» (Шарль Эрмит). Нильс Хенрик Абель 5 августа 1802, Фанге — 6 апреля 1829, Фроланд близ Арендаля — знаменитый норвежский математик .

Слайд 8

Уравнением называют равенство, содержащее букву, значение которой надо найти. Чтобы найти неизвестное уменьшаемое , надо сложить вычитаемое и разность. Чтобы найти неизвестное вычитаемое , надо из уменьшаемого вычесть разность. Чтобы найти неизвестное слагаемое , надо из суммы вычесть известное слагаемое. Решить уравнение – значит найти все его корни (или убедиться, что это уравнение не имеет ни одного корня). Корнем уравнения называют значение буквы, при котором из уравнения получается верное числовое равенство.

Слайд 9

Способы решения. Решить уравнение ( y + 64) -38 = 48 можно двумя способами: 1)сначала найти неизвестное уменьшаемое y = 64: y + 64 = 48 + 38, y + 64 = 86, а потом найти неизвестное слагаемое y : y = 86 – 64, y = 22 или 2)сначала упростить выражение, стоящее в левой части уравнения, использовав свойства вычитания: у + 64 – 38 = 48, y + 26 = 48, А затем найти неизвестное слагаемое у: у = 48 – 26, у = 22.

Слайд 10

Решение задачи с помощью уравнения. Маша задумала число. Если к этому числу прибавить 14 и от полученной суммы отнять 12, то получиться 75. Какое число задумала Маша? Решение: (Х + 14) – 12 = 75 Х + 14 = 75 + 12 Х + 14 =87 Х = 87 – 14 Х = 73 Проверка: (73 +14) – 12 = 75 75 = 75.

Слайд 11

Вывод. Я выбрала эту тему, потому что уравнения часто используют в повседневной жизни, и мне хотелось бы изучить эту тему более углубленной. Я думаю что мне своим проектом удалось найти много интересного исторического материала и показать красоту развития данной темы.

nsportal.ru