Математика сравнение – Сравнение, в математике — это… Что такое Сравнение, в математике?

Сравнение чисел. Видеоурок. Математика 1 Класс

Задание 1: Сравнить количество жуков и бабочек на Рис. 1. 

Рис. 1

Первым действием необходимо определить количество жуков и количество бабочек на рисунке.

Итак, жуков на рисунке четыре, а бабочек – три. Определим, какое число больше, а какое меньше.

Четыре больше, чем три. Так как чтобы получить три, нужно от четырех убрать одного жука.

Или три меньше четырех, так как чтобы получить число четыре, нужно добавить к трем один.

Определим, на сколько четыре больше, чем три. Одному жуку не хватает пары, значит, четыре больше трех на один. Математически это имеет следующий вид. Чтобы узнать, на сколько четыре больше трех, нужно из четырех вычесть три, получится один.  

Значит, четыре больше трех на один. Чтобы узнать, на сколько три меньше четырех, также из большего числа четыре вычитаем меньшее число три.

Итак, чтобы сравнить два числа, необходимо из большего вычесть меньшее.

Ответ: Жуков больше, чем бабочек на 1.

Задание 2: Каких фигур на рис. 2 больше и на сколько?

Рис. 2

Для этого посчитаем количество треугольников, кругов и квадратов на данном рисунке. Треугольников – 5, кругов – 2, квадратов – 3. Чтобы узнать, каких фигур больше, мы расставили их парами. Мы видим, что больше всего треугольников, так как не хватает трем пары. Меньше всего кругов.

Сравним числа 5, 2 и 3. Первым действием сравним треугольники и круги.

Рис. 3

Для того чтобы узнать, на сколько треугольников больше кругов, необходимо от большего числа вычесть меньшее. То есть:.

Значит, треугольников больше, чем кругов, на три. Если расставим парами треугольники и круги, увидим, что трем треугольникам не хватает пары, значит, треугольников на три больше, чем кружков.

Сравним количество кружков и квадратов.

Рис. 4

Определим, на сколько два меньше трех. Для этого из большего числа вычтем меньшее.

По рисунку видим, что кружков меньше, чем квадратов, на один, так как одному квадрату не хватает пары.

Сравним количество треугольников и квадратов.

Рис. 5

Определим, на сколько 5 больше 3. Для этого из большего числа вычтем меньшее.

Значит, треугольников больше, чем квадратов, на 2. По рисунку также видно, что двум треугольникам не хватает пары.

Ответ: Треугольников больше, чем квадратов, на 2, больше, чем кругов, на 3.

Итак, для того, чтобы сравнить два числа, нужно определить, какое число больше, какое число меньше. И чтобы узнать, на сколько одно число больше другого, необходимо из большего числа вычесть меньшее.

 

Список литературы

1. Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
2. Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
3. Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Фестиваль педагогических идей (Источник).

2. Фестиваль педагогических идей (Источник).

3. Фестиваль педагогических идей (Источник).

 

Домашнее задание

1. Примеры на повторение.

2 + 3=            7 + 1 =

4 – 2=            3 – 1 =

7 – 5 =           4 – 1 =

3 + 3 =           5 + 4=

2. Сравнить следующие числа:

3 и 4;             8 и 4;

5 и 3;             3 и 7;

7 и 2;             6 и 8;

1 и 9;             9 и 5.

3. Ответить на вопросы:

МАТЕМАТИКА  (10)     РИСОВАНИЕ  (9)

В каком слове больше букв? 

В каком из этих слов больше одинаковых букв?

4. Запишите числа от  большего к меньшему:

5, 3, 8, 4,1, 2, 9, 6

interneturok.ru

Сравнение чисел / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Сравнение чисел

В этом разделе мы разместили материалы по сравнению чисел.

Ты познакомишься с равенствами и неравенствами, научишься сравнивать лю­бые два числа и выражения, записывать результат сравнения, ис­пользуя знаки >, < и =, узнаешь, как отличить равенство и неравенство и как правильно их читать.

В этой же главе ты научишься уменьшать и увеличивать числа.

Запись, в которой есть знак =, называется равенством. Например, 4 + 5 = 9	Равенства
Запись, в которой есть знаки > или < называется неравенством. Например, 4 + 5 > 6	Неравенства
Чтобы уменьшить на несколько единиц, нужно из большего числа вычесть меньшее.При уменьшении числа — вычитание. Знак минус.	Уменьшить на…
Чтобы увеличить число на какое-то число, нужно добавить это число. Добавить, значит, прибавить. Увеличить. При увеличении числа — сложение. Знак плюс.	Увеличить на…

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Равенства и неравенства

Уменьшить на… Увеличить на…

Правило встречается в следующих упражнениях:

1 класс

Страница 21, Моро, Волкова, Степанова, Учебник, 2 часть

3 класс

Страница 36. Вариант 1. № 4, Моро, Волкова, Проверочные работы

Страница 37. Вариант 2. № 4, Моро, Волкова, Проверочные работы

---

© 2019 — budu5.com, Буду отличником!

budu5.com

Сравнение учебников математики. 1-й класс. Часть I. : swayn

1. Преамбула.
1.1. Объекты исследования.
К сравнению выбраны следующие учебники/курсы математики за 1-й класс:

1. Петерсон Л.Г., 2012 г., М., «Ювента», 3 учебника, 3 рабочих тетради.
Яркий представитель т.н. «развивающего» направления. Долгое время активно продвигался в качестве лучшего постсоветского учебника математики для начальной школы. В ангажированных педагогических кругах принято считать, что курс Петерсон — для одаренных и успешных детей [1], в отличии от курса Моро, предназначенного для массового потребителя
2. Моро М.И., 2015, М., «Просвещение», 2 учебника, 2 рабочих тетради.
Наиболее распространенный учебник математики. Современный представитель «классической» учебной литературы. Является переработкой советского учебника 80-х к современным требованиям преподавания. Выполнен при участии Марии Игнатьевны Моро, автора классического советского курса математики для начальной школы.
3. Моро М.И., 1982, М., «Просвещение». Наиболее известный сегодня советский учебник математики (80-е годы).
4. Пчелко А.С., 1967,М., «Просвещение» Советский учебник арфиметики 60-х годов, классика советской послевоенной учебной литературы.

1.2. Цель работы.
Требуется, для перечисленных выше учебников, оценить:
1. Научное содержание текстов учебника: корректность используемых терминов и понятий, соответствие содержания учебника желаемому результату обучения.
2. Методологический уровень учебника: последовательность изложения материала, доступность выбранной методики изложения для учащихся.
3. Структуру учебника: его компоновку, содержание, качество иллюстраций.

Естественно, данная оценка, хотя и будет опираться на объективные факты, является именно моей оценкой учебников и ни чем более.
Надеюсь, что проделанная работа принесет некоторую пользу не только мне, но и читателям.

Сравнению структуры советских и современных учебников начальной и основной школ будет посвещена отдельная общая статья, выводы которой  будут справедливы в отношении практически всего корпуса современной учебной литературы.

Статья о сравнении учебников будет публиковаться частями, по мере появления у меня свободного времени для соответствующей  работы.
Окончательно, сравнительная оценка учебников будет приведена в систематизированном виде в завершающей части статьи.

2. Курс Л.Г. Петерсон.
2.1. Введение.
Первым будет рассмотрен «развивающий» курс математики первого класса для «успешных» детей под редакцией Л.Г. Петерсон.
Курс состоит из трех учебных пособий, 64 стр., 64 стр., 96 стр., и трех рабочих тетрадей, 64 стр. каждая.
Исходные материалы не привожу, дабы не нарушать авторское право издательства.
При желании, читатель может самостоятельно найти  данный учебный курс в сети.

Предваряя дальнейшие материалы, обращаю внимание, что, в данный момент (с 2014 года), курс исключен из федерального перечня учебников, рекомендованного к применению в школах [2], но продолжает использоваться в течение 5 лет с момента опубликования приказа в тех школах, в которых он был закуплен и, далее, может использоваться педагогами по их желанию.

Перед тем, как выносить суждение по данному курсу в целом, предлагаю оценить ряд материалов из рассматриваемых учебников.

2.2. Серьезные математические ошибки в учебнике

На уроке 9 (стр. 16) понятие суммы дается, еще до введения понятия числа, как объединение непересекающихся множеств. Причем, в данном случае, элементы множеств изображены как однотипные на множестве.

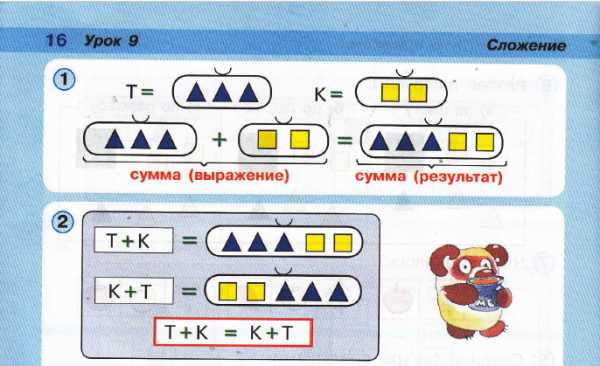
Рисунок 1. Сумма.

С точки зрения математики, вообще-то, Т + К ≠ К + Т,  при такой подаче, если не оговорено отдельно не учитывать состав и порядок элементов.

Это разные размещения, но равные сочетания. Как 11122 и 22111, например.

Автор, вплоть до конца третьей книги, даже после знакомства учащихся с числами, продолжает применять предложенную им оригинальную концепцию сложения.

Введение определения суммы в таком виде, очевидно, не является математически строгим, путает учащихся, способствует формированию у них ложных представлений как о суммировании, в частности, так и о работе с множествами, в целом.

На уроке 11 (стр. 18), разность определяется автором как исключение элементов из множества элементов по заданному списку критериев.

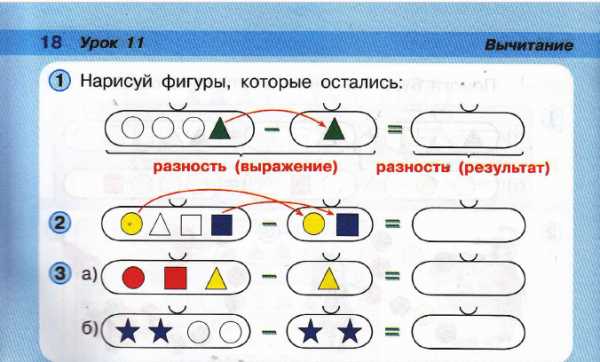
Рисунок 2. Разность.

Например, по мнению автора, в п. 2, при вычитании из четырех геометрических фигур двух, это должны быть желтый круг и синий квадрат. На самом деле, нет. Автор снова ошибается. Разность, в её арифметическом понимании, это операция исключения из множества заданного количества элементов, а не исключения элементов по заданным критериям.

Вообще, в курсе математики начальных классов, ребенок, проводя арифметические действия, должен работать с количественным, а не качественным описанием множеств. На примере рассмотренного выше определения разности, надо работать не с классами кружков и квадратиков, к тому же, дифференцированных по признаку цвета, а с классом геометрических фигур. Лучшей подачей темы была бы классическая её подача: разность на примере одинаковых кружков или, если обязательно хочется красиво проиллюстрировать учебник, одинаковых ягодок или коробочек. Ключевое слово — одинаковых.

Со стр. 36, урок 24, вводится, для счета по ней, числовая прямая, которая активно используется в дальнейшем при счете (т.н. «счет по линейке»). Данный метод имеет как плюсы (складывается представление о «числовой прямой»), так и минусы («счет по линейке» препятствует развитию абстрактного мышления). По моему мнению, в качестве основного метода счета данный метод, при обучении, использоваться не должен. Для усвоения конкретного счета предпочтительнее использование предметного счетного материала («палочек»), с постепенным отходом от таковых и переходом к «чистой» арифметике.

На уроке 18, стр. 34-37, часть III, автор, в теме «единицы счета», касается концепции «составных именованных чисел», которая, как мне кажется, скорее, вредна в начальных классах, нежели полезна.

Рисунок 3. Именованные числа.

Разберем данную концепцию на примере, а), рис. 5. Красный квадрат содержит неизвестное количество черных точек. Таким образом, арифметические операции раздельно проводятся с красными квадратами и черными точками.

Предположим (в рассматриваемом учебнике нет даже этого), что задано правило, по которому устанавливается соответствие между красными квадратами и черными точками. Например, в одном красном квадрате 10 черных точек (в 1 см 10 мм и т.п.). Согласно правилам работы, с составными именованными числами, принятым в элементарной арифметике до, примерно, конца 60-х годов прошлого века, квадраты (или сантиметры) и точки (миллиметры), в таком случае, все равно, учитываются отдельно, после чего лишние точки перекидываются в квадраты (миллиметры свыше 10 переводятся в сантиметры).

Сейчас общепринятой является другая методика работы с составными именованными числами. Например, 3 см 4 мм + 4 см 9 мм, вычисляются не

3 см 4 мм + 4 см 9 мм = 7 см 13 мм = 8 см 3 мм, а

3 см 4 мм + 4 см 9 мм = 34 мм + 49 мм = 83 мм = 8 см 3 мм,

т.е. составные именованные числа приводятся к минимальной общей размерной единице и все вычисления происходят уже после такого приведения типа составных чисел. И это правильно. А вот занимать этими проблемами детей первого класса обучения – неправильно. И, тем более, неправильно учить их устаревшей методике работы с составными именованными числами.

2.2. Неоднозначные и спорные места в учебнике

На стр. 20, урок 13, требуется угадать значения букв классов фигур для их группировки.

Рисунок 4. Угадай задуманные слова.

Далее угадывание значения букв классов как прием обучения (чему? умению угадать ход мысли автора?) встречается довольно-таки часто…

Правила оформления задач (стр. 44, урок 23, часть II), как мне кажется, излишне формальны для первого класса:

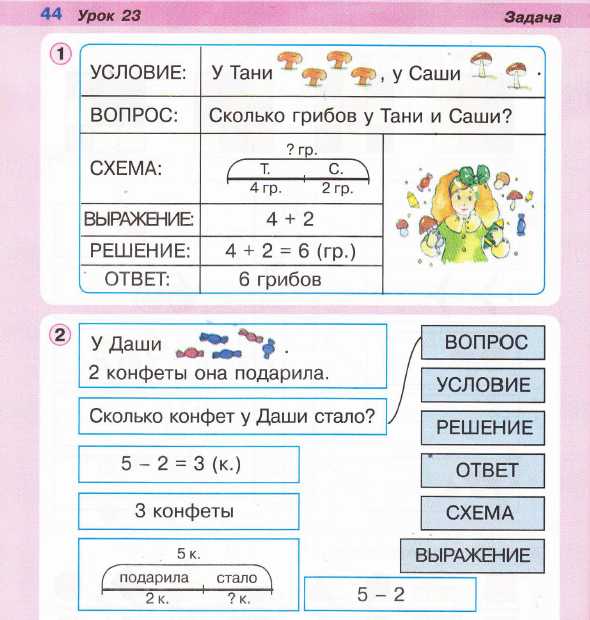
Рисунок 5. Правила оформления задач.

Впрочем, именно этот момент – вопрос вкуса, допускаю, что такого рода требования к формализации решения, при условии, конечно, последовательного формального изложения учебного материала (чего нельзя сказать о данном учебнике), были бы логичны и обоснованы.

Стр. 62, урок 32, нумерация двузначных чисел, с непонятной целью вводится обозначение десятков треугольниками, а единиц точками. В дальнейшем это авторское условное обозначение активно используется как в учебнике, так и в рабочей тетради (РТ 3, 29, 1, стр. 37)

Рисунок 6. Авторские условные обозначения.

По моему мнению, не следует умножать сущности без необходимости. Тем более, в учебнике математики для первого класса.

Сложение с переходом через десяток вводится табличным способом. По моему мнению, подобный подход возможен, но не является лучшим, так как не способствует развитию абстрактного мышления, предпочтителен, как мне кажется, классический метод загрузки «таблицы сложения» в голову учащимся, обучение — через дополнение числа до 10 и закрепление материала количеством выполненных примеров. Ниже пример таблицы сложения из РТ 3, 38,1 стр. 46.

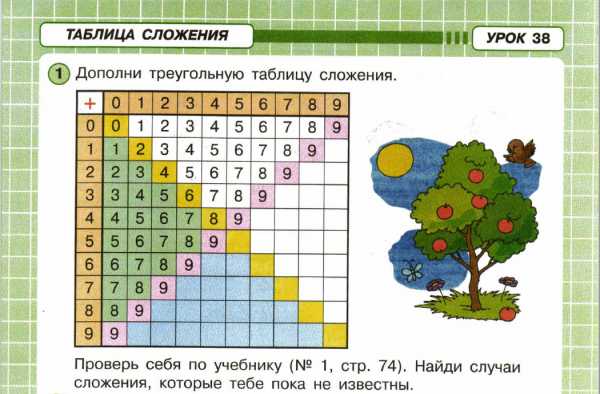
Рисунок 7. «Треугольная таблица сложения».

2.3. Несколько слов о рабочих тетрадях

Рабочие тетради, в целом, соответствуют уровню учебников – столь же невнятные, неоднородные по уровню подачи материала, полные раскрасок, шарад, веселых картинок и заданий от не по возрасту легких, вот, например, для детей среднего детсадовского возраста (РТ 1, стр. 28),

Рисунок 8. Один, два, много.

до не по возрасту сложных, например, требование выхода на уровень сложного планирования работ, для первого класса, как мне кажется, преждевременно (РТ 1, стр. 54, урок 33)

Рисунок 9. Изучаем 6 по плану.

2.4. Резюме.

Учебник перегружен дополнительным материалом в ущерб основному, излишнее внимание уделяется раскраскам, прописям и рисованию по клеточкам. Раскраски и прописи продолжают использоваться при обучении до конца первого класса.

Наличие большого количества качественных математических головоломок, с одной стороны, является одной из немногих положительных сторон рассматриваемого учебника, а, с другой стороны, отвлекает учащегося от усвоения базовых понятий арифметики.

Качественно, учебник содержит серьезные математические ошибки при подаче материала, недостаточен в части подачи основного материала программы и избыточен в части дополнительного материала, содержит большое количество авторской математической символики, не встречающейся в общепринятом дискурсе, и не может быть рекомендован для изучения арифметики в начальной школе.

2.5. Справочно.

Учебники Петерсон давно и заслужено подвергались профессиональной критике, которая, к сожалению, долгое время, никак не влияла на распространение убеждений о качестве учебной литературы подобного рода и необходимости её скорейшего повсеместного распространения. Подробнее с содержательной критикой данного учебного курса можно ознакомиться, например, тут [3]. Позволю привести, в завершение, цитату  уважаемого академика Виктора Анатольевича Васильева, по поводу его полемики с Л.Г. Петерсон:

«Помимо непосредственной работы со школьной математикой, важно еще и понимание самой математики и того, что является математикой, а что — нет; понимание того, что является математическим мышлением и/или полезно для него, а что — нет; наконец и просто общечеловеческий здравый смысл. По моим уже многолетним наблюдениям, для того, чтобы написать полноценный учебник для n-го класса, необходимо (но, разумеется, не достаточно) свободно владеть материалом за 2, 5n или даже 3n классов.

К сожалению, убедить в этом не только автора, но и многих других представителей педагогического сообщества довольно трудно.»[4]

2.6. Краткое содержание учебников курса.

Учебник плохо систематизирован: отсутствует оглавление, как по книгам, так и в целом, что существенно увеличило время, затраченное на анализ текстов учебника. Вероятно, аналогичные трудности навигации по тексту, при поиске необходимого материала, испытывают, при использовании учебника, учащиеся и их родители.
Для дальнейшего использования, прикладываю содержание, составленное самостоятельно

1 часть:

Работа с последовательностями, группами, размером, сходствами и различиями. Понятия суммы и разности. Числа до 6.

2 часть:

Числа до 9. Ноль. Вводится понятие «Задача». В учебнике появляются классические текстовые задачи. Работа с геометрическим материалом.

3 часть:

Длина, масса, объем. Составные именованные числа. 10. Счет десятками. Счет от 10 до 20.

Двузначные числа. Сложение без перехода через десяток.

Табличное сложение с переходом через десяток

Обычное сложение с переходом через десяток.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:

[1] «Автора к доске!» Российская Газета 2010.08.03
[2] Приказ Министерства образования и науки РФ от 31 марта 2014 г. № 253
[3] В.А. Васильев. Экспертиза учебников 2005-2010 г.
[4] В.А. Васильев. Докладная записка в связи с письмом Л.Г. Петерсон от 22.12.2008

swayn.livejournal.com

математика / Сравнение чисел / Математика

Возможно, здесь есть какое-то более короткое решение, но числа довольно близки друг к другу, поэтому какие-то вычисления могут потребоваться.

Итак, надо сравнить $%\sqrt[3]{51}$% и $%2+\sqrt[3]{5}$%. Возведём в куб каждое из чисел, пользуясь тем, что функция $%y=x^3$% монотонно возрастает. Знак неравенства останется тем же, а сравнить теперь надо $%51$% и $%8+5+3(4\sqrt[3]{5}+2\sqrt[3]{5}^2)$%. Это равносильно задаче сравнения между собой чисел $%19/3$% и $%2\sqrt[3]{5}+\sqrt[3]{5}^2$%.

Рассмотрим квадратное уравнение $%x^2+2x-19/3=0$%. Его положительный корень равен $%x=\sqrt{22/3}-1$%. Если мы сумеем сравнить это число с $%\sqrt[3]{5}$%, то задача будет решена. Дело в том, что на положительной полуоси квадратный трёхчлен возрастает, и отсюда будет следовать нужный нам вывод.

Фактически нам нужно сравнить $%x^3$% и $%5$%. Эта задача выглядит проще изначальной, потому что осталась всего одна квадратичная иррациональность. Однако возводить число $%x$% в куб напрямую не очень желательно. Здесь нам может прийти на помощь алгебра: возведение в куб мы осуществим в буквенном виде.

Мы знаем, что $%x^2=19/3-2x$%. Домножим на $%x$%, и далее избавимся от $%x^2$% по тому же принципу: $%x^3=19x/3-2x^2=19x/3-2(19/3-2x)=19x/3-38/3+4x=(31x-38)/3$%. Мы сравниваем это число с $%5$%, то есть $%31x-38$% с $%15$%, или $%31x$% с $%53$%. Вспоминаем, что $%x=\sqrt{22/3}-1$%, то есть сравнить надо $%31\sqrt{22/3}$% и $%53+31=84$%. Это делается возведением в квадрат, и после домножения на $%3$% и сокращения на $%2$% требуется сравнить $%31^2\cdot11=961\cdot11=10571$% и $%3\cdot42\cdot84=10584$%. Второе число оказывается чуть больше (фактически, только здесь нам потребовались небольшие вычисления на уровне перемножения чисел «столбиком»).

Итак, мы установили, что $%x < \sqrt[3]{5}$%. Это значит, что если мы подставим последнее из чисел в квадратный трёхчлен $%x^2+2x-19/3$%, то результат будет больше нуля. Значит, $%19/3 < 2\sqrt[3]{5}+\sqrt[3]{5}^2$%, откуда $%\sqrt[3]{51} < 2+\sqrt[3]{5}$%.

Возможно, кто-то из участников форума сможет предложить менее трудоёмкое решение.

Добавление. Вот ещё один способ решения — он более искусственный, но зато почти не требует вычислений.

Положим $%y=\sqrt[3]{51}-\sqrt[3]{5}$%. Мы хотим доказать, что $%y < 2$%.

Из формулы $$a-b=\frac{a^3-b^3}{a^2+ab+b^2}=\frac{a^3-b^3}{(a-b)^2+3ab}, $$ применённой для чисел $%a=\sqrt[3]{51}$% и $%b=\sqrt[3]{5}$%, следует, что $$y=\frac{46}{y^2+3\sqrt[3]{255}}.$$ Для начала проверим, что $%\sqrt[3]{255} > 19/3$%. Это видно из следующего простого вычисления: $%(19/3)^3=(6+1/3)^3=6^3+3\cdot6^2/3+3\cdot6/3^2+1/3^3=216+36+2+1/27 < 255$%. Таким образом, из предыдущих формул следует, что $$y < \frac{46}{y^2+19},$$ то есть $%y^3+19y < 46$%. Это значит, что $%y < 2$%, так как функция $%f(x)=x^3+19x$% возрастает, а $%f(2)=46$%.

math.hashcode.ru

Материал по математике (2 класс) по теме: Сравнение величин. Уравнения.

Сравнение величин. Уравнения.

19см * 2дм                          60мм * 60см                             9 + Х =14

40см * 4дм                          10мм * 1см                               Х + 7 =10

1дм3см * 30см                    12мм * 1см                              7 – Х = 2

1дм5см * 50см                    9см * 1дм                                 5 – Х = 4

2дм * 12см                          56мин * 1ч                                Х – 1 = 0

7дм * 70см                          1ч * 100мин                               10 – Х = 5

1см * 9мм                            20см * 2дм5см                         Х + 5 = 0

20мм * 2см                          45см * 5дм                                Х + 3 = 4

1см8мм * 18мм                   54мм * 5см                               60 + Х = 90

2см1мм * 3см                      80мм * 8см                                Х + 3 = 13

9мм * 1см                             50мин * 1ч                                 18 = Х + 7

1см * 10мм                          70мин * 1ч10мин                       Х + 7 =14

1дм * 10см                          1см2мм * 14мм                          Х + 8 = 18

1дм * 10мм                          2м6дм * 30дм                            Х – 3 = 7

1м * 99см                            12мм * 2см                                47 – Х = 40

1м * 9дм                              26дм * 1м                                  50 – Х = 40

10см * 1м                             1ч * 59мин                                 Х – 8 = 2

1м * 100см                           1м * 59см                                   Х + 3 = 13

1дм * 100мм                        5дм-20см                                    Х + 28 = 28                    

1см * 10мм                          6см-40мм                                    Х – 0 = 14

3м2дм * 32дм                                                                          10 – Х = 6

2м8дм * 30дм                                                                          64 – Х = 4

1дм2см * 14см                                                                        Х – 9 = 17

2дм3см * 23см                                                                         Х + 2 = 20

7м * 9дм                                                                                   Х – 4 = 12

1м * 99см                                                                                 16 – Х = 16

25мм * 3см

48см * 4дм

16мм * 1см

5м * 4м9дм

3см * 29мм

38мм * 4см

5дм * 1м

1см8мм * 20мм

23мм * 2см

45см * 4дм5см

36см * 4дм

1дм * 100мм

24мм * 3см

nsportal.ru

Сравнение чисел. Математика, 6 класс: уроки, тесты, задания.

1.	Целое число и 0 Сложность: среднее	1
2.	Положительное и отрицательное число (десятичные дроби) Сложность: среднее	1
3.	Смешанное число между двумя целыми числами Сложность: лёгкое	1
4.	Сравнение Сложность: среднее	2
5.	Сравнение отрицательных десятичных дробей Сложность: среднее	2
6.	Наибольшее/наименьшее число Сложность: среднее	2
7.	Предложение в виде неравенства Сложность: среднее	2
8.	Числа в порядке возрастания Сложность: среднее	4
9.	Сравнение буквенных выражений Сложность: сложное	3
10.	Сравнение отрицательных обыкновенных дробей (звёздочка) Сложность: сложное	3
11.	Сравнение отрицательных десятичных дробей (звёздочка) Сложность: сложное	3

www.yaklass.ru

Целые числа, сравнения — дискретная математика

---

Z = {…, -3, -2, -1, 0, 1, 2, 3, …}, N={0,1,2,3,…}, N₊ = {1,2,3,…}
Теорема (деления целых чисел): Пусть b∈N₊. Пусть всякое a∈Z единственным образом представимо в виде a=b*q+r, 0≤0Теорема: Для всяких целых a≥1, h≥r, при некотором S≥0 существует единственное представление a в виде a=a_Sh^S + a_S-1h^S-1 + … + a₁h¹ + a₀, где 0≤a_i≤h-1 (i=0,1,…,S-1), 1≤a_S≤h-1.

Замечание: Представление a=a_Sh^S + a_S-1h^S-1 + … + a₁h¹ + a₀ есть представление целого числа a в h- ичной системе счисления.
a=(a_S,a_S-1, …, a

1, a₀)

Определение: Натуральное число p≤r простое, если p делится только на 1 и на само себя.

Замечание: Существует бесконечно много простых чисел.

Теорема (Основная теорема арифметики): Всякое целое число, большее 1, можно единственным образом представить в виде произведения простых множителей (с точностью до их порядка).

Замечание: по теореме о факторизации a=p₁^a1*p₂^a2*…*p_k^ak — каноническая факторизация (p₁ < p₂<…<p_k). Иногда в каноническую факторизацию включают отсутствующий множитель в нулевой степени для всех простых чисел от «2» до «p_k».

Факторизация простых чисел считается технически трудно осуществимой. Например, число b -120 десятичных знаков для факторизации потребует миллионы лет компьютерного времени.

Определение: Общий делитель ОД (a,b,…,l) для a,b,…,l делит все эти числа. Наибольший общий делитель НОД (a,b,…,l) есть максимум из всех общих делителей для a,b,…,l.

НОД (0,0,…,0)=0.

Теорема: Если a>1, b>1 и их одиночные факторизации a=p₁^a1*p₂^a2*…*p_S^aS, b=p₁^a1*p₂^a2*…*p_S^aS, где p₁,p₂,…,p_s есть все различные простые делители для a и b, то НОД(a,b)=p₁^min(a1,b1)*p₂^min(a2,b2)*…*p_S^min(aS,bS).

Замечание: Теорема переносится на несколько чисел.

Теорема: ∀a₁,…,a_n∈Z, ∃ λ₁, …, λ_n∈Z такие, что НОД (a₁,…,a_n)=∑λ_i*a_i.

Замечание: ∀a₁, a₂∈Z, ∃λ₁, λ₂∈Z такие, что НОД (a

1,a₂)=λ₁*a₁ + λ₂a₂.

Существует расширенный алгоритм Евклида для вычисления λ₁ и λ₂.

Определение: Общее кратное ОК (a,b,…,l) чисел a,b,…,l есть всякое число, кратное каждому из чисел a,b,…,l, т.е. число, делящееся на каждое из a,b,…,l. Наименьшее общее кратное НОК (a,b,…,l) есть минимум из всех общих кратных для a,b,…,l.

Теорема: Если a=p₁^a1*p₂^a2*…*p_S^aS и b=p₁^a1*p₂^a2*…*p_S^aS есть канонические факторизации для a и b, где p₁,p₂,…,p_s есть все различные простые делители для a и b, то НОК(a,b) = p₁^max(a1,b1)*p₂^max(a2,b2)*…*p_S^max(aS,bS).

Замечание: [a₁,…,a_n] = a₁,…,a_n/(a₁,…,a_n).

Определение: Функция Эйлера a и φ(a), которые взаимно просты с a.

Замечание: Целые a и b взаимно просты если НОД(a,b)=1.

Определение: Целые числа a и b сравнимы по mod m (a≡b(mod m)), если (a-b):m.

Теорема: Следующие утверждения эквивалентны:
1) (a≡b(mod m)).
2) (a-b):m.
3) Остатки от деления a и b на m одинаковы, т.е. a и b при делении на дают один и тот же остаток.

Замечание: Отношение сравнения целых чисел есть отношения эквивалентности.

Определение: Класс вычетов по mod m есть множество всех чисел, сравнимых между собой по mod m.

Замечание: Класс C_r = {a = m*q + r: q ∈Z, 0≤z≤m-1}.

Определение: Вычет по mod m есть любое число из класса вычетов по mod m.
Пусть m=5.
…-10,-5,0,5,10,… класс C₀
…-9,-4,1,6,11,… класс C₁
……
…-6,-1,4,9,14,… класс C₄

Полная система вычетов есть любой набор вычетов по одному из каждого класса.
Наименьшая неотрицательная полная система вычетов Z_m = {0,1,..,m-1}.

Теорема: Если НОД(a,m) и x пробегает полную систему вычетов для Z_m.

Замечание: Можно ввести операции над классами вычетов, связав их с операциями в Z_m.
a + b(mod m) = rest(a+b, m)
a * b(mod m) = rest(a*b, m)
где операция rest — остаток. Это модульные операции.

all4study.ru