Умножение матриц
Каталин Дэвид
Чтобы можно было умножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Алгоритм умножения матриц
Умножаем элементы в строках первой матрицы на элементы в столбцах второй матрицы.
- Умножаем элементы первой строки на элементы первого столбца.
- Умножаем первый элемент первой строки на первый элемент первого столбца.
- Умножаем второй элемент первой строки на второй элемент первого столбца.
- Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и первого столбца второй матрицы.
- Складываем полученные произведения.
- Полученный результат будет первым элементом первой строки произведения матриц.
- Умножаем элементы первой строки первой матрицы на элементы второго столбца второй матрицы.
- Умножаем первый элемент первой строки на первый элемент второго столбца.
- Умножаем второй элемент первой строки на второй элемент второго столбца.
- Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и второго столбца второй матрицы.
- Складываем полученные произведения.
- Полученный результат будет вторым элементом первой строки произведения матриц.
- Применяя тот же самый алгоритм, умножаем элементы первой строки первой матрицы на элементы остальных столбцов второй матрицы. Полученные числа составят первую строку вычисляемой матрицы.
- Вторая строка вычисляемой матрицы находится аналогично умножением элементов второй строки первой матрицы на элементы каждого столбца второй матрицы: результаты записываются в новую матрицу после каждого суммирования.
- Делаем это с каждой строкой первой матрицы, пока все строки новой матрицы не будут заполнены.
Пример 7
$A= \begin{pmatrix} 1 & 2 & 2\\ 3 & 1 & 1 \end{pmatrix}$
Заметим, что матрица A имеет 3 столбца, а матрица B имеет 3 строки, значит, их можно перемножить.
$A \cdot B=$ $\begin{pmatrix} \color{red}1 &\color{blue}2 & \color{green}2\\ \color{red}3 &\color{blue}1 & \color{green}1 \end{pmatrix} \begin{pmatrix} \color{red}4 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \\ \color{green}1 & \color{green}5 \end{pmatrix}=$ $\begin{pmatrix} \color{red}{1\cdot4}+\color{blue}{2\cdot3}+\color{green}{2\cdot1} & \color{red}{1\cdot2}+\color{blue}{2\cdot1}+\color{green}{2\cdot5}\\ \color{red}{3\cdot4}+\color{blue}{1\cdot3}+\color{green}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}+\color{green}{1\cdot5} \end{pmatrix}=$ $\begin{pmatrix} 12 & 14\\ 16 & 12\\ \end{pmatrix}$$B \cdot A = \begin{pmatrix} \color{red}4 &\color{blue}2 \\ \color{red}3 & \color{blue}1 \\ \color{red}1 & \color{blue}5 \end{pmatrix} \begin{pmatrix} \color{red}1 &\color{red}2 & \color{red}2\\ \color{blue}3 &\color{blue}1 & \color{blue}1 \end{pmatrix}=$
$\begin{pmatrix} \color{red}{4\cdot1}+\color{blue}{2\cdot3} & \color{red}{4\cdot2}+\color{blue}{2\cdot1} & \color{red}{4\cdot2}+\color{blue}{2\cdot1}\\ \color{red}{3\cdot1}+\color{blue}{1\cdot3} & \color{red}{3\cdot2}+\color{blue}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}\\ \color{red}{1\cdot1}+\color{blue}{5\cdot3} & \color{red}{1\cdot2}+\color{blue}{5\cdot1} & \color{red}{1\cdot2}+ \color{blue}{5\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 10 & 10 & 10 \\ 6 & 7 & 7 \\ 16 & 7 & 7 \end{pmatrix}$
Заметим, что $A \cdot B \neq B \cdot A$
Пример 8
$A= \begin{pmatrix} 5 & 2 \\ 3 & 1 \end{pmatrix} B= \begin{pmatrix} 4 & 6 \\ 5 & 2 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}5 & \color{blue}2 \\ \color{red}3 & \color{blue}1 \end{pmatrix} \cdot \begin{pmatrix} \color{red}4 & \color{red}6 \\ \color{blue}5 & \color{blue}2 \end{pmatrix} =\begin{pmatrix} \color{red}{5\cdot4}+\color{blue}{2\cdot5} & \color{red}{5\cdot6}+\color{blue}{2\cdot2} \\ \color{red}{3\cdot4}+\color{blue}{1\cdot5} & \color{red}{3\cdot6}+\color{blue}{1\cdot2} \end{pmatrix} =$ $\begin{pmatrix} 30 & 34\\ 17 & 20 \end{pmatrix}$
$B \cdot A= \begin{pmatrix} \color{red}4 & \color{blue}6 \\ \color{red}5 & \color{blue}2 \end{pmatrix} \cdot \begin{pmatrix} \color{red}5 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \end{pmatrix} =\begin{pmatrix} \color{red}{4\cdot5}+\color{blue}{6\cdot3} & \color{red}{4\cdot2}+\color{blue}{5\cdot1} \\ \color{red}{5\cdot5}+\color{blue}{2\cdot3} & \color{red}{5\cdot2}+\color{blue}{2\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 38 & 14\\ 31 & 12 \end{pmatrix}$
Опять-таки $A \cdot B \neq B \cdot A$.
$A= \begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix} B= \begin{pmatrix} 5 & 2 & 1 \\ 4 & 3 & 2 \\ 2 & 1 & 5 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}{1} & \color{blue}{4} & \color{green}{3} \\ \color{red}{2} & \color{blue}{1} & \color{green}{5}\\ \color{red}{3} & \color{blue}{2} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{5} & \color{red}{2} & \color{red}{1} \\ \color{blue}{4} & \color{blue}{3} & \color{blue}{2} \\ \color{green}{2} & \color{green}{1} & \color{green}{5} \end{pmatrix}=$
$\begin{pmatrix} \color{red}{1\cdot5} + \color{blue}{4\cdot4} + \color{green}{3\cdot2} & \color{red}{1\cdot2} + \color{blue}{4\
www.math10.com
1.3.4. Примеры решения задач по теме «Обратная матрица»
Задача 1.
Найти обратную матрицу для матрицы
И проверить выполнение условий А А-1 = А-1А = Е.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Убедимся, что матрица А – невырожденная. ΔА = 1·4 — 2·(-1) ≠ 0, следовательно, А-1 существует.
Вычислим алгебраические дополнения к элементам А:
Применим способ вычисления обратной матрицы:
.
Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам Транспонированной матрицы! |
Найдем произведения А А-1 и А-1А:
Таким образом, найденная матрица А-1 отвечает определению обратной матрицы.
Ответ: .
Задача 2.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Следовательно, матрица А невырожденная, и обратная матрица существует.
Вычислим алгебраические дополнения к элементам матрицы А:
Обратная матрица имеет вид:
Ответ: .
Задача 3.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Вычислим определитель матрицы А разложением по первому столбцу:
.
Следовательно, обратная матрица для матрицы А существует.
Найдем алгебраические дополнения к элементам матрицы А:
Значит,
.
Ответ: .
Задача 4.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
.
Ответ:
Задача 5.
При каких X, Y, Z матрица
Является обратной к матрице
Указание
Необходимым условием того, что В = А-1, является требование АВ = Е.
Решение
Проверим невырожденность матрицы А:
Необходимым условием того, что В = А-1, является требование АВ = Е.
Найдем АВ:
Для того, чтобы выполнялось условие АВ = Е, X, Y, Z должны быть решением системы уравнений
Проверим, будет ли равно единичной матрице произведение ВА:
Значит, при найденных значениях
Ответ: X = -3, Y = -3, Z = 4.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
3. Обратная матрица. Решение матричных уравнений
Матрица  называется обратной к квадратной матрице
называется обратной к квадратной матрице  ,
если
,
если
,
где 
 . Обратная
матрица существует только в том случае,
если,
и ее элементы находятся по формуле
. Обратная
матрица существует только в том случае,
если,
и ее элементы находятся по формуле 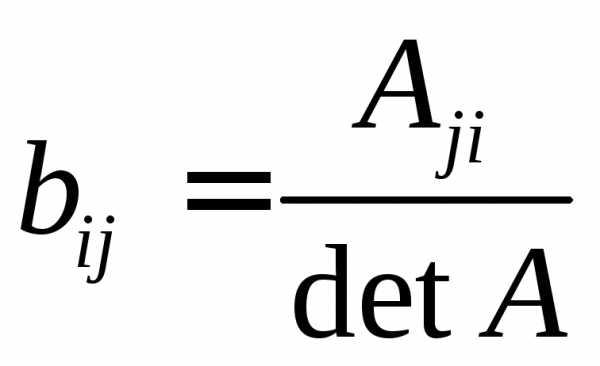 ,
,
где  — алгебраическое дополнение к элементу
— алгебраическое дополнение к элементу .
.
Внимание! Алгебраические дополнения вычисляются к элементам строки, а записываются в столбец.
Если
,
то матрица называетсявырожденной,
в противном случае невырожденной, т.е. обратная матрица существует только
для невырожденных матриц.
называетсявырожденной,
в противном случае невырожденной, т.е. обратная матрица существует только
для невырожденных матриц.
Обозначается
обратная матрица 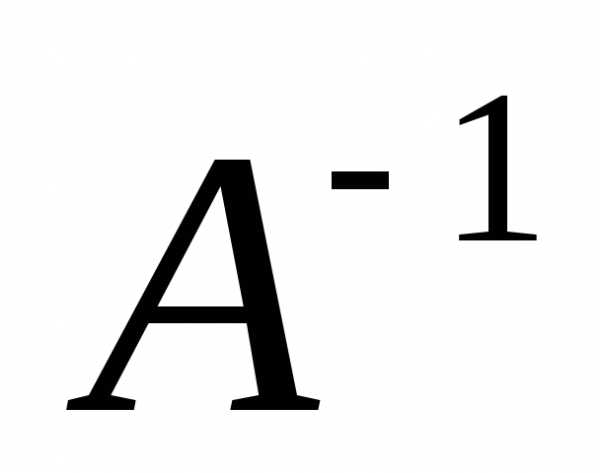 ,
т.е.
,
т.е.
,
при этом ее
определитель 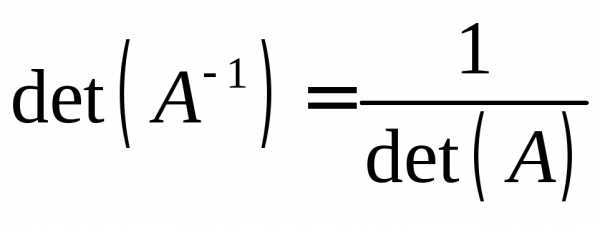 .
.
Для невырожденных
матриц  и
и выполнены соотношения
выполнены соотношения
,
.
Введение обратной матрицы позволяет решать матричные уравнения. В конечном счете, матричные уравнения сводятся к двум простейшим уравнениям:
или .
Если матрица  — квадратная, невырожденная, то эти
уравнения имеют единственное решение,
которое можно получить с помощью обратной
матрицы. Так как при умножении матриц
коммутативный закон не выполняется,
указанные уравнения имеют различные
решения.
— квадратная, невырожденная, то эти
уравнения имеют единственное решение,
которое можно получить с помощью обратной
матрицы. Так как при умножении матриц
коммутативный закон не выполняется,
указанные уравнения имеют различные
решения.
При поиске решения
первое из уравнений надо умножать на
обратную матрицу 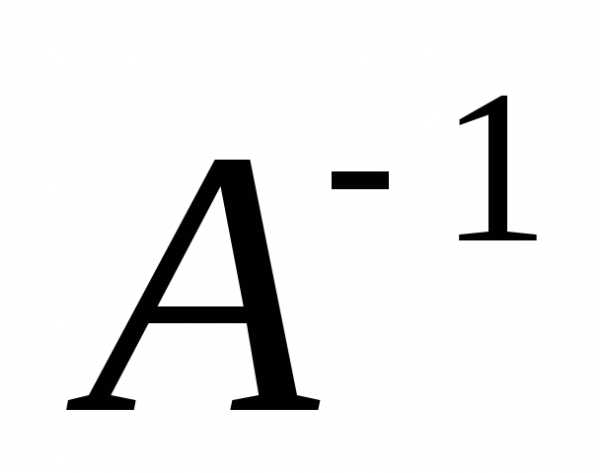 слева, а второе справа, т.е.
слева, а второе справа, т.е.
, (5)
. (6)
►Пример 5. Найти
решение матричного уравнения
,
то есть определить матрицу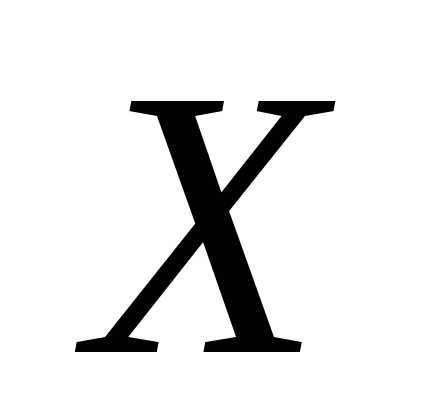 ,
если
,
если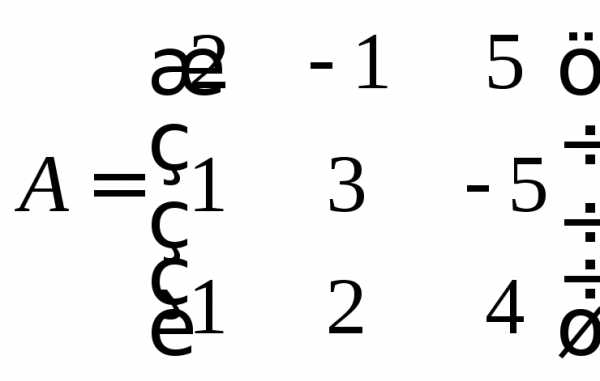 ;
;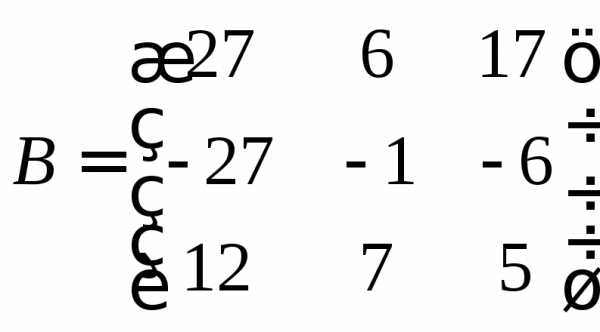 .
.
Решение.
Решение в матричном
виде определяется формулой (5), т.е.
,
если матрица невырожденная. Вычислим определитель
матрицы
невырожденная. Вычислим определитель
матрицы :
:
.
Следовательно,
матрица  невырожденная, и для нее существует
обратная матрица. Проведем вычисления,
необходимые для построения обратной
матрицы. Вычислим алгебраические
дополнения:
невырожденная, и для нее существует
обратная матрица. Проведем вычисления,
необходимые для построения обратной
матрицы. Вычислим алгебраические
дополнения:

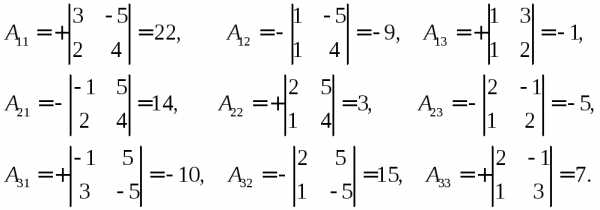
Составим обратную
матрицу 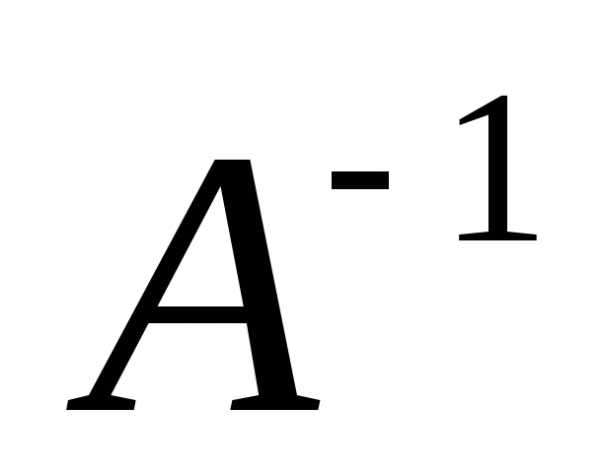 и
найдем неизвестную матрицу
и
найдем неизвестную матрицу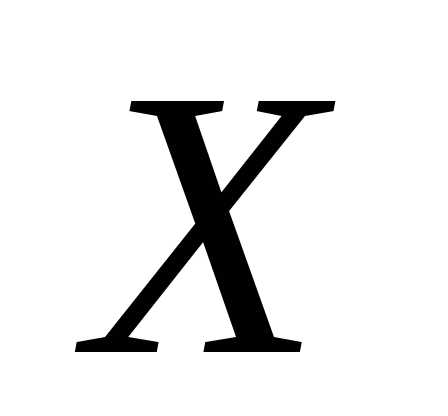 .
.
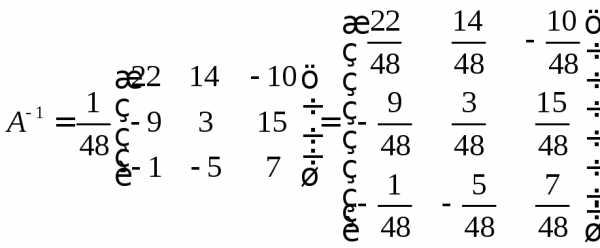 ,.
◄
,.
◄
При вычислениях
множитель 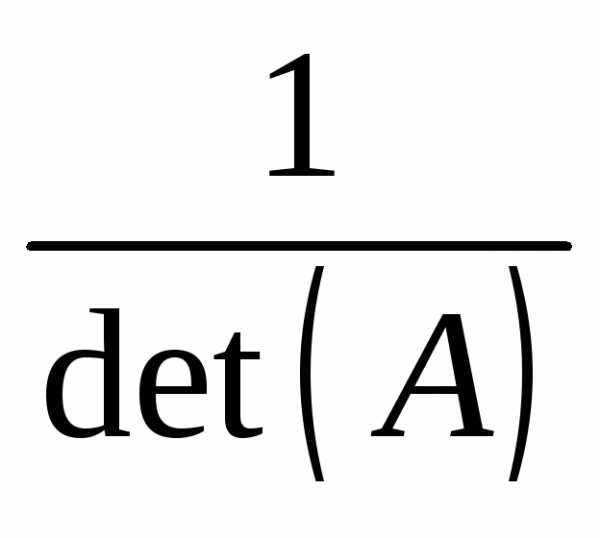 лучше оставлять перед матрицей и
проводить умножение полученной матрицы
на него на последнем этапе вычислений.
лучше оставлять перед матрицей и
проводить умножение полученной матрицы
на него на последнем этапе вычислений.
►Пример 6. Найти решение матричного уравнения
,
если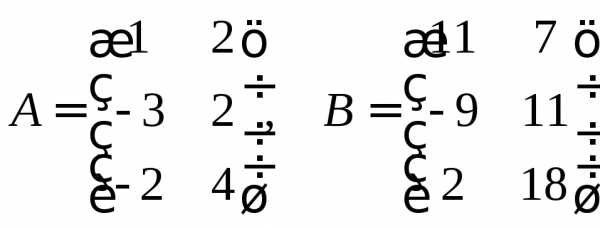 .
.
Решение.
Формулой (5)
воспользоваться нельзя, так как матрица  не квадратная, следовательно, для нее
не существует обратной матрицы. Умножим
обе части уравнения на транспонированную
матрицу
не квадратная, следовательно, для нее
не существует обратной матрицы. Умножим
обе части уравнения на транспонированную
матрицу слева,
получаем
слева,
получаем
.
Матрица 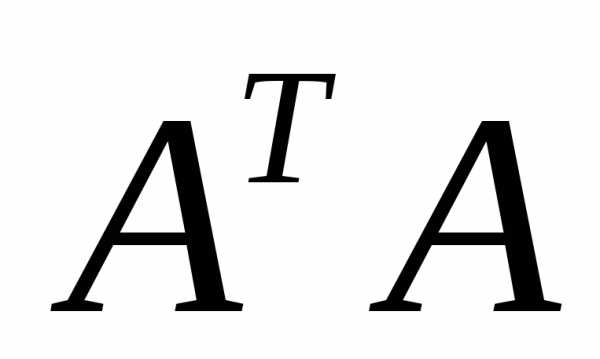 − квадратная и, если ее определитель
не равен нулю, то решение заданного
уравнения имеет вид
− квадратная и, если ее определитель
не равен нулю, то решение заданного
уравнения имеет вид
. .
Проведем вычисления:
.
Определитель
полученной матрицы
.
Следовательно, обратная матрица к
матрице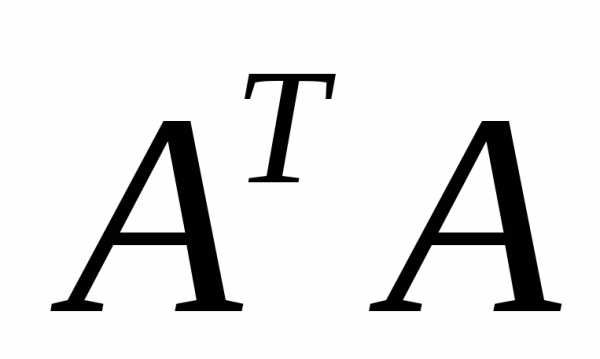 существует, и можно найти матрицу
существует, и можно найти матрицу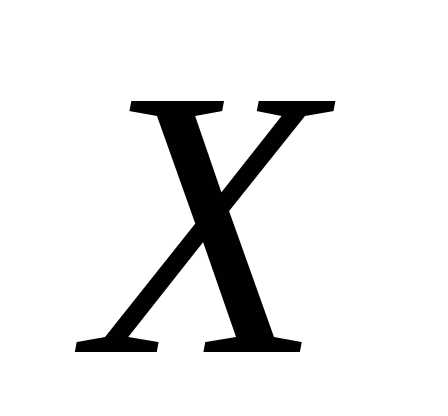 .
.
,
,
.
Итак, неизвестная
матрица 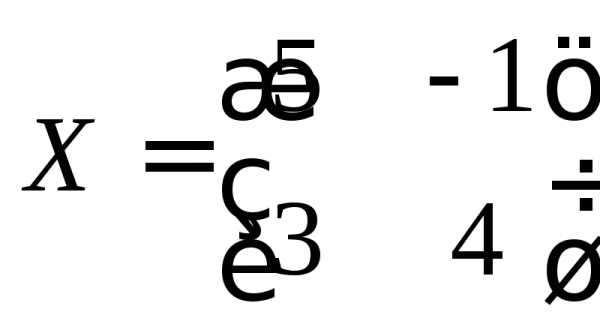 .
◄
.
◄
Упражнения.
1. Для заданных матриц найти обратную матрицу:
а)  ;
б)
;
б)  ; в)
; в) 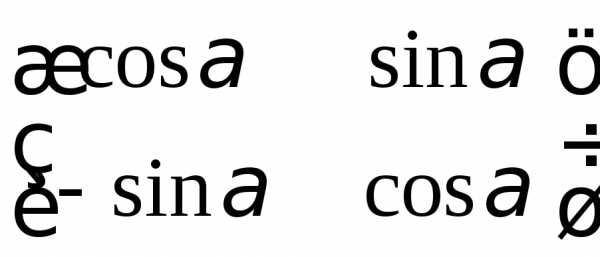 ; г)
; г) 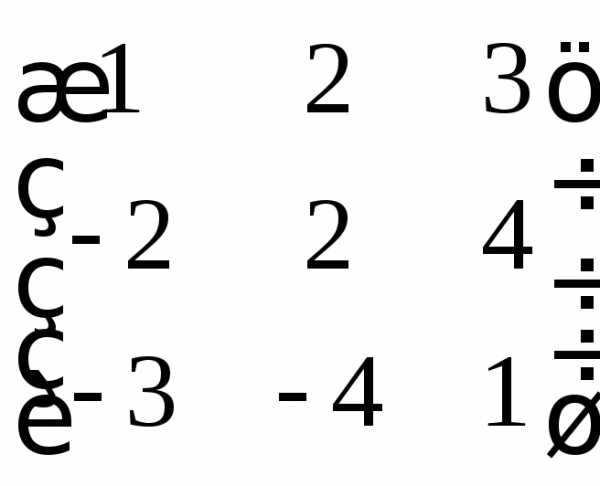 ; д)
; д)  .
.
Ответы:
а) 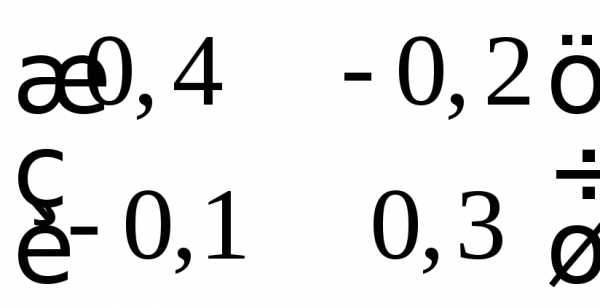 ;
б)
;
б) 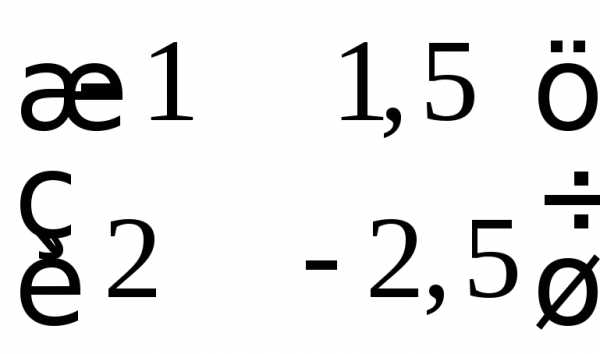 ; в)
; в) 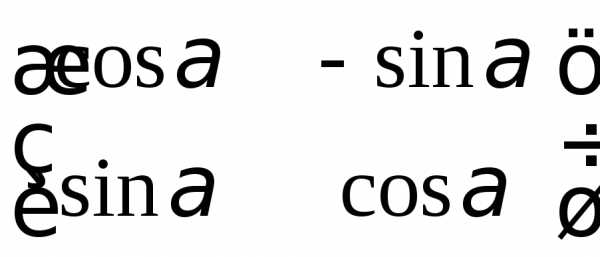 ;
г)
;
г) 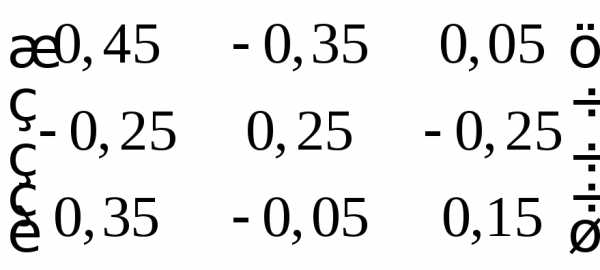 ;
;
д) 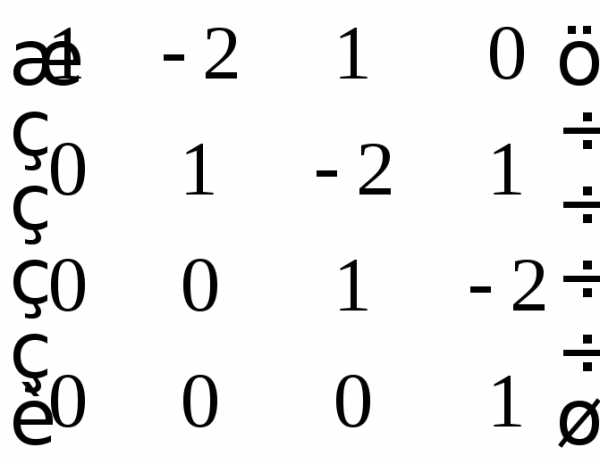 .
.
2. Найти неизвестную матрицу из уравнений:
а) ; б); в) ;
г) ; д).
Ответы:
а) 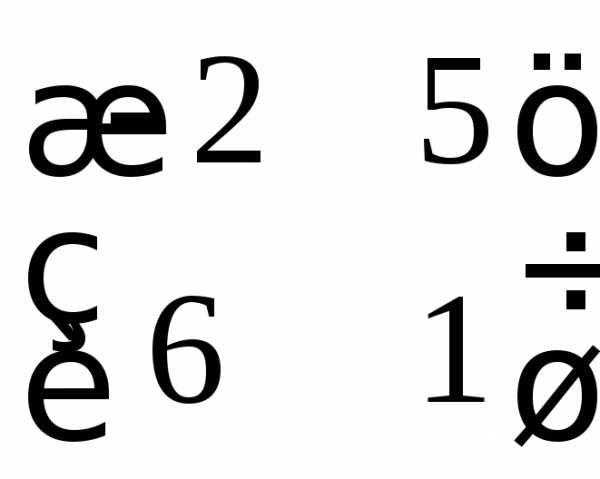 ;
б)
;
б)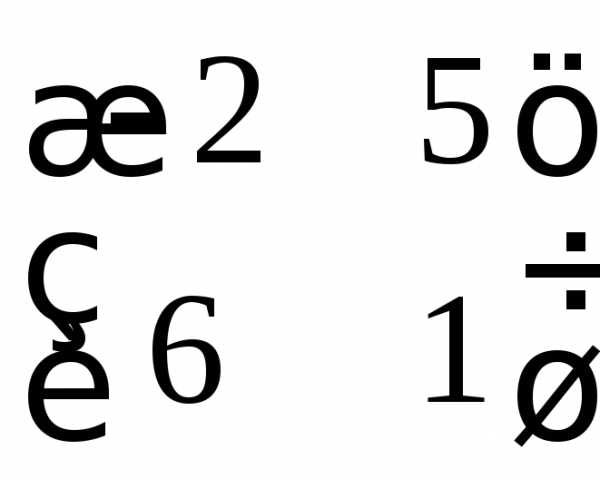 ;
в)
;
в)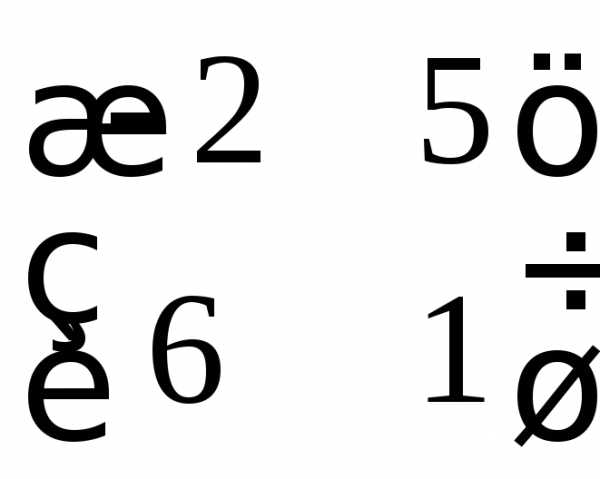 ;
г)
;
г) ;
д)
;
д) .
.
studfiles.net
2.3. Решить матричное уравнение
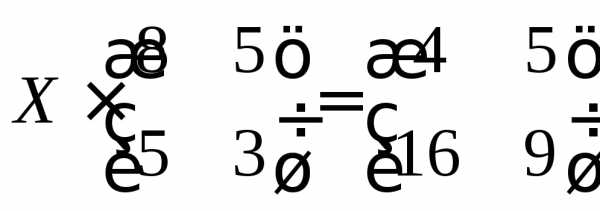
В общем виде уравнение решается
Умножим обе стороны на А-1 справа.
Нам необходимо найти обратную матрицу и выполнить умножение.
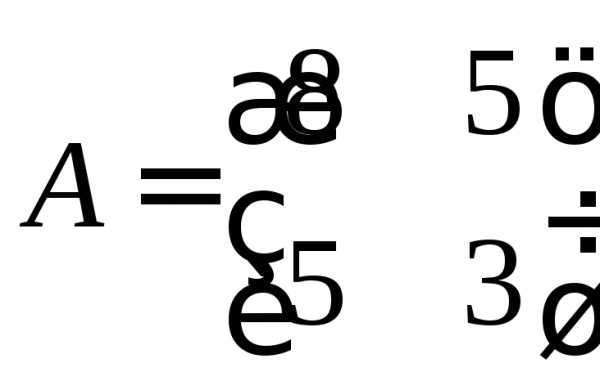 ,
,
,
,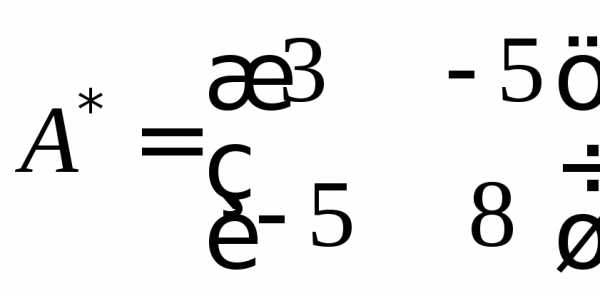
, 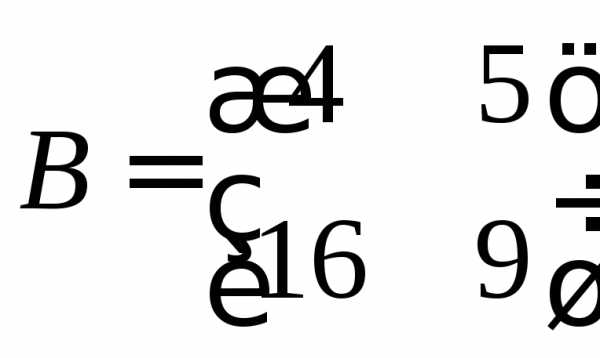
Ответ: 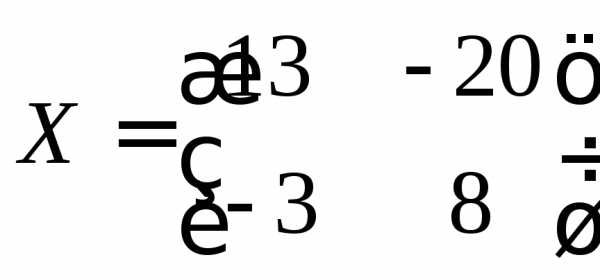 .
Чтоб убедиться в правильности, можно
выполнить проверку.
.
Чтоб убедиться в правильности, можно
выполнить проверку.
Примечание. Имеет больше значение то, с какой стороны находится Х.
Решение систем линейных уравнений
Дана система линейных алгебраических уравнений
Необходимо решить данную систему. Прежде всего, нужно найти определитель матрицы коэффициентов. Если определитель равен нулю, то система не имеет решения.
Далее показано три метода решения.
3.1. Решить методом Гаусса
Для удобства выпишем матрицу коэффициентов
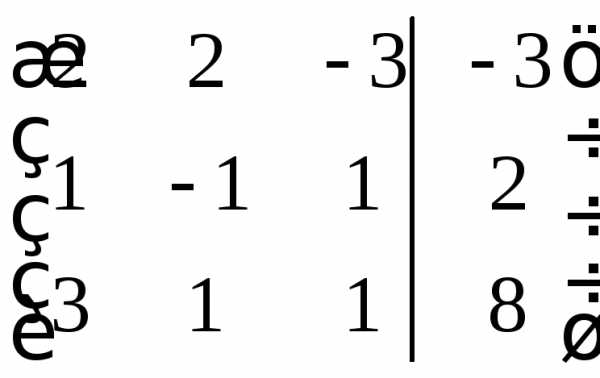
Далее, нам нужно привести матрицу к треугольному виду, т.е. чтоб ниже главной диагонали были нули, а на диагонали – единицы. Для удобства, также поменяем первую и вторую строки местами для того чтоб верхний левый элемент был равен единице (что делать не обязательно).
Ко второй строке прибавим первую, умноженную на (-2), для того, чтоб первый элемент второй строки стал равным нулю. Какими станут значения других элементов этой строки, пока что нас не волнует.
К третьей строке прибавим первую, умноженную на (-3), для того, чтоб первый элемент третьей строки стал равным нулю.
К третьей строке прибавим вторую, умноженную на (-1), для того, чтоб второй элемент третьей строки стал равным нулю.
Приведя матрицу к требуемому виду можно находить значения неизвестных:
Откуда получим ответ
Ответ: 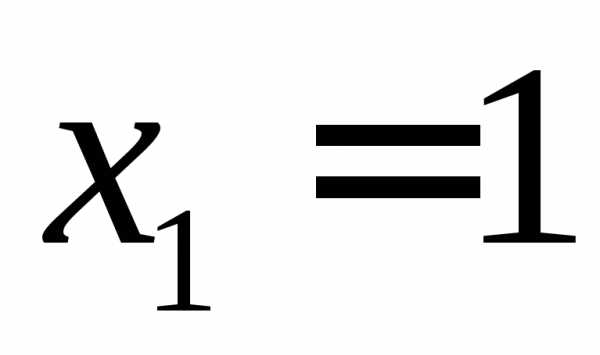 ,
,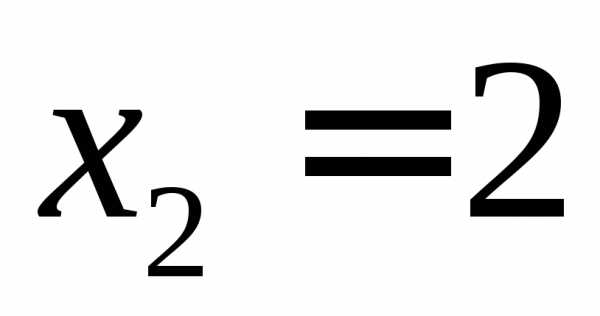 ,
,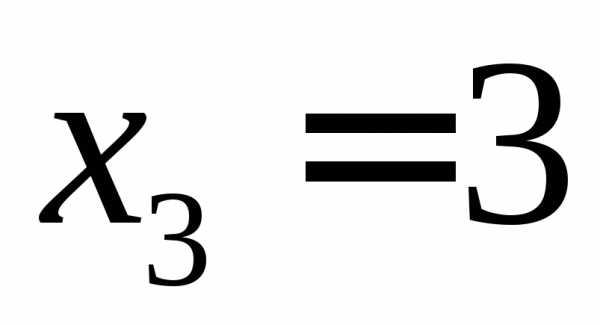 .
.
Ответ можно было также найти при дальнейшем преобразовании матрицы. Для этого нужно привести матрицу коэффициентов при неизвестных к виду единичной матрицы.
Из последнего, можно увидеть, чему равна каждая неизвестная.
Ответ: 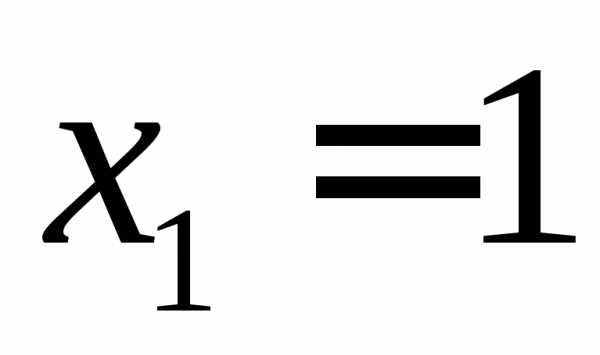 ,
,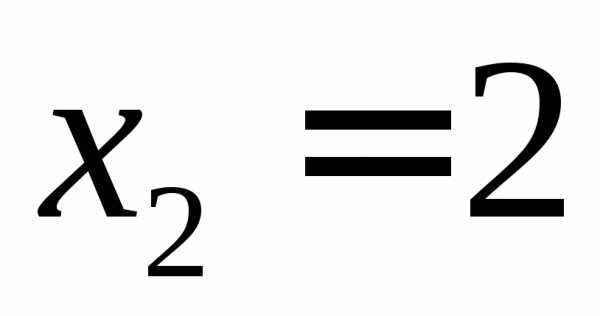 ,
,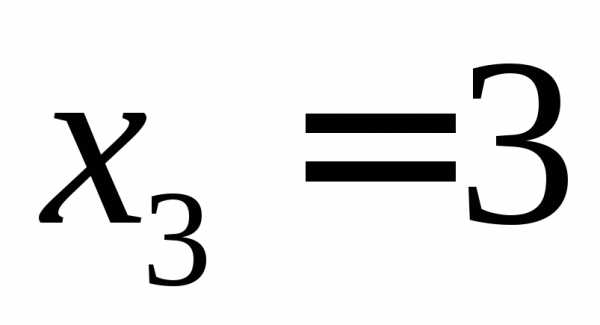 .
.
Примечание. Метод Гаусса, на первый взгляд может показаться запутанным, однако, но является наименее трудозатратным и широко применяется.
3.2. Решить по правилу Крамера.
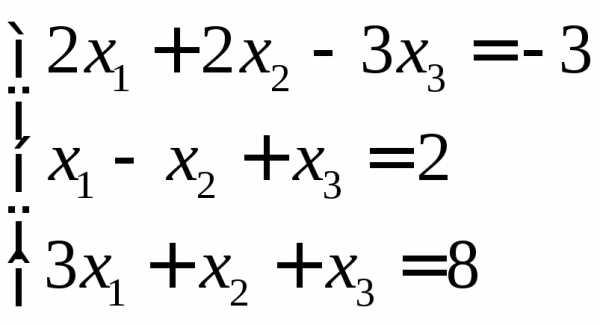
Выпишем матрицу коэффициентов
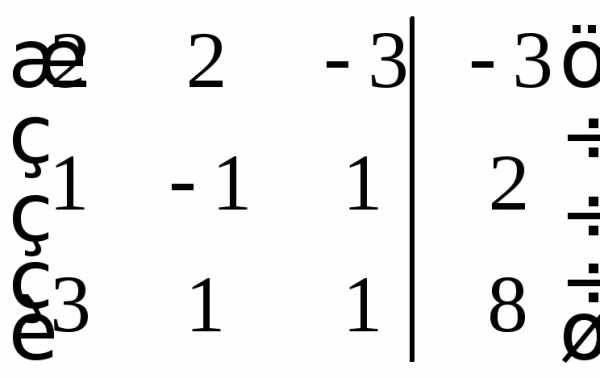
Найдём основной
и дополнительные определители.
Определитель ещё обозначается символом  .
.
Находим неизвестные
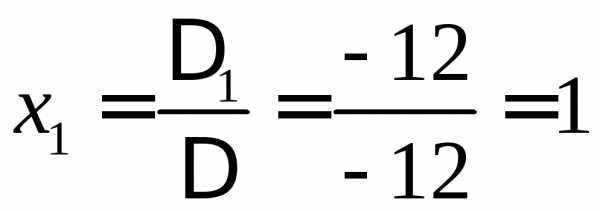 ,
, 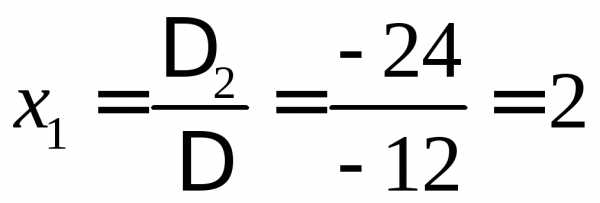 ,
,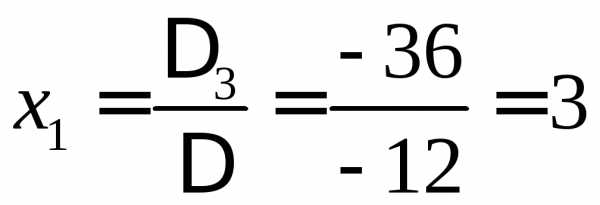
Ответ: 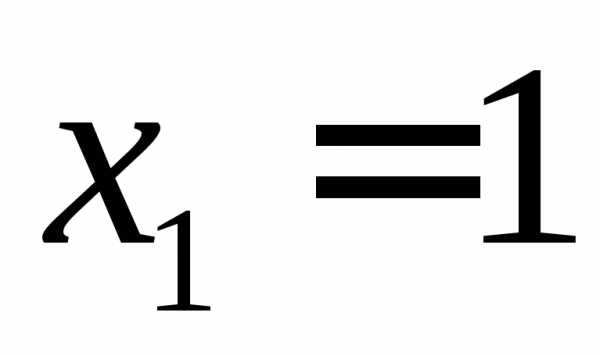 ,
,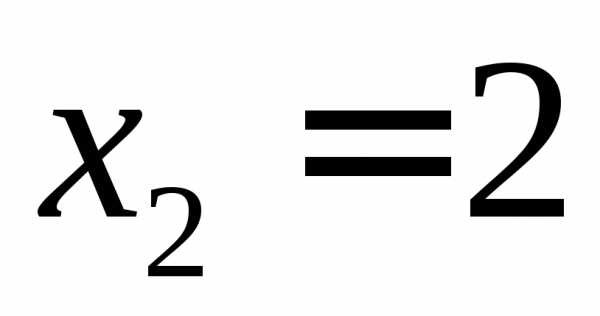 ,
,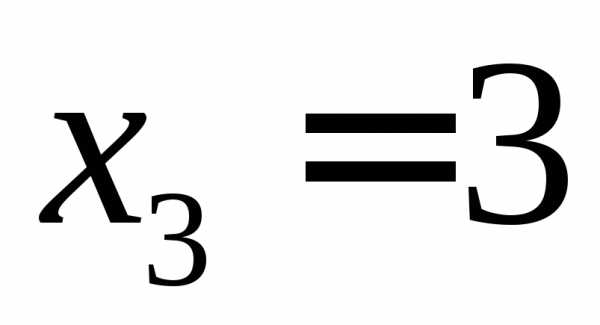 .
.
Данный метод кажется простым, но это только для системы с тремя неизвестными, при увеличении количества уравнений сложность резко возрастает.
3.3. Решить матричным методом.
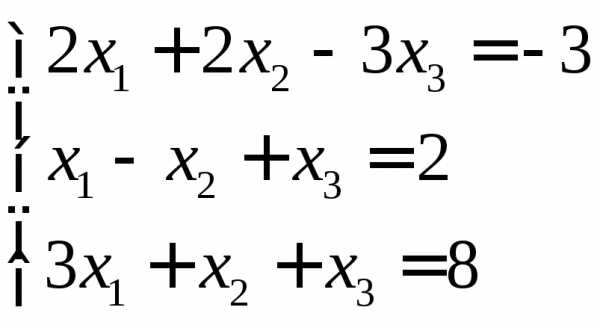
Решение матричного уравнения в общем виде
, где
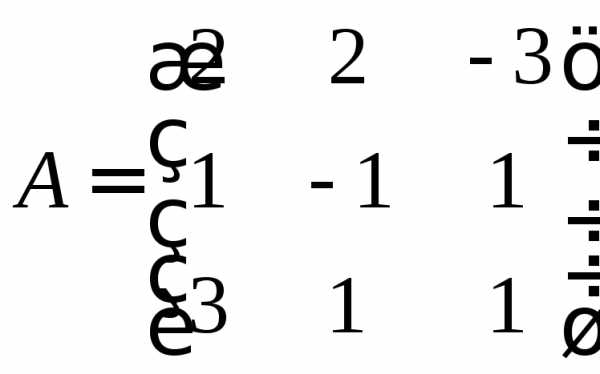 ,
, 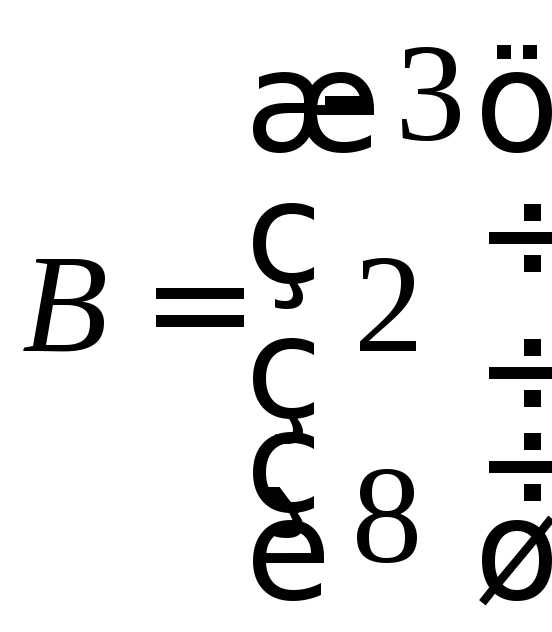
Найдём матрицу, обратную А.
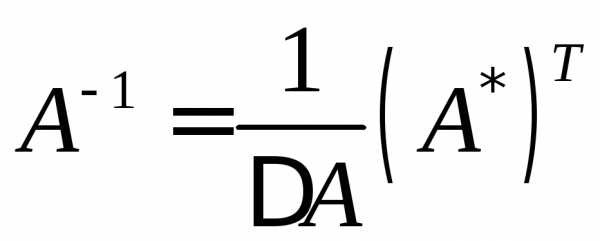
, 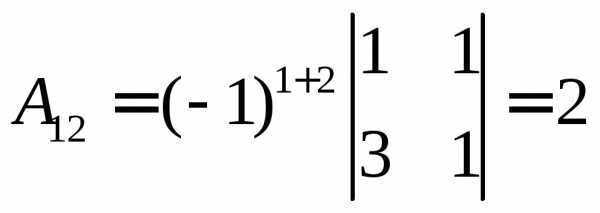 ,
,
, ,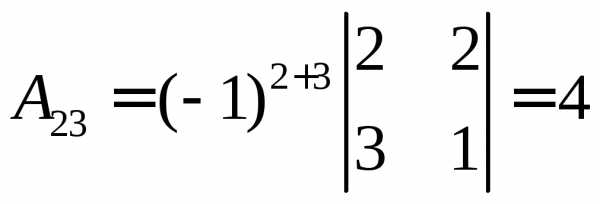
,
Союзная матрица
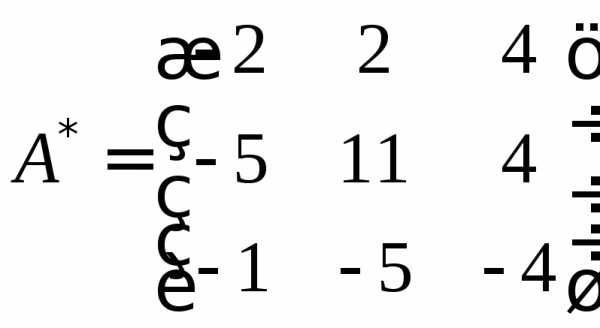
Т.к. элементы матрицы не делятся нацело на 12, оставим делитель за скобками, это не будет ошибкой.
Теперь можем разделить на определитель
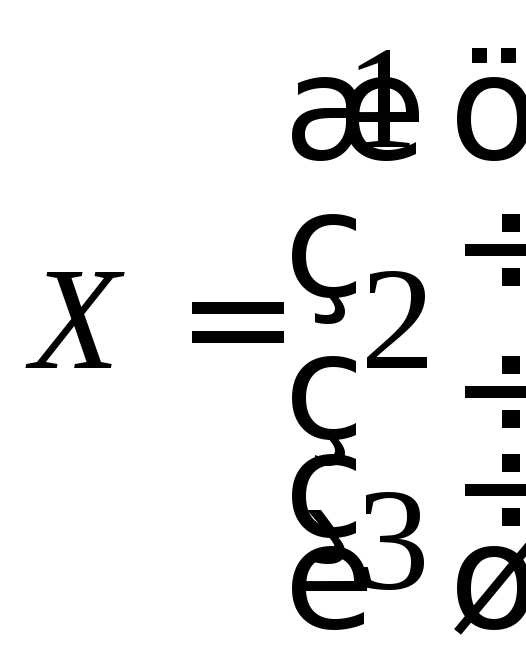
Ответ: 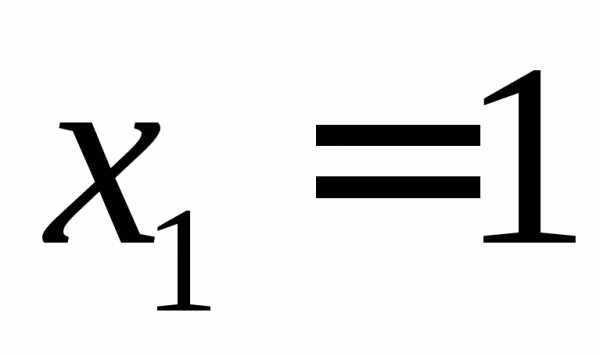 ,
,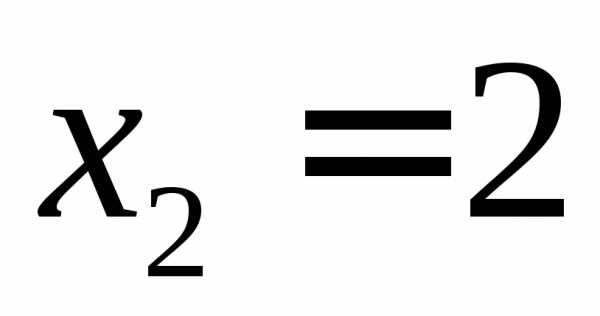 ,
,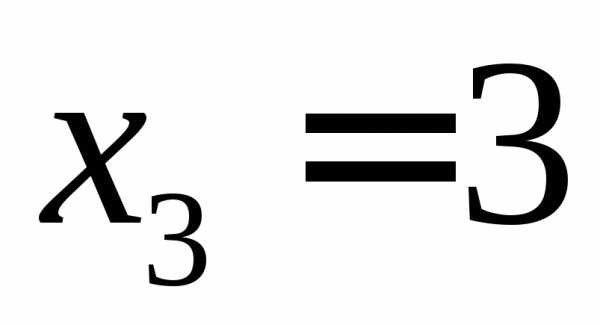 .
.
Примечание. При перемножении матриц и скаляра, действует переместительный закон, но только на скалярное число.
Ранг матрицы. Разрешимость систем
4.1. Определить ранг матрицы
а) 
Найдем определитель данной матрицы
Определитель не равен нулю, значит, ранг матрицы равен ее размерности
Ответ: rank(A) = 3.
б) 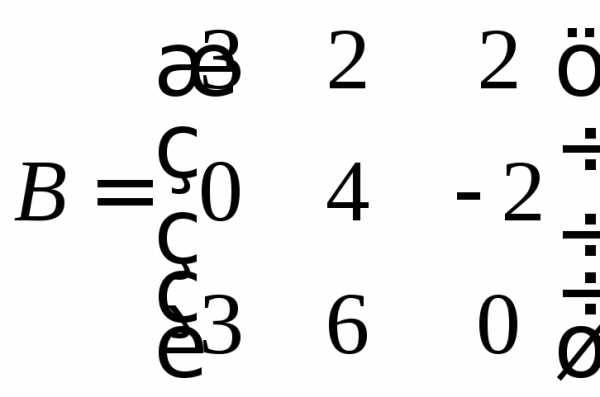
Найдём её определитель
Определитель матрицы равен нулю, значит, ранг матрицы не будет равен её размерности. Из матрицы В составим матрицы меньшей размерности (2х2) путём удаления одной строки и одного столбца. Таких комбинаций будет девять. Если хоть одна такая матрица не даст нулевой определитель, то ранг всей матрицы будет равен двум.
Из матрицы В отбросим первую строку и столбец и найдём определитель получившейся матрицы.
Значит ранг матрицы В равен размерности последней матрицы
Ответ: rank(В) = 2.
в)
Данная матрица прямоугольная, а определитель можно найти только квадратной. Значит будем составлять квадратные матрицы путём отбрасывания лишних столбцов.
1) Возьмём два первых столбца.
2) Возьмём первый и третий столбцы.
3) Возьмём первый и четвёртый столбцы.
Ранг матрицы C равен размерности данной матрицы, несмотря на то, что два первых определителя равны нулю.
Ответ: rank(С) = 2.
Примечание. Данный метод нахождения ранга матрицы становится затруднительным при повышении размерности матрицы. Далее будет показано применение метода Гаусса для нахождения ранга матрицы.
studfiles.net
