Площади подобных треугольников | Треугольники
Утверждение
Площади подобных треугольников относятся как квадраты их соответствующих сторон, то есть отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Дано:
Доказать:
Площадь треугольника ABC может быть найдена, например, по двум сторонам и углу между ними:
Аналогично,
Так как углы подобных треугольников равны, а стороны — пропорциональны, то ∠A=∠A1,
то есть
Теперь можем найти, как относятся площади подобных треугольников:
Так как
то
то есть
Что и требовалось доказать.
Поскольку отношение любых линейных размеров (высот, медиан, биссектрис, периметров) подобных треугольников равно коэффициенту подобия, площади подобных треугольников относятся как квадраты их соответствующих линейных размеров.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Отношение площадей подобных треугольников
Теорема
Доказательство
Дано:  АВС
АВС
 А1В1С1, — коэффициент подобия,
А1В1С1, — коэффициент подобия, 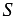
 АВС и
АВС и  А1В1С1.
А1В1С1.Доказать:  .
.
Доказательство:
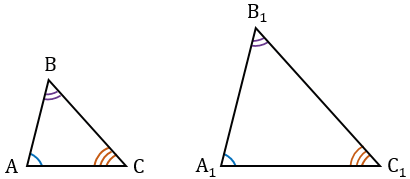
1.  АВС
АВС
 А1В1С1, следовательно,
А1В1С1, следовательно, 
 А1, значит,
А1, значит,  (т.к. площади треугольников, имеющих по равному углу, относятся как произведения сторон, заключающих равные углы). При этом, из подобия треугольников АВС и А1В1С1 следует то, что
(т.к. площади треугольников, имеющих по равному углу, относятся как произведения сторон, заключающих равные углы). При этом, из подобия треугольников АВС и А1В1С1 следует то, что  , значит,
, значит, 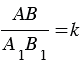 и , тогда,
и , тогда,  .
.Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 543, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 544, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 545, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 546, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 622, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 627, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1077, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1143, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1209*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1308, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Отношение площадей подобных треугольников
Теорема об отношении площадей подобных треугольников
Для подобных треугольников и с коэффициентом подобия справедлива следующая теорема:
ТЕОРЕМАОтношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство. Обозначим через и площади треугольников и с коэффициентом подобия . Так как , то
Из свойств подобных треугольников следует, что . Тогда
Что и требовалось доказать.
Примеры решения задач
ПРИМЕР 1| Задание | |
| Решение | Найдем отношение площадей треугольников и
т.е. . Тогда из подобия треугольников следует
|
| Ответ | см |
| Задание | Треугольники и подобны с коэффициентом подобия . Найти площадь треугольника , если см. |
| Решение | Найдем площадь треугольника по формуле
Поскольку треугольники и подобные, то отношение их площадей равно квадрату коэффициента подобия, т.е. откуда см |
| Ответ | см |
Свойства подобных треугольников
Отношение периметров подобных треугольников
Радиус вписанной окружности треугольника
Гипотенуза прямоугольного треугольника
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников. Вернуться к Списку уроков Тематического планирования.
Урок 32. Отношение площадей
подобных треугольников
Основные дидактические цели урока: закрепить понятия пропорциональных отрезков и подобных треугольников; совершенствовать навыки решения задач на применение свойства биссектрисы треугольника и определения подобных треугольников; рассмотреть теорему об отношении площадей подобных треугольников и показать ее применение в процессе решения задач.
Ход урока
I. Организационный момент
(Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся. Мотивация к учебной деятельности
1. Теоретический опрос.
(Один ученик оформляет доказательство теоремы на доске.)
1) Ответить на вопросы 1—3 учебника.
2) Доказать свойство биссектрисы треугольника.
2. Проверка домашнего задания.
(Учитель проверяет решение задач № 538, 542. Два ученика готовят решение на доске.)
Задача № 538

Наводящие вопросы.
- В каком отношении биссектриса AD треугольника АВС делит сторону ВСР.
- Что можно сказать об отношении отрезков АВ и АС?
- Составьте уравнение, используя отношение отрезков АВ и АС и значение периметра треугольника АВС.
Задача № 542

Наводящие вопросы.
- Какие треугольники называются подобными?
- Чему равно отношение сходственных сторон MN и ВС, KN и AC?
- Чему равны стороны треугольника KMN?
3. Работа по индивидуальным карточкам.
(3—6 учеников работают по карточкам.)
I уровень сложности
- Треугольники KPF и ЕМТ подобны, причем КР : ME = PF : МТ = КЕ : ЕТ, ∠F = 30°, ∠Е = 49°. Найдите остальные углы этих треугольников.
- Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см. Найдите периметр треугольника АВС, если известно, что АВ = 9 см.
II уровень сложности
- ΔВВС подобен ΔАВС (рис. 7.3), AD = 16 см, DC = 9 см. ∠ABC и ∠BDA — тупые. Найдите ВС.
- Периметр треугольника равен 70 см, две его стороны равны 24 см и 32 см. Найдите отрезки, на которые биссектриса треугольника делит его третью сторону.

III уровень сложности
- Диагональ АС делит трапецию ABCD на два подобных треугольника АВС и ACD, ВС = 8 см, AD = 18 см. Найдите АС.
- В равнобедренном треугольнике точка Е — середина основания АС, а точка К делит сторону ВС в отношении 2:5, считая от вершины С. Найдите отношение, в котором прямая BE делит отрезок АК.
- Решение задач по готовым чертежам для подготовки к восприятию нового материала (работа в парах).


Ответы и указания к задачам по готовым чертежам:

(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены три-четыре задачи;
- оценка «4» — правильно решены две задачи;
- оценка «3» — правильно решена одна задача;
- оценка «2» — не ставится.
III. Работа по теме урока
(Учитель делит класс на группы для решения задания творческого характера. После завершения работы заслушиваются и обсуждаются варианты решений.)
Задание. Треугольники АВС и А1В1С1 подобны с коэффициентом подобия k. Найти отношение их площадей.

Вывод. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
IV. Закрепление изученного материала
- Работа в рабочих тетрадях. Решить задачу № 54. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)
- Решить задачу № 545 (работа в парах). (После завершения работы заслушиваются и обсуждаются варианты решений.)
Задача № 545

Вопросы для обсуждения.
- Чему равно отношение площадей подобных треугольников, если их сходственные стороны относятся как 6 : 5?
- Верно ли составлено уравнение исходя из условий задачи?
- Решить задачи № 547, 548 (работа в группах). (После завершения работы заслушиваются и обсуждаются варианты решений.)

V. Самостоятельная работа
I уровень сложности

II уровень сложности

III уровень сложности

VI. Рефлексия учебной деятельности
- Какие треугольники называются подобными?
- Сформулируйте свойство биссектрисы треугольника.
- Что можно сказать о площадях подобных треугольников?
Домашнее задание
- П. 60, вопросы 4 (учебник, с. 158).
- Решить задачи № 543, 544, 546, 549.
- Решить дополнительные задачи.
I уровень сложности: В подобных треугольниках АВС и KMN равны углы В и М, С и N, АС = 3 см, KN = 6 см, MN = 4 см, ∠AX = 30°. Найдите ВС, ∠K; отношение площадей треугольников AВС и KMN; АЕ и BE, если известно, что СЕ — биссектриса треугольника АВС, АВ = 3,5 см.
II уровень сложности: В прямоугольном треугольнике ABC ∠C = 90°, ∠B = 30°, АВ = 12 см, CD — высота. Докажите, что ΔACD подобен ΔАВС, найдите отношение их площадей и отрезки, на которые биссектриса угла А делит катет ВС.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников.
Вернуться к Списку уроков Тематического планирования.
Отношением отрезков AB и CD называется отношение их длин. Отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если их отношения равны.
AB/(A1B1) = CD/(C1D1)
Выясним, пропорциональны ли отрезки на рисунке.
Составим отношения отрезков, учитывая их длины:
AB/AC = 4/12 = 1/3,
AD/DE = 3/9 = 1/3,
DB/BE = 1/5,
Получим, что отрезки AB и AC пропорциональны отрезкам AD и DE. А отрезки AB и AC не пропорциональны отрезкам DB и BE.
Интересное и важное свойство биссектрисы угла треугольника связано с пропорциональностью отрезков.
Пусть дан треугольник АВС, в нем проведена биссектриса АD, докажем, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Дано: ∆ ABC, AD – биссектриса
Доказать: BD/AB = DC/AC
Для доказательства воспользуемся следствиями из формулы площади треугольника:
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
У треугольников ADC и ABD общая высота AH, поэтому
SABD/SADC = BD/DC
2) У треугольников ADC и ABD
∠CAD = ∠BAD, поэтому
SABD/SADC = (AB ∙ AD)/(AC ∙ AD) = AB/AC
3) BD/DC = AB/AC
Или
BD/AB = DC/AC
В геометрии фигуры одинаковой формы называют подобными.
Рассмотрим два треугольника, углы которых равны.
∆ ABC и ∆A1B1C1
∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1
Тогда стороны AB и A1B1, BC и B1C1, CA и C1A1 называются сходственными.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.
∆ ABC ~ ∆A1B1C1
∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1
и AB/(A1B1) = BC/B1C1 = AC/(A1C1) = k
Выясним, как относятся периметры и площади подобных треугольников.
Рассмотрим два подобных треугольника.
∆ ABC ~ ∆A1B1C1
AB/(A1B1) = BC/B1C1 = AC/(A1C1) = k, тогда
AB = kA1B1
BC = kB1C1
AC = kA1C1
Составим отношение периметров этих треугольников и упростим его
PABC/PA1B1C1 = (AB + BC + AC)/(A1B1 + B1C1 + A1C1) = (kA1B1 + k B1C1 + kA1C1)/(A1B1 + B1C1 + A1C1) = k
Вывод: отношение периметров двух подобных треугольников равно коэффициенту подобия.
Теперь рассмотрим отношение площадей подобных треугольников АВС и А1В1С1. ∆ ABC ~ ∆A1B1C1, тогда ∠A = ∠A1, следовательно, по теореме об отношении площадей треугольников, имеющих по равному углу, получим
SABC/SA1B1C1 = (AB ∙ AC)/(A1B1 ∙ A1C1) = AB/(A1B1) ∙ AC/(A1C1)= k ∙ k = k2
Вывод: отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Определение подобных треугольников
Пропорциональные отрезки
Для введения понятия подобия вначале нам необходимо вспомнить понятие пропорциональных отрезков. Вспомним также определение отношения двух отрезков.
Определение 1
Отношением двух отрезков называется отношение их длин.
Понятие пропорциональности отрезков имеет место и для большего числа отрезков. Пусть, к примеру, $AB=2$, $CD=4$, $A_1B_1=1$, $C_1D_1=2$, $A_2B_2=4$, $C_2D_2=8$, тогда
То есть отрезки $AB$, $A_1B_1$, $\ A_2B_2$ пропорциональны отрезкам $CD$, $C_1D_1$, $C_2D_2$.
Подобные треугольники
Вспомним для начала, что вообще представляет себе понятие подобия.
Определение 3
Фигуры называются подобными, если они имеет одинаковую форму, но разные размеры.
Разберемся теперь с понятием подобных треугольников. Рассмотрим рисунок 1.
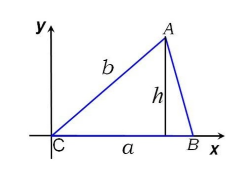
Рисунок 1. Два треугольника
Пусть у этих треугольников $\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1$. Введем следующее определение:
Готовые работы на аналогичную тему
Определение 4
Стороны двух треугольников называются сходственными, если они лежат напротив равных углов этих треугольников.
На рисунке 1, стороны $AB$ и $A_1B_1$, $BC$ и $B_1C_1$, $AC$ и $A_1C_1$ сходственные. Введем теперь определение подобных треугольников.
Определение 5
Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть
\[\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1,\] \[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}\]На рисунке 1 изображены подобные треугольники.
Обозначение: $ABC\sim A_1B_1C_1$
Для понятия подобия существует также понятие коэффициента подобия.
Определение 6
Число $k$, равное отношению сходственных сторон подобных фигур называется коэффициентом подобия этих фигур.
Площади подобных треугольников
Рассмотрим теперь теорему об отношении площадей подобных треугольников.
Теорема 1
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, то есть
\[\frac{S_{ABC}}{S_{A_1B_1C_1}}=k^2\]Доказательство.
Рассмотрим два подобных треугольника и обозначим их площади, соответственно $S$ и $S_1$ (рис. 2).
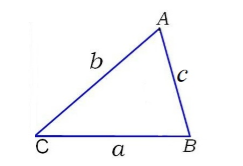
Рисунок 2.
Для доказательства этой теоремы вспомним следующую теорему:
Теорема 2
Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то, по определению,$\angle A=\angle A_1$. Тогда, по теореме 2, получим, что
Так как $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=k$, получим
Теорема доказана.
Задачи, связанные с понятием подобия треугольника
Пример 1
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Стороны первого треугольника $AB=2,\ BC=5,\ AC=6$. Коэффициент подобия данных треугольников $k=2$. Найти стороны второго треугольника.
Решение.
Данная задача имеет два возможных решения.
Пусть $k=\frac{A_1B_1}{AB}=\frac{{B_1C}_1}{BC}=\frac{A_1C_1}{AC}$.
Тогда $A_1B_1=kAB,\ {B_1C}_1=kBC,\ A_1C_1=kAC$.
Следовательно, $A_1B_1=4,\ {B_1C}_1=10,\ A_1C_1=12$
Пусть $k=\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$
Тогда $A_1B_1=\frac{AB}{k},\ {B_1C}_1=\frac{BC}{k},\ A_1C_1=\frac{AC}{k}$.
Следовательно, $A_1B_1=1,\ {B_1C}_1=2,5,\ \ A_1C_1=3$.
Пример 2
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Сторона первого треугольника $AB=2$, соответствующая сторона второго треугольника $A_1B_1=6$. Высота первого треугольника $CH=4$. Найти площадь второго треугольника.
Решение.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то $k=\frac{AB}{A_1B_1}=\frac{1}{3}$.
Найдем площадь первого треугольника.
\[S=\frac{1}{2}AB\cdot CH=\frac{1}{2}\cdot 2\cdot 4=4\]По теореме 1, имеем:
\[\frac{S_{ABC}}{S_{A_1B_1C_1}}=k^2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \[S_{A_1B_1C_1}=36\]Ответ: $36$.
| 1. | Отношение сторон подобных треугольников | 1 вид — рецептивный | лёгкое | 1 Б. | Написание отношения сторон подобных треугольников. |
| 2. | Отношение отрезков | 2 вид — интерпретация | лёгкое | 1 Б. | Вычисление длины отрезка, если известна длина другого отрезка и их отношение. |
| 3. | Отношение отрезков, длина отрезка | 2 вид — интерпретация | лёгкое | 1 Б. | Вычисление длины отрезка по данному отношению и длине другого отрезка. |
| 4. | Пропорциональные отрезки | 2 вид — интерпретация | лёгкое | 2 Б. | Пропорциональные отрезки. Вычисление неизвестного члена пропорции, который находится в числителе. |
| 5. | Подобные треугольники, отношение площадей | 2 вид — интерпретация | среднее | 1 Б. | Нахождение отношений периметров или площадей подобных треугольников. |
| 6. | Длины частей отрезка | 2 вид — интерпретация | среднее | 3 Б. | Вычисление длин частей отрезка, если известна длина всего отрезка и отношение его частей. |
| 7. | Периметры и площади подобных треугольников | 2 вид — интерпретация | среднее | 3 Б. | Вычисление периметра и площади одного из данных подобных треугольников. |
| 8. | Площади подобных треугольников | 2 вид — интерпретация | среднее | 4 Б. | Вычисление площадей подобных треугольников. |
| 9. | Периметр равнобедренной трапеции | 2 вид — интерпретация | среднее | 3 Б. | Вычисление периметра равнобедренной трапеции, подобные треугольники. |
| 10. | Подобные прямоугольные треугольники | 2 вид — интерпретация | среднее | 3 Б. | Вычисление стороны одного из подобных прямоугольных треугольников. |
| 11. | Подобные треугольники | 2 вид — интерпретация | среднее | 3 Б. | Вычисление стороны одного из данных подобных треугольников. |
| 12. | Подобные треугольники, коэффициент подобия (1) | 2 вид — интерпретация | среднее | 4 Б. | Вычисление стороны одного из данных подобных треугольников, коэффициент подобия k < 1. |
| 13. | Подобные треугольники, коэффициент подобия (2) | 2 вид — интерпретация | среднее | 4 Б. | Вычисление стороны одного из данных подобных треугольников, коэффициент подобия k > 1. |
| 14. | Площади подобных треугольников | 3 вид — анализ | сложное | 4 Б. | Использование соотношения площадей подобных треугольников для определения сторон. |
областей параллелограммов и треугольников
Хотя вы можете не увидеть сходства между параллелограммы и Первоначально треугольники, мы увидим, что они на самом деле довольно связанные, когда дело доходит до области. Но насколько они могут быть похожими, если один является трехсторонним многоугольником, а другой это конкретный тип четырехугольника? Давайте начнем рисовать некоторые связи между параллелограммы и треугольники, выясняя, как измерить площади параллелограммов первый.
Области параллелограммов
Напомним, что параллелограммы — это особый тип четырехугольник, противоположные стороны которого не пересекаются. Параллелограммы приходят в виде прямоугольники, ромбы и квадраты. При попытке определить площадь параллелограмм, необходимо будет выделить два основных компонента: база и высота параллелограмма.База параллелограмма может быть на любая сторона фигуры. Высота параллелограмма — это перпендикулярное расстояние между любыми двумя параллельными основаниями. Давайте посмотрим на эти разные части на рисунке ниже.
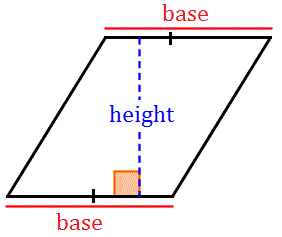
Мы могли бы также выбрать левую и правую стороны параллелограмма в качестве наших баз. В этом случае высота будет идти горизонтально.
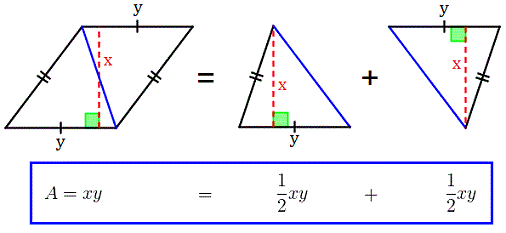
Площадь параллелограмма определяется произведением основания и высоты. То есть площади параллелограммов можно выразить как
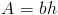
где A представляет площадь, b является основанием и h это высота.
Давайте попрактикуемся в использовании этой формулы, выполнив упражнение ниже.
Упражнение 1
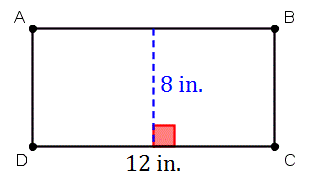
Найдите площадь параллелограмма ABCD .
Ответ:
Во-первых, мы хотим выбрать сторону в качестве основы нашего параллелограмма. В таком случае, мы можем выбрать сторону с надписью 12 дюймов в качестве нашей базы.
Высота нашего параллелограмма — это отрезок, перпендикулярный выбранной нами базе.На схеме мы видим, что существует прямой угол на пересечении DC и пунктирная синяя линия длиной 8 дюймов . Теперь, когда у нас есть меры нашей базы и высоты, мы можем подключить эти значения непосредственно в формула нашей области. Итак, у нас
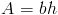

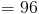
Площадь параллелограмма ABCD составляет 96 квадратных дюймов .Это означает, что мы могли бы идеально соответствовать 96 один дюйм на один дюйм в параллелограмм.
Давайте попробуем еще один пример, чтобы убедиться, что мы понимаем, как использовать формулу площади для параллелограммов.
Упражнение 2
Если площадь параллелограмма EFGH составляет 112 квадратных метров, что должно значение х будет?
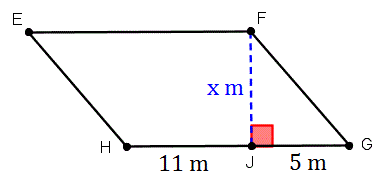
Ответ:
Мы не можем просто «подключить и пыхтеть» для этого упражнения, как мы это делали в первом примере.В этом упражнении нам дана область параллелограмма, и мы должны работать в обратном направлении.
Нам дано, что высота параллелограмма составляет x метров. это переменная, для которой мы будем решать. Нам также дано, что основа нашего параллелограмма, HG , разделен на две меньшие длины: одна, которая 11 метров длиной и еще 5 длиной метров .Давайте объедините их, чтобы узнать, какая у нас база:
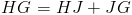
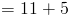
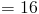
Итак, мы обнаружили, что наша база, b , имеет длину 16 метров в длину. Давайте включим то, что мы знаем, в нашу формулу площади и решим для x .
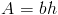
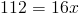
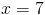
Таким образом, высота параллелограмма EFGH составляет 7 метров .(Обратите внимание, что мы не сказали, что высота была 7 метров в квадрате , потому что мы не говорим о местности; мы говорим о высоте.)
Теперь давайте рассмотрим свойства площади треугольников, чтобы установить связи они с параллелограммами.
Области треугольников
Как и в параллелограммах, основные компоненты площади треугольника являются основой и высота треугольника.Основание треугольника может быть любой стороной. Высота треугольник — это длина высоты треугольника, отведенная к выбранной базе. Высота треугольника — это линия а через вершину, которая перпендикулярна на противоположную сторону треугольника. Давайте рассмотрим эти части в треугольнике ниже.
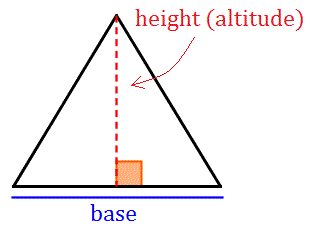
Площадь треугольника составляет половину произведения основания и его соответствующего рост.Таким образом, формула
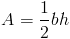
Давайте попрактикуемся в использовании этой формулы, выполнив следующие упражнения.
Упражнение 3
Найти площадь ? KLM .

Ответ:
Основание треугольника, который является сегментом ML , имеет длину 24 сантиметров .Поэтому мы сможем подключить 24 для b , когда мы хотим использовать нашу формулу площади. Длина высоты, или высота, также дана. Мы видим, что высота здесь 7 сантиметров , Таким образом, мы можем подключить 7 к ч . У нас есть оба компонента наша формула, поэтому мы можем подключить эти цифры, чтобы найти область.
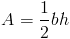
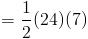
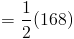
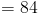
Так, площадь треугольника KLM составляет 84 квадратных сантиметров . Давайте попробуем еще один пример.
Упражнение 4
Найти площадь ? NPQ .
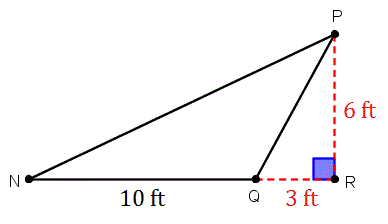
Ответ:
Как мы заметили в предыдущем упражнении, найти площадь треугольника просто, как найти длину основания и высоты. Тем не менее, для этого упражнения, мы должны быть осторожны, чтобы не перепутать значения нашей базы и роста.
Давайте сначала поищем нашу базу.Сегмент NQ является нашей базой с длиной 10 футов . Тем не менее, мы видим, что пунктирная линия продолжается от Q в направлении точки R . Эта строка не часть нашего треугольника. Единственная цель, которой он служит, это помочь нам найти высоту наш треугольник, как мы увидим.
В этом случае наша высота (и высота) лежит снаружи нашего треугольника.Отзыв что по определению высота представляет собой отрезок, перпендикулярный основанию треугольника который проходит через противоположную точку. Так как NQ был выбран в качестве нашего основание, нам нужно было расширить этот сегмент до точки R для того, чтобы возможно иметь линию, перпендикулярную NQ , которая проходит через P .Мы видим, что высота ? NPQ 6 футов . Теперь мы готовы подключить значения нашей базы и высоты в формулу площади для треугольников.
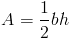
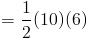
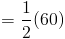
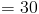
Так, площадь ? NPQ составляет 30 квадратных футов .
Теперь, когда мы знакомы с формулами площадей параллелограммов и треугольников, давайте выясним, каковы отношения между ними.
Соотношение между параллелограммами и треугольниками
Глядя строго на их формулы, мы замечаем, что формула для треугольника имеет дополнительный коэффициент, равный половине, тогда как формула площади для параллелограмма просто основание, умноженное на высоту.Давайте разберемся, как этот дополнительный фактор составляет половину вступает в игру.
Треугольники являются самым основным типом многоугольников, которые составляют все другие типы многоугольников. Другими словами, мы можем вписать определенное количество конгруэнтных треугольников в любой вид многоугольника. Более конкретно, мы узнали, что (n-2) треугольников могут вписывается в n -gon (см. многоугольники).Таким образом, когда мы работаем с параллелограммами, которые являются типом четырехугольника, мы знаем, что мы можем соответствовать (4-2) = 2 конгруэнтных треугольников в параллелограмм.
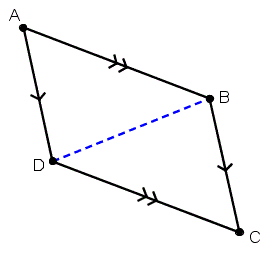
Можно разбить параллелограмм ABCD на два конгруэнтных треугольника:? ABD и? CDB.
Поэтому, если у нас есть параллелограмм того же основания и высоты, что и треугольник, мы знаем, что можем соединить два из этих треугольников, чтобы создать параллелограмм.Давайте посмотрим на это, используя диаграммы ниже.
теорем о подобных треугольниках
1. Теорема о боковом разделении
Если ADE — это любой треугольник, а BC отрисовывается параллельно DE, то AB BD = AC CE
Чтобы показать, что это правда, нарисуйте линию BF параллельно AE, чтобы завершить параллелограмм BCEF:
Треугольники ABC и BDF имеют абсолютно одинаковые углы и поэтому похожи (Почему? См. Раздел под названием AA на странице Как найти, если треугольники похожи.)
- Сторона AB соответствует стороне BD, а сторона AC соответствует стороне BF.
- т. Д. AB / BD = AC / BF
- Но BF = CE
- So AB / BD = AC / CE
Теорема об угловом биссектрисе
Если ABC представляет собой любой треугольник и AD делит пополам (разрезает пополам) угол BAC, то AB BD = AC DC
Чтобы показать, что это правда, мы можем обозначить треугольник следующим образом:
- Угол BAD = Угол ЦАП = x ° Угол
- ADB = y ° Угол АЦП
- = (180 − y) °
Умножьте обе стороны на AB: sin (x) AB BD = sin (y) 1
Разделите обе стороны на sin (x): AB BD = sin (y) sin (x)
По закону синусов в треугольнике ACD: sin (x) DC = sin (180-y) AC
Умножьте обе стороны на AC: sin (x) AC DC = sin (180-y) 1
Разделите обе стороны на sin (x): AC DC = sin (180-y) sin (x)
Но sin (180-y) = sin (y) : AC DC = sin (y) sin (x)
AB BD и AC DC равны sin (y) sin (x) , поэтому:
AB BD = AC DC
В частности, если треугольник ABC является равнобедренным, то треугольники ABD и ACD являются конгруэнтными треугольниками
И тот же результат верен:
AB BD = AC DC
3.Площадь и сходство
Если два одинаковых треугольника имеют стороны в соотношении x: y,
, то их площади находятся в соотношении x 2 : y 2
Пример:
Эти два треугольника похожи со сторонами в соотношении 2: 1 (стороны одного в два раза длиннее другого):
Что можно сказать об их районах?
Ответ прост, если мы просто нарисуем еще три линии:
Мы можем видеть, что маленький треугольник вписывается в большой треугольник четыре раза .
Таким образом, когда длина равна , вдвое больше длины , площадь равна , что в четыре раза больше ,
Так что соотношение их площадей составляет 4: 1
Мы также можем записать 4: 1 как 2 2 : 1
Общий случай:
Треугольники ABC и PQR похожи и имеют стороны в соотношении x: y
Мы можем найти области, используя эту формулу из площади треугольника:
Площадь ABC = 1 2 до н.э. sin (A)
Площадь PQR = 1 2 qr sin (P)
И мы знаем, что длина треугольников находится в соотношении x: y
q / b = y / x, поэтому: q = by / x
и r / c = y / x, поэтому r = cy / x
Кроме того, поскольку треугольники похожи, углы A и P одинаковы:
A = P
Теперь мы можем сделать некоторые вычисления:
Площадь треугольника PQR : 1 2 qr sin (P)
Введите «q = by / x», «r = cy / x» и «P = A»: 1 2 (by) (cy) sin (A) (x) (x)
Упростить: 1 2 bcy 2 sin (A) x 2
Изменить порядок: y 2 x 2 × 1 2 до н.э. sin (A)
Что есть: y 2 x 2 × Площадь треугольника ABC
Таким образом, мы в конечном итоге с этим соотношением:
Площадь треугольника ABC: Площадь треугольника PQR = x 2 : y 2
,Треугольники свойства и типы | GMAT GRE Geometry Tutorial
Нажмите здесь, чтобы посмотреть это проницательное видео.Почему MBA
В серии статей об основных строительных блоках геометрии, после обзора линий, лучей и сегментов, на этот раз мы рассмотрим типы и свойства треугольников.
Определение: Треугольник — это замкнутая фигура, состоящая из трех отрезков.
Треугольник состоит из трех отрезков и трех углов.На рисунке выше AB, BC, CA — три отрезка, а ∠A, ∠B, ∠C — три угла.
Существует три типа треугольников по сторонам и три по углам.
Типы треугольников по сторонам
Равносторонний треугольник : Треугольник, имеющий все три стороны равной длины, является равносторонним треугольником.
Поскольку все стороны равны, все углы тоже равны.
Равнобедренный треугольник : Треугольник, имеющий две стороны равной длины, является равнобедренным треугольником.
Два угла, противоположные равным сторонам, равны.
Треугольник Scalene: Треугольник, имеющий три стороны разной длины, называется разносторонним треугольником.
Типы треугольников по углам
Треугольник с острыми углами: Треугольник с острыми углами называется остроугольным или острым треугольником.
Треугольник с тупым углом: Треугольник, один угол которого тупой, является треугольником с тупым углом или тупым треугольником.
Прямоугольный треугольник: Треугольник, один угол которого является прямым углом, является прямоугольным треугольником или прямоугольным треугольником.
На рисунке выше сторона, противоположная прямому углу, BC называется гипотенузой.
Для прямоугольного ABC,
BC 2 = AB 2 + AC 2
Это называется теоремой Пифагора .
В указанном выше треугольнике 5 2 = 4 2 + 3 2 .Только треугольник, который удовлетворяет этому условию, является прямоугольным треугольником.
Следовательно, теорема Пифагора помогает определить, является ли треугольник прямоугольным.
Типы треугольников
Существуют разные типы прямоугольных треугольников. На данный момент наше внимание сосредоточено только на специальной паре прямоугольных треугольников.
- 45-45-90 треугольник
- 30-60-90 треугольник
45-45-90 треугольник :
Треугольник 45-45-90, как видно из названия, представляет собой прямоугольный треугольник, в котором два других угла составляют 45 ° каждый.
Это равнобедренный прямоугольный треугольник.
В ∆ DEF, DE = DF и ∠D = 90 °.
Стороны в треугольнике 45-45-90 находятся в соотношении 1: 1: √2.
30-60-90 треугольник :
Треугольник 30-60-90, как следует из названия, является прямоугольным треугольником, в котором два других угла составляют 30 ° и 60 °.
Это разносторонний прямоугольный треугольник, поскольку ни одна из сторон или углов не равны.
Стороны в треугольнике 30-60-90 находятся в соотношении 1: √3: 2
Как и любой другой прямоугольный треугольник, эти два треугольника удовлетворяют теореме Пифагора.
Основные свойства треугольников
- Сумма углов в треугольнике равна 180 °. Это называется свойством угловой суммы.
- Сумма длин любых двух сторон треугольника больше, чем длина третьей стороны. Аналогично, разница между длинами любых двух сторон треугольника меньше, чем длина третьей стороны.
- Сторона, противоположная наибольшему углу, является самой длинной стороной треугольника, а сторона, противоположная наименьшему углу, является самой короткой стороной треугольника.
На рисунке выше, ∠B — это самый большой угол, а сторона, противоположная ему (гипотенуза), является самой большой стороной треугольника.
На рисунке выше, ∠A — самый большой угол, а сторона, противоположная ему, BC — самая большая сторона треугольника.
- Внешний угол треугольника равен сумме его внутренних противоположных углов. Это называется свойством внешнего угла треугольника.
Здесь ∠ACD — внешний угол относительно ∆ABC.
Согласно свойству внешнего угла, ∠ACD = ∠CAB + ∠ABC.
Сходство и конгруэнтность в треугольниках
Фигуры с одинаковым размером и формой являются конгруэнтными фигурами. Если две формы совпадают, они остаются конгруэнтными, даже если они перемещены или повернуты. Формы также остаются конгруэнтными, если мы отражаем формы, создавая зеркальные изображения. Две геометрические фигуры совпадают, если они точно покрывают друг друга.
Фигуры с одинаковой формой, но с пропорциональными размерами являются похожими фигурами.Они остаются похожими, даже если они перемещены или повернуты.
Сходство треугольников
Два треугольника называются схожими, если соответствующие углы двух треугольников конгруэнтны, а длины соответствующих сторон пропорциональны .
Он записан как ∆ ABC ∼ ∆ XYZ и обозначен как ∆ ABC ‘, аналогичный’ ∆ XYZ.
Здесь ∠A = ∠X, ∠B = ∠Y и ∠C = ∠Z И
AB / XY = BC / YZ = CA / ZX
Необходимые и достаточные условия для сходства двух треугольников:
(1) Критерий боковой стороны (SSS) для сходства:
Если три стороны треугольника пропорциональны соответствующим трем сторонам другого треугольника, то треугольники называются схожими.
Здесь, ∆ PQR ∼ ∆ DEF как
PQ / DE = QR / EF = RP / FD
(2) Критерий бокового угла (SAS) для подобия :
Если соответствующие две стороны двух треугольников пропорциональны и один включенный угол равен соответствующему включенному углу другого треугольника, то треугольники аналогичны.
Здесь, Δ LMN ∼ Δ QRS, в котором
∠L = ∠Q
QS / LN = QR / LM
(3) Угол-угол-угол (AAA) критерий подобия:
Если три соответствующих угла двух треугольников равны, то оба треугольника похожи.
Здесь Δ TUV ∼ Δ PQR как
∠T = ∠P, ∠U = ∠Q и ∠V = ∠R
Конгруэнтность треугольников
Два треугольника называются конгруэнтными, если все стороны одного треугольника равны соответствующим сторонам другого треугольника и соответствующие углы равны.
Он записывается как ∆ ABC ≅ ∆ XYZ и обозначается как ∆ ABC ‘, совпадающий с’ ∆ XYZ.
Необходимые и достаточные условия для конгруэнтности двух треугольников:
(1) Критерий боковой стороны (SSS) для конгруэнтности :
Если три стороны треугольника равны соответствующим трем сторонам другого треугольника, то треугольники называются конгруэнтными.
Здесь ∆ ABC ≅ ∆ XYZ как AB = XY, BC = YZ и AC = XZ.
(2) Критерий бокового угла (SAS) для конгруэнтности :
Если две стороны и угол, включенный между двумя сторонами треугольника, равны соответствующим двум сторонам и включенному углу другого треугольника, то треугольники являются конгруэнтными.
Здесь ∆ ABC ≅ ∆ XYZ как AB = XY, ∠A = ∠X и AC = XZ.
(3) Критерий угла-стороны-угла (ASA) для конгруэнции : Если два угла и включенная сторона треугольника равны соответствующим двум углам и включенной стороне другого треугольника, то треугольники являются конгруэнтными.
На рисунке выше ∆ ABD ≅ ∆ CBD, в котором
∠ABD = ∠CBD, AB = CB и ∠ADB = ∠CDB.
(4) Критерий конгруэнции прямоугольного гипотенузы : Если гипотенуза и одна сторона прямоугольного треугольника совпадают с соответствующим гипотенузой и стороной другого прямоугольного треугольника, то треугольники являются конгруэнтными.
Здесь ∠B = ∠Y = 90 ° и AB = XY, AC = XZ.
Площадь треугольника:
Площадь треугольника определяется по формуле
Площадь треугольника = (1/2) * Основание * Высота
Чтобы найти площадь треугольника, мы рисуем перпендикулярную линию от основания к противоположной вершине, которая дает высоту треугольника.
Таким образом, площадь ∆ PQR = (1/2) * (PR * QS) = (1/2) * 6 * 4 = 12 кв. Единиц.
Для прямоугольного треугольника легко найти область, поскольку есть сторона, перпендикулярная основанию, поэтому мы можем рассматривать ее как высоту.
Высота ∆ XYZ равна XY, а его площадь составляет (1/2) * XZ * XY кв.
Теперь, как мы можем найти область тупого треугольника LMN?
Для тупого треугольника, мы расширяем основание и рисуем линию, перпендикулярную от вершины к расширенному основанию, которая становится высотой треугольника.
Следовательно, площадь ∆ LMN = (1/2) * LM * NK кв. Единиц.
Решить следующие
1)
∆ ABC — это прямоугольный треугольник, а CD ⊥ AB (⊥ означает «перпендикулярно»).
Найти i) ∠ACD и ii) ∠ABC.
A. 25, 35
B. 35, 35
C. 25, 25
D. 35, 25
Ответ : C
Объяснение :
Рассмотрим ∆ ACD.
∠ADC + ∠DAC + ∠ACD = 180 ° (так как сумма углов в треугольнике равна 180 °)
90 + 65 + ∠ACD = 180 ° → ∠ACD = 25 °
∠ACD + ∠DCB = 90 ° → 25 + ∠DCB = 90 → ∠DCB = 65 °
В ∆ BCD, ∠DCB + ∠CBD + ∠BDC = 180 ° (снова сумма всех углов в треугольнике)
65 + BCBD + 90 = 180 → ∠CBD = 25 ° = ∠ABC.
2) Определите, правильны ли следующие треугольники
A. Оба являются правыми треугольниками
B. ∆ ABC не является прямоугольным треугольником, ∆ DEF является прямоугольным треугольником
C. ∆ ABC является прямоугольным треугольником, ∆ DEF не является прямоугольным
D. Оба не являются прямоугольными треугольниками
Ответ: B
Объяснение :
Триплет, удовлетворяющий теореме Пифагора, представляет собой множество сторон, образующих прямоугольный треугольник.
3)
Если ∆ ABC = 3 (∆ DEF), что из следующего является правильным?
А.∠E = ∠F = 40 °, ∠D = 120 ° И DE = DF = 2 и EF = 3
B. ∠E = ∠F = 40 °, ∠D = 110 ° И DE = DF = 2 и EF = 3
C. ∠E = ∠F = 40 °, ∠D = 100 ° И DE = DF = 2 и EF = 3
D. ∠E = ∠F = 40 °, ∠D = 110 ° И DE = DF = 3 и EF = 3
Ответ: C
Объяснение :
AB и AC равны → углы противоположны равны.
Следовательно, ∠B = ∠C = 40 ° → ∠A = 100 °.
∆ ABC = 3 (∆ DEF) → ∆ ABC и ∆ DEF аналогичны.
Когда два треугольника похожи, их соответствующие углы равны, а соответствующие стороны пропорциональны.
→ DE = DF = 6/3 = 2 и EF = 3
→ ∠E = ∠F = 40 ° и ∠D = 100 °
,Если все три стороны имеют одинаковую длину, это называется равносторонний треугольник. Очевидно, что все равносторонние треугольники также обладают всеми свойствами равнобедренного треугольника.
Недвижимость
- Неравная сторона равнобедренного треугольника обычно называется «основанием» треугольника.
- Углы основания равнобедренного треугольника всегда равны. На рисунке выше углы ∠ABC и ∠ACB всегда одинаковы
- Когда 3-й угол является прямым углом, он называется «равнобедренный треугольник».
- Высота — это перпендикулярное расстояние от основания до самой верхней вершины.
Построение равнобедренного треугольника
Можно построить равнобедренный треугольник заданных размеров, используя только компас и линейку. Смотрите эти три конструкции:Решение равнобедренного треугольника
 Базу, ногу или высоту равнобедренного треугольника можно найти, если вы знаете два других. перпендикулярный биссектриса
основания образует
высота над уровнем моря
треугольника, как показано справа.Это образует два
конгруэнтные прямоугольные треугольники
это может быть решено с помощью
Теорема Пифагора
как показано ниже.
Базу, ногу или высоту равнобедренного треугольника можно найти, если вы знаете два других. перпендикулярный биссектриса
основания образует
высота над уровнем моря
треугольника, как показано справа.Это образует два
конгруэнтные прямоугольные треугольники
это может быть решено с помощью
Теорема Пифагора
как показано ниже.Нахождение базы
Чтобы найти базу с учетом ноги и высоты, используйте формулу: где:L — длина ноги
A — высота
Нахождение ноги
Чтобы найти длину ноги с учетом базы и высоты, используйте формулу: где:B — длина основания
A — высота над уровнем моря
Высота над уровнем моря
Чтобы найти высоту с учетом базы и ноги, используйте формулу: где:L длина ножки
B основание
Внутренние углы
 Если вам дали
внутренний угол
равнобедренного треугольника вы можете найти два других.
Если вам дали
внутренний угол
равнобедренного треугольника вы можете найти два других.
Например, Нам дан угол на вершине, как показано справа 40 °. Мы знаем, что внутренние углы всех треугольников добавляют к 180 °. Таким образом, два базовых угла должны составлять до 180-40 или 140 °. Поскольку два базовых угла совпадают (одинаковая мера), каждый из них составляет 70 °.
 Если нам дан базовый угол, скажем, 45 °, мы знаем, что базовые углы совпадают (та же мера)
и внутренние углы любого треугольника всегда прибавляют к 180 °. Таким образом, угол наклона должен быть 180-45-45 или 90 °.
Если нам дан базовый угол, скажем, 45 °, мы знаем, что базовые углы совпадают (та же мера)
и внутренние углы любого треугольника всегда прибавляют к 180 °. Таким образом, угол наклона должен быть 180-45-45 или 90 °.
Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Треугольные центры
Конгруэнтность и Сходство
Решение треугольников
Викторины и упражнения на треугольник
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
