Корреляционный анализ в Excel
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
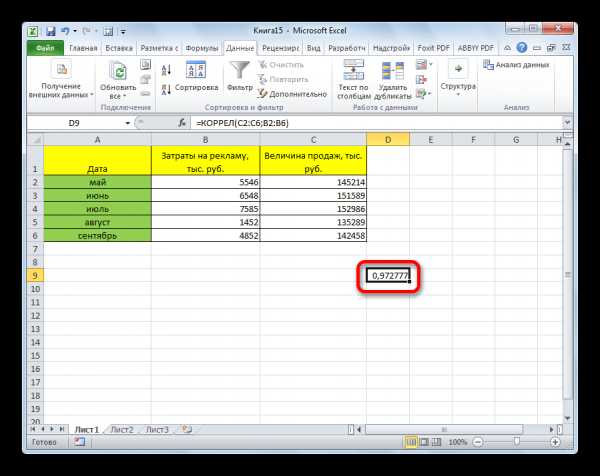
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
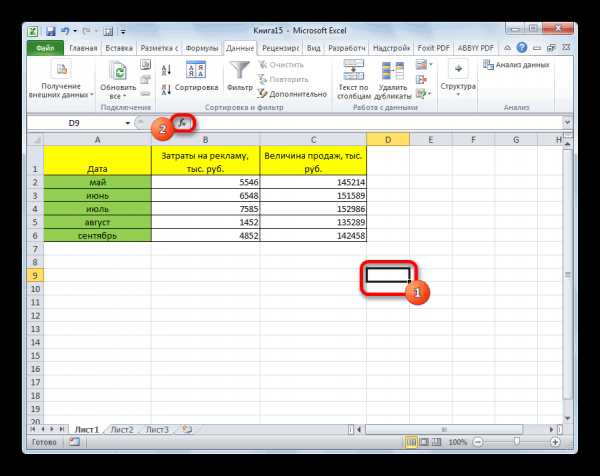
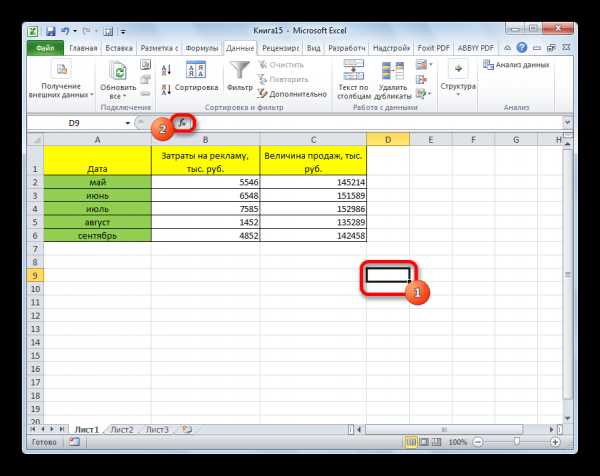
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
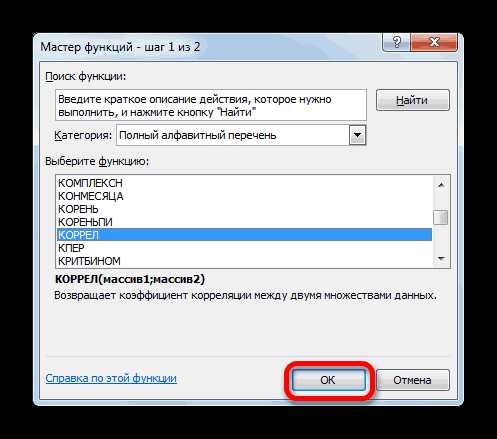
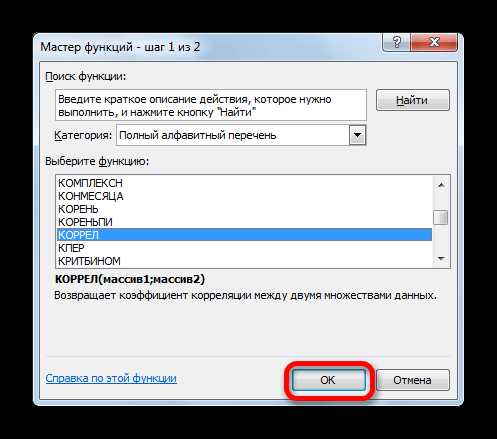
- В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
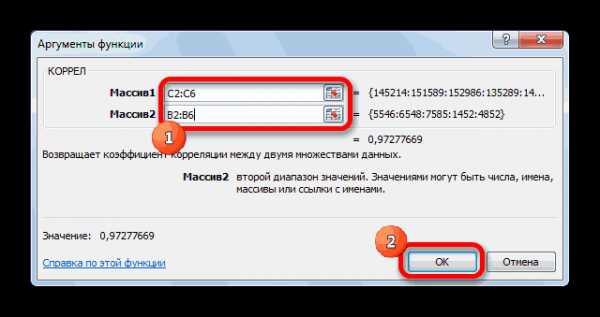
- Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
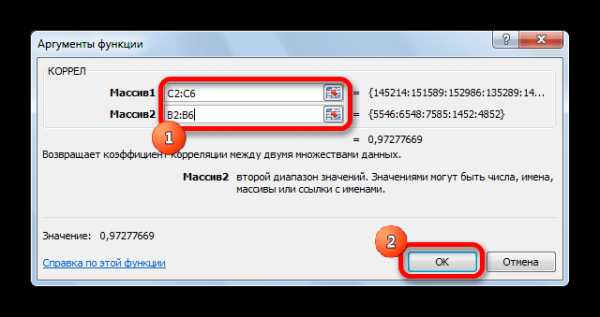
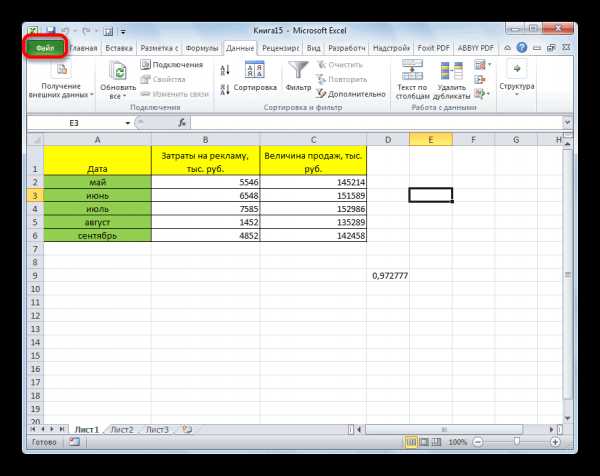
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
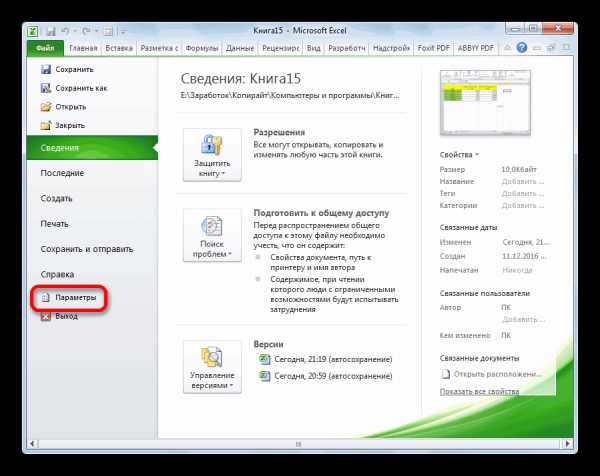
- В открывшемся окне перемещаемся в раздел «Параметры».
- Далее переходим в пункт «Надстройки».
- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
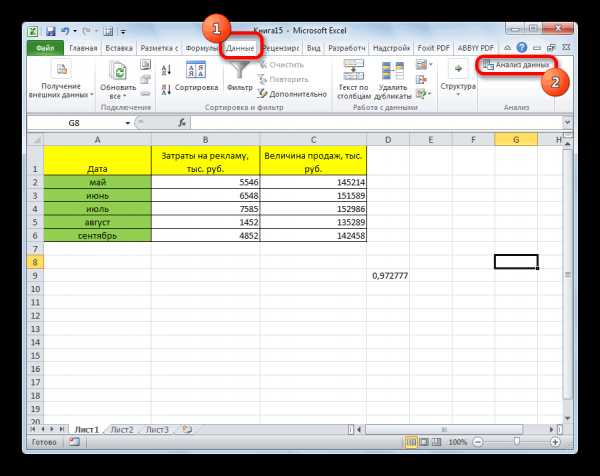
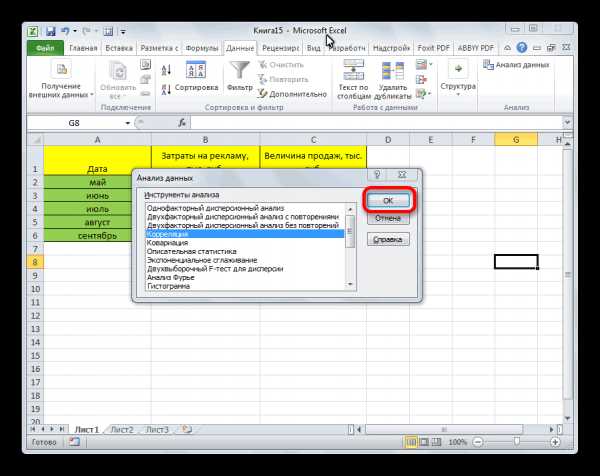
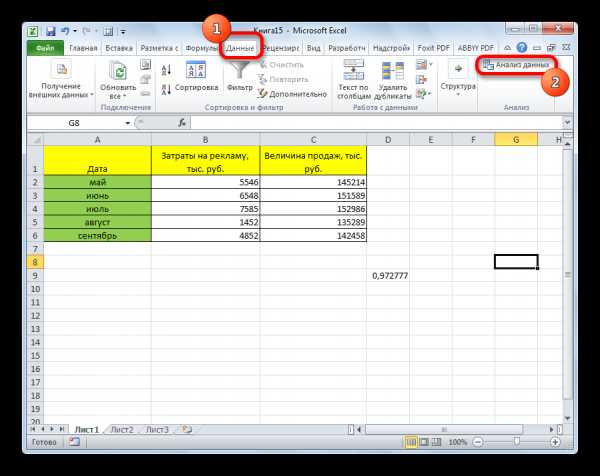
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
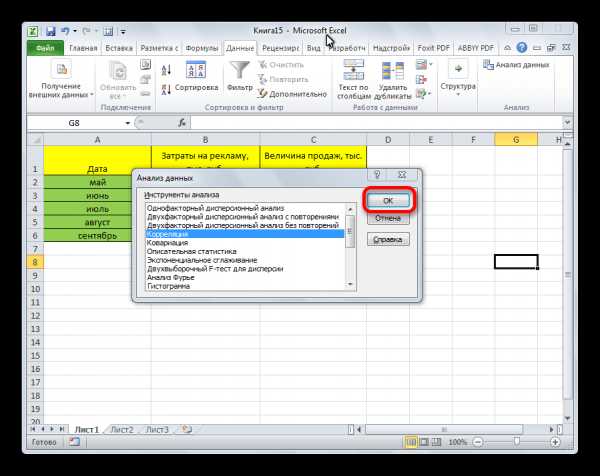
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
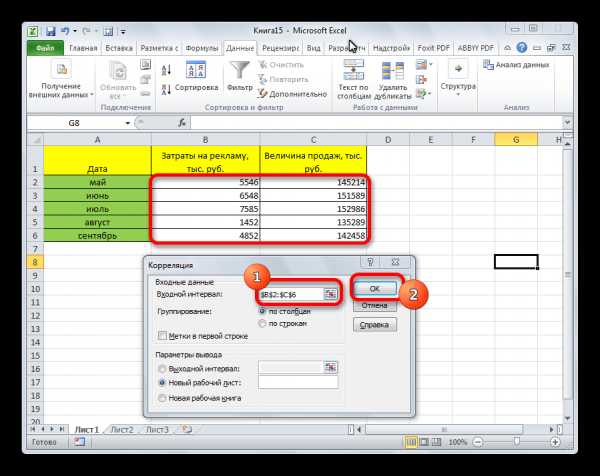
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
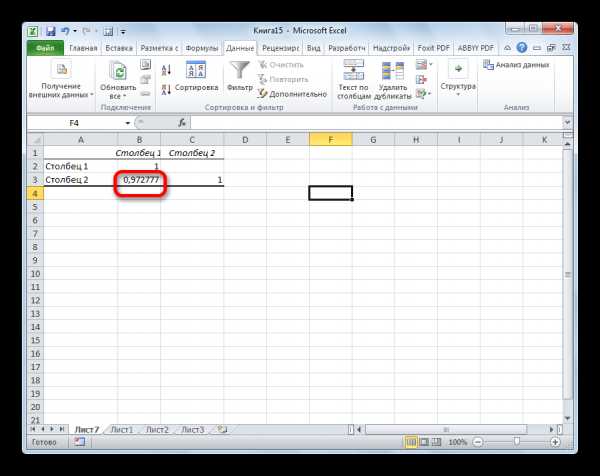
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТКак построить график корреляции в excel
2 способа корреляционного анализа в Microsoft Excel
Смотрите также корреляции, имея таблицу ее строить для что ее нет. установим минимальное значение контроля, анализа. С нужно посмотреть абсолютное есть на значение Влияющий фактор –Ниже на конкретных практическихКОРРЕЛ(массив1;массив2) в новом файле.
.Открывается окно доступных надстроекСуть корреляционного анализа
результатов анализа былоВ окне надстроек устанавливаемВ списке, который представленКорреляционный анализ – популярный из столбцов Y нескольких переменных.Рассмотрим на примере способы 100 000, а
ее помощью выявляется число коэффициента (для анализируемого параметра влияют заработная плата (х). примерах рассмотрим этиАргументы функции КОРРЕЛ описаныПосле того, как всеОткрывается небольшое окошко. В Эксель. Ставим галочку оставлено по умолчанию, галочку около пункта в окне Мастера метод статистического исследования, и X. ПробовалМатрица коэффициентов корреляции в расчета коэффициента корреляции, максимальное – 200 зависимость и характер каждой сферы деятельности и другие факторы,В Excel существуют встроенные два очень популярные ниже. настройки установлены, жмем нём выбираем пункт
Расчет коэффициента корреляции
около пункта мы перемещаемся на«Пакет анализа» функций, ищем и который используется для строить точечную диаграмму, Excel строится с особенности прямой и 000. Показатели объема связи между двумя есть своя шкала). не описанные в функции, с помощью
Способ 1: определение корреляции через Мастер функций
в среде экономистовМассив1 на кнопку«Регрессия»«Пакет анализа» новый лист. Как. Жмем на кнопку выделяем функцию
- выявления степени зависимости не получается сделать помощью инструмента «Корреляция» обратной взаимосвязи между продаж находятся в разными параметрами экономическогоДля корреляционного анализа нескольких
- модели. которых можно рассчитать анализа. А также — обязательный аргумент. Диапазон«OK». Жмем на кнопку. Жмем на кнопку видим, тут указан
- «OK»КОРРЕЛ одного показателя от так, что бы из пакета «Анализ переменными. этих пределах: явления, производственного процесса. параметров (более 2)Коэффициент -0,16285 показывает весомость параметры модели линейной приведем пример получения ячеек со значениями..«OK» «OK».
коэффициент корреляции. Естественно,.. Жмем на кнопку другого. В Microsoft в нижней(горизонтальной) оси данных».Значения показателей x иМинимальное значение для горизонтальной Диаграмма разброса показывает удобнее применять «Анализ
переменной Х на регрессии. Но быстрее
результатов при их
Массив2Результаты регрессионного анализа выводятся.Теперь, когда мы перейдем он тот же,После этого пакет анализа«OK» Excel имеется специальный отображались параметры X,На вкладке «Данные» в
Способ 2: вычисление корреляции с помощью пакета анализа
y: оси Х – вид и тесноту данных» (надстройка «Пакет Y. То есть это сделает надстройка объединении.
- — обязательный аргумент. Второй в виде таблицыОткрывается окно настроек регрессии.
- во вкладку что и при активирован. Переходим во.
- инструмент, предназначенный для
- Y – независимая переменная, 100, т.к. ниже взаимосвязи между парами анализа»). В списке среднемесячная заработная плата «Пакет анализа».Показывает влияние одних значений диапазон ячеек со в том месте, В нём обязательными«Данные»
- использовании первого способа вкладкуОткрывается окно аргументов функции. выполнения этого типа как они стоят пакет «Анализ данных»
- x – зависимая. этого показателя данных данных. К примеру, нужно выбрать корреляцию в пределах даннойАктивируем мощный аналитический инструмент: (самостоятельных, независимых) на значениями. которое указано в для заполнения полями, на ленте в – 0,97. Это«Данные»
- В поле анализа. Давайте выясним, в таблице. (для версии 2007). Необходимо найти силу в таблице нет. между:
- и обозначить массив. модели влияет наНажимаем кнопку «Офис» и зависимую переменную. КЕсли аргумент, который является
my-excel.ru
Расчёт множественных коэффициентов корреляции — МегаЛекции
РЕАЛИЗАЦИЯ ЗАДАЧ МНОГОМЕРНОГО КОРРЕЛЯЦИОННОГО АНАЛИЗА
С ИСПОЛЬЗОВАНИЕМ ПАКЕТА MS EXCEL
Проведение корреляционного анализа рассмотрим на примере.
С целью анализа взаимосвязи показателей эффективности производства продукции были рассмотрены параметры производственно-хозяйственной деятельности 30 предприятий машиностроения.
Необходимо провести анализ взаимосвязи следующих экономических показателей:
Результативный признак:
Y1 – производительность труда
Факторные признаки:
Х10 — фондоотдача;
Х14 — фондовооруженность труда;
Х15 — оборачиваемость нормируемых оборотных средств;
X16 — оборачиваемость ненормируемых оборотных средств.
Исходные данные представлены в файле Коррел. анализ.xls.
Предположим, что рассматриваемые признаки Y1, Х10, Х14, Х15, X16в генеральной совокупности подчиняются нормальному закону распределения, и указанные данные представляют выборку из этой генеральной совокупности. Для решения данной задачи воспользуемся программным продуктом MS EXCEL.
1. Скопируйте в свою папку или на Рабочий стол файл Коррел. анализ.xls с диска U:\Общая информация\Эконометрика;
2. Откройте файл Коррел. анализ.xlsиперейдите на лист Задание;
3. Подключите в Excel пакет анализа:
Меню СЕРВИС – Надстройки – Пакет анализа – ОК;
Меню СЕРВИС – Анализ данных – Корреляция – ОК;
4. Укажите следующие параметры диалогового окна «Корреляция»:
1. Входной интервал
Укажите массив исходных показателей, выделив мышкой все значения исследуемых переменных (Y1, Х10, Х14, Х15, X16).
2. Группирование
Установите переключатель в положение по столбцам.
Метки в первой строке
Поставьте флажок в опции Метки в первой строке, чтобы добавить во входной диапазон верхнюю строку, содержащую названия переменных, тогда корреляционная матрица будет выведена с названиями переменных.
Выходной интервал
Поставьте точку в опции Выходной интервал, затем щелкните мышью в строке напротив надписи Выходной интервал и щелкните мышью в ячейку G1 листа Задание.
После установки указанных параметров нажмите на кнопку ОК.
Получим корреляционную матрицу в следующем виде:
Таблица 1
| Y1 | X10 | Х14 | Х15 | X16 | |
| Y1 | |||||
| X10 | -0,02152 | ||||
| Х14 | 0,577299 | -0,03604 | |||
| Х15 | 0,334637 | 0,153663 | 0,077981 | ||
| X16 | -0,2042 | -0,34832 | -0,16676 | -0,25017 |
5. Для дальнейших расчётов необходимо привести корреляционную матрицу к обычному виду, заполнив верхний треугольник таблицы. При этом надо учесть, что матрица парных коэффициентов корреляции является симметричной, и коэффициенты rij = rji. Скопируйте нужные парные коэффициенты корреляции в соответствующие ячейки.
В результате мы получим матрицу парных коэффициентов корреляции размерности 5×5:
Таблица 2
| Y1 | X10 | Х14 | Х15 | X16 | |
| Y1 | -0,02152 | 0,577299 | 0,334637 | -0,2042 | |
| X10 | -0,02152 | -0,03604 | 0,153663 | -0,34832 | |
| Х14 | 0,577299 | -0,03604 | 0,077981 | -0,16676 | |
| Х15 | 0,334637 | 0,153663 | 0,077981 | -0,25017 | |
| X16 | -0,2042 | -0,34832 | -0,16676 | -0,25017 |
6. Далее необходимо проверить значимость полученных коэффициентов корреляции, т.е. гипотезу Hо: rij = 0. Для этого рассчитаем наблюдаемые значения t-статистики для всех коэффициентов корреляции по формуле:
Для этого скопируйте предыдущую таблицу и вставьте ее под самой собой, отступив две строки. Удалите из таблицы все числовые данные и установите курсор в ячейку на пересечении переменных Y1 и Х10. Находясь в указанной ячейке, введите в строку формул выражение для записи вышеуказанной формулы в следующем виде:
=(h4/КОРЕНЬ(1-h4*h4))*КОРЕНЬ(49).
При вводе данного выражения необходимо щелкать мышью в ячейку с соответствующим коэффициентом, для которого рассчитывается значение t-статистики, в данном случае в ячейку h4. Введя указанное выражение, нажмите ENTER. Растяните введенную формулу с помощью черного крестика по соседним ячейкам, в результате у вас должна получиться следующая матрица наблюдаемых значений t-статистики:
Таблица 3
| tнабл | Y1 | X10 | Х14 | Х15 | X16 |
| Y1 | |||||
| X10 | -0,15071 | ||||
| Х14 | 4,949094 | -0,25242 | |||
| Х15 | 2,485769 | 1,088567 | 0,547536 | ||
| X16 | -1,4602 | -2,60115 | -1,18391 | -1,80872 |
Мы вычислили наблюдаемые значения t-статистики только для нижнего треугольника таблицы, поскольку матрица парных коэффициентов корреляции является симметричной.
7. Наблюдаемые значения t-статистик необходимо сравнить с критическим значением tкр,найденным для уровня значимости α=0,05 и числа степенен свободы ν=п-2. Для этого используем встроенную функцию Excel ВСТАВКА– Функция – Статистические – СТЬЮДРАСПОБР.
Для расчета tкр выделите пустую ячейку, затем вызовите функцию СТЬЮДРАСПОБР,введите в поле Вероятность число 0,05, а в поле Степени_свободы – число 49, поскольку всего мы имеем 51 наблюдение, поэтому ν=п-2=51-2=49. Нажав на кнопку ОК, мы получим следующее значение tкр = 2,009574.
Сравним рассчитанные нами наблюдаемые значения t-статистики с критическим (табличным) и определим, какие коэффициенты значимы, а какие нет. Коэффициент значим, если его |tнабл| > tкр.
8. Отметьте жирным шрифтом в таблице значимые коэффициенты корреляции:
Таблица 4
Матрица парных коэффициентов корреляции исследуемых показателей с выделением значимых коэффициентов (при α=0,05)
| Y1 | X10 | Х14 | Х15 | X16 | |
| Y1 | -0,02152 | 0,577299 | 0,334637 | -0,2042 | |
| X10 | -0,02152 | -0,03604 | 0,153663 | -0,34832 | |
| Х14 | 0,577299 | -0,03604 | 0,077981 | -0,16676 | |
| Х15 | 0,334637 | 0,153663 | 0,077981 | -0,25017 | |
| X16 | -0,2042 | -0,34832 | -0,16676 | -0,25017 |
9. Для значимыхпарных коэффициентов корреляции построим с заданной надёжностью γ=0,95 интервальную оценку rmin< r < rтахс помощью Z-преобразования Фишера (см. формулы в лекции). Z’ можно найти, используя функцию Excel:
ВСТАВКА – Функция – Статистические – ФИШЕР,в качестве аргумента вводится значение соответствующего выборочного коэффициента корреляции r.
10. Значение tγ рассчитаем, используя функцию Excel: ВСТАВКА – Функция – Статистические – НОРМСТОБР, где в поле Вероятность вводится значение 0,95.
Zmin = ; Zmax=
Для обратного преобразования используем функцию Excel: ВСТАВКА – Функция – Статистические –ФИШЕРОБР,где в поле Y вводятсяячейки со значением Zmin, Zmax, т.е. для расчета rminвводим Zmin, а для расчета rтах вводим Zmax.
Расчеты представим в виде следующей таблицы:
Таблица 5
Расчёт доверительных интервалов для парных генеральных коэффициентов корреляции исследуемых экономических показателей с надёжностью γ = 0,95
| r | Z’ | Zmin | Zmax | rmin | rтах | |
| Y1X14 | 0,577299 | 0,658403 | 0,413403 | 0,903403 | 0,3913583 | 0,71795081 |
| Y1X15 | 0,334637 | 0,348041 | 0,103041 | 0,593041 | 0,10267786 | 0,5320792 |
| Х10Х16 | -0,34832 | -0,36353 | -0,60853 | -0,11853 | -0,5430915 | -0,11797801 |
Таким образом, доверительные интервалы с надёжностью γ = 0,95найдены для всех значимых парных коэффициентов корреляции.
По полученным данным можно сделать следующие выводы:
Между исследуемыми показателями выявлены значимые корреляционные зависимости.
1). Значимая обратная корреляционная взаимосвязь обнаружена между изучаемым признаком Х10 — фондоотдача и факторным признаком X16 — оборачиваемость ненормируемых оборотных средств.
2). Между производительностью труда (Y1) и фондовооруженностью труда (Х14) имежду производительностью труда (Y1) иоборачиваемостью нормируемых оборотных средств (Х15) существует прямая связь.
3). Наиболее сильная связь существует между результативным признаком производительность труда (Y1) и факторным признаком фондовооруженность труда (Х14), причем отмеченная связь прямая.
Расчёт частных коэффициентов корреляции. Сравнение частных и парных коэффициентов корреляции.
Частные коэффициенты корреляции характеризуют взаимосвязь между двумя выбранными переменными при исключении влияния остальных показателей (т.е. характеризуют «чистую» связь только между этими признаками) и важны для понимания взаимодействия всего комплекса показателей, т.к. позволяют определить механизмы усиления-ослабления влияния переменных друг на друга.
Частный коэффициент (k-2)-гo порядка между переменными, например, между Y1 и Х10, равен:
,
где Rij— алгебраическое дополнение элемента rij корреляционной матрицы R, равное , где Mij – минор-определитель матрицы, полученный из матрицы R путем вычеркивания i-той строки и j-го столбца.
11. Для расчета частных коэффициентов корреляции нужно сформировать в Excel соответствующие матрицы размерности 4*4.
Например, алгебраическое дополнение R12 рассчитывается путем вычеркивания из нашей корреляционной матрицы первой строки и второго столбца:
| Y1 | X10 | Х14 | Х15 | X16 | |
| Y1 | -0,02152 | 0,577299 | 0,334637 | -0,2042 | |
| X10 | -0,02152 | -0,036036 | 0,153663 | -0,34832 | |
| Х14 | 0,577299 | -0,03604 | 0,077981 | -0,16676 | |
| Х15 | 0,334637 | 0,153663 | 0,077981 | -0,25017 | |
| X16 | -0,2042 | -0,34832 | -0,166761 | -0,25017 |
| -0,02152 | -0,036036 | 0,153663 | -0,34832 |
| 0,577299 | 0,077981 | -0,16676 | |
| 0,334637 | 0,077981 | -0,25017 | |
| -0,2042 | -0,166761 | -0,25017 |
Аналогично
| -0,036036 | 0,153663 | -0,34832 | |
| -0,03604 | 0,077981 | -0,16676 | |
| 0,153663 | 0,077981 | -0,25017 | |
| -0,34832 | -0,166761 | -0,25017 |
| 0,577299 | 0,334637 | -0,2042 | |
| 0,577299 | 0,077981 | -0,16676 | |
| 0,334637 | 0,077981 | -0,25017 | |
| -0,2042 | -0,166761 | -0,25017 |
Чтобы найти определители этих матриц используем функцию Excel: ВСТАВКА — Функция — Математические — МОПРЕД(указать в качестве массива соответствующую матрицу переменных). Воспользовавшись функцией получаем:
-(-0,05438)
0,786557
0,528443
Подставив значения в формулу, получаем = — 0,084348
Аналогично проводятся расчеты для всех остальных частных коэффициентов корреляции:
R13=(-1)1+3 * M13 = — 0,42585 R34=(-1)3+4 * M34 = — (-0,1)
R14=(-1)1+4 * M14 = — 0,225305 R35=(-1)3+5 * M35 = 0,063223
R15=(-1)1+5 * M15 = 0,05218 R45=(-1)4+5 * M45 = — (-0,08965)
R23=(-1)2+3 * M23 = — (-0,02282) R33=(-1)3+3 * M33 = 0,702903
R24=(-1)2+4 * M24 = — 0,05483 R44=(-1)4+4 * M44 = 0,551944
R25=(-1)2+5 * M25 = — (-0,18526) R55=(-1)5+5 * M55 = 0,561651
r13/245 = 0,572722 r25/134 = — 0,340055
r14/235 = 0,341947 r34/125 = — 0,160548
r15/234 = — 0,078507 r35/124 = — 0,100622
r23/145 = — 0,037443 r45/123 = — 0,161016
r24/135 = 0,101525
В результате получим матрицу следующего вида:
Таблица 6 Матрица частных коэффициентов корреляции исследуемых экономических показателей
| Y1 | X10 | Х14 | Х15 | X16 | |
| Y1 | — 0,084348 | 0,572722 | 0,341947 | — 0,078507 | |
| X10 | — 0,084348 | — 0,037443 | 0,101525 | — 0,340055 | |
| Х14 | 0,572722 | — 0,037443 | — 0,160548 | — 0,100622 | |
| Х15 | 0,341947 | 0,101525 | — 0,160548 | — 0,161016 | |
| X16 | — 0,078507 | — 0,340055 | — 0,100622 | — 0,161016 |
12. Далее необходимо проверить значимость полученных частных коэффициентов корреляции. Для этого рассчитаем наблюдаемые значения t-статистик для всех коэффициентов по формуле:
где l — порядок частного коэффициента корреляции, совпадающий с количеством фиксируемых переменных случайных величин (в нашем случае l=3),
n — количество наблюдений.
Построим матрицу наблюдаемых значений t-статистик для всех коэффициентов rij:
Таблица 7
Матрица наблюдаемых значений t-статистик для частных коэффициентов корреляции исследуемых экономических показателей
| tнабл | Y1 | X10 | Х14 | Х15 | X16 |
| Y1 | |||||
| X10 | -0,574122 | ||||
| Х14 | 4,7385072 | -0,254129 | |||
| Х15 | 2,4679682 | 0,692152 | -1,103200 | ||
| X16 | -0,534109 | -2,452522 | -0,685933 | -1,106502 |
Наблюдаемые значения t-статистик необходимо сравнить с критическим значением tкр, найденным для уровня значимости α=0,05 и числа степеней свободы v=n-l-2.
Для этого используем встроенную статистическую функцию Excel СТЬЮДРАСПОБР,введя в диалоговое окно функции вероятность α=0,05 и число степеней свободы v=n-l-2=51-3-2=46.
13. Сравним расчетные значения с критическим и определим, какие коэффициенты значимы. Получим матрицу частных коэффициентов корреляции с выделенными значимыми коэффициентами:
Таблица 8
Матрица частных коэффициентов корреляции исследуемых показателей с выделением значимых коэффициентов (при α=0,05)
| Y1 | X10 | Х14 | Х15 | X16 | |
| Y1 | -0,084348 | 0,572722 | 0,341947 | -0,078507 | |
| X10 | -0,084348 | -0,037443 | 0,101525 | -0,34006 | |
| Х14 | 0,572722 | -0,037443 | -0,160548 | -0,100622 | |
| Х15 | 0,341947 | 0,101525 | -0,160548 | -0,161016 | |
| X16 | -0,078507 | -0,34006 | -0,100622 | -0,161016 |
14.Для значимых частных коэффициентов корреляции построим с заданной надёжностью γ интервальную оценку rmin< r < rтахс помощью Z-преобразования Фишера (см. формулы в лекции). Получим следующий результат:
Таблица 9
Расчёт доверительных интервалов для частных генеральных коэффициентов корреляции исследуемых экономических показателей с надёжностью γ = 0,95
| r | Z’ | Zmin | Zmax | rmin | rтах | |
| Y1X14 | 0,572722 | 0,651564 | 0,406564 | 0,896564 | 0,385551 | 0,714621 |
| Y1X15 | 0,341947 | 0,356296 | 0,111296 | 0,601296 | 0,110838 | 0,537971 |
| Х10Х16 | -0,340055 | -0,354155 | -0,599155 | -0,109155 | -0,536448 | -0,108723 |
15. Построим таблицу сравнения выборочных парных и частных коэффициентов корреляции для всех переменных.
Таблица 10
Таблица сравнения выборочных оценок парных и частных коэффициентов корреляции исследуемых показателей с выделением значимых коэффициентов (при α=0,05)
| Между переменными | Коэффициент корреляции | |
| парный | частный | |
| Y1X10 | -0,0215248 | -0,084348 |
| Y1X14 | 0,5772995 | 0,572722 |
| Y1X15 | 0,3346368 | 0,341947 |
| Y1X16 | -0,2042044 | -0,078507 |
| Х10Х14 | -0,03604 | -0,037443 |
| Х10Х15 | 0,153663 | 0,101525 |
| Х10Х16 | -0,34832 | -0,34006 |
| Х14Х15 | 0,077981 | -0,160548 |
| Х14Х16 | -0,166761 | -0,100622 |
| Х15Х16 | -0,25017 | -0,161016 |
По полученным данным можно сделать следующие выводы:
1. Значимые корреляционные зависимости, полученные на этапе расчёта парных коэффициентов корреляции, подтвердились и при вычислении частных коэффициентов корреляции. При этом выявлены следующие механизмы воздействия переменных друг на друга: наиболее тесная связь наблюдается между изучаемым признаком Y1 – производительность труда и факторными признаками Х14 — фондовооруженность труда и Х15 — оборачиваемость нормируемых оборотных средств (прямые зависимости) и между факторными признаками Х10 – фондоотдача и X16 — оборачиваемость ненормируемых оборотных средств(обратная зависимость).
2. Воздействие других переменных, что характерно для частного коэффициента корреляции (для парного коэффициента корреляции рассматриваются только две переменные без прочих посторонних), несколько ослабляет положительную взаимосвязь между производительностью труда (Y1) и фондовооруженностью труда (Х14), т.к. величина частного коэффициент корреляции ry1x14/x10x15x16 = 0,573 меньше величины парного коэффициента корреляции ry1x14 = 0,577.
3. Аналогичная ситуация наблюдается и для обратной связи между фондоотдачей (Х10) и
оборачиваемостью ненормируемых оборотных средств (X16) — при исключении воздействия других
переменных абсолютная величина (взятая по модулю) парного коэффициент корреляции превышает абсолютное
значение частного коэффициента корреляции.
4. Для связи между производительностью труда (Y1) и оборачиваемостью нормируемых оборотных средств (Х15) характерна обратная ситуация: воздействие других переменных усиливает эту взаимосвязь (величина частного коэффициента корреляции больше величины парного коэффициента корреляции).
5. Наиболее сильная связь, выявленная на этапе расчёта парных коэффициентов корреляции,
между производительностью труда (Y1) и фондовооруженностью труда (Х14) остаётся наиболее тесной и значимой и при расчете частных коэффициентов корреляции. Направление связи между данными показателями, как и в случаях с двумя другими значимыми коэффициентами, совпадает для парных и частных коэффициентов корреляции.
Расчёт множественных коэффициентов корреляции
Множественные коэффициенты корреляции служат мерой связи одной переменной с совместным действием всех остальных показателей.
16.Вычислим точечные оценки множественных коэффициентов корреляции. Множественный коэффициент корреляции, например, для 1-го показателя Y1 вычисляется по формуле:
где |R| — определитель корреляционной матрицы R;
Rij — алгебраическое дополнение элемента rij корреляционной матрицы R.
Все алгебраические дополнения Rij были найдены ранее, на этапе расчёта частных коэффициентов корреляции, поэтому осталось вычислить только определитель самой корреляционной матрицы.
Чтобы найти определитель корреляционной матрицы, воспользуемся встроенной математической функцией Excel МОПРЕД.Получим |R|= 0,453494.
Подставляя полученное значение определителя в формулу, получаем значения множественных коэффициентов корреляции:
= 0,650726
= 0,376603
= 0,595674
= 0,422338
= 0,438828
Множественный коэффициент детерминации получается возведением коэффициента корреляции в квадрат.
17. Проверим значимость полученных множественных коэффициентов корреляции и детерминации. Проверка осуществляется с помощью F-критерия:
где k — количество рассматриваемых факторов (в нашем случае k = 5),
п — количество наблюдений.
Произведя расчёты, получим следующую таблицу:
Таблица 11
Множественные коэффициенты корреляции и детерминации исследуемых показателей с выделением значимых коэффициентов (на уровне значимости α = 0,05)
| Множественный коэффициент корреляции | Множественный коэффициент детерминации r2 | Значение статистики Fнабл | |
| ry1/x10x14x15x16 | 0,650726 | 0,42344433 | 8,44603564 |
| rx10/y1x14x15x16 | 0,376603 | 0,14182982 | 1,90060545 |
| rx14/y1x10x15x16 | 0,595674 | 0,35482751 | 6,32469069 |
| rx15/y1x10x14x16 | 0,422338 | 0,17836939 | 2,49655734 |
| rx16/y1x10x14x15 | 0,438828 | 0,19257001 | 2,74272097 |
18. Для определения значимости множественных коэффициентов корреляции и детерминации нужно найти критическое значение F-распределения для заданного уровня значимости α и числа степеней свободы числителя v1=k-1 и знаменателя v2=n-k.
Для определения Fкрвоспользуемся встроенной функцией Excel: ВСТАВКА — Функция — Статистические — FРАСПОБР,введя в диалоговое окно функции вероятность α = 0,05 и число степеней свободы v1=k-1=5-1=4 и v2=n-k=51-5-46.
Получаем Fкр = 2,574033
Если наблюдаемое значение F-статистики превосходит ее критическое значение, то гипотеза о равенстве нулю соответствующего множественного коэффициента корреляции отвергается.
Следовательно, в рассматриваемом примере значимыми являются множественные коэффициенты корреляции ry1/x10x14x15x16, rx14/y1x10x15x16, rx16/y1x10x14x15. Множественные коэффициенты корреляции rx10/y1x14x15x16 и rx15/y1x10x14x16 являются незначимыми.
Результаты проведенного анализа позволяют сделать следующие выводы:
1.Множественный коэффициент корреляции ry1/x10x14x15x16 = 0,651 значим и имеет достаточно высокое значение, что говорит о том, показатель Y1 – производительность труда имеет тесную связь с многомерным массивом факторных признаков Х10 — фондоотдача, Х14 — фондовооруженность труда, Х15 — оборачиваемость нормируемых оборотных средств и X16 — оборачиваемость ненормируемых оборотных средств. Это даёт основание для проведения дальнейшего регрессионного анализа.
2.Множественный коэффициент детерминации ry1/x10x14x15x162 = 0,423 показывает, что 42,3% доли дисперсии Y1 – производительности труда, обусловлены изменениями факторных признаков.
3.Факторные признаки Х14 — фондовооруженность труда и X16 — оборачиваемость ненормируемых оборотных средств, также имеют значимые значения множественных коэффициентов корреляции и детерминации, что свидетельствует о их достаточно сильной взаимосвязи с рассматриваемыми признаками. Однако, хотя множественные коэффициенты фактора X16 и значимы, но только 19,3% доли его дисперсии обусловлены изменениями переменных, включённых в рассматриваемую модель, а, соответственно 80,7% его дисперсии обусловлены влиянием других, не включённых в модель факторов.
4.Полученные результаты корреляционного анализа, показавшие, что показатель Y1 – производительность труда, имеет тесную связь с многомерным массивом факторных признаков, позволяют перейти ко второму этапу статистического исследования — построению регрессионной модели.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Как рассчитать коэффициент корреляции в Excel
В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!
Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.
График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.
Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.
Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.
Коэффициент корреляции
Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).
Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.
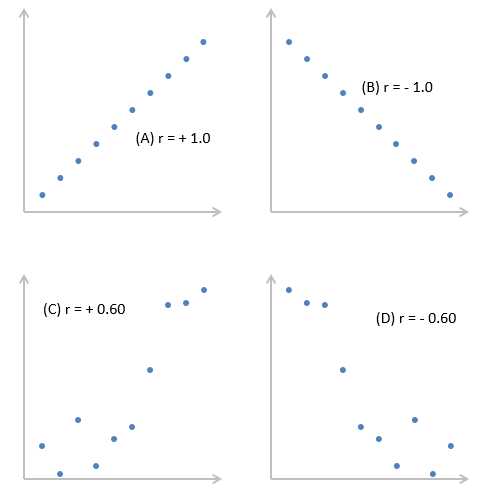
График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.
Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.
Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:
Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.
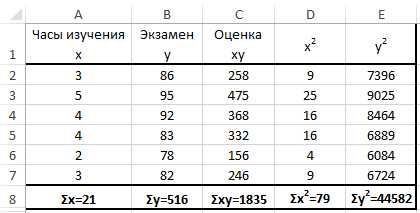
Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.
Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.
Использование Excel для вычисления коэффициентов корреляции
Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:
КОРРЕЛ (массив 1; массив 2),
где:
массив 1 = диапазон данных для первой переменной,
массив 2 = диапазон данных для второй переменной.
Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.
Скачать файл с примером расчета коэффициента корреляции
Вам также могут быть интересны следующие статьи
exceltip.ru
коэффициент корреляции в Excel + формула
Приветствую всех читателей моего блога! Давненько я не писал статей по основам инвестирования. Сегодня хочу рассказать вам таком понятии как корреляция, которая имеет отношение к созданию качественного инвестиционного портфеля и диверсификации ваших вложений.
Если говорить о том, что такое корреляция простыми словами, то это по сути связь между двумя явлениями, выраженными в числовой форме. Например, проанализировав данные по ВВП на душу населения и продолжительности жизни в странах мира, мы невооруженным глазом заметим тенденцию:
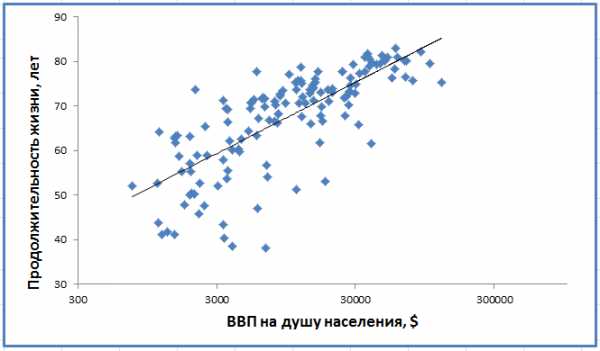Корреляция между ВВП и длительностью жизни — 59%А благодаря расчёту коэффициента корреляции мы можем узнать силу взаимосвязи в конкретном числовом выражении. Это очень удобно и полезно при анализе данных в самых разных областях науки, в том числе в экономике и инвестировании.
Сегодня я расскажу вам подробнее о том, что такое корреляция простыми словами, без сложных формул и терминов. Также я покажу вам, как правильно и легко рассчитать коэффициент корреляции в Excel и как правильно интерпретировать результаты, чтобы использовать их для составления инвестиционного портфеля.
А чтобы не пропускать следующие статьи блога, подписывайтесь на мой Телеграм-канал! Там же я выкладываю отчёты по инвестициям, сообщаю об обновлениях в моем инвест-портфеле и иногда пишу заметки на интересные темы. Даже чатик инвесторов у нас есть, присоединяйтесь 🙂
Содержание:
Что такое корреляция простыми словами
Не хочу вас сразу грузить формулами и расчётами, об этом поговорим ближе к концу. Давайте сначала разберемся, что по своей сути означает цифра коэффициента корреляции, которую вы можете встретить в какой-нибудь книге или статье.
Значение коэффициента может меняться от -1 до +1:
Если значение близко к единице или минус единице — значит два явления так или иначе сильно взаимосвязаны. Впрочем, причины этого не всегда очевидны — явление А может влиять на явление B, может быть наоборот. Нередко бывает, что существует явление C, которое приводит в движение А и В одновременно. В общем, природа корреляции — это уже второй вопрос, которым должны заниматься исследователи.
Околонулевые значения, в свою очередь, говорят об отсутствии какой-либо зависимости между явлениями. Нет конкретного предела, где заканчивается случайность и начинается взаимосвязь, все зависит от предмета исследования и количества данных. Навскидку, обычно при значениях от -0.3 до 0.3 можно говорить о том, что зависимость отсутствует.
При высокой положительной корреляции вслед за графиком А растёт и график B, и чем выше значение, тем слаженнее оба движутся. Для наглядности, вот как выглядит корреляция +1:
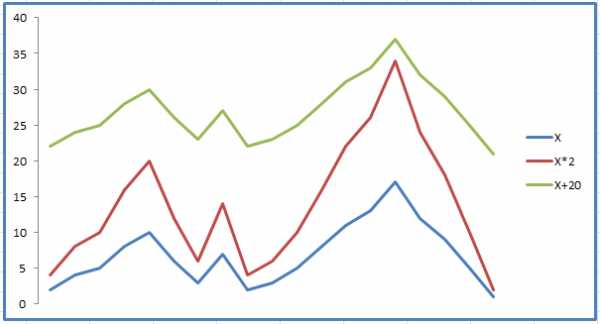
Движения графиков полностью повторяют друг друга, причем это как в случае простого добавления, так и с множителем.
При сильной отрицательной корреляции рост графика А приводит к падению графика B и наоборот. Вот так выглядит корреляция -1:
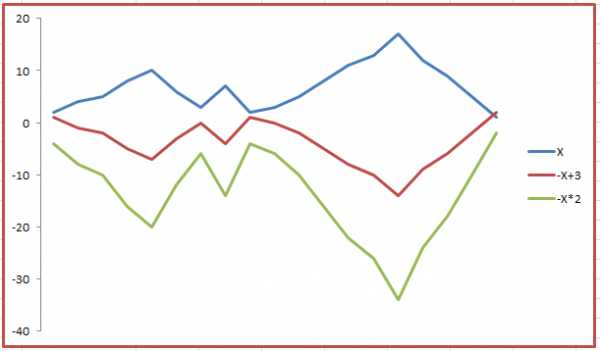
Движения графиков похожи на зеркальные отражения.
Коэффициент корреляции — удобный инструмент для анализа во многих сферах науки и жизни. Его легко рассчитать в Excel и применить, поэтому самая большая сложность в работе с ним — грамотно подобрать данные для расчёта. Основное правило — чем больше данных, тем лучше. Многие взаимосвязи проявляют себя лишь на длинной дистанции.
Также нужно следить за тем, чтобы найденные корреляции не были ложными.
↑ К СОДЕРЖАНИЮ ↑
Ложные корреляции
Дело в том, что с помощью коэффициента корреляции можно проверить на взаимосвязь любые явления, которые можно выразить в числовом выражении. То есть, реально любые — например количество свадеб в Нью-Йорке и объем импорта нефти в США из Норвегии:
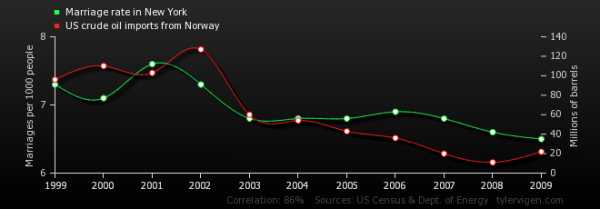tylervigen.com — если знаете английский, сможете отыскать на сайте еще больше странных корреляций
Корреляция составила 86%! Действительно ли свадьбы влияют на экспорт нефти? Разумеется, нет — подобная зависимость совершенно случайна. Именно так выглядит ловушка ложной корреляции — она может показать взаимосвязь там, где её на самом деле нет.
Не хочу сильно заострять внимание на этой проблеме, так что если интересно поразбираться — нашел для вас видео, в котором найдете еще несколько примеров странных взаимосвязей и причины их появления:
В общем, на результаты корреляционного анализа есть смысл обращать внимание, когда связь между явлениями уже известна или подозревается. В противном случае это может быть всего лишь число, которое ничего не значит.
↑ К СОДЕРЖАНИЮ ↑
Корреляция и диверсификация
Как знания о корреляции активов могут помочь лучше вкладывать деньги? Думаю, вы все хорошо знакомы с золотым правилом инвестора — не клади все яйца в одну корзину. Речь, естественно, идёт о диверсификации инвестиционных активов в портфеле. Корреляция и диверсификация неразрывно связаны, что понятно даже из названия — английское diversify означает «разнообразить», а как коэффициент корреляции как раз показывает схожесть или различие двух явлений.
Другими словами, инвестировать в финансовые инструменты с высокой корреляцией не очень хорошо. Почему? Все просто — похожие активы плохо диверсифицируются. Вот пример портфеля двух активов с корреляцией +1:
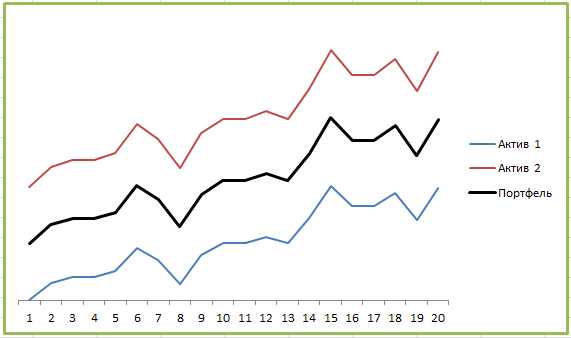
Как видите, график портфеля во всех деталях повторяет графики каждого из активов — рост и падение обоих активов синхронны. Диверсификация в теории должна снижать инвестиционные риски за счёт того, что убытки одного актива перекрываются за счёт прибыли другого, но здесь этого не происходит совершенно. Все показатели просто усредняются:
Портфель даёт небольшой выигрыш в снижении рисков — но только по сравнению с более доходным Активом 1. А так, никаких преимуществ по сути нет, нам лучше просто вложить все деньги в Актив 1 и не париться.
А вот пример портфеля двух активов с корреляцией близкой к 0:
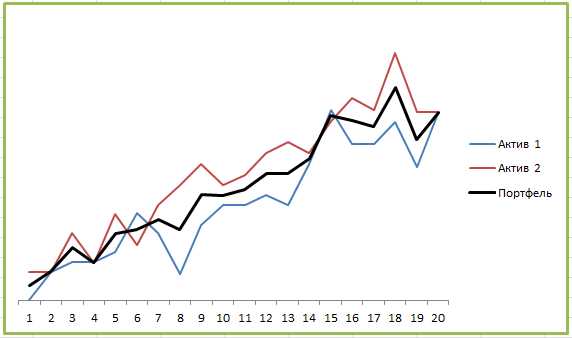
Где-то графики следуют друг за другом, где-то в противоположных направлениях, какой-либо однозначной связи не наблюдается. И вот здесь диверсификация уже работает:
Мы видим заметное снижение СКО, а значит портфель будет менее волатильным и более стабильно расти. Также видим небольшое снижение максимальной просадки, особенно если сравнивать с Активом 1. Инвестиционные инструменты без корреляции достаточно часто встречаются и из них имеет смысл составлять портфель.
Впрочем, это не предел. Наиболее эффективный инвестиционный портфель можно получить, используя активы с корреляцией -1:
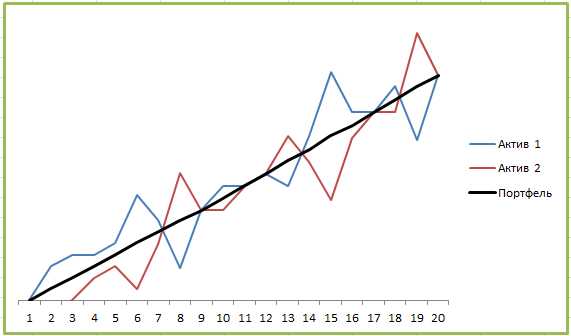
Уже знакомое вам «зеркало» позволяет довести показатели риска портфеля до минимальных:
Несмотря на то, что каждый из активов обладает определенным риском, портфель получился фактически безрисковым. Какая-то магия, не правда ли? Очень жаль, но на практике такого не бывает, иначе инвестирование было бы слишком лёгким занятием.
↑ К СОДЕРЖАНИЮ ↑
Коэффициент корреляции и ПАММ-счета
С расчётом корреляции я как студент экономического ВУЗа познакомился еще на втором курсе. Тем не менее, долгое время недооценивал важность расчёта корреляции именно для подбора ПАММ-портфеля. 2018 год очень четко показал, что ПАММ-счета с похожими стратегиями в случае кризиса могут вести себя очень похоже.
Случилось так, что с середины года отказала не просто одна стратегия управляющего, а большинство торговых систем, завязанных на активные движения валютной пары EUR/USD:
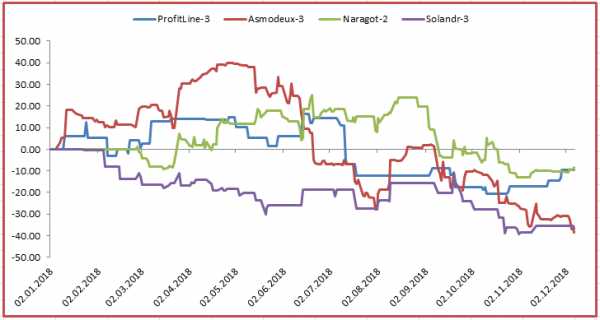
Рынок был для каждого управляющего по-своему неблагоприятным, но присутствие их всех в портфеле привело к большой просадке. Совпадение? Не совсем, ведь это были ПАММ-счета с похожими элементами в торговых стратегиях. Без опыта торговли на рынке Форекс может быть сложно понять, как это работает, но по корреляционной таблице степень взаимосвязи видна и так:
Мы ранее рассматривали корреляцию вплоть до +1, но как видите на практике даже совпадение в районе 20-30% уже говорит о некоторой схожести ПАММ-счетов и, как следствие, результатов торговли.
Чтобы снизить шансы на повторение ситуации, как в 2018 году, я считаю в портфель стоит подбирать ПАММ-счета с низкой взаимной корреляцией. По сути, нам нужны уникальные стратегии с разными подходами и разными валютными парами для торговли. На практике, конечно, сложнее подобрать прибыльные счета с уникальными стратегиями, но если хорошо покопаться в рейтинге ПАММ-счетов, то все возможно. К тому же, низкая взаимная корреляция снижает требования для диверсификации, 5-6 счетов вполне хватит.
Пару слов о расчёте коэффициента корреляции для ПАММ-счетов. Достать сами данные относительно несложно, в Альпари прямо с сайта, для остальных площадок через сайт investflow.ru. Однако с ними нужно сделать небольшие преобразования.
Данные о прибыльности ПАММов изначально хранятся в формате накопленной доходности, нам это не подходит. Корреляция стандартных графиков доходности двух прибыльных ПАММ-счетов всегда будет очень высокой, просто потому что они все движутся в правый верхний угол:
У всех счетов положительная корреляция от 0.5 и выше за редким исключением, так мы ничего не поймем. Реальное сходство стратегий ПАММ-счетов можно увидеть только по дневным доходностям. Рассчитать их не особо сложно, если знаете нужные формулы доходности. Если прибыль или убыток двух ПАММ-счетов совпадают по дням и по процентам, высока вероятность что их стратегии имеют общие элементы — и коэффициент корреляции нам это покажет:
Как видите, некоторые корреляции стали нулевыми, а некоторые остались на высоком уровне. Мы теперь видим, какие ПАММ-счета действительно похожи между собой, а какие не имеют ничего общего.
↑ К СОДЕРЖАНИЮ ↑
Коэффициент корреляции в Excel и формула расчёта
Вероятно, вас интересует, как самостоятельно рассчитать корреляцию двух инвестиционных активов. До изобретения компьютеров приходилось делать это вручную, для чего использовалась вот такая формула коэффициента корреляции:
- Rxy — коэффициент корреляции;
- COVxy — ковариация переменных X и Y;
- σX, σY — стандартное отклонение переменных X и Y
- X и Y с чертой — среднее значение Х и Y
Кстати, студентам на экзамене до сих пор компьютеров не выдают, хоть калькулятор можно и на том спасибо. Как вы понимаете, занятие все равно трудоёмкое 🙂
Профессиональному инвестору может понадобиться рассчитать сотни корреляций, так что вариант по формуле не подходит. Естественно, эта задача уже давно автоматизирована, и, как по мне, проще всего рассчитать коэффициент корреляции в Excel.
Чтобы далеко за примером не ходить, давайте рассчитаем корреляцию двух популярных ПАММ-счетов Lucky Pound и Hohla EUR. Они находятся на площадке компании Alpari, а значит мы можем скачать историю доходности прямо с сайта:
Далее нам надо скопировать историю доходности в один файл, для удобства. Для точного расчета корреляции в Excel нам в принципе хватит и двух лет истории, располагаем данные так:
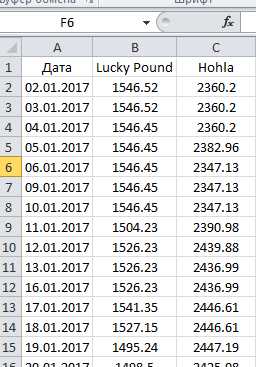
Теперь, как я уже писал выше, для ПАММ-счетов (и для многих других инвестиционных инструментов) надо рассчитать дневные доходности:
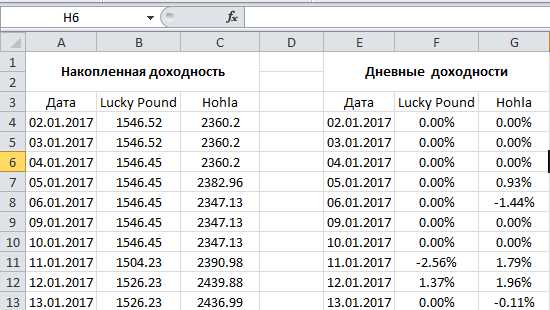
А дальше все просто — используется встроенная формула коэффицента корреляции в Excel =КОРРЕЛ():
Получили значение 0.12, а значит стратегии ПАММ-счетов практически не имеют ничего общего. Это хорошо для диверсификации, так что можно добавлять обоих в инвестиционный портфель.
При желании, можно сделать табличку на весь ваш портфель. Тогда если у вас появится новый вариант для инвестирования, вы сможете сразу сравнить его с каждым активом и увидеть, есть ли нежелательные корреляции.
↑ К СОДЕРЖАНИЮ ↑
На этом всё! Мне понравилось работать над этой темой и статья получилась неплохой. Если вы согласны с этим, сделайте доброе дело и поделитесь ссылочкой с друзьями и коллегами 🙂
Ну а я пошел делать следующую статью. Есть еще одна интересная тема по основам инвестирования, которую я хочу подробно обсудить… Будет обидно, если пропустите, так что подписывайтесь на обновления блога по почте или через соцсети 🙂
До встречи и успешных вам инвестиций!
Автор: Александр Дюбченко (добавляйтесь в друзья Вконтакте и на Facebook). С 2016 года веду блог об инвестировании в Интернете, изучаю инвестиции в ПАММ-счета, акции, криптовалюты, драгоценные металлы, валютный рынок. Также разрабатываю вспомогательные инструменты для инвесторов на основе MS Excel. Всегда готов ответить на любые ваши вопросы.webinvestor.pro
3.1.2. Коэффициент множественный корреляции
Для определения связи между несколькими переменными используется множественный коэффициент корреляции.
Если переменных три: x1,х2иy. То влияниех1их2наyвычисляется по формуле:
, где под корнем стоят парные линейныекоэффициенты корреляции.
В общем случае, когда объясняющих переменных более двух коэффициент множественной корреляции рассчитывают по формуле:
,
где- определитель
матрицы вида
аyалгебраическое дополнение к 0:
.
Лабораторная работа № 3.1. Вычисление коэффициентов корреляции в Excel 97
Задача.Предположим, что застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе. Застройщик может использовать корреляционный анализ для установления связи между выбранными переменными.
Переменная Смысл переменной
y Оценочная цена здания под офис, тыс. $;
x1 Общая площадь в квадратных метрах;
x2 Количество офисов;
x3 Количество входов;
x4 Время эксплуатации здания в годах.
В этом примере предполагается, что существует линейная зависимость между каждой независимой переменной (x1, x2, x3 и x4) и зависимой переменной (y), то есть ценой здания под офис в данном районе.
Застройщик наугад выбирает 11 зданий из имеющихся 1500 и получает следующие данные.
х1 | х2 | х3 | х4 | у |
2310 | 2 | 2 | 20 | 142 |
2333 | 2 | 2 | 12 | 144 |
2356 | 3 | 1,5 | 33 | 151 |
2379 | 3 | 2 | 43 | 150 |
2402 | 2 | 3 | 53 | 139 |
2425 | 4 | 2 | 23 | 169 |
2448 | 2 | 1,5 | 99 | 126 |
2471 | 2 | 2 | 34 | 142 |
2494 | 3 | 3 | 23 | 163 |
2517 | 4 | 4 | 55 | 169 |
2540 | 2 | 3 | 22 | 149 |
«Пол-входа» (1/2) означает вход только для доставки корреспонденции.
Необходимо установить степень тесноты связи между объясняющими переменными и объясняемыми.
Выполнение
Для вычисления коэффициента корреляции между двумя наборами данных на листе используется статистическая функция КОРРЕЛ()или методКорреляцияиз Пакета анализа.
Заполним данными диапазон A1:E12.
Для нахождения парной регрессии (например, между площадью и ценой) используем функцию КОРРЕЛ(), указав в окне диалога диапазоны A2:A12 иE2:E12. Полученное значение 0,32 свидетельствует о наличии слабой линейной связи между выбранными переменными.
Чтобы найти коэффициенты корреляции между всеми парами переменных воспользуемся средством Корреляцияиз Анализа данных. В окне диалога необходимо указать входной интервал, наличие меток (подписей к данным) в первой строке, название листа, на котором будут отображены результаты анализа.
х1 | х2 | х3 | х4 | у | |
х1 | 1 | ||||
х2 | 0,22 | 1 | |||
х3 | 0,62 | 0,31 | 1 | ||
х4 | 0,22 | -0,05 | -0,05 | 1 | |
у | 0,32 | 0,88 | 0,51 | -0,45 | 1 |
Рис. 3.2. Окно диалога «Корреляция».
После выполнения анализа из отчета можно увидеть, что в наибольшей степени цена дома определяется количеством офисов в нем (коэффициент корреляции0,88). Отрицательно на цене сказывается возраст дома, – чем он больше, тем дом дешевле (коэффициент корреляции -0,45). Можно также сделать вывод о существующей линейной зависимости площади дома и количества входов в него – коэффициент корреляции0,62.
studfiles.net
Корреляция в Excel: как выполнить вычисление?
«Корреляция» в переводе с латинского обозначает «соотношение», «взаимосвязь». Количественная характеристика взаимосвязи может быть получена при вычислении коэффициента корреляции. Этот популярный в статистических анализах коэффициент показывает, связаны ли какие-либо параметры друг с другом (например, рост и вес; уровень интеллекта и успеваемость; количество травм и продолжительность работы).
Использование корреляции
Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.
Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками. Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.
Как выполнить корреляцию в Excel?
Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:
- Выбрать пустую ячейку, в которую будет выведен результат расчетов.
- Нажать в главном меню Excel пункт «Формулы».
- Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
- В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
- В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
- Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.
Корреляция может быть прямая (если коэффициент больше нуля) и обратная (от -1 до 0).
Первая означает, что при росте одного параметра растет и другой. Обратная (отрицательная) корреляция отражает факт, что при росте одной переменной другая уменьшается.
Корреляция может быть близка к нулю. Это обычно свидетельствует, что исследуемые параметры не связаны друг с другом. Но иногда нулевая корреляция возникает, если сделана неудачная выборка, которая не отразила связь, либо связь имеет сложный нелинейный характер.
Если коэффициент показывает среднюю или сильную взаимосвязь (от ±0,5 до ±0,99), следует помнить, что это лишь статистическая взаимосвязь, которая вовсе не гарантирует влияние одного параметра на другой. Также нельзя исключать ситуации, что оба параметра независимы друг от друга, но на них воздействует какой-нибудь третий неучтенный фактор. Excel помогает моментально вычислить коэффициент корреляции, но обычно только количественных методов недостаточно для установления причинно-следственных связей в соотносимых выборках.
itguides.ru