Построение графиков сложных функций
Пояснительная записка к работе
«Построение графиков сложных функций»
Выполнил: Черемисин Дмитрий ученик 11Б класса
Преподаватель: Черемисина Галина Артуровна
Образовательное учреждение: МОУ-гимназия №13 п. Краснообска Новосибирского района Новосибирской области
Предмет: алгебра, алгебра и начала анализа
Тема: график сложной функции
Класс: 9 — 10 — 11 классы
Цель руководителя:
привить навыки эффективного использования ИКТ в школе и в жизни;
продолжать формировать интерес к математике посредством рассмотрения внепрограммного материала;
воспитывать осознанное отношение к процессу работы, прививать чувство ответственности за качество выполняемого проекта;
содействовать развитию у учащихся умения систематизировать материал;
осуществлять самоконтроль за процессом выполнения и оформления работы
Самостоятельная работа старшеклассника-гимназиста – это особым образом организованная деятельность, включающая в свою структуру такие компоненты, как:
уяснение цели поставленной учебной задачи;
четкое и системное планирование самостоятельной работы;
поиск необходимой учебной и научной информации;
освоение информации и её логическая переработка;
выработка собственной позиции;
представление, обоснование и защита полученного результата;
проведение самоанализа и самоконтроля.
Этот проект позволит учителю эффективно использовать ИТ в процессе преподавания, делая с их помощью уроки более увлекательными и насыщенными.
Цель работы:
Овладеть умением представлять сложную функцию в виде композиции двух функций
Освоить приём построения эскиза графика функции без применения производной
Показать возможность использования схемы построения графиков сложных функций вида y = f(φ(x))
В работе рассматриваются функции вида y = f(φ(x)), где φ(x) – любая из основных элементарных функций, а f – любая из следующих операций над ними: прибавление к функции какого-либо числа, умножение функции на число, деление единицы на функцию, возведение функции в положительную степень, извлечение корня из функции, нахождение показательной функции от функции, логарифмирование функции, нахождение модуля функции, нахождение тригонометрических функций от функции.
Эта работа может быть предложена в качестве развивающего компонента на уроках алгебры (демонстрация презентации при изучении темы «Исследование функции» и в рамках предметной недели).
Разрешение на публикацию работы моего сына есть!
infourok.ru
График сложных функции
Разделы: Математика
Цель урока:
Систематизировать и расширить знания учащихся по теме: “Графики функций”
Задачи урока:
- Использовать графики функций в задачах с параметром.
- Расширить знания при построении графиков функций, связанных с модулем.
- Исследовать и строить графики суперпозиции функций.
- Получить новые знания при построении графиков суммы, разности, произведения, частного функций.
План урока:
- Формулировка темы, цели, задач урока.
- Обсуждение домашнего задания с приобщением задач с параметром.
- Исследование и построение графиков функций, связанных с модулем (работа у доски, в парах, в группах).
- Исследование и построение графиков суммы и произведения функций.
- Исследование и построение графиков суперпозиции функций.
- Домашнее задание в виде творческой работы.
- Итоги урока. Рефлексия.
1. Обсуждение домашнего задания:
Построить график функций и описать свойства:
а)
б)
Правильность построения графиков проверяется с помощью мультимедийного проектора. Свойства функций проговариваются учащимися устно.
Дополнительный вопрос учителя по домашнему заданию:
Найдите все значения параметра a , при каждом из которых уравнение
б)
имеет ровно один, ровно два и ровно один корень.
Вопрос к классу: Сформулируйте определение функции.
2. Построение графиков функций, связанных с модулем (работа в тетрадях).
Построить графики следующих функций:
а)
б)
в)
г)
д)
е)
С помощью ранее построенных графиков, постройте графики следующих функций:
а)
б)
в)
г)
д)
е)
Укажите особенности графиков функций.
Правильность построения графиков проверяется с помощью мультимедийного проектора. Работа в парах, с последующей проверкой и оценкой.
Вывод:
Для построения графика функции надо сохранить ту часть графика функции, точки которой находятся на оси ОХ или выше, и симметрично отразить относительно оси ОХ ту часть графика функции, которая расположена ниже оси ОХ.
Для построения графика функции надо сохранить ту часть графика функции, точки которой находятся на оси ОУ или справа от нее, и симметрично отразить эту часть относительно оси ОУ.
Вопрос классу: Сформулируйте определение графика функции?
Работа в группах.
Построить график и описать свойства следующих функций:
а)
б)
в)
г)
д)
е)
ж)
з)
Работают 6 групп, два — три человека работают у доски. Заранее желательно обсудить какая функция является исходной.
Правильность построения графиков проверяется с помощью мультимедийного проектора.
Учащиеся, работавшие у доски, должны назвать особенности построенных графиков функций. Уполномоченные в группах должны назвать вертикальные и горизонтальные асимптоты для графиков своих функций.
Вопрос классу: Сформулируйте определение сложной функции?
3. Два учащихся выполняют задание у доски:
Построить графики и описать свойства следующих функций:
а)
б)
В это время идет исследование:
Как построить график суммы функций ?
- Найти область определения функции.
- Произвести сложение ординат точек графиков.
Например: Постройте график функции
Учащиеся самостоятельно выполняют эту работу. Возможны консультации в парах и группах.
Проверка с помощью мультимедийного проектора.
Здесь же, с помощью проектора, рассмотреть другой пример графика суммы функций
По аналогии обсудить: как построить график разности функций.
Как построить график произведения функций ?
- Найти область определения функции.
- Произвести умножение ординат точек графиков.
Например: Постройте график функции
Учащиеся самостоятельно выполняют эту работу. Возможны консультации в парах и группах.
Проверка с помощью мультимедийного проектора. С помощью проектора рассмотреть другой пример графика произведения функций
По аналогии обсудить: как построить график частного функций.
Рассмотреть с помощью проектора график функции
4. С помощью проектора, проверить правильность построения графиков суперпозиции функций (проанализировать работу двух учащихся, которые ранее работали у доски, показать особенности графиков).
Построить графики суммы, разности произведения функций, график сложной функции (подсказка в учебнике после п.2).
Итог урока:
Построение графиков функций один из самых интересных вопросов в курсе алгебры. Графики сложных функций чаще всего получаются очень красивыми и необычными. Поэтому изучение этого материала приносит не только практическую пользу
(например: в физике при изучении волновых явлений), но и эстетическое наслаждение.
Рефлексия:
- Что вам понравилось (или не понравилось) на уроке?
- Что нового вы узнали?
- Ваши пожелания?
Приложение.
25.03.2008
Поделиться страницей:urok.1sept.ru
Построение графиков сложных функций
Разделы: Информатика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (261,1 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Время реализации практикума 4 часа.
Цели урока:
- образовательная: закрепить знания по формированию массивов данных в табличной форме, отработать навык построения графиков сложных функций;
- развивающая: развивать алгоритмическое мышление; умение применять полученные знания при решении задач; умение рассуждать; развивать познавательный интерес;
- воспитательная: прививать учащимся навык самостоятельности в работе, воспитывать трудолюбие, чувство уважения к науке.
Тип урока: Урок обобщения и изучение нового материала.
Форма урока: Комбинированная.
Учебно-методическое оснащение урока:
- ПК, проектор;
- ПО: MS Windows, MS Excel;
- Технологические карты.
План урока.
1. Организационный этап.
2. Объявление темы и целей урока.
3. Повторение изученного материала.
4. Основная часть.
4.1. Построение трехмерных поверхностей (гиперболического параболоида, эллиптического параболоида).
4.2. Построение графиков сложных тригонометрических функций, заданными параметрическими уравнениями. (построение графика фигуры Лиссажу).
5. Закрепление полученных знаний. Компьютерный практикум.
5.1. Построение трехлепестковой розы.
5.2. Построение графика четырехлепестковой розы.
6. Проверка работы учащихся.
7. Подведение итогов урока.
8. Домашнее задание.
Ход урока
| № | Этапы урока | Действие учителя | Действия учащихся |
| 1 | Организационный этап. | Проверка наличия учащихся, готовность к
уроку. Постановка целей и задач урока |
|
| 2 | Объявление темы и целей урока | Сегодня мы познакомимся с разными сложными графиками и научимся строить графики трехмерных поверхностей и сложные тригонометрические функции. | Слайд № 1, Слайд № 2. |
| 3 | Повторение изученного материала. | Вопросы учащимся Слайд № 3. |
Отвечают на вопросы Слайд № 3. |
| 4 | 4. Основная часть. | Знакомит с поверхностью
эллипти?ческого параболоида. Параболоиды в мире техники и литературы. Материал из Википедии Слайд № 4, 5,6. |
Слайд № 4, 5,6. |
| 5 | 4.1. Построение трехмерных поверхностей (гиперболического параболоида, эллиптического параболоида). | Пример с подробным объяснением учителя. Построение графика гиперболического параболоида. Выдает Технологическая карта № 1 (приложение 1) С подробным объяснением учителя. Построение графика эллиптического параболоида. Выдает Технологическая карта № 2. (приложение 3) |
Получают Технологическая карта № 1. (приложение 1) Строят график. гиперболического параболоида. (приложение 2)
Строят график эллиптического параболоида. (приложение 4) |
| 6 | 4.2. Построение графиков сложных тригонометрических функций, заданными параметрическими уравнениями. (построение графика фигуры Лиссажу ). | Ознакомление с полярной системой
координат. Посмотреть связь между декартовыми и
полярными координатами. Использование
параболоидов в мире технике и
литературе.Знакомятся с графиками сложных
функций. (Материал из Википедии – свободной энциклопедии). Показывает Слайд № 7 — 14 С подробным объяснением учителя. Построение графика фигуры Лиссажу Выдает Технологическая карта № 3. (приложение 5) |
Получают Технологическая карта № 3. (приложение 5)
Слайд № 7 — 14
Строят график фигуры Лиссажу (приложение 6) |
| 7 | Закрепление полученных знаний.
Компьютерный практикум. 5.1. Построение трехлепестковой розы. (1 вариант) |
Самостоятельно строят график
трехлепестковой розы. Выдает Технологическая карта № 4. (приложение 7) |
Получают Технологическая карта № 4. (приложение 7) Строят график (приложение 8) |
| 8 | 5.2. Построение графика четырехлепестковой розы. (2 вариант) | Самостоятельно строят график четырехлепестковой розы. | Строят график (приложение 9) |
| 9 | Проверка работы учащихся. | Проверяет работу. | Сдают по желаниюКонтрольные точки 1,2,3,4,5. (все графики) |
| 10 | Подведение итогов урока. | Подводятся итоги урока, выставляются оценки с аргументацией (используются контрольные точки). Постановка задач для следующего урока. | |
| Домашнее задание. | Повторить материал по теме “Построение графиков в электронных таблицах” |
Ход урока
1. Организационный этап.
Проверка наличия учащихся, готовность к уроку.
Постановка целей и задач урока
2. Объявление темы и целей урока. Слайд № 1,2.
Учитель: Сегодня мы будем строить необычные графики, графики трехмерных поверхностей: гиперболического параболоида, эллиптического параболоида. Построение графиков является частным случаем построения диаграмм. Графики позволяют анализировать закономерности изменения величин. Мы будем работать с электронными таблицами, которые позволяют обрабатывать большие массивы числовых данных. В результате вы получите интересные, красивые графики, сложные графики. Построив их, вы сможете рассмотреть проекции фигуры на плоскость.
3. Повторение изученного материала. Слайд № 3.
Вопросы:.
- Назначение электронных таблиц, применение в каких отраслях жизни?
- Перечислите основные функции электронных таблиц.
- Какими способами можно включить Мастер диаграмм?
- Назовите основные типы диаграмм?
- Как связана таблица и построенная диаграмма?
- Что такое диаграмма и какие действия возможны с ней?
- В формулах вы будите использовать ссылки.
Вопросы:
- Какие основные типы ссылок вы знаете?
- Назовите различия между относительными и абсолютными ссылками проявляются при копировании формулы из активной ячейки в другую ячейку?
4. Основная часть. Использование этих графиков в мире техники и в литературе. Слайды № 4,5,6.
4.1. Построение трехмерных поверхностей (гиперболического параболоида, эллиптического параболоида).
Пример с подробным объяснением учителя.
Задание 1. График гиперболического параболоида описывается уравнением z = (х/а)2 — (у/в)2, а эллиптического параболоида z = (х/а)2 + (у/в)2. Диапазон изменения переменных х и у – квадрат (-5;5)C (-5;5) с шагом 0,5. Переименуйте Лист 2, в “График 2” для гиперболического параболоида
Технология работы. Выдается технологическая карта с подробным построением графика.
Технологическая карта № 1. Приложение 1.
Контрольная точка 1. Представьте преподавателю результаты работы.
Приложение 2
Задание 2. Построение графика эллиптического параболоида z = (х/а)2 + (у/в)2. Диапазон изменения переменных х и у – квадрат (-5;5)C (-5;5) с шагом 0,5.
Построить график согласно таблице на Листе 3.
Технология работы. Выдается технологическая карта с подробным построением графика.
Технологическая карта № 2. Приложение 3.
Контрольная точка 2. Представьте преподавателю результаты работы.
Приложение 4.
4.2. Построение графиков сложных тригонометрических функций, заданными параметрическими уравнениями (графика фигуры Лиссажу).
Ознакомление с полярной системой координат. Посмотреть связь между декартовыми и полярными координатами. Использование параболоидов в мире технике и литературе.
(Материал из Википедии – свободной энциклопедии). Слайды № 4-17.
Задание № 3. Построить график фигуры Лиссажу. Пример с подробным объяснением учителя.
Технология работы. Выдается технологическая карта с подробным построением графика.
Технологическая карта № 3. Приложение 5.
Контрольная точка 3. Представьте преподавателю результаты работы.
Приложение 6.
5. Закрепление полученных знаний. Компьютерный практикум.
При решении этих задач закрепляются умения учащихся заполнять таблицы и строить график.
5.1. Построение трехлепестковой розы.
Задание 4. Построить график трехлепестковой розы r=sin 3a, для этого необходимо заполнить столбец х=r*cos a, у=r*sin a. Осуществить переход от градусной меры в радианную по формуле =ПИ()/180*ячейку с градусной мерой. Перейти на Лист 5 и переменуйте в “График 5”.
Технология работы.
Выдается технологическая карта с подробным построением графика.
Технологическая карта № 4. Приложение 7.
Контрольная точка 5. Представьте преподавателю результаты работы.
Приложение 8.
5.2. Построение четырехлепестковой розы
Задание 5. Построить график четырехлепестковой розы r=sin 2a, для этого необходимо заполнить столбец х=r*cos a, у=r*sin a. Осуществить переход от градусной меры в радианную по формуле =ПИ()/180*ячейку с градусной мерой. Перейти на Лист 6 и переменуйте в “График 6”.
Контрольная точка 6. Представьте преподавателю результаты работы
Приложение 9.
6. Проверка работы учащихся.
Учащиеся демонстрируют подготовленные файлы выполненной работы.
7. Подведение итогов урока.
Научились строить графики сложных функций, получили практические навыки работы с большими таблицами.
Подводятся итоги урока, выставляются оценки с аргументацией (используются контрольные точки). Постановка задач для следующего урока.
8. Домашнее задание.
Повторить материал по теме “Построение графиков в электронных таблицах”.
5.05.2012
urok.1sept.ru
3.2. Построение графика сложной функции.
В данном задании предлагается построить график сложной функции, заданной в виде массива точек, используя два подхода: аппроксимацию и сглаживание.
1. Откройте новый файл в Origin.
2. Импортируйте файл ASCIIm_t.dat, находящийся в папкеLab1. Файл содержит набор данных сложной функции.Важно:При импорте используйте команду менюFile/Import/Single ASCII. В окне диалога установить указанный разделитель числа (рис. 17) (запятая). После этого импорт осуществится корректно.
3. Для построения графика данной функции используйте два похода:
а) Постройте график, используя нелинейную функцию для аппроксимации. Для этого отобразите зависимость в виде Plot, Scatterи, затем, вAnalysisзадайте функцию Гаусса (см. рис.10). Удалите появившееся окно подписи данной функции;
б) Постройте график, используя сглаживание. Для этого отобразите зависимость в виде Plot, Line/Spline. Удалите элементGap to Symbol(см. рис.14).
4. Нанесите подписи осей и поясняющие подписи. Для поясняющих подписей используйте следующий шаблон: функция М,функция ГауссаиСплайн. Для подписи осей используйте следующий шаблон: ось ординатфункция М, ось абсциссПараметр Т. Итоговые графики должны выглядеть, как на рис. 18.
5. Вставьте графики как рис. 3а,б и данные в таблицу 3 файла отчета <фамилия>_0.doc.
6. Сохраните файл отчета.
7. Сохраните файл обработки (файл ORIGIN). Для этого откройте меню<File> и выберете команду<Save Project>. В появившемся окне сохранения в верхней левой части укажите рабочую папкуМиЭЭТ/<Номер группы>, а внизу введите название файла <фамилия И.О.>_0. Тип файла оставьте без изменения (OPJ). Нажмите кнопку<Сохранить>.
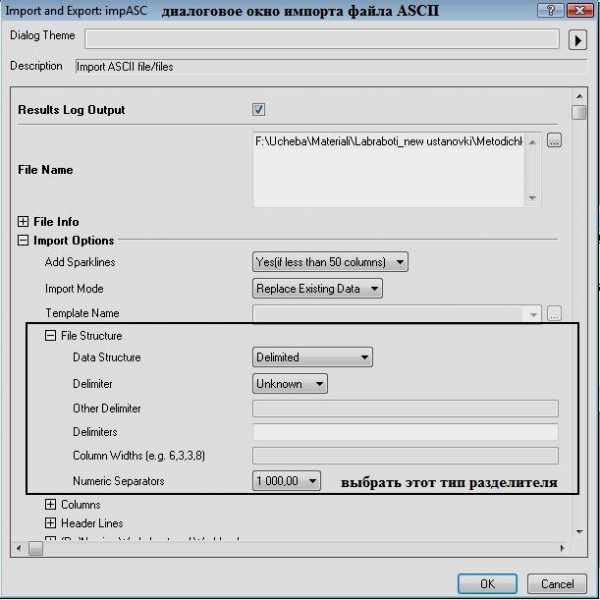
Рис. 17. Диалоговое окно импорта файлаASCII
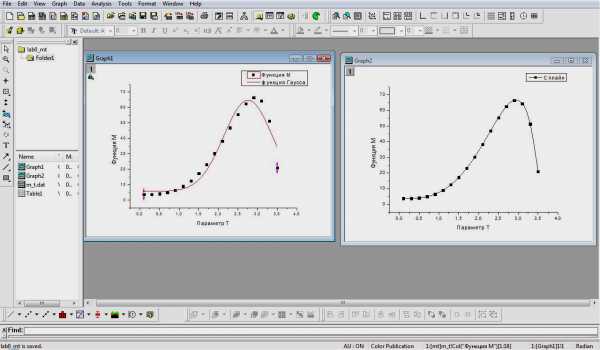
Рис. 18. Итоговое окно графика функции М(T)
В заключении, напишите выводы по проделанной работе в поле Вывод:отчета. Сохраните и распечатайте отчет.
Лабораторная работа №1
Исследование электропроводности
ТВЕРДЫХ ДИЭЛЕКТРИКОВ
1. Цель работы
Изучение электропроводности твердых диэлектриков:
1. Определение удельного поверхностного сопротивления и удельного объемного сопротивления твердых диэлектриков в зависимости от температуры.
2. Определение энергии активации носителей заряда в диэлектрике.
2. Теоретическое введение
2.1. Основные определения и формулы
По своему назначению электроизоляционные материалы под воздействием постоянного напряжения совершенно не должны пропускать электрический ток, т. е. должны быть непроводящими. Иными словами, удельное сопротивление электроизоляционных материалов в идеальном случае должно быть бесконечно большим.
Однако все практически применяемые электроизоляционные материалы при приложении постоянного напряжения пропускают некоторый, обычно очень незначительный, ток, называемый током утечки. Поэтому, чем больше удельное сопротивление электроизоляционного материала, тем выше его качество как изолятора, так как более незначительным будет ток утечки.
I
Iабс
Iсм Iскв
0 t
Рис 1. Зависимость тока через диэлектрик от времени при постоянном напряжении
Ток утечки, протекающий через участок изоляции при установившемся процессе электропроводности, т.е. спустя достаточно большой промежуток времени после приложения к этому участку постоянного напряжения, также является постоянным и называется сквозным током (рис. 1).До момента установления равновесного состояния в диэлектрике протекают процессы смещения связанных зарядов, создавая поляризационные токи, или токи смещения. Токи смещения упругосвязанных зарядов при электронной и ионной поляризациях столь кратковременны, что их обычно не удается зафиксировать. Токи смещения различных видов замедленной поляризации называют абсорбционными токами. При постоянном напряжении абсорбционные токи протекают только в момент включения и выключения напряжения, при переменном напряжении — в течение всего времени нахождения материала в электрическом поле.
Сопротивление участка изоляции Rизравно отношению приложенного к этому участку изоляции постоянного напряженияUк сквозному токуIизчерез этот участок
Rиз = U/Iиз, Ом. (1)
Проводимость изоляции Gиз– величина, обратнаяRиз:
 .
(2)
.
(2)
Помимо объемной проводимости изоляции Gv, количественно определяющей возможность прохождения тока через толщу изоляции, следует учитывать также поверхностную проводимость изоляцииGs, характеризующую наличие повышенной электропроводности на поверхности раздела твердого диэлектрика с окружающей средой. Этот слой создается вследствие неизбежных загрязнений, увлажнения и т.п.
Соответственно вводятся понятия объемного Rvи поверхностногоRs сопротивлений изоляции и объемногоIи поверхностногоIs токов:
 ;
;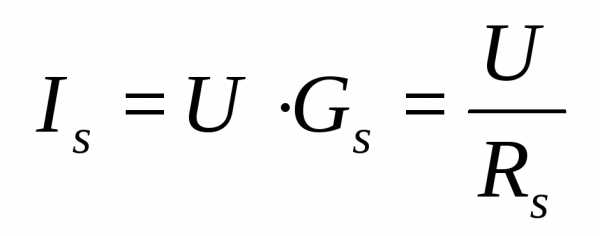 .
(3)
.
(3)
Очевидно (рис. 2), что , так что,
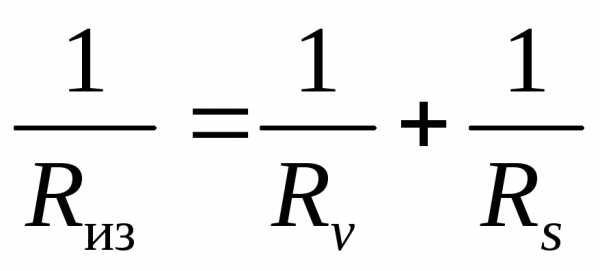 (4)
(4)
или
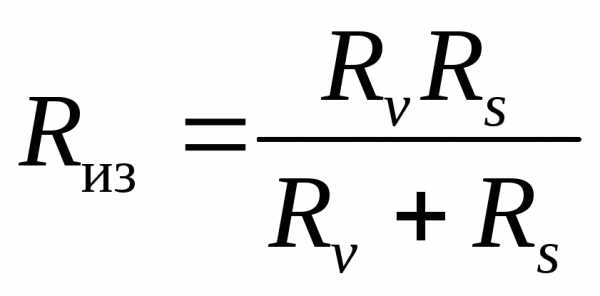 , (5)
, (5)
т.е. сопротивление изоляции определяется как результирующее двух сопротивлений — объемного и поверхностного, включенных параллельно друг другу между электродами.
Is
Iиз I Iиз
Рис. 2. Объемный и поверхностный токи утечки через участок изоляции
Для участка изоляции с постоянным поперечным сечением Sи толщинойh(форма плоского конденсатора) объемное сопротивление рассчитывается по формуле
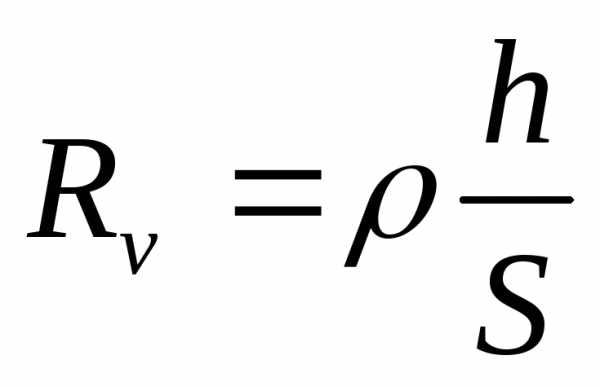 ,
(6)
,
(6)
где  — характеризующая материал величина,
называемая удельным объемным сопротивлением
(иногда обозначается также
— характеризующая материал величина,
называемая удельным объемным сопротивлением
(иногда обозначается также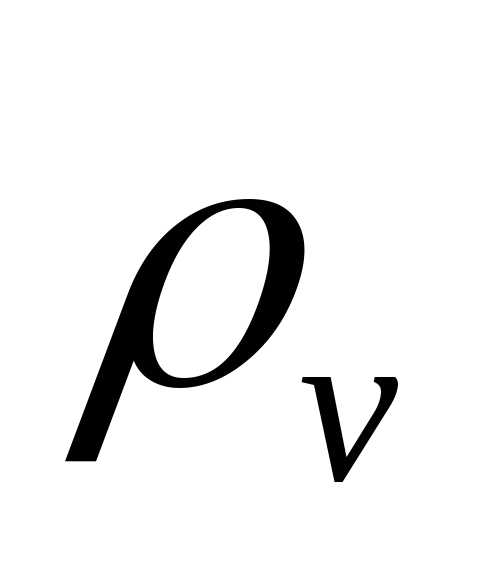 ).
Отсюда
).
Отсюда
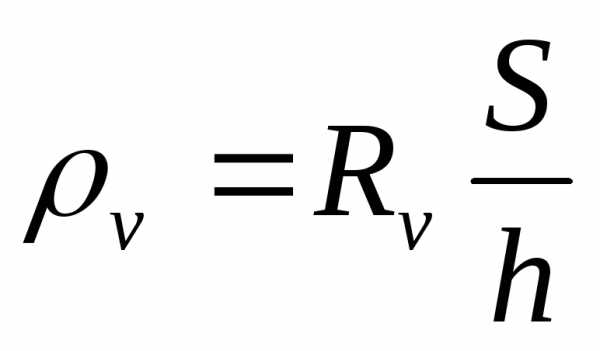 .
(7)
.
(7)
Если Rvвыражено в Омах,h– в метрах иS– в квадратных метрах, то единица измеренияv– Ом•м.
Для определения удельного поверхностного
сопротивления 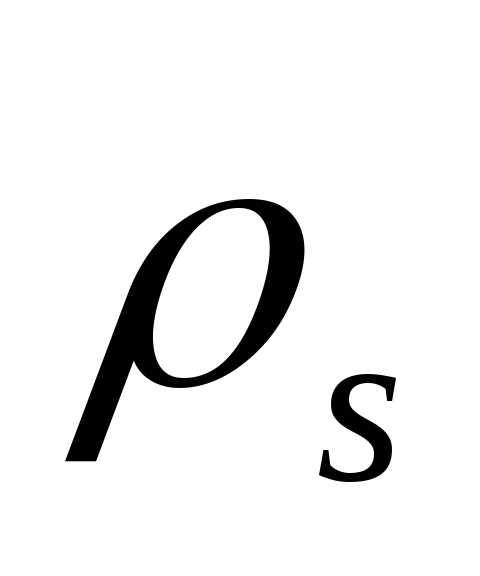 плоского образца на поверхности
диэлектрика помещаются два электрода
с правильными прямыми кромками длинойв, находящиеся на расстоянииадруг от друга (рис. 3,а). Сопротивление
плоского образца на поверхности
диэлектрика помещаются два электрода
с правильными прямыми кромками длинойв, находящиеся на расстоянииадруг от друга (рис. 3,а). Сопротивление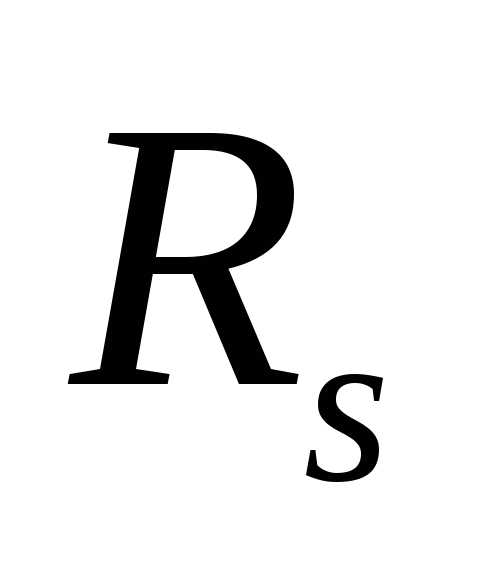 участка поверхности между электродами
равно
участка поверхности между электродами
равно
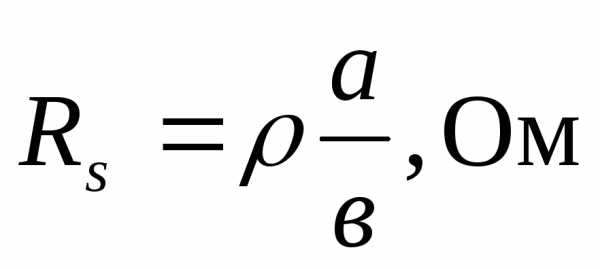 ,
(8)
,
(8)
где коэффициент пропорциональности и есть удельное поверхностное сопротивление. Отсюда
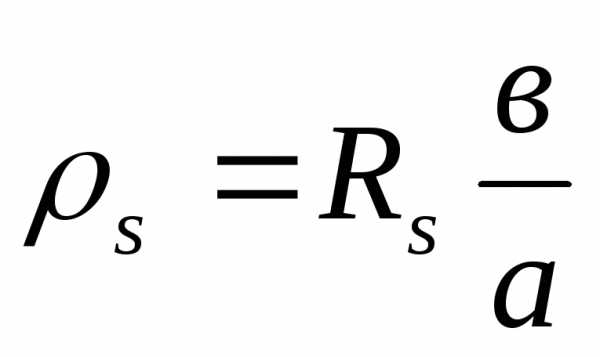 ,
Ом (9)
,
Ом (9)
Очевидно, что при в=а, формула
(9) дает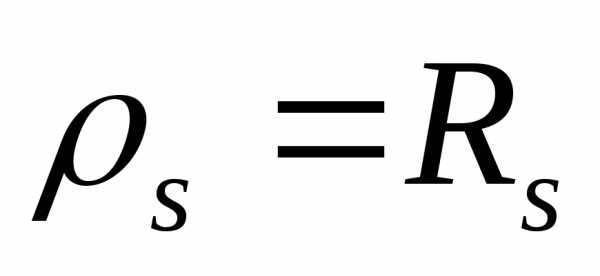 ,
т. е. можно сказать, что
,
т. е. можно сказать, что – сопротивление квадрата любой величины
на поверхности диэлектрика, если ток
идет от одной стороны квадрата к
противоположной стороне; единица
измерения для
– сопротивление квадрата любой величины
на поверхности диэлектрика, если ток
идет от одной стороны квадрата к
противоположной стороне; единица
измерения для – Ом.
– Ом.
Для более точного определения величины 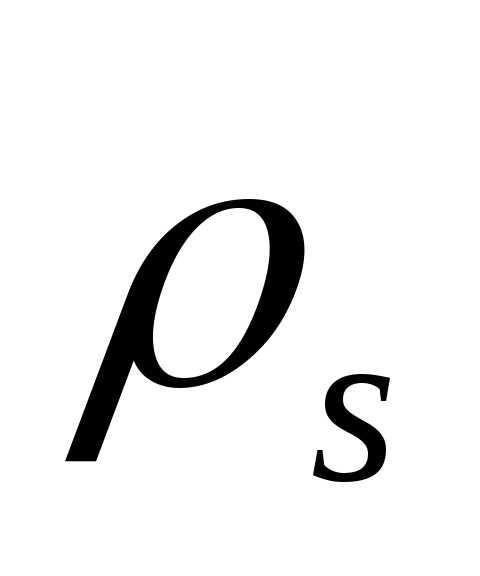 может быть измерено поверхностное
сопротивление
может быть измерено поверхностное
сопротивление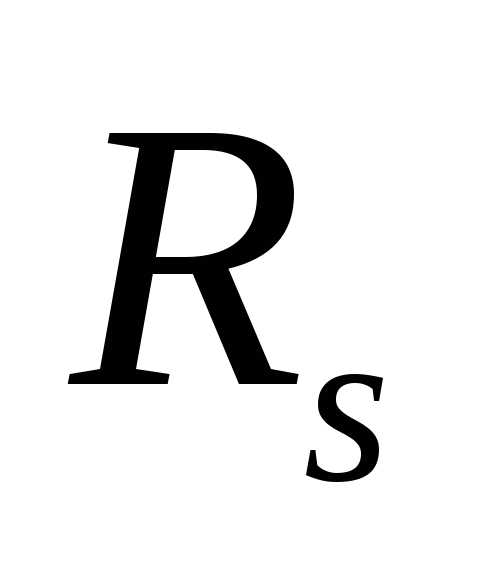 между помещенными на поверхности
диэлектрика электродами в виде двух
коаксиальных колец (рис. 3,б).
между помещенными на поверхности
диэлектрика электродами в виде двух
коаксиальных колец (рис. 3,б).
В этом случае связь между 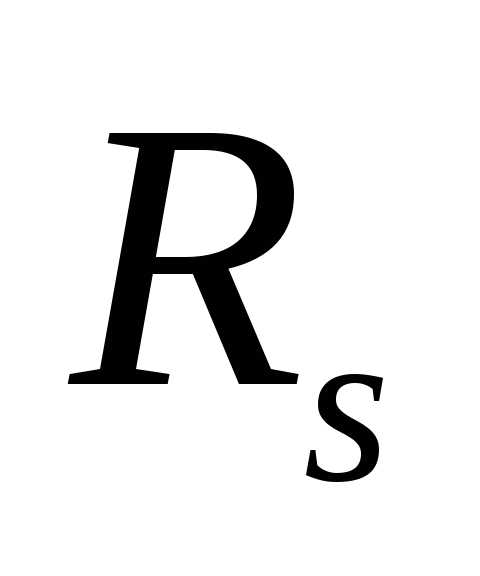 и
и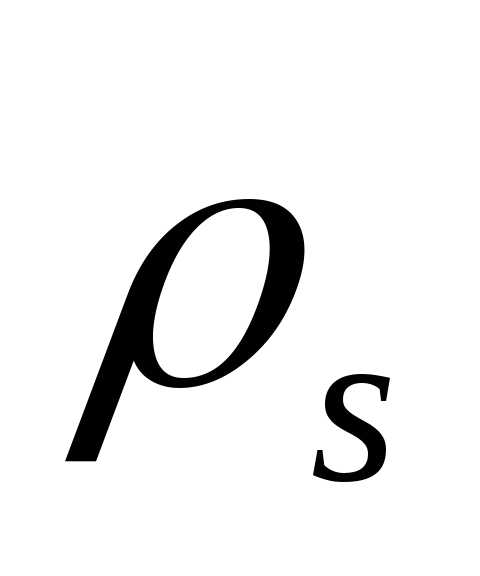 определяется уравнением
определяется уравнением
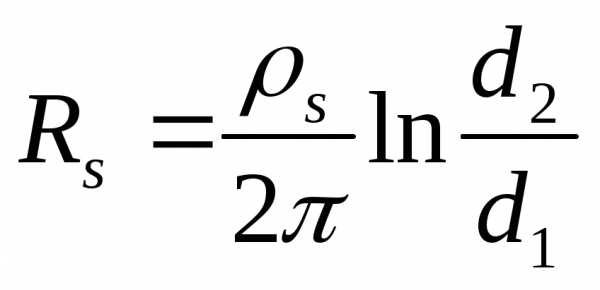 ,
(10)
,
(10)
где 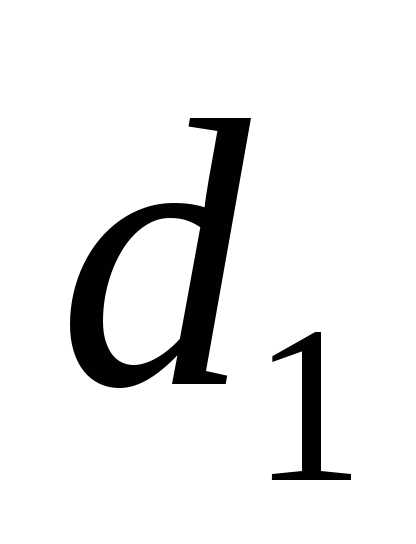 – диаметр внутреннего электрода,
– диаметр внутреннего электрода,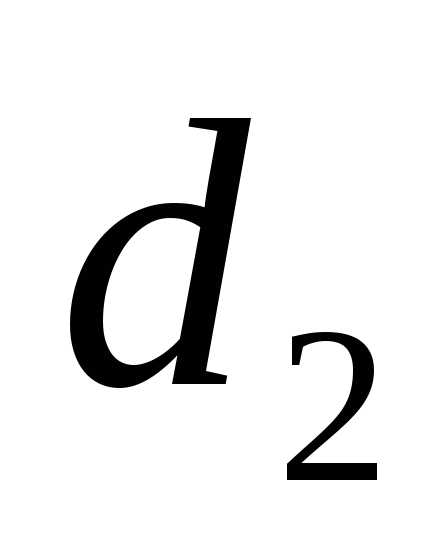 – внутренний диаметр кольцевого
электрода. Отсюда:
– внутренний диаметр кольцевого
электрода. Отсюда:
 . (11)
. (11)
Величина удельного поверхностного сопротивления очень сильно зависит от условий измерения и состояния поверхности диэлектрика.
1
d2
2 d1
в
а
а
б
Рис. 3. Расположение электродов на поверхности диэлектрика при
определении поверхностного сопротивления Rs: а – для электродов
прямоугольной формы; б – для круглых электродов: 1 – диэлектрик,
2 – электроды
studfiles.net
Выступление на НПК по теме «Построение графиков сложных функций»
Исследовательская работа по теме:
«Построение графиков сложных функций»
Выполнила:
Ганиева Айгуль Азатовна
9 б класс
МБОУ СОШ №3
Руководитель: Гайнутдинова
Ольга Николаевна
Проблемный вопрос:
Как можно построить графики сложных функций?
Цели и задачи
Овладеть умением представлять сложную функцию в виде композиции двух функций
Освоить приём построения эскиза графика функции без применения производной
Показать возможность использования схемы построения графиков сложных функций вида y=f(φ(x))
изучить области, в которых применяется функция и её свойства
Введение
Во многих задачах график является лишь вспомогательным элементом решения.
Построение графика сложной функции вида y = f(φ(x)) без использования производной можно осуществлять элементарными способами по некоторой схеме.
Все указанные операции можно проводить непосредственно над графиками основных элементарных функций (понимая под этим выполнение операций над соответствующими координатами), поскольку эти графики известны. Как правило, график функции y = f(φ(x)) трудно, а порой и просто невозможно построить, используя общую схему исследования функции.
Формула для задания сложной функции
y=f(g(x)) –
– сложная функция
g(x) – внутренняя функция
Пример.
g(x) = х2 — 4 – внутренняя функция
f(t) = – внешняя функция
f(t) – внешняя функция
Мы предположили, что функциональные зависимости существуют во всех сферах жизни человека. Сейчас мы попытаемся это доказать.
Основная часть
Схема построения графика сложной функции
Построение графиков функций вида
Построение графиков функций вида
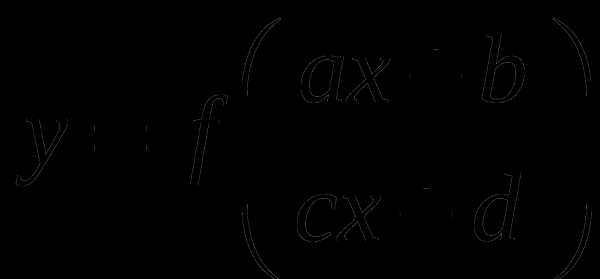
Построение графиков функций вида
Схема построения графика сложной функции у = f(φ(x))
Найти область определения исследуемой сложной функции, а также граничные значения функции.
Построить график внешней и внутренней функции.
Построить график функции у1 = φ(х). Отметить на этом графике характерные точки, т. е. нули и точки разрыва, найти граничные точки, одну — две промежуточные точки;
Произвести заданные операции над ординатами выбранных точек.
Нанести полученные точки и предельные значения на рисунок, помещённый под графиком функции у1 = φ(х) так, чтобы у1 была продолжением оси у.
Соединить полученные точки сплошной линией в тех промежутках, в которых функция непрерывна, и учесть (если она имеется) симметрию графика относительно точки или прямой.
Построение графиков функций вида

Сначала надо построить график линейной функции (внутренней функции)
Найти точки пересечения графика с осью x и y.
Затем в той системе координат надо построить график внешней функции, используя точки пересечения первого графика.


Построение графиков функций вида

Применение функций в точных науках
Графики зависимости физических величин,
параболоиды,
отображение звуковых волн с помощью периодической функции
Периодическая функция
F(x)=F(x±nT)
Звук, колебания за просторами Земли.
Фазы звуковой волны
Для описания относительных временных свойств двух звуковых волн (или разных частей одной волны) вводится понятие фазы звуковой волны.
Графики пословиц
«Посев хуже недосева», «Каши маслом не испортишь»,
«Чем дальше в лес, тем больше дров», «Горяч на почине, да скоро остыл»
Дни солнцестояния
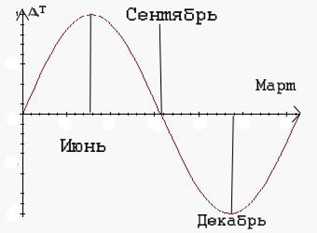
С помощью графика мы можем увидеть, что точки, где график, похожий на график синуса, пересекает ось времени соответствуют 23 сентября и 21 марта
Основные результаты
Для построения графика функции любой сложности необходимо знать и применять свойства элементарных функций (область определения, нули функции, четность и нечетность, периодичность и т. д.).
График сложной функции y = f(φ(x)) можно построить с помощью упрощенной схемы, если использовать операции над графиками (понимая под этим выполнение операций над соответствующими координатами).
Я надеюсь, что мои исследования убедили Вас в том, что функция является неотъемлемой частью нашей жизни и наук в целом.
Эта работа может быть предложена в качестве развивающего компонента на уроках алгебры (демонстрация презентации при изучении темы «Исследование функции» и в рамках предметной недели).
Рене Декарта сказал:
“Прямая – есть кратчайшее расстояние между двумя точками”.
И следуя этому правилу, я призываю вас в своем развитии по восходящей линии, не страшась усталости, не обходя трудностей, идти по прямой от точки не знания к точке знания.
Список ресурсов:
Гусев В.А., Мордкович А.Г. Математика: Справочные материалы. – М.: Просвещение, 1988
Гурский И. П. Графики сложных функций
Дворянинов С. В. О построении графиков сложных функций на основе свойства монотонности. Журнал «Математика в школе»
Дорофеев Г.В. Пособие по математике для поступающих в вузы. – М.: Наука, 1972
Костюкова Н.К. Научно-исследовательская работа учащихся. – М.: Математика в школе №5, 1999
Райхмист Р.Б. Графики функций: задачи и упражнения. – М.: Школа — Пресс, 1997
Рывкин А.А. Справочник по математике – М.: Высшая школа, 1987
Факультативный курс по математике — М.: Просвещение, 1991
http://mathem.by.ru/index.html
infourok.ru
Методы построения графиков функций | Обучонок
Автор публикации:
Климов Даниил СергеевичЧПОУ Красноярский кооперативный техникум экономики, коммерции и права
В данном методическом материале по математике на тему «Методы построения графиков функций» дается определение функции, рассматриваются способы задания функций: табличный, словесный, графический и аналитический.
В методическом материале по математике (алгебре) «Методы построения графиков функций» проводится разбор методов построения графиков функций: параллельный перенос, отражение, выполняется построение графиков четной и нечетной функций.
Оглавление
Введение
Глава 1. Определение функций.
Глава 2. Способы задания функций
Глава 3. Методы построения графиков функций
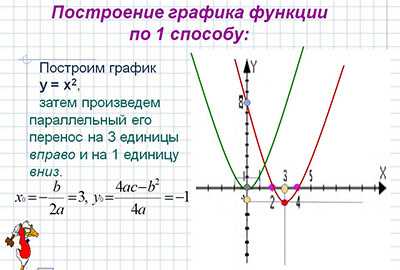
3.1. Параллельный перенос.
3.2. Отражение.
3.3. Построение графиков четной и нечетной функций.
Список источников
Введение
Изучение действий функций и построение их графиков является важным разделом математики.
Свободное владение техникой построения графиков часто помогает решить многие задачи и порой является единственным средством их решения.
Кроме того, умение строить графики функций представляет собой большой самостоятельный интерес.
Глава 1. Определение функций
Величины, участвующие в одном и том же явлении, могут быть взаимосвязаны, так что изменение одних из них влечёт за собой изменение других. Например, увеличение (или уменьшение) радиуса круга ведёт к обязательному увеличению (или уменьшению) его площади.
В таких случаях говорят, что между переменными величинами существует функциональная зависимость, причём одну величину называют функцией, или зависимой переменной (е часто обозначают буквой у), а другую — аргументом, или независимой переменной (её обозначают буквой х).
Функциональную зависимость между х и у принято обозначать символом y=f (x). Если значению х соответствует больше, чем одно значение у, то такая функция называется многозначной.
Переменная величина у есть функция аргумента х, то есть y=f (x), если каждому возможному значению х соответствует одно определённое значение у.
Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f (x).
Горизонтальную ось Ох называют осью абсцисс, вертикальную ось Оу — осью ординат.
Графическое изображение функции имеет важное значение для её изучения. На графике функции часто непосредственно видны такие её особенности, которые можно было бы установить лишь путём длительных вычислений. Если между величинами х и у существует функциональная связь, то безразлично, какую из этих величин считать аргументом, а какую — функцией.
Глава 2. Способы задания функций
1). Табличный способ. При этом способе ряд отдельных значений аргумента х1, х2, …, хk и соответствующий ему ряд отдельных значений функции у1, у2, …, уk задаются в виде таблицы.
Несмотря на простоту, такой способ задания функции обладает существенным недостатком, так как не дает полного представления о характере функциональной зависимости между х и у и не является наглядным.
2). Словесный способ. Обычно этот способ задания иллюстрируют примером функции Дирихле у = D (х): если х — рациональное число, то значение функции D (х) равно 1, а если число х — иррациональное, то значение функции D (х) равно нулю.
Таким образом, чтобы найти значение D (x0) при заданном значении х = х0, необходимо каким — либо способом установить, рационально или иррационально число х0.
3). Графический способ. Функциональная зависимость может быть задана с помощью графика функции у = f (x).
Преимуществом такого способа задания является наглядность, позволяющая установить важные черты поведения функции. Недостаток графического способа заключается в невозможности применения математического аппарата для более детального исследования функции.
4). Аналитический способ. При аналитическом способе задания известна формула, по которой по заданному значению аргумента х можно найти соответствующее значение функции у. В математике чаще всего используется именно аналитический способ задания функций.
Преимуществами такого способа задания являются компактность, возможность подсчета значения у при любом значении х и возможность применения математического аппарата для более детального исследования поведения функции. Однако аналитическому способу задания функции присуща недостаточная наглядность и возможная трудность вычисления значений функции.
Глава 3. Методы построения графиков функций
Исследование функции дает возможность найти область определения и область изменения функции, области ее убывания или возрастания, асимптоты, интервал знакопостоянства и др.
Однако при рассмотрении графиков многих функций часто можно избежать проведения подобного исследования, используя ряд методов, упрощающих аналитическое выражение функции и облегчающих построение графика.
Изложению именно таких методов посвящается эта глава, которая может служить практическим руководством при построении многих функций.
Параллельный перенос
Перенос вдоль оси ординат.
f (x) => f (x) — b
Пусть требуется построить график функции у = f (х) — b. Нетрудно заметить, что ординаты этого графика для всех значений x на ЅbЅ единиц меньше соответствующих ординат графика функций у = f (х) при b>0 и на ЅbЅ единиц больше — при b
Следовательно, график функции у = y (х) — b можно получить параллельным переносом вдоль оси ординат графика функции у = f (х) на ЅbЅ единиц вниз при b>0 или вверх при b
Перемещение графика связано с его перерисовыванием, что бывает затруднительно, особенно в случае сложных графиков. Перенос же графика на ЅbЅ единиц вниз или вверх вдоль оси ординат эквивалентен соответствующему противоположному переносу оси абсцисс настолько же единиц.
Именно этим способом мы будем пользоваться. Тогда представив исходную функцию в виде у + b = f (х), сформулируем следующее правило.
Для построения графика функции y + b = f (x) следует построить график функции y = f (x) и перенести ось абсцисс на ЅbЅ единиц вверх при b>0 или наЅbЅ единиц вниз при b
Полученный в новой системе координат график является графиком функции y = f (x) — b.
Перенос вдоль оси абсцисс.
f (x) => f (x + a)
Пусть требуется построить график функции у = f (x + a). Рассмотрим функцию y = f (x), которая в некоторой точке x = x1 принимает значение у1 = f (x1).
Очевидно, функция у = f (x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.е. x2 = x1 — a, причем рассматриваемое равенство справедливо для совокупности всех значений из области определения функции.
Следовательно, график функции у = f (x + a) может быть получен параллельным перемещением графика функции y = f (x) вдоль оси абсцисс влево наЅaЅ единиц при a>0 или вправо на ЅaЅ единиц при a
Для построения графика функции y = f (x + a) следует построить график функции y = f (x) и перенести ось ординат на ЅaЅ единиц вправо при a>0 или наЅaЅ единиц влево при a
Отражение
Построение графика функции вида y = f (-x). f (x) => f (-x)
Очевидно, что функции y = f (-x) и y = f (x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку.
Иначе говоря, ординаты графика функции y = f (-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f (x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х.
Таким образом, получаем следующее правило.
Для построения графика функции y = f (-x) следует построить график функции y = f (x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f (-x)
Построение графика функции вида y = — f (x).
f (x) => — f (x)
Ординаты графика функции y = — f (x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f (x) при тех же значениях аргумента.
Таким образом, получаем следующее правило.
Для построения графика функции y = — f (x) следует построить график функции y = f (x) и отразить его относительно оси абсцисс.
Построение графиков четной и нечетной функций.
Как уже отмечалось, для четной функции y = f (x) во всей области изменения ее аргумента справедливо соотношение f (x) = f (-x).
Следовательно, функция такого рода принимает одинаковое значение при всех значениях аргумента, равных по абсолютной величине, но противоположных по знаку. График четной функции симметричен относительно оси ординат.
Для построения графика четной функции y = f (x) следует построить ветвь графика этой функции только в области положительных значений аргумента (хі0). График функции y = f (x) в области отрицательных значений аргумента симметричен построенной ветви относительно оси ординат и получается отражением ее относительно этой оси.
Для нечетной функции y = f (x) в области всех значений аргумента справедливо равенство f (-x) = — f (x).
Таким образом, в области отрицательных значений аргумента ординаты графика нечетной функции равны по величин, но противоположны по знаку ординатам графика той же функции при соответствующих положительных значениях х. График нечетной функции симметричен относительно начала координат.
Для построения графика нечетной функции y = f (x) следует построить ветвь графика этой функции только в области положительных значений аргумента (хі0).
График функции y = f (x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат и может быть получен отражением этой ветви относительно оси ординат с последующим отражением в области отрицательных значений относительно оси абсцисс.
Список источников
1. Алгебра и начала математического анализа: учебник для 10-11 кл. общеобразовательных учреждений / под редакцией А.Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын, Б. М. Ивлев, С. И. Шварцбурд; 23-изд.-М.: Просвещение, 2014 -384с.
Если страница Вам понравилась, поделитесь ссылкой с друзьями:
obuchonok.ru
Табличный процессор Мicrosoft Еxcel: построение графиков сложной функции
Федеральное агентство по образованию
Санкт-Петербургский государственный торный институт им. Г.В. Плеханова
(технический университет)
Кафедра информатики и компьютерных технологий
Расчётно-графическая работа 2
Тема: ТАБЛИЧНЫЙ ПРОЦЕССОР MICROSOFT EXCEL
ПОСТРОЕНИЕ ГРАФИКОВ СЛОЖНОЙ ФУНКЦИИ
Функция ЕСЛИ
Функция ПИ
Выполнил: студент группы ТО-07 ________________ /Гориченко А.М./
ОЦЕНКА: ___________
Дата: _____________
Проверила: ст. преп. каф. ИиКТ _________________ /Онушкина И.О./
Санкт-Петербург
2007
Задание
Построить график функции
; шаг изменения x принять равным 0,1.
Результат работы в Microsoft Excel оформить в Microsoft Word:
1) в режиме отображения данных;
2) в режиме отображения формул.
Результаты вычислений в Microsoft Excel в режиме отображения данных
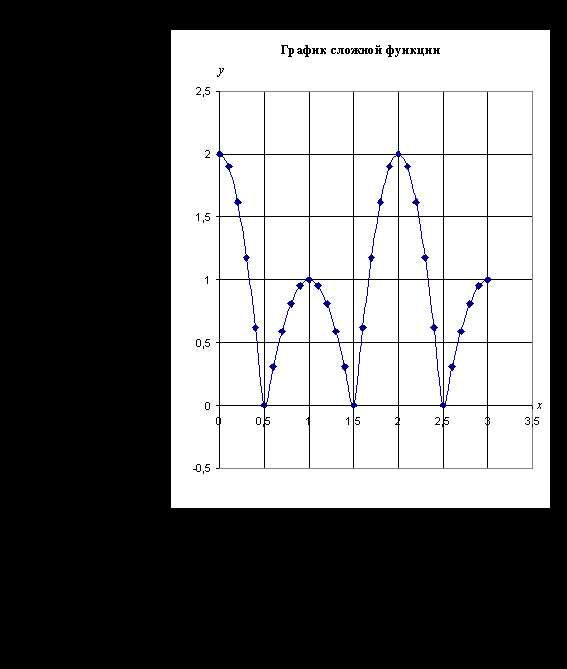
Рис. 1. Результаты вычислений в Microsoft Excel в режиме отображения данных
График сложной функции
Результаты вычисления в Microsoft Excel в режиме отображения формул

Рис. 2. Результаты вычисления в Microsoft Excel в режиме отображения формул
Содержание
Задание. 2
Результаты вычислений в Microsoft Excel в режиме отображения данных. 2
Результаты вычисления в Microsoft Excel в режиме отображения формул. 3
vunivere.ru
