Дисперсия и среднее квадратическое отклонение. Ковариация и коэффициент корреляции
Пройденное нами математическое ожидание случайной величины есть (как было выяснено) ее среднее значение, т.е. центр, вокруг которого группируются значения случайной величины. Но для описания поведения с.в. недостаточно знать ее математическое ожидание. Например, случайные величины Х и Y с законами распределения
Х | −0.01 | 0.01 |
Р | 1/2 | 1/2 |
имеют, как нетрудно посчитать, одинаковые средние значения: M(X)=
Пусть имеется с.в. Х и пусть его среднее значение равно числу а : М(Х)= а . Надо характеризовать величину уклонения значений с.в. Х от среднего, т.е. от числа а. Можно ввести новую с.в. Y=Х−а , которая при каждом испытании будет нам показывать, на сколько и в какую сторону уклонилось значение с.в. Х от своего центра. Поэтому назовем с.в. уклонением случайной величины Х. Но нам удобнее было бы иметь для характеристики разброса не случайную величину, а только какое-нибудь одно число (как это было с математическим ожиданием). Какое? Казалось бы разумным в качестве такого числа взять среднее отклонение с.в. Х от своего центра, т.е. среднее значение уклонения Y, т.е. математическое ожидание с.в. Y. Посчитаем его, пользуясь свойствами математического ожидания:
М(Y) = М(Х−а) = М(Х) −М(а) = М(Х) −а = М(Х) −М(Х) = 0 !
(восклицательный знак здесь не факториал, а выражение эмоции). Итак, среднее значение уклонения любой случайной величины от своего среднего равно нулю, а потому не может быть взято в качестве меры отклонения различных случайных величин от своего среднего значения. Равенство нулю среднего отклонения от центра объясняется тем, что разные по знаку уклонения компенсируют друг друга (поэтому математическое ожидание действительно является центром случайной величины). Разумнее всего в качестве отклонения от центра взять не само уклонение, а его абсолютную величину, т.е. ввести случайную величину
Дисперсией случайной величины Х ( обозначается D(X) ) называется среднее значение квадрата отклонения с.в. Х от своего среднего значения a=M(X):
D(X)=М{[X−M(X)]2}=M((X−a)2).
Как уже было сказано, дисперсия характеризует не само среднее отклонение с.в. Х от ее центра, а средний квадрат такого отклонения. Чтобы получить все же аналог самого среднего отклонения, нужно извлечь квадратный корень из дисперсии. Тогда получим новую числовую характеристику случайных величин
Средним квадратическим отклонением случайной величины Х (обозначается σ(Х), σ − греческая буква «сигма») называется квадратный корень из ее дисперсии:
.
Отметим тот приятный факт, что (в отличии от дисперсии) среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.
Из формулы D(X)=М{[X−M(X)]2}, являющейся определением дисперсии, легко вывести следующую формулу
D(X)=М(X 2) − [M(X)]2,
которая более удобна для практического вычисления дисперсии. Вспоминая правило вычисления математического ожидания функции от случайной величины (в данном случае это М(X 2)), из этой формулы легко получить конкретные выражения для дисперсии как для дискретных, так и для непрерывных случайных величин.
Х | х1 | х2 | … | xn |
Р | p1 | p2 | … | pn |
Тогда
.
2) Пусть Х – непрерывная случайная величина с плотностью вероятности f(x). Тогда
.
Понятно, что если н.с.в. Х сосредоточена на некотором отрезке [a,b] (т.е. по принятому выше определению плотность ее вероятности f(x) обращается в 0 вне этого отрезка), то формула для дисперсии переходит в следующую:
.
Рассмотрим свойства дисперсии, которые справедливы как для дискретных, так и для непрерывных случайных величин. Некоторые из них аналогичны свойствам математического ожидания, а некоторые нет. Выводятся они из формулы D(X)=М(X 2) − [M(X)]2 и свойств математического ожидания.
Если С = const – постоянная величина, то ее дисперсия равна нулю:
D(C) = 0.
Постоянный множитель выносится за знак дисперсии с квадратом:
D(c ∙X ) = c 2 ∙D(X).
Отсюда при с = −1, в частности, следует, что D(−X) = D(X).
Дисперсия суммы двух случайных величин Х и Y вычисляется по формуле:
D(X+Y) = D(X)+D(Y)+2∙M{[X−M(
Величина
cov(Х,Y) = M{[X−M(X)]∙[Y−M(Y)]},
стоящая в правой части формулы для дисперсии суммы случайных величин, называется корреляционным моментом или ковариацией случайных величин Х и Y. Учитывая введенное понятие, формула для дисперсии суммы случайных величин может быть записана в виде
D(X+Y) = D(X) + D(Y) + 2 ∙ cov(Х,Y).
Ковариация обладает следующим важным свойством.
Утверждение. Если случайные величины Х и Y независимы, то их ковариация равна 0.
Доказывается это утверждение достаточно просто, если вспомнить, что для независимых величин математическое ожидание их произведение равно произведению их математических ожиданий.
Из приведенного утверждения вытекает важное
Следствие. Если ковариация двух случайных величин не равна 0, то эти величины зависимы (в том смысле, что не являются независимыми случайными величинами).
Итак, ненулевая ковариация говорит о зависимости случайных величин. Обратное, к сожалению, неверно. Можно привести примеры как зависимых, так и независимых случайных величин, ковариация которых равна 0. Если ковариация двух случайных величин равна нулю, то они называются некоррелированными случайными величинами, а если не равна 0, то коррелированными. Таким образом, из независимости следует некоррелированность, а обратное, вообще говоря, неверно. Однако известно, что если с.в. Х и с.в. Y
Ковариация случайных величин можно рассматривать как меру связи (точнее, меру коррелированности) случайных величин.
Из приведенного выше утверждения, а также формулы для дисперсии суммы случайных величин вытекает следующее свойство дисперсии.
Дисперсия суммы независимых случайных величин равна сумме их дисперсий: если Х и Y − независимые случайные величины, то
D(X+Y)=D(X)+D(Y).
Дисперсия разности независимых случайных величин тоже равна сумме их дисперсий: если Х и Y − независимые случайные величины, то
D(X−Y)=D(X)+D(Y).
Дисперсию произведения независимых случайных величин можно вычислить по формуле:
.
Пусть Х – случайная величина, k и b – числа. Тогда
D(kX+b)=k2D(X).
Пример. Даны законы распределения независимых случайных величин Х и Y:
0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Найти дисперсию случайной величины 2Х−Y+5.
Пример(снова к задаче об автосалоне). Найди дисперсию и среднее квадратическое отклонение введенных ранее случайных величин Х (число продаж в день) и Y (ежедневная прибыль автосалона).
Решение. Мы уже находили среднее ежедневное число продаж и среднюю ежедневную прибыль автосалона: M(X)=1, M(Y)=50 у.е. . Учитывая указанный ранее закон распределения с.в. Х:
Х | 0 | 1 | 2 | 3 |
Р | 0.4 | 0.3 | 0.2 | 0.1 |
по формуле для дисперсии д.с.в. получим:
D(X )= 02∙0.4+12∙0.3+22∙0.2+32∙0.1 − 12 = 1 .
Тогда среднее квадратическое отклонение . Теперь исследуем ежедневную прибыль. ПосколькуY=100 ∙X − 50, то, используя свойства дисперсии, получим D(Y)=1002 ∙D(X)=10000. Тогда среднее квадратическое отклонение у.е. . Попробуем проанализировать по этим данным стабильность работы автосалона. При средней ежедневной прибыли в 50 у.е. среднее отклонение от нее (в ту или иную сторону) составляет 100 у.е., т.е. 200% от средней прибыли . Казалось бы предприятие работает крайне нестабильно. Однако все не так плохо (хотя и не очень уж хорошо), что показывает следующий
Пример(напоследок к задаче об автосалоне). Найди дисперсию и среднее квадратическое отклонение с.в. Y − ежемесячной прибыли автосалона.
Решение. Пусть Y1− прибыль автосалона в 1-ый
день месяца, …, Y30− прибыль автосалона в последний 30-ый
день месяца. Все эти с.в. независимы друг от друга, дисперсия каждой из них
была вычислена ранее (равна 10000),
и ясно, что месячная прибыль есть сумма
ежедневных прибылей: Y=Y1+…+Y30 . Пользуясь соответствующим свойством
дисперсии, получим D(Y)=D(Y1)+…+D(Y30)=30 ∙10000=300000.
Тогда среднее квадратическое отклонение
ежемесячной прибыли автосалона
у.е.
. Посчитаем, какой процент теперь это
составляет от среднейежемесячной прибыли M(Y).
Пользуясь
соответствующим свойством математического
ожидания, получим М(Y)=М(Y1)+…+М(Y30)=30 ∙50=1500.
Теперь уже среднее отклонение от средней
прибыли составляет 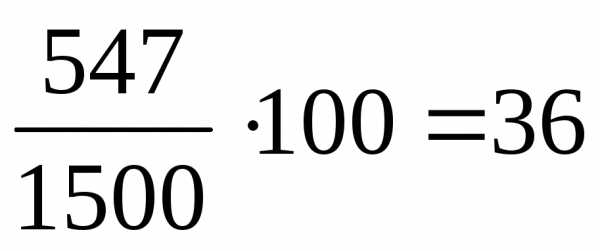 %,
что, конечно, значительно меньше прежних
200%. Хотя тоже много и работа предприятия
оставляет желать лучшего.
%,
что, конечно, значительно меньше прежних
200%. Хотя тоже много и работа предприятия
оставляет желать лучшего.
Пример. В ящике 5 белых шаров и 7 черных. Наугад вынимаю 3 шара. Найти дисперсию и среднее квадратическое отклонение с.в. Х – числа белых шаров среди вынутых.
Рассмотрим теперь нахождение дисперсии в часто встречающихся ситуациях (аналогичных рассмотренным в свойствах матожидания). Пусть производится n независимых испытаний, в каждом из которых некоторое событие А может появиться с вероятностью, зависящей в общем случае от номера испытания. Пусть р1– вероятность появления событий А в 1-oм испытании, …, рn– вероятность появления событий А в n-oм испытании. Обозначим q1=1–p1, …, qn=1–pn (это вероятности того, что событие А не произойдет в соответствующих испытаниях). Рассмотрим с.в. Х – число появлений события А во всех n испытаниях (число успехов в n испытаниях). Тогда дисперсия числа успехов:
.
Доказательство. Отметим, что ранее уже была доказана соответствующая формула для математического ожидания: . Формулу для дисперсии получим тем же способом. Рассмотрим вспомогательные случайные величины:Х1 – число появлений события А в 1-ом испытании, …, Хn – число появлений события А в n-ом испытании . Все введенные с.в. могут принимать значения 0 или 1 (событие А в испытании может появиться или нет), причем значение 1 по условию принимается в k-ом испытании с вероятностью pk (вероятность появления события А в k-ом испытании), а значение 0 с вероятностью (1– pk) (вероятность противоположного события – не появления события А в k-ом испытании), k=1,…, n. Поэтому эти величины имеют следующие законы распределения:
, … ,
Поэтому средние значения этих величин: М(Х1)=0∙q1+1∙ р1= р1 , …, М(Хn)=0∙qn+1∙ рn= рn . Учитывая формулу для дисперсии д.с.в., получим D(Х1)=02∙q1+12∙ р1 – р12= р1∙(1–p1)= р1∙q1 , …, D(Хn)= рn∙qn . Ясно, что общее число появлений события А во всех испытаниях равно сумме сумме «успехов» по всем испытаниям: Х=Х1+Х2+…+Xn . Пользуясь свойством дисперсии суммы независимых случайных величин, получаем: D(Х)=D(Х1)+D(Х2)+…+D(Xn)= р1∙q1+…+ рn∙qn , что и требовалось доказать.
Пример (о тех же стрелках). Первый стрелок попадает в мишень с вероятностью р1=0.5, второй с вероятностью р2=0.6, а третий с вероятностью р3=0.7 . Найти дисперсию и среднее квадратическое отклонение числа попаданий в мишень при одном залпе этих стрелков по мишени.
Решение. Этот пример в точности укладывается в изложенную схему. Событие А в данном случае – попадание в мишень. В каждом из трех испытаний (выстрелы стрелков) оно появляется со своей вероятностью (р1=0.5 либо р2=0.6, либо р3=0.7) . С.в. Х – общее число попаданий в мишень есть общее число появлений события А. Поэтому D(Х)= р1∙q1+р2∙q2+р3∙q3=0.5∙0.5+0.6∙0.4+0.7∙0.3=0.7 , .
Математическое ожидание числа успехов в схеме Бернулли. Пусть производится n независимых испытаний, в каждом из которых некоторое событие А может появиться с одной и той же вероятностью р, а q=1–p. Рассмотрим с.в. Х – число появлений события А во всех n испытаниях. Тогда дисперсия числа успехов:
.
Эта формула следует из предыдущего свойства, так как в рассматриваемом случае вероятности успеха в каждом испытании одинакова: р1=р2=…=рn=р .
Сделаем важное
Замечание. Из полученной формулы получаем, что среднее квадратическое отклонение числа успехов от среднего их числа равно, а потому это отклонение неограниченно растет с ростом числа испытанийn. Однако из выведенной ранее формулы видно, что при этом неограниченно растет и само среднее число успехов. Однако относительное среднее отклонениенеограниченно убывает с ростом числа испытаний, стремясь к 0.
Пример (о том же стрелке). Стрелок попадает в мишень с вероятностью р=0.6 . Найти дисперсию и среднее квадратическое отклонение числа попаданий в мишень при трех выстрелах.
Пример. Найти дисперсию с.в. Х – числа появлений события А в двух независимых испытаниях, если вероятности появления этого события одинаковы в каждом испытании, а среднее число появлений события в этих испытаниях равно 1.2 .
Пример. Д.с.в. Х принимает значения {–1, 0, 1} . Найти закон распределения этой с.в., если М(Х)=0, D(X)=2/3 .
Пример. Плотность вероятности н.с.в. Х задана формулой:
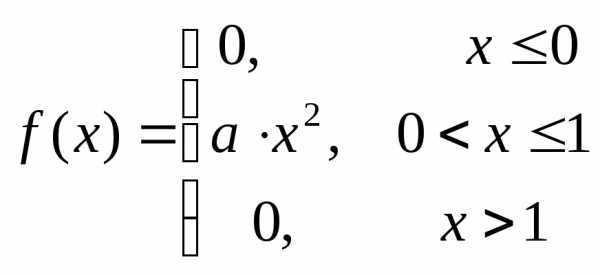 .
.
Найти значение параметра а, математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
Ответ: а=3, М(Х)=3/4, D(Х)=3/80.
Вернемся снова к вопросу о зависимости (точнее, коррелированности) произвольных случайных величин Х и Y, мерой которой, как сказано выше, может выступать их ковариация cov(Х,Y) = M{[X−M(X)]∙[Y−M(Y)]}. Из этой формулы для ковариации легко вывести более удобную формулу:
cov(Х,Y) = M(X∙Y)−M(X)∙M(Y).
В случае дискретной системы случайных величин Х и Y с законом распределения
Х \ Y | y1 | y2 | y3 | … | ym |
x1 | p11 | p12 | p13 | … | p1m |
x2 | p21 | p22 | p23 | … | p2m |
… | … | … | … | … | … |
xn | pn1 | pn2 | pn3 | … | pnm |
математическое ожидание произведения случайных величин M(X∙Y) (это первое слагаемое в выражении для ковариации) вычисляется по формуле:
.
Поэтому формула для ковариации в этом случае имеет вид:
,
где вероятности принятия своих значений случайными величинами Х и Y вычисляются по формулам, которые ранее нами выводились (см. тему «Понятие о системе случайных величин»):
,
Оказывается, что в качестве меры зависимости случайной величины более удобной является другая величина (которая будет названа коэффициентом корреляции), тесно связанная с ковариацией и выражающаяся через нее. Коэффициентом корреляции случайных величин Х и Y (обозначается rXY) называется число, равное
.
Коэффициент корреляции действительно более удобен (по сравнению с ковариацией) для выражения тесноты связи между с.в. Х и Y, так как является безразмерной величиной и обладает следующими полезными свойствами.
Если с.в. Х и Y независимы, то rXY=0 ( потому если
 ,
то с.в.Х и Y зависимы).
,
то с.в.Х и Y зависимы).
Это свойство полностью аналогично соответствующему свойству ковариации и сразу следует из формулы для коэффициента корреляции.
Коэффициент корреляции любых случайных величин Х и Y заключен между (−1) и 1: |rXY|≤1 .
Коэффициент корреляции случайных величин Х и Y равен (−1) или 1 (т.е. |rXY|=1 ) в том и только случае, когда между величинами Х и Y имеется линейная функциональная связь (что означает существование таких чисел а и b, что Y=a ∙X+b.
Относительный (и принципиальный) недостаток коэффициента корреляции состоит в том, что он точно показывает только наличие именно линейной связи между случайными величинами. Коэффициент корреляции может оказаться по модулю даже не близким к 1, однако между случайными величинами все равно может оказаться самая сильная связь − функциональная (хотя, конечно, не линейная).
Таким образом, коэффициент корреляции позволяет судить (хотя и не в полной мере) о степени зависимости случайных величин:
если Х и Y независимы, то rXY=0 ;
если rXY ≠ 0 , то Х и Y зависимы ;
если rXY = ±1 , то Х и Y линейно зависимы ;
studfiles.net
Математическое ожидание. Дисперсия и среднее квадратическое отклонение случайной величины
Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач достаточно знать лишь некоторые числовые параметры, выражающие наиболее характерные свойства (черты) закона распределения случайной величины. Такие числа носят название числовых характеристик случайной величины.
Математическим ожиданием (или средним значением) (или ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
Если дискретная случайная величина X принимает конечное число значений , то ее математическое ожидание находится по формуле
(3)
Если же дискретная случайная величина X принимает бесконечное (счетное) число значений, то
, (4)
при этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится, т. е. сходится ряд .
Математическое ожидание непрерывной случайной величины X с плотностью вероятности , находится по формуле
, (5)
при этом математическое ожидание существует, если интеграл в правой части равенства абсолютно сходится (это значит, что сходится интеграл ).
Дисперсией (рассеянием) (или ) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
.
Из определения вытекает часто используемая формула:
.
Если —дискретная случайная величина, то ее дисперсия вычисляется по формуле:
, (т. е. ) (6)
в случае конечного числа значений, принимаемых случайной величиной X, и по формуле
, (т. е. ) (7)
в случае счетного числа значений.
Если X — непрерывная случайная величина сплотностью , то
(или ). (8)
Средним квадратическим отклонением случайной величины называется величина .
Среднее квадратическое отклонение есть мера рассеяния значений случайной величины около ее математического ожидания.
Мода и медиана
Кроме математического ожидания и дисперсии в теории вероятностей применяется еще ряд числовых характеристик, в частности, мода и медиана случайной величины.
Модой дискретной случайной величины X называется ее наиболее вероятное значение.
Модой непрерывной случайной величины X называется такое ее значение , при котором плотность распределения имеет максимум, т. е. .
На рис. 3 и 4 показана мода для дискретной и непрерывной случайной величины.
Рис. 3 Рис. 4
Если многоугольник распределения (кривая распределения) имеет два или несколько максимумов, то распределение называется двухмодальным или многомодальным.
Иногда встречаются распределения, которые имеют минимум, но не имеют максимум. Такие распределения называются антимодальными.
Медианой непрерывной случайной величины X (обозначение: ) называется такое ее значение , для которого одинаково вероятно, окажется ли случайная величина меньше или больше , т. е.
. (9)
Геометрически вертикальная прямая , проходящая через точку с абсциссой, равной , делит площадь фигуры под кривой распределения на две равные части (рис. 5). Каждая из этих площадей равна , т. к. площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке равна , т. е. .
Рис. 5
Для дискретной случайной величины медиана обычно не определяется.
Решение задач
Пример 1.Производится три независимых опыта, в каждом из которых событие A появляется с вероятностью 0,4. Рассматривается случайная величина X – число появлений события A в трех опытах. Построить ряд и многоугольник распределения, функцию распределения случайной величины X. Найти: 1) вероятность событий: A={X<2}; B={ }; C={ }; 2) математическое ожидание , дисперсию , среднее квадратическое отклонение случайной величины X.
Решение.Случайная величина X может принимать значения ; ; ; . Соответствующие им вероятности найдем, воспользовавшись формулой Бернулли. При n=3, ; имеем: ; ;
; .
Отсюда ряд распределения случайной величины X имеет вид:
(Контроль: ).
Многоугольник распределения случайной величины X представлен на рис.6.
Рис. 6 Рис. 7
Найдем функцию распределения F(x). По определению функции распределения имеем: если , то ;
если , то ;
если , то ;
если , то ;
если , то
.
Итак,
График функции F(x) изображен на рис. 7.
1) Сначала вычислим искомые вероятности непосредственно:
;
;
.
Эти же вероятности найдем, воспользовавшись формулами:
и . Тогда ;
;
2) Найдем математическое ожидание случайной величины X. Используя формулу (3), получим . Вычислим дисперсию. По формуле (6) имеем:
=0,72. Тогда среднее квадратическое отклонение .
Пример 2.Дан ряд распределения дискретной случайной величины X:
Найти моду.
Решение.Так как дискретная случайная величина X принимает значение с наибольшей вероятностью по сравнению с двумя соседними значениями, то мода случайной величины X равна 20, т. е. .
Пример 3.Дана функция
Рис. 8
Показать, что может служить плотностью вероятности некоторой случайной величины X.. Найти математическое ожидание и дисперсию случайной величины X.
Решение.Используя свойство нормированности плотности распределения, найдем, что
,
кроме того, . Следовательно, может служить плотностью вероятности некоторой случайной величины. Так как прямая является осью симметрии соответствующей дуги кривой (см. рис.8), то математическое ожидание случайной величины X равно , т. е. . Найдем дисперсию, воспользовавшись формулой (8). Двукратным интегрированием по частям получим:
Пример 4.Дана плотность вероятности случайной величины X;
Найти функцию распределения F(X), вероятность попадания случайной величины X в промежуток , числовые характеристики величины X: .
Решение.Найдем функцию распределения случайной величины X, для этого воспользуется соотношением (1).
Если x < 0, то .
Если , то .
Если x > a, то .
Итак,
По формуле (*) имеем .
Найдем математическое ожидание случайной величины X. Согласно формуле (5)
.
Теперь отыщем дисперсию. По формуле (8)
Отсюда среднее квадратическое отклонение .
Пример 5.Найти моду, медиану, математическое ожидание и функцию распределения случайной величины X с плотностью вероятности
Решение.Найдем точку максимума функции : ; отсюда при . Точка является точкой максимума функции , так как , если и , если . Следовательно, мода .
Медиану определим из условия (9): (или ).
В данном случае по формуле (2): , т. е. .
Таким образом, приходим к уравнению: или . Отсюда, .
Воспользовавшись формулой (5), вычислим математическое ожидание случайной величины X:
Найдем функцию распределения случайной величины X.
Прежде всего заметим, что если x < 0, то
Если же то т. е. .
megaobuchalka.ru
Среднее квадратическое отклонение
 =
=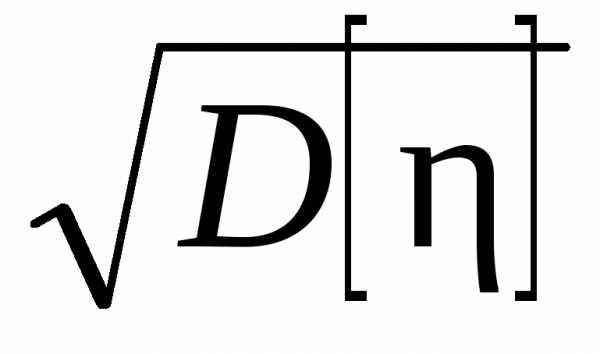 =
=
Вероятность
попадания в интервал 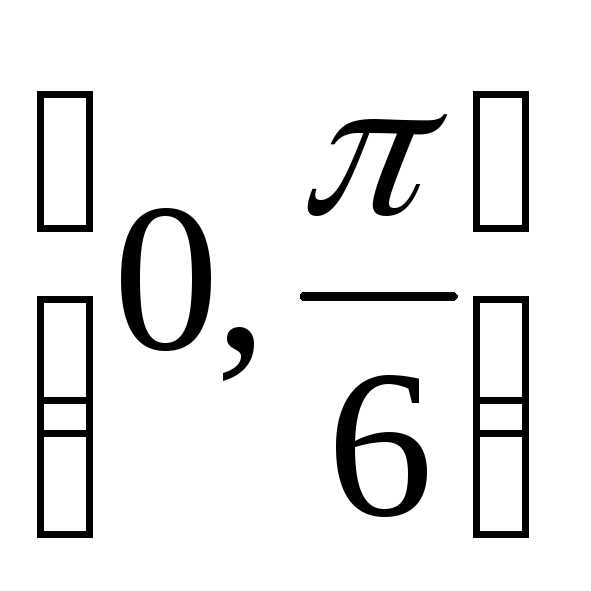
P
Пример 5.8. Случайная величина распределена по нормальному закону с плотностью вероятности
f(x)= 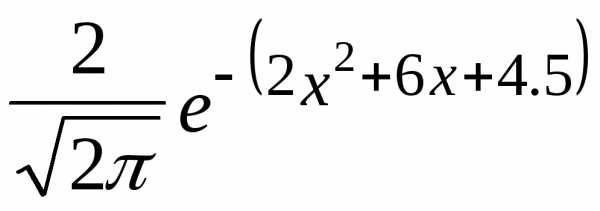 .
.
Найти её математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания в интервал [-2;-1]. Построить кривую плотности вероятности этой случайной величины.
Решение.
1. По виду формулы
плотности вероятности определяем, что
случайная величина распределена по
нормальному закону, для которого
плотность вероятности f(x)
=  .
Приведем заданную функцию к стандартному
виду:
.
Приведем заданную функцию к стандартному
виду:
f(x)= 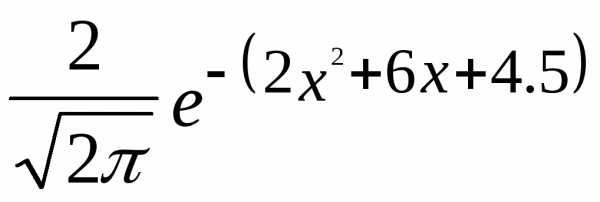 =
=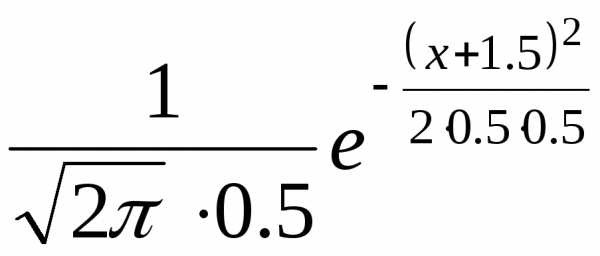 .
.
Отсюда
следует, что m =
-1.5;σ= 0.5.
Известно, что параметрm– математическое ожиданиеM[],
аσ- среднее
квадратическое отклонениеσ.
Следовательно,M[]
= -1.5,σ=0.5,D[]
=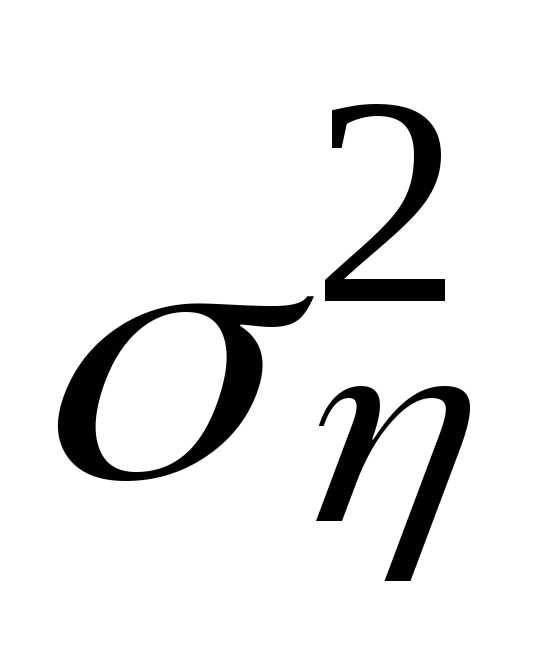 =0.25.
=0.25.
2. Найдем
вероятность попадания заданной случайной
величины в интервал [-2,-1]. По свойствам
функции распределения вероятность
попадания случайной величины в интервал 
,
где F(x) – функция распределения случайной величины. Для нормально распределенной случайной величины функция распределенияF(x) может быть выражена через её нормированную функцию Ф(х) формулой:
F(x)=
Ф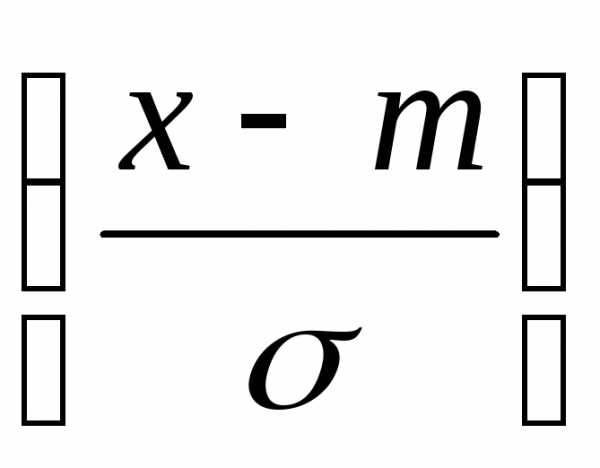 .
(5.5)
.
(5.5)
Функция Ф(х) табулирована (см. табл. В Приложения).
Таким образом,
Р. (5.6)
Для решаемой задачи:=0,5 т.е.
Учитывая, что Ф(-х)=1- Ф(х), и найдя в табл.В Приложения Ф(1)=0.8413, получим
Р(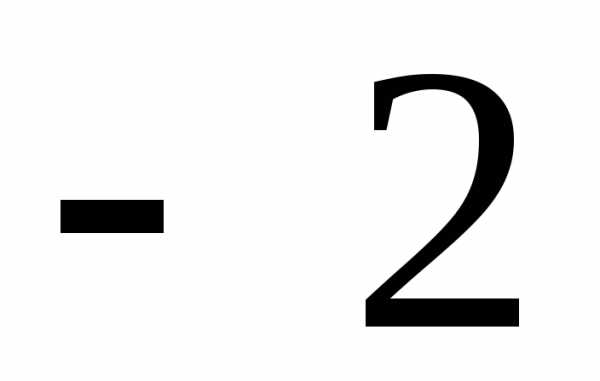 -1)=2Ф(1)-1=0,6826.
-1)=2Ф(1)-1=0,6826.
3. Построим
кривую плотности вероятности. Для этого
на графике построим сначала кривую
нормированной плотности вероятности
(на рис. 5.6 штриховая линия 1), т.е.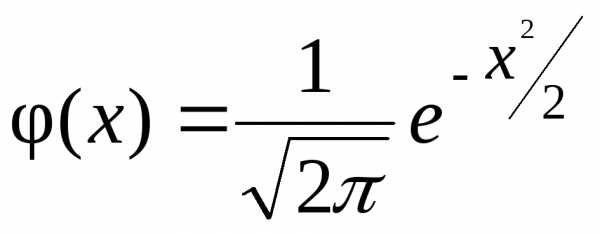 .
Затем сожмем её по оси ординат и растянем
по оси абсцисс вσраз (т.е. максимум увеличится в два раза).
Получим пунктирную линию 2. И, наконец,
сдвинем по оси абсцисс на величинуmвлево, т.е. в данном случае максимум
графика будет в точкех=-1,5.
Окончательный результат на рисунке
изображен сплошной линией.
.
Затем сожмем её по оси ординат и растянем
по оси абсцисс вσраз (т.е. максимум увеличится в два раза).
Получим пунктирную линию 2. И, наконец,
сдвинем по оси абсцисс на величинуmвлево, т.е. в данном случае максимум
графика будет в точкех=-1,5.
Окончательный результат на рисунке
изображен сплошной линией.
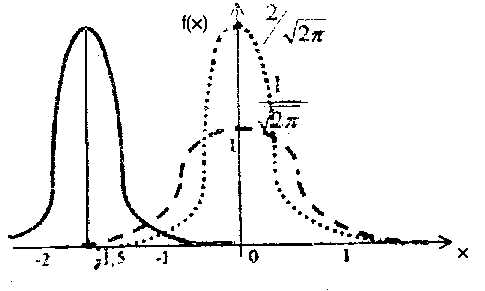
Рис. 5.6.
Пример 5.9.Найти математическое ожидание и среднее квадратическое отклонение случайной величины, распределенной по нормальному закону,
если P{X>60}=0,98 иP{X<90}=0,84.
Решение.Для определения искомых числовых характеристик следует найти параметры распределения предлагаемой случайной величины, так как для нормально распределенной случайной величины математическое ожидание совпадает с параметромm, а среднее квадратическое отклонение с параметром σ. Для этого воспользуемся формулой, выражающей вероятность попадания случайной величины в данные в условиях интервалы через функцию распределения. Преобразуем задания в условии задачи равенства:
из P{x>60}= 0,98 получимр{х60} = 1-р(х>60) = 1-0,98. Отсюда
P{x60}=0,02.
По формуле (5.5) преобразуем левую часть , получим
F(60)=
Ф(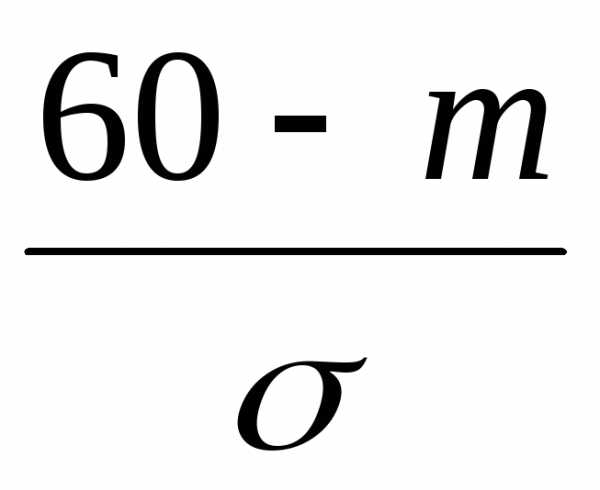 )=
0,02.
)=
0,02.
Теперь по таблицам Ф(х) (табл. В Приложения) необходимо найти значениех, при котором Ф(х) равняется 0,02. Такого значения в таблице нет, это означает, что искомое значение – отрицательное. Используя формулу
Ф(-х)= 1-Ф(х), (5.7)
можно записать
Ф(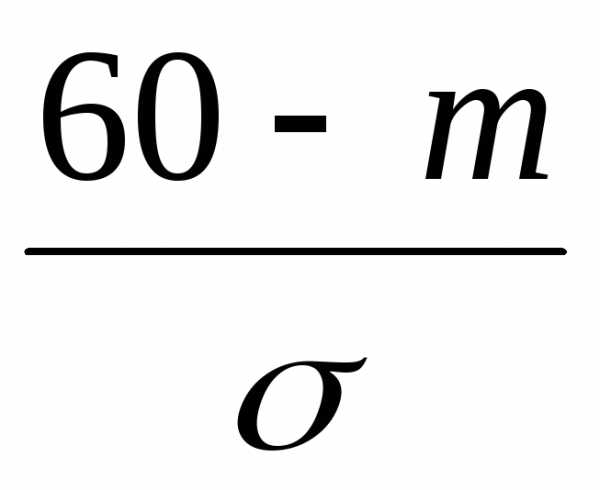 )=
1-Ф(
)=
1-Ф( )=
0,02,
)=
0,02,
т.е. Ф( )=
0,98.
)=
0,98.
По
табл.В Приложения находим, что Ф(х)=
0,98 соответствует значению х=2,056,
т.е. 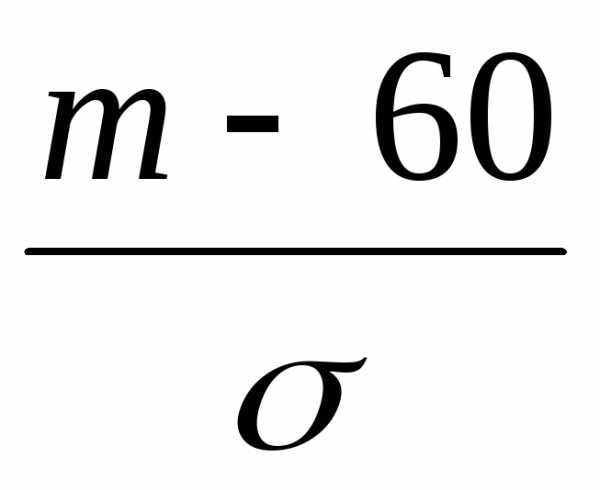 =
2,056.
=
2,056.
Таким
образом, m-2.056 =60.
=60.
Из второго условия
следует P{X<90}=F(90)=Ф(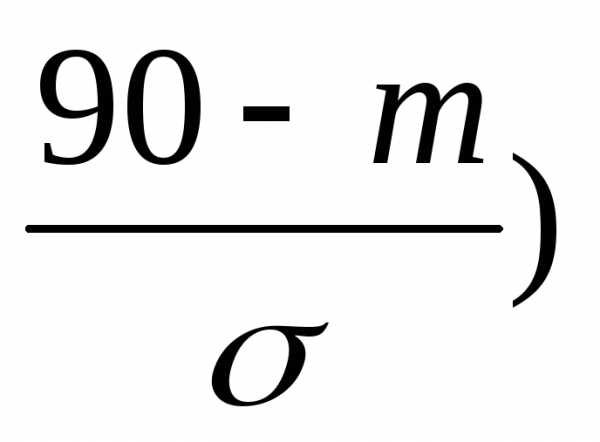 =
0,84 ; по табл. В Приложения находим
аргумент для значения функции 0,84 и
получаем
=
0,84 ; по табл. В Приложения находим
аргумент для значения функции 0,84 и
получаем 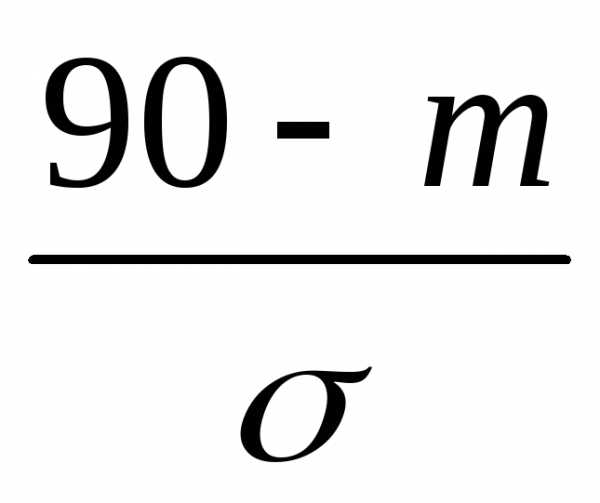 =0,995
, отсюда m+0,995
σ=90. Таким образом получаем систему
уравнений относительно параметров
=0,995
, отсюда m+0,995
σ=90. Таким образом получаем систему
уравнений относительно параметров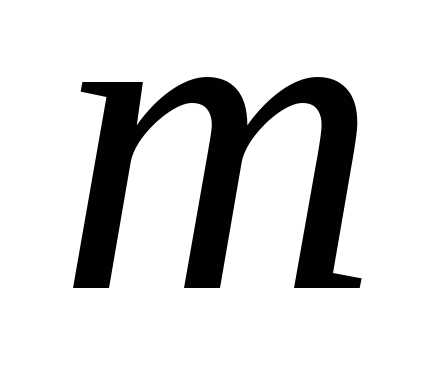 и σ:
и σ:

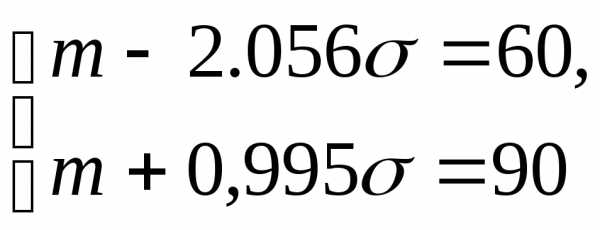
Находим из системы искомые параметры: 3,051 σ=30,σ@9,83,m=60+2,05×9,83@80,15.
Итак, =80,15, аσ=9,83.
studfiles.net
§ 2. Математическое ожидание, дисперсия и среднеквадратическое отклонение случайной величины, их свойства
24
Замечание 1. Значения функцииf (t) называют обычноплотностью вероятности случайной величиныX . Такое название объясняется следующими обстоятельствами:
f (t)= limF(t + | t) − F(t) . |
|
|
t →0 | t | F(t+ t) − F(t) |
|
F(t+ t) − F(t) = P(t≤ X< t+ t) | есть “средняя | ||
|
| t |
|
вероятность”, т.е. вероятность P(t ≤ X < t + | t) , отнесенная к единице длины. | ||
Замечание 2. Понятие интегральной функции распределения имеет место и для дискретных случайных величин. График этой функции в таком случае имеет ступенчатый вид.
Для описания дискретной случайной величины понятие дифференциальной функции распределения неприменимо.
Определение 1. ПустьX – дискретная случайная величина, закон распределения которой имеет вид:
| x | x1 |
| x2 |
| … | xn | (1) |
| p | p1 |
| p2 |
| … | pn | |
|
|
|
| |||||
Математическим ожиданием дискретной случайной величины X на- | ||||||||
зывается число |
|
| n |
|
|
| ||
|
|
|
|
|
|
| ||
|
|
| M ( X) = ∑ xi pi . |
|
| (2) | ||
i =1
Определение 2. ПустьX – непрерывная случайная величина иf (t) – ее дифференциальная функция распределения.Математическим ожиданием непрерывной случайной величины X называется число
+∞ |
|
M ( X) = ∫t f(t) dt | (3) |
−∞
(имеется ввиду, что интеграл (3) сходится).
Математическое ожидание, как дискретной, так и непрерывной случайной величины, имеет следующий вероятностный смысл.
Пусть проведено N испытаний, в результате чего получены значения случайной величиныX :x1 ,x2 , …,xN . Среднее арифметическое этих чисел
x1 + x2 +… + xN при большихn близко кM (X ) .
N
25
Поясним вышесказанное на примере дискретной случайной величины X . ЕслиX имеет распределение (1), то в результатеN испытаний (N – большое) мы получимp1 N раз значениеx1 ,p2 N раз – значениеx2 , …,
pN N раз – значениеxN . Среднее арифметическое полученных в результате испытаний значений равно:
x1 p1 N+ x2 p2 N+… + xN pN N | N | |
= ∑xi pi = M( X) . | ||
N | ||
i =1 |
В связи с этим математическое ожидание называют также средним значением случайной величины.
Замечание. Математическое ожидание является постоянным, не зависящим от опыта числом, характеризующим определенное свойство случайной величины, а именно – устойчивость среднего арифметического полученных в результате испытаний значений.
Свойства математического ожидания
1.M (C) = C, где C= const.
2. | M ( X+Y) = M( X) + M(Y) | для произвольных случайных величин | X |
|
| и Y (зависимых или независимых). |
|
3. | M (λ X )= λ M (X ) для | любой случайной величины X и произ- | |
| вольного числа λ . |
| |
4. | M ( X Y) = M( X) M(Y) | для независимых случайных величин X | и |
Y .
Определение 3. ПустьX – дискретная случайная величина с распре-
делением (1). Дисперсией дискретной случайной величины Xназывается число:
n |
|
D(X )= ∑(xi − M (X ))2 pi , | (4) |
i =1 |
|
где M (X ) – математическое ожидание случайной величиныX . |
|
Определение 4. ПустьX – непрерывная случайная величина и | f (t) – |
ее дифференциальная функция распределения. Дисперсией непрерывной случайной величины X называется число:
+∞ |
|
D( X) = ∫(t− M( X))2 f(t) dt | (5) |
−∞
(если интеграл сходится), M (X ) – математическое ожидание случайной величиныX .
26
Данные выше определения можно объединить следующим образом: дисперсия случайной величины X есть математическое ожидание случайной
величины ( X − M (X ))2 .
Истолкование дисперсии случайной величины как математического ожидания квадрата отклонения X отM (X ) позволяет описать вероятностный смысл дисперсии следующим образом.
Дисперсия характеризует среднее значение квадрата отклонения значений X от ее математического ожидания. Чем больше эти отклонения по абсолютной величине, тем больше дисперсия, и обратно. Дисперсия измеряет меру рассеяния значений случайной величины относительно математического ожиданияX .
Свойства дисперсии
1.D(C)= 0 , гдеC = const .
2.D(λ X )= λ2 D(X ) для любой случайной величиныX и произволь-
ного числа λ .
3. D(X +Y )= D(X )+ D(Y ) для независимых случайных величинX и
Y .
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величиныX и квадратом ее математического ожи-
дания, т.е. |
|
D(X )= M (X 2 )−[M (X )]2 . | (6) |
Доказательство. | свойства2,3 для |
| |
D( X) = M[X− M( X)]2 = M( X2 − 2 X M( X) +[M( X)]2 ) | матем. ожидания |
= |
= M (X 2 )− 2M (X )M (X )+[M (X )]2 = M (X 2 )−[M (X )]2 .
Определение. Средним квадратическим отклонением случайной величиныX называют квадратный корень из ее дисперсии, т.е.
Среднее квадратическое отклонение, как и дисперсия, является мерой рассеяния значений случайной величины относительно математического ожидания. Среднее квадратическое отклонение измеряется в тех же единицах, что и случайная величина X , в то время как дисперсия имеет измерение
X 2 . Поэтому иногда предпочтительнее иметь дело сσ (X ) , а не сD(X ) .

27
Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин, т.е.
σ(X1 + X 2 +…+ X n )= σ 2 (X1 )+σ 2 (X 2 )+…+σ 2 (X n ) .
Доказательство.
Пусть X = X1 + X 2 +…+ X n .
свайство3
D(X )= D(X1 )+ D(X 2 )+…+ D(X n ).
σ(X )= D(X )= D(X1 )+…+ D(X n )= σ 2 (X1 )+…+σ 2 (X n ) .
Примеры решения задач
Пример 1.
Пусть X – количество очков при бросании игральной кости. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величиныX .
Решение. Закон распределения имеет вид:
x |
|
| 1 |
|
|
|
| 2 |
|
| 3 |
|
|
| 6 |
|
| 5 |
| 6 |
|
| Σ | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
p |
| 1 6 |
|
|
| 1 6 |
|
| 1 6 |
|
|
| 1 6 |
|
| 1 6 |
| 1 6 |
|
| 1 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| + 3 1 |
| + 4 1 |
|
|
|
|
| = 21 |
|
|
| ||
M ( X) = ∑xi pi =1 1 | + 2 | 1 |
| +5 | 1 | + 6 | 1 | = | 7 | = 3,5. | |||||||||||||||
|
| i =1 |
|
|
|
| 6 |
|
| 6 |
| 6 |
| 6 |
|
| 6 |
| 6 6 2 |
| |||||
Дисперсию вычислим по формуле: |
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
| D(X )= M (X 2 )−[M (X )]2 . |
|
|
|
|
|
| |||||||||||
Закон распределения случайной величины X 2 | имеет вид: |
|
| ||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
x2 |
|
| 1 |
|
|
|
| 4 |
|
| 9 |
|
|
| 16 |
|
| 25 |
| 36 |
|
| Σ | ||
p |
| 1 6 |
|
|
| 1 6 |
|
| 1 6 |
|
|
| 1 6 |
|
| 1 6 |
| 1 6 |
|
| 1 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
M ( X2 ) | = 1 (1 +4 | + 9+16+ 25+ 36) | = 91 , |
|
|
|
|
|
|
|
|
| |||||||||||||
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| |
D(X )= | 91 | − |
| 7 2 | = | 182 −147 | = | 35 | ≈ 2,92 , |
|
|
|
|
|
|
| |||||||||
6 |
|
|
| 12 |
| 12 |
|
|
|
|
|
|
| ||||||||||||
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
σ(X )= | D(X )= | 2,92 ≈1,71. |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||

28
Пример 2.
Случайная величина X – задана дифференциальной функцией распределенияf (t)= cost в интервале(0;π2). Вне этого интервалаf (t)= 0 . Най-
ти математическое ожидание величины Y = X 2 .
Решение.
+∞ |
|
|
| +∞ | |
M ( X) = ∫t f(t) dt. | Если X * =ϕ(X )M (X * )= ∫ϕ(t) | ||||
−∞ |
|
|
| −∞ | |
+∞ | π 2 |
| u = t2 , du= 2tdt, |
| |
|
| ||||
M ( X2 ) = ∫t2 f(t) dt= ∫t2 | cos t dt= |
| |||
dv = cos t dt, v | = sint |
| |||
−∞ | 0 |
|
| ||
|
|
|
|
| π 2 | π 2 |
|
|
|
|
| u = t, du= dt, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
= t2 sint | − 2 ∫tsin t dt= |
|
| = |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||
|
|
|
|
| 0 | 0 |
|
|
|
|
|
| dv = sin t dt, |
| v = −cost |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
= | π | 2 |
|
|
| π | 2 |
| π 2 |
|
|
|
|
| π | 2 | − 2 sint |
| π | 2 |
| π 2 | − 2 . |
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||
4 | − 2 | −t cost |
| + |
| ∫cost dt | = | 4 |
|
| = | 4 |
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
| Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
| Найти | дисперсию |
| случайной | величины X , | заданной |
| интегральной | |||||||||||||||||||||||||||||||
функцией |
|
|
|
|
|
|
|
| 0, |
|
|
|
|
|
| при t ≤ −2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
| F(t)= |
|
|
|
|
|
|
|
| при − 2 < t≤ 2, |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
| t 4+1 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| при t ≥ 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
Решение. |
| Найдем дифференциальную функцию распределения случайной | |||||||||||||||||||||||||||||||||||||||
величины X |
| ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
f (t)= F (t) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| 0, |
|
|
| при t ≤ −2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 4 , | при − 2 < t≤ 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
|
|
|
|
|
|
|
| f (t) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0, |
|
|
| при t ≥ 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
| 2 |
|
| 2 |
|
|
|
|
|
|
| t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| M ( X) |
| ⌠ |
|
| ⌠ 1 | t dt = |
| 2 |
| = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
| = t f(t) dt= |
|
| 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
| ⌡ |
|
| ⌡ 4 |
|
|
|
|
| −2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
| −2 |
|
| −2 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
| D( X) = M[X− M( X)] | 2 |
|
|
|
| 2 |
| ⌠ |
| 2 |
|
|
| 1 |
| ⌠ | 2 |
|
|
| t |
| 2 |
| 16 |
| 4 |
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||
|
|
| = | M ( X |
|
| ) = t |
| f (t) dt= |
|
| t |
| dt = |
|
|
|
|
|
| = |
| = |
| . | ||||||||||||||||
|
|
|
|
|
| 4 |
| 12 |
|
| 12 | 3 | |||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ⌡ |
|
|
|
|
|
| ⌡ |
|
|
| −2 |
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| −2 |
|
|
|
|
|
|
|
| −2 |
|
|
|
|
|
|
|
|
|
|
|
|
| |
studfiles.net
Определение. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.
Пример. Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Наугад выбирают 1000 изделий. Пусть Х – число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины Х.
Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна Р = 0,96.
Таким образом, закон распределения может считаться биноминальным.
Пример. Найти дисперсию дискретной случайной величины Х – числа появлений события А в двух независимых испытаниях, если вероятности появления этого события в каждом испытании равны и известно, что М(Х) = 0,9.
Т. к. случайная величина Х распределена по биноминальному закону, то
Пример. Производятся независимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0,63.
По формуле дисперсии биноминального закона получаем:
Пример. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно Р1=0,3; P2=0,4; P3=0,5; P4=0,6. Найти математическое ожидание и дисперсию числа отказавших приборов.
Принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4.
Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем .
1) Не отказал ни один прибор.
2) Отказал один из приборов.
0,302.
3) Отказали два прибора.
4) Отказали три прибора.
5) Отказали все приборы.
Получаем закон распределения:
X | 0 | 1 | 2 | 3 | 4 |
X2 | 0 | 1 | 4 | 9 | 16 |
P | 0,084 | 0,302 | 0,38 | 0,198 | 0,036 |
Математическое ожидание:
Дисперсия:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
5.1. Математическое ожидание. Дисперсия и среднее квадратическое отклонение случайной величины
Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач достаточно знать лишь некоторые Числовые параметры, выражающие наиболее характерные свойства (черты) закона распределения случайной величины. Такие числа носят название Числовых характеристик случайной величины.
Математическим ожиданием (или средним значением) (или ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
Если дискретная случайная величина X принимает конечное число значений , то ее математическое ожидание находится по формуле
(3)
Если же дискретная случайная величина X принимает бесконечное (счетное) число значений, то
, (4)
При этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится, т. е. сходится ряд .
Математическое ожидание непрерывной случайной величины X с плотностью вероятности , находится по формуле
, (5)
При этом математическое ожидание существует, если интеграл в правой части равенства абсолютно сходится (это значит, что сходится интеграл ).
Дисперсией (рассеянием) (или ) случайной величины Называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
.
Из определения вытекает часто используемая формула:
.
Если — Дискретная случайная величина, то ее дисперсия вычисляется по формуле:
, (т. е. ) (6)
В случае конечного числа значений, принимаемых случайной величиной X, и по формуле
, (т. е. ) (7)
В случае счетного числа значений.
Если X — непрерывная случайная величина С Плотностью , то
(или ). (8)
Средним квадратическим отклонением Случайной величины Называется величина .
Среднее квадратическое отклонение есть мера рассеяния значений случайной величины около ее математического ожидания.
matica.org.ua
Дисперсия случайной величины. Среднее квадратическое отклонение
Мы рассмотрели число, которое характеризует поведение случайной величины в среднем. Но среднее значение далеко не всегда дает даже общее представление о поведении случайной величины.
Есть еще одна характеристика, которая зачастую несет не менее важную информацию, — это разброс (или рассеивание) случайной величины вокруг ее среднего значения. Вспомним известную шутку о том, что средняя температура по больнице, 36,6°. Ведь это вполне может быть так, если часть больных имеет повышенную температуру, а часть пониженную. Тогда чем же будет отличаться поведение случайной величины, равной температуре больного человека, от поведения величины, равной температуре здорового? И та, и другая величины подвержены колебаниям вокруг некоторого среднего значения (возможно, даже одинакового), но очевидно, что у больных величина этих колебаний будет больше. Попробуем выяснить, какое выражение может претендовать на роль средней меры рассеивания случайной величины вокруг ее среднего значения.
Дисперсиейслучайной величины называется математическое ожиданиеквадрата ее отклонения:
Дисперсия дискретной случайной величины вычисляется по формуле:
или
Средним квадратическим отклонением(стандартом) случайной величины называется арифметический корень из дисперсии, т.е.
Пример 4.10. Найти дисперсию числа очков, выпадающих при бросании игральной кости.
Решение:
Закон распределения случайной величины Х и ее математическое ожидание М(Х) = 3,5 были приведены в примере 4.7.
Вычислим дисперсию:
Дисперсия непрерывной случайной величины определяется равенством:
.
Свойства дисперсии:
1.Дисперсия постоянной величины С равна нулю:
D (С) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D (X + Y) = D (X) + D (Y).
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.
Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:
D (X + C) = D (X).
4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D (X — Y) = D (X) + D (Y).
Литература:
1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.64 – 66, 75 – 94.
2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с. 83 – 141.
Контрольные вопросы:
1. Что называют случайной величиной?
2. Какую величину называют дискретной случайной величиной?
3. Какую величину называют непрерывной случайной величиной?
4. Как задают закон распределения дискретной случайной величины?
5. Что такое многоугольник распределения?
6. Что называют функцией распределения случайной величины?
7. Какими свойствами обладает функция распределения?
8. Какие числовые характеристики случайной величины вы знаете? Дайте им определения, укажите методы их нахождения, перечислите свойства.
Задания для самостоятельного решения
Задание 4.1. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Задание 4.2. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий: а) ровно три; б) менее трех; в) более трех; г) хотя бы одно.
Задание 4.3. Дана функция распределения непрерывной случайной величины Х:
Найти плотность распределения.
Задание 4.4. Дана функция распределения непрерывной случайной величины Х:
Найти плотность распределения.
Задание 4.5. Случайные величины X и Y независимы. Найти дисперсию случайной величины Z = 3X + 2Y, если известно, что D(X) = 5, D(Y) = 6.
Задание 4.6. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:
Тема 5
infopedia.su

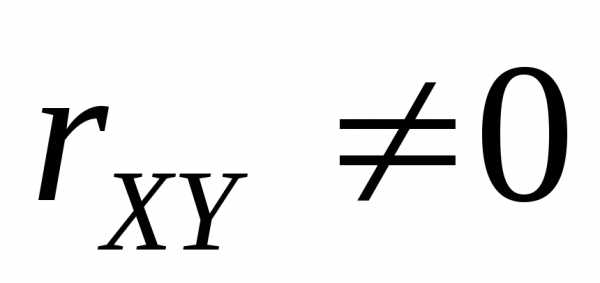 ,
то с.в.Х и Y зависимы).
,
то с.в.Х и Y зависимы).