Обратная синусу функция – , , , , , , , —

Свойства обратных тригонометрических функций

Названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.

Так как геометрически значение обратной тригонометрической функции связано с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку, то названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.

Арксинус

Арксинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \sin \alpha=a,\;|a|\leqslant 1,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)

• Областью определения функции арксинус является отрезок \( [-1;1]. \)
• Областью значений функции арксинус является отрезок \( [-\frac{\pi}{2};\frac{\pi}{2}]. \)
• Арксинус строго возрастающая функция.
• \( \sin \left (\arcsin a \right )=a,\;|a|\leqslant 1. \)
• \( \arcsin\left (\sin \alpha \right )=\alpha,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
• Арксинус является нечетной функцией: \( \arcsin(-a)=-\arcsin a,\;|a| \leqslant 1. \)
• \( \arcsin a>0,\;a\in(0;1]. \)
• \( \arcsin a=0,\;a=0. \)
• \( \arcsin a<0,\;a\in[-1;0). \)

Арккосинус

Арккосинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \cos \alpha=a,\;|a|\leqslant 1,\;\alpha\in[0;\pi]. \)

• Областью определения функции арккосинус является отрезок \( [-1;1]. \)
• Областью значений функции арккосинус является отрезок \( [0;\pi]. \)
• Арккосинус строго убывающая функция.
• \( \cos \left (\arccos a \right )=a,\;|a|\leqslant 1. \)
• \( \arccos\left (\cos \alpha\right )=\alpha,\;\alpha\in[0;\pi]. \)
• Арккосинус является индифферентной функцией: \( \arccos (-a)=\pi-\arccos a,\;|a|\leqslant 1. \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
• \( \arccos a>0,\;a\in[-1;1). \)
• \( \arccos a=0,\;a=1. \)

Арктангенс

Арктангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{tg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)

• Областью определения функции арктангенс является вся числовая прямая: \( \mathbb{R}. \)
• Областью значений функции арктангенс является интервал \( \left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
• Арктангенс строго возрастающая функция.
• \( \text{tg}\left (\text{arctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
• \( \text{arctg}\left (\text{tg}\,\alpha \right ) =\alpha,\;\alpha\in\left ( -\frac{\pi}{2};\frac{\pi}{2} \right ). \)
• Арктангенс является нечетной функцией: \( \text{arctg}\left (-a \right ) =-\text{arctg}\,a,\;a\in\mathbb{R}. \)
• \( \text{arctg}\,a>0,\;a\in(0;\infty ). \)
• \( \text{arctg}\,a=0,\;a=0. \)
• \( \text{arctg}\,a<0,\;a\in(-\infty;0). \)

Арккотангенс

Арккотангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{ctg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (0;\pi \right ). \)

• Областью определения функции арккотангенс является вся числовая прямая: \( \mathbb{R}. \)
• Областью значений функции арккотангенс является интервал \( \left (0;\pi \right ). \)
• Арккотангенс строго убывающая функция.
• \( \text{ctg}\left (\text{arcctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
• \( \text{arcctg}\left (\text{ctg}\,\alpha \right ) =\alpha,\;\alpha\in\left (0;\pi \right ). \)
• Арккотангенс является индифферентной функцией: \( \text{arcctg}\left (-a \right ) =\pi-\text{arcctg}\,a,\;a\in\mathbb{R}. \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
• \( \text{arcctg}\,a>0,\;a\in\mathbb{R}. \)

Основные соотношения

• \( \arcsin a+\arccos a=\frac{\pi}{2},\;|a|\leqslant 1. \)
• \( \text{arctg}\,a+\text{arcctg}\,a=\frac{\pi}{2},\;a\in\mathbb{R}. \)

Решение простейших тригонометрических уравнений

В общем виде

\( \sin x=a,\;|a|\leqslant 1\Rightarrow x=(-1)^k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)

или \( \left[\begin{matrix} x&=&\arcsin\,a+2\pi k,&\;k\in\mathbb{Z}\\ x&=&\pi-\arcsin\,a+2\pi l,&\;l\in\mathbb{Z} \end{matrix}\right. \)

\( \cos x=a,\;|a|\leqslant 1\Rightarrow x=\pm\arccos\,a+2\pi k,\;k\in\mathbb{Z} \)

\( \text{tg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arctg}\,a+\pi k,\;k\in\mathbb{Z} \)

\( \text{ctg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arcctg}\,a+\pi k,\;k\in\mathbb{Z} \)

Частные случаи

\( \sin x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)

---

\( \cos x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)

---

\( \text{tg}\, x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)

---

\( \text{ctg}\, x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)

\( \sin x=1\Rightarrow x=\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)

---

\( \cos x=1\Rightarrow x=2\pi k,\;k\in\mathbb{Z} \)

---

\( \text{tg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)

---

\( \text{ctg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)

\( \sin x=-1\Rightarrow x=-\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)

---

\( \cos x=-1\Rightarrow x=\pi+2\pi k,\;k\in\mathbb{Z} \)

---

\( \text{tg}\, x=-1\Rightarrow x=-\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)

---

\( \text{ctg}\, x=-1\Rightarrow x=\frac{3\pi}{4}+\pi k,\;k\in\mathbb{Z} \)

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

Выражение через логарифм обратных тригонометрических функций

Формулы обратных тригонометрических функций

Обратные тригонометрические функции выражаются через натуральные логарифмы следующим образом:

Здесь стоит подчеркнуть, что все эти функции многозначны и обозначают всю совокупность значений в целом. Везде подразумевается, что квадратный корень имеет два знака: «+» и «–», а логарифм имеет бесконечное множество значений, отличающихся на 2πin, где n — целое. То есть, например, под арксинусом имеется в виду вся совокупность значений:
.
Такое правило распространяется на все многозначные функции комплексного переменного и их названия начинаются с большой буквы. Названия с маленькой буквы означают однозначную ветвь функции, заданной на определенной области Римановой поверхности.

Ниже приводится вывод этих формул.

Арксинус

Пусть   f = arcsin z.

Чтобы выразить arcsin z через элементарные функции, решаем уравнение:

Выразим sin f   через комплексные переменные:

Умножим на 2 i e^if


Решаем квадратное уравнение

Логарифмируем


Умножаем на -i

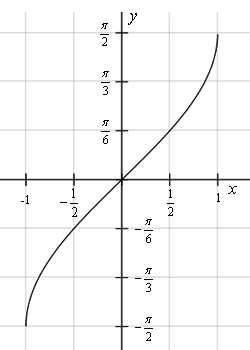
На рисунке изображена главная ветвь арксинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз.

Далее следует разобраться со знаком &pm;. С точки зрения комплексных переменных, квадратный корень всегда имеет два значения, различающихся знаком плюс и минус. Поэтому корень всегда подразумевает неоднозначность. Выберем такой знак, чтобы формула была справедлива для главного значения арксинуса. То есть для действительных значения арксинуса f = arcsin z должны находится в интервале

Рассмотрим знак +. Положим z = 0.

То есть знак + соответствует главному значению арксинуса, которое имеет множество значений при

Если мы возьмем знак –, то

То есть знак – соответствует ветви арксинуса, которая имеет множество значений при

Остальные ветви получаются вследствие многозначности логарифма. Выразим выражение под знаком логарифма через модуль r и аргумент φ:

где n — целое. Тогда

То есть многозначность логарифма дает ветви, которые отстоят друг от друга на величину 2π, что соответствует периоду синуса.

Итак,

Арккосинус

Выполняем аналогичные вычисления для арккосинуса. Пусть   f = arccos z.

Рассмотрим уравнение:

Умножим на 2 e^if



Логарифмируем

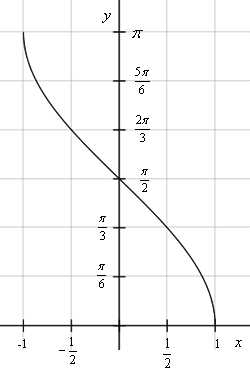
На рисунке изображена главная ветвь арккосинуса. Остальные ветви получились бы, если продлить перевернутую синусоиду вверх и вниз.

Если взять знак +, то при z = 0 имеем:

Знак + соответствует главному значению арккосинуса, которое имеет множество значений при

Если бы мы взяли знак –, то

То есть знак – соответствует ветви арккосинуса, которая имеет множество значений при .

Итак,

Арктангенс

Для арктангенса, пусть   f = Arctg z.

Рассмотрим уравнение:

Умножим числитель и знаменатель на e^if и выполняем преобразования




Логарифмируем:
;
.

Рассмотрим действительные z. Представим комплексную функцию под знаком логарифма в алгебраической форме:
,
где .

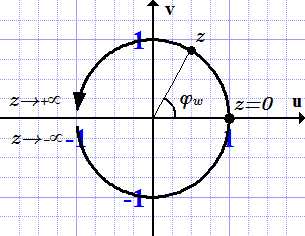
Комплексная функция при действительных z.

При . Это соответствует главному значению арктангенса, .

При . При этом аргумент функции возрастает от до : . Тогда
.

При . При этом аргумент функции убывает от до : . Тогда .

На рисунке изображена главная ветвь арктангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси.

Все это соответствует главному значению арктангенса, у которого
;
.

Итак,
.
Мы можем образовать листы Римановой поверхности, подчинив их условию:
.
Тогда лист с , при действительных z, даст нам главное значение арктангенса. На остальных листах к функции w добавится множитель , что приведет к увеличению значения арктангенса на . Эти значения соответствуют другим ветвям арктангенса.

Арккотангенс

Пусть   f = arcctg z.

Рассмотрим уравнение:
или

Это уравнение такое, как для тангенса, только нужно заменить z на :
;
.

Также рассмотрим действительные z. Представим комплексную функцию под знаком логарифма в алгебраической форме:
,
где .

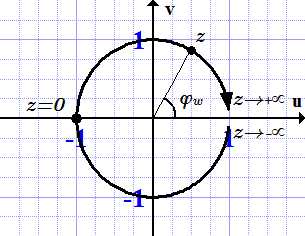
Комплексная функция при действительных z.

При . Это соответствует главному значению арккотангенса, .

При . При этом аргумент функции убывает от до : . Тогда .

При . При этом аргумент функции возрастает от до : . Тогда .

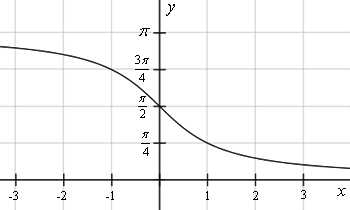
На рисунке изображена главная ветвь арккотангенса. Остальные ветви расположены периодически вверх и вниз по вертикальной оси.

Все это соответствует главному значению арккотангенса, у которого
;
.

Итак,
.
Мы можем образовать листы Римановой поверхности, подчинив их условию:
.
Тогда лист с , при действительных z, даст нам главное значение арккотангенса. На остальных листах к функции w добавится множитель , что приведет к увеличению значения арккотангенса на . Эти значения соответствуют другим ветвям арктангенса.

Автор: Олег Одинцов.     Опубликовано: 23-07-2014   Изменено: 13-04-2019

1cov-edu.ru

Обратные тригонометрические функции | Подготовка к ЕГЭ по математике

Обратные тригонометрические функции (аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям.

 

Функция арксинус

Арксинусом числа , где называется такое значение угла x, для которого

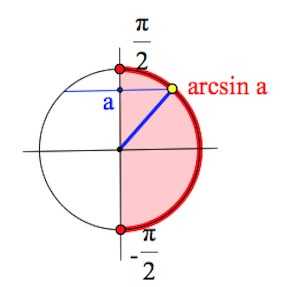
Пример 1.

Найти

Решение:

Отмечаем на оси синусов , проводим горизонталь:

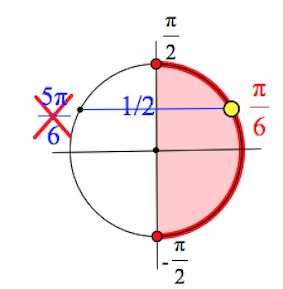
Получили две серии точек на круге.

Значения синусов в них –

Нам подходит лишь одна единственная точка, что входит в отрезок , то есть точка

Ответ:

Пример 2.

Найти

Решение:

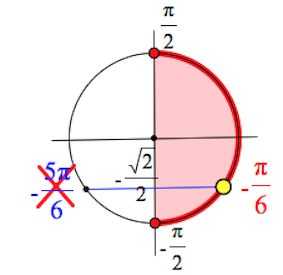
Обратите внимание, положение точки на круге совпадает с положением точки , однако мы берем  точку , так как по определению арксинус принадлежит

Ответ: 

Функция арккосинус

 

Арккосинусом числа , где   называется такое значение угла x, для которого

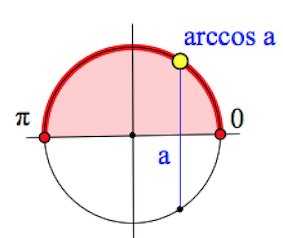
Пример. 

Найти

Решение: 

Отмечаем на оси косинусов значение , проводим вертикаль:

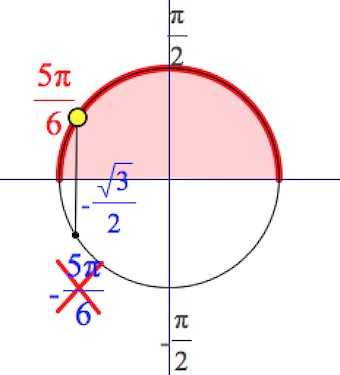
Выходим на две серии точек круга (значения косинусов в них – ), но берем лишь ту, что из , а именно

Ответ: 

Функция арктангенс

 

Арктангенсом числа , где называется такое значение угла x, для которого

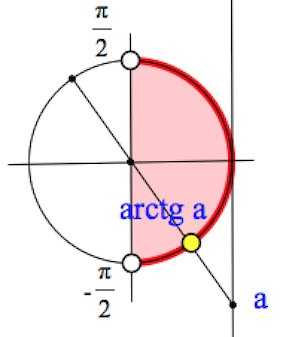
Пример.

Найти

Решение:

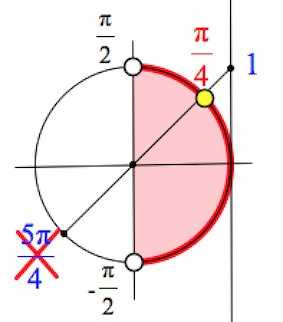
Ответ:  

Функция арккотангенс

 

Арккотангенсом числа ,    называется такое значение угла x, для которого

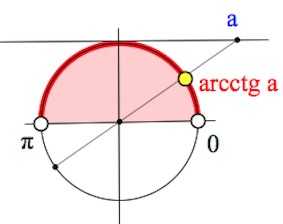
Пример.

Найти

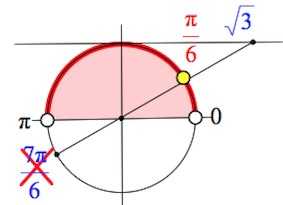
Ответ: 

 

egemaximum.ru

Обратные тригонометрические функции, все формулы

Основные обратные тригонометрические функции:

1. – арксинус;

2. – арккосинус;

3. – арктангенс;

4. – арккотангенс.

Арксинус является нечетной функцией, то есть: .

Для арккосинуса справедливо следующее равенство

   

Арктангенс функция нечетная, поэтому для нее справедливо следующее равенство

   

Для функции арккотангенс справедливо следующее равенство

   

Для вычисления значений обратных тригонометрических функций можно пользоваться таблицей

Основные соотношения между обратными тригонометрическими функциями

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Обратные тригонометрические функции — это… Что такое Обратные тригонометрические функции?



Обратные тригонометрические функции

        аркфункции, круговые функции, решают следующую задачу: найти дугу (число) по заданному значению её тригонометрической функции. Шести основным тригонометрическим функциям соответствуют шесть О. т. ф.: 1) Arc sin

х («арксинус x») — функция, обратная sin х; 2) Arc cos x («арккосинус x») — функция, обратная cos х; 3) Arc tg x («арктангенс x») — функция, обратная tg х; 4) Arc ctg x («арккотангенс x») — функция, обратная ctg x; 5) Arc sec x («арксеканс x») — функция, обратная sec x; 6) Arc cosec x («арккосеканс x») — функция, обратная cosec x. Согласно этим определениям, например, х = Arc sin a есть любое решение уравнения sin х = a, т.е. sin Arc sin a = a. Функции Arc sin x и Arc cos x определены (в действительной области) для |х| ≤ 1, функции Arc tg х и Arc ctg х — для всех действительных х, а функции Arc sec х и Arc cosec х:—для |х| ≥ 1; две последние функции малоупотребительны.

         Так как тригонометрические функции периодические, то обратные к ним функции являются многозначными функциями. Определённые однозначные ветви (главные ветви) этих функций обозначаются так: arc sin

х, arc cos x,…, arc cosec x. Именно, arc sin х есть та ветвь функции Arc sin х, для которой — π/2 ≤ arc sin х ≤ π/2. Аналогично, функции arc cos х, arc tg х и arc ctg х определяются из условий: 0 ≤ arc cos х ≤ π, — π/2 x π/2, 0 x π. На рис. изображены графики функций у = Arc sin x, у = Arc cos x, у = Arc tg x, у = Arc ctg x; главные Arc cos x = ± arc cos x +2πn,ветви этих функций выделены жирной линией. О. т. ф. Arc sin х,… легко выражаются через arc sin

x,…, например         

         n = 0, ±1, ±2, …

        

         Известные соотношения между тригонометрическими функциями приводят к соотношениям между О. т. ф., например из формулы

        

        вытекает, что

        

        Производные О. т. ф. имеют вид

                                             О. т. ф. могут быть представлены степенными рядами, например         

        эти ряды сходятся для —1 ≤ x ≤ 1.

         О. т. ф. можно определить для произвольных комплексных значений аргумента; однако их значения будут действительными лишь для указанных выше значений аргумента. О. т. ф. комплексного аргумента могут быть выражены с помощью логарифмической функции, например

        

        

         Лит.: Новоселов С. И., Обратные тригонометрические функции, 3 изд., М., 1950.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Обратные гиперболические функции
• Обратный клапан

Смотреть что такое «Обратные тригонометрические функции» в других словарях:

• ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — функции, обратные тригонометрическим (см.). Функцией, обратной синусу, является арксинус, функцией, обратной косинусу, является арккосинус и т. д. Обозначаются так: Arcsin x (арксинус x), Arccos x (арккосинус x) и т.д …   Большая политехническая энциклопедия

• ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — общее название функций арксинуса, арккосинуса, арктангенса, арккотангенса, арксеканса, арккосеканса, каждая из которых выражает величину дуги (или угла), соответствующей данному значению х тригонометрической функции, название которой получается… …   Большой Энциклопедический словарь

• Обратные тригонометрические функции — (круговые функции, аркфункции)  математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: арксинус (обозначение: arcsin) арккосинус (обозначение: arccos)… …   Википедия

• обратные тригонометрические функции — общее название функций арксинуса, арккосинуса, арктангенса, арккотангенса, арксеканса, арккосеканса, каждая из которых выражает величину дуги (или угла), соответствующей данному значению х тригонометрической функции, название которой получается… …   Энциклопедический словарь

• ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — функции, обратные тригонометрическим функциям. Обычно рассматривают следующие О. т. ф.: Arcsin х (арксинус х) ф ция, обратная sin х; Arccos х (арккосинус х) ф ция, обратная cos Л; Arctg х (арктангенс х) ф ция, обратная tg х; Arcctg х… …   Большой энциклопедический политехнический словарь

• ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ, — аркфуикции, круговые функции, функции, обратные тригонометрическим функциям. Шести основным тригонометрич. функциям соответствуют шесть О. т. ф.: арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс; обозначаются соответственно… …   Математическая энциклопедия

• ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — общее назв. функций арксинуса, арккосинуса, арктангенса, арккотангенса, арксеканса, арккосеканса, каждая из к рых выражает величину дуги (или угла), соответствующей данному значению х тригонометрич. функции, название к рой получается… …   Естествознание. Энциклопедический словарь

• Обратные гиперболические функции — Обратные гиперболические функции  определяются как обратные функции к гиперболическим функциям. Эти функции определяют площадь сектора единичной гиперболы x2 − y2 = 1 аналогично тому, как обратные тригонометрические функции определяют длину… …   Википедия

• Тригонометрические функции — Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения …   Википедия

• Тригонометрические функции —         один из важнейших классов элементарных функций.          Для определения Т. ф. обычно рассматривают окружность единичного радиуса с двумя взаимно перпендикулярными диаметрами A A и B B (рис. 1). От точки А по окружности откладываются дуги …   Большая советская энциклопедия

Книги

• Математика обратные тригонометрические функции Решение задач Учебное пособие, Далингер В., В учебном пособии рассмотрен общий подход к определению обратной тригонометрической функции и построению ее графиков, на этой основе изложены теоретические основы обратных тригонометрических… Подробнее  Купить за 549 руб
• Математика: обратные тригонометрические функции. Решение задач 2-е изд., испр. и доп. Учебное пособие для СПО, Виктор Алексеевич Далингер, В учебном пособии рассмотрен общий подход к определению обратной тригонометрической функции и построению ее графиков, на этой основе изложены теоретические основы обратных тригонометрических… Серия: Профессиональное образование Издатель: ЮРАЙТ, Подробнее  Купить за 369 руб электронная книга
• Обратные тригонометрические функции, С. И. Новоселов, В настоящем втором издании книга подверглась значительной переработке. Наиболее существенные изменения заключаются в следующем: 1. В теории обратных тригонометрических функций последовательно… Издатель: Государственное учебно-педагогическое издательство Министерства Просвещения РСФСР, Подробнее  Купить за 250 руб

Другие книги по запросу «Обратные тригонометрические функции» >>

dic.academic.ru

Обратные тригонометрические функции | Математика, которая мне нравится

I. Рассмотрим функцию , где (см. рис. 48).

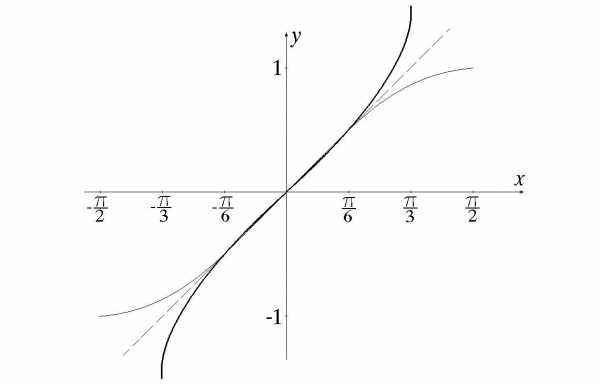
Рис. 48

Множество значений этой функции — .

Рассмотрим функцию , где . Эта функция — функция, обратная функции .

II. Рассмотрим функцию , где (см. рис. 49).

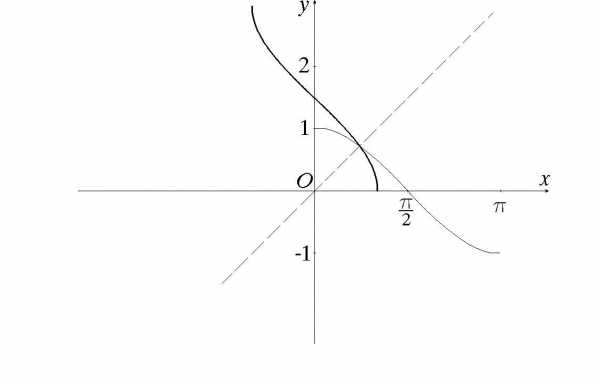
Рис. 49

Функция — обратная функция.

III. Рассмотрим функцию , где (см. рис. 50).

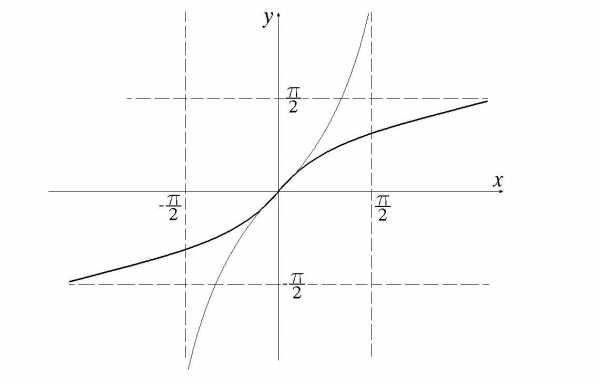
Рис. 50

Функция — обратная функция.

IV. Рассмотрим функцию , где (см. рис. 51).

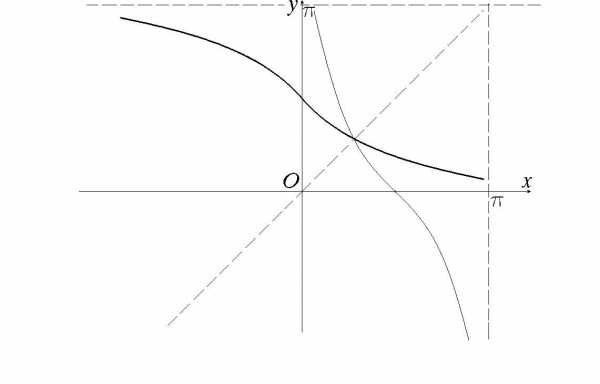
Рис. 51

Функция — обратная функция.

Функции и строго возрастают, и строго убывают. Функции и нечетные.

Это следует из общего утверждения:

Утверждение. Функция, обратная нечетной функции, является нечетной функцией.

Доказательство. Пусть — нечетная функция, — обратная к ней. Пусть . Тогда . Следовательно, . Отсюда . И это верно для любого числа из области определения .

Теорема. Для любого

   

   

Доказательство.

   

Так как на отрезке синус строго монотонен, то из равенства синусов двух чисел этого отрезка вытекает равенство этих чисел.

   

Второе равенство доказывается аналогично.

Теорема.

   

   

Доказательство.

   

Первое равенство доказывается аналогично.

Задачи.

1) Найдите значения выражений

1.

2.

3.

2) Постройте графики функций

1.

2.

3.

3) Докажите, что для любого значения из промежутка справедливо неравенство

hijos.ru