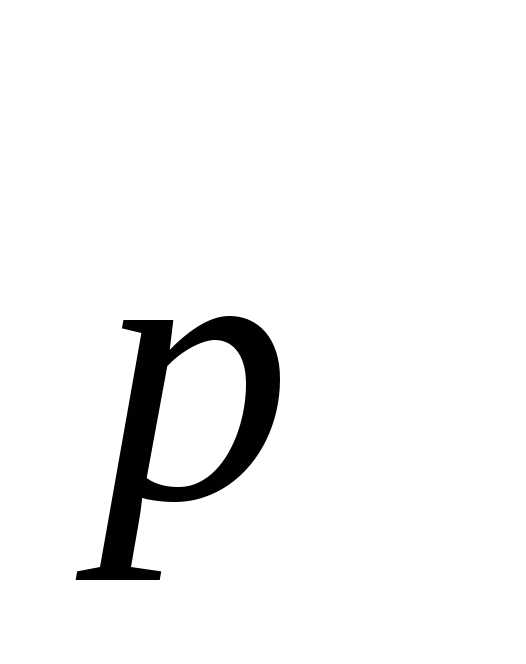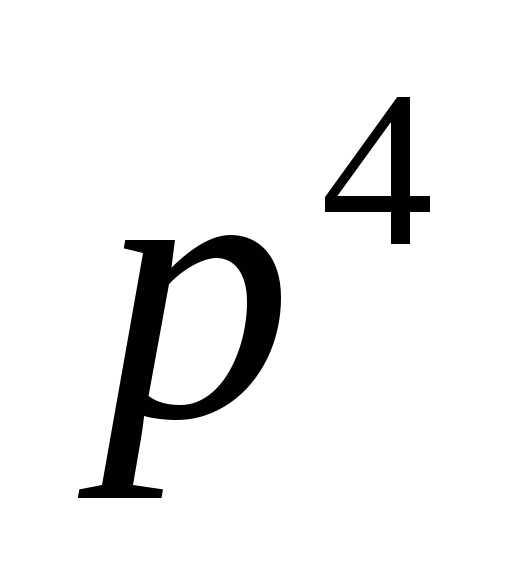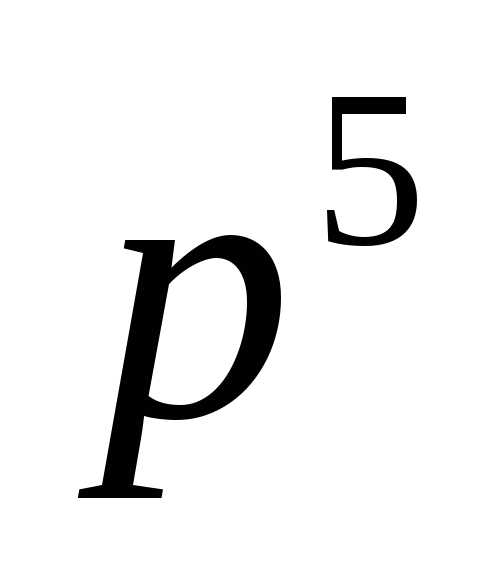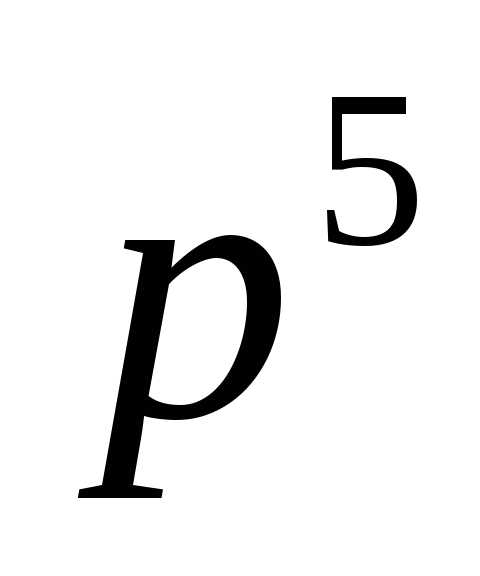[Python] #Наименьшее число m, такое, что m! делится без
#Наименьшее число m, такое, что m! делится без остатка на 10 — это m=5 (5! = 120). Аналогично, наименьшее число m, такое, что m! делится без остатка на 25 — это m=10. В общем случае, значение функции s(n) равно наименьшему числу m, такому что m! без остатка делится на n. Определим функцию S(M, N) = ∑s(n) для всех n ∈ [M, N]. К примеру, S(6, 10) = 3 + 7 + 4 + 6 + 5 = 25. Найдите S(610000000, 620000000).
#главная функция
def S(N,M):
result = 0
list = generate_base(int(math.sqrt(M))+1000)
for i in range (N, M + 1):
result += s(factorization(i, list))
return result
#функция принимает число n в виде словаря простых чисел и их степеней и выдает минимальное m такое, что m!%n==0
def s(n):
result = 0
for (num, exp) in n.items():
tmp = get_fact(num, exp)
if tmp > result:
result = tmp
return result
#функция принимает число и степень, и возвращает минимальное m такое, что m! %(число**степень) == 0
def get_fact(num, exp):
a = 1
res = num
while(a < exp):
res += num
a += get_exp(res, num)
return res
def get_exp(num, base):
exp = 1
while ((num//base)%base == 0):
num = num//base
exp += 1
return exp
#разложить число на простые множители
def factorization(num, list):
dict = {}
i = 0
a = list[i]
while a*a <= num:
if num % a == 0:
if dict.get(a):
dict[a] += 1
else:
dict[a] = 1
num //= a
else:
i += 1
a = list[i]
if num != 1:
if dict.get(num):
dict[num] += 1
else:
dict[num] = 1
return dict
#создать список простых чисел
def generate(n):
lst=[2]
for i in range(3, n+1, 2):
if (i > 10) and (i%10==5):
continue
for j in lst:
if j*j — 1 > i:
lst.append(i)
break
pastebin.com
5. Нумерация вычислимых функций
Определение
5.1. Пусть f – n—местная
функция, вычислимая по программе P с геделевым номером m = (P).
Число m будем называть индексом функции f.
Вычислимую функцию от n переменных с индексом m будем обозначать символом 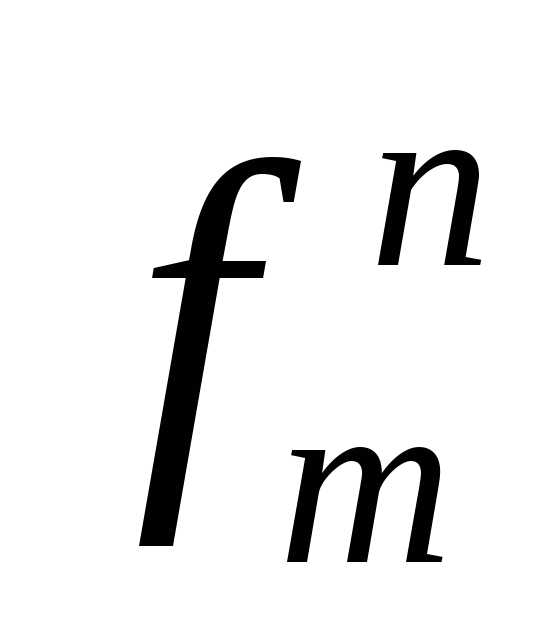 .
.
Из определения 5.1 следует, что каждая n—местная вычислимая функция f представлена в перечислении
Ниже
мы в основном будем рассматривать
одноместные вычислимые функции 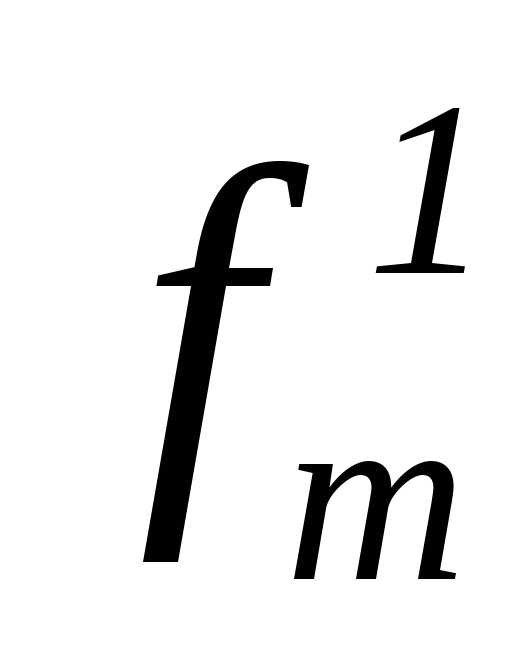
Теорема 5.1. Существует невычислимая всюду определенная функция.
Доказательство.
Пусть  — некоторое перечисление всех вычислимых
функций:
— некоторое перечисление всех вычислимых
функций:
Положим
Функция g отличается от любой вычислимой функции 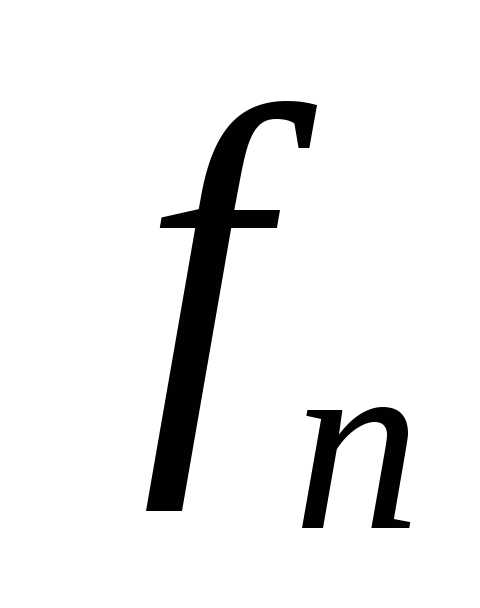 в точкеn.
Действительно, если функция
в точкеn.
Действительно, если функция 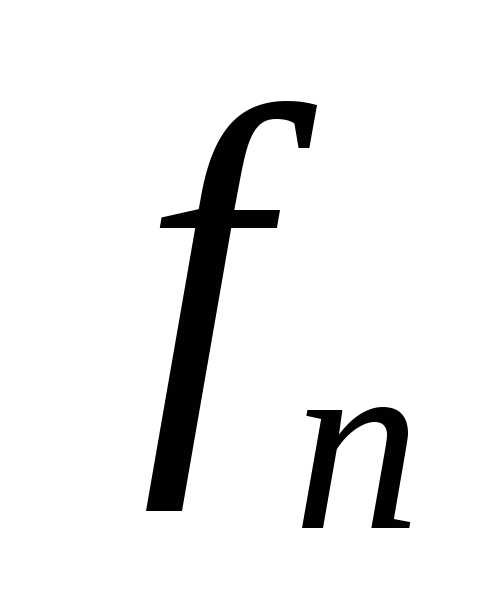 определена в точкеn,
то
.
Если
определена в точкеn,
то
.
Если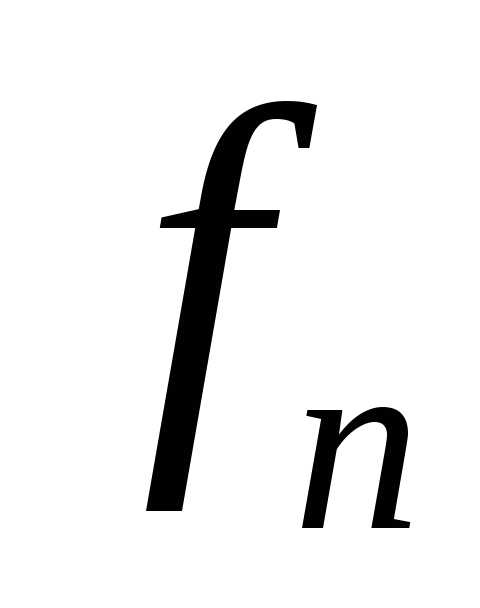 не определена в точкеn,
то g отличается от
не определена в точкеn,
то g отличается от 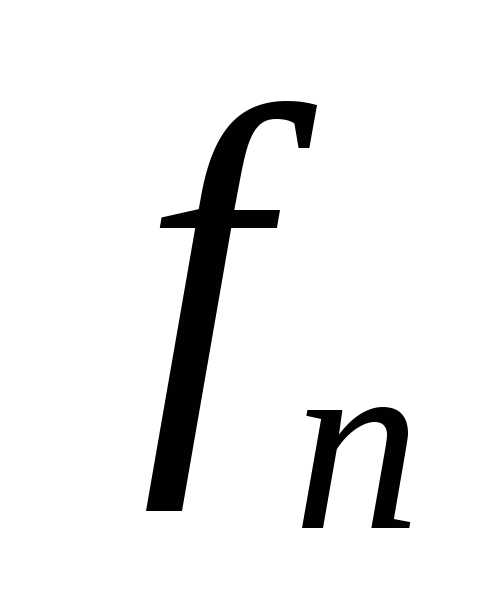
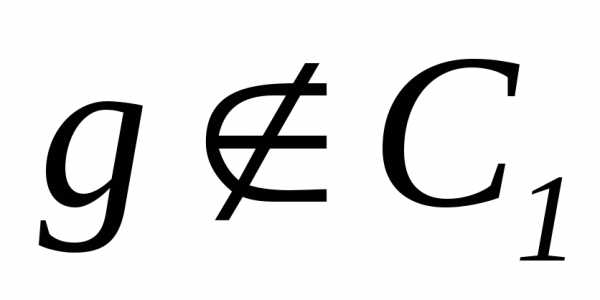 и, следовательно, g — невычислимая всюду определенная
функция.
и, следовательно, g — невычислимая всюду определенная
функция.Метод построения функции в теореме 5.1 является примером диагональной конструкции, открытой Кантором.
6. Универсальные программы
В этом разделе мы докажем несколько неожиданный результат, состоящий в том, что существуют универсальные программы, то есть программы, которые в некотором смысле реализуют все другие программы. Этот результат является одним из основных результатов теории вычислимости.
Определение 6.1. Универсальной функцией для n-местных вычислимых функций называется (n+1)-местная функция
.
Для
примера рассмотрим функцию 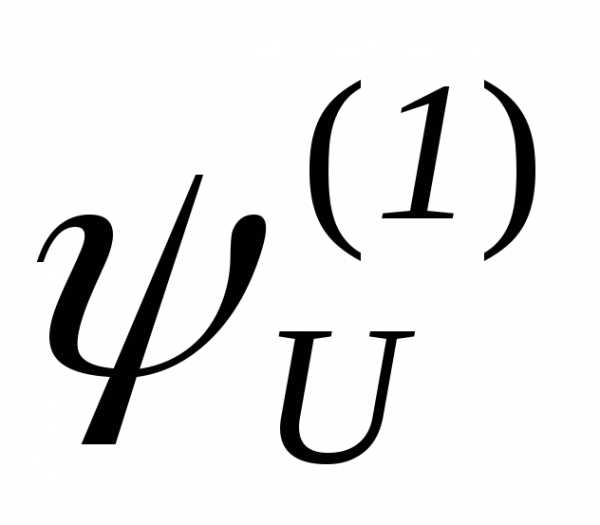
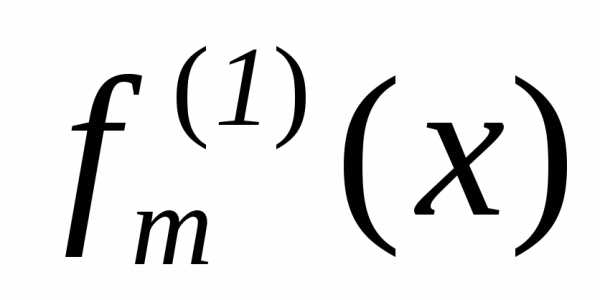 .
Таким образом, название функции
.
Таким образом, название функции вполне соответствует классу вычисляемых
ею одноместных функций.
вполне соответствует классу вычисляемых
ею одноместных функций.Ниже
для простоты вместо 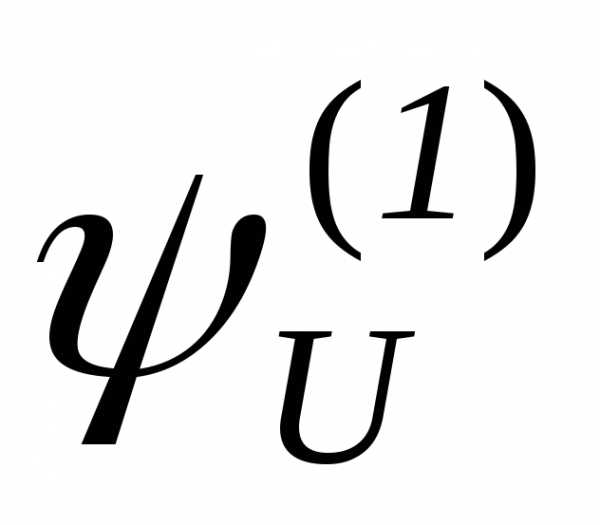 будем писать
будем писать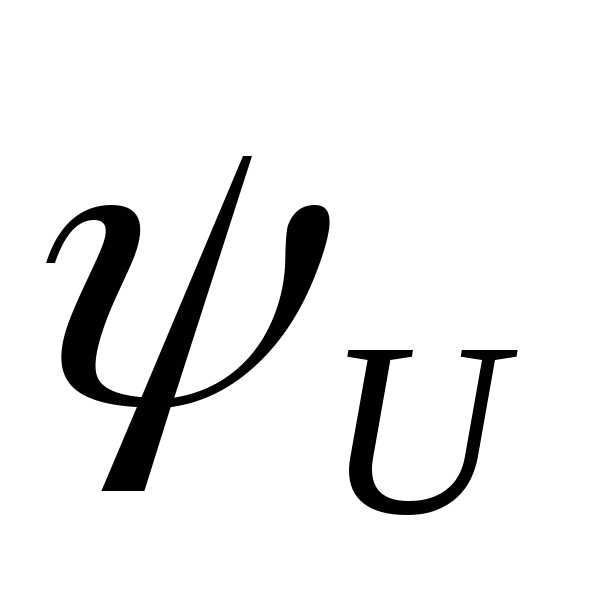 .
.
Теорема
6.1. Для
каждого натурального числа n универсальная функция 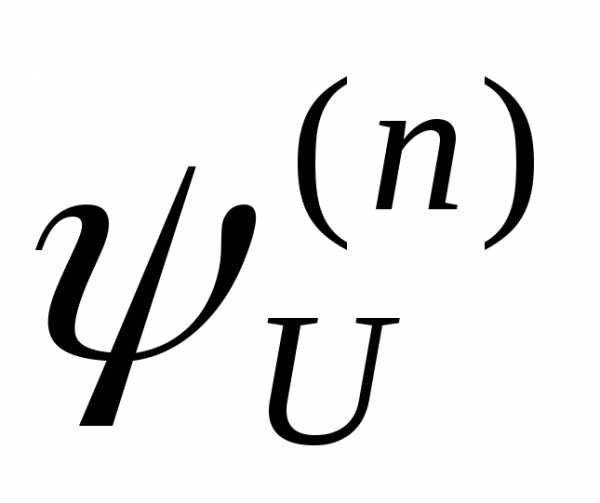 вычислима.
вычислима.
Доказательство. Покажем, как можно вычислить значение
функции
для заданного числаm и фиксированного набора (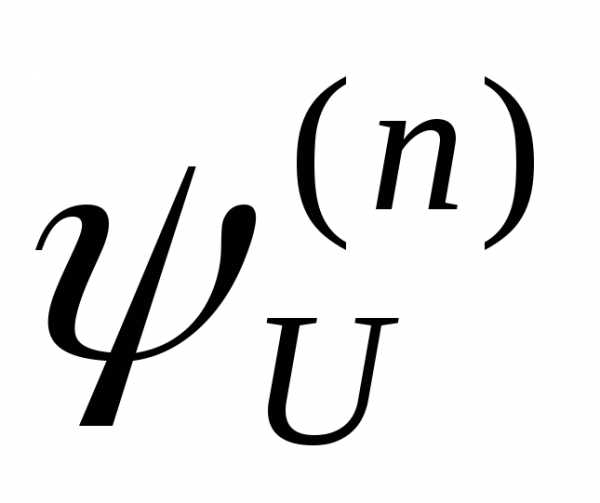 вычислима.
вычислима.
Определение
6.2. Любая
программа Р(n),
вычисляющая функцию 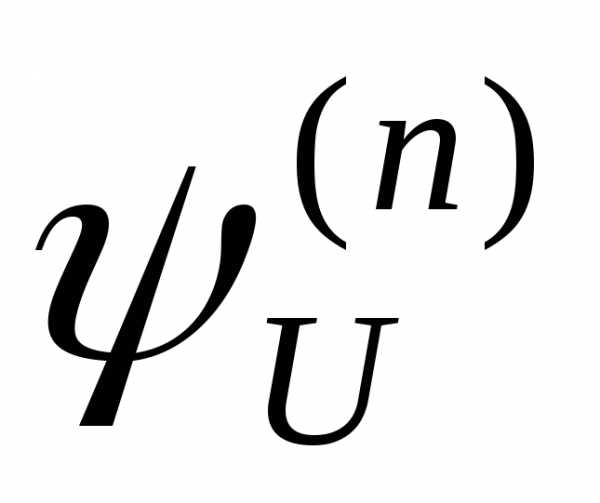 ,
называется универсальной программой.
,
называется универсальной программой.
Универсальные программы полностью соответствуют своему названию. Действительно, так как универсальная программа Р(n) позволяет вычислить любую n—местную вычислимую функцию, то, по сути дела, программа Р(n) заменяет абсолютно все программы для вычисления n—местных функций.
Проиллюстрируем теперь, как использовать вычислимость универсальных функций в диагональных построениях.
7. Алгоритмически неразрешимые проблемы
Основным стимулом, приведшим к выработке понятия алгоритма и созданию теории алгоритмов, явилась потребность доказательства неразрешимости многих проблем, возникших в различных областях математики. Специалист, решая задачу, всегда должен считаться с возможностью того, что она может оказаться неразрешимой.
При доказательстве неразрешимости той или иной проблемы часто используется так называемый метод сводимости, заключающийся в следующем. Пусть, например, в результате некоторых рассуждений удалось показать, что решение проблемы Pr1 приводит к решению другой проблемы
Ниже доказывается неразрешимость ряда известных проблем.
Теорема
7.1. Проблема
«функция  всюду определена» неразрешима.
всюду определена» неразрешима.
Доказательство. Пусть g — характеристическая функция этой проблемы
Нам надо показать, что функция g невычислима.
От противного, предположим, что g — вычислимая функция. Рассмотрим функцию
Функция f всюду определена и отличается от каждой
вычислимой функции 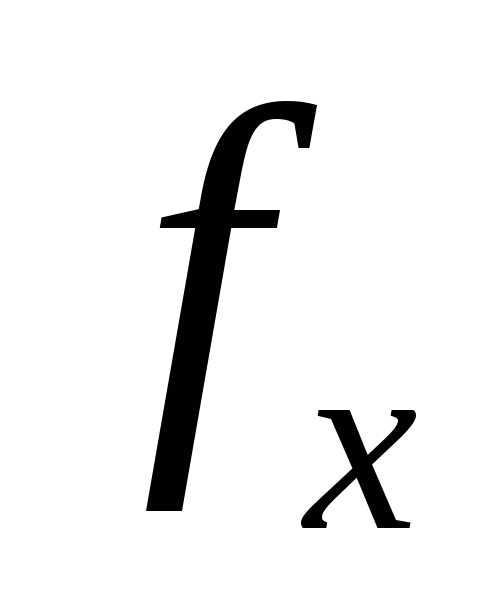 .
.
Применяя g и универсальную функцию 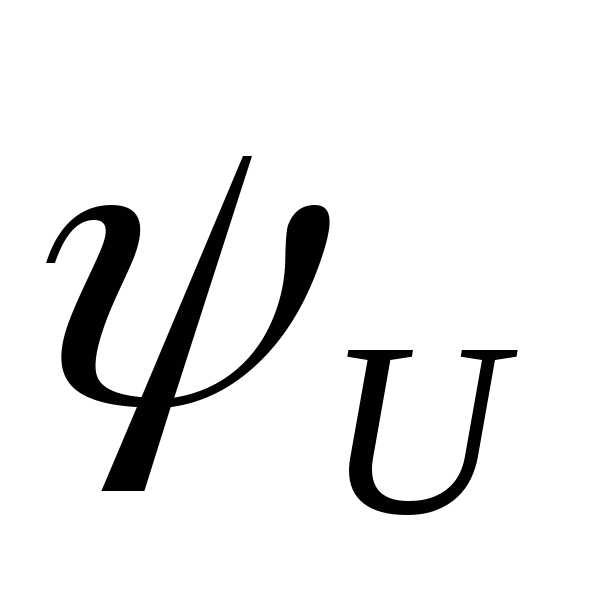 , запишем f в виде:
, запишем f в виде:
Из
вычислимости функций g и 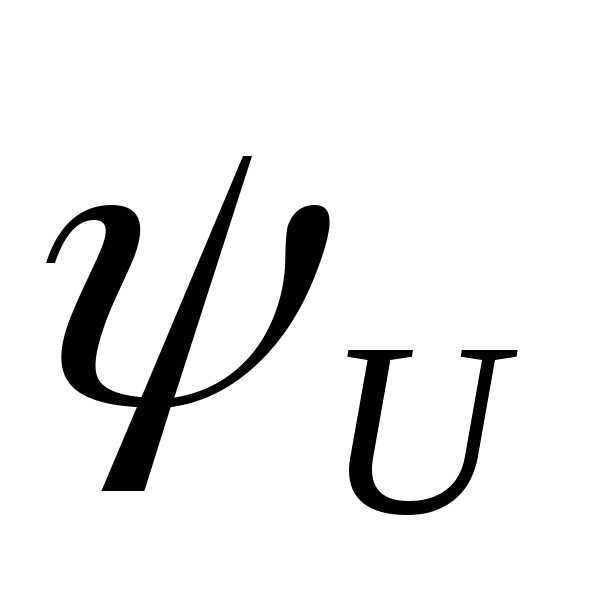 по тезису Черча следует вычислимость
функцииf.
по тезису Черча следует вычислимость
функцииf.
Полученное
противоречие доказывает невычислимость
функции g.
Таким образом, проблема «функция 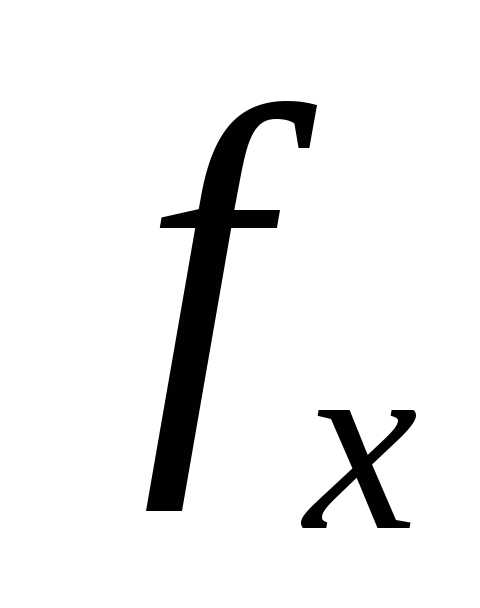 всюду определена» неразрешима.
всюду определена» неразрешима.
Обозначим
область определения 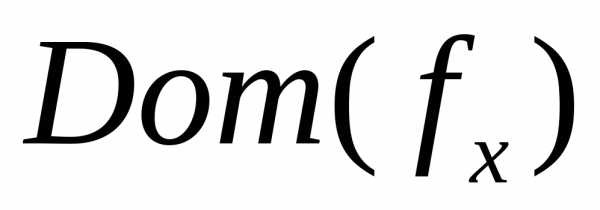
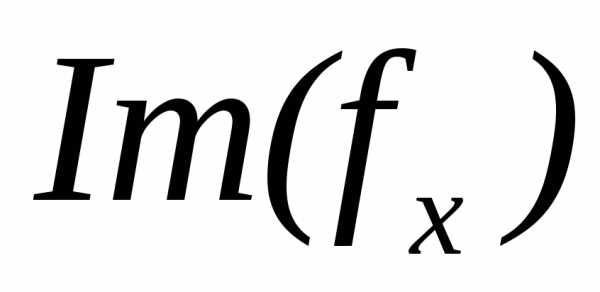 функции
функции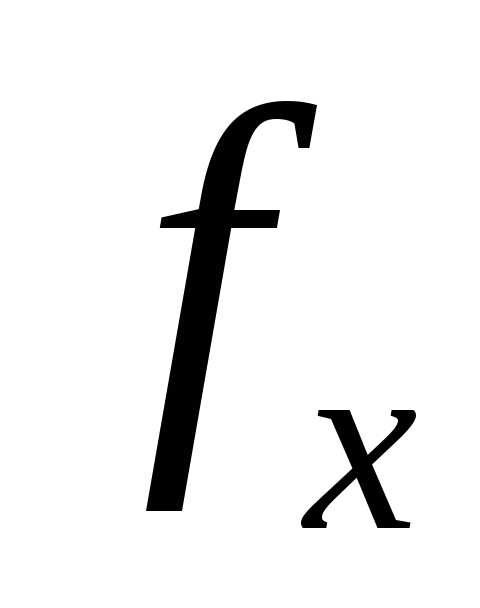 через
через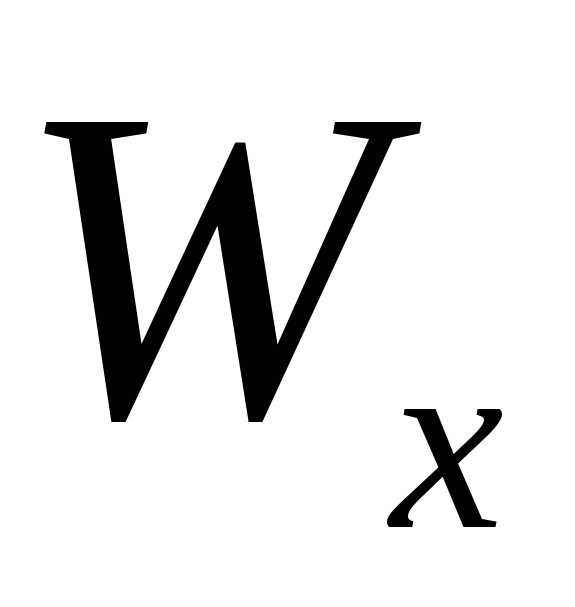 и
и соответственно.
соответственно.Теорема
7.2. Проблема
« »
неразрешима.
»
неразрешима.
Доказательство. Характеристическая функция этой проблемы задается следующим образом:
Предположим, что функция g вычислима, и приведем это предположение к противоречию.
Рассмотрим функцию
Так
как функция g вычислима, то по тезису Черча функция f также вычислима. С другой стороны, для
любого x область определения Dom(f)
функции f отлична от области определения 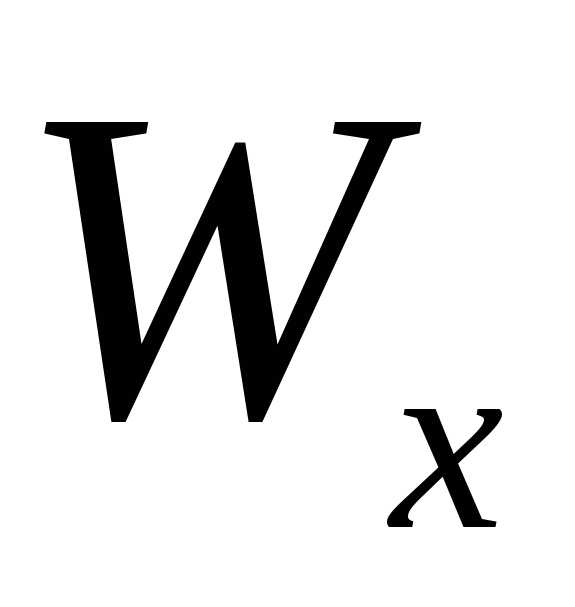 ,
и, следовательно,
,
и, следовательно,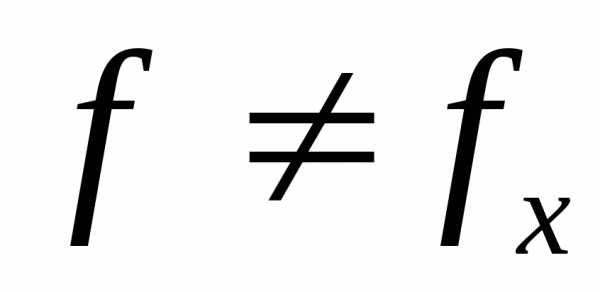 .
.
Таким
образом, предположение о вычислимости
характеристической функции g неверно. Поэтому проблема « »
неразрешима.
»
неразрешима.
Замечание
7.1. Доказанная
теорема вовсе не утверждает, что мы не
можем для любого конкретного числа a сказать, будет ли определено значение 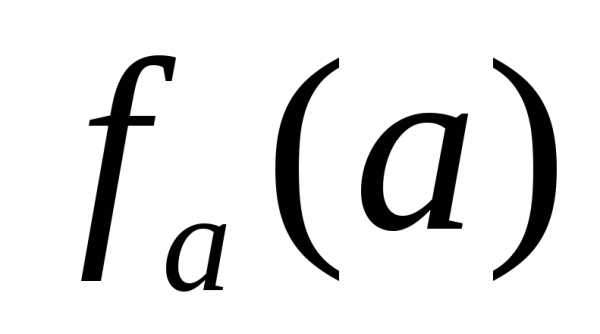 .
В теореме лишь утверждается, что не
существует единого общего метода решения
вопроса о том, будет ли значение
.
В теореме лишь утверждается, что не
существует единого общего метода решения
вопроса о том, будет ли значение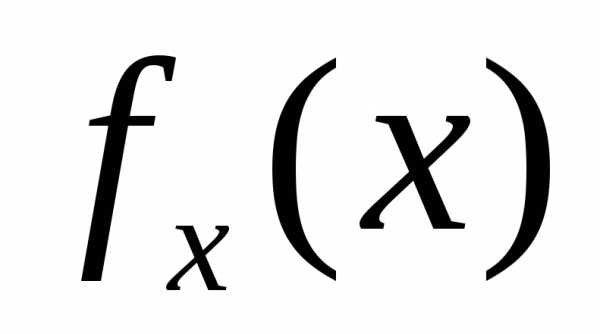 определено.
определено.
Замечание
7.2. Проблему
« »
называют такжепроблемой
самоприменимости.
Такое название связано с формулировкой
проблемы в форме: «Остановится ли МНР,
работая по программе
»
называют такжепроблемой
самоприменимости.
Такое название связано с формулировкой
проблемы в форме: «Остановится ли МНР,
работая по программе 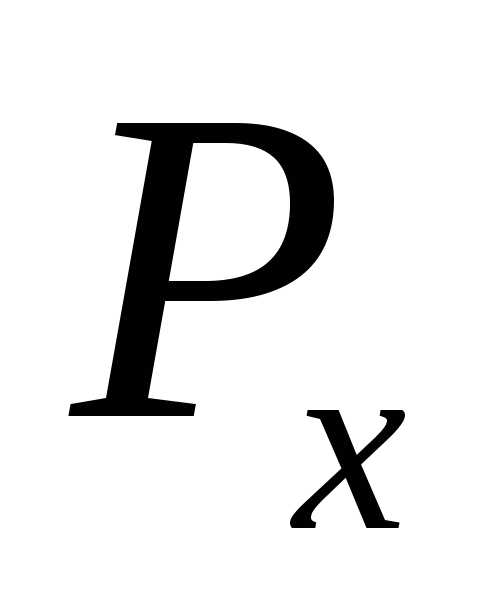 с начальной конфигурацией (x)?».
Другими словами: «Применима ли программа
к своему кодовому номеру?».
с начальной конфигурацией (x)?».
Другими словами: «Применима ли программа
к своему кодовому номеру?».
Теорема
7.3. Проблема
« »
неразрешима.
»
неразрешима.
Доказательство.
Если бы проблема « »
была разрешима, то была бы разрешима
более простая проблема «
»
была разрешима, то была бы разрешима
более простая проблема « »,
что противоречит доказанной выше
теореме.
»,
что противоречит доказанной выше
теореме.
Замечание 7.3. Доказанную теорему часто интерпретируют как утверждение о неразрешимости проблемы остановки, в которой говорится, что не существует общего метода, устанавливающего, остановится ли некоторая конкретная программа, запущенная с некоторым конкретным набором начальных данных.
Смысл этого утверждения для теоретического программирования очевиден: не существует общего метода проверки программ на наличие в них бесконечных циклов.
В
доказательстве теоремы мы показали,
что проблема остановки « »,
по крайней мере, не проще, чем проблема
самоприменимости «
»,
по крайней мере, не проще, чем проблема
самоприменимости « ».
Мы свели вопрос о неразрешимости одной
проблемы к другой. Это прием часто
используется при доказательстве
неразрешимости проблем.
».
Мы свели вопрос о неразрешимости одной
проблемы к другой. Это прием часто
используется при доказательстве
неразрешимости проблем.
studfiles.net
11.3. Машины произвольного доступа и вычислимые функции
Опишем другую алгоритмическую модель, представляющую собой идеализированную ЭВМ и предложенную в 70-х годах XX века с целью моделирования реальных вычислительных машин и анализа сложности вычислений.
Машина произвольного доступа (МПД) состоит из бесконечного числа регистров R1, R2, …, в каждом из которых может быть записано натуральное число из . Пусть есть число, записанное в регистре , . Состоянием машины или Конфигурацией назовем последовательность чисел . Функционирование машины заключается в изменении конфигураций путем выполнения Команд в порядке их написания.
Машина имеет следующие типы команд.
Команды обнуления. Для всякого имеется команда . Действие команды заключается в замене содержимого регистра на 0. Содержимое других регистров не меняется. Обозначение действия
:
:= 0.
Команды прибавления единицы. Для всякого имеется команда . Действие команды заключается в увеличении содержимого регистра на 1. Содержимое других регистров не меняется. Обозначение действия :
:= + 1.
Команды переадресации. Для всех имеется команда . Действие команды заключается в замене содержимого регистра числом — хранящимся в регистре . Содержимое других регистров не меняется (включая и ). Обозначение действия :
:= или à .
Команды условного перехода. Для всяких имеется команда . Действие этой команды заключается в:
Сравнении содержимого регистров и , затем:
А) если = , то МПД переходит к выполнению команды с номером (идентификатором) Q в списке команд;
B) если ¹ , то МПД переходит к выполнению следующей команды в списке команд.
Конечная, упорядоченная последовательность команд данных типов составляет Программу МПД.
Пусть зафиксирована начальная конфигурация чисел и программа . Тогда однозначно определена последовательность конфигураций , где есть конфигурация, полученная из конфигурации применением команды . Пусть на некотором шаге выполнена команда и получена конфигурация . Тогда, если не есть команда условного перехода, то следующая конфигурация есть конфигурация, полученная из применением команды . Если есть команда условного перехода, т. е. IT = J(M, N, Q), то получается из применением команды , если = в конфигурации и команды , если ¹. Последовательность конфигураций будет обозначаться также P(A1, A2, …) или и называться Вычислением.
Вычисление (работа машины) останавливается, если:
Выполнена последняя команда, т. е. T = S И не есть команда условного перехода;
Если IT = J(M, N, Q), = в конфигурации и Q > S;
Если IT = J(M, N, Q), ¹ в конфигурации и T = S.
Если вычисление остановилось, то последовательность содержимого регистров называется Заключительной конфигурацией. Если последовательность конечна, то говорим, что МПД применима к начальной конфигурации и пишем P(A1, A2, …)¯ или . В противном случае говорим, что МПД неприменима к и пишем P(A1, A2, …) или .
Будем рассматривать только такие начальные конфигурации, в которых имеется конечное число элементов, отличных от нуля. Будем писать вместо для таких конфигураций. Ясно, что любого T конфигурация будет содержать конечное число отличных от нуля элементов, если этим свойством обладает конфигурация .
Теперь условимся, что понимать под вычислением функций на МПД. Рассмотрим частичные функции F типа . Пусть — фиксированная программа. Пусть . Будем говорить, что вычисление дает результат B, если и в заключительной конфигурации . Обозначение: . Будем говорить, что программа Р вычисляет функцию F, если для любых выполнимо
.
Назовем функцию F вычислимой (на МПД), если существует программа Р, которая вычисляет F. Класс вычислимых (на МПД) функций обозначим Е.
Заметим, что любая программа Р для любого N ³ 1 на начальных конфигурациях вида определяет N-местную частичную функцию , такую, что для всех
Ясно, что разные программы могут вычислять одну и ту же функцию.
Распространим понятие алгоритмической вычислимости на предикаты, заданные на множестве . Пусть — произвольный такой предикат. Определим характеристическую функцию предиката p соотношением:
Будем называть предикат p разрешимым, если его характеристическая функция вычислима, и не разрешимым в противном случае.
Это понятие соответствует вопросу о наличии алгоритма для проверки свойства, определяемого предикатом.
Теперь распространим понятие вычислимости на функции, отличные от рассматриваемого типа.
Пусть D — некоторое множество, и — функция от N переменных. Зафиксируем эффективное кодирование множества D натуральными числами , т. е. зададим инъективную функцию . Пусть — ее обратная. Тогда для функции можно однозначно определить функцию , где или
,
Для любых .
Будем называть функцию F вычислимой тогда и только тогда, когда функция F* вычислима.
Пример 11.1. Кодирование множества целых чисел Z. Пусть
Таким образом, можно считать определенным понятие вычислимости целочисленных функций. Позднее будут рассмотрены эффективные кодирования и других областей.
Рассмотрим примеры вычислимых функций (на МПД).
А) Функция F(X, Y) = X + Y. Эта функция может быть вычислена следующей программой при начальной конфигурации (X, Y, 0, 0, …). P = I1 I2 I3 I4, где I1 = J(3, 2, 5), I2 = S(1), I3 = S(3), I4 = J(1, 1, 1). Данная программа прибавляет 1 к X до тех пор, пока R3 не станет равным Y.
B) Функция
Эта функция может быть вычислена программой Р = I1 I2 I3 I4 I5 I6, где I1 = J(1, 2, 6), I2 = S(3), I3 = S(2), I4 = S(2), I5 = J(1, 1, 1), I6 = T(3, 1).
Данная программа прибавляет 1 к R3 и 2 к R2 до тех пор, пока R2 не станет равным X, тогда R3 даст результат.
Поскольку доказательства вычислимости конкретных функций связаны с предъявлением конкретных программ, их вычисляющих, то следует ввести некоторые соглашения о составлении и записи программ. Аналогично композиции машин Тьюринга можно ввести композицию программ МПД.
Пусть . Будем говорить, что Р имеет стандартный вид, если для всякой команды условного перехода J(M, N, Q) выполнимо . Две программы Р и назовем эквивалентными, если они определяют одни и те же N-местные функции, т. е. для всех .
Утверждение 11.2. Для всякой программы Р существует эквивалентная ей программа стандартного вида .
Доказательство. Пусть . Тогда определим где для любого
.
Ясно, что удовлетворяет нужным требованиям, что требовалось доказать.
Пусть теперь даны две программы P и Q стандартного вида. Образуем программу (где , ) с учетом нумерации, т. е. команды J(M, N, Q) заменены на J(M, N, S + Q). Тогда результат действия программы PQ совпадает с результатом вычисления по программе P, к которому применена программа Q.
Заметим, что для всякой программы Р существует минимальное натуральное число R(P) такое, что для всех , входящих в команды из Р, т. е. S(N), Z(N), T(M, N), J(M, N, Q) выполнено M, N < R(P). Это число иногда называют Ширина, ранг программы Р.
Смысл числа R(P) состоит в том, что регистры с T > R(P) в ходе вычисления по программе Р не будут менять свое содержание и не будут влиять на содержимое регистров , поэтому их можно использовать для других вычислений.
Заметим также, что можно организовывать вычисление, используя программу Р, в случае, когда входы программы находятся в регистрах , а результат заносится в . Далее для простоты положим, что регистры отличны от .
Пусть Р вычисляет F в стандартном понимании вычислимости. Тогда программа
Будет вычислять и результат запишет в . Данную программу обозначим .
Пример 11.3. Функция F(X, Y) = Xy — вычислимая функция. Пусть Н — программа, вычисляющая функцию X + Y (пример а) ). Тогда вычисляется программой
Программа Р вычисляет Xy по правилу
Как следует из изложенного, язык программ МПД содержит основные процедуры языков программирования и позволяет устраивать композицию (соединение) программ и использовать программы в качестве подпрограмм других программ. Это является основанием для предположения о том, что введенный класс вычислимых функций в точности отвечает классу алгоритмически вычислимых функций. Данное предположение называется Тезисом Черча (для МПД). Так же как и тезис Тьюринга, данный тезис доказать нельзя, однако принятие его позволяет истолковывать утверждения о несуществовании МПД для решения конкретных задач как утверждения о несуществовании алгоритмов вообще.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
summation — Нахождение числа $ M $, что $ S_N
Given that
$u_n=\frac{1}{n^2-n+1}- \frac{1}{n^2+n+1}$
$S_n=\sum_{n=N+1}^{2N}u_n$
Find a number $M$ such that $S_N<10^{-20}$ for all $N>M$
I did:
$S_N = \sum_{n=N+1}^{2N}u_n = \sum_{n=0}^{2N}u_n — \sum_{n=0}^{N}u_n$
Using method of difference and by further simplification I get :
$S_N= 1 — \frac{1}{(2N)^2+2N+1}- 1 + \frac{1}{N^2+N+1}$
$S_N= \frac{1}{N^2+N+1}- \frac{1}{4N^2+2N+1}$
Then:
$S_N < \frac{1}{10^{20}}$
I did an assumption that:
$frac{1}{10^{20}}\approx 0$
Because without the assumption I end up with : $4N^4+7N^3+7N^2+3N+1 > 10^{20}(3N^2+N)$ which is like way too hard
I think it’s pretty good approximation for such a question
Therefore :
$frac{1}{N^2+N+1}< \frac{1}{4N^2+2N+1}$
$4N^2+2N+1 < N^2+ N+1$
$3N^2+N<0$
$frac{-1}{3}< N < 0$
So :
$M=\frac{-1}{3}$
$frac{3N^2+N}{(N^2+N+1)(4N^2+2N+1)}< \frac{1}{10^{20}}.$
This is wrong. The correct answer is very large, it’s:
$M=10^{10}.$
I have no idea how this number came, please help.
Учитывая, что
$u_n = \гидроразрыва{1}{п^2- п + 1}- \гидроразрыва{1}{п^2 + п + 1}$
$S_n = \sum_{n = N + 1}^{2N}u_n$
Найти число $M$ , что $S_N < 10^{- 20}$ для всех $N > M$
я сделал:
$S_N = \sum_{n = N + 1}^{2N}u_n = \sum_{n = 0}^{2N}u_n — \sum_{n = 0}^{ N}$ u_n
Используя метод разницы и путем дальнейшего упрощения я получаю:
$S_N = 1 — \гидроразрыва{1}{(2N)^2 + 2n + 1}- 1 + \frac{1}{N^2 + N + 1}$
$S_N = \frac{1}{N^2 + N + 1}- \frac{1}{4N^2 + 2N + 1}$
После этого:
$S_N < \гидроразрыва{1}{10^{20}}$
я сделал предположение, что:
$\гидроразрыва{1}{10^{20}}\ок 0$
Потому что без предположения я в конечном итоге с: $4N^4 + 7N^3 + 7N^2 + 3n + 1 > 10^{20}(3N^2 + N)$ , который является подобный путь слишком жесткий
Я думаю, что это довольно хорошее приближение для такого вопроса
Поэтому:
$\гидроразрыва{1}{N^2 + N + 1}< \гидроразрыва{1}{4N^2 + 2n + 1}$
$4N^2 + 2n + 1 < N^2 + N + 1$
$3N^2 + N < 0$
$\гидроразрыва{-1}{3}< < N 0$ Долл. США
So:
$M = \frac{-1}{3}$
$frac{3N^2 + N}{(N^2 + N + 1) (4N^2 + 2N + 1)}< \frac{1}{10^{20}}.$
Это неправильно. Правильный ответ очень большой, это:.
$M = 10^{10}$
Я понятия не имею, как пришел этот номер, пожалуйста, помогите.
math.stackovernet.com
Предел последовательности — теоремы и свойства
Последовательности
Числовой последовательностью называется закон (правило), согласно которому, каждому натуральному числу ставится в соответствие число .
Число называют n-м членом или элементом последовательности.
Далее мы будем считать, что элементами последовательности являются действительные числа.
Более подробно см. страницу Определение числовой последовательности >>>.
Последовательность называется ограниченной, если существует такое число M, что для всех действительных n.
Верхней гранью последовательности называют наименьшее из чисел, ограничивающее последовательность сверху. То есть это такое число s, для которого для всех n и для любого , найдется такой элемент последовательности , превосходящий s′: .
Нижней гранью последовательности называют наибольшее из чисел, ограничивающее последовательность снизу. То есть это такое число i, для которого для всех n и для любого , найдется такой элемент последовательности , меньший i′: .
Верхнюю грань также называют точной верхней границей, а нижнюю грань – точной нижней границей. Понятия верхней и нижней граней справедливы не только к последовательностям, но и к любым множествам действительных чисел.
Определение предела последовательности
Число a называется пределом последовательности , если для любого положительного числа существует такое натуральное число N, зависящее от , что для всех натуральных выполняется неравенство
.
Предел последовательности обозначается так:
.
Или при .
С помощью логических символов существования и всеобщности определение предела можно записать следующим образом:
.
Открытый интервал (a – ε, a + ε) называют ε — окрестностью точки a.
Последовательность, у которой существует предел называется сходящейся последовательностью. Также говорят, что последовательность сходится к a. Последовательность, не имеющая предела, называется расходящейся.
Точка a не является пределом последовательности , если существует такое , что для любого натурального n существует такое натуральное m > n, что
.
.
Это означает, что можно выбрать такую ε — окрестностью точки a, за пределами которой будет находиться бесконечное число элементов последовательности.
Более подробно материал изложен на странице
Определение предела последовательности >>>.
Свойства конечных пределов последовательностей
Основные свойства
Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.
Если число a не является пределом последовательности , то существует такая окрестность точки a, за пределами которой находится бесконечное число элементов последовательности.
Теорема единственности предела числовой последовательности. Если последовательность имеет предел, то он единственный.
Если последовательность имеет конечный предел, то она ограничена.
Если каждый элемент последовательности равен одному и тому же числу C: , то эта последовательность имеет предел, равный числу C.
Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.
Доказательства основных свойств приведены на странице
Основные свойства конечных пределов последовательностей >>>.
Арифметические действия с пределами
Пусть существуют конечные пределы и последовательностей и . И пусть C – постоянная, то есть заданное число. Тогда
;
;
;
, если .
В случае частного предполагается, что для всех n.
Если , то .
Доказательства арифметических свойств приведены на странице
Арифметические свойства конечных пределов последовательностей >>>.
Свойства, связанные с неравенствами
Если и элементы последовательности, начиная с некоторого номера, удовлетворяют неравенству , то и предел a этой последовательности удовлетворяет неравенству .
Если и элементы последовательности, начиная с некоторого номера, принадлежат замкнутому интервалу (сегменту) , то и предел a также принадлежит этому интервалу: .
Если и и элементы последовательностей, начиная с некоторого номера, удовлетворяют неравенству , то .
Если и, начиная с некоторого номера, , то .
В частности, если, начиная с некоторого номера, , то
если , то ;
если , то .
Если и , то .
Пусть и . Если a < b, то найдется такое натуральное число N, что для всех n > N выполняется неравенство .
Доказательства свойств, связанных с неравенствами приведены на странице
Свойства пределов последовательностей, связанные с неравенствами >>>.
Бесконечно большая и бесконечно малая последовательности
Бесконечно малая последовательность
Последовательность называется бесконечно малой последовательностью, если ее предел равен нулю:
.
Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.
Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Для того, чтобы последовательность имела предел a, необходимо и достаточно, чтобы , где – бесконечно малая последовательность.
Доказательства свойств бесконечно малых последовательностей приведены на странице
Бесконечно малые последовательности – определение и свойства >>>.
Бесконечно большая последовательность
Последовательность называется бесконечно большой последовательностью, если для любого положительного числа существует такое натуральное число N, зависящее от , что для всех натуральных выполняется неравенство
.
В этом случае пишут
.
Или при .
Говорят, что стремится к бесконечности.
Если , начиная с некоторого номера N, то
.
Если же , то
.
Если последовательность являются бесконечно большой, то, начиная с некоторого номера N, определена последовательность , которая является бесконечно малой. Если являются бесконечно малой последовательностью с отличными от нуля элементами, то последовательность является бесконечно большой.
Если последовательность бесконечно большая, а последовательность ограничена, то
.
Если абсолютные значения элементов последовательности ограничены снизу положительным числом ( ), а – бесконечно малая с неравными нулю элементами, то
.
Более подробно определение бесконечно большой последовательности с примерами приводится на странице
Определение бесконечно большой последовательности >>>.
Доказательства свойств бесконечно больших последовательностей приведены на странице
Свойства бесконечно больших последовательностей >>>.
Критерии сходимости последовательностей
Монотонные последовательности
Последовательность называется строго возрастающей, если для всех n выполняется неравенство:
.
Соответственно, для строго убывающей последовательности выполняется неравенство:
.
Для неубывающей:
.
Для невозрастающей:
.
Отсюда следует, что строго возрастающая последовательность также является неубывающей. Строго убывающая последовательность также является невозрастающей.
Последовательность называется монотонной, если она неубывающая или невозрастающая.
Монотонная последовательность ограничена, по крайней мере, с одной стороны значением . Неубывающая последовательность ограничена снизу: . Невозрастающая последовательность ограничена сверху: .
Теорема Вейерштрасса. Для того чтобы неубывающая (невозрастающая) последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной сверху (снизу ). Здесь M – некоторое число.
Поскольку любая неубывающая (невозрастающая) последовательность ограничена снизу (сверху), то теорему Вейерштрасса можно перефразировать следующим образом:
Для того чтобы монотонная последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной: .
Монотонная неограниченная последовательность имеет бесконечный предел, равный для неубывающей и для невозрастающей последовательности.
Доказательство теоремы Вейерштрасса приведено на странице
Теорема Вейерштрасса о пределе монотонной последовательности >>>.
Критерий Коши сходимости последовательности
Условие Коши. Последовательность удовлетворяет условию Коши, если для любого существует такое натуральное число , что для всех натуральных чисел n и m, удовлетворяющих условию , выполняется неравенство
.
Последовательности, удовлетворяющие условию Коши, также называют фундаментальными последовательностями.
Критерий Коши сходимости последовательности. Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
Доказательство критерия сходимости Коши приведено на странице
Критерий Коши сходимости последовательности >>>.
Подпоследовательности
Теорема Больцано – Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность. А из любой неограниченной последовательности – бесконечно большую подпоследовательность, сходящуюся к или к .
Доказательство теоремы Больцано – Вейерштрасса приведено на странице
Теорема Больцано – Вейерштрасса >>>.
Определения, теоремы и свойства подпоследовательностей и частичных пределов рассмотрены на странице
Подпоследовательности и частичные пределы последовательностей>>>.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
В.А. Зорич. Математический анализ. Часть 1. Москва, 1997.
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Москва, 2005.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Формулы для расчета системы типа «m из n» при m n 5
Общее число элементов, n | |||||
m | 1 | 2 | 3 | 4 | 5 |
1 | | | |||
2 | – | | | ||
3 | – | – | | | |
4 | – | – | – | | |
5 | – | – | – | – | |
5.5.2. Мостиковые схемы
Мостиковой структуройназывается параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей (рис. 5.8, а, б). Работоспособность такой системы зависит не только от количества отказавших элементов, но и от их положения в структурной схеме. При одновременном отказе элементов 1 и 4, или 2 и 5, или 2, 3 и 4 и т. д. схема (рис. 5.8) окажется неработоспособной. Но отказ элементов 1 и 5, или 2 и 4, или 1, 3 и 4, или 2, 3 и 5 к отказу системы не приводит.
а) б)
Рис. 5.8. Мостиковые схемы
Д
3
ля расчёта надёжности мостиковых систем можно воспользоватьсяметодом прямого перебора, как для систем «m из n» (п. 5.5.1), но при анализе работоспособности каждого состояния системы необходимо учитывать не только число отказавших элементов, но и их положение в схеме (табл. 5.3). Вероятность безотказной работы системы определяется как сумма вероятностей всех работоспособных состояний: 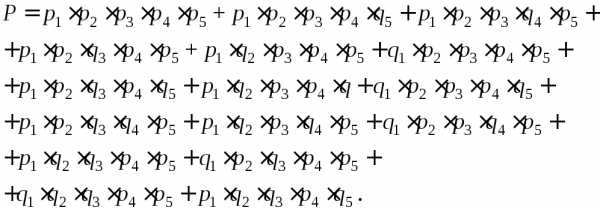 (5.21)
(5.21)
Для элементов с равной надёжностью
(5.22)
Метод прямого перебора
эффективен только при малом количестве
элементов n,
поскольку число состояний системы
составляет 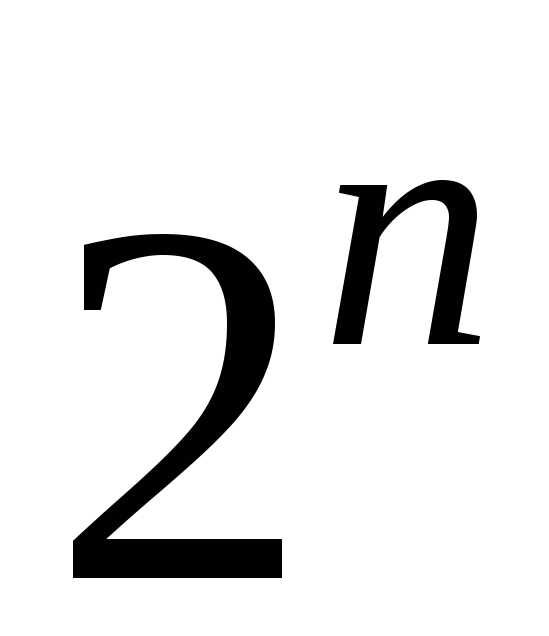 .
Например, для схемы на рис. 5.8, б их
количество составит уже
.
Например, для схемы на рис. 5.8, б их
количество составит уже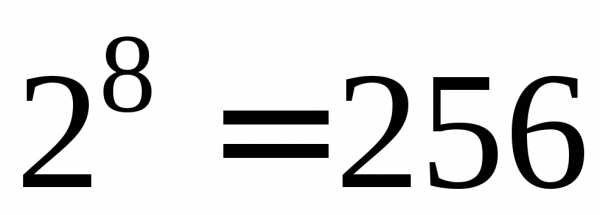 .
Если рассматривать только сочетания,
отвечающие работоспособному (или
неработоспособному) состоянию системы
в целом, то это упростит расчёт.
.
Если рассматривать только сочетания,
отвечающие работоспособному (или
неработоспособному) состоянию системы
в целом, то это упростит расчёт.
При расчете мостиковых систем используется также метод логических схем с применением алгебры логики (булевой алгебры). Суть этого метода в составлении для ТС формулы алгебры логики, определяющей условие работоспособности системы. для каждого элемента и системы в целом рассматриваются два противоположных события – отказ и сохранение работоспособности.
Таблица 5.4
Таблица состояний мостиковой системы
№ сост. | Состояние элементов | Состояние системы | Вероятность состояния | |||||
1 | 2 | 3 | 4 | 5 | в общем случае | при равнонадежных элементах | ||
1 | + | + | + | + | + | + | | |
2 | + | + | + | + | – | + | ||
3 | + | + | + | – | + | + | ||
4 | + | + | – | + | + | + | ||
5 | + | – | + | + | + | + | ||
6 | – | + | + | + | + | + | ||
Окончание табл. 5.4
№ сост. | Состояние элементов | Состояние системы | Вероятность состояния | |||||
1 | 2 | 3 | 4 | 5 | в общем случае | при равнонадежных элементах | ||
7 | + | + | + | – | – | – | ||
8 | + | + | – | + | – | + | ||
9 | + | – | + | + | – | + | ||
10 | – | + | + | + | – | + | ||
11 | + | + | – | – | + | + | ||
12 | + | – | + | – | + | + | ||
13 | – | + | + | – | + | + | ||
14 | + | – | – | + | + | + | ||
15 | – | + | – | + | + | + | ||
16 | – | – | + | + | + | – | ||
17 | + | + | – | – | – | – | ||
18 | + | – | + | – | – | – | ||
19 | – | + | + | – | – | – | ||
20 | + | – | – | – | + | – | ||
21 | – | + | – | – | + | + | ||
22 | – | – | – | + | + | – | ||
23 | + | – | – | + | – | + | ||
24 | – | + | – | + | – | – | ||
25 | – | – | + | – | + | – | ||
26 | – | – | + | + | – | – | ||
27 | + | – | – | – | – | – | ||
28 | – | + | – | – | – | – | ||
29 | – | – | + | – | – | – | ||
30 | – | – | – | + | – | – | ||
31 | – | – | – | – | + | – | ||
32 | – | – | – | – | – | – | ||
Для составления логической схемы можно воспользоваться методами минимальных путей и минимальных сечений.
Метод минимальных путей дает точное значение только для сравнительно простых систем с небольшим числом элементов. Для более сложных систем результат расчета является нижней границей вероятности безотказной работы.
Метод минимальных сеченийприменяется для расчёта верхней границы вероятности безотказной работы системы.
Метод минимальных путей для расчета вероятности безотказной работы рассматривается на примере простейшей мостиковой схемы (рис. 5.8, а).
Минимальным путемназывается последовательный набор работоспособных элементов системы, который обеспечивает её работоспособность, а отказ любого из них приводит к ее отказу.
Минимальных путей в системе может быть несколько или один. система с последовательным соединением элементов (рис. 5.1) имеет только один минимальный путь, включающий все элементы. В системе с параллельным соединением (рис. 5.2) число минимальных путей совпадает с числом элементов и каждый путь включает один из них.
Для мостиковой системы из пяти элементов (рис. 5.8, а) минимальных путей четыре: (элементы 1 и 4), (2 и 5), (1, 3 и 5), (2, 3 и 5). Логическая схема такой системы (рис. 5.9) составляется таким образом, чтобы все элементы каждого минимального пути были соединены друг с другом последовательно, а все минимальные пути – параллельно.
Рис. 5.9. Логическая схема Рис. 5.10. Логическая схема
мостиковой системы по методу мостиковой системы по методу
минимальных путей минимальных сечений
Затем для логической схемы составляется функция алгебры логики по общим правилам расчета вероятности безотказной работы, но вместо символов вероятностей безотказной работы элементов Рi и системы Р используются символы события (сохранения работоспособности элемента ai и системы А). Так, «отказ» логической схемы рис. 5.9 состоит в одновременном отказе всех четырех параллельных ветвей, а «безотказная работа» каждой ветви – в одновременной безотказной работе ее элементов. Последовательное соединение элементов логической схемы соответствует логическому умножению («И»), параллельное – логическому сложению («ИЛИ»). Следовательно, схема на рис. 5.9 соответствует утверждению: система работоспособна, если работоспособны элементы 1 и 4, или 2 и 5, или 1, 3 и 5, или 2, 3 и 4. Функция алгебры логики запишется:
(5.23)
В выражении (5.23) переменные а рассматриваются как
булевы, т. е. могут принимать только два
значения: 0 или 1. Тогда при возведении
в любую степень k любая переменная a сохраняет свое значение: 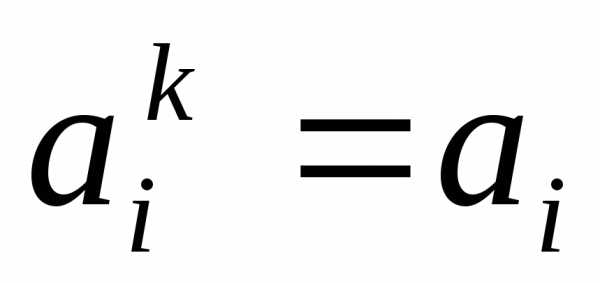 .На основе этого
свойства формула, описыващая функцию
алгебры логики (5.23), может быть преобразована
к виду
.На основе этого
свойства формула, описыващая функцию
алгебры логики (5.23), может быть преобразована
к виду
(5.24)
Заменив в выражении (5.24)
символы событий  их вероятностями
их вероятностями  ,
получим уравнение для определения
вероятности безотказной работы системы
,
получим уравнение для определения
вероятности безотказной работы системы
(5.25)
Для системы равнонадёжных
элементов (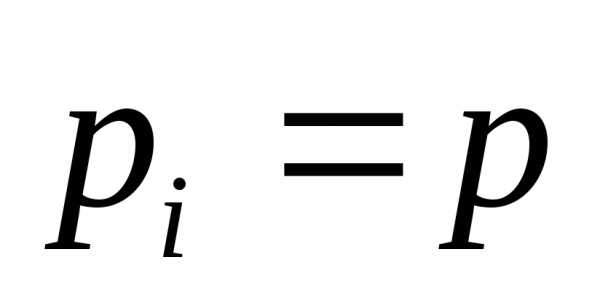 )
выражение (5.25) легко
преобразуется в формулу (5.22).
)
выражение (5.25) легко
преобразуется в формулу (5.22).
Минимальным сечением называется набор неработоспособных элементов, отказ которых приводит к отказу системы, а восстановление работоспособности любого из них – к восстановлению работоспособности системы. Как минимальных путей, так и минимальных сечений может быть несколько. Очевидно, система с параллельным соединением элементов имеет только одно минимальное сечение, включающее все её элементы (восстановление любого восстановит работоспособность системы). В системе с последовательным соединением элементов число минимальных путей совпадает с числом элементов и каждое сечение включает один из них.
В мостиковой системе (рис. 5.8, а) минимальных сечений четыре (элементы 1 и 2), (4 и 5), (1, 3 и 5), (2, 3 и 4). Логическая схема системы (рис. 5.9) составляется таким образом, чтобы все элементы каждого минимального сечения были соединены друг с другом параллельно, а все минимальные сечения – последовательно. Аналогично методу минимальных путей составляется функция алгебры логики.
Безотказная работа логической системы (рис. 5.10) заключается в безотказной работе всех последовательных участков, а отказ каждого из них – в одновременном отказе всех параллельно включенных элементов. Так как схема метода минимальных сечений формулирует условия отказа системы, в ней последовательное соединение соответствует логическому «ИЛИ», а параллельное – логическому «И». Схема рис. 5.10 соответствует формулировке: система откажет, если откажут элементы 1 и 2, или 4 и 5, или 1, 3 и 5, или 2, 3 и 4. Функция алгебры логики запишется
(5.26)
После преобразований с использованием свойств булевых переменных выражение (5.26) приобретает форму (5.24), а после замены событий их вероятностями переходит в выражение (5.25).
Таким образом, для мостиковой системы из пяти элементов верхняя и нижняя границы вероятности безотказной работы, полученные методами минимальных сечений и минимальных путей, совпали с точными значениями (5.22), полученными методом прямого перебора. Для сложных систем это может не произойти, поэтому методы минимальных путей и минимальных сечений следует применять совместно.
При анализе надежности ТС можно воспользоваться методом разложения относительно особого элемента, основанным на известной в математической логике теореме о разложении функции логики по любому аргументу.
Согласно этой теореме, можно записать:
(5.27)
где 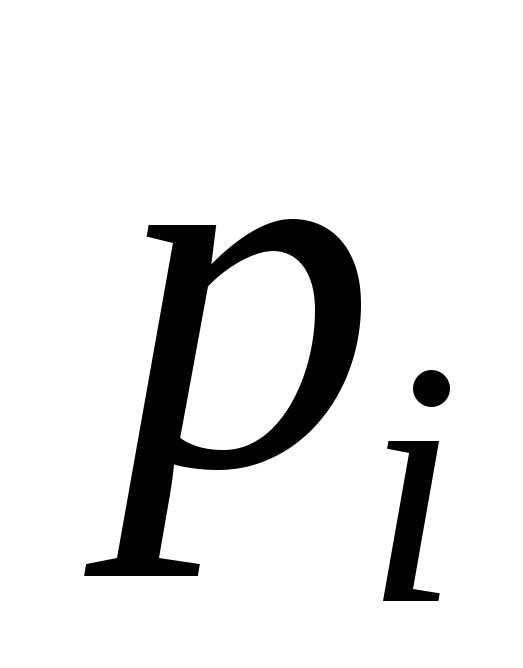 и– вероятности безотказной работы и
отказаi-го
элемента;
и– вероятности безотказной работы и
отказаi-го
элемента; 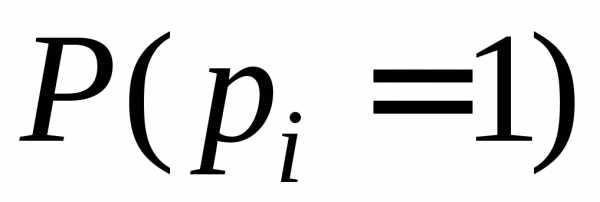 и– вероятности работоспособного состояния
системы при условии, чтоi-й
элемент абсолютно надежен и что i-й
элемент отказал.
и– вероятности работоспособного состояния
системы при условии, чтоi-й
элемент абсолютно надежен и что i-й
элемент отказал.
Для мостиковой схемы (рис.
5.8, а) в качестве особого целесообразно
выбрать диагональный элемент 3. При 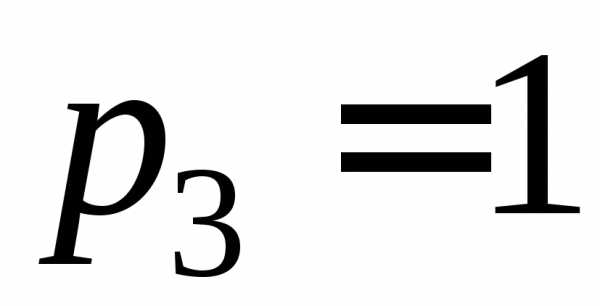 мостиковая схема превращается в
параллельно-последовательное соединение
(рис. 5.11, а), а при
мостиковая схема превращается в
параллельно-последовательное соединение
(рис. 5.11, а), а при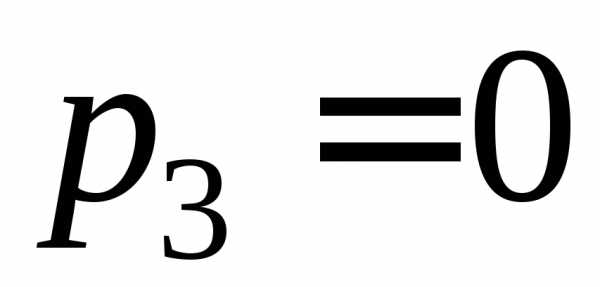 – в последовательно-параллельное (рис.
5.11, б).
– в последовательно-параллельное (рис.
5.11, б).
а)
б)
Рис. 5.11. Преобразование мостиковой схемы при абсолютно надежном (а) и отказавшем (б) центральном элементе
Для преобразованных схем можно записать:
, (5.28)
. (5.29)
Тогда на основании формулы (5.27) получается:
(5.30)
Легко убедиться, что для равнонадёжных элементов формула (5.30) обращается в формулу (5.22).
Этим методом можно воспользоваться и при разложении относительно нескольких «особых» элементов. Например, для двух элементов (i, j) выражение (5.27) примет вид:
(5.31)
Для мостиковой схемы (рис. 5.8, б) вероятность безотказной работы при разложении относительно диагональных элементов 3 и 6 определяется выражением (5.31):
(5.32)
Выражения для определения
вероятности 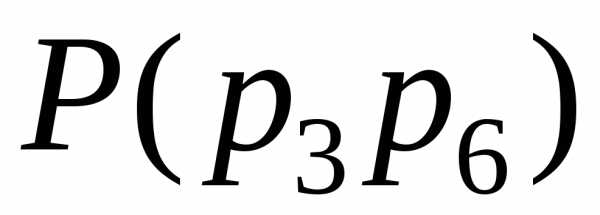 можно составить, выполнив предварительно
преобразованные схемы (например, рис.
5.11, а, б).
можно составить, выполнив предварительно
преобразованные схемы (например, рис.
5.11, а, б).
studfiles.net
В этой главе мы узнаем о лямбда-исчислении. Лямбда-исчисление описывает понятие алгоритма. Ещё до появления компьютеров в 30-е годы двадцатого века математиков интересовал вопрос о возможности создания алгоритма, который мог бы на основе заданных аксиом дать ответ о том верно или нет некоторое логическое высказывание. Например у нас есть базовые утверждения и логические связки такие как “и”, “или”, “для любого из”, “существует один из”, с помощью которых мы можем строить из базовых высказываний составные. Некоторые из них окажутся ложными, а другие истинными. Нам интересно узнать какие. Но для решения этой задачи прежде всего необходимо было понять а что же такое алгоритм?
Ответ на этот вопрос дали Алонсо Чёрч (Alonso Church) и Алан Тьюринг (Alan Turing). Чёрч разработал лямбда-исчисление, а Тьюринг теорию машин Тьюринга. Оказалось, что задача автоматического определения истинности формул в общем случае не имеет решения.
В основе лямбда-исчисление лежит понятие функции. Мы можем составлять сложные функции из простейших, а также подставлять в функции аргументы, которые могут быть как константами так и другими функциями. Как только мы составили выражение мы можем передать его вычислителю. Он подставляет аргументы в функции и возвращает такое выражение, в котором невозможно далее проводить подстановки аргументов. Этот процесс проведения подстановок считается вычислением алгоритма.
В рамках теории машин Тьюринга алгоритм описывается по-другому. Машина Тьюринга имеет внутреннее состояние, Состояние содержит некоторое значение, которое изменяется по ходу работы машины. Машина живёт не сама по себе, она читает ленту символов. Лента символов – это большая цепочка букв. На каждую букву машина реагирует серией действий. Она может изменить значение состояния, обновить букву в ленте или перейти к следующему или предыдущему символу. Есть состояния, которые обозначают конец работы, они называются терминальными. Как только машина дойдёт до терминального состояния мы считаем, что вычисление алгоритма закончилось. После этого мы можем считать результат из состояний машины.
Функциональные языки программирования основаны на лямбда-исчислении. Поэтому мы будем говорить именно об этом описании алгоритма.
Составление термов
Можно считать, что лямбда исчисление это такой маленький язык п
anton-k.github.io