Разность логарифмов | Логарифмы
Разность логарифмов с одинаковыми основаниями равна логарифму частного от деления выражения, стоящего под знаком логарифма уменьшаемого, на выражение под знаком логарифма вычитаемого.
Формула перехода от разности логарифмов к логарифму частного:
(x>0, y>0).
Это свойство в некоторых случаях позволяет найти разность логарифмов, даже если точные значения логарифмов уменьшаемого и вычитаемого по отдельности вычислить невозможно.
Примеры.
Это свойство верно, в том числе, и для десятичных и натуральных логарифмов.
Разность десятичных логарифмов равна десятичному логарифму частного от деления выражений, стоящих под знаками логарифмов уменьшаемого и вычитаемого:
Примеры.
Разность натуральных логарифмов равна натуральному логарифму частного от деления выражений, стоящих под знаками логарифмов уменьшаемого и вычитаемого:
Переход от разности логарифмов к логарифму частного верен и для большего количества слагаемых:
Например,
Переход от разности логарифмов к логарифму частного используется не только в вычислениях, но и для упрощения выражений, в ходе решения логарифмических уравнений, неравенств и их систем.
www.logarifmy.ru
Сумма логарифмов | Логарифмы
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения выражений, стоящих под знаками логарифмов слагаемых:
(x>0, y>0).
С помощью этого свойства в некоторых случаях можно найти, чему равна сумма логарифмов, даже если логарифм каждого слагаемого не является рациональным числом.
Например,
Это свойство верно, в частности, и для десятичных и натуральных логарифмов.
Сумма десятичных логарифмов равна десятичному логарифму произведения выражений, стоящих под знаками логарифмов слагаемых:
Например,
Сумма натуральных логарифмов равна натуральному логарифму произведения выражений, которые стоят под знаками логарифмов в слагаемых:
Переход от суммы логарифмов к логарифму произведения верен и в случае когда количество слагаемых больше двух:
Например,
Это свойство логарифмов широко используется при упрощении выражений, в ходе решения логарифмических уравнений и неравенств.
www.logarifmy.ru
2. Логарифмы и их свойства
,
при условии, что 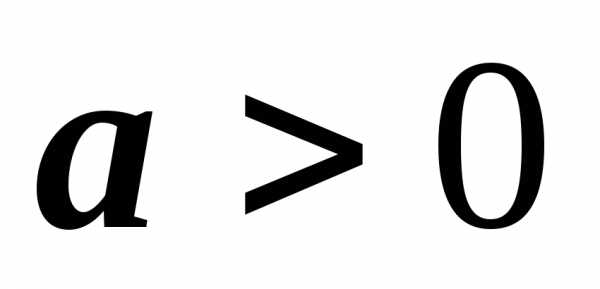 ,
,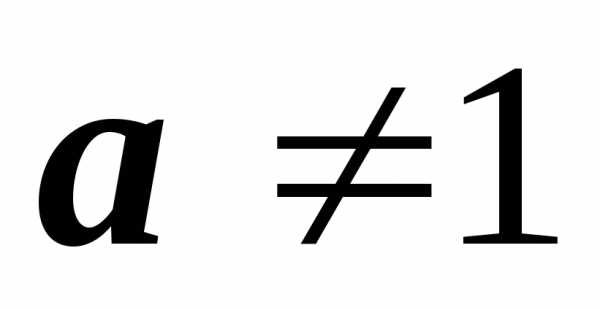 ,
,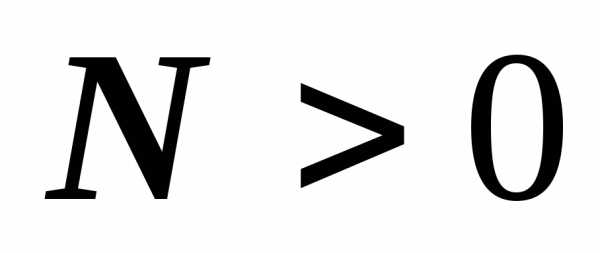

Из определения логарифма
следует, что 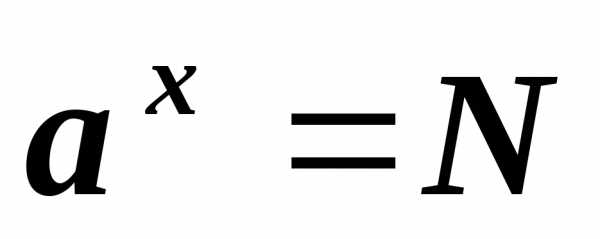 ,
т.е. — это равенство является основным
логарифмическим тождеством.
,
т.е. — это равенство является основным
логарифмическим тождеством.
Логарифмы по основанию 10
называются десятичными логарифмами.
Вместо 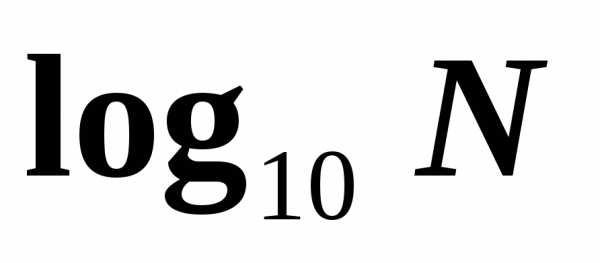 пишут
пишут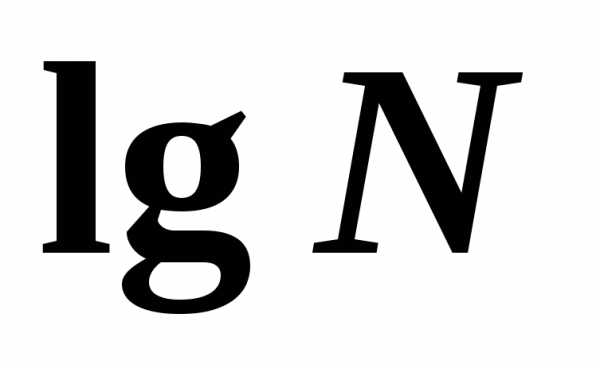 .
.
Логарифмы по основанию e называются натуральными и обозначаются.
Основные свойства логарифмов.
Логарифм единицы при любом основании равен нулю
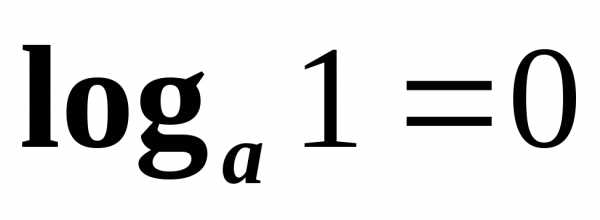
Логарифм произведения равен сумме логарифмов сомножителей.
3) Логарифм частного равен разности логарифмов
Логарифм степени равен логарифму модуля основания, умноженному на показатель степени.
Логарифм корня равен логарифму модуля подкоренного выражения, деленному на множитель корня.
Зависимость между логарифмами с различными основаниями определяется формулой.
Множитель 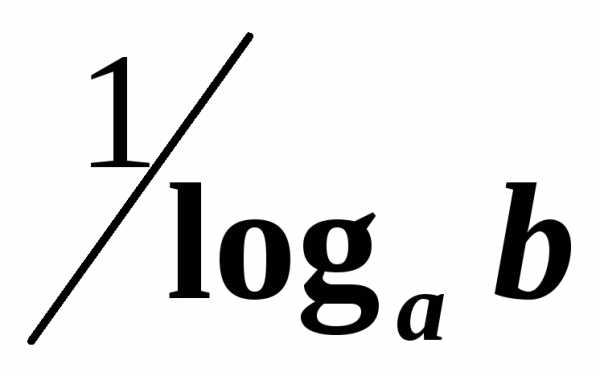
С помощью свойств 2-5 часто удается свести логарифм сложного выражения к результату простых арифметических действий над логарифмами.
Например,
Такие преобразования логарифма называются логарифмированием. Преобразования обратные логарифмированию называются потенцированием.
Глава 2. Элементы высшей математики.
1. Пределы
Пределом функции является конечное число А, если при
стремлении xx0для каждого наперед заданного 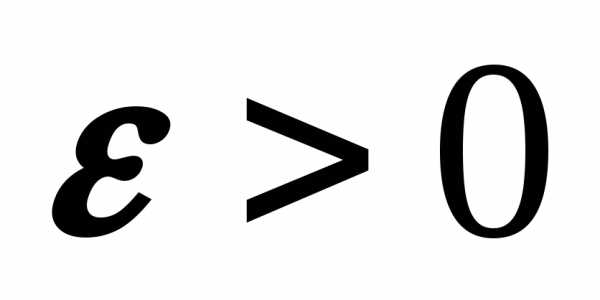 ,
найдется такое число
,
найдется такое число  ,
что как только
,
что как только 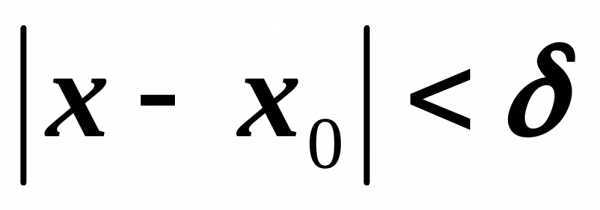 ,
то
,
то 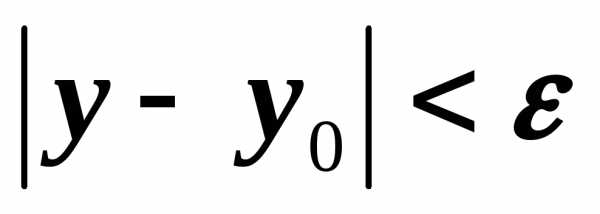 .
.
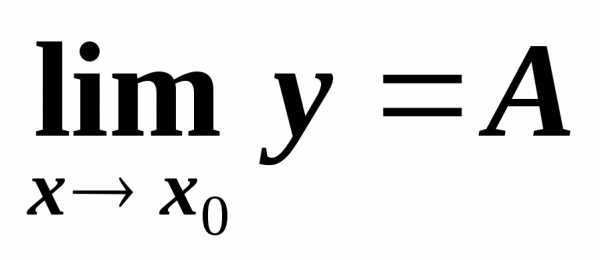
Функция, имеющая предел, отличается от него на бесконечно малую величину: , где- б.м.в., т.е..
Пример. Рассмотрим функцию 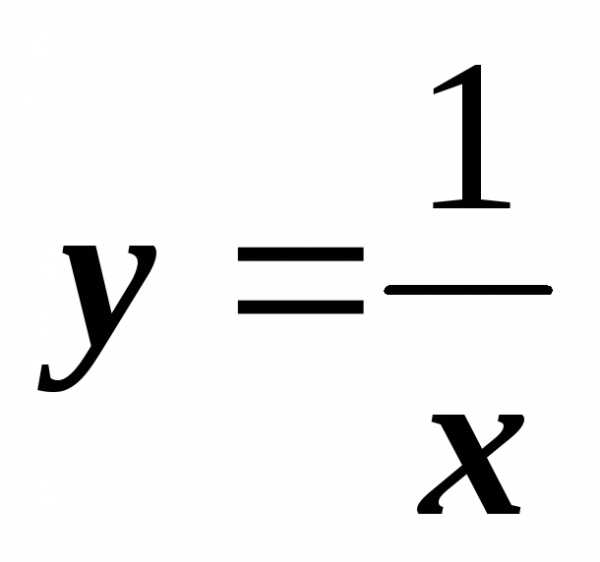 .
.
При стремлении
,
функцияy стремится к нулю: 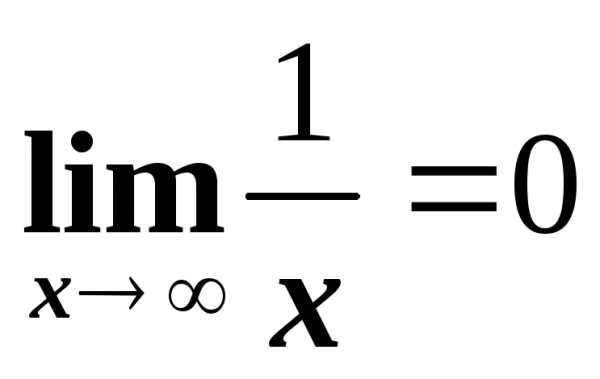
1.1. Основные теоремы о пределах.
Предел постоянной величины равен этой постоянной величине
.
Предел суммы (разности) конечного числа функций равен сумме (разности) пределов этих функций.
.
Предел произведения конечного числа функций равен произведению пределов этих функций.
Предел частного двух функций равен частному пределов этих функций, если предел знаменателя не равен нулю.
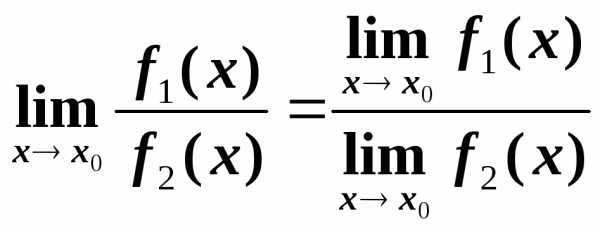
Замечательные пределы
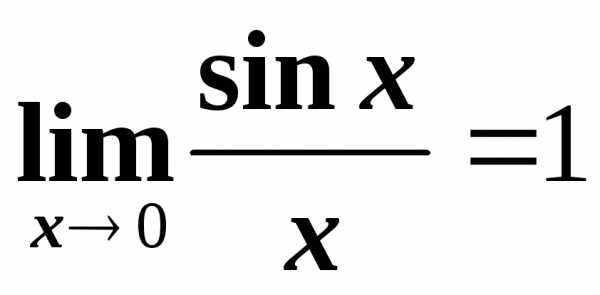 ,
, 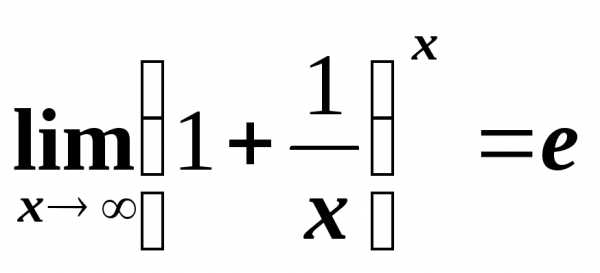 ,
где
,
где
1.2. Примеры вычисления пределов
Пример 1
Однако, не все пределы вычисляются так
просто. Чаще вычисление предела сводится
к раскрытию неопределенности типа:  или
или 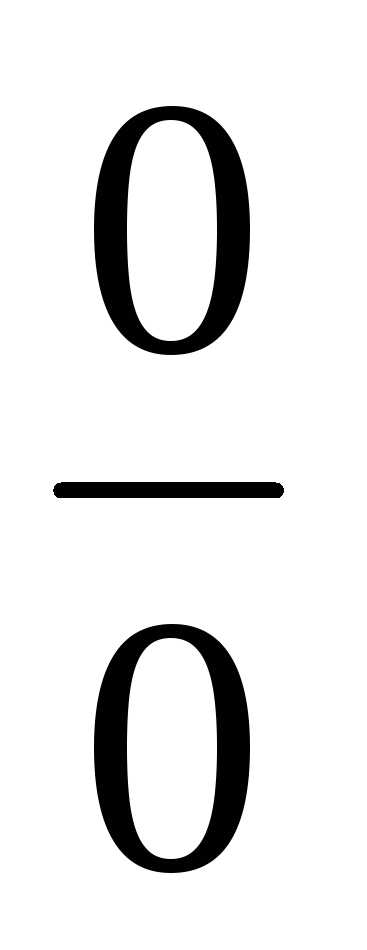 .
.
Пример 2
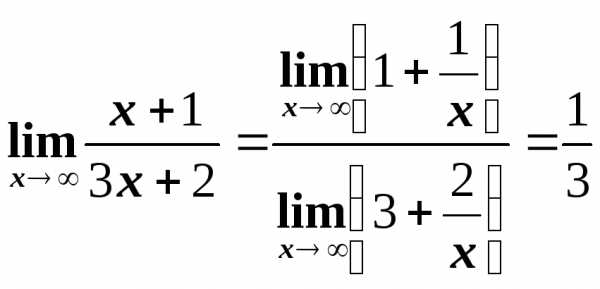 .
.
Пример 3
.
2. Производная функции
Пусть мы имеем функцию
,
непрерывную на отрезке 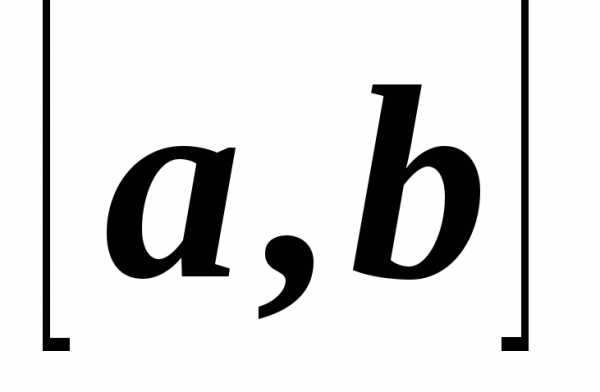
Аргумент  получил некоторое приращение
получил некоторое приращение 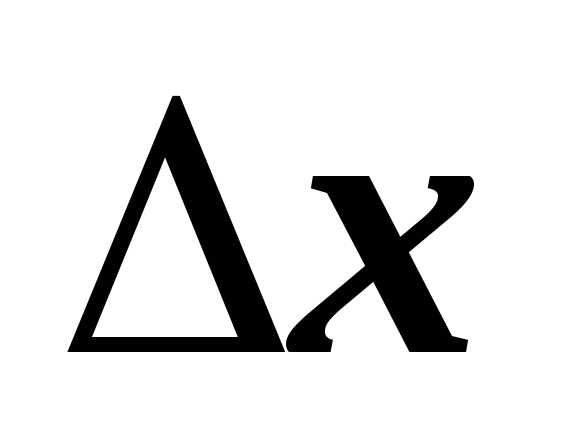 .
Тогда и функция получит приращение
.
Тогда и функция получит приращение  .
.
Значению аргумента  соответствует значение функции
.
соответствует значение функции
.
Значению аргумента 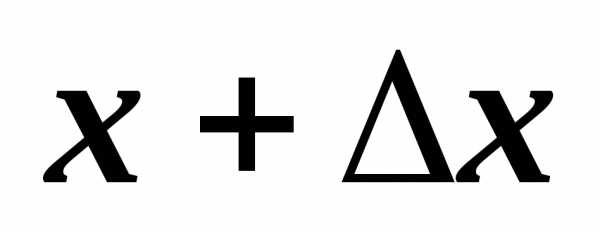 соответствует значение функции
.
соответствует значение функции
.
Следовательно, .
Найдем предел этого отношения при 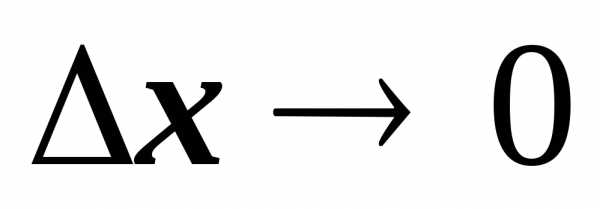 .
Если этот предел существует, то он
называется производной данной функции.
.
Если этот предел существует, то он
называется производной данной функции.


Определение 3Производной данной функции  по
аргументу
по
аргументу  называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента произвольным
образом стремится к нулю.
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента произвольным
образом стремится к нулю.
Производная функцииможет быть обозначена следующим образом:
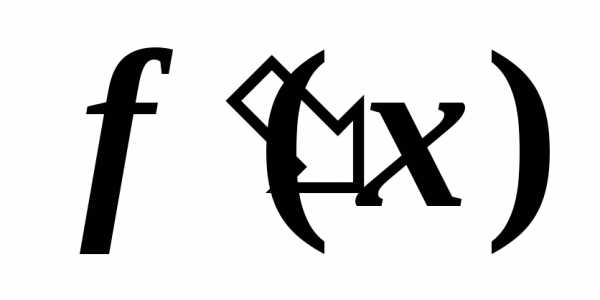 ;
;  ;
; 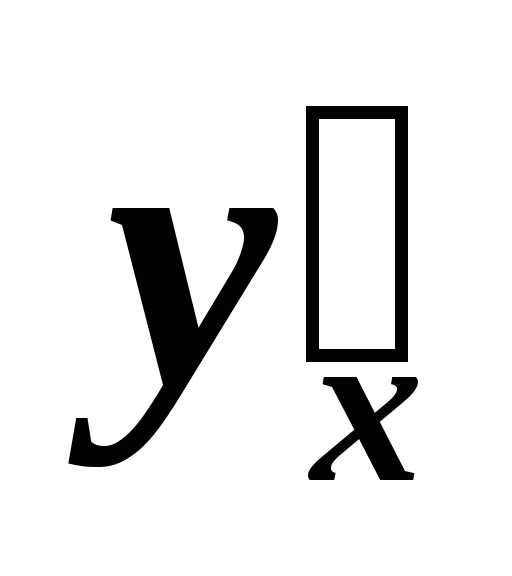 ;
; 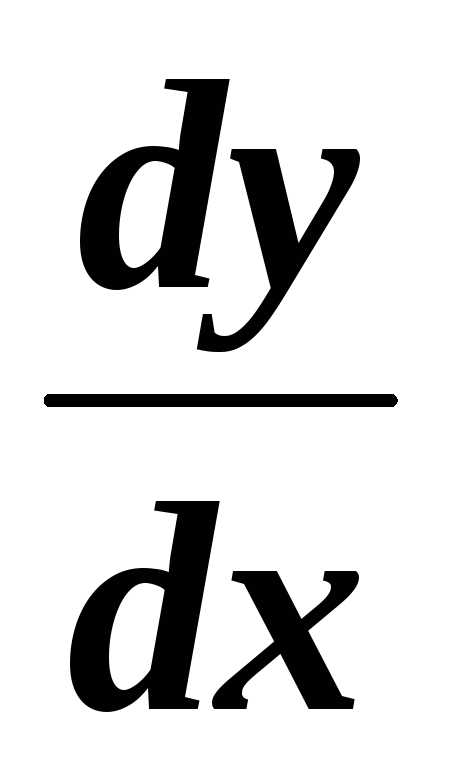 .
.
Определение 4Операция нахождения производной от функции называетсядифференцированием.
2.1. Механический смысл производной.
Рассмотрим прямолинейное движение некоторого твердого тела или материальной точки.
Пусть в некоторый момент времени 
 движущаяся
точка
движущаяся
точка 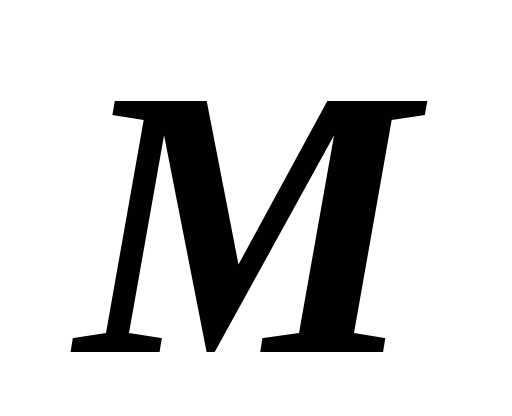 находилась на расстоянии
находилась на расстоянии  от начального положения
от начального положения 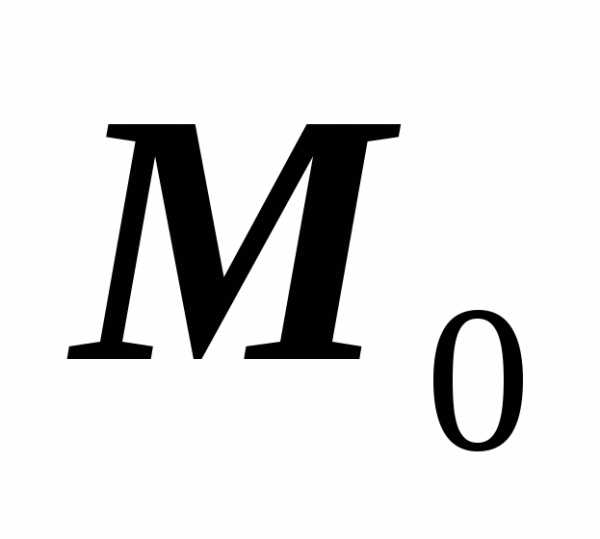 .
. 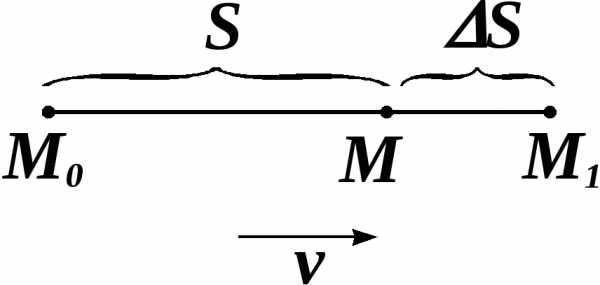
Через некоторый
промежуток времени  она переместилась на расстояние
она переместилась на расстояние  .
Отношение
.
Отношение 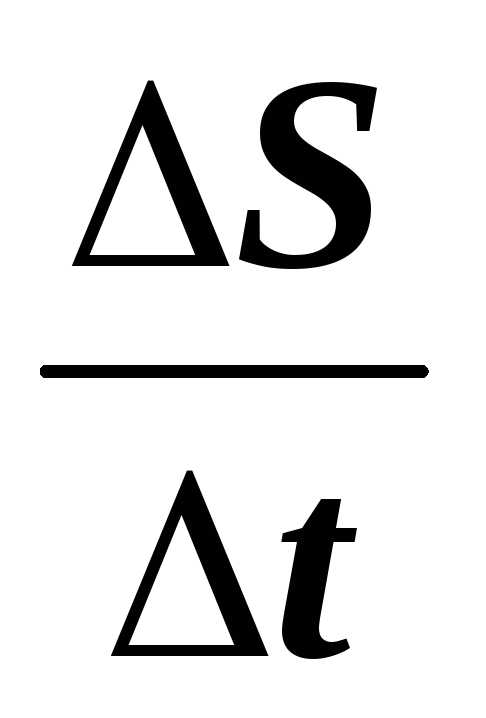 =
=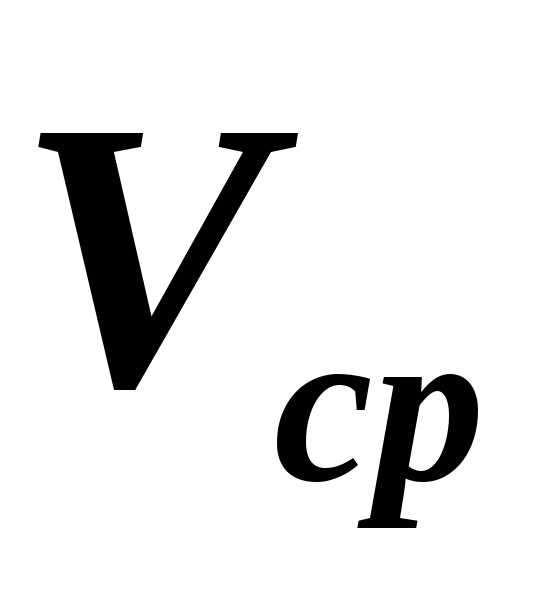 — средняя скорость материальной точки
— средняя скорость материальной точки 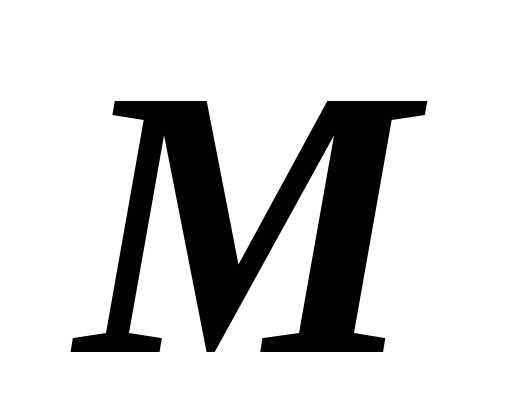 .
Найдем предел этого отношения, учитывая
что
.
Найдем предел этого отношения, учитывая
что 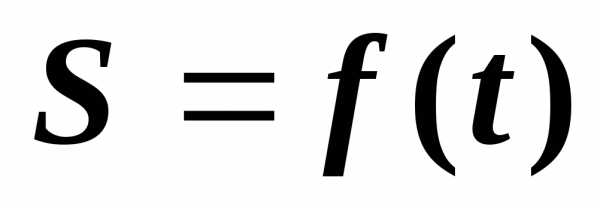 .
.
Следовательно, определение мгновенной скорости движения материальной точки сводится к нахождению производной от пути по времени.
2.2. Геометрическое значение производной
Пусть у нас есть графически заданная некоторая функция .
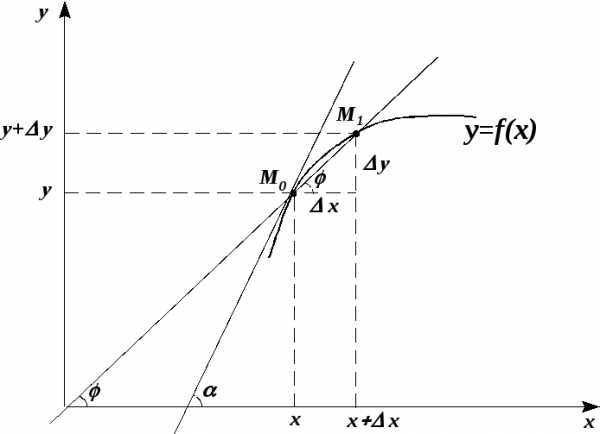
Рис. 1. Геометрический смысл производной
Если 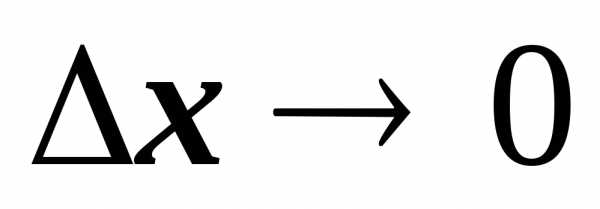 ,
то точка
,
то точка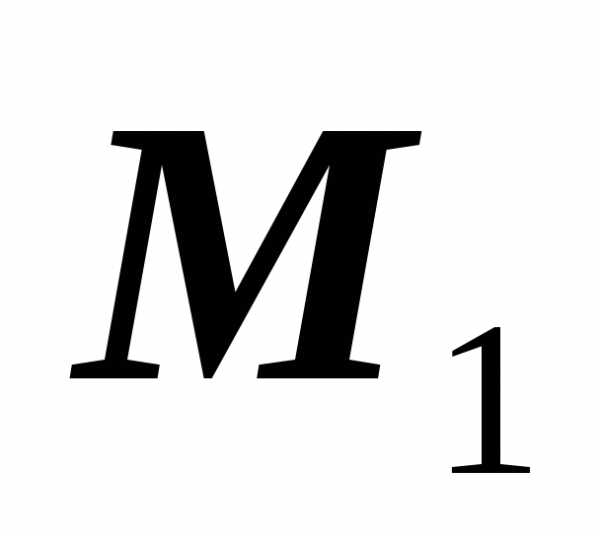 ,
будет перемещаться по кривой, приближаясь
к точке
,
будет перемещаться по кривой, приближаясь
к точке 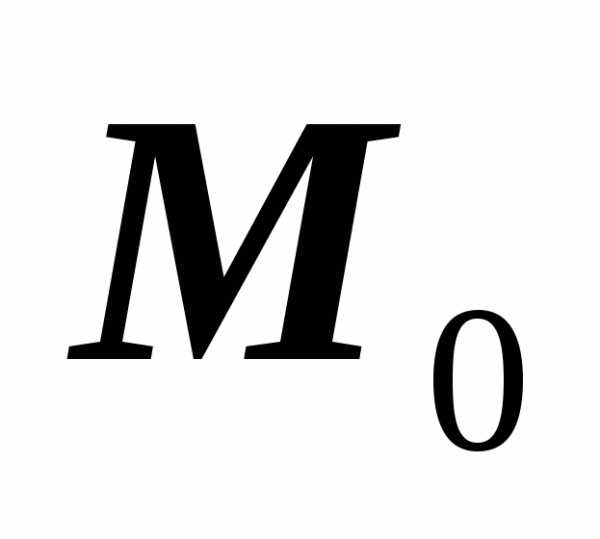 .
.
Следовательно ,
т.е. значение производной при данном
значении аргумента  численно равняется тангенсу угла
образованного касательной в данной
точке с положительным направлением оси
численно равняется тангенсу угла
образованного касательной в данной
точке с положительным направлением оси 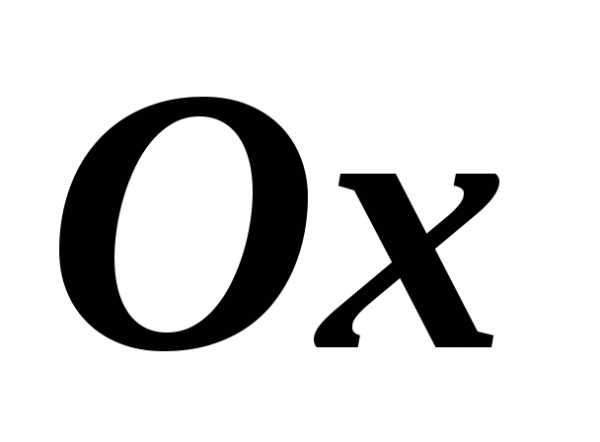 .
.
2.3. Таблица основных формул дифференцирования.
Степенная функция
Показательная функция
Логарифмическая функция
Тригонометрическая функция
Обратная тригонометрическая функция
2.4. Правила дифференцирования.
Производная от
Производная суммы (разности) функций
Производная произведения двух функций
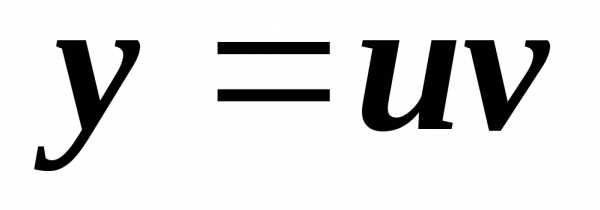
Производная частного двух функций
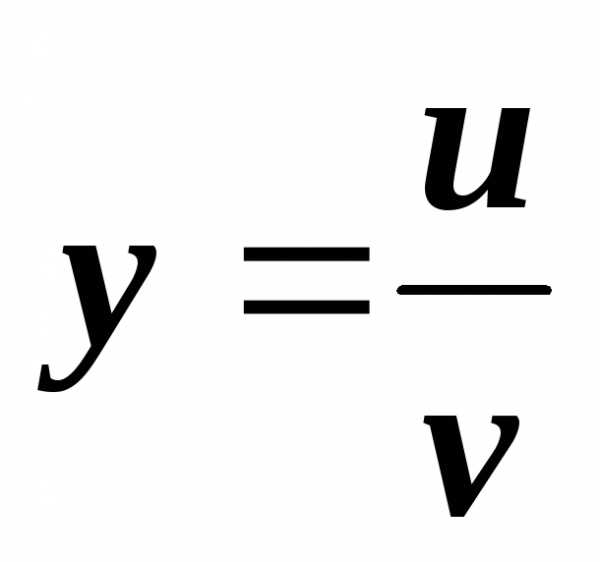
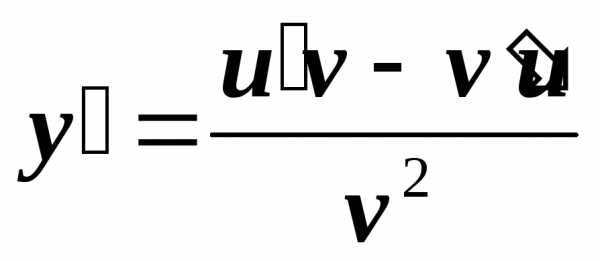
2.5. Производная от сложной функции.
Пусть дана функция такая, что ее можно представить в виде
и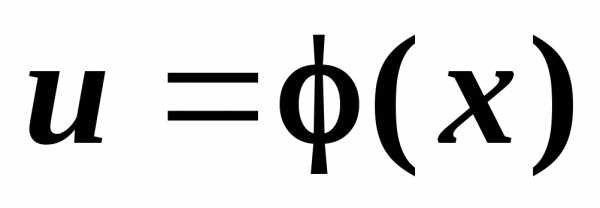 ,
где переменная
,
где переменная является промежуточным аргументом,
тогда
является промежуточным аргументом,
тогда
Производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по x.
Пример1.
Пример2.
3. Дифференциал функции.
Пусть есть
,
дифференцируемая на некотором отрезке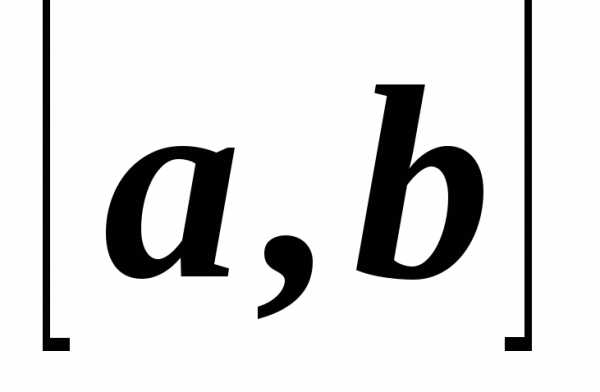 и пустьу этой функции есть производная
и пустьу этой функции есть производная
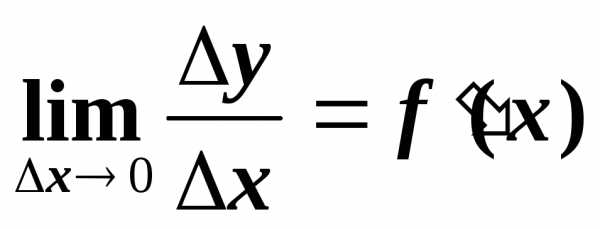 ,
,
тогда можно записать
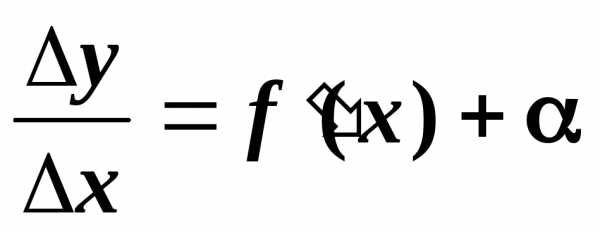 (1),
(1),
где  — бесконечно малая величина,
— бесконечно малая величина,
так как при
Умножая все члены равенства (1) на 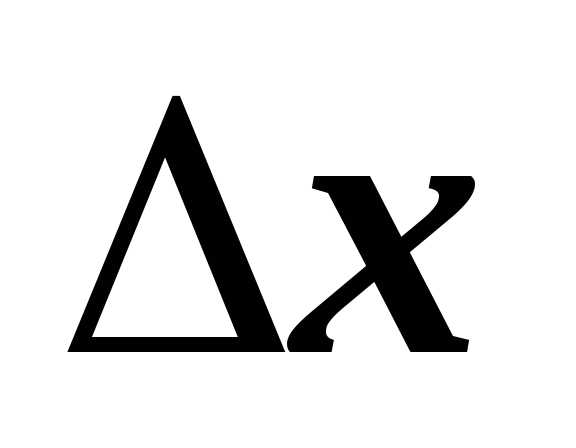 имеем:
имеем:
,
где  —
б.м.в. высшего порядка.
—
б.м.в. высшего порядка.
Величина 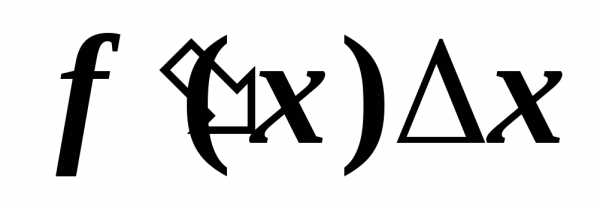 называется дифференциалом функции
называется дифференциалом функции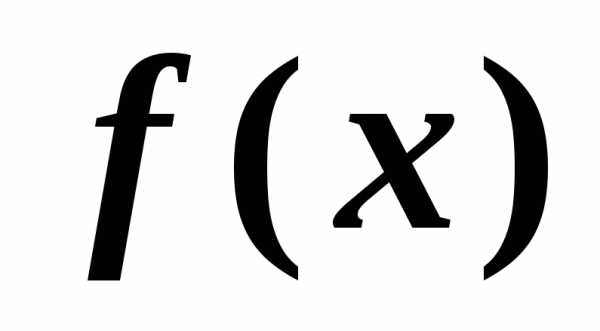 и обозначается
и обозначается
.
3.1. Геометрическое значение дифференциала.
Пусть дана функция .
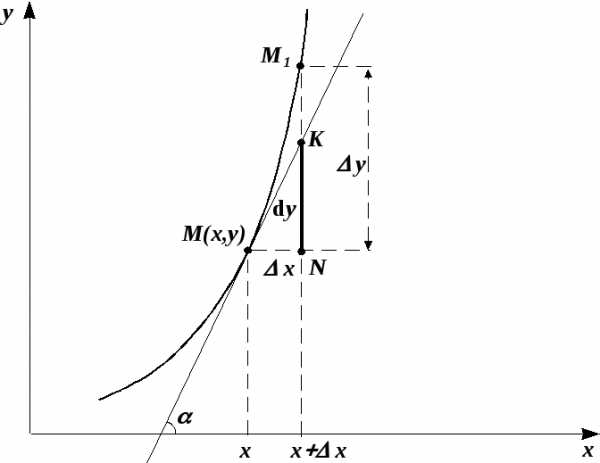
Рис.2. Геометрический смысл дифференциала.
.
Очевидно, что дифференциал функции 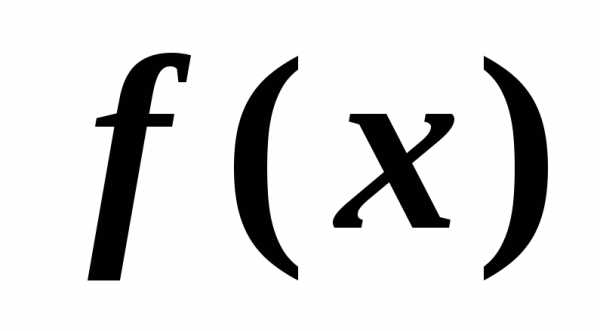 равен приращению ординаты касательной
в данной точке.
равен приращению ординаты касательной
в данной точке.
3.2. Производные и дифференциалы различных порядков.
Если есть , тогданазывается первой производной.
Производная от первой производной называется производной второго порядка и записывается .
Производной n-го порядка
от функции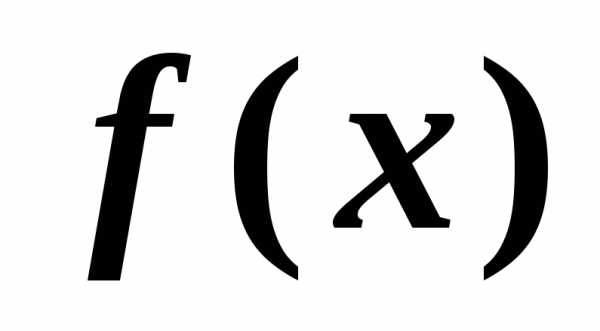 называется производная (n-1)-го
порядка и записывается:
называется производная (n-1)-го
порядка и записывается:
.
Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка.
. 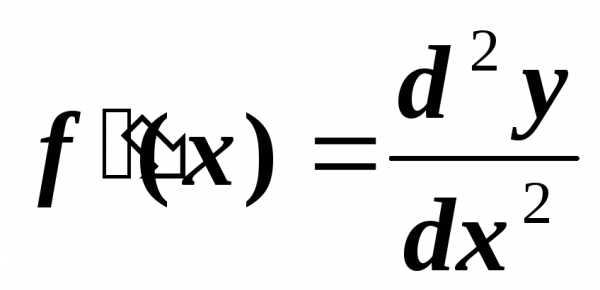
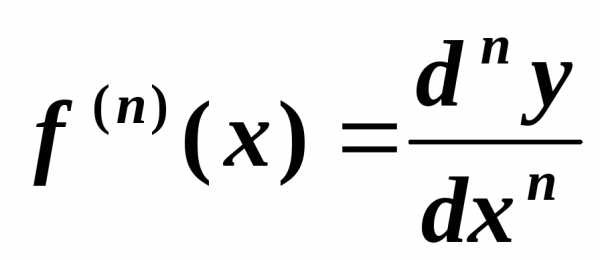 .
.
3.3 Решение биологических задач с применением дифференцирования.
Задача1. Исследования показали, что рост колонии микроорганизмов подчиняется закону, гдеN– численность микроорганизмов (в тыс.),t–время (дни).
а) Рассчитать численность популяции через 7 дней от посева.
б) Будет ли в этот период численность колонии увеличиваться или уменьшаться?
Решение
а)
б)
Ответ. Численность колонии будет увеличиваться.
Задача 2. Вода в озере периодически тестируется для контроля содержания болезнетворных бактерий. Черезtдней после тестирования концентрация бактерий определяется соотношением
.
Когда в озере наступит минимальная концентрация бактерий и можно будет в нем купаться?
РешениеФункция достигает max или min, когда ее производная равна нулю.
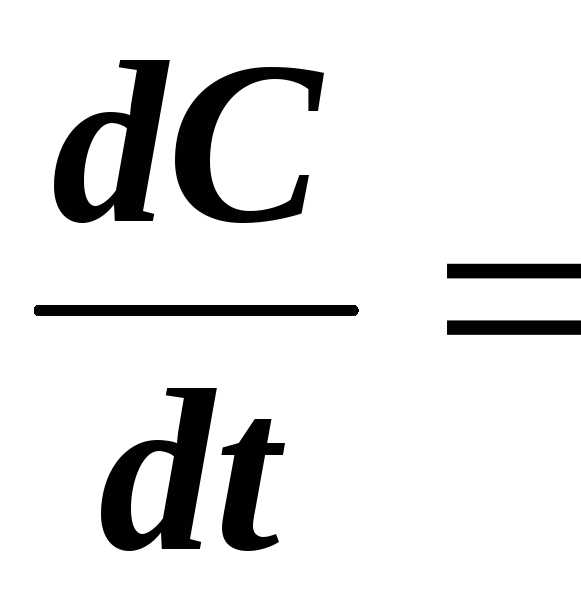 ,
,
Определим max или min будет через 6 дней. Для этого возьмем вторую производную.

Ответ: Через 6 дней будет минимальная концентрация бактерий.
studfiles.net
Логарифм равен логарифму | Логарифмы
Уравнения, в которых один логарифм равен другому логарифму, можно считать простейшими в случае, когда основания этих логарифмов равны:
При решении любого логарифмического уравнения следует определить его ОДЗ либо выполнить проверку найденных корней. В уравнениях вида «логарифм равен логарифму» нахождение ОДЗ может быть упрощено.
Под знаком логарифма должно стоять положительное число, следовательно,
ОДЗ:
По свойству логарифмической функции, из того что равны логарифмы по одному основанию
следует, что выражения, стоящие под знаками логарифмов, также равны:
А раз они равны между собой, если одно из выражений положительно, то другое — также положительно. Следовательно, для нахождения области допустимых значений уравнения достаточно выбрать только одно из двух условий (разумеется, выбирают то неравенство, которое проще решить).
Примеры.
ОДЗ:
Так как логарифмы по одинаковому основанию равны, приравниваем выражения, стоящие под знаками логарифмов:
Первый корень не входит в ОДЗ.
Ответ:2.
Если разность логарифмов равна нулю, уравнение может быть представлено в виде «логарифм равен логарифму»:
Поэтому в ОДЗ достаточно записать лишь одно условие:
Поскольку равны логарифмы с одинаковыми основаниями, выражения, стоящие под знаками логарифмов, тоже равны:
Второй корень не входит в ОДЗ.
Ответ: 1,5.
www.logarifmy.ru
Логарифмы в математике, основные понятия и определения
Определение и основные понятия логарифмов
Например. , поскольку .
В 8 веке индийский математик Вирасена (792-853), исследуя степенные зависимости, опубликовал фактически таблицу логарифмов (целочисленных показателей) для оснований 2, 3, 4. Дальнейшее развитие теория логарифмов получила в средневековой Европе, где была выдвинута идея замены трудоемкого умножения на простое сложение. Впервые эта идея увидела свет в книге «Arithmetica integra» (1544) немецкого математика Михаэля Штифеля (1487-1567). В 1614 году шотландский математик Джон Непер (1560-1617) опубликовал сочинение «Описание удивительной таблицы логарифмов», в котором ввел термин «логарифм», а также описал его свойства. Общепринятого обозначения логарифма не было до конца 19 века, хотя специальные обозначения для натурального и десятичного логарифмов появились значительно ранее.
Натуральный логарифм — логарифм по основанию :
Десятичный логарифм — логарифм по основанию 10:
Свойства логарифмов
Следующие свойства приведены для произвольных величин , при которых логарифм существует.
- Основное логарифмическое тождество:
Например. .
- Если основание логарифма и подлогарифмическая функция равны, то логарифм равен единице:
Например. .
- Логарифм по любому основанию от единицы равен нулю:
Например. .
- Логарифм произведения равен сумме логарифмов от каждого из сомножителей:
Например. .
- Логарифм частного равен разности логарифмов от делимого и делителя соответственно:
Например. .
- .
Например. .
- .
Например. .
- .
Например. .
- .
Например. .
- Переход к новому основанию:
Например. .
- .
Например. .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Логарифм частного | Логарифмы
Чему равен логарифм частного? Это зависит от знаков делимого и делителя.
При положительных делимом и делителе
логарифм частного равен разности логарифмов делимого и делителя.
В этом случае формула логарифма частного может быть записана как
где x>0, y>0.
Например,
Если в ходе решения логарифмических уравнений, неравенств либо их систем требуется осуществить переход от логарифма частного к разности логарифмов, следует учесть область допустимых значений.
Когда на области допустимых значений переменные положительны, проблемы при таком переходе не возникают.
Например, в системе
область допустимых значений —
откуда
При таких условиях можем преобразовать логарифм частного как
и система примет вид:
после чего её легко решить, например, способом сложения.
Если же делимое и делитель в частном под знаком логарифма могут принимать как положительные, так и отрицательные значения, формула перехода от логарифма частного к разности логарифмов выглядит так:
Таким образом, в общем случае логарифм частного равен разности логарифмов модулей делимого и делителя.
Например, в выражении
область допустимых значений —
Поэтому при переходе от логарифма частного к разности логарифмов переменные нужно записывать под знаком модуля:
www.logarifmy.ru
Логарифм произведения | Логарифмы
Логарифм произведения — результат сложения логарифмов с одинаковыми основаниями. Если выражения, стоящие под знаками логарифмов, положительны, формула
является тождеством, то есть
при x>0, y>0 логарифм произведения равен сумме логарифмов множителей:
Например,
Как и другие свойства логарифмов, переход от логарифма произведения к к сумме логарифмов может быть использован для преобразований в ходе решения логарифмических уравнений, неравенств и их систем. Если на области допустимых значений переменные, входящие в произведение под знаком логарифма, положительны, проблем не возникает.
Например, для системы
область допустимых значений x>0, y>0. Поэтому
и систему можно преобразовать как
Если же область допустимых значений включает в себя не только положительные значения переменных, формула перехода от логарифма произведения к сумме логарифмов выглядит так:
Таким образом, в общем случае
логарифм произведения равен сумме логарифмов модулей множителей.
Примеры.
Здесь область допустимых значений
поэтому при переходе от логарифма произведения к сумме логарифмов множителей переменную x берем по модулю:
Область допустимых значений
следовательно,
www.logarifmy.ru
