Параллелограмм. Свойства и признаки параллелограмма
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
6. Точка пересечения диагоналей является центром симметрии параллелограмма
7. Диагонали параллелограмма и стороны
связаны следующим соотношением:
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны:
2. Противоположные углы попарно равны:
3. Диагонали пересекаются и в точке пересечения делятся пополам
4. Противоположные стороны равны и параллельны:
5.
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:
Формулы площади параллелограмма смотрите здесь.
Хорошую подборку задач на нахождение углов и длин в параллелограмме
смотрите здесь.
egemaximum.ru
Паралелограм та його властивості. Ознаки паралелограма
Паралелограм та його властивості. Ознаки паралелограма
Великий клас чотирикутників становлять паралелограми.
Чотирикутник, у якого протилежні сторони паралельні, називається паралелограмом.
Висотою паралелограма називається відрізок, що є перпендикуляром до прямої, яка містить протилежну сторону.
У паралелограма з кожної його вершини можна провести по дві висоти. Висоти, проведені з вершин тупих кутів паралелограма, лежать у паралелограмі; висоти, проведені з гострих тупих кутів паралелограма, лежать зовні паралелограма.
Властивості паралелограма
У паралелограмі протилежні сторони рівні.
У паралелограмі протилежні кути рівні.
У паралелограмі сума кутів, прилеглих до однієї сторони, дорівнює 180°.
Діагоналі паралелограма перетинаються і точкою перетину діляться навпіл.
Діагоналі паралелограма ділять його на два рівні трикутники.
Ознаки паралелограма
Якщо діагоналі чотирикутника перетинаються й у точці перетину діляться навпіл, то цей чотирикутник паралелограм.
Якщо в чотирикутнику дві протилежні сторони паралельні і рівні, то цей чотирикутник паралелограм.
Якщо в чотирикутнику протилежні сторони попарно рівні, то цей чотирикутник паралелограм.
Якщо в чотирикутнику протилежні кути попарно рівні, то цей чотирикутник паралелограм.
Властивість діагоналей паралелограма
:Діагоналі паралелограма перетинаються й у точці перетину діляться навпіл.
Властивість протилежних сторін і кутів паралелограма:
У паралелограма протилежні сторони й кути рівні.
Це цікаво.
Якщо провести бісектриси двох протилежних кутів паралелограма, то вони будуть паралельні або співпадуть.
Якщо провести бісектриси двох кутів, прилеглих до однієї сторони паралелограма, то вони будуть перпендикулярні.
shkolyar.in.ua
Параллелограмм. Определение, свойства и признаки
Свойства параллелограмма
1. Противоположные стороны тождественны.
Доказательство
Первым делом проведем диагональ AC. Получаются два треугольника: ABC и ADC.
Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.
AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.
Следовательно, \triangle ABC = \triangle ADC (по второму признаку: \angle 1 = \angle 2, \angle 3 = \angle 4 и AC — общая).
И, значит, \triangle ABC = \triangle ADC, то AB = CD и AD = BC.
Доказано!
2. Противоположные углы тождественны.
Доказательство
Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4. Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4. Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C, \angle B = \angle D.
Доказано!
3. Диагонали разделены пополам точкой пересечения.
Доказательство
Проведем еще одну диагональ.
По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD. Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).Доказано!
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.
AB = CD; AB || CD \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC?
\triangle ABC = \triangle ADC по свойству 1: AB = CD, AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC.
Но если \triangle ABC = \triangle ADC, то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 — накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.
AB = CD, AD = BC \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим данный признак. Еще раз проведем диагональ AC.
По свойству 1 \triangle ABC = \triangle ACD.
Из этого следует, что: \angle 1 = \angle 2 \Rightarrow AD || BC и \angle 3 = \angle 4 \Rightarrow AB || CD, то есть ABCD — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.
\angle A = \angle C, \angle B = \angle D \Rightarrow ABCD — параллелограмм.
Доказательство
2 \alpha + 2 \beta = 360^{\circ} (поскольку ABCD — четырехугольник, а \angle A = \angle C, \angle B = \angle D по условию).
Получается, \alpha + \beta = 180^{\circ}. Но \alpha и \beta являются внутренними односторонними при секущей AB.
И то, что \alpha + \beta = 180^{\circ} говорит и о том, что AD || BC.
При этом \alpha и \beta — внутренние односторонние при секущей AD. И это значит AB || CD.
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.
AO = OC; BO = OD \Rightarrow параллелограмм.
Доказательство
BO = OD; AO = OC, \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD, \Rightarrow \angle 3 = \angle 4, и \Rightarrow AB || CD.
Аналогично BO = OD; AO = OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8, и \Rightarrow AD || BC.
Четвертый признак верен.
academyege.ru
Параллелограмм — это… Что такое Параллелограмм?
Параллелограмм
Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Свойства
- Противоположные стороны параллелограмма равны.
- .
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- .
- Сумма углов, прилежащих к одной стороне, равна 180°.
- Точка пересечения диагоналей является центром симметрии параллелограмма.
- Сумма всех углов равна 360°.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон:
пусть а — длина стороны AB, b — длина стороны BC, и — длины диагоналей; тогда
Доказательство
Проведя диагональ BD, мы получим два треугольника: ABD и BCD, которые равны, т.к. одна сторона у них общая, а соответственные углы при стороне BD равны как накрест лежащие при параллельных прямых , , где BD — секущая. Из равенства треугольников следует: и ∠A = ∠С Противоположные углы ∠B и ∠D также равны, т.к. они представляют собой суммы равных углов.
Наконец, углы, прилежащие к одной стороне, например ∠A и ∠D, дают в сумме 180°, так как это углы внутренние односторонние при параллельных прямых.
По теореме косинусов: Поскольку , то Складывая полученные равенства:
- Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.
Признаки параллелограмма
Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:
1. Если в четырёхугольнике противоположенные стороны попарно равны, то четырёхугольник параллелограмм 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник параллелограмм 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник параллелограмм
Площадь параллелограмма
- , где a — сторона, h — высота проведенная к этой стороне.
- , где a и b — стороны, а — угол между сторонами a и b.
- .
См. также
dic.academic.ru
Площа паралелограма
Паралелограмом називають чотирикутник у якого протилежні сторони паралельні між собою. Основні задачі в школі з даної теми полягають у обчисленні площі паралелограма, його периметру, висоти, діагоналей. Вказані величини та формули для їх обчислення будуть наведені нижче.
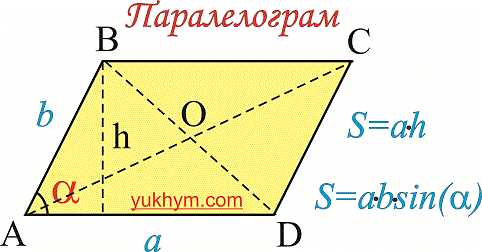
Властивості паралелограма
Протилежні сторони паралелограма, як і протилежні кути рівні між собою: AB=CD, BC=AD,
Діагоналі паралелограма в точці перетину діляться на дві рівні частини :
АО=OC, OB=OD.
Кути, прилеглі до будь-якої сторони (сусідні кути) в сумі рівні 180 градусів.
Кожна з діагоналей паралелограма ділять його на два однакові за площею і геометричнирівні трикутникими розмірами трикутники.
Ще одна чудова властивість, яку часту застосовують при розв’язуванні задач полягає в тому, що сума квадратів діагоналей в паралелограмі рівна сумі квадратів усіх сторін:
AC^2+BD^2=2*(AB^2+BC^2).
Основні ознаки паралелограмів:
1. Чотирикутник у якого протилежні сторони попарно паралельні є паралелограмом.
2. Чотирикутник з рівними протилежними сторонами є паралелограмом.
3. Чотирикутник з рівними і паралельними протилежними сторонами є паралелограмом.
4. Якщо діагоналі чотирикутника в точці перетину діляться навпіл то це паралелограм .
5. Чотирикутник у якого протилежні кути попарно рівні є паралелограмом
Бісектриси паралелограма
Бісектриси протилежних кутів у паралелограмі можуть бути паралельними або співпадати.
Бісектриси сусідніх кутів (прилеглі до однієї сторони) перетинаються під прямим кутом (перпендикулярні).
Висота паралелограма
Висота паралелограма — це відрізок, який проведений з кута перпендикулярно до основи. З цього слідує, що з кожного кута можна провести дві висоти.
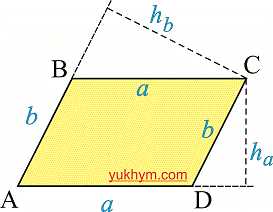
Формула площі паралелограма
Площа паралелограма рівна добутку сторони на висоту проведену до неї. Формула площі наступна
Друга формула не менш популярна при обчисленнях і визначається так: Площа паралелограма рівна добутку сусідніх сторін на синус кута між ними
На основі наведених формул Ви будете знати, як обчислити площу паралелограма.
Периметр паралелограма
Формула для обчислення периметру паралелограма має вигляд
тобто периметр рівний подвоєному значенню суми сторін. Задачі на паралелограм будуть розглянуті в сусідніх матеріалах, а поки що вивчайте формули. Більшість задач з обчислення сторін, діагоналей паралелограма достатньо прості і зводяться до знання теореми синусів та теореми Піфагора.
yukhym.com
понятие и свойства, примеры изображений
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны. На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.
Как вы уже успели догадаться, параллелограмм является выпуклым четырехугольником. Рассмотрим основные свойства параллелограмма.
Свойства параллелограмма
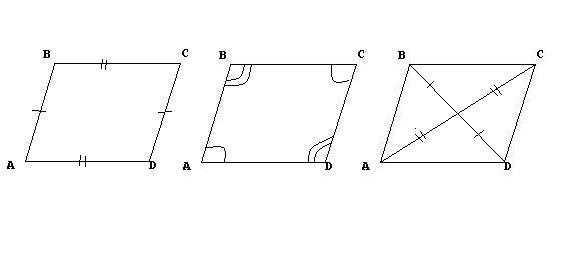
1. В параллелограмме противоположные углы и противоположные стороны равны. Докажем это свойство — рассмотрим параллелограмм, представленный на следующем рисунке.
Диагональ BD разделяет его на два равных треугольника: ABD и CBD. Они равны по стороне BD и двум прилежащим к ней углам, так как углы накрест лежащие при секущей BD параллельных прямых BC и AD и AB и CD соответственно. Следовательно, AB = CD и
BC = AD. А из равенства углов 1, 2 ,3 и 4 следует, что угол A = угол1 +угол3 = угол2 + угол4 = угол С.
2. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.
Тогда треугольник AOB и треугольник COD равны между собой, по стороне и двум прилежащим к ней углам. (AB=CD так как это противоположные стороны параллелограмма. А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.
Все основные свойства проиллюстрированы на следующих трех рисунках.
Нужна помощь в учебе?
Предыдущая тема: Выпуклый многоугольник: теорема и задача
Следующая тема:   Признаки параллелограмма: доказательства и рисунки
Все неприличные комментарии будут удаляться.
www.nado5.ru
Параллелограмм. Определение, свойства и признаки
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Свойства параллелограмма
1. Противоположные стороны тождественны
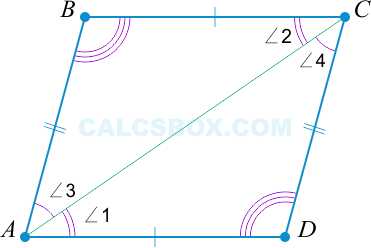
Первым делом проведем диагональ \( AC \). Получаются два треугольника: \( ABC \) и \( ADC \).
Так как \( ABCD \) — параллелограмм, то справедливо следующее:
\( AD || BC \Rightarrow \angle 1 = \angle 2 \) как лежащие накрест.
\( AB || CD \Rightarrow \angle3 = \angle 4 \) как лежащие накрест.
Следовательно, \( \triangle ABC = \triangle ADC \) (по второму признаку: \( \angle 1 = \angle 2, \angle 3 = \angle 4 \) и \( AC \) — общая).
И, значит, \( \triangle ABC = \triangle ADC \), то \( AB = CD \) и \( AD = BC \).
2. Противоположные углы тождественны

Согласно доказательству свойства 1 мы знаем, что \( \angle 1 = \angle 2, \angle 3 = \angle 4 \). Таким образом сумма противоположных углов равна: \( \angle 1 + \angle 3 = \angle 2 + \angle 4 \). Учитывая, что \( \triangle ABC = \triangle ADC \) получаем \( \angle A = \angle C \), \( \angle B = \angle D \).
3. Диагонали разделены пополам точкой пересечения
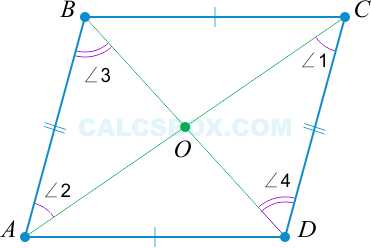
По свойству 1 мы знаем, что противоположные стороны тождественны: \( AB = CD \). Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \( \triangle AOB = \triangle COD \) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, \( BO = OD \) (напротив углов \( \angle 2 \) и \( \angle 1 \)) и \( AO = OC \) (напротив углов \( \angle 3 \) и \( \angle 4 \) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
\( AB = CD \); \( AB || CD \Rightarrow ABCD \) — параллелограмм.
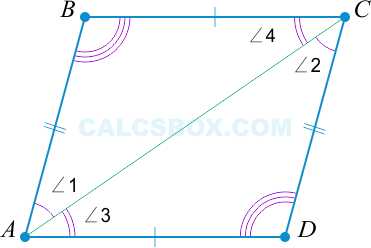
Рассмотрим подробнее. Почему \( AD || BC \)?
\( \triangle ABC = \triangle ADC \) по свойству 1: \( AB = CD \), \( \angle 1 = \angle 2 \) как накрест лежащие при параллельных \( AB \) и \( CD \) и секущей \( AC \).
Но если \( \triangle ABC = \triangle ADC \), то \( \angle 3 = \angle 4 \) (лежат напротив \( AD || BC \) (\( \angle 3 \) и \( \angle 4 \) — накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
\( AB = CD \), \( AD = BC \Rightarrow ABCD \) — параллелограмм.
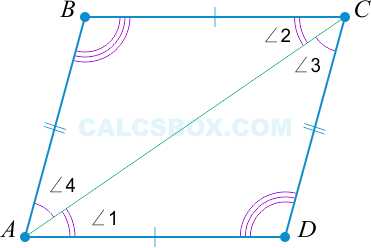
Рассмотрим данный признак. Еще раз проведем диагональ \( AC \).
По свойству 1 \( \triangle ABC = \triangle ACD \).
Из этого следует, что: \( \angle 1 = \angle 2 \Rightarrow AD || BC \) и \( \angle 3 = \angle 4 \Rightarrow AB || CD \), то есть \( ABCD \) — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
\( \angle A = \angle C \), \( \angle B = \angle D \Rightarrow ABCD \) — параллелограмм.
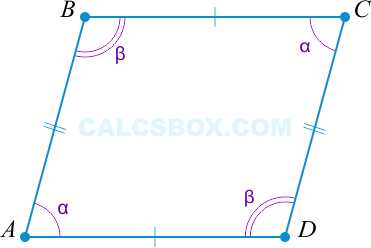
\( 2 \alpha + 2 \beta = 360^{\circ} \) (поскольку \( \angle A = \angle C \), \( \angle B = \angle D \) по условию).
Получается, \( \alpha + \beta = 180^{\circ} \). Но \( \alpha \) и \( \beta \) являются внутренними односторонними при секущей \( AB \).
И то, что \( \alpha + \beta = 180^{\circ} \) говорит и о том, что \( AD || BC \).
При этом \( \alpha \) и \( \beta \) — внутренние односторонние при секущей \( AB || CD \).
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
\( AO = OC \); \( BO = OD \Rightarrow \) параллелограмм.
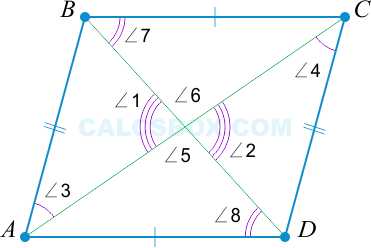
\( BO = OD \); \( AO = OC \), \( \angle 1 = \angle 2 \) как вертикальные \( \Rightarrow \triangle AOB = \triangle COD \), \( \Rightarrow \angle 3 = \angle 4 \), и \( \Rightarrow AB || CD \).
Аналогично \( BO = OD \); \( AO = OC \), \( \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 \), и \( \Rightarrow AD || BC \).
Четвертый признак верен.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
