Как выразить из формулы одну величину через другие онлайн – Выразить переменную из уравнения | Онлайн калькулятор

Подготовка к ЕГЭ. Выразить переменную из формулы.

В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ, в некоторых случаях необходимо только выразить неизвестную величину. Способов выведения неизвестной из формулы много. Если посмотреть страницы Интернета, то мы увидим множество рекомендаций по этому поводу. Это говорит о том, что единого подхода к решению этой проблемы научное сообщество еще не выработало, а те способы, которые используются, как показывает опыт работы в школе – все они малоэффективны. До 90% учащихся выпускных классов не умеют правильно выразить неизвестное. Те же, кто умеют это делать – выполняют громоздкие преобразования. Очень странно, но физики, математики, химики имеют разные подходы, объясняя методы переноса параметров через знак равенства (предлагают правила треугольника, креста или пропорций др.) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с разными трактовками решения данной проблемы, последовательно посещая уроки этих предметов. Эту ситуацию описывает типичный диалог в сети:

Научите выражать из формул величины. 10 класс, мне стыдно не знать, как из одной формулы делать другую.

Да не переживай — это проблема многих моих одноклассников, хоть я и в 9 кл. Учителя показывают это чаще всего методом треугольника, но мне кажется, что это неудобно, да и запутаться легко. Покажу наиболее простой способ, которым я пользуюсь…

Допустим, дана формула:

S=vt

Ну более простая….тебе из этой формулы нужно найти время. Ты берешь и в эту формулу подставляешь числа только разные, исходя из алгебры. Допустим:

S=vt

45=9*5

и тебе наверное хорошо видно, что чтобы найти время в алгебраическом выражении 5 нужно 45/9 т.е переходим к физике: t=s/v

У большинства учащихся формируется психологический блок. Часто учащиеся отмечают, что при чтении учебника трудности в первую очередь вызывают те фрагменты текста, в которых много формул, что «длинные выводы все равно не понять», но при этом возникает чувство неполноценности, неверия в свои силы.

Я, предлагаю следующее решение данной проблемы – большинство учащихся все — таки могут решать примеры и, следовательно, расставлять порядок действий. Используем это их умение.

1. В той части формулы, где содержится переменная, которую нужно выразить, надо расставь порядок действий, причем в одночленах, не содержащих искомую величину этого делать не будем.

2. Затем в обратной последовательности вычислений перенесите элементы формулы в другую часть формулы ( через знак равенства) с противоположным действием ( « минус» — «плюс», «разделить» — « умножить», « возведение в квадрат» – «извлечение корня квадратного»).

То есть найдем в выражении последнее действие и перенесем одночлен или многочлен, исполняющий это действие, через знак равенства первым, но уже с противоположным действием. Таким образом, последовательно, находя последнее действие в выражении, перенесите из одной части равенства в другую все известные величины. В заключение перепишем формулу так, чтобы неизвестная переменная стояла слева.

Получаем четкий алгоритм работы, точно знаем, сколько преобразований необходимо выполнить. Можем для тренировки использовать уже известные формулы, можем выдумывать свои. Для начала работы над усвоением данного алгоритма была создана презентация.

Опыт работы с учащимися показывает, что данный способ хорошо воспринимается ими. Реакция учителей на мое выступление на фестивале «Учитель профильной школы» также говорит о положительном зерне, заложенном в этой работе.

infourok.ru

Решение «буквенных» уравнений в Wolfram|Alpha

Задача «выразить х из уравнения (с несколькими неизвестными)» встречается довольно часто. Ее можно рассматривать, как решение уравнения с буквенными коэффициентами. Поэтому логично, что Wolfram|Alpha использует для решения таких «буквенных» уравнений запрос

solve, который обычно служит для решения уравнений с одним неизвестным.

Вот простой пример такой задачи.

Дано:

Найти x.

Запрос solve применительно к этому уравнению дает такой результат:

solve 2x+3y-1=0

Здесь Wolfram|Alpha отдает приоритет отысканию переменной y. Возможно, полагая, что y это — функция, а x — ее аргумент? Кстати, тот же самый результат дает и запрос solve 2x+3y-1.

Если же из данного уравнения нужно найти именно х, то это следует указать явно. И вот, каким образом:

solve 2x+3y-1 for x

При этом, в отличие от первого варианта, здесь Wolfram|Alpha дает возможность посмотреть пошаговое решение задания с подробным текстовым комментарием:

(Эта замечательная особенность Wolfram|Alpha уже обсуждалась в одном из предыдущих постов Математика с Wolfram|Alpha: шаг за шагом…)

Итак, рассмотренный выше пример уже дает представление о том, как легко Wolfram|Alpha справляется с «буквенными» уравнениями. Однако, пойдет ли дело так же гладко, если вместо x и y взять другие буквы?

Запрос solve 2a+3b-1 дает следующее:

Однако, абсолютно аналогичный по структуре запрос solve 2n+3m-1 выводит совсем другой результат:

Конечно же! Логика здесь есть: Wolfram|Alpha по умолчанию считает неизвестным то, что обозначено буквой, расположенной ближе к концу алфавита. Но, если вы не уверены в своем знании английского алфавита, тогда, решая в Wolfram|Alpha буквенное уравнение, лучше каждый раз явно указывать неизвестную величину.

Естественно, теперь возникает вопрос: а что будет, если взять уравнение, которое содержит не два буквенных обозначения, а больше? Например, такое:

Как и следовало ожидать, здесь Wolfram|Alpha по запросу

solve (без указания неизвестного) выводит решение квадратного уравнения относительно x:

solve a*x^2+b*x+c*b^2=0

Если же из данного уравнения нужно найти b, то запрос должен быть таким:

solve a*x^2+b*x+c*b^2=0 for b

Аналогичным образом следует поступить, если ищем c:

solve a*x^2+b*x+c*b^2=0 for c

Также ясно, что решение кубического уравнения

даст запрос solve a*x^3+b*x^2+c*x+d

А вот, если нас интересует, как выражается из данного уравнения a, то запрос формулируем иначе:

solve a*x^3+b*x^2+c*x+d=0 for a

Под конец, хочется задать Wolfram|Alpha вопрос посложнее. Например, сможет ли система решить такое «буквенное» уравнение?

Запрос solve без явного указания неизвестного выводит решение этого уравнения относительно z:

solve a-(a-e*((x*v-a*(w+x))/(w*x)))=e*(((a-e*((x*v-a*(w+x))/(w*x)))(y+z)-z*v)/(y*z))

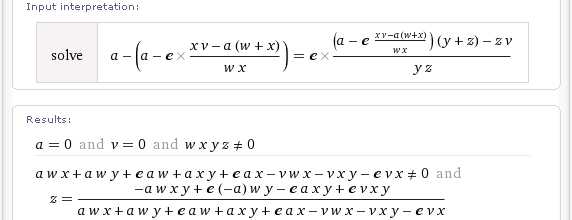
Если же нужно найти, к примеру, w, тогда, естественно, получим:

Что же касается решения трансцендентных «буквенных» уравнений, то все зависит от вида конкретного уравнения. Если уравнение допускает аналитическое решение, тогда это решение получается точно так же, как и ранее. Если же нет, тогда, по-возможности, Wolfram|Alpha выдает неявное решение в графическом виде.

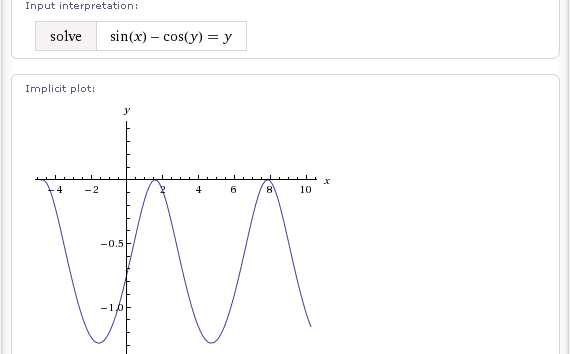
Рассмотрим несколько типичных примеров.

solve cos(x)-sin(y)=y^2

solve sin(x)-cos(y)=y

solve sin(x)-cos(y^2)+x=0 for y

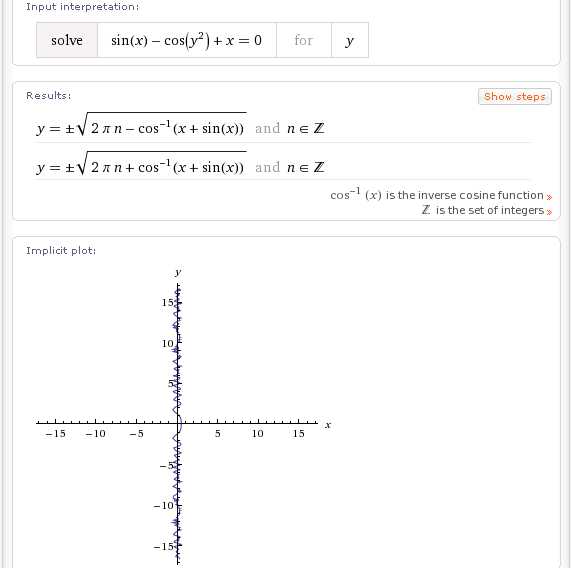
Некоторые решения оказываются довольно неожиданными и по-своему красивыми:

solve sin(x)-cos(y)+xу=0 for y

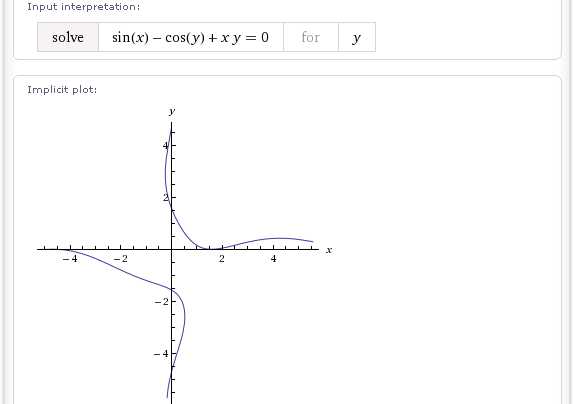
solve sin(x)-cos(y)+x^2=0 for x

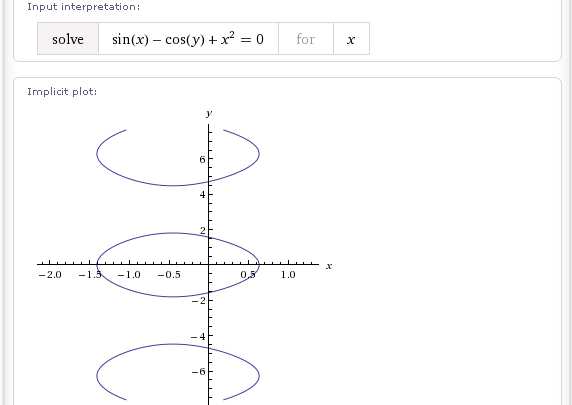
solve sin(x)-cos(y)+log(x)=0 for x

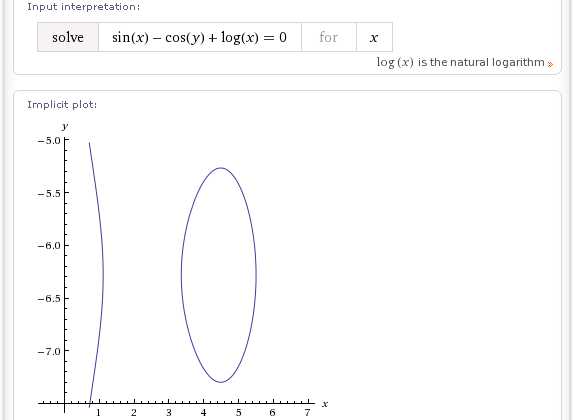
solve sin(x)-cos(y)+log(y)=0

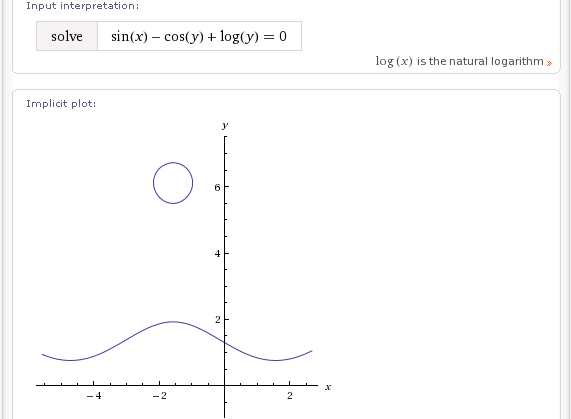
solve sin(x)-cos(y)+e^x=0

solve sin(x)-cos(y)+x^y=0

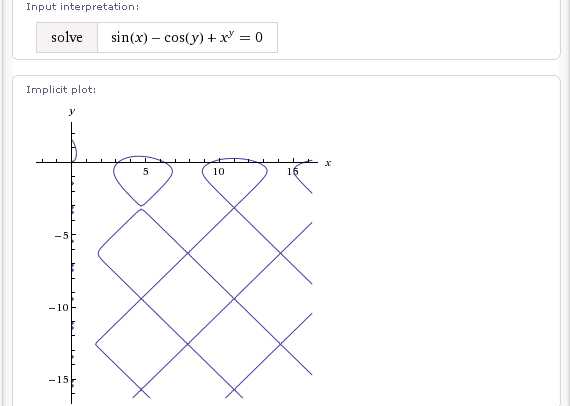
И т.д. и т.п.

www.wolframalpha-ru.com

Документ без названия

Тема 5. Выражение из формул одних величин через другие

Теория

Запись какого либо правила с помощью букв называют формулой.

Запишем правило нахождение пути по скорости и времени движения в буквенном виде. Обозначим путь буквой s, скорость — буквой v и время — буквой t. Получим равенство s = vt — это равенство называют формулой пути.

По формуле пути можно решать различные задачи.

Полезно вспомнить:

1. Чтобы найти неизвестное слагаемое надо из суммы вычесть известное:

а + х = в; х = в-а

2. Чтобы найти неизвестный сомножитель надо произведение разделить на известный:

а*х=в; х=в:а

3. Чтобы найти неизвестный делитель надо делимое разделить на частное:

а:х=в; х=а:в

4. Чтобы найти неизвестное делимое надо делитель умножить на частное:

х:а=в; х=а*в

Практика

1. Автомобиль движется со скоростью 60 км/ч. За какое время он пройдет путь в 600 км?

Решение. Заменим в формуле s = vt буквы s и v их значениями: s = 600, v = 60. Получим уравнение: 600 = 60t. Из него находим, что t = 600:60, то есть t = 10. Значит, чтобы проехать 600 км, автомобиль должен двигаться 10 ч.
Ответ: за 10 ч.

2. Из формулы скорости газовых молекул  выразите давление газа p.

Решение: ;

3. Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошел человек, сделавший 4000 шагов, если длина его шага составляет примерно 55 см? Ответ выразите в километрах.

Решение.

s = 4000·55см = 220000см = 2200м = 2,2км.

Ответ: 2,2 км.

4. Выразите из формулы скорости равноускоренного движения v = v₀ + at время t.

Решение.

Выполним два шага: 1) сначала выразим at; 2) Затем время t. 

1) at = v — v₀;  2) .  Ответ: .

Реши сам

1. (Демо 2010 Задание 5) Из формулы периода обращения  выразите время
вращения t. Ответ:______

2. Выразите из формулы F = 1,8C + 32 переменную С. Ответ:______

3. Выразите из формулы l = 1 + 7,8t переменную t. Ответ:______

4. Из формулы  выразите переменную v. Ответ:______

5. Из формулы  выразите переменную t. Ответ:______

6. Из формулы  выразите переменную V. Ответ:______

7. Из формулы  выразите переменную A. Ответ:______

8. Из формулы  выразите переменную b. Ответ:______

9. Из формулы  выразите переменную a. Ответ:______

10. Выразите из формулы скорости равноускоренного движения v = v₀ + at ускорение a. Ответ:______

11. Выразите из формулы пути равномерного движения s = s₀ + at скорость v. Ответ:______

12. Из формулы давления газа  выразите скорость молекул v. Ответ:______

13. Объем цилиндра вычисляется по формуле V = πR²H, где R – радиус основания, Н – высота цилиндра. Выразите из этой формулы радиус R. Ответ:______

14. Из формулы пути равноускоренного движения  выразите время t Ответ:______

 

algebra.belem.ru

Формулы и их преобразование

Из курса математики вам уже известны некоторые формулы. Посмотрите на вторую строку таблицы, на формулу S = l·b. Она показывает, что площадь прямоугольника S вычисляется умножением его длины l на ширину b. То есть формула показывает, что величины S, l, b связаны друг с другом.

Как вычислить …	Формула
… площадь прямоугольника	S = l·b
… объём параллелепипеда, цилиндра	V = S·h

Итак, формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.

Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная символом b.

Исходная формула	Выразили « b »	Выразите « c »
a = b · c	b = a : c	c = …
a = c · b	b = a : c	c = …
a = b : c	b = a · c	c = …
a = c : b	b = c : a	c = …
a = b + c	b = a – c	c = …
a = c + b	b = a – c	c = …
a = b – c	b = a + c	c = …
a = c – b	b = c – a	c = …

Начертите такую же таблицу в тетради и заполните третью колонку, выразив в ней величину, обозначенную символом с.

Вычислять значение величины по формуле вы уже умеете. Познакомимся теперь, как можно находить границы истинности результата при вычислениях по формуле. Допустим, мы измеряли длину, ширину и высоту спичечного коробка линейкой и получили такие результаты:

l = 5,0 см ± 0,1 см	b = 3,5 см ± 0,1 см	h = 1,5 см ± 0,1 см
Перепишем эти же равенства в виде неравенств:
4,9 см < l < 5,1 см	3,4 см < b < 3,6 см	1,4 см < h < 1,6 см

Применив две формулы V = S · h = l·b · h , вычислим наименьшее Vmin и наибольшее Vmax значения объёма спичечного коробка:

Vmin = 4,9 см · 3,4 см · 1,4 см Vmin ≈ 23 см³

Vmax = 5,1 см · 3,6 см · 1,6 см Vmax ≈ 29 см³

Тогда результат вычисления объёма коробка с учётом погрешности измерений исходных величин запишется в виде неравенства:

23 см³ < Vкор < 29 см³

На числовой прямой это неравенство будет выглядеть так:

Соответственно, истинное значение объёма коробка заключено между значениями Vmin и Vmax. Другими словами, оно лежит где-то в интервале между 23 см³ и 29 см³ (нами он отмечен синей штриховкой).

Итак, мы познакомились с тем, как можно находить границы истинности результата, подставляя в формулу наименьшие и наибольшие значения входящих в неё величин.

questions-physics.ru

Как выразить величину из формулы

В физике величинами являются количественные колляции предметов и показатели взаимодействий тел между собой и окружающей средой, скажем длина, масса, скорость, время, углы и проч. Эти параметры могут быть зависимыми либо самостоятельными один от иного. Отношения многих связанных величин представлены в знаменитых формулах, из которых неизменно дозволено выразить всякую переменную.

Инструкция

1. Выражение величины из формулы производится с подмогой математических операций – переноса членов, деления на одно число обе части записи и др. То есть, следует упрощать и трудиться с формулой, как с алгебраическим уравнением. Исполняя данные действия, необходимо также рассматривать смену знака, правила итога величины из под корня, возведения в степень.

2. В особенно простом случае при наличии выражения вида v = 2*g + 11 для поиска величины g исполните следующие действия. Перенесите все члены, не содержащие переменную g в одну (класснее левую) часть данного уравнения, не забывая поменять их знак при переносе на противоположный: -2*g = 11 – v. Остальные величины и константы перенесите за знак равенства. Если при желанной величине стоит показатель, как в данном случае (-2), поделите на эту константу обе части уравнения: g = -(11 – v)/2.

3. При выражении из формулы величины, возведенной в степень, как, скажем, в дальнейшем варианте: S = a*t?/4, исполните вначале выше описанные действия. Поставьте переменную в степени по левую сторону уравнения, причем для итога константы из знаменателя дроби умножьте на это число обе части формулы : a*t? = 4*S. Поделите уравнение на переменную а и получится: t? = 4*S/а. Дабы убрать степень желанной переменной, возьмите корень этой же степени (тут квадратный) как с левой, так и с правой части выражения: t = ?4*S/а. Встречается и обратная обстановка, когда желанная величина стоит под знаком корня, в этом случае требуется исполнить возведение каждого уравнения в степень, указанную при корне. Так, выражение ??S = v + g преобразуется в вид S = (v + g)?.

4. При наличии трудных выражений, полученных в итоге многократных подстановок разных формул, зачастую появляются затруднения в выражении незнакомой величины. Скажем, в конструкции вида S = (?t?*k/(1+g))*f – 15 при поиске величины k желанно провести заблаговременное облегчение уравнения с подмогой вступления подстановочной переменной. Примите за х выражение в огромных скобках: х = (?t?*k/(1+g)), тогда первоначальное уравнение будет выглядеть так: S = х*f – 15. Отсель легко находится х = (S + 15)/f. Дальше верните взамен х скобочное выражение (?t?*k/(1+g)) = (S + 15)/f . Позже чего дозволено продолжать облегчения с поддержкой схожих подстановок либо сразу выразить желанную

величину : k = ((1+g)*(S + 15)/f )2/t?.

Изредка при решении задач появляется надобность выразить дробное число в процентах. Перевести в проценты дозволено и десятичную дробь, и обычную, и положительную, и неправильную. Разглядим, как это сделать.

Инструкция

1. Нужно понимать, что процент – это одна сотая доля. Следственно выразить дробь в процентах – значит узнать, какую долю от ста выражает эта дробь.

2. Пускай дана десятичная дробь. Скажем, 0.54. Дабы выразить в процентах десятичную дробь, нужно само число умножить на сто (в случае десятичной дроби это обозначает перенести точку на два разряда вправо) и поставить справа от числа знак процента. Получаем, что 0.54=54%. Еще несколько примеров: 1.3=130%, 0.218=21.8%, 0.02=2%.

3. Дабы выразить обычную дробь в процентах, комфортно вначале представить её в виде десятичной дроби. Для этого домножьте числитель и знаменатель на такое число , дабы в знаменателе дроби получилось 10, 100, 1000, и т.д.

4. Запишите число как десятичную дробь. Дальше действуйте согласно пункту 2.

5. Дабы выразить в процентах целое число (либо целую часть неправильной дроби), примитивно умножьте его на сто и поставьте знак процента. В неправильной дроби дозволено отдельно выразить в процентах целую и дробную часть, после этого просуммировать полученные итоги.

6. Разглядим сейчас обратную задачу: как из процентов сделать десятичную дробь.Дабы перевести число в процентах в десятичное число , поделите его на сто. То есть перенесите разрядную точку на два разряда налево.Примеры: 26%=0.26, 0.15%=0.0015, 117%=1.17.

jprosto.ru

Вычисление выражений для заданных значений переменных

Данный калькулятор вычисляет значение выражения, подставляя туда значения переменных из таблицы. Удобно для проверки домашних заданий типа «Найдите значение выражения при a = 0.1, b = 2». Обозначения переменных в выражении должны совпадать с именами переменных в таблице. Если не совпадет — замены не будет и подсчитает неправильно, так что следите.

addimport_exportmode_editdelete

Переменные

Размер страницы: 5102050100chevron_leftchevron_right

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: Lorem ipsum;Lorem ipsum

Точность вычисления

Знаков после запятой: 2

Формула после подстановки

 

Результат расчета

 

Сохранить share extension

Для расчета после подстановки значений переменных используется Математический калькулятор.
Таким образом, аналогично указанному калькулятору, здесь также в математическом выражении допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:

• / — деление
• ^ — возведение в степень

и следующих функций:

• sqrt — квадратный корень
• rootp — корень степени p, например root3(x) — кубический корень
• exp — e в указанной степени
• lb — логарифм по основанию 2
• lg — логарифм по основанию 10
• ln — натуральный логарифм (по основанию e)
• logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
• sin — синус
• cos — косинус
• tg — тангенс
• ctg — котангенс
• sec — секанс
• cosec — косеканс
• arcsin — арксинус
• arccos — арккосинус
• arctg — арктангенс
• arcctg — арккотангенс
• arcsec — арксеканс
• arccosec — арккосеканс
• versin — версинус
• vercos — коверсинус
• haversin — гаверсинус
• exsec — экссеканс
• excsc — экскосеканс
• sh — гиперболический синус
• ch — гиперболический косинус
• th — гиперболический тангенс
• cth — гиперболический котангенс
• sech — гиперболический секанс
• csch — гиперболический косеканс
• abs — абсолютное значение (модуль)
• sgn — сигнум (знак)

planetcalc.ru

Выражение переменной из формулы

Повторить:
1) Порядок действий в математике;
2) Решение линейных уравнений

Вопрос 1. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 2. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 3. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 4. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 5. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 6. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 7. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 8. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 9. Выразите из формулы переменную

A.
B.
C.
D.

Вопрос 10. Выразите из формулы переменную

A.
B.
C.
D.

fizmat.by