Параллелограмм это квадрат у которого – — — — — …

Содержание

Параллелограмм. — Царство математики

Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства параллелограмма:

В параллелограмме противоположные стороны и противоположные углы равны.
Диагонали параллелограмма точкой пересечения делятся пополам.
Диагональ параллелограмма делит параллелограмм на два равных треугольника.
Точка пересечения диагоналей — центр симметрии параллелограмма.
Биссектриса любого угла параллелограмма отсекает от него равнобедренный треугольник.
Биссектрисы параллелограмма, проведенные из противоположных углов, параллельны.
Биссектрисы параллелограмма, проведенные из соседних углов, перпендикулярны.
Угол между высотами, проведенными из тупого угла параллелограмма, равен острому углу параллелограмма.
Угол между высотами, проведенными из острого угла параллелограмма, равен тупому углу параллелограмма.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон параллелограмма.
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

Частные случаи параллелограмма: прямоугольник, квадрат, ромб. Следовательно, все эти фигуры обладают свойствами, присущими параллелограмму.

Прямоугольник — параллелограмм, у которого все углы равны.

Отличительное свойство прямоугольника: диагонали прямоугольника равны.

Ромб — параллелограмм, у которого все стороны равны.

Отличительное свойство ромба: диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Квадрат — параллелограмм, у которого все стороны и углы равны.

Отличительное свойство квадрата: диагонали квадрата равны, взаимно перпендикулярны и делят углы квадрата пополам.

Площадь параллелограмма:

Площадь параллелограмма через сторону и высоту, проведенной к этой стороне:
S=a·h_a=b·h_b_.
Площадь параллелограмма через стороны и угол между ними: S=a·b·sinφ.
Площадь параллелограмма через диагонали и угол между ними: S=0,5·d₁·d₂·sinφ.
Площадь параллелограмма через радиус вписанной окружности и сторону(верна только для параллелограмма, в который можно вписать окружность): S=2·a·r.
Площадь параллелограмма через радиус вписанной окружности и угол между сторонами(верна только для параллелограмма, в который можно вписать окружность): S=4r²/sinφ.

anasta8ia.ru

Квадрат и его свойства

Главная
Геометрия
Свойства выпуклых многоугольников. Параллелограмм, прямоугольник, квадрат, ромб
Квадрат и его свойства

Квадрат — это параллелограмм, у которого все стороны равны и все углыпрямые. Следовательно, у квадрата есть все пять свойств параллелограмма. Квадрат — это прямоугольник, у которого все стороны равны. Следовательно, у квадрата есть ещё два свойства — свойства прямоугольника. Квадрат — это ромб, у которого все углы прямые. Следовательно, у квадрата есть ещё три свойства — свойства ромба. Всего у квадрата десять свойств.

Первые пять свойств квадрата как параллелограмма: а) диагональ квадрата делит его на два равных треугольника, б) противоположные стороны квадрата равны, в) противоположные углы квадрата равны, г) сумма углов, прилежащих к одной стороне, равна 180°.

Свойства квадрата как прямоугольника: д) диагонали квадрата равны, е) у квадрата две оси симметрии — прямые, соединяющие середины его сторон.

Свойства квадрата как ромба: ж) диагонали квадрата взаимно перпендикулярны, з) диагонали квадрата делят углы квадрата пополам, и) у квадрата еще две оси симметрии — его диагонали.

диагональ

прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне многоугольника

параллелограмм

четырёхугольник, у которого противоположные стороны попарно параллельны

перпендикулярные прямые

прямые, образующие при пересечении четыре прямых угла

прямой угол

угол с градусной мерой равной 90°

прямоугольник

параллелограмм, у которого все углы прямые

ромб

параллелограмм, у которого все стороны равны

стороны

смежные отрезки, соединяющие вершины многоугольника

треугольник

фигура, состоящая из трёх точек, не лежащих на одной прямой и трёх отрезков, попарно соединяющих эти точки

угол

фигура, состоящая из точки и двух исходящих из неё лучей

blitztest.ru

Квадрат. Свойства квадрат. Признаки квадрата.

Категория: Справочные материалы

Елена Репина 2013-07-26 2013-09-20

Квадрат – ромб, у которого все углы прямые.

или

Квадрат – прямоугольник с равными сторонами.

или

Квадрат – параллелограмм, у которого все стороны равны и все углы равны.

Свойства квадрата

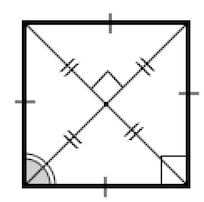
Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.

Признаки квадрата

Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.

Описанная окружность

Около квадрата можно описать окружность. Сторона и радиус окружности связаны соотношением:

Вписанная окружность

В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:

Площадь квадрата

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Автор: egeMax | Нет комментариев

egemaximum.ru

5.1.2 Параллелограмм, прямоугольник, ромб, квадрат

Видеоурок 1: Прямоугольник, ромб и квадрат. Часть 1

Видеоурок 2: Прямоугольник, ромб и квадрат. Часть 2

Лекция: Параллелограмм, прямоугольник, ромб, квадрат

Четырехугольники

Один подраздел многоугольников мы изучили в прошлом вопросе, сейчас же перейдем к изучению четырехугольников – это многоугольники, у которых 4 стороны, 4 вершины, 4 угла.

В школьном курсе геометрии изучают несколько основных типов четырехугольников – это параллелограмм, прямоугольник, ромб, квадрат и трапецию. В этом же вопросы мы рассмотрим все, кроме трапеции, поскольку все первые 4 типа многоугольников имеют некоторые похожие черты – у них противолежащая пара сторон параллельна.

Отличительная особенность всех четырехугольников – это то, что сумма всех углом равна 360 градусов.

Ну давайте начнем характеризовать все четырехугольники, имеющиеся в теме.

Параллелограмм

Исходя из названия, можно судить, что у данного четырехугольника что-то параллельное. Это совершенно верно, параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны.

Все четырехугольники характеризуются своими свойствами, поэтому давайте ознакомимся со свойствами параллелограмма:

Если у четырехугольника присутствуют перечисленные свойства, то он является параллелограммом:

Какой — то Один признак выполнен
Все свойства параллелограмма можно использовать

Для любого параллелограмма справедлива следующая формула, по которой ясно, что сумма квадратов сторон диагоналей равна сумме квадратов всех сторон:

Данное свойство вытекает из теоремы Пифагора для двух прямоугольных треугольников.

Любую сторону можно найти по известным величинам диагоналей и углов между ними:

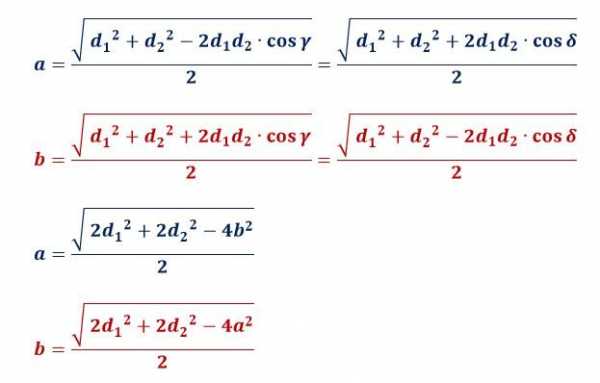
Найти стороны параллелограмма можно не только через диагонали, но и через высоты и площади:

Одними из наиболее важных формул являются формулы для нахождения диагоналей найти их можно по известным сторонам и углу между ними:

Но на самом деле самыми важными формулами являются формулы для нахождения площадей:

Квадрат

Правильный четырехугольник – это квадрат. Как известно, у всех правильных фигур равны стороны и равны углы. Квадрат можно назвать частным случаем параллелограмма, поскольку все свойства и признаки параллелограмма видны и у квадрата.

Свойства квадрата:

Все стороны равны.
Все углы равны 90 градусам.
Диагонали квадрата равны и пересекаются под прямым углом, а точка их пересечения делит их пополам.

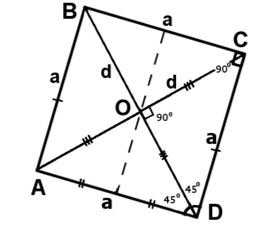
Отличительной особенностью диагонали квадрата является то, что она есть гипотенузой прямоугольного треугольника с катетами, равными сторонам квадрата, а гипотенузой равной диагонали. Именно поэтому из теоремы Пифагора диагональ квадрата всегда в раз больше его стороны.

Так как у квадрата все стороны равны, то найти периметр и площадь этой фигуры не составляет ни малейшего труда:

Прямоугольник

Эта фигура характеризуется тем, что все её углы прямые, то есть по 90 градусов.

Свойства прямоугольника:

У прямоугольника все противолежащие стороны параллельны и равны между собой.
Все углы прямые.
Точка пересечения диагоналей делит их на равные части.

Квадрат диагонали прямоугольника равен сумме квадратов его сторон:

Как можно было понять, данная формула была выведена из теоремы Пифагора, поскольку в основе прямоугольника лежат 2 прямоугольных треугольника.

Формулы нахождения сторон по известным величинам диагоналей, а также площадей:

Формулы сторон прямоугольника

Формулы периметра прямоугольника

Формулы площадей

Ромб

И наконец-то мы подошли к последнему из параллелограммов, который называется ромбом.

У ромба, как и у квадрата, все стороны равно, но, как и у любого параллелограмма, его стороны попарно параллельны.

Отличительной особенностью ромба считается то, что его диагонали, пересекаясь под прямым углом, делятся пополам.

Не имеет смысла перечислять все свойства ромба, поскольку они аналогичны свойствам параллелограмма, а так же квадрата.

У ромба так же существует связь между длинами диагоналей и его сторон. Поскольку в основании ромба лежат 4 прямоугольных треугольника, то можно было вывести формулу связи диагоналей и сторон через теорему Пифагора:

Формулы для сторон ромба

Формулы площадей ромба

cknow.ru

Параллелограмм — это… Что такое Параллелограмм?

Параллелограмм

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства

Противоположные стороны параллелограмма равны.
.
Противоположные углы параллелограмма равны.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
.
Сумма углов, прилежащих к одной стороне, равна 180°.
Точка пересечения диагоналей является центром симметрии параллелограмма.
Сумма всех углов равна 360°.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон:

пусть а — длина стороны AB, b — длина стороны BC, и — длины диагоналей; тогда

Доказательство

Проведя диагональ BD, мы получим два треугольника: ABD и BCD, которые равны, т.к. одна сторона у них общая, а соответственные углы при стороне BD равны как накрест лежащие при параллельных прямых , , где BD — секущая. Из равенства треугольников следует: и ∠A = ∠С Противоположные углы ∠B и ∠D также равны, т.к. они представляют собой суммы равных углов.

Наконец, углы, прилежащие к одной стороне, например ∠A и ∠D, дают в сумме 180°, так как это углы внутренние односторонние при параллельных прямых.

По теореме косинусов: Поскольку , то Складывая полученные равенства:

Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:

1. Если в четырёхугольнике противоположенные стороны попарно равны, то четырёхугольник параллелограмм 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник параллелограмм 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник параллелограмм

Площадь параллелограмма

, где a — сторона, h — высота проведенная к этой стороне.

, где a и b — стороны, а — угол между сторонами a и b.

См. также

med.academic.ru

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).

Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.

Прямоугольник — это четырехугольник, у которого каждый угол является прямым.

Квадрат — это частный случай прямоугольника.

Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника

1. Прямоугольник — это параллелограмм

Свойство объясняется действием признака 3 параллелограмма (то есть \( \angle A = \angle C \), \( \angle B = \angle D \))

2. Противоположные стороны равны

\( AB = CD,\enspace BC = AD \)

3. Противоположные стороны параллельны

\( AB \parallel CD,\enspace BC \parallel AD \)

4. Прилегающие стороны перпендикулярны друг другу

\( AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB \)

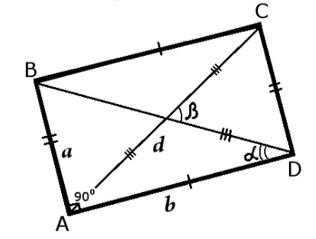
5. Диагонали прямоугольника равны

\( AC = BD \)

Согласно свойству 1 прямоугольник является параллелограммом, а значит \( AB = CD \).

Следовательно, \( \triangle ABD = \triangle DCA \) по двум катетам (\( AB = CD \) и \( AD \) — совместный).

Если обе фигуры — \( ABC \) и \( DCA \) тождественны, то и их гипотенузы \( BD \) и \( AC \) тоже тождественны.

Значит, \( AC = BD \).

Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.

Докажем и это.

\( \Rightarrow AB = CD \), \( AC = BD \) по условию. \( \Rightarrow \triangle ABD = \triangle DCA \) уже по трем сторонам.

Получается, что \( \angle A = \angle D \) (как углы параллелограмма). И \( \angle A = \angle C \), \( \angle B = \angle D \).

Выводим, что \( \angle A = \angle B = \angle C = \angle D \). Все они по \( 90^{\circ} \). В сумме — \( 360^{\circ} \).

6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон

Это свойство справедливо в силу теоремы Пифагора.

\( AC^2=AD^2+CD^2 \)

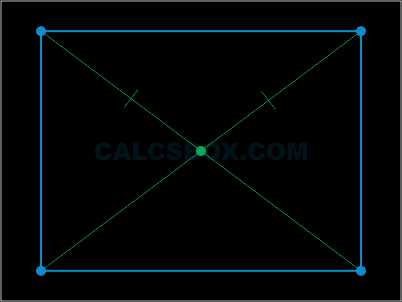
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника

\( \triangle ABC = \triangle ACD, \enspace \triangle ABD = \triangle BCD \)

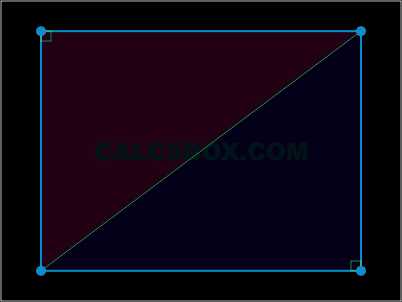
8. Точка пересечения диагоналей делит их пополам

\( AO = BO = CO = DO \)

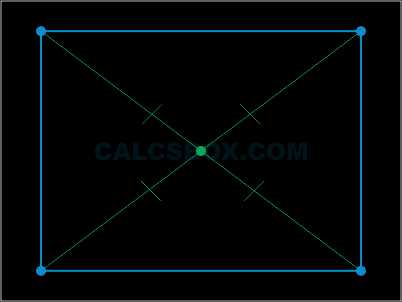
9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности

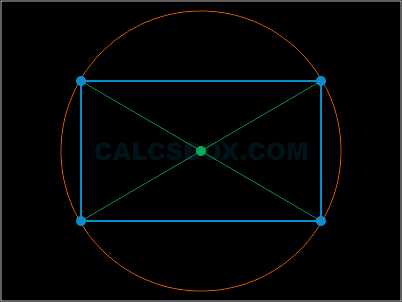
10. Сумма всех углов равна 360 градусов

\( \angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ} \)

11. Все углы прямоугольника прямые

\( \angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ} \)

12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника

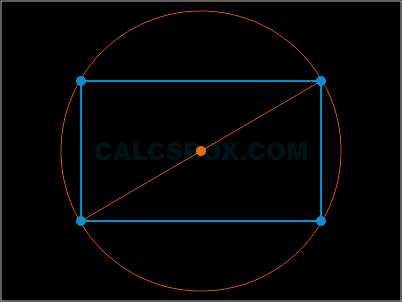
13. Вокруг прямоугольника всегда можно описать окружность

Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна \( 180^{\circ} \)

\( \angle ABC = \angle CDA = 180^{\circ},\enspace \angle BCD = \angle DAB = 180^{\circ} \)

14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом)

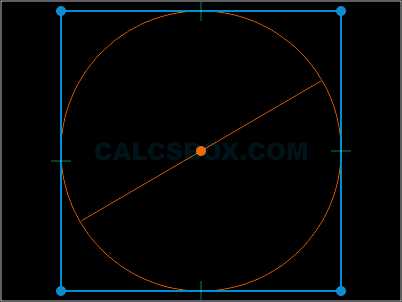
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

доказать, что параллелограмм у которого углы равны а диагонали перпендикулярны является квадратом

Все тут расписывать, честно говоря, лень, но подскажу: Углы равны, диагонали перпендикулярны. Противолежащие стороны тоже равны (параллелограмм, все же) . Стороны треугольников, которые образуют диагонали, тоже равны. Отсюда можно сделать вывод о равенстве всех 4-х треугольников, на которые параллелограмм разделен диагоналями (по признаку о стороне и 2-м прилежащим к ней углам) . Ну а раз они равны — равны и стороны параллелограмма. А что есть параллелограмм, у которого все стороны равны? Это квадрат. PROFIT!

а нафиг доказывать, нарисовал и все видно сразу …

Математика Докажите, что если диагонали параллелограмма равны и перпендикулярны, то этот параллелограмм является квадратом. Подробное решение тут —->>> <a rel=»nofollow» href=»https://www.youtube.com/watch?v=E04Rxy9Obo4″ target=»_blank»>https://www.youtube.com/watch?v=E04Rxy9Obo4</a>

touch.otvet.mail.ru