Работа с матрицами с – Работа с матрицами в C#

Работа с матрицами

Диапазон можно использовать как значение переменной, например x := 0,0.01..1.

Если разность прогрессии равна единице (то есть элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают. Например, чтобы сформировать по приведенной выше формуле матрицу размером 6 . 6, перед этой формулой надо указать i := 0..5 j := 0..5. При формировании матрицы путем присвоения значения ее элементам размеры матрицы можно не задавать заранее.

Всем неопределенным элементам автоматически присваиваются нулевые значения.

Например, формула M5,5 := 1 создает матрицу M размером 6 х 6, у которой все элементы, кроме расположенного в правом нижнем углу, равны 0.

Стандартные и пользовательские функции

Произвольные зависимости между входными и выходными параметрами задаются при помощи функций. Функции принимают набор параметров и возвращают значение, скалярное или векторное (матричное). В формулах можно использовать стандартные встроенные функции, а также функции, определенные пользователем.

Чтобы использовать функцию в выражении, надо определить значения входны параметров в скобках после имени функции. Имена простейших математических функций можно ввести с панели инструментов Calculator (Счет).

Информацию о других функциях можно почерпнуть в справочной системе. Вставить в выражение стандартную функцию можно при помощи команды

Insert.Function (Вставка.Функция). В диалоговом окне Insert Function (Встав-

ка функции) слева выбирается категория, к которой относится функция, а справа — конкретная функция. В нижней части окна выдается информация о выбранной функции. При вводе функции через это диалоговое окно автоматически добавляются скобки и заполнители для значений параметров.

Пользовательские функции должны быть сначала определены. Определение

задается при помощи оператора присваивания. В левой части указывается имя пользовательской функции и, в скобках, формальные параметры — переменные, от которых она зависит. Справа от знака присваивания эти переменные должны использоваться в выражении. При использовании пользовательской функции в последующих формулах ее имя вводят вручную. В диалоговом окне Insert Function (Вставка функции) оно не отображается.

Решение уравнений и систем

Для численного поиска корней уравнения в программе Mathcad используется

функция root. Она служит для решения уравнений вида f(x) = 0, где f(x) — выражение, корни которого нужно найти, а х — неизвестное. Для поиска

studfiles.net

Функции для работы с матрицами в Excel

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

Формулы массива

Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).

Порядок применения формулы массива:

1. Выделить диапазон, где должен появиться результат действия формулы.
2. Ввести формулу (как и положено, со знака «=»).
3. Нажать сочетание кнопок Ctrl + Shift + Ввод.

В строке формул отобразится формула массива в фигурных скобках.

Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.



Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+h3). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

Условие задачи:

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:h21). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

exceltable.com

36. Функции для работы с матрицами в табличном процессоре.

Средства MS Excel оказываются весьма полезны в линейной алгебре, прежде всего для операций с сматрицами и решения систем линейных уравнений.

Матрицы

Значительная часть математических моделей различных объектов и процессов записывается в достаточно простой и компактной матричной форме. В частности, при решении линейных уравнений мы имеем дело с матрицами и арифметическими действиями с ними. Что же такое матрица? Как выполняются действия с матрицами?

Матрицей размера m × n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Матрицы обозначаются прописными (заглавными) буквами латинского алфавита. Числа, составляющие матрицу, называются элементами матрицы и обозначаются строчными буквами с двойной индексацией: aij , где I – номер строки, а j – номер столбца.

Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой:

а из одного столбца – матрицей (вектором)-столбцом:

Если число строк матрицы равно числу столбцов и равно n, то такую матрицу называют квадратной n-го порядка. Например, квадратная матрица 2-го порядка:

Если у элемента матрицы aij номер столбца равен номеру строки (i=j), то такой элемент называется диагональным. Диагональные элементы образуют главную диагональ матрицы

Квадратная матрица с равными нулю всеми недиагональными элементами называется диагональной. Квадратная матрица называется единичной, если она диагональная, и все диагональные элементы равны единице. Различают единичные матрицы первого, второго, третьего и т. д. порядков

Матрица любого размера называется нулевой или нуль-матрицей, если все её элементы равны нулю

Как и над числами, над матрицами можно проводить ряд операций, причём в случае с матрицами некоторые из операций являются специфическими.

Транспонирование

Транспонированной называется матрица (АТ), в которой столбцы исходной матрицы (А) заменяются строками с соответствующими номерами.

В сокращённой записи, если А= (aij), то АТ= (aji).

Для обозначения транспонированной матрицы иногда используют символ «’» (A’). Транспонированием называется операция перехода от исходной матрицы (А) к транспонированной (АТ).

Из определения транспонированной матрицы следует, что если исходная матрица А имеет размер m×n, то транспонированная матрица АТ имеет размер n×m.

Для осуществления транспонирования в Excel используется функция ТРАНСП, которая позволяет поменять ориентацию массива на рабочем листе с вертикальной на горизонтальную и наоборот.

Функция имеет вид ТРАНСП (массив). Здесь массив – это транспонируемый массив или диапазон ячеек на рабочем листе. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и т. д. Рассмотрим это на примере.

Предположим, что диапазон ячеек A1:E2 введена матрица размера 2×5

Необходимо получить транспонированную матрицу.

1. Выделите (указателем мыши при нажатой левой кнопке) блок ячеек под транспонированную матрицу (52). Например, A4:B8.

2. Нажмите на панели инструментов Стандартная кнопку Вставка функции.

3. В появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Ссылки и массивы, а в рабочем поле Функция – имя функции ТРАНСП . После этого щелкните на кнопке ОК.

studfiles.net

Работа с векторами и матрицами.

Полученную переменную можно использовать для дальнейших вычислений, например:

>> x = 3 — a x =

2

Вы можете использовать стандартные математические операторы (+, -,*, /, ^) и функции, такие как sin, cos, tan (тангенс), cot (котангенс), log (натуральный

логарифм), log10(десятичный), log2, exp … Для изменения порядка выполнения операций используйте ( ). Аргументы функции задаются в круглых скобках.

Записав начальные буквы имени функции, и, нажав клавишу TAB, будет выведен список функций начинающихся с этих букв (если таковые есть) либо слово будет

дописано до конца.
>> sin
sin	sinc	single sinh	sinsml	sinusoid
sin_tr	sinfo	singvals sinint	sint	sinv

Во время работы вы можете получить справку по интересующей вас функции, набрав

>>help имя_функции

MATLAB это система, работающая с матрицами. Все численные

вычисления производятся в матричной форме. Система MATLAB выполняет сложные и трудоемкие операции над векторами и матрицами даже в режиме

прямых вычислений без какого-либопрограммирования. Ею можно пользоваться

как мощнейшим калькулятором, в котором наряду с обычными арифметическими

и алгебраическими действиями могут использоваться такие сложные операции, как инвертирование матрицы, вычисление ее собственных значений и принадлежащих им векторов, решение систем линейных уравнений, вывод графиков двумерных и трехмерных функций и многое другое. Интересно отметить, что даже обычные числа и переменные в MATLAB рассматриваются как матрицы размера 1×1, что дает единообразные формы и методы проведения

операций над обычными числами и массивами. Это также означает, что большинство функций может работать с аргументами в виде векторов и матриц.

При необходимости вектора и матрицы преобразуются в массивы, и значения

вычисляются для каждого их элемента.

studfiles.net

7 Работа с матрицами

7.1 Векторные и матричные операции

Некоторые из операторов MathCad имеют особые значения в применении к векторам и матрицам. Например, символ умножения * при применении к векторам означает скалярное умножение и умножение матриц — когда применяется к матрицам.

Векторные и матричные операторы доступны на панели Символьная. Если результатом является вектор, то это обязательно вектор-столбец, а не вектор-строка.

Таблица 7.1

Команды работы с векторами и матрицами

Обозначение	Клавиши	Пояснения
x * y	Ctrl+*	Векторное произведение трехмерных векторов x и y
An	^	Степень матрицы. Для квадратной матрицы А и целого положительного n вычисляется n-я степень матрицы А, при n отрицательном n-я степень обратной матрицы А.
|A|	|	Определитель матрицы.

А^-1 – обратная матрица – такая матрица, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Е — единичная матрица — квадратная матрица, элементыглавной диагоналикоторой равны единице, а остальные элементы равны нулю:

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

А^Т — транспонированная матрица — матрица, полученная из исходной матрицызаменой строк на столбцы.

Формально, транспонированная матрица для матрицы размеров— матрицаразмеров, определённая как A^T[i,j] = A[j,i].

Например,

и      

7.2 Функции, возвращающие специальные характеристики матриц

max(V) — возвращает максимальный по значению элемент матрицы V;

min(V) — возвращает минимальный по значению элемент матрицы V;

cols(V) — возвращает число столбцов матрицы V;

rows(V) — возвращает число строк матрицы V;

tr(V) — возвращает след (сумму диагональных элементов) квадратной матрицы V;

csort(V,n) — возвращает матрицу с переставленными строками в соответствии с элементами N-го столбца, расположенными по возрастанию;

rsort(V,n) — возвращает матрицу с переставленными столбцами в соответствии с элементами N-ой строки, расположенными по возрастанию.

7.3 Упражнения к теме 7

1. Переставить столбцы матрицы по элементам первой строки, по элементам второго столбца.

2. Найти сумму матриц и.

3. Найти матрицу 2А+5В, если и.

4. Найти произведения матриц АВ и ВА, если и.

5. Найти значение матричного многочлена , если, аЕ — единичная матрица третьего порядка.

6. Дана матрица . Найти обратную матрицу.

7. Найти матрицу , еслии.

8. Вычислить |А|, А^т, В^-1, А³, если

Найти максимальный элемент матрицы С=А*В.

Пример выполнения упражнения 1. Для решения системы уравнений включим панель инструментов Матрица: Вид — Панели инструментов — Матрица или воспользуемся кнопкой на панели Математическая . Вводим«D :=», далее можно воспользоваться комбинацией клавиш: «Ctrl» + «M» или выбрать пиктограмму на панели Матрица . На экране появляется менюВставка матрицы (рис. 6.2). Вводим число столбцов 3 и число строк 3, щелкаем ОК. Вводим элементы матрицы, перемещаясь по таблице с помощью клавиши Tab.

Вводим с клавиатуры функцию rsort, вводим аргументы D и 0 (т.к. по умолчанию нумерация строк и столбцов в MathCad начинается с 0), щелкаем знак «=», получаем результат:

studfiles.net

Раздел 2 — Работа с матрицами в Scilab(230114)

А.В.Сорокин

Среда вычислений Scilab: Первые шаги

2.Работа с матрицами в среде Scilab

2.1Задание матриц

Матрица в среде Scilab может вводиться несколькими способами:

—>a=[1 2 3; 2 3 4; 4 5 6] <Enter>

или

—>a=[1 2 3; <Enter> 2 3 4; <Enter> 4 5 6] <Enter>

Результат — матрица размере 3х3

a11	a12	a13
a a	a	a
21	22	23
a	a	a
31	32	33

1

Вектор столбец можно вводить b 2 несколькими способами

3

—>b=[1;2;3] <Enter>

или

—>b=[1 2 3]’ <Enter>

Таким образом матрица и вектор начинается с символа [ , а заканчивается символом ]. Разделение на элементы внутри строки осуществляется пробелом или символом ,. Разделение на строки осуществляется символом ;.

Обращаться к элементам матрицы или вектора можно так a(1,2) есть элемент a12 , b(2) есть элементb2 .

2.2Операции над матрицами и векторами

+- поэлементное сложение элементов матриц

— — поэлементное вычитание элементов матриц * — матричное умножение

Если одним из операндов является число, то элементы другого операнда (матрицы)

a	a		a c	a c
умножаются на это число. Если a 11	12		и c – число, то a c 11	12
a21	a22		a21c	a22c

.* — поэлементное умножение матриц / — матричное деление справа

Запись b/a означает ba 1

./ — поэлементное деление справа

24

А.В.Сорокин

Если	a	a		b
	a 11	12		и b 11
	a21	a22		b21

Среда вычислений Scilab: Первые шаги

			a11				a12
b					b		b
12		, то запись a ./ b означает результат	11			12
b22			a21				a22
							b22
			b21

\ — матричное деление слева Запись a\b означает a 1b

.\ — поэлементное деление слева

								b11
	a			b
Если		a			b		, то запись a .\ b означает результат			a
	a 11	12		и b 11	12			11
	a21	a22		b21	b22			b21
								a21

^ — возведение в степень

a

a

a

a

a

a

,

a

a

1

— т.е.

Если a 11

12

, то, a^211

12

11

12

a ^ ( 1)11

12

a21

a22

a21

a22

a21

a22

a21

a22

1

a

a

x

x

вычисление обратной,

2

, т.е. такая матрица

x

, что

a ^ ( 1/ 2)

11

12

11

12

a21

a22

x21

x22

x x a

.^ — поэлементное возведение в степень

1

1

a11

a12

a. ^ (1/ 2)

a112

a122

Если a

, то

1

1

a21

a22

a 2

a

2

21

22

‘- операция транспонирования матрицы a ‘aT

2.3 Примеры работы с матрицами

Пусть матрицы a и b заданы

—>a=[1 2; 3 4]

—>b=[2 1; 3 5] b =

21

35

Сложение и разность матриц

—>c=a+bc =

—>d=a-bd =

25

А.В.Сорокин		Среда вычислений Scilab: Первые шаги
* — матричное умножение
—>f=a*b
f =
8	11
18	23

.* — поэлементное умножение матриц

—>g=a.*b g =

2 2

920

/- матричное деление справа

—>h=a/b h =

-0.14290.4286 0.4286 0.7143

проверка правильности выполнения операции

—>j=h*b j =

1.0000 2.0000

3.0000 4.0000

./ — поэлементное деление справа

—>k=a./b

k =
0.5000	2.0000
1.0000	0.8000

\ — матричное деление слева

—>v=a\b

v=

-1.00003.0000 1.5000-1.0000

проверка правильности выполнения операции

>> j=a*v
j =
2.0000	1.0000
3.0000	5.0000

.\ — поэлементное деление слева

—>m=a.\b

m=

2.0000 0.5000

1.0000		1.2500
^ — возведение в степень
—>a2=a^2
a2 =
7	10
15	22

проверка правильности выполнения операции

—>a*a

26

А.В.Сорокин

Среда вычислений Scilab: Первые шаги

ans =

7 10

15 22

—>x=b^(1/2) x =

1.3251	0.2852
0.8557	2.1808
—>x*x
ans =
2.0000	1.0000
3.0000	5.0000

.^ — поэлементное возведение в степень

—>y=a.^2

транспонирование матрицы

—>at=a’ at =

13

24

Примечание. С матрицами можно строить выражение с использованием арифметических функций. При этом функция будет вычисляться от каждого элемента матрицы.

a	a		sin(a )		sin(a	)
Пример. Если a 11	12		, то sin(a)	11	12	.
a21	a22		sin(a21 )		sin(a22 )

2.4. Работа с блочными матрицами

Среда Scilab позволяет работь с блочными матрицами, что иногда бывает очень полезным.

Например, даны четыре матрицы: a 1				2 , b [3] ,c [4] ,d 5	6 . На основе них
можно построить блочную матрицу
a	b
	используя команду
c	d
—>[ a b ; c d] <Enter>
Или блочную матрицу		a	b
		d	c

используя команду

—>[ a b ; d c] <Enter>

27

А.В.Сорокин

Среда вычислений Scilab: Первые шаги

При построении блочной матрицы размеры соответствующих блоков должны быть согласованы.

Одной еще интересной возможностью является разбиение матрицы на блоки используя оператор двоеточие ( : ) для индексов матрицы.

k:n=[k k+1 k+2 … n-2n-1n], k<n

k:m:n=[k k+m k+2m … n-2mn-mn], еслиn-kнацело делится на m и m>0

2:5=[2 3 4 5] 2:2:12=[2 4 6 8 10 12]

k:-1:n=[kk-1k-2… n+2 n+1 n], k>n

k:m:n=[k k-mk-2m… n+2m n+m n], еслиk-nнацело делится на m и m<0

7:-1:3=[34 5 6 7]13:-2:1=[1311 9 7 5 3 1]

13:1=[ ] 2:-1:7=[]

Рассмотрим это на примере:

a11	a12	a13
Пусть имеется матрица a a	a	a		. Тогда
21	22	23
a	a	a
31	32	33
команда
—>s=a(1:2,2:3)<Enter>

2		3	, т.е. блок	a	a
помещает в переменную s матрицу s				12	13
	4	5		a22	a23

Если необходимо построить матрицу	a	a		, то это можно сделать командой
	11	13
	a31	a33
—>a([1 3],[1 3])

Конструкция [1 3] означает, что из матрицы a будут выбраны элементы с индексами 1 и 3. Например

—>a([1 2 3],[1 2 3])

или

—>a(1:3,1:3)

будем соответствовать всей матрице. А команды

—>a([3 2 1],[3 2 1])

или

—>a(3:-1:1,3:-1:1)

28

А.В.Сорокин			Среда вычислений Scilab: Первые шаги
			a33		a32	a31
матрице с переставленными строками и столбцами a a					a	a	.
				23	22	21
			a		a	a
				13	12	11
команда
—>a([1 3 2],[1 2 3])
выдаст следующую матрицу
a11	a13	a12
a a	a	a
21	23	22
a	a	a
31	33	32

Для построения из матрицы a матрицы с вычеркнутой 2-ойстрокой можно поступить следующим образом:

—>b=a([1 3], : )

или

—>b=a([1 3], 1:3)

Другим способом удаления строки или столбца является помещение на его место пустой матрицы [ ].

—>a(2, :)=[ ]

Какой способ является предпочтительным, зависит от типа конкретной решаемой задачи.

Используя описанные выше команды можно вычислять миноры матрицы. Рассмотрим

a11	a12	a13
это на вычислении определителя матрицы a a	a	a		раскладываемого по первой
21	22	23
a	a	a
31	32	33

строке:

d=a(1,1)*(-1)^(1+1)*det(a(2:3,2:3))+a(1,2)*(-1)^(1+2)*det(a(2:3,[13]))+a(1,3)*(-1)^(1+3)*det(a(2:3,1:2))

Здесь det( ) обозначает функцию вычисления определителя матрицы.

Реализуем метод Крамера для вычисления решения x системы

Ax b

где

29

А.В.Сорокин															Среда вычислений Scilab: Первые шаги
				a11			a12	a13				b1					x1
			A a				a	a			,	b b			,		x x		.
				21			22		23				2				2
				a			a	a				b					x
				31			32	33					3				3
формулами
	b a			a						a		b a							a		a	b
		1	12	13							11	1	13							11	12	1
	det b2		a22	a23				det		a12		b2	a23					det a21			a22	b2
	b a			a						a		b a							a		a	b
x		3	32	33		,	x				13	3	33			,	x			31	32	3
1			det A				2				det A						3			det A

последовательность команд будет такой

—>da=det(a)

—>x1=det([b a(:,2:3)])/da—>x2=det([a(:,1) b a(:,3)])/da—>x3=det([a(:,1:2) b])/da—>x=[x1;x2;x3]

Для проверки необходимо проверить вектор невязки на нуль

Ax b 0 ?

т.е. выполнить команду

—>e=a*x-b

По-другомуметод Крамера можно было бы реализовать так

—>da=det(a)

—>сa=a, ca(:,1)=b—>x1=det(ca)/da—>сa=a, ca(:,2)=b—>x2=det(ca)/da—>сa=a, ca(:,3)=b—>x2=det(ca)/da—>x=[x1;x2;x3]

2.5 Создание стандартных матрицы в среде Scilab

Определение размеров матрицы можно делать с помощью функции size —>[n,m]=size(A)

n = 3

m=

3

Для определения длины вектора наряду с функцией size можно использовать функцию length

30

А.В.Сорокин	Среда вычислений Scilab: Первые шаги
—>k=length(b)
k =
3

В среде Scilab имеется три функции, позволяющие создавать следующие матрицы: Для создания единичной матрицы порядка n можно использовать команду eye(n)

—>E=eye(3,3)

Команда

—>E=eye(2,3)

создает матрицу

Для создания матрицы порядка n состоящей из единиц можно использовать команду ones(n)

—>I=ones(3,3)

Команда

—>I=ones(3,2)

создает матрицу

Для создания матрицы порядка n состоящей из нулей можно использовать команду zeros(n)

—>Z=zeros(3,3)

31

А.В.Сорокин		Среда вычислений Scilab: Первые шаги
Z =
0	0	0
0	0	0
0	0	0

Команда

—>Z=zeros(1,3)

создает матрицу

Z =

0 0 0

2.6 Функции для обработки матриц

Функция det используется для вычисления определителя матрицы

—>a=[1 2; 2 1];—>d=det(a)

d=

= — 3

Функция rank используется для вычисления ранга матрицы

—>a=[1 2; 2 1];—>r=rank(a) r=

= 2

Функция inv используется для вычисления обратной матрицы

—>a=[1 2; 2 1];—>ia=inv(a)

ai =

-0.3333		0.6667
0.6667		-0.3333
—>a*ia
ans =
1	0
0	1

Используя эту функцию, можно решать систему линейных алгебраических уравнений ax b с помощью команды

—>x=inv(a)*b

В качестве альтернативы такого способа решения можно предложить два других

32

А.В.Сорокин		Среда вычислений Scilab: Первые шаги
—>x=a\b
и
—>x=a^(-1)*b
Функция diag используется как для получения из матрицы вектора диагональных
элементов
—>a=[1 2; 2 3];
—>h=diag(a)
h =
1
3
так и для построения матрицы с заданной диагональю
—>t=diag(h)
t =
1	0
0	3

Функция sum используется для суммирования элементов матрицы и вектора :

Суммирование элементов вектора

—>b=[1 2 3]—>s=sum(b) s =

6

Суммирование элементов столбцов

—>a=[1 2;

	3 4]
—>s=sum(a,1)
s =
4	6

Суммирование элементов строк

—>s=sum(a,2)s =

3

7

Функция prod используется для вычисления произведения элементов матрицы и вектора

:

Вычисление произведения элементов вектора

—>b=[1 2 3]—>p=prod(b) p =

6

Вычисление произведения элементов столбцов

—>a=[1 2; 3 4]

—>p=prod(a,1)p =

33

studfiles.net

4.4. Работа с матрицами

Векторы и матрицы рассматриваются в программе MathCad как одномерные и двумерные массивы данных. Число строк и столбцов матрицы задается в диалоговом окне Insert Matrix (Вставка матрицы), которое открывают командой Insert ► Matrix (Вставка ► Матрица). Вектор задается как матрица, имеющая один столбец.

После щелчка на кнопке ОК в формулу вставляется матрица, содержащая вместо элементов заполнители. Вместо каждого заполнителя надо вставить число, переменную или выражение.

Для матриц определены следующие операции: сложение, умножение на число, перемножение и прочие. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы. Например, выражение М+3, где М — матрица, означает, что к каждому элементу матрицы прибавляется число 3. Если требуется явно указать необходимость поэлементного применения операции к матрице, используют знак векторизации, для ввода которого служит кнопка Vectorize (Векторизация) на панели инструментов Matrix (Матрица). Например:

–обычное произведение матриц.

– поэлементное произведение матриц с использованием векторизации.

Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля. Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Subscript (Индекс) на панели инструментов Matrix (Матрица).

Пара индексов, определяющих элемент матрицы, разделяется запятой. Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки, например М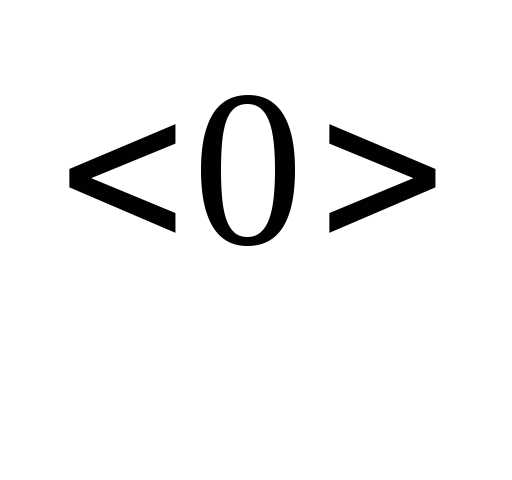. Для его ввода используется кнопка Matrix Column (Столбец) на панели инструментов Matrix (Матрица).

Чтобы задать общую формулу элементов матрицы, типа М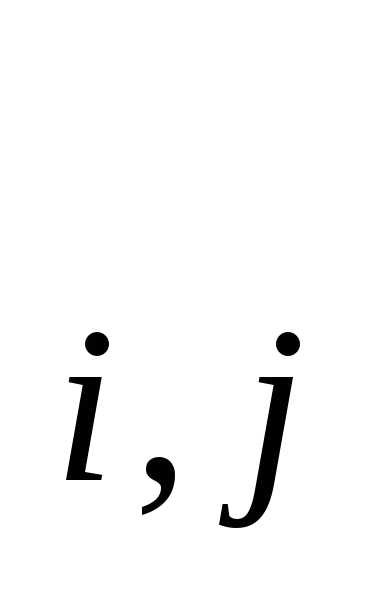:= i+j, используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента, через запятую значение второго и через точку с запятой значение последнего элемента. Точка с запятой при задании диапазона отображается как две точки (..). Диапазон можно использовать как значение переменной, например х := 0,0.01..1.

Если разность прогрессии равна единице (то есть, элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают. Например, чтобы сформировать по приведенной выше формуле матрицу размером 6x6, перед этой формулой надо указать i := 0..5 j := 0..5. При формировании матрицы путем присвое­ния значения ее элементам, размеры матрицы можно не задавать заранее. Всем неопределенным элементам автоматически присваиваются нулевые значения. Например, формула М_5,5 := 1 создает матрицу М размером 6x6, у которой все эле­менты, кроме расположенного в правом нижнем углу, равны 0.

Часть векторных и матричных функций Mathcad, использующих массивы в качестве параметров, приведена в таблице 5. (Более полную таблицу см. в Приложении 2.) В таблице введены следующие обозначения: А и В — массивы (векторы или матрицы), v и u — векторы; М и N -квадратные матрицы; z — скалярное выражение; n, m, k и s — целые числа. Символом  отмечаются операторы и функции, применимые к составным массивам.

Таблица 5. Векторные и матричные функции Mathcad.

Имя функции	Описание
Rows(A)	Возвращает число строк в массиве А ()
cols(A)	Возвращает число столбцов в массиве А ()
length(v)	Возвращает число элементов в векторе v ()
last(v)	Возвращает индекс последнего элемента в векторе v ()
max(A)	Возвращает наибольший элемент .в массиве А
min(A)	Возвращает наименьший элемент в массиве А
lsolve(M,v)	Возвращает вектор решения х (Мх=v)

studfiles.net