Периметр трапеции чему равен – Периметр трапеции | Формулы и расчеты онлайн

Содержание

Периметр трапеции — энциклопедический справочник и словарь для студента от А до Я

Формула периметра произвольной трапеции ABCD (рис. 1), в которой \(\ A B=a, B C=b, C D=C, A D=d \), имеет вид:

\(\ P_{A B C D}=a+b+c+d \)

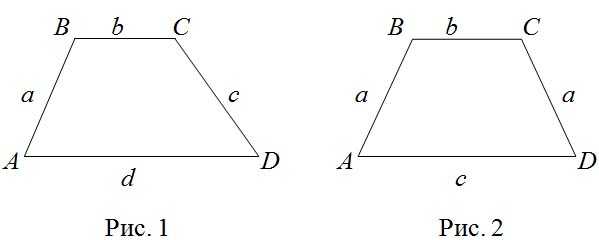
В случае, если трапеция ABCD – равнобокая (рис. 2), то есть \(\ A B=C D=a, B C=b, A D=C \) формула для периметра трапеции примет вид:

\(\ P_{A B C D}=2 a+b+c \)

Примеры решения задач

ПРИМЕР 1

Задание

Найти периметр равнобокой трапеции ABCD, стороны которой соответственно равны AB=CD=2 см, BC=3 см и AD=5 см.

Решение

Обозначим a=2 см, b=3 см и c=5 см. Для нахождения периметра заданной равнобокой трапеции воспользуемся формулой:

\(\ P_{A B C D}=2 a+b+c \)

Подставляя в неё исходные данные, получим

\(\ P_{A B C D}=2 \cdot 2+3+5=12 \) (см)

Ответ

Периметр трапеции равен \(\ P_{A B C D}=12 \mathrm{см} \)

ПРИМЕР 2

Задание

Найти периметр прямоугольной трапеции, если её основания равны соответственно 9 дм и 6 дм, а меньшая боковая сторона равна 4 дм.

Решение

Сделаем рисунок (рис. 3).

Обозначим \(\ A B=4, B C=6, A D=9 \) Опустим высоту из вершины C:

\(\ C H=A B=4 \)

Так как \(\ \mathrm{AH}=\mathrm{BC} \), то \(\ \mathrm{HD}=\mathrm{AD}-\mathrm{BC} \) , то есть

\(\ \mathrm{HD}=9-6=3 \)

Далее рассмотрим треугольник CHD, он прямоугольный, CD – гипотенуза. Найдем ее по теореме Пифагора:

\(\ C D=\sqrt{C H^{2}+H D^{2}} \)

Подставляя в последнее равенство известные значения катетов, получим

\(\ C D=\sqrt{4^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5(\mathrm{см}) \)

Периметр данной прямоугольной трапеции найдем по формуле

\(\ P_{A B C D}=a+b+c+d \)

В данном случае она примет вид:

\(\ P_{A B C D}=A B+B C+C D+A D \)

Подставляя длинны сторон трапеции в последнее равенство, получим

\(\ P_{A B C D}=4+6+5+9=24(\mathrm{см }) \)

Ответ

\(\ P_{A B C D}=24 \mathrm{см} \)

sciterm.ru

Формула периметра трапеции

Периметр трапеции равен сумме длин всех четырех сторон

Трапе́ция (от др. -греч. τράπέζιου — «столик» ; τράπεζα — «стол, еда» ) — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Иногда трапеция определяется как четырёхугольник, у которого произвольная пара противолежащих сторон параллельна, в этом случае параллелограмм является частным случаем трапеции

Периметр произвольной трапеции

Периметр произвольной трапеции, в которой AB=a, BC=b, CD=c, AD=d, имеет вид:

\[ \LARGE P_{ABCD} = a + b + c + d \]

где:
P — периметр трапеции
a, b, c, d — стороны трапеции

Периметр равнобокой трапеции

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

Периметр произвольной трапеции, в которой AB=CD=a, BC=b, AD=c, имеет вид:

\[ \LARGE P_{ABCD} = 2 \cdot a + b + c \]

где:
P — периметр трапеции
a, b, c, d — стороны трапеции

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны: ∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны: AC = BD

3. Одинаковые углы между диагоналями и основаниями: ∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°: ∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Также можно найти периметр трапеции, не зная длин оснований, но имея среднюю линию m. Средняя линия по определению представляет собой полусумму оснований трапеции, поэтому умножив ее на два, можно подставить ее вместо оснований в формулу периметра: \( P = 2 \cdot m + c + d \).

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

Формулы периметра трапеции и примеры применения

Сделаем рисунок (рис. 3).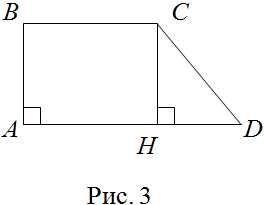

Обозначим . Опустим высоту из вершины :

Так как , то , то есть

Далее рассмотрим треугольник , он прямоугольный, – гипотенуза. Найдем ее по теореме Пифагора:

Подставляя в последнее равенство известные значения катетов, получим

(см)

Периметр данной прямоугольной трапеции найдем по формуле

В данном случае она примет вид:

Подставляя длинны сторон трапеции в последнее равенство, получим

(см)

ru.solverbook.com

Как найти периметр трапеции равнобедренной и прямоугольной

Прежде, чем приступить к расчету периметра трапеции, необходимо дать определение понятиям «периметр» и «трапеция», а так же изучить виды трапеций.

Периметр – это сумма длин всех сторон геометрической фигуры.

Так же в литературе имеется определение, согласно которому периметр – это длина линии, ограничивающей прямоугольную фигуру.

Трапеция – четырехугольник, две стороны которого параллельны (основания трапеции), а две другие стороны.

Виды трапеций

равнобедренная;
прямоугольная.

Если боковые стороны трапеции равны, трапеция называется равнобедренной.

В случае, когда одна из боковых сторон оказывается перпендикулярной основаниям – трапеция прямоугольная.

Определение периметра равнобедренной трапеции

Периметр равнобедренной трапеции определяется по формуле:

Периметр ABCD = a+b+c+d=2*a+b+d , где a, c – длина боковых сторон; b, d – длина сторон, являющихся основаниями.

Таким образом, если стороны равнобедренной трапеции равны – а=с=4см, b=5см, d=6см, периметр составит 19 см.: Периметр ABCD = 2*4+5+6=19 см.

Определение периметра прямоугольной трапеции

Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:

Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.

опустим высоту из вершины С, высота CH = AB = 5см;
исходя из рисунка 3, AH = BC = 7 см;
HD = AD – AH = 10 – 7 = 3 см;
далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.

Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же, для определения длины различных сторон трапеции могут помочь следующие формулы:

формула расчета длины основания через среднюю линию;
формулы длин сторон через высоту и угол при нижнем основании трапеции;
формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
формулы длин сторон равнобедренной трапеции через площадь.

Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.

kakumno.ru

Как найти периметр прямоугольной трапеции

Трапеция – это такой четырехугольник, у которого 2 параллельных основания, а остальные стороны не параллельны друг другу. У прямоугольной трапеции один угол прямой, как вы уже наверняка догадались.

Шаг 1. Формула вычисления периметра прямоугольной трапеции

Периметр прямоугольной трапеции вычисляется с помощью суммирования длин всех сторон, что весьма логично. Тут она от остальных фигур ну ничем не отличается:

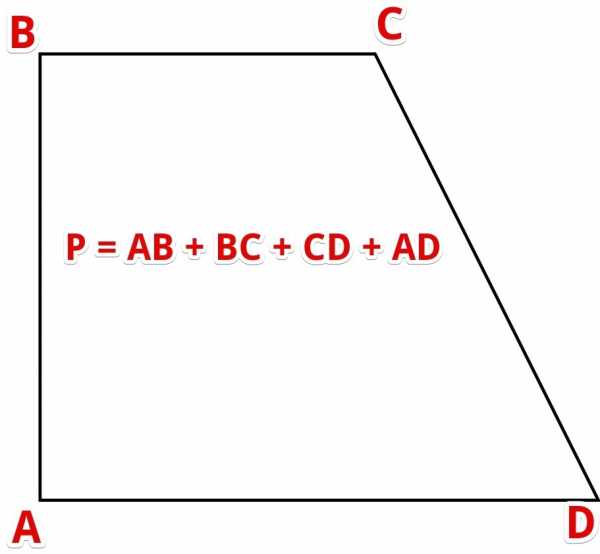
Шаг 2. Решение задач на тему определения периметра прямоугольной трапеции

Задача №1

Нужно найти периметр прямоугольной трапеции, когда даны длины всех сторон. Тут всё просто. Складываем все 4 значения, и готово. Это самый лёгкий вариант нахождения периметра. Остальные задачи в итоге всё равно сводятся к нему, но нужно рассмотреть и остальные варианты, интересно же!

Задача №2

Нужно найти периметр всё той же прямоугольной трапеции, но в этом случае мы знаем длину нижнего основания AD, которая равна a. Одна из боковых сторон CD, которая не перпендикулярна ему, равна d. Угол между этим основанием и стороной равен Альфа.

Решение задачи №2

Катеты находятся по таким формулам: CE = CD*sin(ADC), в свою очередь ED = CD*cos(ADC). Верхнее основание вычисляется так: BC = AD — ED = a — CD*cos(ADC) = a — d*cos(Альфа). Длина перпендикулярной стороны считается по формуле: AB = CE = d*sin(Альфа). После этих действий вы будете обладать драгоценными знаниями о длине всех сторон трапеции.

Задача №3

Требуется найти периметр трапеции, когда даны длины его оснований. AD = a, BC=c. Также мы знаем длину перпендикулярной стороны AB, которая равна b. Острый угол при неперпендикулярной стороне равен Альфа.

Решение задачи №3

Для начала проведите высоту трапеции на большее основание, начало которой будет лежать в вершине С. После этого восхитительного действия мы получаем отрезок CE и делим трапецию на 2 фигуры: прямоугольник

ABCE, а также треугольник ECD (прямоугольный). Гипотенузой треугольника в нашем случае будет известная нам сторона CD, один из катетов будет равен перпендикулярной боковой стороне нашей трапеции (опираемся на правило прямоугольника, по которому параллельные стороны равны). Длина другого отрезка будет равна разности оснований трапеции. И опять вроде всё просто.

Для начала снова проводим перпендикуляр CE и так же получаем прямоугольник ABCE вместе с треугольником CED. Осталось найти длину гипотенузы того треугольника, который мы получили, мы с уверенностью можем сказать, что CD = AB/sin(ADC) = b/sin(Альфа). Мы снова нашли все длины сторон. Осталось только их сложить. Надеемся, вы сможете сделать это без нас.

imdiv.com

Трапеция. Свойства, признаки, площадь. Средняя линия трапеции

Трапеция — четырехугольник, у которого две стороны параллельны, а две другие — нет.

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.

Если боковые стороны равны, трапеция называется равнобедренной.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме оснований:

Как видим, теория очень проста. А задачи, в которых применяются свойства трапеции, весьма разнообразны. В этой статье разобраны и стандартные задачи (номер и ), и более интересные.

. Найдите высоту трапеции , опущенную из вершины , если стороны квадратных клеток равны .

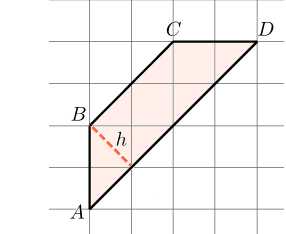
Высота трапеции — это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины .

Ответ: .

. Основания трапеции равны и , боковая сторона, равная , образует с одним из оснований трапеции угол . Найдите площадь трапеции.

Это стандартная задача. Углы и — односторонние, значит, их сумма равна , и тогда угол равен . Из треугольника найдем высоту . Катет, лежащий напротив угла в , равен половине гипотенузы. Получаем, что и площадь трапеции равна .

. Основания трапеции равны и . Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Скажите, что вы видите на чертеже? Можно сказать, что изображена трапеция , и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, и , в которых проведены средние линии.

Мы помним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны.

Из треугольника находим: .

Ты нашел то, что искал? Поделись с друзьями!

В следующей задаче мы тоже воспользуемся свойством средней линии треугольника.

. Основания трапеции равны и . Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем — среднюю линию трапеции, . Легко доказать, что отрезок , соединяющий середины диагоналей трапеции, лежит на средней линии. Дальше все просто. Найдем отрезки и , являющиеся средними линиями треугольников и , а затем отрезок . Он равен .

. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного , отсекает треугольник, периметр которого равен . Найдите периметр трапеции.

Периметр треугольника равен сумме его сторон, то есть .

Периметр трапеции равен .

На сколько периметр трапеции больше периметра треугольника? Чему равен периметр трапеции?

Ответ: .

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Как найти периметр трапеции

Трапеция – это четырехугольник, у которого две стороны параллельны. Для вычисления периметра трапеции необходимо сложить все стороны трапеции.

Ваши действия

Способ 1 из 3: Основная формула

Основная формула. Для вычисления периметра любой двумерной геометрической фигуры необходимо сложить все стороны этой фигуры. Трапеция имеет четыре стороны, поэтому периметр трапеции вычисляется по формуле: P = T + B + L + R
- где P — периметр, Т — верхняя сторона (верхнее основание), B — нижняя сторона (нижнее основание), L — левая боковая сторона, R – правая боковая сторона.
Сложите все стороны трапеции. Таким образом вы найдете периметр трапеции.
- Пример: дана трапеция с нижним основанием 3 см, верхним основанием 2 см и боковыми сторонами 1 см каждая. Найдите периметр трапеции.
  - T = 2 см, B = 3 см, L = 1 см, R = 1 см
  - Р = Т + В + L + R = 2 + 3 + 1 + 1 = 7 см
  - Окончательный ответ: периметр трапеции равен 7 см.
Основная формула годится в случаях, когда вам даны значения всех четырех сторон трапеции. В противном случае вам нужно найти недостающее значение или воспользоваться другой формулой.
- Вы можете найти периметр, если вам даны оба основания, высота и оба угла, прилежащих к нижнему основанию.
- Вы также можете найти периметр, если вам дано верхнее основание, обе боковые стороны и оба угла, прилежащих к нижнему основанию.

Способ 2 из 3: Боковые стороны не даны

Формула. Если вам не даны боковые стороны L и R, необходимо воспользоваться другой формулой. Заметим, что в этой формуле будут использоваться высота и оба угла, прилежащих к нижнему основанию: P = T + B + H * [(1/sin a₁) + (1/sin a₂)]
- где P — периметр, Т — верхняя сторона (верхнее основание), B — нижняя сторона (нижнее основание), Н — высота, a₁ и a₂ — углы, прилежащие к нижнему основанию (в градусах).
Сложите обратные величины синусов углов. Для нахождения синусов углов используйте калькулятор или таблицу.
- Пример: дана трапеция с нижним основанием 10 см, верхним основанием 5 см и высотой 8 см. Углы, прилежащие к нижнему основанию, равны 30 градусов и 45 градусов.
  - (1/sin a₁) + (1/sin a₂) = 1/sin(30) + 1/sin(45) = 2 + 1,414 = 3,414
Your ads will be inserted here by
Easy Plugin for AdSense.
Please go to the plugin admin page to
Paste your ad code OR
Suppress this ad slot.
Умножьте это значение на высоту трапеции. Высота трапеции Н – линия, соединяющая оба основания и пересекающая их под прямым углом.
- Пример: H = 8 см
  - H * [(1/sin a₁) + (1/sin a₂)] = 8 * 3,414 = 27,312
К этому значению прибавьте верхнее и нижнее основания B и Т.
- Пример: Т = 5 см; B = 10 см.
  - P = T + B + H * [(1/sin a₁) + (1/sin a₂)] = 5 + 10 + 27,312 = 42,312
Запишите ответ. Вы нашли периметр трапеции. Теперь запишите ответ, поставив соответствующие единицы измерения.
- Пример: периметр трапеции равен 42,312 см.

Способ 3 из 3: Высота или основание не даны

Разбейте трапецию на части. Вы можете найти периметр трапеции, если вам не дано нижнее основание, но даны три другие стороны и два угла, прилежащих к нижнему основанию. Вам нужно визуально разделить трапецию на три части: прямоугольник в центре и два треугольника по бокам. Для этого проведите две высоты из углов, прилежащих к верхнему основанию.
- Примечание: в итоге для вычисления периметра вы будете использовать основную формулу. Но до этого мы покажем, как найти нижнее основание трапеции.
- После разделения трапеции на три части, объедините два боковых треугольника так, чтобы они образовали один треугольник. Сейчас забудьте про среднюю часть трапеции (в виде прямоугольника) и сосредоточьтесь на этом треугольнике.
Определите, является ли полученный треугольник равносторонним. Если два данных угла, прилежащих к нижнему основанию, равны 60 градусов каждый, то треугольник является равносторонним, то есть у него все углы и все стороны одинаковы.
- Если ваш треугольник равносторонний, вы можете вычислить нижнее основание (для этого сложите верхнее основание и боковую сторону трапеции) и найти периметр трапеции.
- Пример X: дана трапеция с верхним основанием 7 см и двумя боковыми сторонами, равными 4,5 см каждая. Два угла, прилежащих к нижнему основанию, равны 60 градусов каждый.
  - Когда вы разобьете трапецию на части, вы получите равносторонний треугольник, у которого каждая сторона равна 4,5 см.
Найдите угол (если необходимо). Если треугольник не является равносторонним, найдите угол между его боковыми сторонами. Для этого вычтите сумму известных углов из 180 градусов.
- Пример Y: дана трапеция с верхним основанием 12 см, правой боковой стороной 5 см, левой боковой стороной 7 см и углами, прилежащими к нижнему основанию, равными 50 и 87 градусов соответственно.
  - Когда вы разобьете трапецию на части, вы получите треугольник с правой боковой стороной 5 см, левой боковой стороной 7 см и углами, прилежащими к основанию, равными 50 и 87 градусов.
  - Третий угол = 180 – (87 + 50) = 43 градусов.
Вычислите площадь треугольника. Теперь, когда вам известны две стороны и угол между ними, вы можете найти площадь треугольника по формуле: Площадь треугольника = (1/2) * S₁ * S₂ * sin(a)
- Пример Y: A = (1/2) * 7 см * 5 см * sin(43) = (1/2) * 7 * 5 * 0,68 = 11,9 кв. см.
Найдите основание треугольника. Теперь, когда вам известна площадь треугольника, боковые стороны и все три угла, вы можете найти основание треугольника. Для этого выберите один угол, прилежащий к основанию, и соответствующую боковую сторону. Вычислите основание треугольника по формуле: B = Площадь треугольника / (1/2 * S₁ * sin(a)
- Пример Y: B = 11,9 / [1/2 * 7 см * sin(87)] = 11,9 / 3,4951 = 3,405 см
Сложите значения основания треугольника и верхнего основания трапеции. Таким образом вы найдете нижнее основание трапеции.
- Пример X: Верхнее основание T = 7 см.
  - Основание треугольника равно 4,5 см.
  - Нижнее основание трапеции = 7 см + 4,5 см = 11,5 см.
- Пример Y: Верхнее основание T = 12 см.
  - Основание треугольника равно 3,405 см.
  - Нижнее основание трапеции = 12 + 3,405 = 15,405 см.
Используйте основную формулу для вычисления периметра трапеции. Теперь, когда вам известны все стороны трапеции, сложите их, чтобы найти периметр трапеции.
- Пример X: Нижнее основание трапеции = 11,5 см; T = 7 см; L = 4,5 см; R = 4,5 см.
  - Р = Т + В + L + R = 7 + 4,5 + 4,5 + 11,5 = 27,5 см.
  - Периметр трапеции равен 27,5 см.
- Пример Y: Нижнее основание трапеции = 15,405 см; Т = 12 см; L = 7 см; R = 5 см.
  - Р = Т + В + L + R = 12 + 15,405 + 7 + 5 = 39,405 см
  - Периметр трапеции равен 39,405 см.

Что вам необходимо

Калькулятор
Карандаш
Бумага