Площадь круга пи равна – Площадь круга равна пи

Почему площадь круга равна пи эр квадрат?

Несколько историй для детей про визуализацию математики из книги Стивена Строгаца «Удовольствие от х»

В школе нам не объясняли почему площадь круга равна пи эр квадрат.
Просто говорили, что это так. Между тем ребенок запомнит это гораздо лучше, если поймет, как к этому пришли. Точнее – увидит.

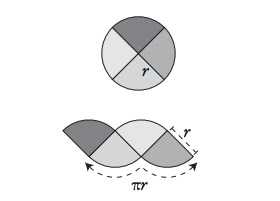
Можно разрезать круг на четыре части и сложить его иначе. Понятно, что площадь круга от этого не изменится. Видно, что две нижние дуги имеют общую длину, равную половине длины окружности исходного круга (потому что другая половина окружности приходится на две дуги сверху). Поскольку длина всей окружности в π раз больше диаметра, то ее половина в π раз больше половины диаметра, то есть радиуса r. Вот почему на рисунке показано, что πr — суммарная длина дуг фестонов в нижней части фигуры.
Во-вторых, прямые стороны кусочков имеют длину r, так как каждая из них первоначально была радиусом окружности

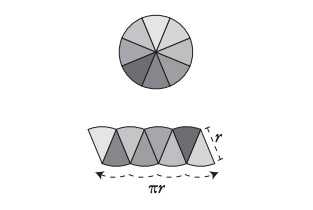
Повторим это же уже с восемью отрезками круга. Теперь фигура приобрела менее странную форму. Дуги сверху и снизу по-прежнему существуют, но они не столь ярко выражены. Еще одно усовершенствование: левая и правая стороны изогнутой фигуры стали более вертикальными, чем раньше. Несмотря на все изменения, два факта остаются постоянными: дуги внизу по-прежнему имеют длину πr, а каждая сторона — длину r. И конечно, площадь фигуры та же — это площадь исходного круга, так как это просто фигура, составленная из восьми частей круга.

По мере увеличения числа отрезков происходит нечто чудесное: фестоны все больше и больше разглаживаются, превращая фигуру в прямоугольник. Дуги становятся более плоскими, а стороны — почти вертикальными.

В пределе бесконечно большого числа частей фигура превратится в прямоугольник. Но, как и прежде, два факта все еще остаются неизменными: нижняя сторона прямоугольника равна πr, а высота — r. А площадь прямоугольника равна его ширине, умноженной на высоту, то есть произведение πr и r дает площадь прямоугольника, равную πr2

Или другая история, которую гораздо легче понять, выкладывая камушки.

1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25

Суммы нечетных чисел всегда оказываются идеальными квадратами.

А объяснение этому чуду довольно простое.

____

Или классическая история с маленьким Гауссом.
Однажды в Германии, в конце XVIII века, для того чтобы заставить учеников поработать, учитель дал им задание подсчитать сумму всех натуральных чисел от 1 до 100. Какова же было его удивление, когда уже через несколько минут один ученик сказал ему ответ: искомая сумма равна 5050.

Можно объяснить это тем, что Гаусс заметил, что гораздо проще складывать числа попарно.
1 + 100 = 2 + 99… И таких пар 50.

А можно визуализировать задачу через камушки. Для простоты скажем ребенку, что нужно посчитать сумму всех натуральных чисел от 1 до 10.

Очевидно, что можно просто дополнить пирамиду такой же пирамидой до прямоугольника.

Всего то – десять умножить на одиннадцать. И разделить на два

71sergey.livejournal.com

Почему площадь круга равна пи эр квадрат? / Интересное / magSpace.ru

Несколько историй для детей про визуализацию математики из книги Стивена Строгаца «Удовольствие от х»

В школе нам не объясняли почему площадь круга равна πr²
Просто говорили, что это так. Между тем ребенок запомнит это гораздо лучше, если поймет, как к этому пришли. Точнее – увидит.

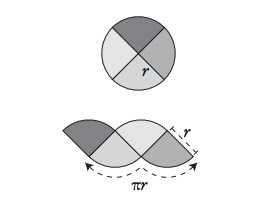
Можно разрезать круг на четыре части и сложить его иначе. Понятно, что площадь круга от этого не изменится. Видно, что две нижние дуги имеют общую длину, равную половине длины окружности исходного круга (потому что другая половина окружности приходится на две дуги сверху). Поскольку длина всей окружности в π раз больше диаметра, то ее половина в π раз больше половины диаметра, то есть радиуса r. Вот почему на рисунке показано, что πr

— суммарная длина дуг фестонов в нижней части фигуры. 

Во-вторых, прямые стороны кусочков имеют длину r, так как каждая из них первоначально была радиусом окружности

Повторим это же уже с восемью отрезками круга. Теперь фигура приобрела менее странную форму. Дуги сверху и снизу по-прежнему существуют, но они не столь ярко выражены. Еще одно усовершенствование: левая и правая стороны изогнутой фигуры стали более вертикальными, чем раньше. Несмотря на все изменения, два факта остаются постоянными: дуги внизу по-прежнему имеют длину πr, а каждая сторона — длину r. И конечно, площадь фигуры та же — это площадь исходного круга, так как это просто фигура, составленная из восьми частей круга.

По мере увеличения числа отрезков происходит нечто чудесное: фестоны все больше и больше разглаживаются, превращая фигуру в прямоугольник. Дуги становятся более плоскими, а стороны — почти вертикальными.

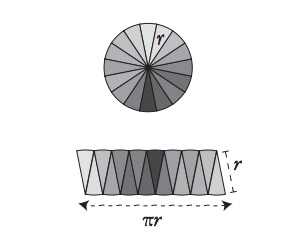
В пределе бесконечно большого числа частей фигура превратится в прямоугольник. Но, как и прежде, два факта все еще остаются неизменными: нижняя сторона прямоугольника равна πr, а высота — r. А площадь прямоугольника равна его ширине, умноженной на высоту, то есть произведение πr и r дает площадь прямоугольника, равную πr²

Или другая история, которую гораздо легче понять, выкладывая камушки.

1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25

Суммы нечетных чисел всегда оказываются идеальными квадратами.

А объяснение этому чуду довольно простое.

____

Или классическая история с маленьким Гауссом.

Однажды в Германии, в конце XVIII века, для того чтобы заставить учеников поработать, учитель дал им задание подсчитать сумму всех натуральных чисел от 1 до 100. Какова же было его удивление, когда уже через несколько минут один ученик сказал ему ответ: искомая сумма равна 5050.

Можно объяснить это тем, что Гаусс заметил, что гораздо проще складывать числа попарно. 
1 + 100 = 2 + 99… И таких пар 50.

А можно визуализировать задачу через камушки. Для простоты скажем ребенку, что нужно посчитать сумму всех натуральных чисел от 1 до 10.

Очевидно, что можно просто дополнить пирамиду такой же пирамидой до прямоугольника.

Всего то – десять умножить на одиннадцать. И разделить на два.

magspace.ru

Площадь круга — Википедия

Площадь круга радиуса

r равна πr². Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к его диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть ¹⁄₂ × 2πr × r).

Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Евдокс Книдский в пятом столетии до нашей эры обнаружил, что площади кругов пропорциональны квадратам их радиусов.^[1] Великий математик Архимед использовал методы евклидовой геометрии, чтобы показать, что площадь внутри окружности равна площади прямоугольного треугольника, основание которого имеет длину окружности, а высота равна радиусу окружности, в своей книге

Измерение круга^[en]. Длина окружности равна 2πr, а площадь треугольника равна половине основания на высоту, что даёт πr². До Архимеда Гиппократ Хиосский первый показал, что площадь круга пропорциональна квадрату его диаметра в его попытках квадрирования гиппократовых луночек^[2] Однако он не установил константу пропорциональности.

Использование многоугольников[править]

Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна половине длины окружности на радиус.^[3]

Доказательство Архимеда[править]

Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.

Не больше[править]

Круг с вписанными квадратом и восьмиугольником. Показан зазор

Предположим, что площадь круга C больше площади треугольника T = ¹⁄₂cr. Пусть E означает превышение площади. Впишем^[en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G₄ больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G₈. Продолжаем деление, пока общий зазор G_n не станет меньше E. Теперь площадь вписанного многоугольника P_n = C − G_n должна быть больше площади треугольника.

Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина

h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт ¹⁄₂nhs. Но h < r и ns < c, так что площадь многоугольника должна быть меньше площади треугольника ¹⁄₂cr, получили противоречие.

Не меньше[править]

Окружность с описанным квадратом и восьмиугольником. Показан зазор

Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G₄ больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше

D. Площадь многоугольника P_n должна быть меньше T.

Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.

Таким образом, площадь круга в точности равна площади треугольника.

Доказательство перегруппировкой[править]

Площадь круга после перегруппировки Анимация перегруппировки

Следуя Сато Мошуну ^[4] и Леонардо да Винчи ^[5], мы можем использовать вписанные правильные многоугольники другим способом. Положим, мы вписали шестиугольник. Разрежем шестиугольник на шесть треугольников, делая сечения через центр. Два противоположных треугольника содержат общие диаметры. Сдвинем теперь треугольники, чтобы радиальные стороны стали смежными. Теперь пара треугольников образует параллелограмм, в котором стороны шестиугольника образуют две противоположные стороны длиной

s. Две радиальные стороны становятся боковыми сторонами, а высота параллелограмма равна h (как в доказательстве Архимеда). Фактически, мы можем собрать все треугольники в один большой параллелограмм, располагая в ряд полученные параллелограммы (из двух треугольников). То же самое будет верно, если мы будем увеличивать число сторон. Для многоугольника с 2n сторонами параллелограмм будет иметь основание ns и высоту h. С ростом числа сторон длина основания параллелограмма увеличивается, стремясь к половине окружности, а высота стремится к радиусу. В пределе параллелограмм становится прямоугольником с шириной πr и высотой r.

Приближения площади круга единичного радиуса перегруппировкой треугольников.</span>

многоугольник			параллелограмм
n		сторона		основание		высота		площадь
4		1,4142136		2,8284271		0,7071068		2,0000000
6		1,0000000		3,0000000		0,8660254		2,5980762
8		0,7653669		3,0614675		0,9238795		2,8284271
10		0,6180340		3,0901699		0,9510565		2,9389263
12		0,5176381		3,1058285		0,9659258		3,0000000
14		0,4450419		3,1152931		0,9749279		3,0371862
16		0,3901806		3,1214452		0,9807853		3,0614675
96		0,0654382		3,1410320		0,9994646		3,1393502
∞		1/∞		π		1		π

Интегрирование[править]

Площадь круга путём интегрирования

Используя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2πt dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.

Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:

Быстрая аппроксимация[править]

Вычисления, проведённые Архимедом, были трудоёмкими и он остановился на многоугольнике с 96 сторонами. Более быстрый метод использует идеи Снелла (1621), позднее развитые Гюйгенсом (1654) ^[6].

Метод удвоения Архимеда[править]

Если задан круг, пусть u_n будет периметром вписанного правильного n-угольника, а U_n — периметром описанного правильного n-угольника. Тогда u_n и U_n являются нижней и верхней границей длины окружности, которые становятся точнее с ростом n, а их среднее значение (u_n + U_n)/2 становится особенно хорошей аппроксимацией длины окружности. Чтобы вычислить u_n и U_n для больших n, Архимед вывел следующие формулы:

   (среднее геометрическое)

   (среднее гармоническое).

Начав с шестиугольника, Архимед удваивал n четыре раза, дойдя до 96-угольника, который дал ему хорошую аппроксимацию длины окружности круга.

В современных обозначениях можно воспроизвести эти вычисления (и пойти дальше). Для единичной окружности вписанный шестиугольник имеет периметр u₆ = 6, а описанный шестиугольник имеет периметр U₆ = 4√3. Удваиваем семь раз, получаем

Удвоения Архимеда семь раз; n = 6×2^k.

k		n		un		Un		(un + Un)/4
0		6		6,0000000		6,9282032		3,2320508
1		12		6,2116571		6,4307806		3,1606094
2		24		6,2652572		6,3193199		3,1461443
3		48		6,2787004		6,2921724		3,1427182
4		96		6,2820639		6,2854292		3,1418733
5		192		6,2829049		6,2837461		3,1416628
6		384		6,2831152		6,2833255		3,1416102
7		768		6,2831678		6,2832204		3,1415970

(здесь (u_n + U_n)/2 аппроксимирует длину единичной окружности, которая равна 2π, так что (u_n + U_n)/4 аппроксимирует π)

Последняя строка таблицы содержит ³⁵⁵⁄₁₁₃ — лучшее рациональное приближение, то есть не существует приближения лучшего этого со знаменателем до 113.
Число ³⁵⁵⁄₁₁₃ является прекрасным приближением для π, нет рационального числа более близкого к π со знаменателем до 16604.^[7]

Улучшение Снелла-Гюйгенса[править]

Снелл предложил (а Гюйгенс доказал) более тесные границы, чем у Архимеда:

Для n = 48 формула даёт приближение лучше (около 3,14159292), чем метод Архимеда для n = 768.

Развитие формулы удваивания Архимеда[править]

Круг с подобными треугольниками, описанным, вписанным и дополнительным

Пусть одна сторона вписанного правильного n-угольника имеет длину s_n и пусть точки A и B — её концы. Пусть A′ — противоположная A точка на окружности, так что A′A является диаметром, а A′AB является вписанным треугольником, опирающимся на этот диаметр. По теореме Фалеса этот треугольник является прямоугольным (угол B прямой). Пусть длина A′B равна c_n и эту длину будем называть дополнением s_n. Тогда c_n²+s_n² = (2r)². Пусть точка C делит дугу AB пополам, и пусть C′ является противоположной C точкой окружности. Тогда длина CA равна s_2n, длина C′A равна c_2n, а C′CA снова является прямоугольным треугольником, опирающимся на диаметр C′C. Поскольку C делит дугу AB пополам, диаметр C′C перпендикулярен хорде AB, которую он пересекает, скажем, в точке P. Треугольник C′AP тогда прямоуголен и подобен C′CA, поскольку у них общий угол C′. Получаем, что все три соответствующие стороны находятся в одной и той же пропорции. В частности, мы имеем C′A : C′C = C′P : C′A и AP : C′A = CA : C′C. Центр окружности O делит A′A пополам, так что треугольник OAP подобен A′AB и длина OP равна половине длины A′B. В результате получаем

В первом равенстве отрезок C′P равен сумме C′O+OP, что равно r+¹⁄₂c_n, а отрезок C′C является диаметром и его длина равна 2r. Для единичного круга получаем знаменитую формулу удвоения Людольфа Ван Цейлена

Если мы теперь построим правильный описанный n-угольник со стороной ″B″, параллельной AB, то OAB и OA″B″ являются подобными с отношением подобия A″B″ : AB = OC : OP. Обозначим описанную сторону S_n, тогда отношение превращается в S_n : s_n = 1 : ¹⁄₂c_n. (Мы снова используем факт, что OP равен половине of A′B.) Получаем

Обозначим периметр вписанного многоугольника через u_n = ns_n, а описанного через U_n = nS_n. Комбинируя равенства, получим

так что

Получили среднее геометрическое.

Можно также вывести

или

Получили среднее гармоническое.

Аппроксимация случайными бросаниями[править]

Площадь единичного круга методами Монте-Карло. После 900 бросаний получаем 4×⁷⁰⁹⁄₉₀₀ = 3,15111…

Если более эффективные методы недоступны, можно прибегнуть к «бросанию дротиков». Этот метод Монте-Карло использует факт, что при случайных бросаниях точки равномерно по площади квадрата, в котором расположен круг, число попаданий в круг приближается к отношению площади круга на площадь квадрата. Следует принимать этот метод как последнюю возможность вычисления площади круга (или фигуры любой формы), поскольку для получения приемлемой точности требует огромного числа испытаний. Для получения точности 10⁻ⁿ необходимо около 100ⁿ случайных испытаний ^[8].

Конечная перегруппировка[править]

Как мы видели, разбив диск на бесконечное число кусков мы можем из них затем собрать прямоугольник. Интересный факт был открыт относительно недавно Лацковичем ^[9], что мы можем разбить круг на большое, однако конечное число кусков, а затем перегруппировать их в квадрат той же площади. Сам вопрос о таком конечном разбиении носит название «Квадратура круга Тарского».

Мы можем растянуть круг до формы эллипса. Поскольку это растяжение является линейным преобразованием плокости, оно изменяет площадь, но сохраняет отношения площадей. Этот факт можно использовать для вычисления площади произвольного эллипса, отталкиваясь от площади круга.

Пусть единичный эллипс описан квадратом со стороной 2. Преобразование переводит круг в эллипс путём сжатия или растяжения горизонтального и вертикального диаметров до малой и большой оси эллипса. Квадрат становится прямоугольником, описанным вокруг эллипса. Отношение площади круга к площади квадрата равно π/4, и отношение площади эллипса к площади прямоугольника будет тоже π/4. Если a и b — длины малой и большой осей эллипса. Площадь прямоугольника будет равна ab, а тогда площадь эллипса — πab/4.

Мы можем распространить аналогичные техники и на большие размерности. Например, если мы хотим вычислить объём внутри сферы, и мы знаем формулу для площади сферы, мы можем использовать приём, аналогичный «луковичному» подходу для круга.

Метод треугольника[править]

Круг, развернутый треугольник Круг и треугольник имеют одну площадь.

Этот метод является модификацией доказательства, использующего окружности. Представим себе разворачивание концентричных кругов в отрезки, получим прямоугольный треугольник с высотой r и основанием 2πr (получаемое из внешней окружности круга).

Вычисление площади треугольника даст площадь круга:

Площадь = ½ * основание * высота= ½ * 2 π r * r = π r².

• Archimedes в переводе Хиса (T. L. Heath) The Works of Archimedes. — Dover, c. 260 BCE, год публикации 2002. —. — ISBN 978-0-486-42084-4.
  
• Petr Beckmann A History of Pi. — St. Martin’s Griffin, 1976. — ISBN 978-0-312-38185-1.
• J. Gerretsen, P. Verdenduin Fundamentals of Mathematics, Volume II: Geometry. — MIT Press, 1983. —. — ISBN 978-0-262-52094-2.
• Miklós Laczkovich Equidecomposability and discrepancy: A solution to Tarski’s circle squaring problem // Journal für die reine und angewandte Mathematik. — 1990. —. —.
• Serge Lang Math! : Encounters with High School Students. — Springer-Verlag, 1985. — ISBN 978-0-387-96129-3.
• David Eugene Smith, Yoshio Mikami A history of Japanese mathematics. — Chicago: Open Court Publishing, 1914. —. — ISBN 978-0-87548-170-8.
• J. M.Thijsse Computational Physics. — Cambridge University Press, 2006. —. — ISBN 978-0-521-57588-1.

1. ↑ James Stewart. Single variable calculus early transcendentals.. — 5th.. — Toronto ON: Brook/Cole, 2003. — С. 3. — ISBN 0-534-39330-6.
2. ↑ Thomas L. Heath A Manual of Greek Mathematics. — Courier Dover Publications, 2003. —. — ISBN 0-486-43231-9..
3. ↑ Hill, George. Лекции по кеометриидля начинающих, страница 124 (1894).
4. ↑ Smith, Mikami, 1914
5. ↑ Beckmann, 1976
6. ↑ Gerretsen, Verdenduin, 1983
7. ↑ Не все лучшие рациональные приближения сводятся к непрерывным дробям!
8. ↑ Thijsse, 2006
9. ↑ Laczkovich, 1990

Внешние ссылки[править]

www.wiki-wiki.ru

Ответы@Mail.Ru: Найдите площадь круга

Площадь круга равна = Пи* радиус в квадрате

Площадь = пи умноженое на радиус в квадрате а) 22/7*36 б) 22/7*7^2

<a rel=»nofollow» href=»http://www.fxyz.ru/формулы_по_геометрии/формулы_площади/площадь_круга/» target=»_blank» >смотри здесь</a>

1) площадь круга равна ПR(в квадрате) . получаем 3,14*36=113,04 2)диаметр-это половина радиуса, соответственно радиус равен 2D=14*2=28. ПЛОЩАДЬ ЕГО РАВНА: 3,14*784=2461,76

touch.otvet.mail.ru

Помогите Длинна окружности равна 16пи см. Найти площадь круга, ограниченного этим кругом

длина окружности эт 2пирадиус то есть радиус 8, площадь пи*радиус в квадрате, площадь=64пи

8 пи в квадрате

Радиус=16пи/2пи=8см. Площадь=64пи

Просто: c=2пr r=16п/2п=8 S=пr^2 S=п8^2=64п

L= 2пR=16п значит R=8 S=пR^2 значит S=64п

длинна окружности равна 2 пи умноженное на радиус… выражаем радиус…. а площадь круга равна 2 пи умноженное на радиус в квадрате… вот и все!!!!

touch.otvet.mail.ru