Полная таблица неопределенных интегралов – Решим задачи, контрольные, курсовые… — Таблица неопределенных интегралов

Таблица первообразных. Таблица интегралов. Таблица неопределенных интегралов.

Интеграл степенной функции.	Интеграл степенной функции.
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
—
Интеграл экспоненциальной функции.	Интеграл экспоненты, где a-постоянное число.
Интеграл сложной экспоненциальной функции.	Интеграл экспоненциальной функции.
—
Интеграл, равняющийся натуральному логарифму.	Интеграл : «Длинный логарифм».
	Интеграл : «Длинный логарифм».
Интеграл : «Высокий логарифм».	Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логарифму.
Интеграл : «Высокий логарифм».
—
Интеграл косинуса.	Интеграл синуса.
Интеграл, равный тангенсу.	Интеграл, равный котангенсу.
—
Интеграл, равный как арксинусу, так и арккосинусу

dpva.ru

Понятие и свойства неопределённого интеграла, таблица интегралов

Неопределённый интеграл: 8 фактов, которые надо знать студенту

Факт 1. Интегрирование — действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x).

Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений x из этого промежутка выполняется равенство F ‘(x)=f(x), то есть данная функция f(x) является производной от первообразной функции F(x)..

Например, функция F(x) = sin x является первообразной для функции

f(x) = cos x на всей числовой прямой, так как при любом значении икса (sin x)’ = (cos x).

Определение 2. Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись

∫ 

f(x)dx

,

где знак ∫  называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.

Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то

∫ 

f(x)dx = F(x) +C

,                 (1)

где C — произвольная постоянная (константа).

Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция — «быть дверью». А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции «быть дверью», то есть её неопределённым интегралом, является функция «быть деревом + С», где С — константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции «сделана» из первообразной функции при помощи

формулы, которую мы узнали, изучая производную.

Тогда таблица функций распространённых предметов и соответствующих им первообразных («быть дверью» — «быть деревом», «быть ложкой» — «быть металлом» и др.) аналогична таблице основных неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов перечисляются распространённые функции с указанием первообразных, из которых «сделаны» эти функции. В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы.

Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C, а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C, например, так: 5x³+С. Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x

³+4 или 5x³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.

Поставим задачу интегрирования: для данной функции f(x) найти такую функцию F(x), производная которой равна f(x).

Пример 1.Найти множество первообразных функции

Решение. Для данной функции первообразной является функция

так как

Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x) dx, т.е.

или

                     (2)

Следовательно, функция — первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции

и вообще

где С – произвольная постоянная. В этом можно убедиться дифференцированием.

Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.

---

Теорема (формальное изложение факта 2). Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C , где С

– произвольная постоянная.

---

В следующем примере уже обращаемся к таблице интегралов, которая будет дана в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.

Пример 2.  Найти множества первообразных функций:

1)   

2)

3)

Решение. Находим множества первообразных функций, из которых «сделаны» данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.

1) Применяя формулу (7) из таблицы интегралов при n = 3, получим

2) Используя формулу (10) из таблицы интегралов при

n = 1/3,  имеем

3) Так как

то по формуле (7) при n = -1/4 найдём

Под знаком интеграла пишут не саму функцию f, а её произведение на дифференциал dx. Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,

, ;

здесь в обоих случаях подынтегральная функция равна , но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной x, а во втором — как функция от z.

Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.

Пусть требуется найти кривую

y=F(x) и мы уже знаем,что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.

Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F'(x). Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy.

Назовём график первообразной функции от f(x) интегральной кривой. Если F'(x)=f(x), то график функции y=F(x) есть интегральная кривая.

Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых

, как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C.

Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.

---

Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.

                  (3)

Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.

---

Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.

  (4)

---

Факт 7. Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.

  (5)

---

Факт 8. Пользусь таблицей неопределённых интегралов, свойствами неопределённого интеграла и методами интегрирования, можно отыскать неопределённый интеграл любой функции.

Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами:

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

 

Продолжение темы «Интеграл»

Поделиться с друзьями

function-x.ru

Таблица неопределенных интегралов

Функции, содержащие a 2   + x 2   , a 2   — x 2   , a + bx 2

1)     = arctgx + C

2)     =  1  a arctg  x  a + C

4)     =   1 ab arctg(x  b  a ) + C   при a > 0 и b > 0

Если a и b отрицательны, то знак «−» выносится за интеграл, а если a и b разных знаков, то использовать следущую формулу (№5)

6)     = ln x 2   +  a  b + C

7)     =  x  b —  a  b  , затем см. №4 или №5

9)     = — —  b  a  , затем см. №4 или №5

10)     = +  , затем см. №4 или №5

Функции, содержащие a + bx

1)     a + bx  dx = (a + bx) 3   + C

2)     x a + bx  dx = — 2(2a — 3bx) (a + bx) 3   + C

3)     x 2   a + bx  dx = 2(8a 2   — 12abx + 3b 2   x 2   ) (a + bx) 3   + C

4)     xdx a + bx = — a + bx + C

5)     a + bx = 2(8a 2   — 4abx + 3b 2   x 2   ) a + bx + C

7)     dx x a + bx = 2 -a arctg a + bx -a + C , при a

Функции, содержащие

3)     x  dx =  1  3 + C

6)       dx =   x a 2   + C

11)       dx x 2   = − + C

Функции, содержащие

1)       dx = arcsinx + C

2)       dx = arcsin  x  a + C

3)       dx =     x a 2   + C

5)       xdx =     1 + C

6)     = −  x  2 +  1  2 a 2   arcsin  x  a + C

7)     dx =  x  2 +  1  2 a 2   arcsin  x  a + C

8)     dx =  x  8 (5a 2   — 2x 2   ) +  3  8 a 4   arcsin  x  a + C

9)     x dx = −  1  3 + C

10)     x dx = −  1  5 + C

11)     x 2   dx =  x  8 (2x 2   — a 2   ) +  1  8 a 4   arcsin  x  a + C

12)     =   x — arcsin  x  a + C

14)       dx x 2   = − + C

17)     dx = −  1  x — arcsin  x  a + C

Функции, содержащие

2)       dx = −     x a 2   + C

6)     x  dx =  1  3 + C

7)     x  dx =  1  5 + C

11)       dx x = arcsecx + C

12)       dx x =  1  a arcsec  x  a + C

14)       dx x 3   = + arcsec  x  a + C

15)     dx = — a*arccos  a  x + C

Функции, содержащие ,

Функция, содержащая интегрируется подстановкой t = x — a.

Тогда получает вид , и интеграл находят в группе

для функций, содержащих . Если его в таблице нет,

то стараются привести его к виду, имеющемуся в таблице.

То же можно сказать и о функции, содержащей выражение .

В этом случае подстановка t = x + a приводит радикал к виду

Функции, содержащие a + bx + cx 2     (c > 0)

1)     = 2 arctg 2cx + b + C , если b 2

Функции, содержащие a + bx — cx 2     (c > 0)

2)       dx = 1 c arcsin   2cx — b + C

Другие алгебраические функции

2)      a — x  b + x dx = + (a + b)arcsin  x + b  a + b + C

3)      a + x  b — x dx = − — (a + b)arcsin  b — x  a + b + C

4)      1 + x  1 — x dx = − + arcsinx + C

5)     dx = 2arcsin  x — a  b — a + C

Показательные и тригонометрические функции

1)     a x   dx = + C

2)     e x   dx = e x   + C

3)     e ax   dx = + C

4)     sinx dx = -cosx + C

5)     cosx dx = sinx + C

6)     tgx dx = -ln|cosx| + C

7)     ctgx dx = ln|sinx| + C

8)     secx dx = ln|secx + tgx| + C = ln tg(  π  4 +  x  2 ) + C

9)     cosecx dx = ln|cosecx — ctgx| + C = ln tg  x  2 + C

10)     sec 2   x dx = tgx + C

11)     cosec 2   x dx = -ctgx + C

12)     secx*tgx dx = secx + C

13)     cosecx*ctgx dx = -cosecx + C

14)     sin 2   x dx =  x  2 —  1  4 sin2x + C

15)     cos 2   x dx =  x  2 +  1  4 sin2x + C

16)     sin n   x dx = − +  n — 1  n sin n — 2   x dx

Эта формула применяется несколько раз, пока не приведет к интегралу

sinx dx или sin 2   x dx (в зависимости от n, четное или нечетное), затем №4 или №14.

17)     cos n   x dx = +  n — 1  n cos n — 2   x dx

Аналогично предыдущему интегралу, затем №5 или №15.

18)     = −    1    n — 1 +  n — 2  n — 1

Эта формула применяется несколько раз, пока не приведет к интегралу

dx или    dx    sinx (в зависимости от n, четное или нечетное), затем №9.

19)     =    1    n — 1 +  n — 2  n — 1

Аналогично предыдущему интегралу, затем №8.

20)     sinx * cos n   x dx = − + C

21)     sin n   x * cosx dx = + C

22)     sin n   x * cos m   x dx = cos m — 1   x * sin m + 1   x m + n   +  m — 1  m + n sin n   x * cos m — 2   x dx

Применяется несколько раз, пока степень косинуса не будет равна нулю (если m — четное) или единице (если m — нечетное). В первом случае см.№16, во втором — №21. Этой формулой следует пользоваться, когда m n, то лучше пользоваться №23.

23)     sin n   x * cos m   x dx = − cos m + 1   x * sin n — 1   x m + n   +  n — 1  m + n sin n — 2   x * cos m   x dx

Аналогично предыдущему интегралу, затем №17 и №20.

24)     sin(mx)sin(nx)dx = −  sin(m + n)x  2(m + n) +  sin(m — n)x  2(m — n) + C ,   (m ≠ n).

25)     cos(mx)cos(nx)dx =  sin(m + n)x  2(m + n) +  sin(m — n)x  2(m — n) + C ,   (m ≠ n).

26)     sin(mx)cos(nx)dx = −  cos(m + n)x  2(m + n) −  cos(m — n)x  2(m — n) + C ,   (m ≠ n).

27)     =   2 arctg(  a — b  a + b tg  x  2 ) + C , если a > b

29)     =   2 arctg + C , если a > b

31)       dx a 2   cos 2   x + b 2   sin 2   x =  1  ab arctg(  b tgx  a ) + C

32)     e x   sinx dx = + C

33)     e ax   sin(nx) dx = e ax   (a sin(nx) — n cos(nx)) + C

34)     e x   cosx dx = + C

35)     e ax   cos(nx) dx = e ax   (n sin(nx) + a cos(nx)) + C

36)     x e ax   dx = (ax — 1) + C

37)     x n   e ax   dx = —  n  a x n — 1   e ax   dx

Формула применяется несколько раз, пока степень х не станет равной единице, затем см. №36

38)     x a mx   dx = — + C

39)     x n   a mx   dx = —    n    m ln(a) x n — 1   a mx   dx

Формула применяется несколько раз, пока степень х не станет равной единице, затем см. №38

40)     e ax   cos n   dx = e ax   cos n — 1   x(a cosx + n sinx) + e ax   cos n — 2   dx

Формула применяется несколько раз, пока косинус не исчезнет (если четное n) или его степень не станет равной единице (если нечетное n), затем см. №35

41)     sh x dx = ch x + C

42)     ch x dx = sh x + C

43)     th x dx = ln|ch x| + C

44)     cth x dx = ln|sh x| + C

45)     sch x dx = 2arctg e x   + C

46)     csch x dx = ln|th  x  2 | + C

47)     sch 2   x dx = th x + C

48)     csch 2   x dx = -cth x + C

49)     sch x th x dx = sch x + C

50)     csch x cth x dx = -csch x + C

51)     sh 2   x dx = −  x  2 +  1  4 sh3x + C

52)     ch 2   x dx =  x  2 +  1  4 sh3x + C

Логарифмические функции

Даются функции, содержащие только натуральный логарифм. Если требуется найти интеграл от функции, содержащей логарифм при другом основании, то предварительно переводят его в натуральный по формуле

log   a x =  ln(x)  ln(a) , а затем пользуются таблицей.

1)     ln(x)dx = x ln(x) — x + C

2)     = ln|ln(x)| + C

3)     x n   ln(x)dx = x n + 1   (   ln(x)   n + 1 − ) + C

4)     ln n   (x)dx = x ln n   (x) — n ln n — 1   (x)dx

Формулу применять до тех пор, пока не получится интеграл ln(x)dx , затем №1

5)     x m   ln n   (x)dx = ln n   (x) —    n    m + 1 x m   ln n — 1   (x)dx

Формулу применять до тех пор, пока не получится интеграл №3

mateshka.ru

Таблица основных неопределенных интегралов. Правила интегрирования. Интегралы от степенной, показательной, тригонометрических функций

Главные интегралы, которые должен знать каждый студент

Перечисленные интегралы — это базис, основа основ. Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.

Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забывайте при интегрировании добавлять к ответу произвольную постоянную С!

Интеграл от константы

∫Adx=Ax+C (1)

Интегрирование степенной функции

В действительности, можно было ограничиться только формулами (5) и (7), но остальные интегралы из этой группы встречаются настолько часто, что стоит уделить им немного внимания.

∫xdx=x22+C (2)
∫x2dx=x33+C (3)
∫1xdx=2x+C (4)
∫1xdx=ln|x|+C (5)
∫1x2dx=−1x+C (6)
∫xndx=xn+1n+1+C(n≠−1) (7)

Интегралы от показательной функции и от гиперболических функций

Разумеется, формулу (8) (пожалуй, самую удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.

∫exdx=ex+C (8)
∫axdx=axlna+C(a>0,a≠1) (9)
∫shxdx=chx+C (10)
∫chxdx=shx+C (11)

Базовые интегралы от тригонометрических функций

Ошибка, которую часто делают студенты: путают знаки в формулах (12) и (13). Запомнив, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен сosx. Это неверно! Интеграл от синуса равен «минус косинусу», а вот интеграл от cosx равен «просто синусу»:

∫sinxdx=−cosx+C (12)
∫cosxdx=sinx+C (13)
∫1cos2xdx=tgx+C (14)
∫1sin2xdx=−ctgx+C (15)

Интегралы, сводящиеся к обратным тригонометрическим функциям

Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Аналогично, (18) — частный случай (19).

∫11+x2dx=arctgx+C=−arcctgx+C (16)
∫1×2+a2=1aarctgxa+C(a≠0) (17)
∫11−x2dx=arcsinx+C=−arccosx+C (18)
∫1a2−x2dx=arcsinxa+C=−arccosxa+C(a>0) (19)

Более сложные интегралы

Данные формулы тоже желательно запомнить. Они также используются достаточно часто, а их вывод довольно утомителен.

∫1×2+a2dx=ln|x+x2+a2|+C (20)
∫1×2−a2dx=ln|x+x2−a2|+C (21)
∫a2−x2dx=x2a2−x2+a22arcsinxa+C(a>0) (22)
∫x2+a2dx=x2x2+a2+a22ln|x+x2+a2|+C(a>0) (23)
∫x2−a2dx=x2x2−a2−a22ln|x+x2−a2|+C(a>0) (24)

Общие правила интегрирования

1) Интеграл от суммы двух функций равен сумме соответствующих интегралов: ∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx (25)

2) Интеграл от разности двух функций равен разности соответствующих интегралов: ∫(f(x)−g(x))dx=∫f(x)dx−∫g(x)dx (26)

3) Константу можно выносить за знак интеграла: ∫Cf(x)dx=C∫f(x)dx (27)

Легко заметить, что свойство (26) — это просто комбинация свойств (25) и (27).

4) Интеграл от сложной функции, если внутренняя функция является линейной: ∫f(Ax+B)dx=1AF(Ax+B)+C(A≠0) (28)

Здесь F(x) — первообразная для функции f(x). Обратите внимание: эта формула подходит только для случая, когда внутренняя функция имеет вид Ax + B.

Важно: не существует универсальной формулы для интеграла от произведения двух функций, а также для интеграла от дроби:

∫f(x)g(x)dx=?∫f(x)g(x)dx=? (30)

Это не означает, конечно, что дробь или произведение нельзя проинтегрировать. Просто каждый раз, увидев интеграл типа (30), вам придется изобретать способ «борьбы» с ним. В каких-то случаях вам поможет интегрирование по частям, где-то придется сделать замену переменной, а иногда помощь могут оказать даже «школьные» формулы алгебры или тригонометрии.

Простой пример на вычисление неопределенного интеграла

Пример 1. Найти интеграл: ∫(3×2+2sinx−7ex+12)dx

Воспользуемся формулами (25) и (26) (интеграл от суммы или разности функций равен сумме или разности соответствующих интегралов. Получаем: ∫3x2dx+∫2sinxdx−∫7exdx+∫12dx

Вспомним, что константу можно выносить за знак интеграла (формула (27)). Выражение преобразуется к виду

3∫x2dx+2∫sinxdx−7∫exdx+12∫1dx

А теперь просто воспользуемся таблицей основных интегралов. Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, экспоненту и константу 1. Не забудем добавить в конце произвольную постоянную С:

3×33−2cosx−7ex+12x+C

После элементарных преобразований получаем окончательный ответ:

x3−2cosx−7ex+12x+C

Проверьте себя дифференцированием: возьмите производную от полученной функции и убедитесь, что она равна исходному подинтегральному выражению.

Сводная таблица интегралов

∫Adx=Ax+C

∫xdx=x22+C

∫x2dx=x33+C

∫1xdx=2x+C

∫1xdx=ln|x|+C

∫1x2dx=−1x+C

∫xndx=xn+1n+1+C(n≠−1)

∫exdx=ex+C

∫axdx=axlna+C(a>0,a≠1)

∫shxdx=chx+C

∫chxdx=shx+C

∫sinxdx=−cosx+C

∫cosxdx=sinx+C

∫1cos2xdx=tgx+C

∫1sin2xdx=−ctgx+C

∫11+x2dx=arctgx+C=−arcctgx+C

∫1×2+a2=1aarctgxa+C(a≠0)

∫11−x2dx=arcsinx+C=−arccosx+C

∫1a2−x2dx=arcsinxa+C=−arccosxa+C(a>0)

∫1×2+a2dx=ln|x+x2+a2|+C

∫1×2−a2dx=ln|x+x2−a2|+C

∫a2−x2dx=x2a2−x2+a22arcsinxa+C(a>0)

∫x2+a2dx=x2x2+a2+a22ln|x+x2+a2|+C(a>0)

∫x2−a2dx=x2x2−a2−a22ln|x+x2−a2|+C(a>0)

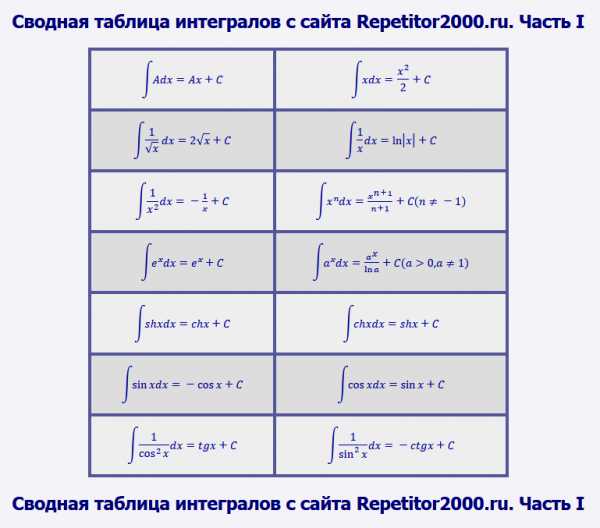
Скачайте таблицу интегралов (часть I) по этой ссылке

Скачайте таблицу интегралов (часть II) по этой ссылке

Если Вы учитесь в ВУЗе, если у Вас возникли сложности с высшей математикой (математический анализ, линейная алгебра, теория вероятностей, статистика), если Вам нужны услуги квалифицированного преподавателя, зайдите на страничку репетитора по высшей математике. Будем решать Ваши проблемы вместе!

Возможно, вас заинтересуют также

www.repetitor2000.ru

Полная таблица интегралов

Применяя таблицу производных и правила взятия интегралов, можно составить такую таблицу интегралов:

1).

 

2).  ∫cosx dx=sinx+c

 

3). ∫sinx dx=-cosx+c

 

4). 

5).

6).

7).

8).

9).

10).

11).

12).

13).

14).

Таблица интегралов незаменима при вычислении интегралов поэтому советуем Вам запомнить её или записать её в тетрадь.

tendey.kz

Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Элементы математического анализа

Первообразная

      Определение 1. Функцию   F (x) ,   определенную на интервале   (a, b),   называют первообразной функции   f (x) ,   определенной на интервале   (a, b),   если для каждого выполнено равенство

F’ (x) = f (x) .

      Например, из справедливости равенства

(sin 2x)’ = 2 cos 2x

вытекает, что функция   F (x) = sin 2x   является первообразной функции   f (x) = 2 cos 2x .

      Замечание. Функция   F (x) = sin 2x   не является единственной первообразной функции   f (x) = 2 cos 2x ,   поскольку функция   F (x) = sin 2x + 10 ,   или функция   F (x) = sin 2x – 3 ,   или функции вида   F (x) = sin 2x + c ,   где   c   – любое число, также являются первообразными функции   f (x) = 2 cos 2x .

      Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.

      Теорема 1. Если функция   F (x)   является первообразной функции   f (x)   на интервале   (a, b) ,   то любая другая первообразная функции   f (x)   на интервале   (a, b)   имеет вид

F (x) + с ,

где   c   – некоторое число.

Неопределенный интеграл

      Определение 2. Множество всех первообразных функции   f (x)   называют неопределенным интегралом от функции   f (x)   и обозначают

(1)

      Обозначение (1) читается так: «Неопределенный интеграл от функции   f (x)   по   dx» .

      Если   F (x)   является первообразной   f (x) ,   то в силу теоремы 1 смысл формулы (1) заключается в следующем:

(2)

      Однако для упрощения формулу (2) принято записывать в виде

(3)

подразумевая, но не указывая специально, что   c   – любое число.

      В формуле (3) функцию   f (x)   называют подынтегральной функцией, выражение   f (x) dx   нызывают подынтегральным выражением, а число   c   называют постоянной интегрирования.

      Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.

Правила интегрирования. Замена переменной в неопределенном интеграле

      Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.

      Правило 1 (интеграл от произведения числа на функцию). Справедливо равенство

где   k   – любое число.

      Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.

      Правило 2 (интеграл от суммы функций). Интеграл от суммы функций вычисляется по формуле

то есть интеграл от суммы функций равен сумме интегралов от этих функций.

      Правило 3 (интеграл от разности функций). Интеграл от разности функций вычисляется по формуле

то есть интеграл от разности функций равен разности интегралов от этих функций.

      Правило 4 (интегрирование при помощи замены переменной). Из справедливости формулы

вытекает, что      

(4)

если все входящие в формулу (4) функции   f (φ (x)),   φ’ (x),   F (φ (x))   определены.

      Доказательство правила 4. Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы (4):

      Мы получили подынтегральную функцию из левой части формулы (4), что и требовалось.

      Замечание. Рассмотрим частный случай формулы (4), когда функция   φ (x)   является линейной функцией, то есть

φ (x) = kx + b ,

что   k   и   b   – произвольные числа, .

      В этом случае

φ’ (x) = k ,

и формула (4) принимает вид

(5)

      Формула (5) часто используется при решении задач.

Таблица интегралов

      Следующая таблица неопределенных интегралов составлена на основе таблицы производных часто встречающихся функций, а также на основе таблицы производных сложных функций

Основная формула	Обобщения
	, где   k – любое число
где   n – любое число, не равное   – 1	, где   n, k, b – любые числа, ,
	где   n – любое число,
,   x > 0	, где   k, b – любые числа, , kx + b > 0
	где   φ (x) > 0
	, где   k, b – любые числа,
где   a – любое положительное число, не равное 1	, где  a – любое положительное число, не равное 1,   k, b – любые числа,
	, где  a – любое положительное число, не равное 1
	, где   k, b – любые числа,
	, где   k, b – любые числа,
	, где   k, b – любые числа, ,
	,
	, где   k, b – любые числа, ,
	,
| x | < 1	где   k, b – любые числа, , | kx + b | < 1
	| φ (x) | < 1
	где   a, b – любые числа,
	, где   k, b – любые числа,
	где   a, b – любые числа,

Основная формула: Обобщения: , где   k – любое число

Основная формула: где   n – любое число, не равное   – 1 . Обобщения: , где   n, k, b – любые числа, , _____ где   n – любое число,

Основная формула: ,   x > 0 Обобщения: , где   k, b – любые числа, ,   kx + b > 0 _____ где   φ (x) > 0

Основная формула: Обобщения: , где   k, b – любые числа, _____

Основная формула: , где   a – любое положительное число, не равное 1 . Обобщения: , где  a – любое положительное число, не равное 1,   k, b – любые числа, _____ , где  a – любое положительное число, не равное 1

Основная формула: Обобщения: , где   k, b – любые числа, _____

Основная формула: Обобщения: , где   k, b – любые числа, _____

Основная формула: где   Обобщения: , где   k, b – любые числа, , _____ , где

Основная формула: где   Обобщения: , где   k, b – любые числа, , _____ ,

Основная формула:   | x | < 1 Обобщения: где   k, b – любые числа, , | kx +b | < 1 _____ где   | φ (x) | < 1 _____ где   a, b – любые числа,

Основная формула: Обобщения: , где   k, b – любые числа, _____ _____ где   a, b – любые числа,

Примеры решения задач

      Пример 1. Вычислить интеграл

      Решение. Воспользовавшись свойствами степеней, а затем правилами интегрирования и формулами из таблицы неопределенных интегралов формулами из таблицы неопределенных интегралов, получаем

Ответ.

      Пример 2. Значение первообразной   F (x)   функции   f (x) = – 4 sin x   в точке   x = 0   равно   9.   Найти .

      Решение. Поскольку Поскольку

то

      Подставляя в формулу (6) значение   x = 0 ,   находим значение постоянной интегрирования   c:

F (0) = 4 cos 0 + c = 9,

4 + c = 9,     c = 5.

      Следовательно,

F (x) = 4 cos x + 5

      Поэтому

      Ответ.  7

      Пример 3. Найти первообразную   F (x)   функции

если   F (2π) = 2e + 3.

      Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов

для функции   φ (x) = cos x ,   получаем

      Следовательно,

(7)

      Подставляя в формулу (7) значение   x = 2π,   находим значение постоянной интегрирования   c:

      Итак,

c = 3e +3 .

      Ответ. 

      Пример 4. Вычислить интеграл

      Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов

для функции   φ (x) = e^x,   получаем

      Ответ. 

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Таблица интегралов — Помощь в обучении

Добавлено в закладки: 0

К Вашему вниманию предоставлена таблица неопределенных интегралов. Интеграл является одним из основных понятий математического анализа. В таблицах ниже мы попытались предоставить все основные формулы нахождения неопределенных интегралов, которые помогут Вам решить задания по теме нахождение неопределенных интегралов.

Таблица основных неопределенных интегралов

\(\int 0dx=C\)

\(\int 1dx=x+C\)

\(\int  x^{n} dx= \frac{ x^{n+1} }{n+1}+C, n \neq -1,\)

\(\int  \frac{dx}{x} =ln |x| + C\)

\(\int  a^{x}dx  = \frac{a^{x}}{ln a} + C\)

\(\int  e^{x}dx  = e^{x} + C\)

\(\int sinxdx  = -cosx + C\)

\(\int cosxdx  = sinx + C\)

\(\int  \frac{dx}{ sin^2 x} = -ctgx + C\)

\(\int  \frac{dx}{ cos^2 x} = tgx + C\)

\(\int  \frac{dx}{ \sqrt{a^2-x^2} } = arcsin \frac{x}{a} + C, |x|<|a|\)

\(\int  \frac{dx}{a^2+x^2}= \frac{1}{a} arctg \frac{x}{a}+C\)

\(\int  \frac{dx}{a^2-x^2}= \frac{1}{2a} ln  |\frac{a+x}{a-x}|+C,  | x |  \neq a\)

\(\int  \frac{dx}{ \sqrt{x^2 \pm a^2} } = ln | x+ \sqrt{x^2 \pm a^2}  | + C\)

Таблица интегралов от рациональных функций

\(\int  x^{n} dx= \frac{ x^{n+1} }{n+1}+C\)

\(\int  (ax+b)^{n} dx= \frac{ (ax+b)^{n+1} }{a(n+1)}+C\)

\(\int  \frac{dx}{x} =ln |x| + C\)

\(\int  \frac{dx}{ax+b} = \frac{1}{a} ln |ax+b| + C\)

\(\int  \frac{ax+b}{cx+d}dx = \frac{a}{c}x +  \frac{bc-ad}{c^2} ln |cx+d| + C\)

\(\int  \frac{dx}{(x+a)(x+b)} = \frac{1}{a-b} + ln | \frac{x+b}{x+a} | + C\)

\(\int  \frac{dx}{x^2-a^2} = \frac{1}{2a} ln | \frac{x-a}{x+a} | + C\)

\(\int  \frac{xdx}{(x+a)(x+b)} = \frac{1}{a-b} ( aln | x+a |-b ln | x+b | )+ C\)

\(\int  \frac{xdx}{x^2-a^2} = \frac{1}{2} ln | x^2-a^2 | + C\)

\(\int  \frac{dx}{x^2+a^2} = \frac{1}{a} arctg (\frac{x}{a})  + C\)

\(\int  \frac{xdx}{x^2+a^2} = \frac{1}{2} ln | x^2+a^2 | + C\)

\(\int  \frac{dx}{(x^2+a^2)^2} = \frac{1}{2a^2} \frac{x}{x^2+a^2}+ \frac{1}{2a^3}arctg (\frac{x}{a}) + C\)

\(\int  \frac{xdx}{(x^2+a^2)^2} = -\frac{1}{2} \frac{1}{x^2+a^2}+ C\)

\(\int  \frac{xdx}{(x^2+a^2)^3} = -\frac{1}{4} \frac{1}{(x^2+a^2)^2}+ C\)

\(\int  \frac{dx}{ax^2+bx+c} = \frac{2}{ \sqrt{4ac-b^2} } arctg \frac{2ax+b}{\sqrt{4ac-b^2}} + C , (b^2-4ac)<0\)

\(\int  \frac{xdx}{ax^2+bx+c} = \frac{1}{ 2a } ln |ax^2+bx+c| — \frac{b}{2a}  \int  \frac{dx}{ax^2+bx+c} + C \)

\(\int  \frac{xdx}{ax+b} = \frac{1}{ a^2 } (b+ax-b ln  | ax+b | ) + C \)

\(\int  \frac{x^2dx}{ax+b} = \frac{1}{ a^3 } ( \frac{1}{2} (ax+b)^2 — 2b(ax+b) + b^2ln  | ax+b | ) + C \)

\(\int  \frac{dx}{x(ax+b)} = \frac{1}{ b } ln  |  \frac{ax+b}{x}  | ) + C\)

\(\int  \frac{dx}{x^2(ax+b)} = — \frac{1}{bx} + \frac{a}{ b^2 } ln  |  \frac{ax+b}{x}  | ) + C\)

\(\int  \frac{xdx}{(ax+b)^2} = \frac{1}{a^2} (ln  |ax+b| +  \frac{b}{ax+b} ) + C\)

\(\int  \frac{x^2dx}{(ax+b)^2} = \frac{1}{a^3} (b+ax-2bln  |ax+b| —  \frac{b^2}{ax+b} ) + C\)

Таблица неопределенных интегралов от транцендентных функций

\(\int  e^{x}dx  = e^{x} + C\)

\(\int  a^{x}dx  = \frac{a^{x}}{ln a} + C\)

\(\int  \frac{dx}{xlnx}=ln | lnx | +C\)

\(\int   x^{n} lnx dx =x^{n+1} \big( \frac{lnx}{n+1} — \frac{1}{(n+1)^2}\big)+C\)

\(\int   e^{ax} lnx dx = \frac{1}{a} e^{ax}lnx — \frac{1}{a}\int  \frac{ e^{ax} }{x} dx +C\)

\(\int x^nln^mxdx= \frac{ x^{n+1} }{n+1} ln^mx —  \frac{m}{n+1}\int x^n ln^{m-1}xdx+C\)

\(\int  \frac{x^n}{ln^mx} dx=- \frac{ x^{n+1} }{(m-1)ln^{m-1}x} + \frac{n+1}{m-1} \int  \frac{x^n}{ln^{m-1}x} dx+C\)

\(\int  lnx dx=xlnx-x+C\)

\(\int arcsinx dx=xarcsinx+ \sqrt{1-x^2} +C\)

\(\int arctgx dx=xarctgx-ln\sqrt{1+x^2} +C\)

\(\int  e^{ax}dx  =  \frac{e^{ax}}{a} + C\)

\(\int  xe^{ax}dx  =  \frac{e^{ax}}{a^2} (ax-1)  + C\)

\(\int   \frac{a^{x}}{x^n} dx  =  -\frac{a^x}{(n-1) x^{n-1}} +  \frac{lna}{n-1} \int   \frac{a^{x}}{ x^{n-1} } dx + C\)

\(\int shx dx = chx + C\)

\(\int chx dx = shx + C\)

Таблица интегралов от иррациональных функций

\(\int  \frac{dx}{ \sqrt{ax+b} }  =  \frac{2}{a}  \sqrt{ax+b}  + C\)

\(\int  \sqrt{ax+b}dx  =  \frac{2}{3a}   (ax+b)^{1,5}  + C\)

\(\int  \frac{xdx}{\sqrt{ax+b}}=\frac{2(ax-2b)}{3a^2}(ax+b)^{1,5}+C\)

\(\int  x\sqrt{ax+b}dx= \frac{2(3ax-2b)}{15a^2}(ax+b)^{1,5}+C\)

\(\int  \frac{dx}{(x+c) \sqrt{ax+b}}=\frac{1}{\sqrt{b-ac}}ln|\frac{\sqrt{ax+b}-\sqrt{b-ac}}{\sqrt{ax+b}\sqrt{b-ac}}|+C, (b-ac>0)\)

\(\int  \frac{dx}{(x+c) \sqrt{ax+b}}=\frac{1}{\sqrt{ac-b}}arctg( \sqrt{ \frac{ax+b}{ac-b} } )+C, (b-ac<0)\)

\(\int  \sqrt{ \frac{ax+b}{cx+d} }dx= \frac{1}{c}  \sqrt{(ax+b)(cx+d)}- \frac{ad-bc}{c \sqrt{ac} } arctg \sqrt{ \frac{a(cx+d)}{c(ax+b)} }+C\)

\(\int \frac{dx}{x \sqrt{ax+b}}=\frac{1}{ \sqrt{b} }ln|\frac{\sqrt{ax+b}-\sqrt{b}}{\sqrt{ax+b}+\sqrt{b}}|+C, b>0\)

\(\int \frac{dx}{x \sqrt{ax+b}}=\frac{2}{ \sqrt{-b} }arctg  \sqrt{ \frac{ax+b}{-b} } +C, b<0\)

\(\int \frac{dx}{x^2 \sqrt{ax+b}}=-\frac{ \sqrt{ax+b} }{ bx }-  \frac{a}{2b} \int \frac{dx}{x \sqrt{ax+b}}+C\)

\(\int  \frac{ \sqrt{ax+b} }{x}dx=2 \sqrt{ax+b}+b\int  \frac{ dx }{x\sqrt{ax+b}}+C\)

\(\int  \sqrt{ \frac{a-x}{b+x} } dx= \sqrt{(a-x)(b+x)}-(a+b)arcsin \sqrt{ \frac{x+b}{a+b} }  +C\)

\(\int  \sqrt{ \frac{a+x}{b-x} } dx= -\sqrt{(a+x)(b-x)}-(a+b)arcsin \sqrt{ \frac{b-x}{a+x} }  +C\)

\(\int \frac{dx}{\sqrt{ax^2+bx+c}}dx=-\frac{1}{\sqrt{a}}arcsin\frac{2ax+b}{\sqrt{b^2-4ac}}+C\)

\(\int \sqrt{ax^2+bx+c}dx= \frac{2ax+b}{4a}\sqrt{ax^2+bx+c}+\frac{4ac-b^2}{8a}\int  \frac{dx}{\sqrt{ax^2+bx+c}}+C\)

\(\int \sqrt{x^2+a^2}dx= \frac{x}{2}\sqrt{x^2+a^2}+\frac{a^2}{2}ln | x+\sqrt{x^2+a^2} | +C\)

\(\int \sqrt{x^2-a^2}dx= \frac{x}{2}\sqrt{x^2-a^2}-\frac{a^2}{2}ln | x+\sqrt{x^2-a^2} | +C\)

\(\int  \frac{dx}{\sqrt{x^2+a^2}} = ln | x+\sqrt{x^2+a^2} | +C\)

\(\int  \frac{dx}{\sqrt{x^2-a^2}} = ln | x+\sqrt{x^2-a^2} | +C\)

\(\int  \frac{xdx}{\sqrt{x^2+a^2}} =\sqrt{x^2+a^2}+C\)

\(\int  \frac{\sqrt{x^2-b^2}}{x}dx =\sqrt{x^2-b^2}+barcsin \frac{b}{x} +C\)

\(\int  \sqrt{a^2-x^2}dx = \frac{x}{2} \sqrt{a^2-x^2}+ \frac{a^2}{2} arcsin \frac{x}{a} +C\)

\(\int   \frac{\sqrt{a^2-x^2}}{x}dx = \sqrt{a^2-x^2}+aln |\frac{x}{a+\sqrt{a^2-x^2}}|+C\)

\(\int  \frac{dx}{\sqrt{a^2-x^2}}=arcsin( \frac{x}{a} )+C\)

\(\int  \frac{xdx}{\sqrt{a^2-x^2}}=-\sqrt{a^2-x^2}+C\)

\(\int  \frac{dx}{x\sqrt{a^2-x^2}}= \frac{1}{a}ln|\frac{x}{a+\sqrt{a^2-x^2}}| +C\)

Таблица интегралов от тригонометрических функций

\(\int sinxdx  = -cosx + C\)

\(\int cosxdx  = sinx + C\)

\(\int sin^2xdx= \frac{x}{2} — \frac{1}{4}sin2x + C\)

\(\int cos^2xdx= \frac{x}{2} + \frac{1}{4}sin2x + C\)

\(\int  sin^nxdx= -\frac{1}{n} sin^{n-1}xcosx + \frac{n-1}{n}\int sin^{n-2}xdx + C\)

\(\int  cos^nxdx= \frac{1}{n} cos^{n-1}xsinx + \frac{n-1}{n}\int cos^{n-2}xdx + C\)

\(\int  \frac{dx}{sinx}=ln | tg \frac{x}{2}  |  + C\)

\(\int  \frac{dx}{cosx}=ln |tg (\frac{x}{2}+ \frac{ \pi }{2})| + C\)

\(\int sinxcosxdx=-\frac{1}{4}cos2x + C\)

\(\int sin^2xcosxdx=\frac{1}{3}sin^3x + C\)

\(\int sinxcos^2xdx=-\frac{1}{3}cos^3x + C\)

\(\int sin^2xcos^2xdx=\frac{1}{8}x- \frac{1}{32}sin4x + C\)

\(\int tgxdx=-ln | cosx | + C\)

\(\int ctgxdx=ln | sinx | + C\)

\(\int  \frac{sinx}{cos^2x} dx=\frac{1}{cosx}+C\)

\(\int  \frac{sin^2x}{cos^2x} dx=tgx-x+C\)

\(\int  \frac{sin^2x}{cosx} dx=ln | tg (\frac{x}{2}+ \frac{ \pi }{2} ) | — sinx + C\)

\(\int  \frac{cosx}{sin^2x} dx=- \frac{1}{sinx} +C\)

\(\int  \frac{cos^2x}{sin^2x}dx=-ctgx-x+C\)

\(\int \frac{cos^2x}{sinx}dx=ln| tg \frac{x}{2}|+cosx+C\)

\(\int \frac{dx}{cosxsinx}=ln|tg x|+C\)

\(\int \frac{dx}{sin^2xcosx}=- \frac{1}{sinx}+ln | tg (\frac{x}{2} + \frac{ \pi }{2} ) |  +C\)

\(\int \frac{dx}{sinxcos^2x}=\frac{1}{cosx}+ln | tg \frac{x}{2}|+C\)

\(\int \frac{dx}{sin^2xcos^2x}=tgx-ctgx+C\)

\(\int \frac{dx}{sin^nx}=- \frac{1}{n-1} \frac{cosx}{ sin^{n-1}x}+ \frac{n-2}{n-1}\int \frac{dx}{ sin^{n-2}x} +C\)

\(\int tg^nxdx=\frac{ tg^{n-1}x}{n-1} — \int  tg^{n-2} xdx +C\)

\(\int ctg^nxdx=-\frac{ ctg^{n-1}x}{n-1}-\int ctg^{n-2}xdx+C\)

\(\int sinxcos^nxdx=-\frac{cos^{n+1}x}{n+1}+C\)

\(\int sin^nxcosxdx=\frac{sin^{n+1}x}{n+1}+C\)

www.poreshaem.com