Построить график функции с модулем – Графики функций с модулем

Содержание

Построение графиков функций содержащих модуль? 14

Содержание

Стр.

Введение. 2

1Модуль в математике. 3

2.Графики с модулем. 4

2.1. y=f (|x|)………………………………………. 4

2.2. y=|f (x)|………………………………………. 5

2.3. y=|f (|x|)|……………………………………… 6-7

2.4. |y|=|f (x)|………………………………………. 8

3.Примеры построения.

I…………………………………………… 9

II………………………………………….. 10

III…………………………………………. 11

IV…………………………………………. 12

V………………………………………….. 13

3.6.Вывод………………………………… 14

4.Для чего нужно изучать

построение графиков функций, содержащих модуль? 14

5. Решение уравнений графическим способом.

I…………………………………………… 15

II………………………………………….. 16

III…………………………………………. 17

Заключение. 18

Список литературы. 19

Введение.

С понятием модуль мы познакомились в пятом классе и на протяжении долгих лет продолжаем встречаться с ним. Построение графиков функций, содержащих модуль, не входит в школьную программу. Именно по этому я решила подробно ознакомиться с модулем в графиках функций.

Моя цель: научиться строить графики функций, содержащих модуль, построить множество подобных графиков и понять алгоритм их построения. Узнать, для чего нужно уметь строить графики с модулем.

Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово, которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.

В архитектуре модуль-это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.

Модуль в технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и. т.п.

Модуль объемного сжатия (в физике) — отношение нормального напряжения в материале к относительному удлинению.

1. Модуль в математике:

Модулем рационального числа α называют расстояние (в единичных отрезках) от начала отсчета до точки координатной прямой, соответствующей этому числу: А (α).

α, если α≥0;

|α|= -α, если α<0.

|α|≥0 – модуль числа не отрицателен.

^{Модуль вектора — это длина вектора и обозначается символом |AB|.}

2. Графики с модулем.

Модуль встречается нам в уравнениях и выражениях, в неравенствах и в функциях. Особое внимание я уделяю графикам функций, содержащих модуль потому, что очень интересно строить график и видеть, как он изменяется.

Существует разное расположение модуля в функциях. Рассмотрим некоторые из них:

2.1. y=f (|x|)

І способ. Собственный алгоритм построения:

y=f (|x|) – четная.

По определению модуля получим:

f (x), если x≥0;

y=f (|x|)=

f (-x), если x<0.

a) построить график y=f (x).

b) «стереть» график y=f (x) на промежутке, в котором x<0.

c) построить график y=f (-x).

d) «стереть» график y=f (-x) на промежутке, в котором x≥0.

Полученный график и есть y=f (|x|).

Указание: графики строить на одной координатной плоскости.

2.2. y=|f (x)|

І способ. Собственный алгоритм построения:

По определению модуля получим:

f (x), если f (x)≥0;

y=|f (x)|=

-f (x), если f (x)<0.

a) построить график y=f (x).

b) «стереть» график y=f (x) на промежутке, в котором f (x)<0.

c) построить график y=-f (x).

d) «стереть» график y=-f (x) на промежутке, в котором f (x)≥0.

Полученный график и есть y=|f (x)|.

Указание: графики строить на одной координатной плоскости.

ІІ способ. По определению:

f (x), если f (x)≥0;

y=|f (x)|=

-f (x), если f (x)<0.

a) построить график y=f (x).

Построив множество таких графиков, я пришла к выводу, что модуль отражает симметрично относительно оси ОХ, ту часть графика функции, которая лежит ниже оси ОХ, в верхнюю полуплоскость.

b) отобразим часть графика y=f (x), лежащую ниже оси ОХ, в верхнюю полуплоскость.

c) «стереть» часть графика y=f (x), лежащую ниже оси ОХ.

Полученный график и есть y=|f (x)|.

2.3. y=|f (|x|)|

І способ. Собственный алгоритм построения:

По определению модуля получим:

f (x), если f (x)≥0;

|f (x)|=

-f (x), если f (x)<0;

y=|f (|x|)|=

f (-x), если f (-x)≥0;

|f (-x)|=

-f (-x), если f (-x)<0.

a) построить график y=f (x).

b) «стереть» график y=f (x) на промежутке, в котором f (x)<0.

c) построить график y=-f (x).

d) «стереть» график y=-f (x) на промежутке, в котором f (x)≥0.

e) построить график y=f (-x).

f) «стереть» график y=f (-x) на промежутке, в котором f (-x)<0.

g) построить график y=-f (-x).

h) «стереть» график y=-f (-x) на промежутке, в котором f (-x)≥0.

Полученный график и есть y=|f (|x|)|.

Указание: графики строить на одной координатной плоскости

ІІ способ. По определению:

f (x), если x≥0;

y=f (|x|)=

f (-x), если x<0.

Для построения графика y=|f (|x|)| нужно:

a) построить график y=f (x).

b) «стереть» график y=f (x) на промежутке, в котором x<0.

с) Участки полученного графика, лежащие ниже оси ОХ, отразить в верхнюю полуплоскость.

Построив множество таких графиков, я пришла к выводу, что модуль отразит построенную часть графика симметрично относительно оси ОУ.

Полученный график и есть y=|f (|x|)|.

Указание: графики строить на одной координатной плоскости.

2.4. |y|=|f (x)|

І способ. Собственный алгоритм построения:

Заметим, что функция |y|=|f (x)| — нечетная, имеем:

f (x), если f (x)≥0;

|f (x)|=

-f (x), если f (x)<0.

y, если y≥0;

|y|=

-y, если y<0.

Получили: y= f (x) равную ей –y=-f (x) и

-y= f (x) равную ей y=-f (x).

Тогда:

построить график y= f (x)
построить график y= -f (x)

Полученный график и есть |y|=|f (x)|.

Указание: графики строить на одной координатной плоскости

ІІ способ. По определению:

a) построить график y=|f (x)|.

b) отразить полученный график относительно оси ОХ в нижнюю полуплоскость.

3. Примеры построения:

І. y=x²2|x|3 способ «по алгоритму»

х, если х≥0;

|х|= -х, если х<0.

1.если х≥0, то y=x²-2x-3 – квадратичная функция, график парабола,

ветви направлены вверх,D(y)=R,

вершина (1;-4).

(синий график)

2.если х<0, то y=x²+2x-3 — квадратичная функция, график парабола,

ветви направлены вверх,D(y)=R,

вершина (-1;-4).

(зеленый график)

ІІ. y=|x²2x3| способ «по алгоритму»

x²2x3 , если x²2x3 ≥0;

1. | x²2x3|=

-x²+2x+3, если x²2x3 <0.

X²2x3 ≥0, пусть h≥0, тогда найдем нули h:

x²2x3=0

по теореме Виета:

x₁x₂=-3 x₁=-1;

x₁₊x₂=2 x₂=3.

а)x€(-∞;-1]٧[3;+∞), то y=x²2x3– квадратичная функция, график

парабола,

ветви направлены вверх,D(y)=R,

вершина (1;-4).

(синий график)

b) x€(-1;3), то y=-x²+2x+3 — квадратичная функция, график парабола,

ветви направлены вниз,D(y)=R,

вершина (1;4).

(зеленый график)

ІІІ. |y|=|xІ2|x|3| Способ «по определению»

1.построить график y=xІ2|x|3 (пример І)

(синий график)

2. построить график y=|xІ2|x|3|, т.е.модуль отразит симметрично относительно оси ОХ, ту часть графика y=xІ2|x|3, которая лежит ниже оси ОХ, в верхнюю полуплоскость.

(синий график)

4.построить график |y|=|xІ2|x|3|,т.е. модуль отразит график y=|xІ2|x|3| в нижнюю полуплоскость.

(зеленый график)

IV. |y|=xІ2x3 способ «по алгоритму»

y, если y≥0;

|y|= -y, если y<0.

1.построить график y=x²2x3 – квадратичная функция,

график парабола,

ветви направлены вверх,D(y)=R,

вершина (1;-4).

(синий график)

2.оставить график y=xІ2x3 только на тех промежутках, где y≥0.

3.построить график -y=xІ2x3,для этого преобразуем его, умножив две части на-1. Получим:

y=-x²+2x+3 — квадратичная функция, график парабола,

ветви направлены вниз,D(y)=R,

вершина (1;4).

(зеленый график)

4. оставить график y=-xІ+2x+3 только на тех промежутках, где y<0.

V. y=|xІx|2 способ «по алгоритму»

x²x , если x²x≥0;

1. | x²x|=

-x²+x, если x²x<0.

x²x≥0, пусть h≥0, тогда найдем нули h:

x²x=0

x(x-1)=0

x=0 или x=1

2.Построить график y=xІx2 на промежутке x€(-∞;0]٧[1;+∞),

y=x²x2– квадратичная функция, график парабола,

ветви направлены вверх,D(y)=R,

вершина (0,5;-2,25).

(синий график)

3. Построить график y=-xІ+x+2 на промежутке x€(0;1)

y=-x²+x-2– квадратичная функция, график парабола,

ветви направлены вниз,D(y)=R,

вершина (0,5;-1,25).

(зеленый график)

3.6.Вывод:

Каждый выбирает свой способ построения графиков функций, содержащих модуль. По моему мнению удобней строить такие графики способом «по определению». Этим способом графики строятся очень быстро, но для этого необходимы навыки в работе.

Для некоторых графиков удобен способ «по алгоритму», при таком построении нет опасности запутаться.

4.Для чего нужно изучать

построение графиков функций, содержащих модуль?

Решать уравнения можно не только аналитическим способом, но и графическим способом.

Графический способ: Суть этого способа заключается в том, чтобы построить графики данных функций. В случае, если графики пересекутся, точки пересечений данных графиков будут являться корнями нашего уравнения. В случае, если графики не пересекутся, мы сможем сделать вывод, что уравнение корней не имеет. Этот способ, вероятно, реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.

Другой способ решения уравнений, содержащих модуль — это способ разбиения числовой прямой на промежутки. В этом случае нам нужно разбить числовую прямую так, что по определению модуля, знак абсолютной величины на данных промежутках можно будет снять. Затем, для каждого из промежутков мы должны будем решить данное уравнение и сделать вывод, относительно получившихся корней (удовлетворяют они нашему промежутку или нет). Корни, удовлетворяющие промежутки и дадут окончательный ответ.

5.решение уравнений графическим способом.

І. Решим графически уравнение |x2|=3

Для решения уравнения графическим способом, надо построить графики функцийy=|x -2| и у=3.

Для построения графика функции у =|x — 2|, построим график функции у =| х — 2| — это прямая, пересекающая ось ОХ в точке (2; О), а ось ОУ в точке (о; — 2), а затем часть прямой, лежащую ниже оси ОХ зеркально отразить в оси ОХ.

Графиком функции у = 3 является прямая, параллельная оси ОХ и проходящая через точку (о; 3) на оси ОУ.

Абсциссы точек пересечения графиков функций дадут решения уравнения.

Прямая графика функции у=3 пересеклась с графиком функции y=|x — 2| в точках с координатами (-1; 3) и (5; 3), следовательно решениями уравнения будут абсциссы точек: х= — l, х=5.

Ответ: Х ₁= -1, Х₂ = 5.

ІІ. Решить графически уравнение |1-x|-|2x+3|+x+4=0

1.Представим уравнение в виде |1-x|-|2x+3|=-x-4

2.Построим график y=|1-x|-|2x+3|

Узловые точки: x=1,x=-1,5.

(1-x)

(2x+3)

а) При x<-1,5, (1-x)>0 и (2x+3)<0,т.е. функция примет вид

y=1- x+2x+3,

y=x+4 – графиком является прямая, проходящая через две точки

(0;4), (-4;0).

б) При -1,5≤x<1, (1-x)>0 и (2x+3)>0, т.е. функция примет вид

y=1-x-2x-3, y=-3x-2 – графиком является прямая, проходящая

через две точки (0;-2), (-1;1).

в) При x≥1, (1-x)≤0 и (2x+3)>0, т.е. функция примет вид

y=-1+x-2x-3, y=-x-4 – графиком является прямая, проходящая

через две точки (0;-4), (-4;0).

График функции y=-x-4 совпадает с графиком y=|1-x|-|2x+3|,

при x≥1, поэтому решением являются все x≥1 и x=-4.

Ответ: x≥1 и x=-4.

Нестандартное уравнение:

ІІІ. Решим графически уравнение |4-x|+|(x-1)(x-3)|=1.

Представим уравнение в виде |(x-1)(x-3)|=1-|4-x|.

2. Построим график y=|(x-1)(x-3| и y=1-|x-4|.

а) В графике y=|(x-1)(x-3| раскроем внутренние скобки получим:

y=|x²-4x+3|- квадратичная функция.

Построим этот график «по определению».

Пересечение графика с осью ОХ. При x=0 y=3,

т.е. график пересекается с осью ОУ в точке (0;3). И при x=4 y=3

мы получили первый график.

б) Построим график y=1-|x-4| «по алгоритму»,

Построив, увидим, что данный график пересекает ось ОХ в точках 5 и 3.

При x=4, y=1 и как видно из графика обеих функций пересекаются в одной точке (3;0).

Ответ: (3;0).

Заключение

Разобравшись с построением графиков функций, содержащих модуль, самостоятельно, я убедилась:

как интересно строить такие графики;
приобрела навык в этом деле;
увидела, какие удивительные и красивые бывают графики.

4.я научилась применять построение графиков в решении

сложных уравнений.

В дальнейшем, когда круг знаний функций расширится, я рассмотрю, как изменяет модуль графики. Надеюсь, это будет ещё интересней и увлекательней.

Список литературы

1.К.Вельскер, Л.Лепманн. Учебник математики Х класса.

2.М.И.Башмаков. уравнения и неравенства.

3.Д.И. Аверьянов, П.И. Алтынов, И.И. Баврин и др. Большой справочник Математики для школьников и поступающих в вузы.

textarchive.ru

Урок по теме «Построение графиков квадратичной функции с модулем»

Урок по теме «Построение графиков квадратичной функции с модулем»
Учебник А.Г.Мордкович, базовый уровень, 4 — й урок темы «Функция y = ax 2 + bx + c, ее свойства и график»
Быкасов Андрей Иванович,
учитель математики НОУ «Нефтеюганская православная гимназия», г.Нефтеюганск, Тюменская область

Тема : «Построение графиков
квадратичной функции с модулем »
Цель: обобщить знание свойств квадратичной функции и научить применять свойства квадратичной функции при построении графиков квадратичной функции с модулем
Задачи:
Выявить степень сформированности у учащихся понятия квадратичной функции, её свойств, особенностей её графика.
Создать условия для формирования умения анализировать, сравнивать, классифицировать графики изученных функций.

Продолжить развитие умения построения графиков квадратичной функции с модулем , используя программу AGrapher .
Формировать умение сотрудничать, работая в группе.
Оборудование: проектор, экран , 4 компьютера, программа AGrapher .

Этапы урока
Организационный
Мотивация к учебной деятельности.
Актуализация знаний и фиксация затруднения в пробном действии (работа с графиками функций).
Выявление места и причины затруднения.
Построение проекта выхода из затруднения.
Реализация построенного проекта.
Самостоятельная работа с самопроверкой по эталону.
Включение в систему знаний и повторение.
Рефлексия учебной деятельности. Оценивание работы на уроке.

Домашнее задание.

1. Организационный
На перемене дети садятся по группам. Группы формируются
на добровольной основе, консультант группы определяется
учителем. Каждой группе выдаются листы контроля
результатов деятельности.
Здравствуйте, ребята! Я рада сегодня вас видеть и очень надеюсь на совместную плодотворную работу. Сегодня мы работаем в группах. В каждой группе мною был назначен консультант, который поможет мне оценить в конце урока каждого из вас. В течение всего урока мы будем накапливать баллы: за каждый правильный, точный и логичный ответ Вы будете получать «+» в таблице, лежащей на вашем столе. Здесь мне будет нужна помощь консультантов. В конце урока мы просуммируем «+» и поставим отметки в зависимости от их количества:
более 8 «+»- «5»
6-7 «+»- «4»
4-5 «+»- «3».

2. Мотивация к учебной деятельности . Задача этапа: Создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность.
Если вы хотите научиться плавать, то смело
входите в воду, а если хотите научиться
решать задачи, то решайте их!
Дьёрдь Пойя
Сегодня нам предстоит решение многих задач, вы видите, как можно научится их решению по мнению известного венгерского математика Д.Пойя. Согласны ли вы, что такой подход применим и к нашему уроку?( Да )
Для начала предлагаю вспомнить, что мы знаем о функциях.

За каждое выполненное задание, консультант выставляет «+» в лист контроля (максимум 4 балла)
3 . Актуализация знаний и фиксация затруднения в пробном действии.
1 группа

Запишите формулы и названия функций, которые вы видите на графиках. (Каждые 2 правильно записанные формулы оцениваются «+», максимум 4 балла).
Постройте графики функций:
4 группа
2 группа
Постройте графики функций:
№ 1
№ 2
№ 3
№ 4 .
№ 1
№ 2
№ 3
№ 4
3 группа
Постройте графики функций:
№ 1.
№ 2.
№ 3. №4.
2. 1Актуализация знаний и фиксация з1атруднения в пр№1обном действии.

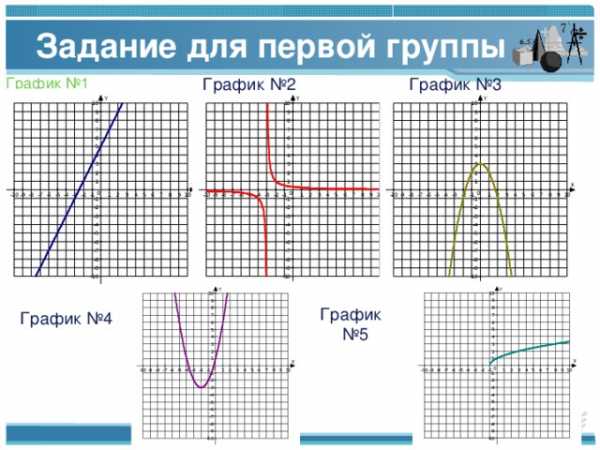
Задание для первой группы
График №1
График №2
График №3
График №5
График №4

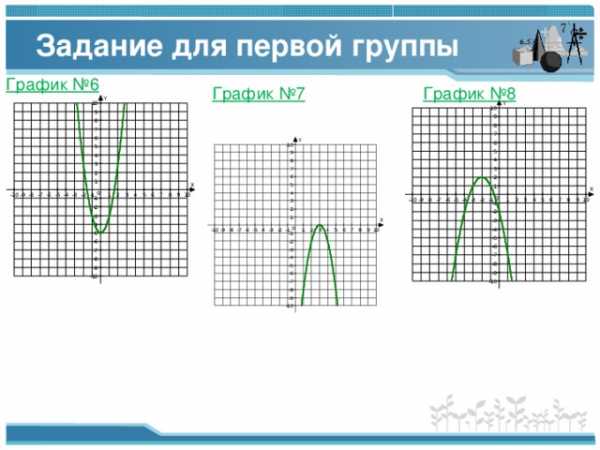
Задание для первой группы
График №6
График №7
График №8

Проверка
1группа
№ 1
№ 2
№ 3
№ 4
№ 5
№ 6
№ 7
№ 8
За каждое правильно выполненные 2 задания, консультант выставляет «+» в лист контроля

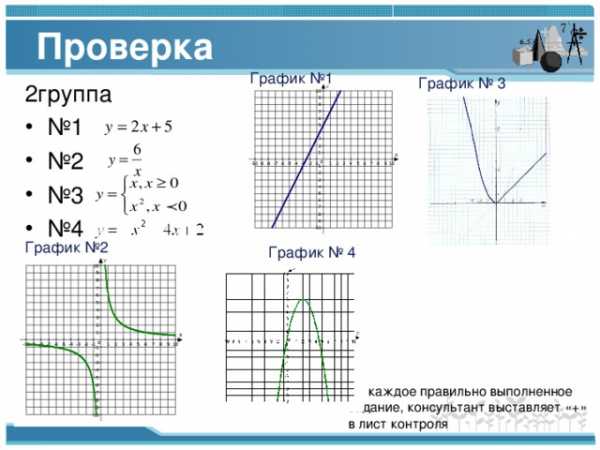
Проверка
График №1
График № 3
2группа
График №2
График № 4
За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

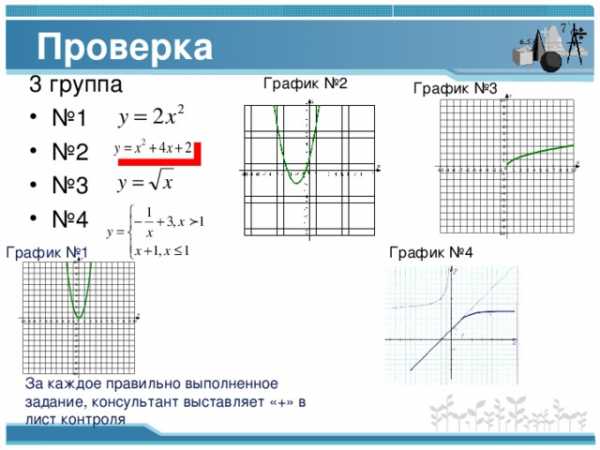
Проверка
3 группа
График №2
График №3
График №4
График №1
За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

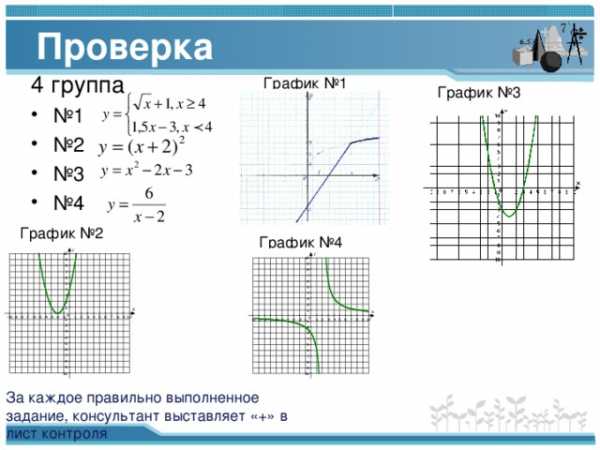
Проверка
4 группа
График №1
График №3
График №2
График №4
За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

3 . Актуализация знаний и фиксация затруднения в пробном действии.
Повторим определение модуля
Как получаем из функции можно получить функцию ?
Постройте графики функций
За каждое правильно выполненное задание, консультант выставляет «+» в лист контроля

3 . Актуализация знаний и фиксация затруднения
в пробном действии.
1 . Организовать актуализацию изученных способов действий, достаточных для построения нового знания.
2. Зафиксировать актуализированные способы действий в речи.

3. Зафиксировать актуализированные способы действий в знаках (эталонах).
Графики каких функций вам знакомы ?( линейная, прямой и обратной пропорциональности, квадратичная, у = )
Как по графику определить вид функции и её формулу? (уметь пользоваться правилами параллельных переносов вдоль осей Ох,Оу, уметь определять коэффициенты, оси симметрии и асимптоты)
Формулы для каких графиков функций вы не смогли определить? Почему?
(последние формулы видим впервые, поэтому не можем определить вид функции и как строить графики)
Давайте попробуем сформулировать цель нашего урока .
(Научиться строить графики нового вида, научиться узнавать их среди других графиков функций, описывать их свойства.)
А я добавлю к вашей цели еще одну: обобщить знание свойств квадратичной функции и научиться применять свойства квадратичной функции в построении графиков с модулем.

Тема урока
«Построение графиков
квадратичной функции с модулем»

4.Построение проекта выхода из затруднения.
Построим графики квадратичных функций с модулем
Выполнив практическую работу, сделаем вывод о свойствах графика
и

5. Реализация построенного проекта.
1.Организовать построение нового способа на примере, вызвавшем затруднение. 2.Организовать фиксацию нового способа действия в речи и с помощью эталона.
3. Зафиксировать преодоление возникшего ранее затруднения.
Каждой группе предлагается построить график одной функции в программе AGrapher , описать её свойства
по алгоритму:
1
2

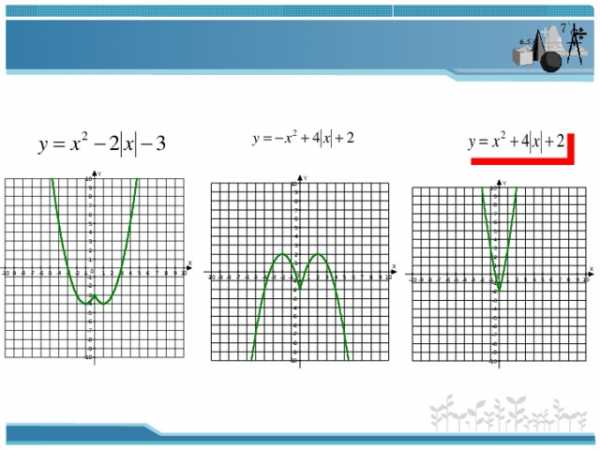
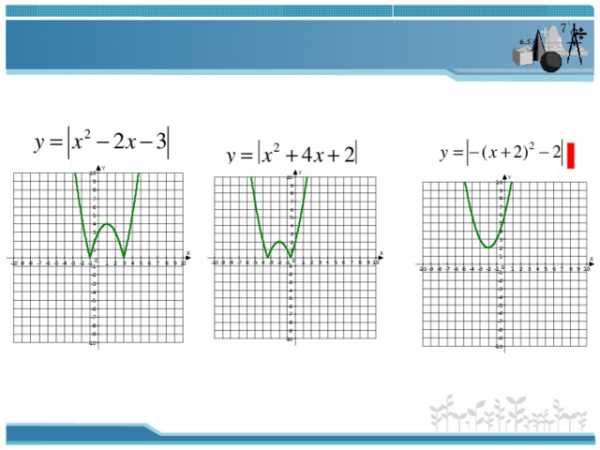
6 .Организовать фиксацию нового способа действия в речи и с помощью эталона.
а) Давайте обобщим способы построения графиков функций, в которых выражение, задающее функцию, находится под знаком модуля, в единый алгоритм (строим график функции без модуля, потом часть графика, находящаяся ниже оси Ох, отображается в верхнюю полуплоскость)
б) Давайте обобщим способы построения графиков функций, в которых аргумент находится под знаком модуля, в единый алгоритм. (строим график функции без модуля, потом часть графика, находящаяся правее оси Оу, отображается в левую полуплоскость)
На основании какого математического понятия мы получаем эти новые способы действия ? (На основании определения модуля выражения)

Сравним полученный нами алгоритм с эталоном .
За каждый правильный ответ, консультант выставляет «+» в лист контроля.

6. Алгоритм построения графика квадратичной функции вида (эталон)
1.Строим график функции у = f (х).
2.Часть графика, для которой, значения функции положительны — оставляем без изменения.
3.Часть графика, для которой, значения функции отрицательны – зеркально отображаем в верхнюю полуплоскость.

Алгоритм построения графика квадратичной функции вида (эталон)
1.Строим график функции у = f (х).
2.Часть графика, для которой, значения аргумента положительны — оставляем без изменения.
3.Часть графика, для которой, значения аргумента положительны – зеркально отображаем в левую полуплоскость.

7 . Самостоятельная работа с самопроверкой по эталону.
Каждой группе выдается задание на построение графиков функций
1 группа
2 группа
3 группа
4 группа
За правильно выполненное задание, консультант выставляет «+» в лист контроля

8. Включение в систему знаний и повторение.
Как построить график квадратичной функции с модулем .(проговаривают алгоритмы)
Графики каких функций мы можем построить с учетом нового знания, полученного сегодня на уроке? (перечисляют функции)

8. Включение в систему знаний и повторение.
Построить графики функций

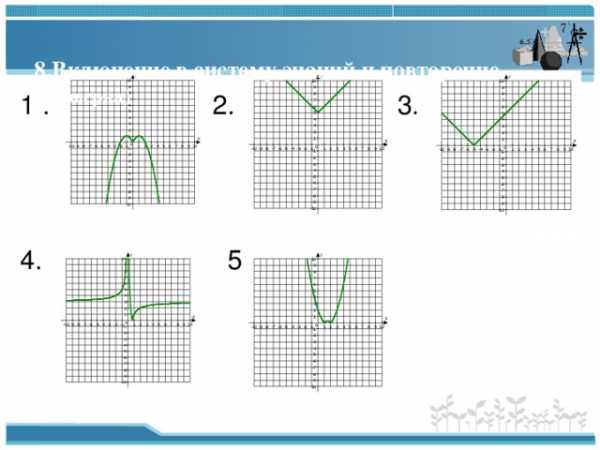
8. Включение в систему знаний и повторение. (проверка)
1 . 2. 3.
4. 5.

9. Подведение итогов, рефлексия
Просуммируем «+» и поставим отметки в зависимости от их количества:
более 8 «+» — «5»
6-7 «+» — «4»
4-5 «+» — «3».
В листе контроля укажите, как вы оцениваете свои достижения поставленных целей на этом уроке
1. Затрудняюсь в построении графика без помощи алгоритма
2. Могу построить строить графики функций с модулями
3. Я все понял и могу объяснить другим

10. Домашнее задание
1. Затрудняюсь в построении графика без помощи алгоритма
Выучить определение модуля. Построить графики функций:
2. Могу построить строить графики функций с модулями
3. Я все понял и могу объяснить другим

Самоанализ урока
Тема урока. «Построение графиков квадратичной функции с модулем».
Цель урока: обобщить знание свойств квадратичной функции и научить применять её свойства в п остроении графиков квадратичной функции с модулем.
Урок четвертый в теме «Функция y = ax 2 + bx + c , ее свойства и график».
Цель урока реализовывалась через формирование у учащихся умения анализировать графики функций и делать выводы. Урок построен в деятельностной технологии обучения.
Обучающиеся знают ряд функций (линейная, обратной пропорциональности, квадратичная, ) умеют определять формулу по графику, умеют строить график, зная формулу.
В ходе урока учащиеся углубляют и расширяют знания о функциях. Учатся обобщать полученные знания и применять их в новых ситуациях. Выполняют исследование свойств графиков с модулем на компьютере при помощи программы AGrapher. Задачи урока были выполнены в ходе организации деятельности учащихся через исследование, сравнение, обобщение графиков различных квадратичных функций с модулем. Для решения задач урока использовала различные формы и методы работы, обучающиеся выполняли самостоятельную работу в группах, выступали с выводами, обобщали знания о функциях. На этапах выявления места и причины затруднений и реализации построенного проекта самостоятельная работа способствовала пониманию как строятся графики функций содержащих модуль
Задачи урока соответствуют особенностям учебного материала.

Самоанализ урока
Содержание учебного материала учитывает возрастные особенности обучающихся и
способствует формированию у школьников компетенций:
учебно-познавательных: обучающиеся формулировали цель урока; выбирали основание для сравнения и обобщения , делали выводы; оценивали свою работу.
коммуникативных: приобретали навыки общения, аргументировали свои выводы; выступали с устными комментариями;
информационных: извлекали необходимую информацию, работая с программой для построения графиков функций, работали над созданием алгоритма построения графиков квадратичной функции с модулем;
Ведущими методами на уроке были частично-поисковый, исследовательский методы. Учащиеся были активны на уроке, работоспособны на всех этапах.
Домашняя работа предложена дифференцированно с учетом уровня усвоения материала и самооценки учащегося.
Считаю, что все используемые на уроке методы, формы, приемы, средства способствовали достижению цели урока.
Цель урока реализована: дети научились строить графики квадратичной функции с модулем и описывать её свойства.
multiurok.ru
Графики функций с модулем

Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа
городского округа город Буй Костромской области
Графики функций
с модулем
Работу выполнила:
Торопова И.В. учитель математики
2004 г.

В курсе математики основной и средней школы незначительное место отводится построению графиков функций, аналитическое выражение которых содержит знак модуля. И поэтому учащиеся испытывают определённые затруднения при их построении.
Впервые с модулем числа учащиеся встречаются в курсе математики 6 класса, и больше не упоминается о нем до 9 класса, и немного заданий на построение графиков таких функций встречается в курсе алгебры и начала анализа 10 класса.
Поэтому, я считаю, что формировать навыки построения графиков функций, аналитическое выражение которых содержит знак модуля, можно начинать с учащимися 7 – 8 классов, проявляющими интерес к изучению математики на занятиях математического кружка или факультатива.
В 7 классе после изучения тем «Линейная функция» и « Прямая пропорциональность» стоит попробовать построить график функции y = |2х|.
Учащиеся уже хорошо умеют строить графики прямой пропорциональности и предварительно надо построить график функции
y = 2х, затем вспомнить с учащимися определение модуля числа и попросить их составить таблицу значений для функции y = |2х| (значения переменной х необходимо взять как положительные так и отрицательные), затем отметить полученные точки на координатной плоскости, соединить их и сравнить полученные графики, ответив на следующие вопросы:
а) Какие значения принимает функция y = |2х| при х≥0, х
б) чем сходны графики функций y = 2х и y = |2х|, чем различаются?
в) Можно ли получить график функции из графика функции y = 2х?
y = 2х y = |2х|

х

-3

-2

-1

0

1

2

3

y

-6

-4

-2

0

2

4

6

х

-3

-2

-1

0

1

2

3

y

6

4

2

0

2

4

6
Учащиеся заметят, что для построения графика функции y = |2х| можно построить график функции y = 2х, затем оставить без изменения часть графика при х≥0, а часть графика расположенную ниже оси х ( при х
Таких заданий можно подобрать много, а способные учащиеся вполне могут построить графики следующих функций: y = |х + 1|, y = |2х + 1|, используя выводы, полученные при построении графика функции y = |2х|.
y = | х + 1| y = |2х + 1|
В 8 классе учащиеся знакомятся с графиком обратной пропорциональности и продолжая формировать умения строить графики, сильным учащимся стоит
построить графики функций типа y = и y = , опираясь на знания, полученные при построении графиков функций, содержащих модуль
в 7 классе.

y = y =

В курсе алгебры 9 класса при изучении темы «Функция. Область определения и область значения функции» ребята знакомятся с графиком функции y = |х| , её областью определения и областью значения. Но заданий в учебнике под редакцией С.А. Теляковского с использованием функции
y = |х| нет, кроме №17 и то предлагаемого на дом. А вот в дидактических материалах для 9 класса авторов Ю.Н. Макарычева, Н.Г. Миндюка,
Л.М. Коротковой предлагаются задания из второго блока, способствующие развитию учащихся в алгоритмическом и логическом плане.
С-8 «График квадратичной функции»
Задание №6
Постройте график функции: а) y = |х| — 3 ; б) y = |х +3| .
y = |х| — 3 y = |х +3|
При построении данных графиков функций можно воспользоваться знаниями, полученными при преобразовании графиков функций y =aх²+n c одной стороны , т. е. график функции y = |х| — 3 можно получить из графика
y = |х| с помощью параллельного переноса вдоль оси Оy на три единицы масштаба вниз, а график функции y = |х +3| из графика функции y = |х| с помощью параллельного переноса вдоль оси Ох на три единицы масштаба влево. Затем сильных учащихся попросить сделать вывод о построении графиков функций вида y = |х| + n ; y = |х — m|.
n>0
y = |х — m| y = |х| + n

m
n
m>0
А с другой стороны (возможно учащиеся и этот способ вспомнят, который чаще всего и используется) построить график функции y = |х — m| можно из графика функции y = х – m , оставив без изменения все части графика, которые лежат выше оси абсцисс, а части расположенные ниже её отобразить симметрично.
С-14 «Графический способ решения систем уравнений» предлагается задание №5, также из второго блока.
Решите графически систему уравнений:
а) y =х²– 3
y = |х|
Ответ: (≈ -2,3; ≈2,3) (≈ 2,3; ≈2,3)
Учащиеся легко с этим заданием справляются, поэтому можно предложить
ёще ряд аналогичных заданий.
Задание: Изобразив схематически графики, выясните, имеет ли решение система уравнений и если имеет, то сколько:
а) y = х²– 3 б) y = х²– 3 в) y = х²– 3 г) y = х²– 3 д) y = х²– 3
y = |х| — 3 y = -|х| y = 4 — |х| y = -|х| — 3 y =-|х| — 4
(3 решения) (2 решения) (2 решения) (1 решение) (нет решения)
Решение.
а)

Отработав навыки построения графика квадратичной функции сильные учащиеся могут попробовать построить графики следующих функций:
а) y = |х²— 1|
Для построения достаточно сначала построить график функции y = х²— 1 , а на интервале (-1; 1) часть графика отобразить симметрично относительно оси абсцисс, остальную часть оставить без изменения.
Аналогичных заданий можно
подобрать достаточно много,
но после их выполнения необходимо
с учащимися сделать вывод о
построении графиков функций
вида y = |f(х)|.
Здесь же надо рассмотреть построение графиков функций вида y = f(|х|). т.е. графики функций содержащие модуль аргумента.
б) y = После его построения учащиеся заметят,
что данный график получается из графика
функции y =путем симметрии относительно уже оси Оy . Необходимо еще раз обратить внимание учащихся, что под знаком модуля находится аргумент и вновь сделать выводы.
в) y = х²— 6|х| + 4

Некоторые учащиеся заметят, что под знаком модуля стоит аргумент, учитывая что х² =|х|², тогда достаточно будет построить график функции для х≥0, а затем полученную кривую отобразить относительно оси у.

И закончить рассмотрение графиков функций в 9 классе, аналитическое выражение которых содержит знак модуля построением графиков вида
y = |f(|х|)|.
Предложить учащимся построить графики следующих функций:
а) y = |х| ; б) y = |х| — 1; в) y = | |х| — 1|.
Задания а) и б) легко учащиеся выполнят, но их выполнение должно натолкнуть их на мысль, что построение графика функции под в) следует выполнять поэтапно: строим график функции y = |х|, затем выполнить параллельный перенос вдоль оси Оу на одну единицу масштаба вниз и наконец, часть графика расположенного под осью Ох симметрично отобразить относительно её.
а) б) в)

Тренировочные упражнения:

а) y = | |2х|-3 | б) y = | 3|х| + 1| в) y =| х²— 4|х| + 3 |
г) y = |х| + х д) y = 2|х| + х е) y =+ 3

Вывод: Для построения графика функции y = |f(|х|)| надо построить график функции y = f(|х|), далее оставить без изменения все части построенного графика, которые лежат выше оси абсцисс, а части, расположенные ниже её, отобразить симметрично относительно этой оси.
Такая работа с графиками закрепит знания учащихся о модуле числа и даст неплохие навыки для их построения.
В 10-11 классах эту работу следует продолжить, т.к. учащиеся основательно знакомятся со свойствами функций и их исследованием.
В 10 классе большое место отводится изучению тригонометрических функций и, конечно же, их графикам. Здесь можно такие задания:

1. Построить графики функций у = cos|x| и у = |cosx|.
Решение.

а)у = cos|x|, cos|x| = cosx, т.к. cos x = cos(-x). Следовательно, график данной функции тот же, что и график функции у = cosx;
б) у=- |cosx|, при cos x ≥ 0 у = cos x. Следовательно, на участке, где
cos x ≥ 0, график будет тот же, что и график функции у = cosx. При cos x у = — cosx. Следовательно, части графика функции у = cos x, расположенные
ниже оси абсцисс, зеркально отобразятся и будут расположены в верхней
полуплоскости.
2. Построить графики функций у = sin[x| и у = |sin x |.

Решение.
Чтобы построить график у = sin|x|, надо построить сначала график
у = sin х при х > 0, а затем построить кривую, симметричную с построенным графиком относительно оси ординат.

3. Построить график функции у = sin х + |sin х |.
4. Построить график функции у =tg|x|.
Решение.

Функция чётная, так как tg|-x| = tg|x|. При х > 0 график искомой функции тот же, что и график функции у = tg x.
5. Построить график функции у = |tgx|.

Решение.
Часть графика функции у = tgx, расположенную в верхней полуплоскости, оставить без изменений, а часть графика, расположенную в нижней полуплоскости, зеркально отобразить относительно оси ОХ.
В теме «Функции и их графики» при изучении нового материала и говоря о преобразовании графиков вновь вспомнить и о графиках функции у = |f(х)| и y = f(|х|):
а) график у = |f(х)| функции получается из графика функции у = f(х) следующим образом: часть графика у = f(х), лежащая над осью Ох, сохраняется, часть его, лежащая под осью Ох, отображается симметрично относительно оси Ох:
б) график функции y = f(|х|) получается из графика функции у = f(х) так: при х≥0 график у = f(х) сохраняется, а при х 0 полученная часть графика отображается симметрично относительно оси Oу:

На следующем уроке рассмотреть построение нескольких таких графиков функций.
а) построить графики функций:
б) построить график функции у = |х-1| + |х+3|.
Решение.
Находим значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль: х — 1 = 0 или х + 3 = 0;
х= 1 или х = -3.
1) при х = -х+ 1-х-3 =-2х-2; у = -2х-2;
2) при -3= -х+ 1 +х + 3 = 4; у = 4;
3) при х>1, у = х-1+х + 3=2х + 2; у= 2х + 2.

В теме «Исследование функций» в учебнике «Алгебра и начала анализа» для учащихся 10-11 классов Колмогорова А.Н. включены функции, содержащие знак модуля, но таких заданий всего два — это №99(а, в), №55(а).

В качестве дополнительного задания на исследования тригонометрических функций сильным учащимся предложить построить график функции
у = 2 – sin| х+|
Решение.
1 способ. Строим график функции у = —sin|х|
Ось ординат переносим на +, а ось абсцисс — на -2.
2 способ. График имеет две ветви, уравнения которых различны.
1) если х+≥ 0, то есть х≥-, то у = 2 – sin( х+).
2) если х+0, то есть х, то у = 2 – sin( -(х+))= 2+ sin( х+).
Область определения функции — вся числовая прямая.
Область значения функции определим из условия -1≤– sin| х+|≤1
-1+2≤ у ≤ 1+2
1≤ у ≤3
Общая точка обеих ветвей графика: х= -; у=- sin| 0|+2=2: точка (-; 2).
Можно учащимся, конечно, предложить построить и исследовать графики таких функций, как у= arcsin| x| , у= arcsin| x-1|, у=arccos| x|, у= arctg| x|, но с этим заданием справятся только сильные учащиеся или проявляющие интерес к данной теме.
И закончить построение таких графиков функций в 11 классе рассмотрением графиков показательной и логарифмической функций типа:

у = 2^|^x^| у =| log _аx |
График функции у = 2^{^x при х≥0 Строим график функции у = log _аx.}
И его зеркальное отображение На интервале (0;1) у = log _аx 0
относительно оси Оу дадут в (кривая расположена под осью Ох)
совокупности график заданной эта часть графика функции симмет
функции. рично отобразится относительно
оси Ох, а остальная часть останется
без изменения.
у = 2^|^x^-1| у = log | x |^|у = |log | x ||
Литература
1. Афанасьева Т.Л., Тапилина Л.А. Алгебра 10 класс (поурочные планы).- Волгоград . -2002. С.13-45.
2. Вирченко Н.А., Ляшко И.И., Швецов К.И. Графики функций: Справочник. –Киев: Наукова думка. -1979. — С.100-107.

3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10-11 класса средней школы. – М.: Просвещение, 1990. – С. 47-54.
4. Макарычев Ю.Н. и др. Дидактические материалы по алгебре для 9 класса. – 5-е изд. – М.: Просвещение, 2000. – С. 10-19. 0>
megdu.ru
Графики функций с модулем

Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа
городского округа город Буй Костромской области
Графики функций
с модулем
Работу выполнила:
Торопова И.В. учитель математики
2004 г.

В курсе математики основной и средней школы незначительное место отводится построению графиков функций, аналитическое выражение которых содержит знак модуля. И поэтому учащиеся испытывают определённые затруднения при их построении.
Впервые с модулем числа учащиеся встречаются в курсе математики 6 класса, и больше не упоминается о нем до 9 класса, и немного заданий на построение графиков таких функций встречается в курсе алгебры и начала анализа 10 класса.
Поэтому, я считаю, что формировать навыки построения графиков функций, аналитическое выражение которых содержит знак модуля, можно начинать с учащимися 7 – 8 классов, проявляющими интерес к изучению математики на занятиях математического кружка или факультатива.
В 7 классе после изучения тем «Линейная функция» и « Прямая пропорциональность» стоит попробовать построить график функции y = |2х|.
Учащиеся уже хорошо умеют строить графики прямой пропорциональности и предварительно надо построить график функции
y = 2х, затем вспомнить с учащимися определение модуля числа и попросить их составить таблицу значений для функции y = |2х| (значения переменной х необходимо взять как положительные так и отрицательные), затем отметить полученные точки на координатной плоскости, соединить их и сравнить полученные графики, ответив на следующие вопросы:
а) Какие значения принимает функция y = |2х| при х≥0, х
б) чем сходны графики функций y = 2х и y = |2х|, чем различаются?
в) Можно ли получить график функции из графика функции y = 2х?
y = 2х y = |2х|

х

-3

-2

-1

0

1

2

3

y

-6

-4

-2

0

2

4

6

х

-3

-2

-1

0

1

2

3

y

6

4

2

0

2

4

6
Учащиеся заметят, что для построения графика функции y = |2х| можно построить график функции y = 2х, затем оставить без изменения часть графика при х≥0, а часть графика расположенную ниже оси х ( при х
Таких заданий можно подобрать много, а способные учащиеся вполне могут построить графики следующих функций: y = |х + 1|, y = |2х + 1|, используя выводы, полученные при построении графика функции y = |2х|.
y = | х + 1| y = |2х + 1|
В 8 классе учащиеся знакомятся с графиком обратной пропорциональности и продолжая формировать умения строить графики, сильным учащимся стоит
построить графики функций типа y = и y = , опираясь на знания, полученные при построении графиков функций, содержащих модуль
в 7 классе.

y = y =

В курсе алгебры 9 класса при изучении темы «Функция. Область определения и область значения функции» ребята знакомятся с графиком функции y = |х| , её областью определения и областью значения. Но заданий в учебнике под редакцией С.А. Теляковского с использованием функции
y = |х| нет, кроме №17 и то предлагаемого на дом. А вот в дидактических материалах для 9 класса авторов Ю.Н. Макарычева, Н.Г. Миндюка,
Л.М. Коротковой предлагаются задания из второго блока, способствующие развитию учащихся в алгоритмическом и логическом плане.
С-8 «График квадратичной функции»
Задание №6
Постройте график функции: а) y = |х| — 3 ; б) y = |х +3| .
y = |х| — 3 y = |х +3|
При построении данных графиков функций можно воспользоваться знаниями, полученными при преобразовании графиков функций y =aх²+n c одной стороны , т. е. график функции y = |х| — 3 можно получить из графика
y = |х| с помощью параллельного переноса вдоль оси Оy на три единицы масштаба вниз, а график функции y = |х +3| из графика функции y = |х| с помощью параллельного переноса вдоль оси Ох на три единицы масштаба влево. Затем сильных учащихся попросить сделать вывод о построении графиков функций вида y = |х| + n ; y = |х — m|.
n>0
y = |х — m| y = |х| + n

m
n
m>0
А с другой стороны (возможно учащиеся и этот способ вспомнят, который чаще всего и используется) построить график функции y = |х — m| можно из графика функции y = х – m , оставив без изменения все части графика, которые лежат выше оси абсцисс, а части расположенные ниже её отобразить симметрично.
С-14 «Графический способ решения систем уравнений» предлагается задание №5, также из второго блока.
Решите графически систему уравнений:
а) y =х²– 3
y = |х|
Ответ: (≈ -2,3; ≈2,3) (≈ 2,3; ≈2,3)
Учащиеся легко с этим заданием справляются, поэтому можно предложить
ёще ряд аналогичных заданий.
Задание: Изобразив схематически графики, выясните, имеет ли решение система уравнений и если имеет, то сколько:
а) y = х²– 3 б) y = х²– 3 в) y = х²– 3 г) y = х²– 3 д) y = х²– 3
y = |х| — 3 y = -|х| y = 4 — |х| y = -|х| — 3 y =-|х| — 4
(3 решения) (2 решения) (2 решения) (1 решение) (нет решения)
Решение.
а)

Отработав навыки построения графика квадратичной функции сильные учащиеся могут попробовать построить графики следующих функций:
а) y = |х²— 1|
Для построения достаточно сначала построить график функции y = х²— 1 , а на интервале (-1; 1) часть графика отобразить симметрично относительно оси абсцисс, остальную часть оставить без изменения.
Аналогичных заданий можно
подобрать достаточно много,
но после их выполнения необходимо
с учащимися сделать вывод о
построении графиков функций
вида y = |f(х)|.
Здесь же надо рассмотреть построение графиков функций вида y = f(|х|). т.е. графики функций содержащие модуль аргумента.
б) y = После его построения учащиеся заметят,
что данный график получается из графика
функции y =путем симметрии относительно уже оси Оy . Необходимо еще раз обратить внимание учащихся, что под знаком модуля находится аргумент и вновь сделать выводы.
в) y = х²— 6|х| + 4

Некоторые учащиеся заметят, что под знаком модуля стоит аргумент, учитывая что х² =|х|², тогда достаточно будет построить график функции для х≥0, а затем полученную кривую отобразить относительно оси у.

И закончить рассмотрение графиков функций в 9 классе, аналитическое выражение которых содержит знак модуля построением графиков вида
y = |f(|х|)|.
Предложить учащимся построить графики следующих функций:
а) y = |х| ; б) y = |х| — 1; в) y = | |х| — 1|.
Задания а) и б) легко учащиеся выполнят, но их выполнение должно натолкнуть их на мысль, что построение графика функции под в) следует выполнять поэтапно: строим график функции y = |х|, затем выполнить параллельный перенос вдоль оси Оу на одну единицу масштаба вниз и наконец, часть графика расположенного под осью Ох симметрично отобразить относительно её.
а) б) в)

Тренировочные упражнения:

а) y = | |2х|-3 | б) y = | 3|х| + 1| в) y =| х²— 4|х| + 3 |
г) y = |х| + х д) y = 2|х| + х е) y =+ 3

Вывод: Для построения графика функции y = |f(|х|)| надо построить график функции y = f(|х|), далее оставить без изменения все части построенного графика, которые лежат выше оси абсцисс, а части, расположенные ниже её, отобразить симметрично относительно этой оси.
Такая работа с графиками закрепит знания учащихся о модуле числа и даст неплохие навыки для их построения.
В 10-11 классах эту работу следует продолжить, т.к. учащиеся основательно знакомятся со свойствами функций и их исследованием.
В 10 классе большое место отводится изучению тригонометрических функций и, конечно же, их графикам. Здесь можно такие задания:

1. Построить графики функций у = cos|x| и у = |cosx|.
Решение.

а)у = cos|x|, cos|x| = cosx, т.к. cos x = cos(-x). Следовательно, график данной функции тот же, что и график функции у = cosx;
б) у=- |cosx|, при cos x ≥ 0 у = cos x. Следовательно, на участке, где
cos x ≥ 0, график будет тот же, что и график функции у = cosx. При cos x у = — cosx. Следовательно, части графика функции у = cos x, расположенные
ниже оси абсцисс, зеркально отобразятся и будут расположены в верхней
полуплоскости.
2. Построить графики функций у = sin[x| и у = |sin x |.

Решение.
Чтобы построить график у = sin|x|, надо построить сначала график
у = sin х при х > 0, а затем построить кривую, симметричную с построенным графиком относительно оси ординат.

3. Построить график функции у = sin х + |sin х |.
4. Построить график функции у =tg|x|.
Решение.

Функция чётная, так как tg|-x| = tg|x|. При х > 0 график искомой функции тот же, что и график функции у = tg x.
5. Построить график функции у = |tgx|.

Решение.
Часть графика функции у = tgx, расположенную в верхней полуплоскости, оставить без изменений, а часть графика, расположенную в нижней полуплоскости, зеркально отобразить относительно оси ОХ.
В теме «Функции и их графики» при изучении нового материала и говоря о преобразовании графиков вновь вспомнить и о графиках функции у = |f(х)| и y = f(|х|):
а) график у = |f(х)| функции получается из графика функции у = f(х) следующим образом: часть графика у = f(х), лежащая над осью Ох, сохраняется, часть его, лежащая под осью Ох, отображается симметрично относительно оси Ох:
б) график функции y = f(|х|) получается из графика функции у = f(х) так: при х≥0 график у = f(х) сохраняется, а при х 0 полученная часть графика отображается симметрично относительно оси Oу:

На следующем уроке рассмотреть построение нескольких таких графиков функций.
а) построить графики функций:
б) построить график функции у = |х-1| + |х+3|.
Решение.
Находим значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль: х — 1 = 0 или х + 3 = 0;
х= 1 или х = -3.
1) при х = -х+ 1-х-3 =-2х-2; у = -2х-2;
2) при -3= -х+ 1 +х + 3 = 4; у = 4;
3) при х>1, у = х-1+х + 3=2х + 2; у= 2х + 2.

В теме «Исследование функций» в учебнике «Алгебра и начала анализа» для учащихся 10-11 классов Колмогорова А.Н. включены функции, содержащие знак модуля, но таких заданий всего два — это №99(а, в), №55(а).

В качестве дополнительного задания на исследования тригонометрических функций сильным учащимся предложить построить график функции
у = 2 – sin| х+|
Решение.
1 способ. Строим график функции у = —sin|х|
Ось ординат переносим на +, а ось абсцисс — на -2.
2 способ. График имеет две ветви, уравнения которых различны.
1) если х+≥ 0, то есть х≥-, то у = 2 – sin( х+).
2) если х+0, то есть х, то у = 2 – sin( -(х+))= 2+ sin( х+).
Область определения функции — вся числовая прямая.
Область значения функции определим из условия -1≤– sin| х+|≤1
-1+2≤ у ≤ 1+2
1≤ у ≤3
Общая точка обеих ветвей графика: х= -; у=- sin| 0|+2=2: точка (-; 2).
Можно учащимся, конечно, предложить построить и исследовать графики таких функций, как у= arcsin| x| , у= arcsin| x-1|, у=arccos| x|, у= arctg| x|, но с этим заданием справятся только сильные учащиеся или проявляющие интерес к данной теме.
И закончить построение таких графиков функций в 11 классе рассмотрением графиков показательной и логарифмической функций типа:

у = 2^|^x^| у =| log _аx |
График функции у = 2^{^x при х≥0 Строим график функции у = log _аx.}
И его зеркальное отображение На интервале (0;1) у = log _аx 0
относительно оси Оу дадут в (кривая расположена под осью Ох)
совокупности график заданной эта часть графика функции симмет
функции. рично отобразится относительно
оси Ох, а остальная часть останется
без изменения.
у = 2^|^x^-1| у = log | x |^|у = |log | x ||
Литература
1. Афанасьева Т.Л., Тапилина Л.А. Алгебра 10 класс (поурочные планы).- Волгоград . -2002. С.13-45.
2. Вирченко Н.А., Ляшко И.И., Швецов К.И. Графики функций: Справочник. –Киев: Наукова думка. -1979. — С.100-107.

3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10-11 класса средней школы. – М.: Просвещение, 1990. – С. 47-54.
4. Макарычев Ю.Н. и др. Дидактические материалы по алгебре для 9 класса. – 5-е изд. – М.: Просвещение, 2000. – С. 10-19. 0>
www.megdu.ru
Построение графика функции, содержащей модуль. Пример 1

ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ, СОДЕРЖАЩЕЙ МОДУЛЬ.

ПРИМЕР 1.

Построить график функции:

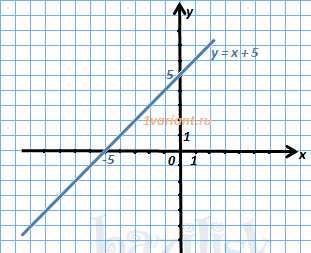
1. Строим график функции .

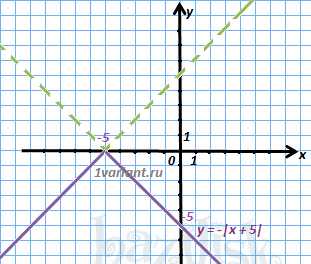
2. График нижней полуплоскости отображаем вверх симметрично относительно оси ОХ и получаем график функции .

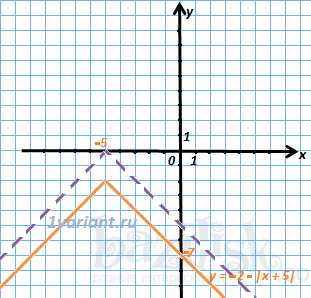
3. График функции отображаем вниз симметрично относительно оси ОХ и получаем график функции .

4. Опускаем график функции на 2 единицы вниз и получаем график .

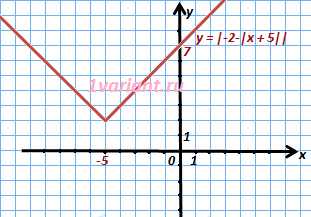
5. Отображаем график функции относительно оси ОХ и получаем график .

6. В итоге график функции выглядит следующим образом

www.1variant.ru
No related posts.