Построение графиков функций геометрическими методами / math5school.ru
График функции y=f(x)+a
График функции y=f(x–a)
График функции y=kf(x), k>0
График функции y=f(kx), k>0
График функции y=–f(x)
График функции y=f(–x)
График функции y=|f(x)|
График функции y=f(|x|)
График функции y=f(x)+a
Способ построения: параллельный перенос графика функции y=f(x) вдоль оси Oy на а единиц вверх, если a>0, и на |a| единиц вниз, если a<0.
График функции y=f(x–a)
Способ построения: параллельный перенос графика функции y=f(x) вдоль оси Ox на а единиц вправо, если a>0, и на |a| единиц влево, если a<0.
График функции y=kf(x), k>0
Способ построения: растяжение графика функции
График функции y=f(kx), k>0
Способ построения: сжатие графика функции y=f(x) вдоль оси Ox относительно оси Oy в k раз, если k>1, и растяжение в 1/k раз, если 0<k<1.
График функции y=–f(x)
Способ построения: симметричное отражение графика функции y=f(x) относительно оси Ox.
График функции y=f(–x)
Способ построения: симметричное отражение графика функции y=f(x) относительно оси Oy.
График функции y=|f(x)|
Способ построения: часть графика функции y=f(x), расположенная ниже оси Ox, симметрично отражается относительно этой оси, остальная его часть остаётся без изменения.
График функции y=f(|x|)
Способ построения: часть графика функции y=f(x), расположенная правее оси Oy и на ней, остаётся без изменения, а остальная его часть заменяется симметричным отображением относительно оси Oy части графика, расположенной правее оси Oy.
Смотрите также:
Таблицы чисел
Алгебраические тождества
Степени
Арифметический корень n-й степени
Логарифмы
Графики элементарных функций
Тригонометрия
Таблицы значений тригонометрических функций
Треугольники
Четырёхугольники
Многоугольники
Окружность
Площади геометрических фигур
Прямые и плоскости
Многогранники
Тела вращения
math4school.ru
График функции y=f(|x|) | Алгебра
График функции y=f(|x|) может быть получен из графика функции y=f(x).
Для этого ту часть графика, которая лежит левее оси Oy, отбрасываем. Часть графика, расположенную правее оси ординат, сохраняем, и её же отображаем симметрично относительно оси Oy.
Точка, лежащая на оси Oy, при таком преобразовании остаётся на месте.
Примеры.
1) Построить график функции y= -x²+2|x|+8.
Решение:
Так как x²=|x|², запишем формулу функции в виде y= —|x|²+2|x|+8.
График функции y= —|x|²+2|x|+8 можно получить из графика функции y= -x²+2x+8. Для этого часть графика, лежащую слева от оси Oy, отбрасываем. Правее оси ординат график сохраняем и это же часть отображаем симметрично относительно оси Oy:
(1; 9) → (-1; 9),
(2; 8) → (-2; 8),
(3; 5) → (-3; 5),
(4; 0) → (-4; 0).
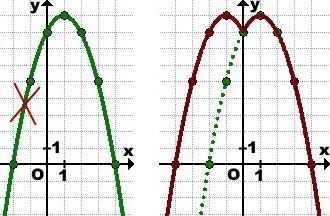
График y= -|x|²+2|x|+8 из графика y= -x²+2x+8.
2) График функции
получен из графика функции y=-4/(x-2).
Всё, что лежит левее оси Oy, отбрасываем, всё, что правее — отображаем симметрично относительно оси ординат:
3) График функции
получен из графика y=√x.
Отбрасывать здесь нечего, поскольку график полностью расположен правее оси ординат. Весь график сохраняем, и его же отображаем симметрично относительно оси Oy:
Геометрические преобразования — быстрый и удобный способ построения графиков на основе графиков элементарных функций. Поскольку в алгебре строить графики приходится достаточно часто, важно вовремя научиться пользоваться этим инструментом.
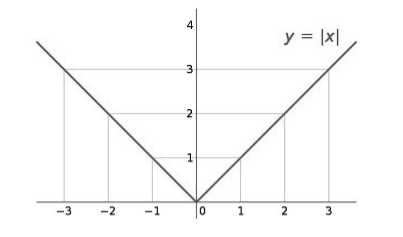
Функции y=|x|, y=[x],y={x}, y=sign(x) и их графики. Функция f(x)=|x|
Функция $f(x)=|x|$
$|x|$ — модуль. Он определяется следующим образом: Если действительное число будет неотрицательным, то значение модуля совпадает с самим числом. Если же отрицательно, то значение модуля совпадает с абсолютным значением данного числа.
Математически это можно записать следующим образом:
Пример 1
Исследуем и построим её график.
- $D\left(f\right)=R$.
- По определению модуля действительного числа, получим, что$E\left(f\right)=[0,\infty )$
- $f\left(-x\right)=|-x|=|x|=f(x)$. Значит, функция четна.
- При $x=0,\ y=0$. Точка $\left(0,0\right)$ — единственное пересечение с координатными осями.
- \[f’\left(x\right)=\left\{ \begin{array}{c} {1,x >0,} \\ {-1,xФункция будет возрастать на промежутке $x\in (0,+\infty )$
Функция будет убывать на промежутке $x\in (-\infty ,0)$
Значения на концах области определения.
\[{\mathop{\lim }_{x\to -\infty } y\ }=+\infty \] \[{\mathop{\lim }_{x\to +\infty } y\ }=+\infty \]
Рисунок 1.
Функция $f(x)=[x]$
Функция $f\left(x\right)=[x]$ — функция целой части числа. Она находится округлением числа (если оно само не целое) «в меньшую сторону».
Пример: $[2,6]=2.$
Пример 2
Исследуем и построим её график.
- $D\left(f\right)=R$.
- Очевидно, что эта функция принимает только целые значения, то есть $\ E\left(f\right)=Z$
- $f\left(-x\right)=[-x]$. Следовательно, эта функция будет общего вида.
- $(0,0)$ — единственная точка пересечения с осями координат.
- $f’\left(x\right)=0$
- Функция имеет точки разрыва (скачка функции) при всех $x\in Z$.
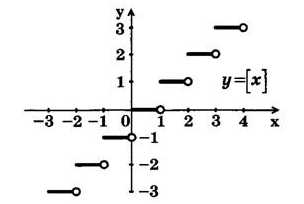
Рисунок 2.
Функция $f\left(x\right)=\{x\}$
Функция $f\left(x\right)=\{x\}$ — функция дробной части числа. Она находится «отбрасыванием» целой части этого числа.
$\{2,6\}=0,6$
Пример 3
Исследуем и построим график функции
$D\left(f\right)=R$.
Очевидно, что эта функция никогда не будет отрицательной и никогда не будет больше единицы, то есть $\ E\left(f\right)=[0,1)$
$f\left(-x\right)=\{-x\}$. Следовательно, данная функция будет общего вида.
Пересечение с осью $Ox$: $\left(z,0\right),\ z\in Z$
Пересечение с осью $Oy$: $\left(0,0\right)$
$f’\left(x\right)=0$
Функция имеет точки разрыва (скачка функции) при всех $x\in Z$
Рисунок 3.
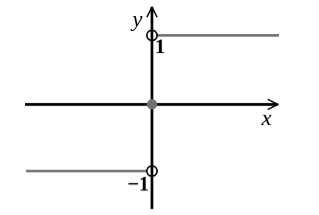
Функция $f(x)=sign(x)$
Функция $f\left(x\right)=sign(x)$ — сигнум-функция. Эта функция показывает, какой знак имеет действительное число. Если число отрицательно, то функция имеет значение $-1$. Если число положительно, то функция равняется единице. При нулевом значении числа, значение функции также будет принимать нулевое значение.
Математически это можно записать следующим образом:
Пример 4
Исследуем и построим график функции
- $D\left(f\right)=R$.
- Непосредственно из определения, получим
- \[\ E\left(f\right)=\left\{-1\right\}\cup \left\{0\right\}\cup \{1\}\]
$f\left(-x\right)=sign\left(-x\right)=-sign(x)$. Следовательно, данная функция будет нечетной.
Пересечение с осью $Ox$: $\left(0,0\right)$
Пересечение с осью $Oy$: $\left(0,0\right)$
$f’\left(x\right)=0$
Функция имеет точку разрыва (скачка функции) в начале координат.

Рисунок 4.
Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=|f(x)|; y=f(|x|). Построение графика обратной функции. Примерно 7-9 класс (13-15 лет)
Преобразование графиков функций у= f(x) в y=-f(x): |
|
|
|
Преобразование графиков функций у= f(x) в y=f(-x): |
|
|
|
Преобразование графиков функций у= f(x) в y=-f(-x): |
|
|
|
Преобразование графиков функций у= f(x) в y=f(x-a): |
|
|
|
dpva.ru
Как построить график функции у = f (x + t) + m, если известен график функции у = f(x)
На этом уроке вы узнаете, как построить график функции у = f (x + t) + m, если известен график функции у = f(x)
Мы умеем строить график функции y = f(x+t), если известен график функции y = f(x).
Правило построения графиков функции y = f(x+t):
y = f(x+t)
y = f(х) сдвигаем:
— при на единиц
— при на единиц
Правило построения графиков функции y = f(x) + m:
y = f(x) + m
y = f(х) сдвигаем:
— при на единиц
— при на единиц
Пример. Построить график функции
Дано:
Решение. 1. Сначала мы должны построить график функции вида в нашем случае это .
Так как -1 < 0, то, соответственно, график сдвигается вдоль оси Ох вправо на 1 единицу (рис. 1).
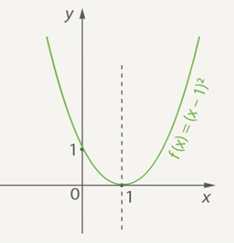
Рис. 1. График функции
2. Теперь построим :
Так как , а 2 > 0, то график, полученный в предыдущем действии, мы сдвигаем вверх 2 единицы (рис. 2).
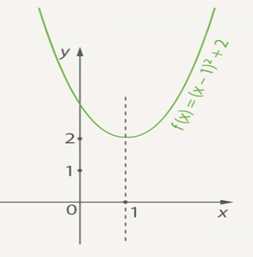
Рис. 2. График функции
Этот график и будет графиком требуемой функции. Точка пересечения с осями – (0; 3).
Пример решен.
В данном примере числа -1 и 2 можно заменить на параметр
interneturok.ru
Как построить график функции y=m*f(x), если известен график функции y=f(x)
Дополнительные сочиненияНа этом уроке мы обсудим построение модификаций графиков вида у = mf(x). Вначале мы вспомним, как строятся ранее изучаемые модификации графиков вида у = f(x±k) и у = f(x)±k. Далее мы рассмотрим построение графика функции вида у = mf(x) на примере функции синуса и сформулируем общее правило для подобных преобразований. В конце урока мы решим несколько примеров на построение схематического графика.
Тема: Тригонометрические функции
Урок: Как построить график функции y=m∙f(x), если известен график функции y=f(x)
1. Преобразование графиков: напоминание
Вспомним известные нам правила преобразования графиков.
1) Построить графики функций
Например:

получаем сдвигом кривой на 1 вправо по оси x;
получаем сдвигом кривой на 1 влево по оси x.
2) Построить графики функций
Например:
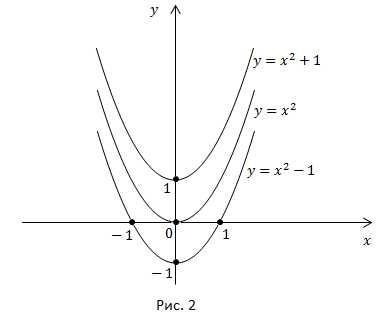
получаем сдвигом кривой на 1 вверх по оси y;
получаем сдвигом кривой на 1 вниз по оси y.
2. Построение графика функции y=m∙f(x) по известному графику y=f(x)
3) Построить график функции
Например:
Поместим значения функций в основных точках в таблицу.
И построим графики функций (рис. 3).
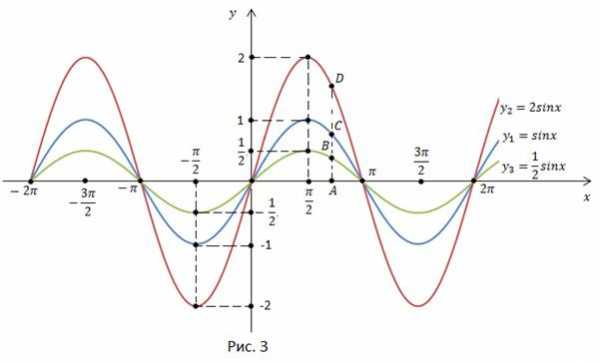
Исходную кривую необходимо растянуть или сжать в m раз. При точки графика остаются без изменения.
Рассмотрим значения функций в основных точках при
0 | 0 | 0 | 0 | ||||
0 | 0 | 0 | 0 | ||||
0 | 0 | 0 | 0 |
И построим графики функций
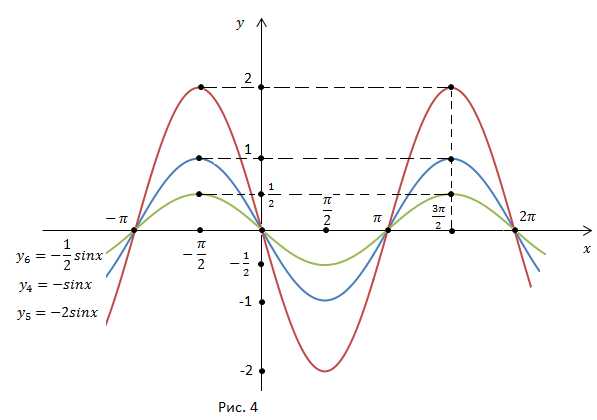
График функции симметричен графику функции относительно оси x.
3. Правило получения кривой y=m∙f(x)
Правило получения кривой из кривой
1. Точки пересечения кривой c осью x сохраняются без изменений.
2. В остальных точках области определения ордината изменяется в m раз (рис. 5).

4. Примеры
Используя правило, построим графики функций:
1)
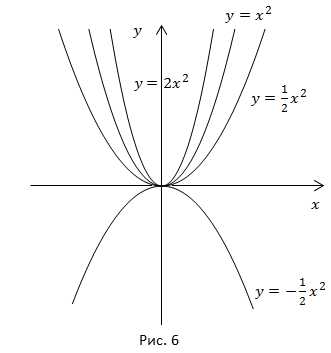
2)
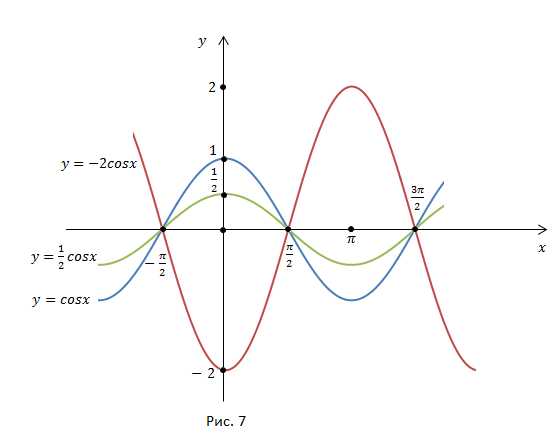
5. Вывод, заключение
Мы вспомнили известные ранее правила преобразования графиков функций и вывели новое правило, по которому из графика функции можно получить график функции , привели несколько примеров.
Правило будет использоваться и в дальнейшем, в частности, при исследовании гармонических колебаний.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М. Л., Мошкович М. М., Шварцбурд С. И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А. Г., Полонский В. Б., Якир М. С. Алгебраический тренажер.-К.: А. С.К., 1997.
7. Саакян С. М., Гольдман А. М., Денисов Д. В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А. П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 17.1 – 17.6.
Дополнительные веб-ресурсы
1. Математика .
2. Интернет-портал Problems. ru .
3. Образовательный портал для подготовки к экзаменам .
dp-adilet.kz
Как построить график функции y=f(kx), если известен график функции y=f(x)
На этом уроке мы рассмотрим построение модификаций графика вида у = f(k∙x). Вначале мы вспомним, как строится график вида у = m*f(x) и общее правило построения таких графиков. Далее мы рассмотрим построение модификаций графиков вида у = f(k∙x) при k>1 на примере функции синуса и сформулируем правило построения. И рассмотрим построение графиков при 0<k<1. В конце урока мы сформулируем общее правило для построения графиков данной модификации при k>0.
Тема: Тригонометрические функции
Урок: Как построить график функции y=f(kx), если известен график функции y=f(x)
Ранее мы рассматривали, как построить график функции когда на число m умножалась вся функция, при этом необходимо было сжать или растянуть исходную кривую в m раз вдоль оси y.
Теперь вместо аргумента x в функцию подставим аргумент и исходную кривую необходимо будет в раз сжать или растянуть вдоль оси x.
Вспомним правило построения графика функции
Дан график необходимо получить график функции
|
|
|||||
|
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
interneturok.ru