Построить график функций y x 3 – Постройте график функции y = x-3

Постройте график функции y = |x| x + |x| – 3x

Задание.
Построить график функции у = \textbar х \textbar  х + \textbar х\textbar  — 3х.

Решение.
Сначала рассмотрим функцию. Она содержит знак модуля, под которым стоим переменная х. в таком случае переменная х может принимать и отрицательное, и положительное значение. Следовательно, графиком функции будет две параболы, ветви которых направлены в противоположные стороны.
Разберем более подробно.
Предположим, что переменная х будет иметь положительно значение. Тогда функция после раскрытия знака модуля будет иметь вид:

   

В случае, когда х будет иметь отрицательное значение, функция будет иметь следующий вид:

   

Нужно построить эти две параболы, но первую на промежутке для положительных значений х, то есть от 0 до плюс бесконечности, а вторую — для отрицательных значений х, то есть от минус бесконечности до 0. Таким образом, эти две параболы будут отделяться осью Оу.

Найдем вершины этих парабол.

   

   

   

   

   

   

Для построения найдем еще точки пересечения с осями координат.
Для параболы :
С осью Оу: х = 0

   

С осью Ох: у = 0

   

   

или
Получили две точки:
(0; 0) и (2; 0).
Для параболы :
С осью Оу: х = 0

   

С осью Ох: у = 0

   

   

или
Получили две точки:
(0; 0) и (—4; 0).

ru.solverbook.com

Постройте график функции и найдите значение k

Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.

Решение:

Разберем как строить график с модулем.

y=|x-3|-|x+3|

Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3

У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.

1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1

У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).

y=—(x-3)-(—(x+3))=-х+3+х+3=6

На интервале (-∞;-3) получился график линейной функции (прямой) у=6

2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3

У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.

y=—(x-3)-(+(x+3))=-х+3-х-3=-2x

На интервале (-3;3) получился график линейной функции (прямой) у=-2х

3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.

х=5
x-3=5-3=2 и x+3=5+3=8

У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).

y=+(x-3)-(+(x+3))=х-3-х-3=-6

На интервале (3;+∞) получился график линейной функции (прямой) у=-6

4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.

5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.

Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.

Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.

Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.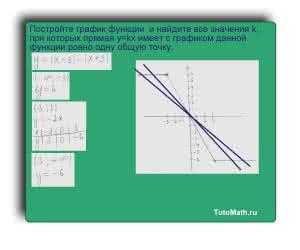

Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.

Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.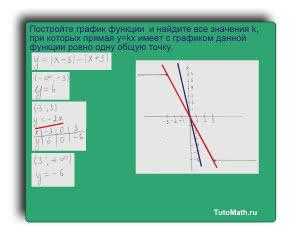

Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.

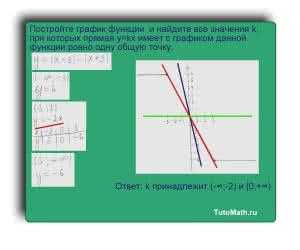
Ответ: при k принадлежащей интервалу (-∞;-2)U[0;+∞) прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

tutomath.ru

Построить график функции y = 3x+1

Задание.
Постройте график функции y = 3x + 1.

Решение.
Поскольку данная функция относится к линейным, а следовательно, ее графиком ее будет прямая, то построить ее можно абсолютно без никаких проблем. Выполним несложные расчеты, для того чтобы найти пару точек, через которые эта прямая будет проходить.
Найти точки можно двумя способами, которые практически равны по сложности.
Первый заключается в нахождении точек прямой, в которых она пересекается с осью Ох и осью Оу.

Первым рассмотрим пересечение с осью Ох. Если функция пересекается с осью Ох, то предположительно х не будет равен 0, а вот координата у будет равна 0. Решим следующее равенство:

   

   

Координаты первой точк5и получились равными .
Вторую точку найдем как пересечение с осью Оу. В этом случае предполагаем, что у не равен нулю, а вот х равен нулю. Подставляем в уравнение х = 0:

   

И вторая точка (0; 1).
Осталось провести через эти точки прямую и график готов.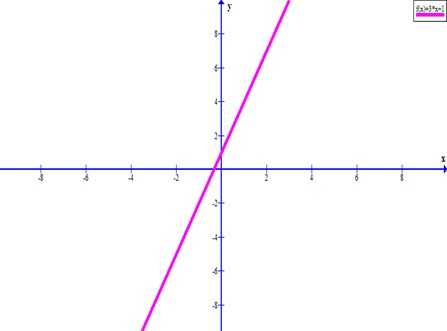

Второй способ очень похож на первый, но вместо подстановки в уравнение значений х = 0 и у = 0, подставляют произвольные значения переменной х и находят значения у.
Например:
при х = 1 функция — точка (1; 4)
при х = -1 функция — точка (-1; -2)

ru.solverbook.com

Постройте график функции y = x^3-x^2

Задание.

Постройте график функции y = x^3 — x^2.

Решение.

Для данного уравнения функции ограничений никаких нет, ни для аргумента, ни для самой функции. Другими словами функция может существовать для любого значения переменной х.
В таком случае вместо этой переменной можно подставить любое значение, найти для него соответствующее значение функции и получить координату точки, через которую пройдет график функции. Такой метод называется методом подбора координат точек. Но в уравнении стоит переменная х в кубе, что тянет за собой несколько необычное поведение функции. Поэтому мы вынуждены выполнить некоторый анализ этого поведения.
Найдем первую производную функции, чтобы узнать на каких промежутках функция будет возрастать или же убывать:

   

Приравняем ее к нулю и решим уравнение:

   

или
Найдем знак производной на полученных трех промежутках и выясним поведение функции на них:
— функция возрастает
— функция убывает
— функция возрастает
Рассчитаем значение функции в точке максимума и минимума:
— точка максимума (0; 0)
— точка минимума
Найдем точки перегиба функции, вычислив вторую производную:

   

   

   

Найдем значение функции для найденного х:

   

— точка перегиба.
Осталось найти точки пересечения с координатными осями и построить график.
Пересечение с осью Ох будем искать, приравняв функцию к нулю:

   

   

или

   

   

Пересечение с осью Оу будем искать, подставив вместо х значение 0. Но для такого значение выше уже были произведены расчеты, поэтому точками пересечения с координатными осями будут:
(0; 0) и (1; 0).

ru.solverbook.com

Строим графики функций, содержащие модуль. Часть 1

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 1. Изобразить график функции y = |x² – 4x + 3|

1) Строим график функции y = x² – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

0x : y = 0.

x² – 4x + 3 = 0.

x₁ = 3, x₂ = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

0y: x = 0.

y = 0² – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x_в = -(-4/2) = 2, y_в = 2² – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

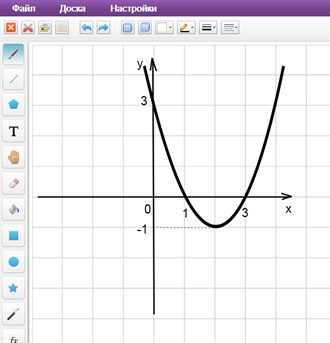
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2, изображен пунктиром).

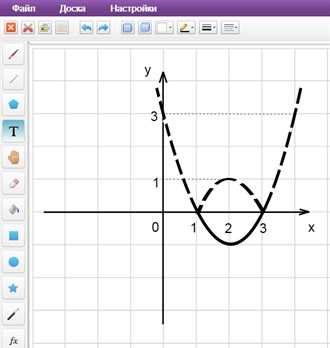
2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x² – 4 · |x| + 3

Так как x² = |x|², то исходную функцию можно переписать в следующем виде: y = |x|² – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x² – 4 · x + 3 (см. также рис. 1).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

4) Окончательный график изображен на рисунке (рис. 3).

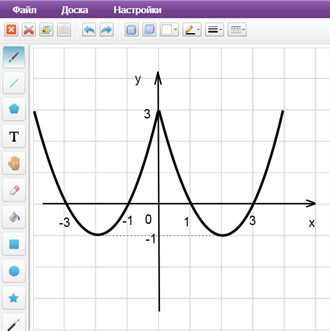
Пример 3. Изобразить график функции y = log₂|x|

Применяем схему, данную выше.

1) Строим график функции y = log₂x (рис. 4).

Далее повторяем пункты 2)-3) предыдущего примера и получаем окончательный график (рис. 5).

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже  являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому , их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x² + 2|x| – 1|.

1) Заметим, что x²= |x|². Значит, вместо исходной функции y = -x² + 2|x| – 1

можно использовать функцию y = -|x|² + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x|² + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x² + 2x – 1 (рис. 6).

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7).

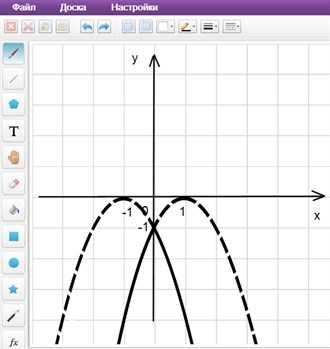
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8).

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a)  Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9).

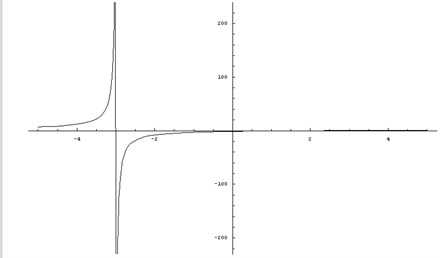
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

Далее повторяем пункты b)-c) из предыдущего примера и получаем следующий график функции (рис. 10).

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11).

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Как построить график функции y=|x|x+|x|-3x?

У автора прозвучало два вопроса: «Как построить график заданной функции и как вообще строить такие графики?»

Поскольку на первый вопрос уже есть ответы, то ограничусь только картинкой графика.

Я немного видоизменю формулу и на ее примере попробую подробно рассказать о методе работы с модулями. А также постараюсь рассказать о других вариантах.

Поскольку модуль при различных Х, ведет себя по разному и решать уравнения с модулями нельзя, то те части уравнения где присутствует модуль переменной, заменяют на обыкновенные иксы. Но при этом альтернативная замена должна при расчете давать такое же значение как и модульная часть.

Предположим у нас такое уравнение:

Здесь под модулем только переменная Х, поэтому мы может разделить координатную ось на две части, та что слева от оси Y (отрицательная) и на ту что справа (положительная). Следовательно для каждой половинки будет свое уравнение.

В данном задании придется подставлять в формулы численные значения Х, поэтому что бы было

проще, понятней и меньше писать, я обозначу уравнения как функции.

N(х)- это Начальное уравнение

L(х)- это уравнение Левой части

P(х)- это уравнение Правой части

S(x)- уравнение Средней части

Рассмотрим, как более простую, правую часть. Здесь иксы всегда положительные, а значит модуль ничего не делает и его можно упустить.

Перейдем к левой части. Не поленимся и заключим в скобки выражения где есть |Х|.Все коэффициенты и знаки вынесем за скобку. В отрицательной зоне модуль Х заменяется на «-Х». Так как при подстановке любого отрицательного числа получится равенство.|Х|=-Х. Например подставим «-2». получим|-2|=-(-2)=2

В результате получили два простеньких квадратных уравнения. Квадратные уравнения решаются по теореме Виета, но в нашем случае это можно сделать в уме. Рассмотрим P(х).

P(х)=-2х^2+4х

х1=0 y=0

х2=2 у=0

Ось этой параболы будет находиться посередине между корнями. Значит Х оси равен 1. Подставим это значение в формулу.

P(1)=-2*1^2+4*1=2

Значит координаты вершины параболы А(1;2)

Строим график.

Аналогично рассматриваем левое уравнение L(х)

L(х)=2х^2-6х

х1=0 y=0

х2=3 у=0

Ось этой параболы по Х равна»1.5″

L(1.5)=2*1.5^2-6*1.5=-4.5

Координаты вершины параболы В(1.5;-4.5)

Строим график.

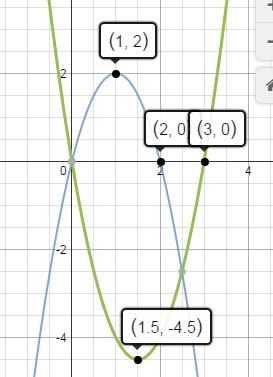
Теперь остается навести нужные части.

Вы обратили внимание, что в точке перехода между зонами есть излом. Это не всегда так. Переход может быть и плавным, и со скачком и, уходить в бесконечность, и могут быть не определенные точки. Например:

Понятно, что Х разделить на Х всегда равен 1, но вот с каким знаком, кроме того появляются неопределенные точки.

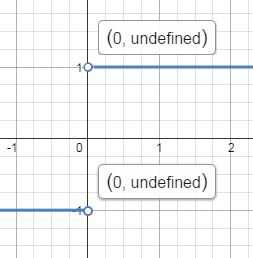
Поэтому если в уравнении есть структура |Х|/Х или Х/|Х|, то всегда будет скачок.

Например:

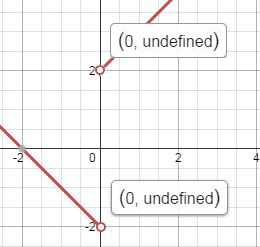
Структура 1/|Х| Всегда приведет к бесконечности. Например:

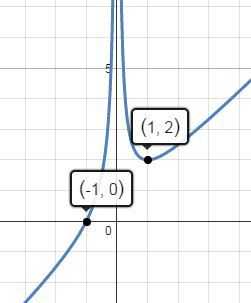
А вот что будет если под модулем будет хотя бы простенькое выражение?

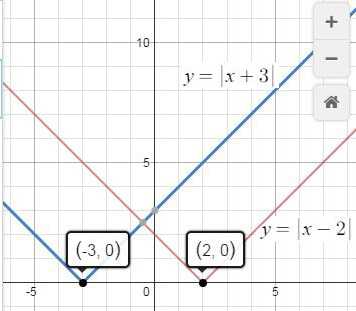
Наши выражения добавят точки излома и еще одну зону между осью Y и этой точкой. Назовем ее средней (S(x)). Может показаться, что на предыдущей картинке ее нет. Но это дело случая, а точнее формулы.

Следует понимать, что от вида выражений зависит, в положительной или отрицательной зонах будет точка излома.

Так для выражений |X-a| и |a-X| точка излома будет в правой части, а для выражений |x+a| и |-X-a| в левой. А также каждый подобный модуль прибавит еще одну точку излома и зону.

Рассмотрим страшное выражение и определим точки излома. И конечно будет еще одна точка х=0

Разобьем нашу ось на зоны и выберем в каждой зоне проверочную точку.

Теперь рассмотрим зоны L, S1, S2. В этих зонах Х будет отрицательным, а значит что мы |Х| заменим на «-Х». А вот скобки придется анализировать. Что бы получить одинаковое численное значение под модулем и в нашей замене, математические выражения должны совпадать, но вот со знаком мы можем не угадать.

Зона L

Предположим что в зоне L формула совпадает с N(х)

?L(х)=|Х|+(Х+3)-(Х-2)-(-Х-6)

Подставим вместо Х значение контрольной точки зоны L, то есть Х=-7

В скобочках получим значения -4;-9;1 Это значит что математическое выражение в третьей скобке правильное. А вот в первой и второй, перед скобкой нужно поставить знак минус, что бы изменить отрицательные значения на положительные. Ведь модуль может дать нам только положительное значение. Для этого меняем в скобке у всех членов знаки на противоположные. Получим следующее.

L(х)=-Х+(-Х-3)-(2-Х)-(-Х-6)=1

Уравнение в этой зоне получилось очень простое. Это прямая линия параллельная оси Х и проходящяя через точку Y=1

Зона S1

Контрольная точка Х=-4

?S1(х)=|Х|+(Х+3)-(Х-2)-(-Х-6)

S1(х)=-Х+(-Х-3)-(2-Х)-(Х+6)=-2Х-11

Зона S2

Контрольная точка Х=-1

?S2(х)=|Х|+(Х+3)-(Х-2)-(-Х-6)

S2(х)=-Х+(Х+3)-(2-Х)-(Х+6)=-5

Зоны с положительными иксами S3 и P. Меняем |Х| на Х

Зона S3

Контрольная точка Х=1

?S3(х)=|Х|+(Х+3)-(Х-2)-(-Х-6)

S3(х)=Х+(Х+3)-(2-Х)-(Х+6)=2Х-5

Зона P

Контрольная точка Х=3

?P(х)=|Х|+(Х+3)-(Х-2)-(-Х-6)

P(х)=Х+(Х+3)-(Х-2)-(Х+6)=-1

Все, строим графики функций.

Теперь остается лишь правильно навести.

Примерно по такой схеме строятся графики функций с модулями.

Но следует помнить, что для более сложных функций нельзя путать модуль функции с модулем ее аргумента.

www.bolshoyvopros.ru

Постройте график функции y = 2 – 3^x

Задание.
Постройте график функции y = 2 — 3^x.

Решение.
Для того, чтобы понять как построить заданную функцию, необходимо рассмотреть ее и выполнить хотя бы небольшой анализ.
Одним из слагаемых функции является число в неизвестной степени. Такие функции принято называть показательными, причем они существуют при любом значении показателя степени.
Проверим функцию на четность. В таком случае нужно подставить в эту функцию вместо переменной х переменную —х и по полученному результату сделать вывод о ее четности:

   

Получили ни четную, ни нечетную функцию.
Также показательная функция не является периодической.
Проще всего построить заданную функцию по нескольким известным точкам, которые найдем, подставив вместо переменной х произвольные значения. Значения будем брать и положительные, и отрицательные.
— точка пересечения с осью Оу
Точку пересечения с осью Ох находить не так просто, но придется найти хотя бы приблизительное значение:

   

   

Решим равенство приближенно. Если подставить х = 0,5, то получим:

   

Если же взять х = 1, то:

   

Следовательно, график будет пересекаться с осью Ох приблизительно в точке (0,7; 0).

   

   

   

   

   

   

Полученных точек достаточно, чтобы получить адекватный график заданной в условии функции.
Нанесем точки на график и соединим линией.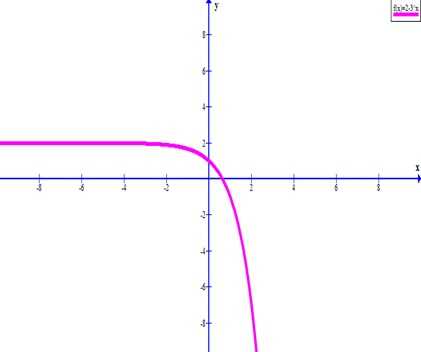

ru.solverbook.com