Построить три изображения многогранника с вырезом – Построить три изображения многогранника с вырезом. | Интерактивное сообщество — Решение задач по инженерной графике

Содержание

Лекция 6. Многогранники | CADInstructor

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Стоимость и возможные формы обучения (очно или дистанционно) смотрите разделе Цены.
Подробнее о репетиторстве.

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра.

Ребра, пересекаясь, образуют вершины.

Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

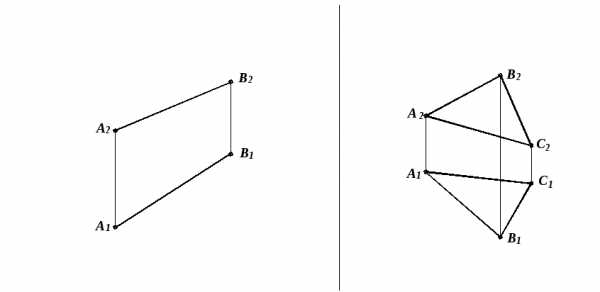
Дана пирамида, основание которой параллельно π₁. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).

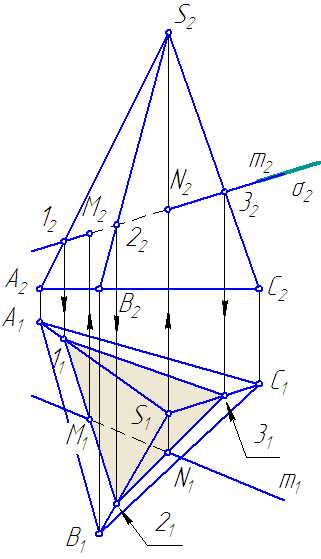
Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

Решение

Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.

В сечении находим точки M и N принадлежащие прямой m.
Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

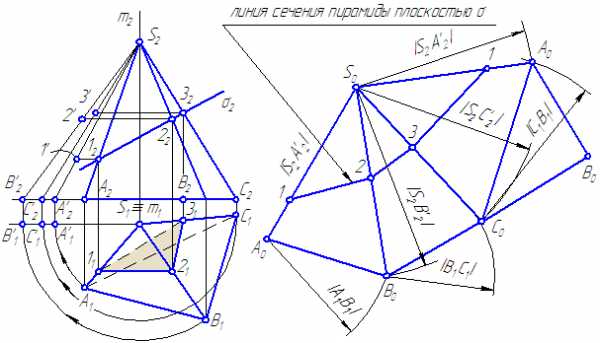
Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки , проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

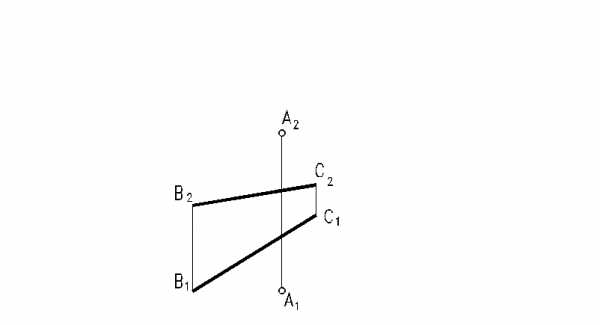
Дана призма, основания которой параллельны плоскости проекций π

Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

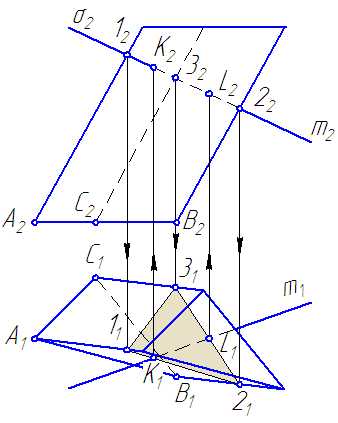
Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы

Порядок построения:

Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
В сечении находим точки K и L принадлежащие прямой m.
Определяем видимость прямой m. Если грань АВ на π₂ видна, то точка К на π₂ видима, грань ВС невидима, следовательно, точка L невидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

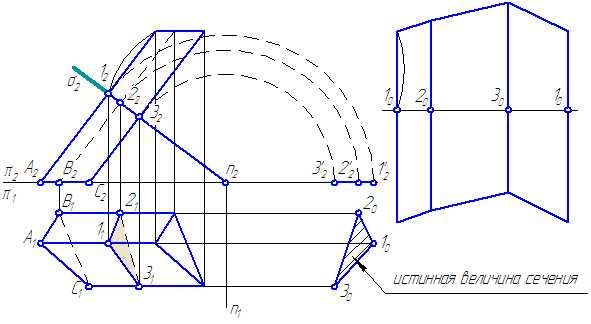
Рисунок 6.4 – Построение развёртки призмы

Порядок построения:

Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
/1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Упражнение

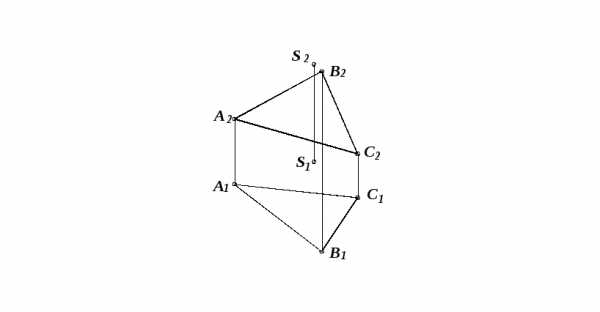
Построить линии пересечения призмы с пирамидой (Рисунок 6.6).

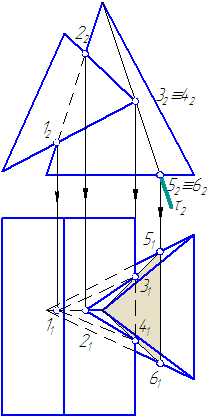
Рисунок 6.6. Построение линии пересечения призмы с пирамидой

Решение

Находим на π₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость τ⊥π₂.
Полученные на π₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Упражнение

Построить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

По двум проекциям построить третью;
На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
Построить развёртку пирамиды с нанесением линии пересечения.

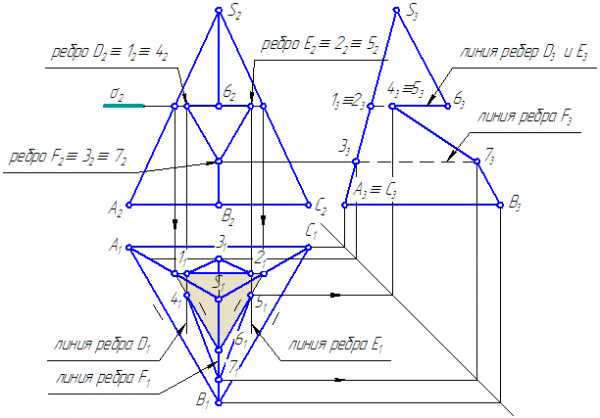
Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки

Решение:

Проводим линии рёбер призмы на всех проекциях.
Введём плоскость σ⊥π₂, σ//π₁:

σ//АВС – основанию пирамиды;
σ пересекает пирамиду сечение подобно ΔА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Грань D₂E₂∩S₂B₂ =6₂.

Ребро F₂∩S₂B₂ =7₂.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

6.4. Задачи для самостоятельной работы

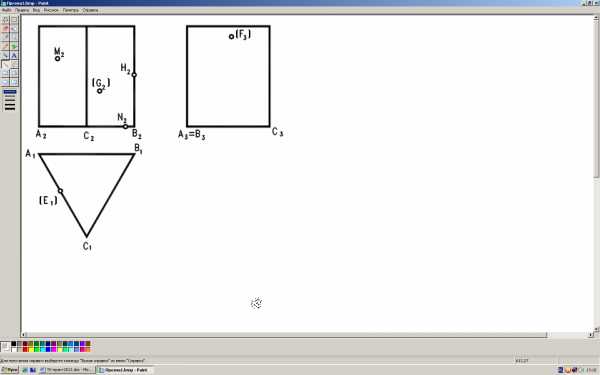
1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

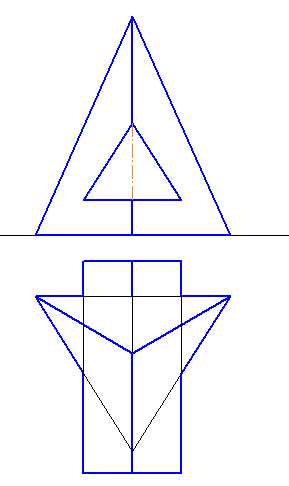
Рисунок 6.8

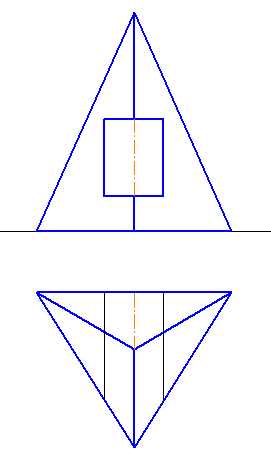
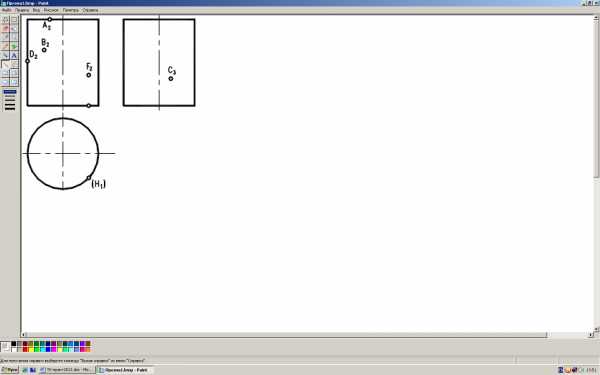
Рисунок 6.9

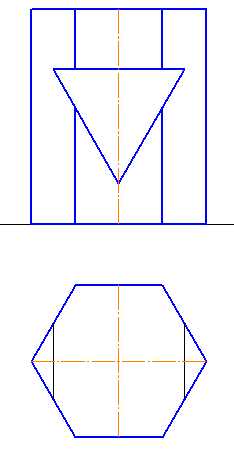
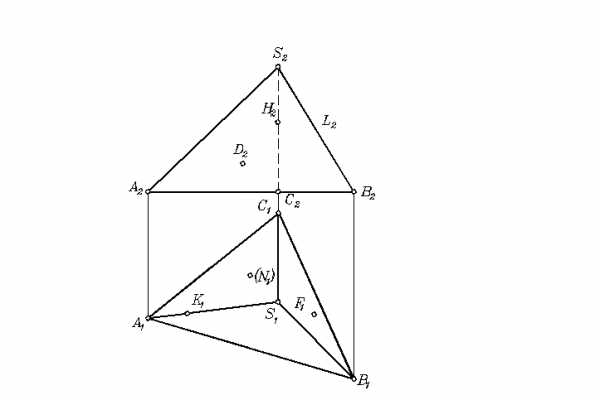
Рисунок 6.10

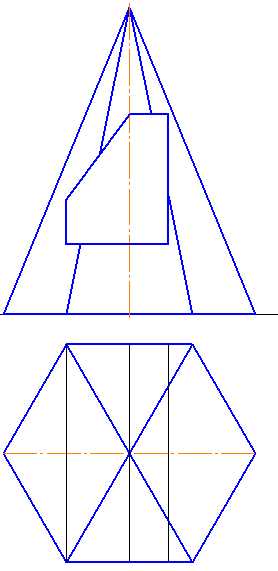
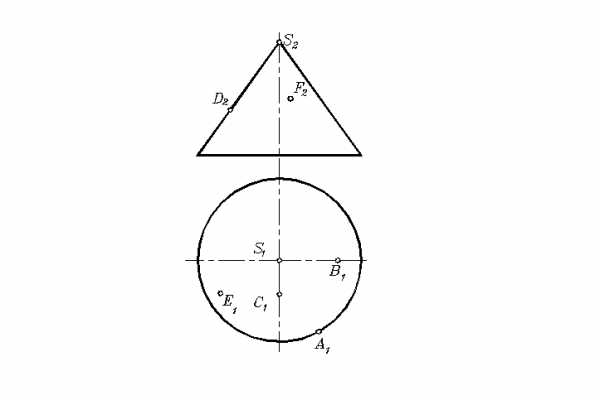
Рисунок 6.11

cadinstructor.org

Построение многогранников — Мегаобучалка

Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником. К наиболее часто используемым в практике многогранникам относятся призма и пирамида.

Чертёж любого многогранника состоит из сочетания многоугольников. Каждая линия на чертеже многоугольника — это либо проекция линии пересечения двух граней (ребра), либо проекция самой грани (плоскости), если эта грань перпендикулярна плоскости проекций. При проецировании многогранника на плоскость чертежа необходимо уметь мысленно разделять его на составные части и правильно определять порядок их изображения.

Вспомним из курса черчения, как изображаются на чертеже плоские фигуры, различно расположенные относительно плоскостей проекций:

— плоская фигура, параллельная плоскости, проецируется на неё без искажения;

— плоская фигура, перпендикулярная к плоскости, проецируется на неё в прямую линию;

— плоская фигура, наклонённая к плоскости, проецируется на неё с искажением.

Плоскости, наклонённые к плоскостям проекций, называются плоскостями общего положения. Рассмотрим построение многоугольников в случае, когда они являются плоскостями общего положения.

Проекцией треугольника в общем случае является треугольник. Чтобы построить на чертеже проекции треугольника, необходимо построить проекции его вершин (точек). Следует помнить, что они должны лежать на одной линии связи. Проекцией четырёхугольника в общем случае будет четырёхугольник. При этом у квадрата, прямоугольника, ромба и параллелограмма сохраняется параллельность противоположных сторон (проекции параллельных прямых — параллельны).

На чертеже четырёхугольника произвольно можно построить только одну его проекцию и три вершины на другой проекции (три точки определяют плоскость). Проекцию четвёртой вершины нужно строить исходя из принадлежности её плоскости четырёхугольника (найти её на одной из диагоналей) (рис. 3.6).

а) б) в) г)

Рис. 3.6

Аксонометрические проекции многогранников, так же как и многоугольников, строятся при помощи координат вершин многогранника.

Построение геометрического тела в аксонометрии начинается с построения плоской геометрической фигуры — многоугольника. При построении правильного шестиугольника в изометрии или диметрии центровые линии заданной фигуры принимаются за координатные оси (рис. 3.7), относительно которых ориентируются вершины рассматриваемой фигуры. Например, координата вершины 1 определяется радиусом R; вершины 6- отрезками R/2 и hдля изометрии (рис. 3.7б) и отрезками R/2 и h/2для диметрии (рис. 3.7в).

а) б) в)

Рис. 3.7

Построим прямоугольную изометрию правильной шестиугольной пирамиды. На свободном месте поля строят основание (рис. 3.7б), из точки пересечения осей проводят отрезок прямой, равный высоте пирамиды (рис. 3.8). Вершину пирамиды соединяют прямыми линиями с вершинами шестиугольного основания.

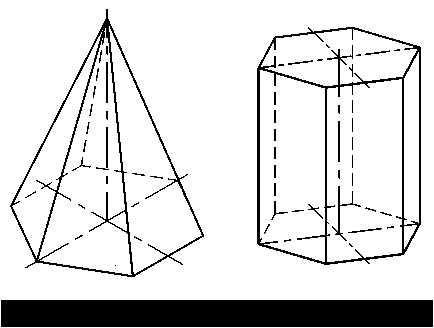Построение прямой шестигранной призмы в диметрии (рис. 3.9) также начинают с построения нижнего основания (рис 3.7в). Затем из каждой вершины нижнего основания проводят вертикальные прямые, на которых откладывают высоту призмы. Полученные точки соединяют отрезками и получают верхнее основание.

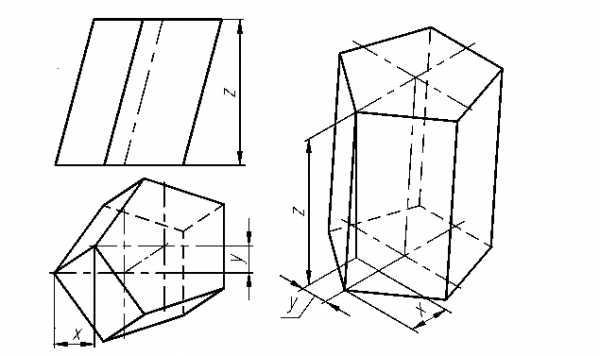
Построение наклонной призмы в аксонометрии начинают с проведения аксонометрических осей и построения нижнего основания. Затем строят одно ребро боковой грани, для чего по координатам определяют верхнюю точку ребра (рис. 3.10). После этого можно построить верхнее основание и провести остальные рёбра боковых граней.

Рис. 3.10

Построение проекций точек, лежащих на поверхности многогранника. При выполнении заданий по проекционному черчению приходится строить линию пересечения двух поверхностей. Для этого необходимо уметь находить точки, расположенные на поверхности геометрических тел.

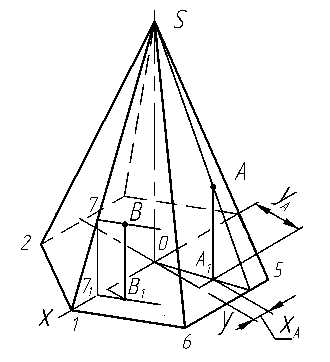
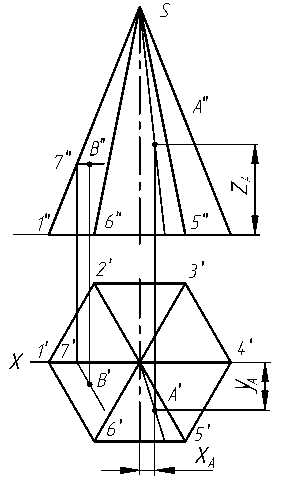На чертеже для построения горизонтальной проекции точки А, расположенной на поверхности пирамиды, через заданную проекцию точки А″ проводят прямую линию и находят её горизонтальную проекцию (рис. 3.11а). На горизонтальной проекции прямой с помощью линии связи находят горизонтальную проекцию А′ точки А. При построении точки А в изометрической проекции необходимо сначала построить на основании пирамиды её проекцию А₁, определяемую координатами X_A и Y_A (рис. 3.11б). Затем через построенную точку А₁ нужно провести линию параллельно вертикальной оси и отложить на ней координату Z_A . Полученная точка А и будет изображением точки А в изометрии. Аксонометрическое изображение является обратимым изображением, что подтверждается возможностью построения аксонометрической координатной ломаной любой точки поверхности, принадлежащей пирамиде.

а) б)

Рис. 3.11

Координатными ломаными пользуются, если нельзя применить какой-либо частный приём. Например, по наглядному изображению точки В(рис. 3.11б), принадлежащей боковой грани пирамиды, можно определить координаты точки и построить её горизонтальную и фронтальную проекции. Для этого через точку В проводим прямую линию, параллельную ребру 1 6, до пересечения с ребром S 1 и получаем точку 7, лежащую в координатной плоскости хОу. Строим проекцию точки 7 на основании пирамиды (точку 7₁) и проводим отрезок прямой параллельно 1 6, на котором определяем точку В₁ .

По координатам точки В, определённым на аксонометрической проекции (рис. 3.11б), можно построить горизонтальную и фронтальную проекции точки В на чертеже (рис. 3.11а).

Тела вращения

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями. Цилиндрическая поверхность вращения образуется при вращении прямой линии g (образующей) вокруг оси i, параллельной образующей (рис. 3.12 а). Если часть цилиндрической поверхности отсечь двумя плоскостями, перпендикулярными к оси вращения, то ограниченное этими плоскостями и цилиндрической поверхностью тело будет являться прямым круговым цилиндром.

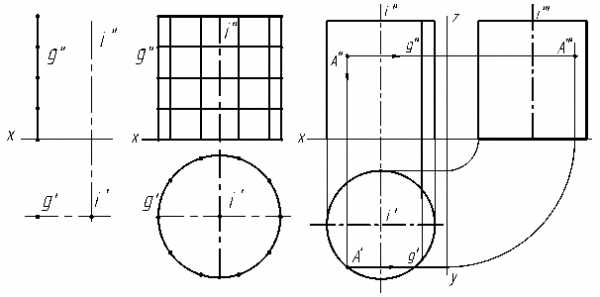
а) б) в)

Рис. 3.12

Отметим на прямой g ряд точек, при вращении каждая точка опишет окружность (параллель). Если на этом цилиндре отметить ряд промежуточных меридианов, то можно получить изображение цилиндра с каркасом, нанесённым на его поверхность (рис. 3.12б).

На рис. 3.12в представлены три проекции прямого кругового цилиндра, ось вращения которого перпендикулярна горизонтальной плоскости. Проводим фронтальную проекцию образующей цилиндра через A″. Она является горизонтально-проецирующей прямой и проецируется в точку на окружности. В этой точке будет находиться и горизонтальная проекция A′ точки A , так как точка видна относительно фронтальной плоскости проекций. Профильная проекция точки A находится в проекционной связи с проекциями A′ и A″. Чтобы найти профильную проекцию A″′, надо провести линию связи из точки A″ и отложить расстояние y от оси z. Все три проекции точки видимы.

Конус — геометрическое тело, ограниченное конической поверхностью и плоскостью. Коническая поверхность образуется вращением прямой g вокруг оси i, которая пересекает эту прямую (рис. 3.13а). Точка S пересечения образующей и оси вращения называется вершиной конической поверхности.

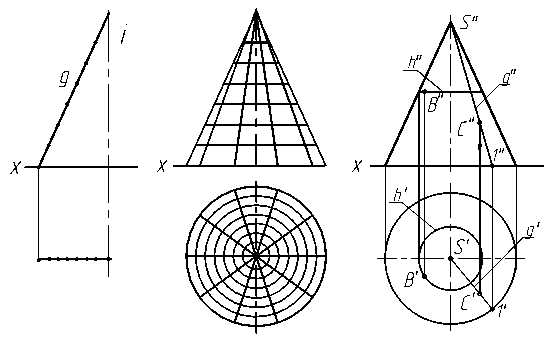
а) б) в)

Рис. 3.13

Отметим на прямой g ряд точек, при вращении каждая из них опишет окружность (параллель). Если на этом конусе отметить ряд промежуточных меридианов, то можно получить изображение конуса с каркасом, нанесённым на его поверхность (рис. 3.13б).

На рис. 3.13в представлены две проекции прямого кругового конуса, ось вращения которого перпендикулярна горизонтальной плоскости проекций. На поверхности задана проекция точки A″. Проводим фронтальную проекцию образующей конуса через A″ и S″ — S″1″. Находим горизонтальную проекцию образующей S′1′, используя линии связи и принадлежность точки 1 окружности основания конуса. Горизонтальная проекция точки A′ находится на пересечении линии связи с горизонтальной проекцией образующей S′1′. Чтобы найти горизонтальную проекцию точки В по заданной В″, проведём через неё параллель h″ и построим h′, которая проецируется на горизонтальную плоскость проекций в окружность. Горизонтальная проекция точки В′ находится на пересечении линии связи с горизонтальной проекцией h′.

Шар — геометрическое тело, ограниченное сферической поверхностью. Сферическая поверхность образуется вращением дуги окружности m вокруг диаметра i (рис. 3.14а). Отметим на дуге m ряд точек, при вращении дуги каждая точка опишет окружность (параллель). Если на этой сфере отметить ряд промежуточных меридианов, то можно получить изображение шара с каркасом, нанесённым на его поверхность (рис. 3.14б).

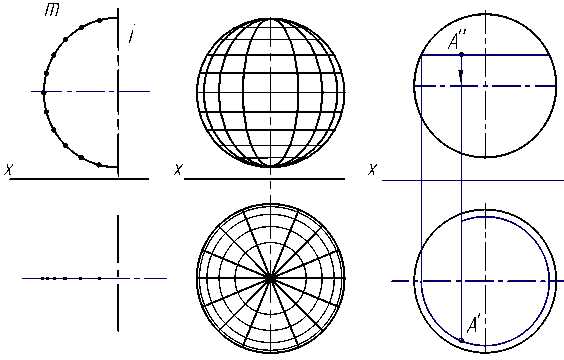
а) б) в)

Рис. 3.14

Рассмотрим нахождение горизонтальной проекции точки А, принадлежащей сфере, по заданной её фронтальной проекции А» (рис. 3.14в). Через фронтальную проекцию точки А» проведём параллель (линия, параллельная горизонтальной плоскости). От точки пересечения параллели и окружности главного меридиана проведём линию связи до горизонтальной проекции главного меридиана (горизонтальная осевая линия). Через найденную точку проведём окружность (горизонтальная проекция параллели). От фронтальной проекции точки проведём линию связи, которая пересечёт окружность в двух точках. Поскольку А» видима, то выбираем точку с большей координатой y и обозначаем А’.

Аксонометрические проекции тел вращения. Основанием ряда геометрических тел вращения является окружность. Чтобы построить геометрическое тело в аксонометрии, надо уметь строить, прежде всего, его основание. Изображения окружностей в изометрии и диметрии во всех трёх плоскостях проекций представляют собой эллипсы. В практике выполнения аксонометрических чертежей допускается сложные лекальные построения эллипсов заменять более простыми построениями овалов, вычерчиваемых при помощи циркуля.

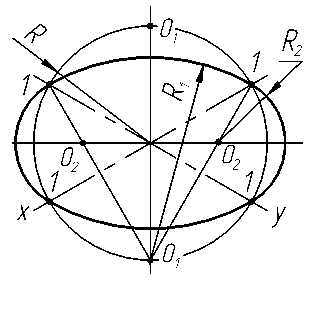Построим изометрическую проекцию окружности радиуса R, расположенной в горизонтальной плоскости, заменив эллипс четырехцентровым овалом (рис. 3.15).

Малая ось эллипса (0₁ 0₁) параллельна оси, отсутствующей в горизонтальной плоскости, т.е. оси z (рис. 3.15). Большая ось перпендикулярна малой. Необходимо также провести аксонометрические оси х, у и вспомогательную окружность радиуса R. Построенный овал должен проходить через точки 1, так как только в этом случае сохранятся размеры вдоль координатных осей.

Центры большой дуги овала (0₁) находятся на пересечении вспомогательной окружности с продолжением малой оси (рис. 3.15). Радиус большой дуги R₁ равен расстоянию от 0₁ до точки 1. Точки пересечения отрезков 0₁1 с большой осью будут центрами 0₂меньших дуг овала. Отрезок 0₂1 равен радиусу меньшей дуги. Проведя теперь меньшие дуги овала, получим четырехцентровой овал.

В прямоугольной диметрии, так же как и в изометрии, малая ось эллипса параллельна той аксонометрической оси, которая перпендикулярна плоскости проекций, где расположена изображаемая окружность.

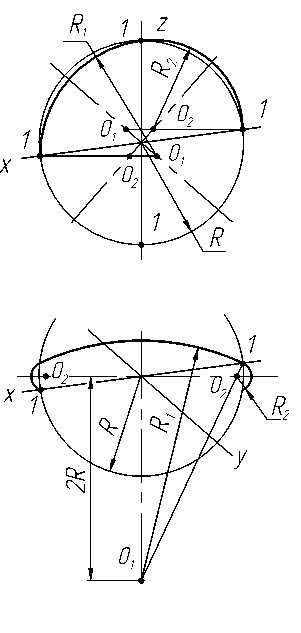Рассмотрим построение в плоскости х0z овала радиусом R (рис. 3.16). Из точки пересечения осей хиz проводим окружность радиуса Rи на пересечении с осями получаем точки 1,которые являются точками касания дуг овала. Затем строим центры дуг, для чего из точек 1, принадлежащих оси х, проводим горизонтальные прямые до пересечения с большой и малой осями эллипса и получаем точки 0₁ и 0₂. Точки 0₁, лежащие на малой оси, являются центрами больших дуг овала, а точки 0₂ — центрами малых дуг. Из центров 0₁ радиусом R₁, равным отрезку 0₁1, проводим большие дуги овала, а из центров 0₂ — малые дуги овала. На рис. 3.17 приведено построение овала в плоскости х0у. На оси х строим точки 1 касания дуг овала. Для нахождения центров 0₁ больших дуг овала от пересечения осей хиувверх и вниз по направлению малой оси откладываем отрезки, равные 2R. Центры малых дуг овала 0₂ находим на пересечении отрезка 0₁1 и большой оси эллипса. Большие дуги овала проводим из центров 0₁ через точки 1, малые дуги — из центров 0₂.

Построение аксонометрической проекции поверхности вращения (конуса, цилиндра) начинают с построения кругового основания. Затем на вертикальной оси откладывают высоту. Для цилиндра (рис. 3.18) строят верхнее основание и проводят очерковые образующие — касательные к двум овалам оснований. У конуса вершину S соединяют касательными с основанием (рис. 3.19).

Для построения точки А на поверхности цилиндра в прямоугольной изометрии сначала строят проекцию точки А₁ на основании цилиндра по координате Х_А , взятой с горизонтальной проекции (рис. 3.12в). От точки А₁ параллельно оси 0z проводят прямую и откладывают координату Z_А, взятую с фронтальной проекции (рис. 3.12в).

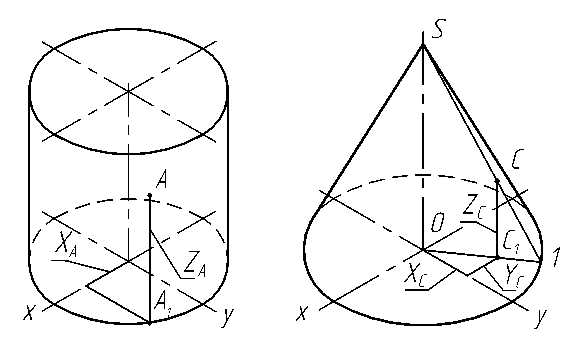
Рис. 3.18 Рис. 3.19

Построение точки С на поверхности конуса в изометрии (рис. 3.19) выполняют в следующей последовательности: строят проекцию точки С₁ на основании конуса по координатам X_А и Y_А , взятым с горизонтальной проекции (рис. 3.13в), от точки С₁ параллельно оси 0z проводят прямую и откладывают координату Z_С, взятую с фронтальной проекции (рис. 3.13в).

Если же по наглядному изображению точки Стребуется определить её координаты, то вначале через заданную точку С проводят образующую S1 и строят её проекцию 01 на основание конуса, а затем из точки С проводят прямую, параллельную оси 0z, и строят точку С₁. Выполненные построения позволяют определить координаты точки С на наглядном изображении.

megaobuchalka.ru

Графическая работа № 4 «Многогранник»

1. По координатам точек A, B, C, S построить три проекции пирамиды SABC, занимающей общее положение. Определить видимость её рёбер.

На фронтальной проекции видимой грани пирамиды построить прямоугольник K₂L₂M₂N₂ размером 2010 мм с двумя вершинами, расположенными на одном из рёбер. Построить горизонтальную и профильную проекции четырёхугольника.
Определить положение рёбер и граней пирамиды относительно плоскостей проекций и занести в таблицу.
Определить натуральную величину ребра многогранника, занимающего общее положение, методом прямоугольного треугольника.

Варианты задания и указания к его выполнению в [2,3]. Образец выполнения работы см. ниже.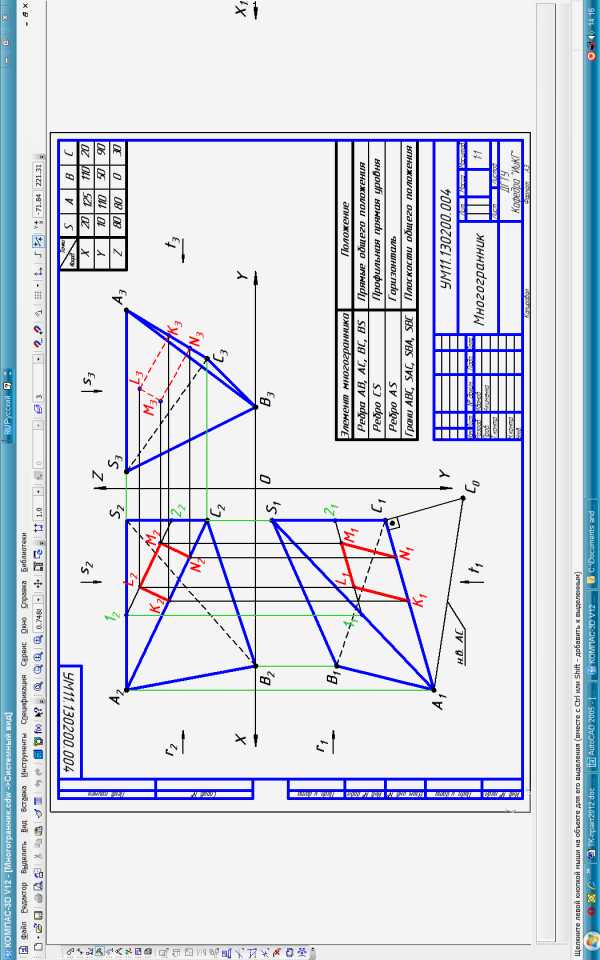

54. Найти недостающие проекции точек, принадлежащих поверхностям призмы, цилиндра, пирамиды, конуса.

ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА

СПОСОБ замены плоскостей проекций

55. Преобразовать горизонталь и фронталь в проецирующие прямые.

56. Преобразовать линию общего положения

в проецирующую прямую.

57. Определить: 1) расстояние от точки S до пл.  АВС; 2) натуральную величину пл.  АВС; 3) угол наклона пл.  АВС к плоскости П₁. Это упражнение аналогично графической работе № 5.

СПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ

58. Определить натуральную величину отрезка АВ и углы наклона его к плоскостям

проекций P₁и P₂..

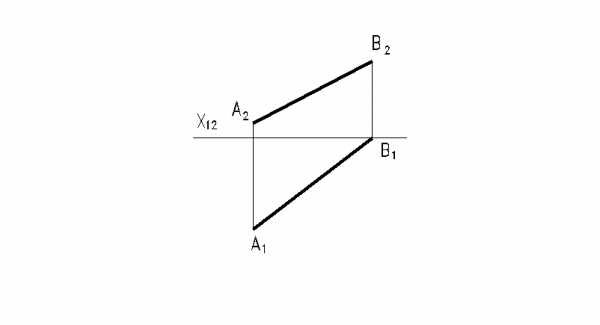
59. Определить расстояние от точки А до прямой ВС.

60. Определить величину двугранного угла при ребре АВ.

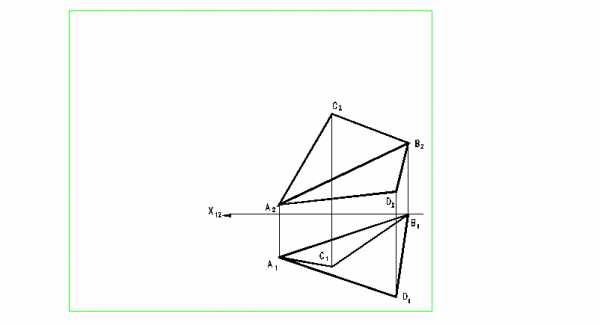
СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ

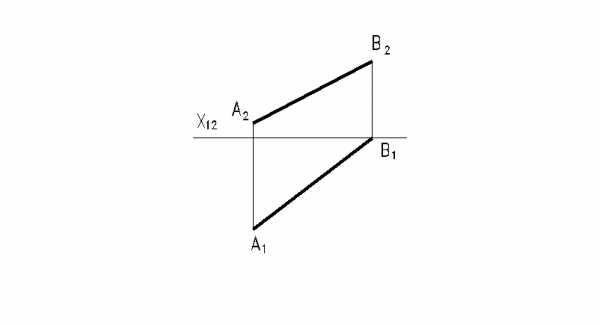
61. Определить натуральную величину отрезка АВ и углы наклона его к плоскостям

проекций P₁и P₂.

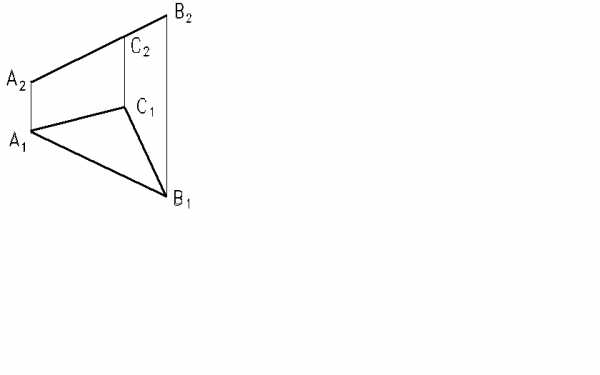
62. Определить натуральную величину треугольника АВС.

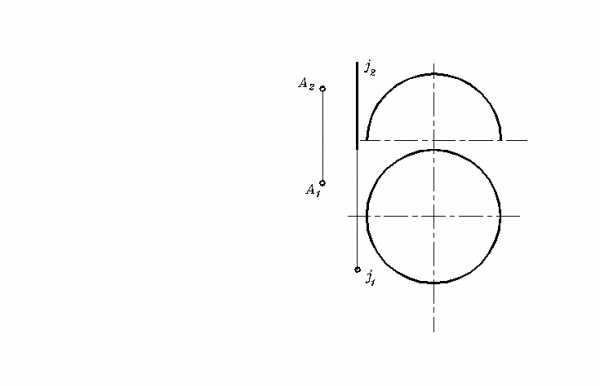
63. Повернуть точку А вокруг вертикальной оси j до совмещения с поверхностью полусферы. Сколько решений имеет задача?

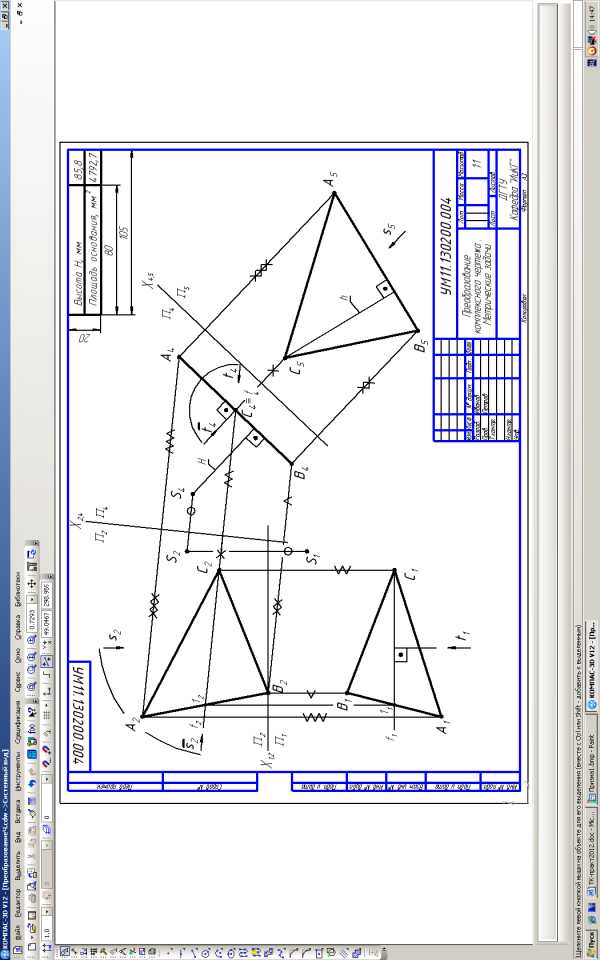
Графическая работа № 5 «Преобразование комплексного чертежа. Метрические задачи»

На двухкартинном чертёже (формат А3) методом замены плоскостей проекций преобразовать плоскость общего положения, заданную треугольником ABC, в проецирующую (и точку S), а затем в плоскость уровня (координаты точек взять из предыдущей работы) и определить:

1. Расстояние от точки S до плоскости треугольника ABC (высоту пирамиды).

Площадь треугольника ABC (основания пирамиды). Данные занести в таблицу.

Для рационального размещения построений на чертёжном формате, работу предварительно выполнить на черновике. В качестве прямой уровня использовать горизонталь или фронталь. Допускается использование масштаба уменьшения. Образец выполнения см. ниже.

Курс Черчения. ВИДЫ, РАЗРЕЗЫ, СЕЧЕНИЯ. (Изображения ГОСТ 2.305-2008)

64. По наглядному изображению детали в диметрии построить шесть основных видов, откладывая от базовых линий размеры детали в направлениях осей X и Z.в масштабе 1:1, а в направлении оси Y— в масштабе 2:1 (в два раза больше). На всех основных видах обозначить проекции точки A. Данное упражнение аналогично графической работе № 6, за исключением того, что наглядное изображение дано в изометрии.

Графическая работа № 6 «Виды основные»

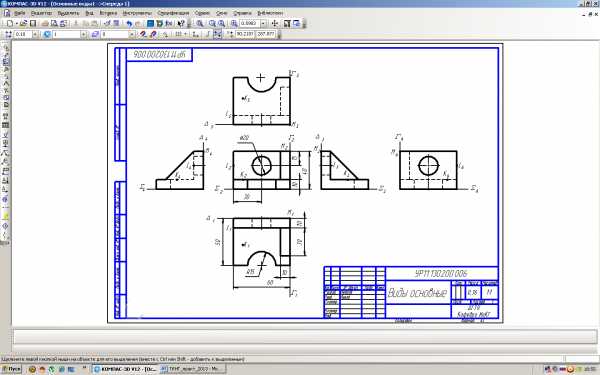
На формате А3 по наглядному изображению детали построить шесть её основных видов. Вид по стрелке принять в качестве главного (спереди).

На видах изобразить невидимые элементы детали штриховыми линиями, а оси отверстий и плоскости симметрии ― штрихпунктирными линиями.

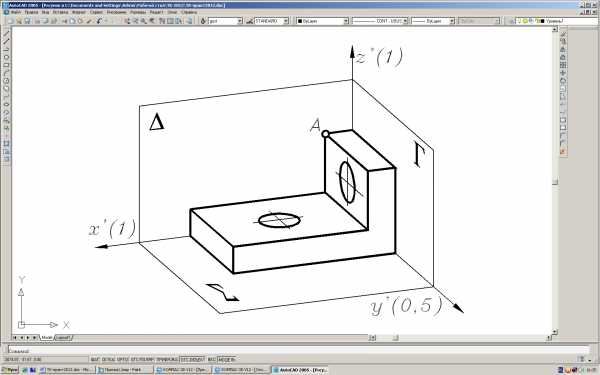
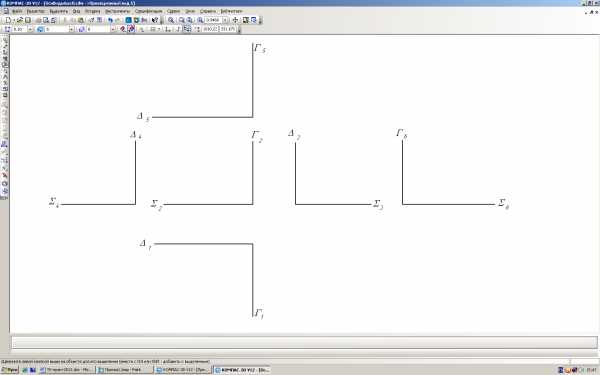
Указать и обозначить на всех видах базовые линии (проекции базовых плоскостей Σ, Δ, Γ), а также проекции заданных точек K, L, M. Образец выполнения см. выше. Варианты задания «Основные виды» и рекомендации по выполнению в [2,15].

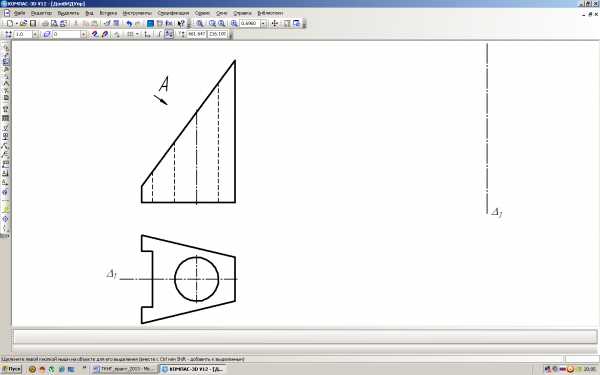
65. Построить фронтальный разрез, вид слева и дополнительный вид А детали, используя базовую плоскость .

studfiles.net

Инженерная графика! Лекции — Стр 6

1.17 Многогранники

Гранной поверхностью называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. Гранные поверхности можно подразделить на два вида: пирамидальные ипризмати-

ческие.

Часть пространства, ограниченная со всех сторон поверхностью, называется телом.

Многогранником называется тело, ограниченное плоскими многоугольниками. Рассмотрение многогранников ограничим рассмотрением призм и пирамид.

Призмой называется многогранник, у которого одинаковые взаимно параллельные грани – основания, а остальные – боковые грани – параллелограммы. Если ребра боковых граней перпендикулярны основанию, то призму называют прямой. Для задания призмы достаточно задать одно ее основание и боковое ребро.

Пирамида представляет собой многогранник, у которого одна грань – произвольный многоугольник, принимающейся за основание, а остальные грани (боковые) – треугольники с общей вершиной, называемой вершиной пирамиды.

Сечение многогранников плоскостью. В сечении гранных поверхно-

стей плоскостями получаются многоугольники, вершины которых определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью.

Многоугольник сечения может быть найден двумя путями:

-вершины многоугольника находятся как точки пересечения прямых (ребер) с секущей плоскостью;

-стороны многоугольника находятся как линии пересечения плоскостей (граней) многогранника с секущей плоскостью.

Вкачестве примера построим сечение призмы фронтальнопроецирующей плоскостью Q (рис. 1.80) .

Секущая плоскость перпендикулярно фронтальной плоскости проекций, следовательно, все линии, лежащие в этой плоскости, в том числе и фигура сечения на фронтальной проекции, совпадут с фронтальным следом Qv

плоскости Q. Таким образом, фронтальная проекция фигуры сечения 1/ 2/ 3/ Определяется при пересечении фронтальных проекций ребер призмы со следомQv. Горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией призмы. Профильная проекция фигуры сечения находится по принадлежностям проекций точек 1,2,3 соответствующим ребрам призмы. Если считать что плоскостьQ отсекает верх призмы, то фигура сечения на

профильной плоскости видна, а если нет, то линия 2//3// изобразится невидимой.

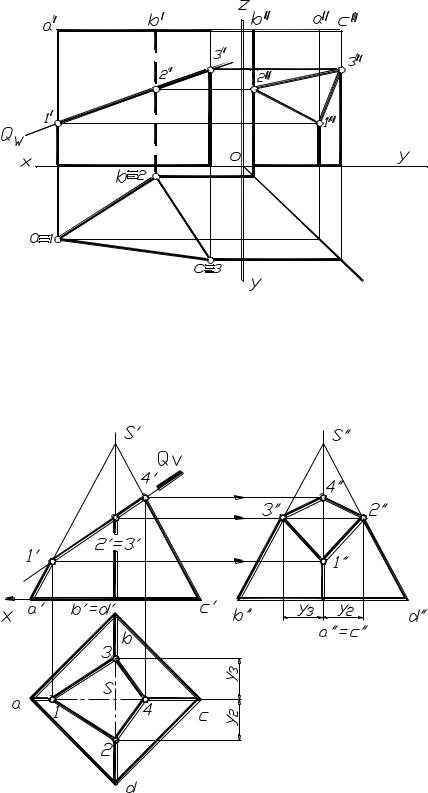
На рисунке 1.81 показано сечение четырехугольной пирамиды фронталь- но-проецирующейплоскостьюQ.

Рис. 1.81

Секущая плоскость перпендикулярна фронтальной плоскости проекций, следовательно, все линии, лежащие в этой плоскости, в том числе и фигура сечения на фронтальной проекции, совпадут с фронтальным следом плоскости. Таким образом, фронтальная проекция фигуры сечения 1,2,3,4

определится при пересечении фронтальных проекций ребер пирамиды со

следом плоскости. Горизонтальные проекции этих точек находим, проводя

проекционные линии связи на горизонтальную проекцию соответствующих

ребер. Если считать что плоскость Q отсекает верх пирамиды, то на фрон-

тальной плоскости фигура сечения видна, если нет, то 3//4//, 4//2// будут

невидимы.

Рис. 1.82

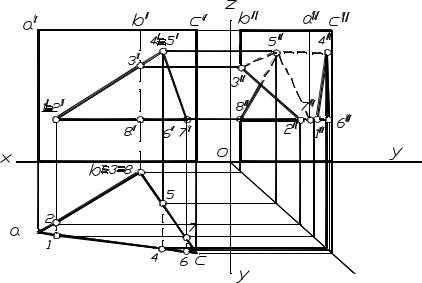
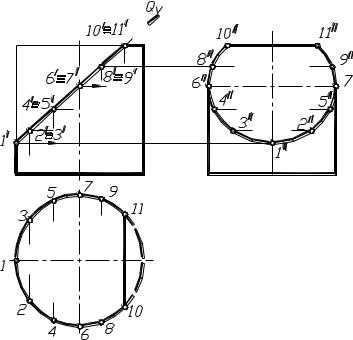
Призма с вырезом. В качестве примера построения сечения многогранника несколькими плоскостями рассмотрим построение призмы с вырезом, образованным треугольной призмой.

На фронтальной проекции отмечаем проекции точек встречи ребра B заданной призмы с гранями призмы выреза: 3/ и 8/, и точки пересечения ребер призмы выреза с гранями заданного тела: 1/2/4/5/6/7/. Находим горизон-

тальные проекции отмеченных точек. Все они находятся на горизонтальной проекции заданной призмы. По двум полученным проекциям точек находим их профильные проекции. С учетом видимости соединяем точки, принадлежащие соответствующим граням заданной призмы. В грани AB: точки 3,2,8, в граниBC: точки 3,5,7,8 и в граниAC: 1,4,6,1.

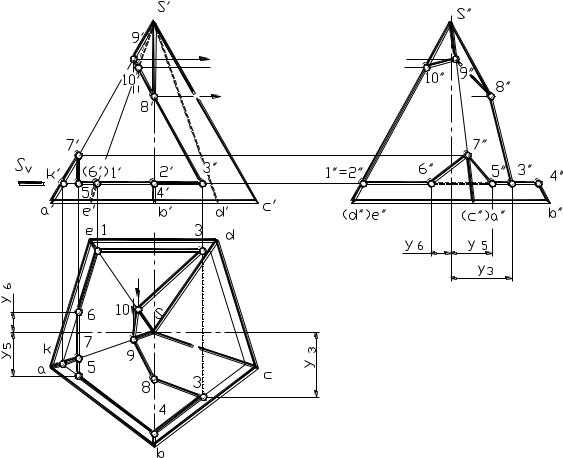
Пирамида с вырезом. На рисунке 1.83 показано построение пирамиды с вырезом (как результат сечения пирамиды несколькими проецирующими плоскостями, образовавшими призматический вырез). Обозначаем на фронтальной проекции точки, одновременно принадлежащие заданной пирамиде и призматическому вырезу. По принадлежности точек ребрам заданной пирамиды находим их горизонтальные и профильные проекции. Точки (3) пересечения ребра призматического выреза с гранями заданной пирамиды можно найти двумя способами. Первый способ заключается в проведении через точки выреза плоскостиS параллельной основанию (след которой обозначается на комплексном чертеже). В сечении пирамиды этой плоскостью

образуется треугольник подобный основанию, проходящий через точку K. Данному треугольнику принадлежат точки 3,1,6,7,5,4,3. Можно также найти точки на поверхности пирамиды проведением через них прямых, связывающих их с вершиной пирамиды и дальнейшим построением проведенных прямых на горизонтальной плоскости проекций и нахождением на них искомых точек. Полученные точки соединяют с учетом видимости в необходимой последовательности по соответствующим граням заданной пирамиды (чтобы две точки принадлежали одной секущей плоскости и одной грани пирамиды).

Рис. 1.83

1.18 Тела вращения

Рассмотрим некоторые из многочисленных поверхностей вращения.

Поверхности, образованные вращением прямой линии. К таковым от-

носятся цилиндр и конус.

Цилиндр вращения – поверхность, полученная вращением прямой вокруг параллельной ей оси и ограниченная двумя взаимно параллельными плоскостями.

Конус вращения – поверхность, образованная вращением прямой (образующая) вокруг пересекающейся с ней осью (направляющая).

Примером поверхностей, образованных вращением окружности вокруг неподвижной осиявляется сфера.

Сфера – поверхность, полученная вращением окружности вокруг ее диаметра.

Сечение цилиндра плоскостью. При сечении цилиндра враще-

ния плоскостью, параллельной оси вращения, в сечении получается пара прямых (образующих). Если секущая плоскость перпендикулярна к оси вращения, в сечении получается окружность. В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс.

Рис. 1.84

На рисунке 1.84 показан пример построения проекций линии сечения цилиндра фронтально проецирующей плоскостью Q, когда в сечении получается эллипс.

Фронтальная проекция фигуры сечения в этом случае совпадает с фронтальным следом плоскости, а горизонтальная – с горизонтальной проекцией поверхности цилиндра – окружностью. Профильная проекция строится по двум имеющимся проекциям – горизонтальной и фронтальной, замеряя игрековые координаты точек относительно оси цилиндра и откладывая их на проекционных линиях связи соответствующих точек.

Сечение конуса плоскостью. В зависимости от положения секущей плоскости в сечении конуса вращения могут получиться различные линии, называемые линиями конических сечений.

Если секущая плоскость проходит через вершину конуса перпендикулярно его основанию, то в сечении получается пара прямых – образующих

(треугольник – рис. 1.85а). В результате пересечения конуса плоскостью, перпендикулярной к оси конуса, получается окружность (рис. 185б). Если секущая плоскость наклонена к оси вращения конуса и не проходит через ее вершину, в сечении конуса могут получиться эллипс (секущая плоскость пересекает все образующие конуса – рис. 1.85в). Парабола образуется, если секущая плоскость параллельна одной из образующих конуса (рис. 1.85г). Гипербола образуется в случае, если секущая плоскость параллельна двум образующим конуса в зависимости от угла наклона секущей плоскости к основанию конуса (рис. 1.85д).

а	б	в	г	д
		Рис. 1.85

Известно, что точка принадлежит поверхности, если она принадлежиткакой-либолинии этой поверхности.Для конуса графически наиболее простыми линиями являются образующие и окружности. Следовательно, если по условию задачи требуется найти горизонтальные проекции точек, принадлежащих поверхности конуса, то нужно через точки провести одну из этих линий.

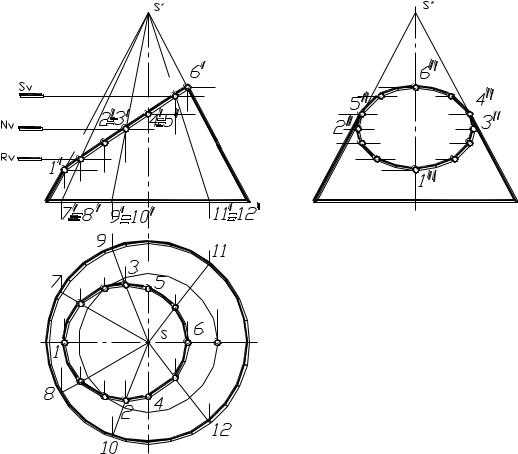
На рисунке 1.86 дан пример построения проекций линии сечения конуса фронтально проецирующей плоскостью, когда в сечении получается эллипс.

Фигура сечения на фронтально плоскости совпадает со следом секущей плоскости. Обозначим характерные точки (точки, принадлежащие фронтальному очерку конуса – 1, 6 и 4, 5 – точки, принадлежащие профильному очерку конуса) и несколько промежуточных (чем больше будет отмечено таких точек, тем точнее получится фигура сечения – эллипс). Горизонтальные и профильные проекции точек 1,4,5,6, находятся без дополнительных построений, так как они принадлежат соответствующим очеркам конуса. Для точек 4 и 5 находятся их профильные проекции из условия принадлежности их профильному очерку конуса, а затем, измерив игрековую координату этих точек от оси конуса, отмечаются их горизонтальные проекции. Для нахождения проекций промежуточных точек можно воспользоваться методом проведения секущих плоскостей, параллельных основанию конуса или проведением через отмеченные точки образующих конуса с последующим нахожде-

нием горизонтальных проекций этих образующих и нахождением на них соответствующих точек. Далее по двум полученным проекциям строятся третью проекции отмеченных точек. Полученные проекции точек соединяются плавной кривой с учетом видимости (на примере верхняя часть конуса отсечена плоскостью Q и поэтому вся фигура сечения на профильной плоскости видна). Если такого отсечения не происходит, то на профильной проекции часть кривой сечения 465 изобразится невидимой линией.

Рис. 1.86

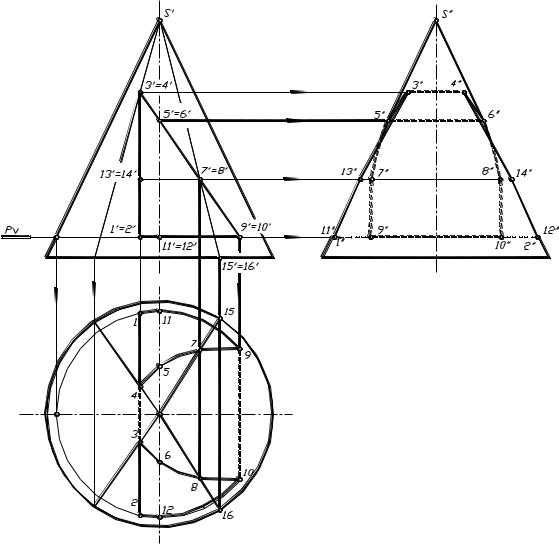
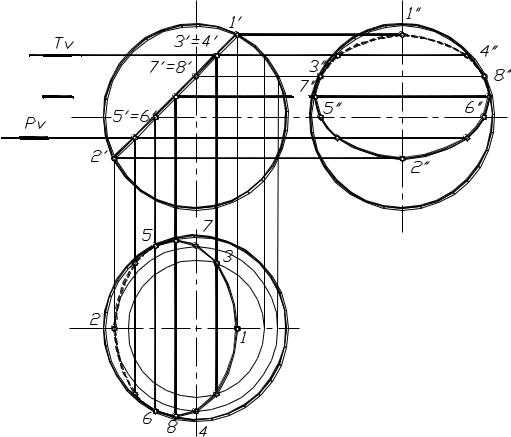
Конус с вырезом. На рисунке 1.87 показан конус, в котором выполнен вырез, образованный тремя плоскостями частного положения, образующих призматический вырез. Фронтальная проекция фигуры сечения совпадает с очерком призматического выреза. Для нахождения горизонтально и профильной проекций выреза отмечаем ряд необходимых точек. Необходимо отметить характерные точки, принадлежащие очеркам конуса, точки перегиба плоскостей выреза и ряд промежуточных для точности построения определенных кривых.

В данном случае отмечаются точки 5,6 и 11,12 , принадлежащие профильному очерку конуса; точки 1, 2, 3, 4, 9,10, являющиеся ребрами (линии перегиба плоскостей выреза) призматического выреза. Для более точного построения части параболы необходимо отметить ряд точек (чем их будет

больше, тем точнее получится кривая) находящихся между точками 3, 9 и 4, 10 (в данном случае это точки 7 и 8). Для построения части выреза, в результате которого образуется часть гиперболы, отмечаются точки, находящиеся между точками 1 и 3, 2 и 4 (в данном случае это точки 13 и 14). Их также необходимо взять достаточное количество.

Построив горизонтальные и профильные проекции отмеченных точек, фигуры проекций выреза соединяются с учетом видимости. На горизонтальной плоскости линии входа и выхода призматического выреза конуса видны. На профильной проекции видимость определяется по граничным точкам 5, 6 и 11, 12. Линия 5, 7, 9, 11 и 6, 8, 10, 12 на профильной проекции не видна, но, учитывая форму выреза, куски линии 5, 7 и 6, 8 до линий 3, 13 и 4, 14 будут видны.

Рис. 1.87

Сечение шара плоскостью. Если шар пересекать плоскостью, то в сечении всегда получается окружность. Эта окружность может проецироваться:

-в прямую, если секущая плоскость перпендикулярна к плоскости проекций;

-в окружность с радиусом, равным расстоянию от оси вращения шара до очерка, если секущая плоскость параллельнакакой-либоплоскости проекций;

-в эллипс, если секущая плоскость не параллельна ни одной из плоскостей проекций.

Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную какойлибо плоскости проекций, и построить окружность, на которой находится эта точка

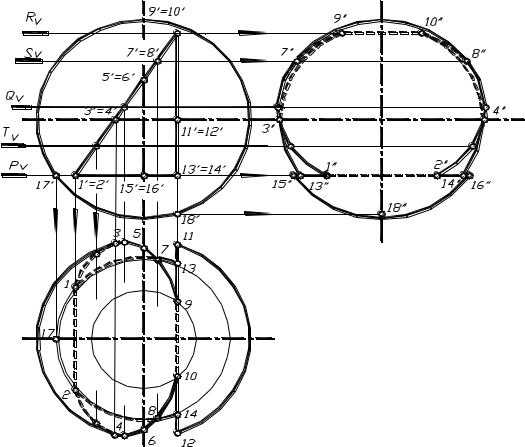
На рисунке 1.88 показано построение проекций линии сечения шара фронтально проецирующей плоскость.

Построение начинаем с определения характерных точек. Точки 1 и 2 находятся на фронтальном очерке шара (главном меридиане). Эти точки – концы малой оси эллипса, а также самая высокая и самая низкая точки. Их горизонтальные и профильные проекции находятся на соответствующих окружностях шара, которые на горизонтальной и профильной плоскостях

совпадают с осями. Точки 7 и 8 находятся на профильном очерке шара (профильном меридиане) и служат для определения видимости на профильной плоскости проекций. Горизонтальные проекции этих точек находятся по фронтальным и профильным. Точки 5 и 6 находятся на горизонтальном очерке шара (экваторе) и служат для определения видимости на горизонтальной плоскости проекций. Профильные проекции этих точек находим по горизонтальным и фронтальным проекциям. Для точного построения линии сечения необходимо найти несколько дополнительных точек. Для их построения используются вспомогательные секущие плоскости (например, плоскости горизонтального уровня T и P), которые в сечении дают окружность на горизонтальной плоскости. Полученные точки соединяют плавной кривой с учетом их видимости.

Шар с вырезом. На рисунке 1.89 показано построение проекций шара с вырезом, образованным тремя плоскостями частного положения, образующими призматический вырез.

Рис. 1.89

Для построения проекций выреза отмечаем необходимые точки. Это точки, принадлежащие очеркам шара, точки перегиба плоскостей выреза, а также ряд промежуточных для более точного построения линий выреза.

studfiles.net

Геометрические тела с вырезом

Пример 1. Вырез на конусе (рис.142).

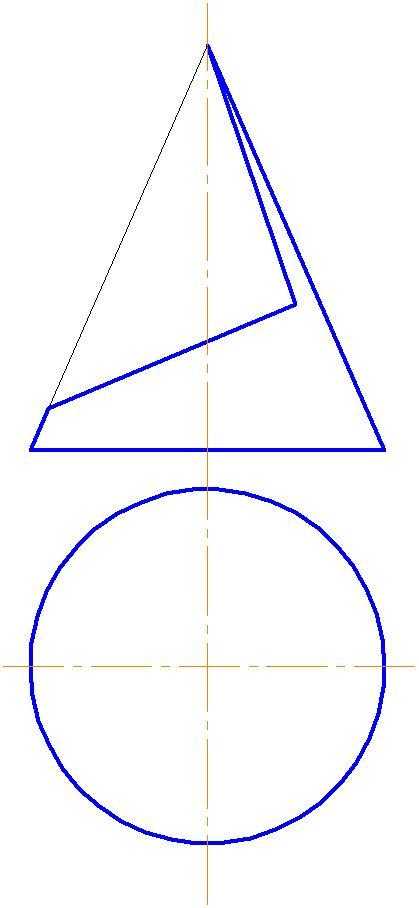
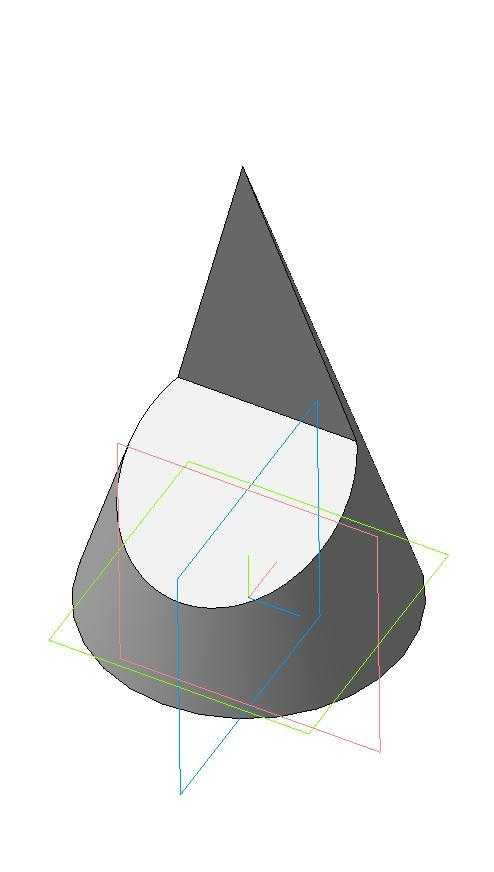Рис.142

Вырез произведен двумя плоскостями. Одна проходит через вершину конуса и рассечет его поверхность по образующим. Вторая плоскость — фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей.

1. Отметим фронтальные проекции характерных точек для построения выреза — А», В», С», M»,N» (рис. 143).

2. Точки D и Е выбраны произвольно для построения эллипса, т.к. линия среза от А до СN представляет собой часть эллипса.

3. Найдем горизонтальные проекции точек А, В, С, D, Е, N. Точки лежат на поверхности конуса, а значит, они лежат на линиях, принадлежащих поверхности конуса. Горизонтальные проекции точек М и В, D и E найдены на окружностях, принадлежащих поверхности конуса. Точки С и N — на образующих S₁ и S₂.

4. Соединяем полученные горизонтальные проекции. S’С’ и S’N‘ – прямые, C’, B’, D’, A’, E’, M’, N’ – кривая линия — часть эллипса (рис.142).

Рис.143 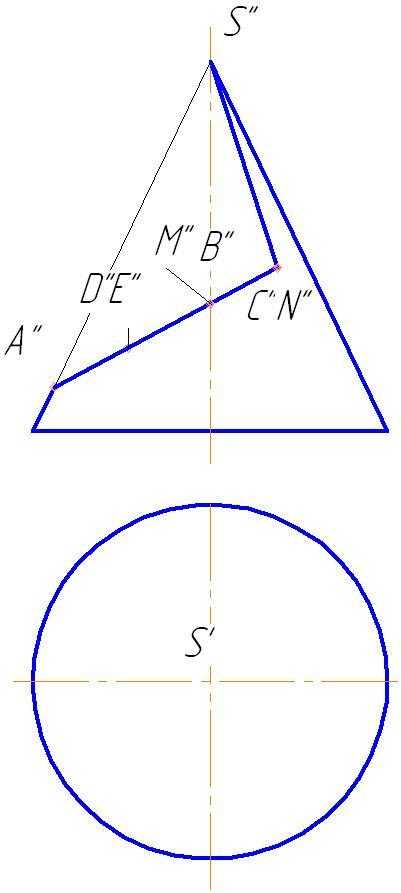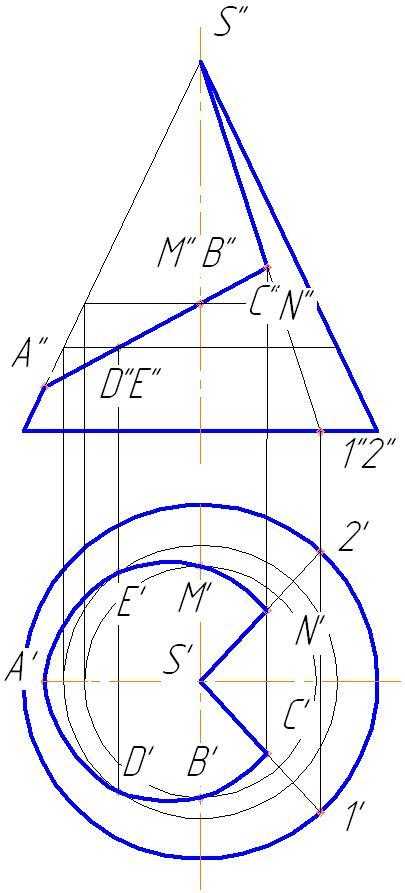Рис.144

Строим профильную проекцию конуса и профильные проекции точек. Соединяем их (рис.145).

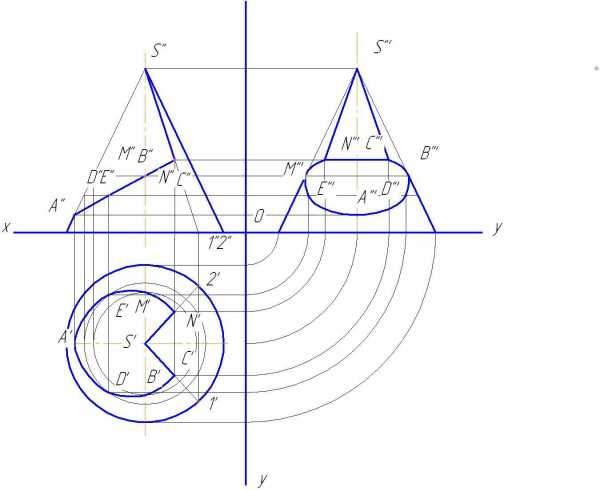
Рис.145

Пример 2. Вырез на цилиндре (рис.146).

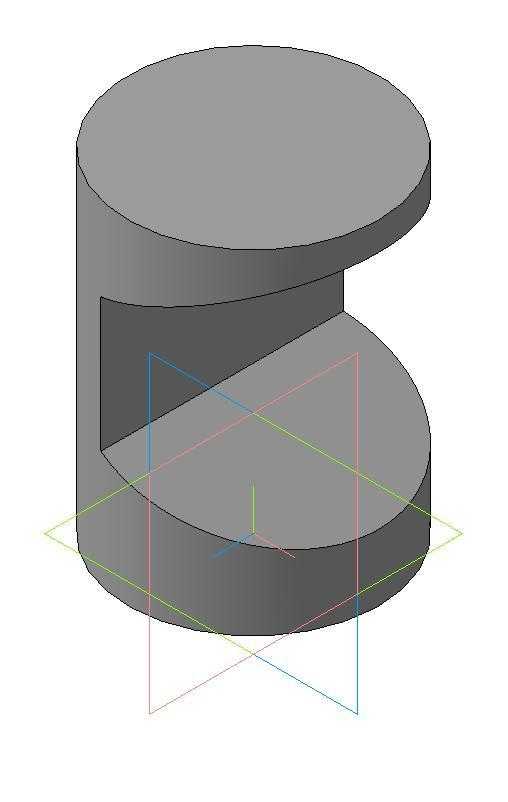
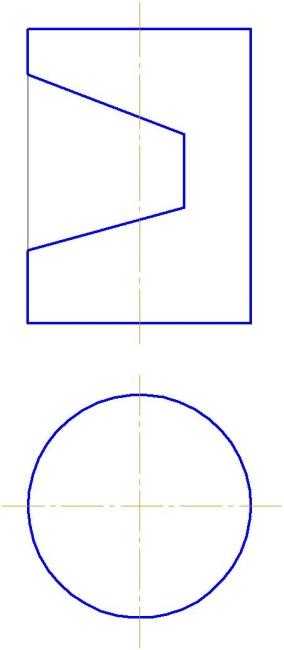
Рис.146

Вырез произведен тремя плоскостями. Наклонные фронтально-проецирующие плоскости рассекут цилиндр по части эллипса, ограниченного прямой. Плоскость, параллельная оси вращения, пересекает поверхность цилиндра по образующим.

1.Отметим на фронтальной проекции выреза фронтальные проекции A»,F»,G»,K»,L»,P». Характерные точки D»,E» ,M»,N» — на оси симметрии цилиндра, B»,C»,T»,V » — отмечены произвольно на линии, принадлежащей поверхности цилиндра. Все точки принадлежат боковой поверхности цилиндра, которая проецируется в окружность на горизонтальной плоскости проекций. Поэтому все горизонтальные проекции точек принадлежат этой окружности (рис.147).

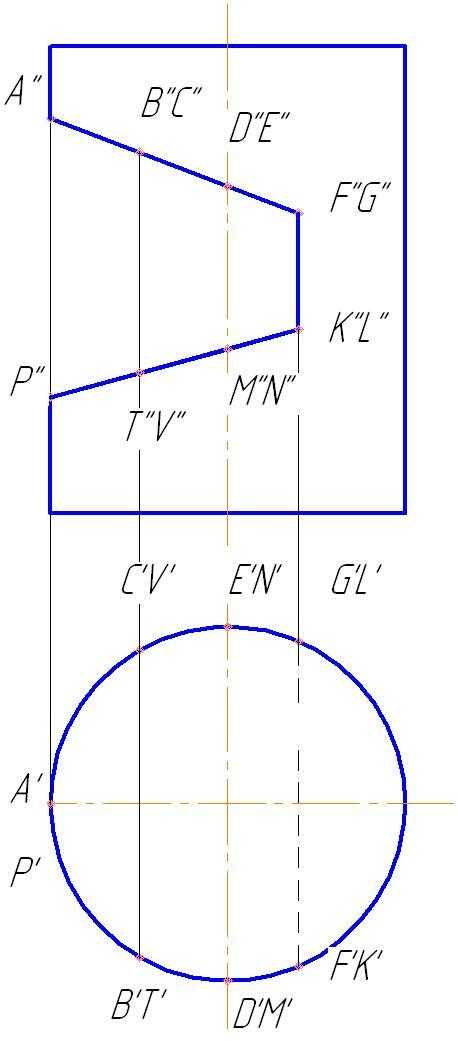Рис.147

Найдем профильные проекции всех точек. Затем полученные точки соединяем. Линия GECABDF — часть эллипса, FK и GL отрезки прямых, GF и KL-отрезки прямых, LNVPTMK — часть эллипса (рис. 148).

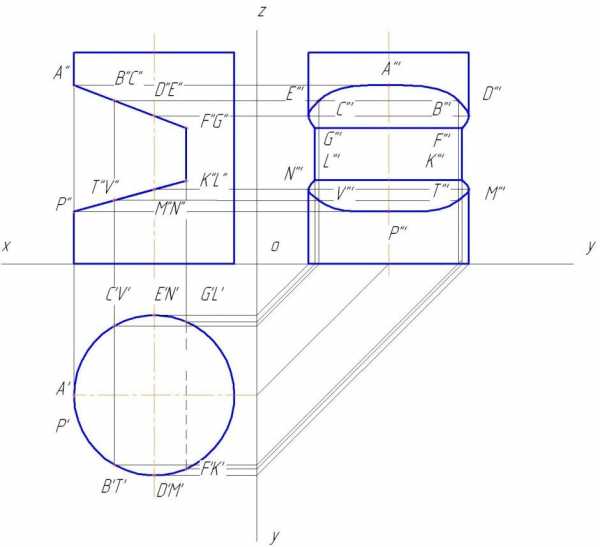Рис.148

Пример 3. Вырез на призме (рис.149).

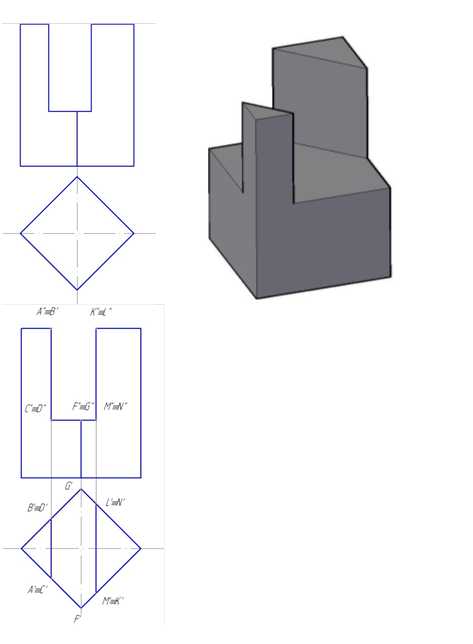Рис.149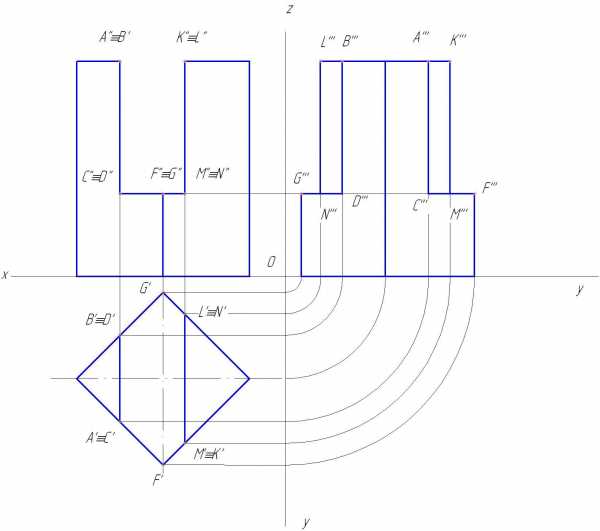Hbc

Рис.150

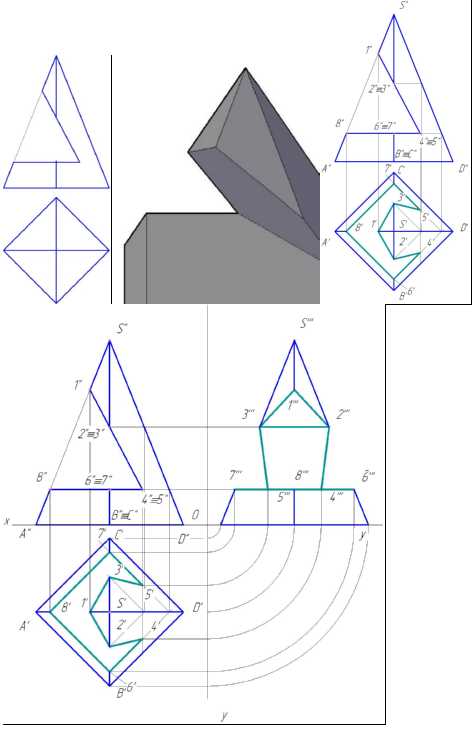
Пример 4. Вырез на пирамиде (рис.150).

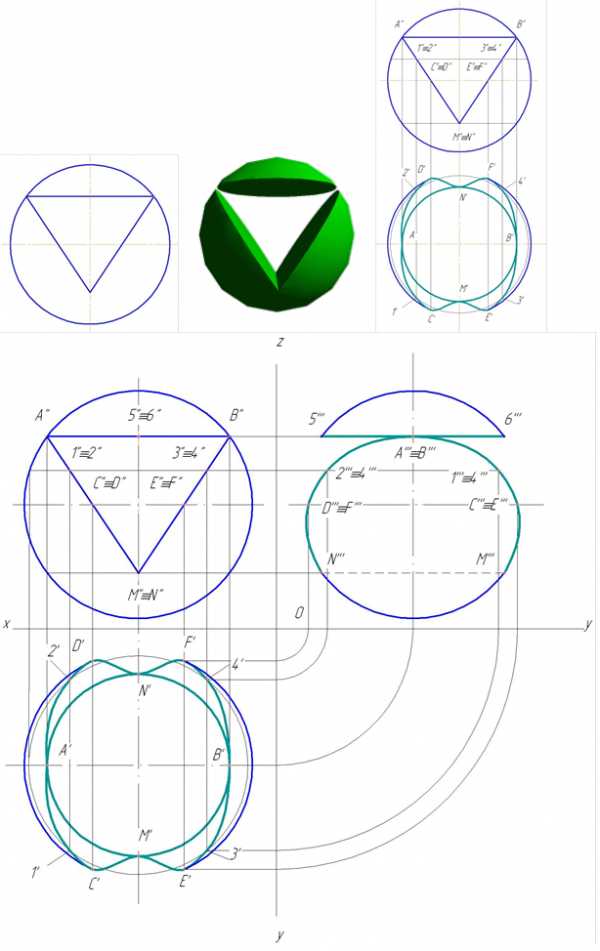
Пример 5. Вырез на сфере (рис. 151

Библиографический список

1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. – М.: Наука, 2000 – 272с.

2. Крылов Н.Н. Начертательная геометрия. – М.: Высшая школа, 2007 – 224с.

3. Локтев О.В. Краткий курс начертательной геометрии. – М.: Высшая школа, 2001 – 130с.

4. Фролов С.А. Начертательная геометрия. М.: Машиностроение, 1983 – 240с.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

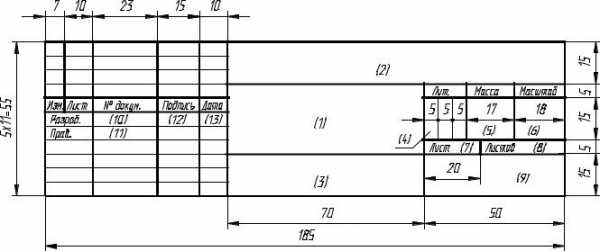
вграфе 10 – фамилию студента;

вграфе 11 – фамилию преподавателя;

Рис. 1. Основная надпись (форма 1)

вграфе 12 – подпись студента;

вграфе 13 – дату выполнения чертежа.

Все остальные графы не заполняются.

Любые сложные детали современных машин представляют собой комбинацию простых тел, ограниченных соответствующими поверхностями. Чаще всего встречаются детали, ограниченные плоскостями, цилиндрическими, коническими или шаровыми поверхностями. Поэтому нужно тщательно изучить свойства этих поверхностей и выработать прочные навыки выполнения и чтения чертежей простейших геометрических тел.

Прежде, чем перейти к решению задач на построение тел с вырезом, рассмотрим отдельные поверхности, правила нахождения точки на поверхности и сечение поверхностей плоскостью.

При решении задач необходимо определять проекции точек или линий, принадлежащих поверхности, при условии, что положение одной из проекций элемента известно. Такие задачи сводятся к нахождению проекций точек, принадлежащих поверхности. Положение проекций прямой линии определяется проекциями двух любых различных ее точек; построение проекций кривой линии, принадлежащей поверхности, сводится к построению проекций ряда определенным образом выбранных точек, которые затем соединяются плавной кривой.

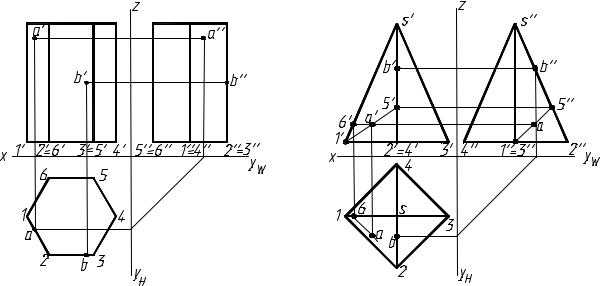
Призмы и пирамиды в трех проекциях, точки на поверхности

Проанализируем чертежи призмы и пирамиды (рис. 3, а, б).

На приведенных чертежах ребра проецируются в виде отрезков прямых или в виде точек. Например, фронтальные и профильные проекции боковых ребер призмы и пирамиды – отрезки прямых. Горизонтальные проекции тех же боковых ребер призмы – точки. Профильные проекции ребер основания призмы – точки 5″=6″ и2″=3″ (рис. 3, а).

Рис. 3

Грани многогранников, которые перпендикулярны плоскостям проекций, проецируются на них в виде отрезков прямых линий. Например, боковые грани призмы (рис. 3, а) на горизонтальной проекции изображаются в виде прямых линий, образующих шестиугольник. В виде прямых линий проецируются на профильную плоскость передняя и задняя грани призмы. Основания изображенных тел проецируются в виде отрезков прямых линий на фронтальную и профильную плоскости проекций.

Профильная проекция точки А (а″) призмы (рис. 3, а) построена с помощью координатыyА, которая замеряется на горизонтальной плоскости. Профильная проекция точкиВ призмы находится на отрезке прямой линии, в которую проецируется боковая грань призмы.

Профильная проекция точки A на грани1S2 пирамиды (рис. 3, б) построена с помощью отрезка прямой15 (1′5′ и1″5″) на грани1S2, на котором находится эта точка. Горизонтальная проекция точкиА построена с помощью горизонтали этой же грани.

Точка B находится на ребре2S пирамиды. Сначала, проведя линию связи до пересечения ее с профильной проекцией ребра, находим профильную проекциюb″ точки. Затем, используя определенную по профильной проекции координатуyВ, строим горизонтальную проекцию точки.

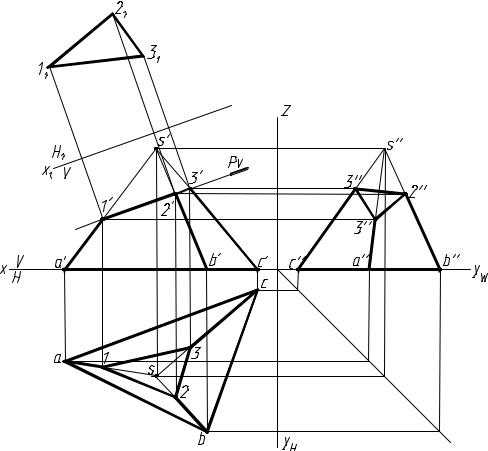
Пересечение многогранников плоскостями

В пересечении гранных поверхностей плоскостями получаются многоугольники, вершины которых определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью.

Многоугольник сечения может быть найден двумя путями:

1.Вершины многоугольника находятся как точки пересечения прямых (ребер) с секущей плоскостью;

2.Стороны многоугольника находятся как линии пересечения плоскостей (граней) многогранника с секущей плоскостью.

Вкачестве примера построим сечение пирамиды фронтально-проеци-рующей плоскостьюP (рис. 4).

Секущая плоскость − фронтально-проецирующая,следовательно, все линии, лежащие в этой плоскости, в том числе и фигура сечения на фронтальной плоскости проекций, совпадут с фронтальным следомPv плоскостиP. Таким образом, фронтальная проекция фигуры сечения1′2′3′ определится при пересечении фронтальных проекций ребер пирамиды со следомPv. Горизонтальные проекции точек1, 2 и3 находим при помощи линий связи на горизонтальных проекциях соответствующих ребер.

studfiles.net

1.3. Проекции геометрических тел

Для того, чтобы при выполнении чертежей представить себе форму детали удобно мысленно расчленять деталь на геометрические тела. Геометрические тела, ограниченные плоскими фигурами – многоугольниками, называют многогранниками (рис. 13). Их плоские фигуры называются гранями, а линии их пересечения – ребрами. Угол, образованный гранями, сходящимися в одной точке – вершине, будет многогранным углом. Например. Призма и пирамида – многогранники. Тела вращения ограничены поверхностями, которые получаются в результате вращения около оси какой-либо линии АВ, называемой образующей.

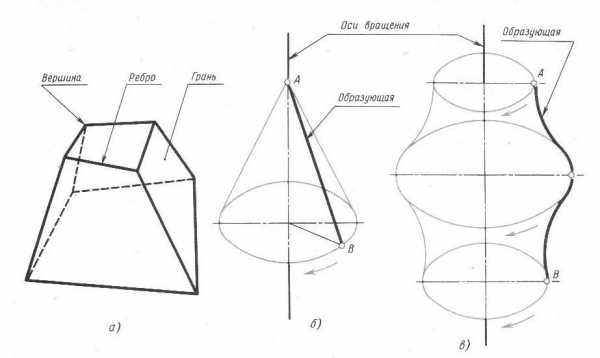
Рис. 13. Многогранные тела и тела вращения

Проекции призм

Построение проекции правильной прямой шестигранной призмы (рис. 14) начинается с выполнения ее горизонтальной проекции – правильного шестиугольника. Из вершин этого шестиугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Эта проекция изображается отрезком горизонтальной прямой. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер – отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых.

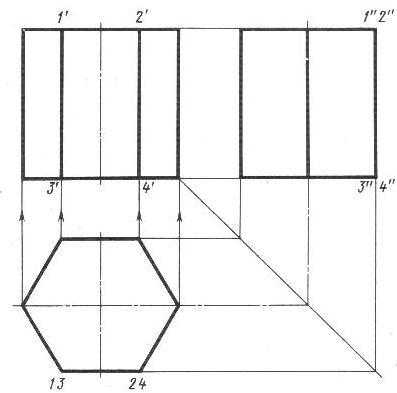
Рис. 14. Проекция шестигранной призмы

Проекции пирамид

Построение проекций трехгранной пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой действительный вид треугольника (рис.15). Фронтальная проекция основания изображается горизонтальным отрезком прямой. Из горизонтальной проекции s вершины пирамиды и получают фронтальную проекцию s’ вершины. Соединяя точку s’ с точками 1’, 2’ и 3’, получают фронтальные проекции ребер пирамиды.

Горизонтальные проекции ребер получают соединяя горизонтальную проекцию s вершины пирамиды с горизонтальными проекциями 1, 2 и 3 вершин основания.

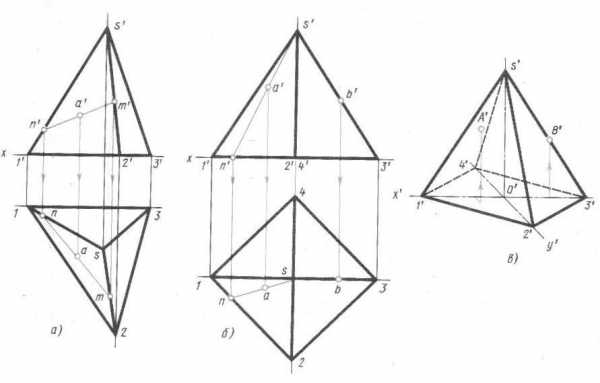
Рис. 15. Проекции пирамиды

Проекции цилиндров

Боковая поверхность прямого кругового цилиндра образованна движением отрезка АВ вокруг вертикальной оси по направляющей окружности. На рис. 16,а дано наглядное изображение цилиндра. Построение горизонтальной и фронтальной проекций цилиндра показано на рис. 16,б и 16,в.

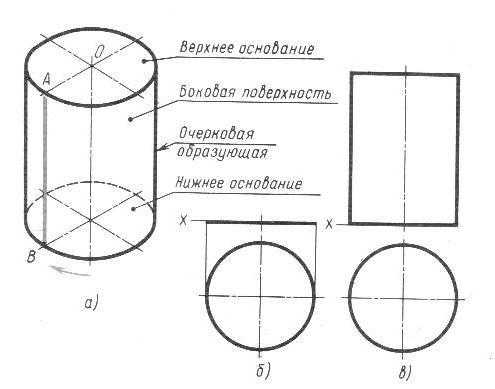
Рис. 16. Проекции цилиндра

Построение начинают с изображения основания цилиндра, т.е. двух проекций окружности. Т.к. окружность расположена на плоскости Н, то она проецируется на эту плоскость без искажения. Фронтальная проекция окружности представляет собой отрезок горизонтальной прямой линии, равный, равный диаметру окружности основания.

После построения основания на фронтальной проекции проводят две очерковые (крайне) образующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра.

Проекции конусов.

Наглядное изображение прямого кругового конуса показано на рис. 17,а. Боковая поверхность конуса образованна вращением образующей BS около оси конуса по направляющей – окружности основания. Последовательность построения двух проекций конуса показана на рис. 17, б и в. Предварительно строят две проекции основания. Горизонтальная проекция основания – окружность. Если предположить, что основание конуса лежит на плоскости Н, то фронтальной проекцией будет отрезок прямой, равный диаметру этой окружности. На фронтальной проекции из середины основания восстанавливают перпендикуляр и на нем откладывают высоту конуса. Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и получают фронтальную проекцию конуса.

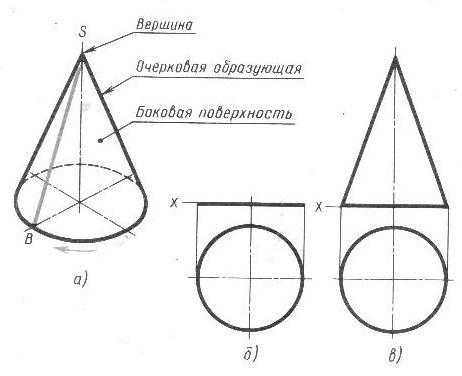
Рис. 17. Проекции конуса

studfiles.net

Лекция 6. Многогранники | CADInstructor

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Упражнение

6.2. Призма. Развертка призмы

Упражнение

6.3. Взаимное пересечение многогранников

Упражнение

Упражнение

6.4. Задачи для самостоятельной работы

Построение многогранников — Мегаобучалка

Графическая работа № 4 «Многогранник»

Инженерная графика! Лекции — Стр 6

Геометрические тела с вырезом

Библиографический список

Оглавление

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Призмы и пирамиды в трех проекциях, точки на поверхности

Пересечение многогранников плоскостями

1.3. Проекции геометрических тел

Добавить комментарий Отменить ответ