Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
- Подробности
- Автор: Administrator
www-formula.ru
Все формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
- Подробности
- Автор: Administrator
www-formula.ru
Как найти сторону треугольника?
Безусловно, чаще всего вопрос о том, как же найти неизвестную сторону треугольника возникает при проведении алгебраических или же геометрических расчетов, но иногда такая необходимость возникает и в обычной жизни, например, при построении каких-либо архитектурных чертежей или проведении расчетов.
В настоящий момент времени есть несколько различных способов решения такой задачи. И каждый способ отличается от предыдущего не только формулой, по которой производится расчет, но и исходными данными, которые необходимы для вычисления.
Способы нахождения сторон треугольника
Итак, самым простым и логичным ответом на вопрос: как находить стороны треугольника, является то, что необходимо найти решение по формуле. В зависимости от исходных данных, формулы могут быть самыми разными. Обычно необходимую сторону треугольника можно вычислить по:
- Двум уже известным сторонам и углу, который находится между ними.
- Двум углам и одной известной стороне.
Как видно, в любом, из двух названных случаях, все равно необходимо знать значения трех показателей. Без их знания никогда не будет возможным найти ответ на вопрос о том, как находить стороны треугольника.
Как найти неизвестную сторону треугольника
Итак, чтобы найти сторону треугольника которая не известна по условию при помощи первого способа необходимо использовать следующую формулу: с=v(а2+b2-2аb*cosC). Что касается обозначений данной формулы, то а и b — это длины известных сторон, cosC угол, находящийся между ними. На самом деле, для решения задачи о том, как найти неизвестную сторону в треугольнике, абсолютно нет никакой необходимости обладать какими-то особыми алгебраическими знаниями, вполне достаточно знать основы.
Для того чтобы найти сторону по второму способу понадобится следующая формула: sinA/a=sinB/b=sinC/с. Обозначения этой формулы аналогичны предыдущей, то есть В и С обозначают известные углы, а С — единственно известную сторону.
Но
elhow.ru
Как найти сторону треугольника — в помощь школьнику :: SYL.ru
Есть несколько способов решения этой геометрической задачи. Они описаны в статье.
При помощи сторон и углов
Итак, первый способ нахождения сторон треугольника — это по нескольким сторонам и углу между ними (и аналогично с углами и одной прилежащей стороной). Данный способ подойдет для старшей школы, так как здесь используются такие понятия, как синус, косинус, квадрат числа и корень. Итак, как найти сторону треугольника, который является произвольным? Для начала нарисуем эту самую фигуру. Теперь давайте обзовем элементы нашей фигуры. Стороны будут a, b и c. Угол, находящийся напротив стороны a, у нас будет «альфа», напротив b -«бета», напротив c — «гамма».
Для того чтобы найти сторону, скажем, a, необходимо вычислить квадратный корень из суммы квадрата b, c и вычесть из нее двойное произведение косинуса угла a на стороны b и c. То есть, для того, чтобы облегчить вид формулы и пояснить, как найти сторону треугольника произвольной формы, можем написать следующее: a=(b*b+c*c-2*b*c*cos»альфа»)^(1/2). Будьте внимательны, ведь если угол, расположенный напротив искомой стороны, будет тупым, то косинус примет отрицательное значение. Еще одна формула нахождения сторон треугольника — по двум углам и сторонам. Сразу приведем формулу-равенство, так как для понимания наглядный вид проще, чем длинная роспись. По-прежнему нам нужно найти сторону a. Тогда, опираясь на обозначения, получим следующее: a=(b*sin»альфа»)/sin»бета»=(b*sin»альфа»)/sin(«альфа»+»гамма»)=(b*sin(«бета»+»гамма»))/sin»бета». Вот таким мудреным способом можно найти неизвестную сторону произвольного треугольника.Равнобедренный треугольник
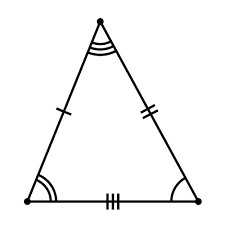
Что такое равнобедренный треугольник? Сам по себе он имеет две одинаковые стороны и так называемое основание. Стороны-близнецы обозначим буквой a, основание — b. Стало быть, раз у треугольника есть два «бедра» одной величины, то и углы на «фундаменте» тоже будут одинаковыми. Их назовем «альфа». Для того чтобы ответить, как найти сторону равнобедренного треугольника, необходимо ввести еще одну величину — угол, образованный между равными «бедрами».
Так как он располагается напротив b, то назвать его лучше всего «бета». Здесь при поиске неизвестных сторон можно пользоваться несколькими формулами. Давайте же посмотрим, какими именно. Первые две — это те, по которым можно вычислить длину стороны основания равнобедренного треугольника. Основана она на знаниях ученика о синусах и косинусах.
Итак, выглядят наши вычисления следующим образом: b=2*a*sin(«бета»/2)=a*(2-2*cos»бета»)^(1/2) или же b=2*a*cos»альфа». Легко все и просто. Особенно, если «набить руку» и попрактиковаться. Теперь можем взглянуть, как вычислить длину равных сторон. Здесь тоже имеется два варианта, они немного сложнее, чем предыдущие. Выглядят громоздко, но пугаться этого не стоит. Как же найти «бедра»? Будем иметь следующий вид формул: a=b/(2*sin(«бета»/2))=b/(2-2*cos»бета»)^(1/2) или же a=b/(2/cos»альфа»). Какую именно запись нужно использовать? Все зависит от поставленной задачи и условий. Конечно же, можно произвести проверку вычислений по всем формулам, если у вас есть абсолютно все данные. Теперь можем двигаться дальше.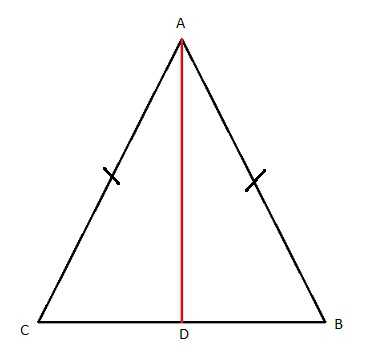
Прямоугольный треугольник
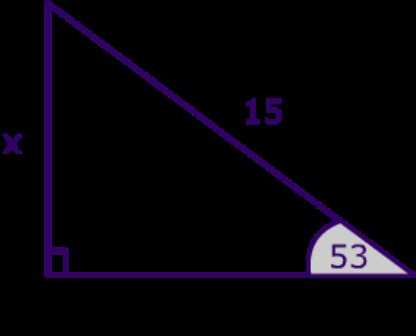
Наверное, каждый школьник, который только начал изучение геометрии, знает, что такое прямоугольный треугольник. С первого взгляда в данной фигуре нет ничего особенного, сложного и непонятного. Но вот когда «теряются» данные о той или иной стороне сего геометрического объекта, начинаются проблемы. Дело все в том, что вопрос: «Как найти сторону прямоугольного треугольника?» — затрагивает не только понятия синуса и косинуса, а еще и тангенсов углов. Таким образом, вычисления становятся намного сложнее и больше. Итак, сначала обозначим два катета нарисованного прямоугольного треугольника через a и b. Углы, лежащие напротив этих сторон, как и принято было прежде, назовем «альфа» и «бета» соответственно. Нашей гипотенузой будет служить сторона c. Угол, лежащий против него, нам не понадобится — он будет прямым. Вариантов вычислений тут несколько. Первый называется классическим. Для катета a формулы выглядит как: a=c*cos»бета»=c*sin»альфа»=b*tg»альфа».
Сторону b найдем аналогичным способом: b=c*cos»альфа»=c*sin»бета»=a*tg»бета». Тогда наша гипотенуза находится при помощи: c=a/sin»альфа»=a/cos»бета» или c=b/cos»альфа»=b/sin»бета». Второй, более простой и привычный метод нахождения сторон прямоугольного треугольника — по теореме Пифагора. Она гласит: сумма квадратов двух катетов равна квадрату гипотенузы. Значит, будем иметь следующее: a=(c*c-b*b)^(1/2), b=(c*c-a*a)^(1/2), c=(b*b+a*a)^(1/2). Вот простой и незамысловатый ответ на вопрос, как найти сторону треугольника. Не пугайтесь огромных вычислений.Итоги
Итак, сегодня мы разобрались, как найти сторону треугольника, и выучили много новых формул. Для того чтобы лучше их запомнить, запишите их на какую-нибудь бумажку, по которой потом будет проще учить все наизусть. Не стоит пугаться «страшных» цифр и больших вычислений. Все проще, чем кажется.
www.syl.ru
Формулы прямоугольного треугольника
Определение и формулы прямоугольного треугольника
ОПРЕДЕЛЕНИЕ Если один из углов треугольника прямой (то есть равен ), то треугольник называетсяВ прямоугольном треугольнике с , гипотенузой и катетами и
Теорема Пифагора:
Площадь прямоугольного треугольника:
Радиус окружности, вписанной в прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника
Примеры решения задач
ПРИМЕР 1| Задание | В прямоугольном треугольнике с катетом 6 см и прилежащим к нему острым углом найти периметр и площадь. |
| Решение | Рассмотрим прямоугольный треугольник . Пусть катет см и . Найдем длину гипотенузы :
Тогда по теореме Пифагора второй катет
Найдем периметр и площадь треугольника
|
| Ответ | см, см |
| Задание | В прямоугольном треугольнике известно, что радиус описанной окружности см, а радиус вписанной окружности см. Найти стороны треугольника. |
| Решение | Рассмотрим прямоугольный треугольник с катетами и гипотенузой . Поскольку радиус описанной окружности равен половине гипотенузы, то
Подставим в формулу для радиуса вписанной окружности известные данные:
откуда , а тогда . Воспользуемся теоремой Пифагора:
Решая квадратное уравнение , получим и . Тогда . |
| Ответ | 5 см, 12 см, 13 см |
Формулы равностороннего треугольника
Определение и формулы равностороннего треугольника
ОПРЕДЕЛЕНИЕТреугольник называется равносторонним, если все его стороны равны.
В равностороннем треугольнике все углы равны между собой и равны :
В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной
В равностороннем треугольнике со стороной радиус описанной окружности равен , радиус вписанной окружности – .
В равностороннем треугольнике высоты совпадают с медианами и биссектрисами и равны .
Площадь равностороннего треугольника равна .
Примеры решения задач
ПРИМЕР 1| Задание | Найти сторону равностороннего треугольника , если биссектриса см. |
| Решение | Так как треугольник равносторонний, то его биссектриса
Тогда сторона треугольника
|
| Ответ | см |
| Задание | Найти высоту равностороннего треугольника , если радиус вписанной окружности равен 3 см. |
| Решение | Зная радиус вписанной окружности в равносторонний треугольник, можно найти его сторону:
Сторона треугольника связана с высотой следующим соотношением
|
| Ответ | см |
ru.solverbook.com
Как найти сторону треугольника, если две другие известны
В геометрии часто бывают задачи, связанные со сторонами треугольников. Например, часто необходимо найти сторону треугольника, если две другие известны.
Треугольники бывают равнобедренными, равносторонними и неравносторонними. Из всего разнообразия, для первого примера выберем прямоугольный (в таком треугольнике один из углов равен 90°, прилегающие к нему стороны называются катетами, а третья — гипотенузой).
Быстрая навигация по статье
Длина сторон прямоугольного треугольника
Решение задачи следует из теоремы великого математика Пифагора. В ней говорится, что сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы: a²+b²=c²
- Находим квадрат длины катета a;
- Находим квадрат катета b;
- Складываем их между собой;
- Из полученного результата извлекаем корень второй степени.
Пример: a=4, b=3, c=?
- a²=4²=16;
- b² =3²=9;
- 16+9=25;
- √25=5. То есть, длина гипотенузы данного треугольника равна 5.
Если же у треугольника нет прямого угла, то длин двух сторон недостаточно. Для этого необходим третий параметр: это может быть угол, высота площадь треугольника, радиус вписанной в него окружности и т.д..
Если известен периметр
В этом случае задача ещё проще. Периметр (P) представляет собой сумму всех сторон треугольника: P=a+b+c. Таким образом, решив простое математическое уравнение получаем результат.
Пример: P=18, a=7, b=6, c=?
1) Решаем уравнение, перенося все известные параметры в одну сторону от знака равенства:
P=a+b+c
c=P-a-b
2) Подставляем вместо них значения и вычисляем третью сторону:
c=18-7-6=5, итого: третья сторона треугольника равна 5.
Если известен угол
Для вычисления третьей стороны треугольника по углу и двум другим сторонам, решение сводится к вычислению тригонометрического уравнения. Зная взаимосвязь сторон треугольника и синуса угла, несложно вычислить третью сторону. Для этого нужно возвести обе стороны в квадрат и сложить их результаты вместе. Затем вычесть из получившегося произведение сторон, умноженное на косинус угла: C=√(a²+b²-a*b*cosα)
Если известна площадь
В этом случае одной формулой не обойтись.
1) Сначала вычисляем sin γ, выразив его из формулы площади треугольника:
S=a*b* sin γ/2
sin γ= 2S/(a*b)
2) По следующей формуле вычисляем косинус того же угла:
sin² α + cos² α=1
cos α=√(1 — sin² α)=√(1- (2S/(a*b))²)
3) И снова воспользуемся теоремой синусов:
C=√((a²+b²)-a*b*cosα)
C=√((a²+b²)-a*b*√(1- (S/(a*b))²))
Подставив в это уравнение значения переменных, получим ответ задачи.
Поделитесь этой статьёй с друзьями в соц. сетях:
podskajem.com