Правила треугольников – Свойства треугольника. В том числе равенство и подобие, равные треугольники, стороны треугольника, углы треугольника, площадь треугольника — формулы вычисления, прямоугольный треугольник, равнобедренный треугольник, высота треугольника.

Тестирование онлайн

• Основные понятия треугольника

Понятие треугольника

Если три точки, не лежащие на одной прямой, соединить отрезками, получим треугольник. Одну из сторон треугольника часто называют его основанием.

Теорема. Сумма углов треугольника равна 180⁰

Если все три угла треугольника острые, то треугольник называется остроугольным.

Если один из углов треугольника тупой, то треугольник называется тупоугольным.

Если один из углов треугольника прямой, то треугольник называется прямоугольным. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами.

В любом треугольнике против большей стороны лежит больший угол; против равных сторон — равные углы, и обратно. Любая сторона треугольника меньше суммы двух других сторон, а также больше разности двух других сторон.

Продолжив одну из сторон треугольника, получим внешний угол. Угол АВD — внешний.

Признаки равенства треугольников

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

Теорема. Два треугольника равны, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого.

Теорема. Два треугольника равны, если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим углам другого.

Теорема. Два треугольника равны, если три стороны одного треугольника соответственно равны трем сторонам другого.

Медиана, биссектриса и высота треугольника

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой. Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам.

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

Замечательные точки треугольника. 1) Биссектрисы треугольника пересекаются в одной точке.

2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

3) Высоты треугольника (или их продолжения) пересекаются в одной точке.
4) Медианы треугольника пересекаются в одной точке.

Равнобедренный треугольник

Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.

Треугольник, у которого все стороны равны, называется равносторонним.

Теорема. В равнобедренном треугольнике углы при основании равны.

Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

fizmat.by

Правило треугольников — Энциклопедия по экономике

Нижний левый треугольник соответствует зоне убытков предприятия до достижения порога рентабельности, верхний правый треугольник — зоне прибылей (не окажет ли нам знание последнего обстоятельства дополнительную помощь при расчете авансовых платежей по налогу на прибыль и общей суммы налога ).  [c.198]

На рис. 10.5 показан выделенный абзац. Обратите внимание на положение верхнего треугольника и левого нижнего треугольника на горизонтальной линейке они указывают на отступ в красной строке и левую границу абзаца. Правый треугольник мы сдвинули влево, но еще не отпустили кнопку мыши (поэтому на экране видна вертикальная пунктирная линия). Как только мы отпустим кнопку, правый край абзаца сместится влево.  [c.96]

На рис. 10.6 мы выделили и взяли три абзаца в рамку (толщиной 0,75 пункта), заполнив ее узором (градация серого 10%). Чтобы рамка была более аккуратной, мы сдвинули влево нижний правый треугольник на горизонтальной линейке (т. е. изменили правую границу абзацев). Обратите внимание, как все наши манипуляции воспроизводятся на панели Обрамление толщина границы рамки, градация серого, утопленные кнопки выбора типа рамки.  [c.97]

Составлялись планы социального развития коллективов методом набора мероприятий (в том числе из прошлогодних планов), утверждались, как правило, «треугольником» и принимались на общих собраниях к действию. Органическая увязка этих планов с производственной деятельностью предприятий была довольно слабой, что обусловливало их второстепенный характер и соответственно второстепенную роль в жизни трудовых коллективов.  [c.153]

Вообще-то, отличие между горизонтальными треугольниками и тройными тройками заключается только во внешней форме моделей и всего в одном пункте правил. Действительно, образующие линии треугольника всегда наклонены в разные стороны (одна линия может быть горизонтальной). У идеальной тройной тройки обе линии должны быть горизонтальными или обе наклонены против тренда старшего уровня. Правда, образующие линии у тройной тройки могут быть наклонены в разные стороны, как и у треугольника, но в этом случае обязательно должно быть нарушено одно из правил треугольника, например, заключительная волна заходит за вершину предыдущей действующей волны. В противном случае эту модель можно будет идентифицировать уже в качестве горизонтального треугольника.  [c.113]

Если политики оценивают потребительский излишек более высоко, чем излишек производителя, данные полные убытки могут не иметь большого политического значения. Однако если кривая спроса очень неэластична, контроль над ценами может привести к чистой потере в потребительском излишке, как показано на рис. 9.4. На этом рисунке треугольник В, площадь которого равна убыткам потребителей, вытесненных с рынка нормированием товаров, больше прямоугольника А, измеряющего выигрыш потребителей, получивших преимущественное право приобрести товар. Потребители оценивают товар очень высоко, а вытесненные с рынка теряют очень много.  [c.270]

Предприятия — риск со знаком — выпускают, как правило, небольшие объемы продукции по низкой цене. Продукция может пользоваться спросом у незначительного круга потребителей, или же единственным заказчиком может выступать государство. Примером подобного предприятия является ОАО Красный треугольник .  [c.62]

Индикатор примечаний — маленький красный треугольник в верхнем правом углу ячейки. Примечание вводится в окно справа от ячейки при выполнении команды меню Вставка > Примечание и выводится после установки указателя на ячейку. Для редактирования примечаний или их удаления служит команда меню Вставка > Изменить примечание.  [c.344]

Если у электродвигателей нет доски зажимов, а просто выведено шесть концов обмотки статора, то при соединении этих концов в звезду или треугольник необходимо придерживаться порядка соединения и маркировки проводов. При этом необходимо помнить, что электродвигатели, выпущенные на двойное напряжение 220/380 В, можно включать в сеть 220 В только при соединении обмоток статора в треугольник, а в сеть 380 В — при соединении обмотки статора в звезду. Нарушение этого правила может привести к повреждению электродвигателя.  [c.18]

Остается добавить, что 75 процентов риска по любой конкретной акции составляют рынок и сектор. Проблема, с которой сталкиваются большинство инвесторов, состоит в том, что они концентрируют 75 процентов своих усилий на оценке конкретных фундаментальных показателей. Чрезвычайно важно покупать акции, когда вы являетесь хозяином положения (рынок имеет бычий настрой). Необходимые рыночные индикаторы мы раскроем в последующих главах. Еще раз, прежде чем предпринимать какие-либо действия в отношении акции, наберите как можно больше очков в свою пользу. Я не знаю, сколько раз знакомые подходили ко мне и просили совета насчет акции, о которой они узнавали от своих друзей. Как правило, они говорили, что это весьма солидный и надежный источник. Мой ответ на это всегда был один и тот же, и его же я повторю и для вас «Если это инсайдерская информация, то у вас ее уже нет. Потому что, как только вы ее получили, она тут же стала внешней, доступной всем, информацией, а те, кто знали о ней, давно уже что-то предприняли». Почти в каждом случае вы можете взглянуть на графики «крестики-нолики» и увидеть, где действовали инсайдеры. Как только вы научитесь пользоваться этим методом, вот уже более ста лет остающимся надежным помощником биржевика, вы поймете, почему график «крестики-нолики» равнозначен инсайдерской информации. Модель Треугольника (см. рису-  [c.59]

Эта фигура отличается от предыдущих тем, что треугольник обычно является фигурой продолжения. Его формирование сигнализирует, что тренд опередил себя (сленг — Прим. автора) и должен на некоторое время консолидироваться. После завершения этой консолидации тренд обычно возобновляет движение в том же направлении. Поэтому при верхнем тренде треугольник является обычно бычьей фигурой. При нижнем тренде треугольник обычно медвежий. Фигура треугольника может принимать разнообразные формы. Наиболее частой является симметричный треугольник (см. рис. 10). Эта фигура характеризуется горизонтальным движением на графике, где действие цены постепенно сужается. Линии тренда, прочерченные вдоль его пиков и падений, начинают сходиться. Каждая линия тренда обычно испытывает два или (чаще) три касания. Как правило, на расстоянии от двух третей до трех четвертей фигуры цены прорываются в направлении предыдущего тренда. Если предыдущий тренд шел вверх, цены, вероятно, прорвут вверх.  [c.37]

Эта ступенька треугольника Б—И — управление правовыми вопросами — стала для меня самым тяжелым уроком, который я когда-либо получал. Мой богатый папа выявил серьезный изъян в моем бизнесе я не оформил юридические права на изделия на «липучках», которые я разработал до того, как начал их выпускать. А именно, я так и не запатентовал некоторые из моих изделий (я не сделал этого, потому что считал, что платить 10 тысяч долларов юристам-патентоведам за такую, как я полагал, мелочь, слишком дорого). Вскоре  [c.385]

Треугольник Б—И и правило 90/10 идут рука об руку  [c.394]

В следующей главе мы рассмотрим еще одну группу моделей — модели продолжения тенденции. Тогда мы поговорим о треугольниках, флагах, вымпелах, клиньях и прямоугольниках. Эти модели, как правило, отражают паузы в существующей тенденции, а не перелом в ее динамике. Обычно они классифицируются как промежуточные и малые (или краткосрочные) по сравнению с основными моделями.  [c.97]

Обратите внимание на то, как часто мы употребляем слово «обычно». Это связано с тем, что интерпретация графических моделей подчинена, скорее, общим закономерностям, чем жестким правилам. В ней всегда существуют исключения. Даже элементарная классификация ценовых моделей становится подчас затруднительной. Обычно треугольники являются моделями продолжения тенденции, однако временами они показывают перелом тенденции. Хотя треугольники, как правило, считаются промежуточными моделями, они иногда появляются на долгосрочных графиках, отражающих развитие основной тенденции. Разновидность треугольника — перевернутый треугольник — обычно обозначает перелом основной восходящей тенденции. Временами даже «голова и плечи» — наиболее известная основная модель перелома -может свидетельствовать о фазе консолидации.  [c.124]

Симметричный треугольник или «спираль» — как правило, модель продолжения тенденции. Она знаменует паузу в уже существующей тенденции, после которой последняя возобновляется. Например, на рис. 6.1 а предшествующая тенденция была восходящей, и после консолидации цен в виде треугольника рост цен скорее всего продолжится. В случае нисходящей тенденции, симметричный треугольник означал бы, что после его завершения падение цен возобновится.  [c.126]

На завершение модели треугольник требуется некоторое время, которое определяется точкой схождения двух линий, то есть вершиной модели. Как правило, прорыв цен должен быть в направлении предыдущей тенденции, на расстоянии от половины до 3/4 ширины треугольника по горизонтали. Под шириной треугольника понимается расстояние от вертикальной линии слева (основания модели) до ее вершины справа. Так как две линии должны соединиться в какой-то точке, отрезок, определяющий время, может быть получен только после проведения двух сходящихся линий. Прорыв вверх обозначается пересечением верхней линии тренда. Если цены остаются внутри треугольника за точкой, находящейся на расстоянии 3/4 ширины, модель начинает терять свой потенциал. Это означает, что цены продолжат неопределенное движение к вершине треугольника, а затем дальше за ее пределы.  [c.126]

Расширяющаяся формация» — относительно редкая модель, которая, если и возникает, то, как правило, в преддверии перелома основной восходящей тенденции, на вершине рынка. Она напоминает расширяющийся треугольник с тремя последовательно возрастающими верхними и двумя опускающимися нижними экстремумами. Расширение ценовых колебаний сопровождается постепенным увеличением торговой активности. Такая формация завершается при пересечении уровня второго спада, которое следует после достижения рынком третьего пика.  [c.137]

Pu . 6.66 Пример модели алмаз на вершине рынка. Левая часть модели представляет собой расширяющийся треугольник, правая — симметричный. Прорыв восходящей линии тренда справа сигнализирует о переломе тенденции. Измерьте алмаз по вертикали в самой широкой его части и отложите полученное расстояние вниз от точки прорыва.  [c.139]

Как правило, такая модель до прорыва успевает пройти две трети расстояния до своей вершины, а иногда даже достигает ее (способность проходить весь путь до вершины также отличает ее от симметричного треугольника). По мере образования клина объем должен уменьшаться, а затем, при прорыве, -увеличиваться. При нисходящей тенденции клин формируется быстрее, чем при восходящей.  [c.146]

Как правило, графики цен на один и тот же товар демонстрируют одинаковую последовательность ценовых моделей, которая может отличаться от последовательности моделей на графиках цен на другие товары. Иными словами, графики определенного товара имеют набор особенностей, присущих только этому товару. Например, на графиках хлопка возникает много закругленных вершин и оснований, которые часто образуют целые последовательные серии, что редко наблюдается на графиках соевых бобов и пшеницы. Изучение графиков соевых бобов за несколько лет показывает, что наиболее распространенными моделями на этом рынке являются треугольники. В свою очередь, конфигурации «голова и плечи» очень часто встречаются на графиках рынка пшеницы. Все товарные активы чаще всего следуют определенным моделям поведения, которые находят свое отражение на графиках.»  [c.153]

При рассмотрении ценовых моделей в главах 5 и б мы уже отмечали, что объем является важным индикатором подтверждения ценовых изменений. Одним из первых признаков образования модели «голова и плечи», свидетельствующей о достижении рынком вершины, служит то, что во время формирования «головы» цены росли при небольшом объеме, а последующее падение цен к линии «шеи» сопровождалось увеличением торговой активности. В процессе образования двойных или тройных вершин объем становился все меньше при достижении ценами каждого последующего пика, зато при снижении цен возрастал. Формирование моделей продолжения тенденции, например треугольников, должно проходить при постепенном снижении объема. Как правило, завершение всех моделей (в точке прорыва) сопровождается увеличением активности рынка, если прорыв не ложный (см. рис. 7.5).  [c.162]

Графический анализ достаточно субъективен и с трудом поддается тестированию. Именно поэтому его не так просто переложить на язык компьютерных программ. Что же касается процедур и правил анализа средних скользящих, то они легко закладываются в компьютерную программу, которая потом может выдавать специальные сигналы, указывающие пользователю на наиболее благоприятные моменты для открытия длинных или коротких позиций. Если результаты графического анализа часто оказываются противоречивыми, у аналитиков могут возникнуть разногласия относительно того, к какому типу относится та или иная ценовая модель к треугольникам или, скажем, алмазам на преобладание каких настроений указывают изменения объема бычьих или медвежьих, то сигналы средних скользящих, наоборот, — точны и недвусмысленны.  [c.208]

В самой общей форме это правило, или принцип, гласит обычно рынок не проявляет себя одинаково два раза подряд. Например, если последний раз при переломе тенденции сформировалась определенная модель, то при следующем переломе в том же направлении она, скорее всего, не повторится. Правило чередования не может подсказать нам, что конкретно произойдет с рынком, но говорит, что именно произойти не должно. Более узкое применение этого правила на практике обычно сводится к определению того, какой тип коррекции следует ожидать. Корректирующие конфигурации имеют тенденцию к чередованию. Иными словами, если корректирующая волна 2 представляла собой простую модель а-Ь-с, то волна 4, скорее всего, образует сложную конфигурацию — например, треугольник. И наоборот, если волна 2 представляет собой сложную модель, волна 4 окажется простой. Примеры правила чередования — на рис. 13.31.  [c.346]

Треугольники, как правило, образуются на четвертых волнах (эта модель всегда предшествует последней волне). Треугольник может также быть корректирующей волной В.  [c.353]

Рис. 13. 37 Еще один пример пятиволнового роста. Обратите внимание на линии канала и пятиволновое разбиение каждой импульсной восходящей волны. Волна 4 сформировала треугольник консолидации, который также состоит из пяти волн. Треугольники, как правило образуются волной 4.

В 70-х годах, когда Стенфордский исследовательский институт образовал Силиконовую Долину, а Северная Каролина строила Исследовательский Треугольник, ни одно учреждение Техаса не имело политики, которая могла бы позволять передавать за деньги в частный сектор права владения или лицензию на интеллектуальную собственность, созданную в ходе финансированного государством исследования. Даже сегодня прибыль представляет собой спорный вопрос для большинства «некоммерческих» университетов, что способствует расширению запрещенной зоны на пути технологии к месту на рынке, где они могут стать прибыльными продуктами. Фундаментальная причина заключается в различии мотивации к новым знаниям. В университетском сообществе знание является венцом всему, целью, а не средством. Чтобы еще усложнить проблему, государственные университеты заявляют об их ответственности перед налогоплательщиками. Те. дескать, уже оплатили их труд и. следовательно, имеют право на долю в результатах. Проблема такого подхода заключается в том, что при этом не учитываются финансовые и управленческие инвестиции, обязательные для превращения идеи в продукт. Готовность безвозмездной передачи идеи обществу исключает дополнительные инвестиции, необходимые для превращения добротной технологии в рыночный продукт. Если какая-либо фирма, университет, сообщество, государство или нация реально хочет, чтобы их граждане извлекли выгоду из исследований, поддержанных на бюджетные деньги, то надо, чтобы это «чреждение нашло партнера из частного сектора, который понимает разницу между изумительной технологией и ходовым продуктом. Этот партнер должен также понимать правила трансфера технологии и роль, которую в этом может сыграть сотрудничество разных секторов.  [c.236]

Как только мощная волна 3 заканчивается, на рисунок рынка начинает оказывать воздействие взятие прибыли. Большинство опытных трейдеров, стоявших ранее в трен-де, начинают снимать обильную прибыль, закрывая свои позиции. Характер волны 4 совершенно отличается от той, какая присуще волне 2. Эллиот отмечал это различие, как правило, чередования если волна 2 является простой, то волна 4 будет сложной, и наоборот. Простой коррекцией обычно обоснованно является движение типа «зигзаг». Если оно происходит в волне 2, волна 4 будет сложной боковой коррекцией (плоская, неправильная, треугольник, удвоенные или утроенные тройки5).  [c.91]

INTU] INTUIT прорвала двойную вершину на 45. Это — пробитие модели треугольника. Такие модели, как правило, приводят именно к таким быстрым взрывным движениям. Основной тренд — восходящий, с ценой, торгуемой над линией медвежьего сопротивления. Тест прорыва максимум графика на 50. Если все «ОК», то покупайте INTU здесь, с защитной остановкой на 38, так как тут уровень прорыва линии восходящего тренда.  [c.56]

Неограничивающие Треугольники (специфика) 5-30 Посттреугольный выброс 5-31 Расширяющиеся Треугольники (общие правила) 5-31  [c.121]

economy-ru.info

Инструкция торговли по модели треугольник: описание и правила построения

Модель треугольника (от англ. triangle model) — один из паттернов графического анализа, популярен среди трейдеров на финансовых рынках. Используется в торговле на среднесрочных и долгосрочных периодах. Дата его возникновения ориентировочная и считается началом 90 годов.

Для того чтобы иметь полное представление о торговле графическими моделями, мы должны хорошее понимать одну из наиболее распространенных моделей на графике. То, что я имею в виду является треугольными торговыми моделями.

Итак, в этом уроке мы обсудим основные треугольные модели и некоторые способы для правильного определения и торговли этих моделей.

Что такое модель треугольника

Модель треугольник — специфическая фигура образованная на ценовом графике, появляющаяся когда верхние и нижние части цены движутся навстречу друг другу, как стороны треугольника. Когда верхний и нижний уровень треугольника взаимодействуют между собой, трейдеры ожидают возможного прорыва из треугольника. Таким образом, многие трейдеры прорыва используют треугольные модели для определения точек входа на прорывах.

Существуют различные виды треугольников, которые можно увидеть на графике Forex. Перед тем, как торговать треугольником вы должны понимать разницу между формированиями. Теперь мы более внимательно взглянем на различные модели треугольников и соответствующие торговые установки. После того, как вы будете обладать этими знаниями, вы будете в состоянии добавить торговую стратегию треугольника к вашему торговому арсеналу.

Восходящий / Нисходящий треугольник

Эти типы треугольников имеют одну плоскую горизонтальную сторону, и одну наклонную сторону, которая движется по направлению к плоской горизонтальной стороне. Модели восходящих и нисходящих треугольников являются зеркальным отражением друг друга. Они определяются по возрастанию или убыванию в зависимости от того, какая сторона является плоской горизонтальной стороной, и с какой стороны находится склон.

Паттерн Восходящего треугольника

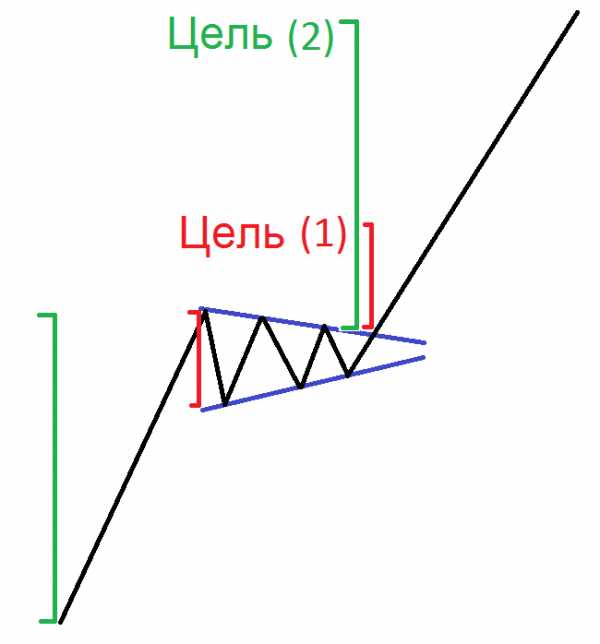
У этой модели треугольника верхняя сторона плоская, а нижняя восходящая. Таким образом, вершины этого треугольника находятся на том же уровне, а днища увеличиваются. Этот тип треугольника, как правило, имеет бычий характер. Если вы заметили этот треугольник на графике, вы должны быть готовы поймать бычье движение цены, равное, по крайней мере, размеру треугольника. Таким образом, прорывы через верхний уровень (плоская сторона) используются для установки точек входа для длинных позиций. Это эскиз модели восходящего треугольника:

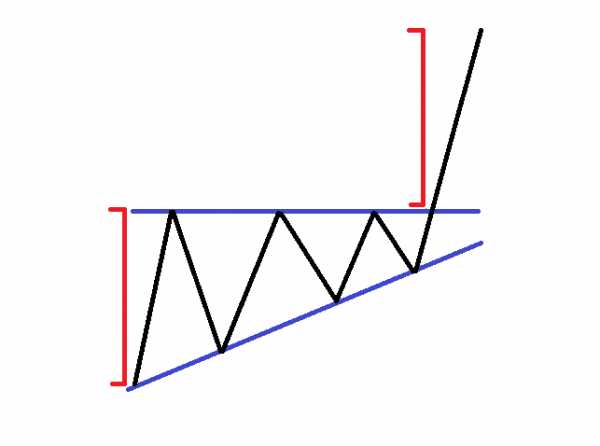
Черные линии выше, показывают на ценовое действие в рамках треугольного формирования. Синие линии относятся к сторонам треугольника, которые содержат ценовое действие. Красные линии соответствуют размеру треугольника и его потенциальной цели, которая обычно представляет собой 1:1 измеренного движения.

Когда формируется восходящий треугольник в бычьем тренде, мы ожидаем продолжение тренда.

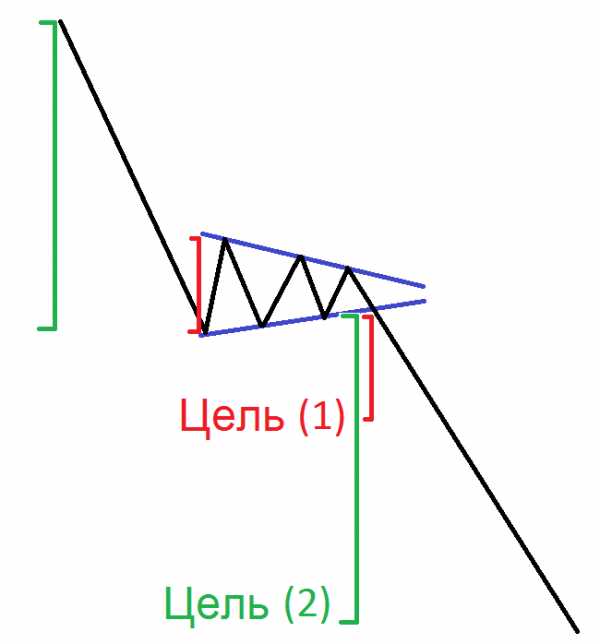
Паттерн Нисходящего треугольника

Как уже отмечалось ранее, восходящий и нисходящий треугольники являются зеркальным отражением друг друга. Таким образом, модель нисходящего треугольника имеет противоположную характеристику. Плоская сторона нисходящего треугольника находится ниже ценового действия. Верхняя сторона треугольника наклонена вниз. В медвежьем рынке, нисходящий треугольник имеет медвежий потенциал, равный по крайней мере, размер формирования. По этой причине, нисходящий треугольник используется для открытия коротких позиций после того, как цена пробила его нижнюю (плоскую) сторону. Давайте взглянем на эскиз нисходящего треугольника:

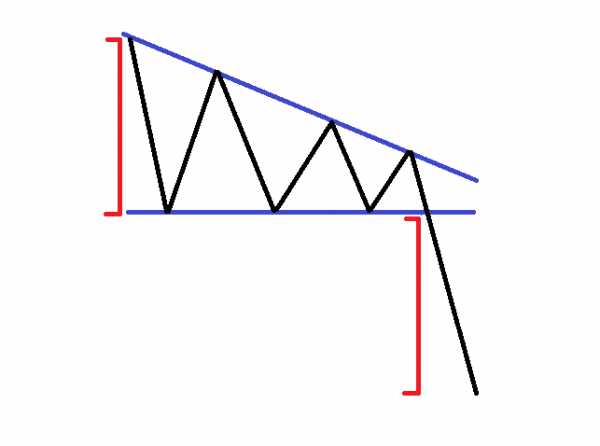
Когда нисходящий треугольник создается во время медвежьей ценовой тенденции, мы ожидаем, что эта тенденция продолжится.

Очень важно отметить, что восходящие и нисходящие треугольники иногда прорываются через наклоненный уровень, что приводит к возникновению ложных сигналов и заманиванию некоторых трейдеров в ловушку. То же самое сохраняется и для горизонтальной ценовой зоны. Вы всегда должны стараться дождаться закрытия свечи, чтобы подтвердить прорыв. Это поможет уменьшить многие ложные сигналы.

Восходящий / Нисходящий Клин

Восходящие и Нисходящие клинья подобны моделям Восходящих и Нисходящих треугольников. Тем не менее, Восходящие и Нисходящие клинья не имеют плоскую сторону. Обе стороны клиньев наклонены в том же самом направлении. Давайте опишем два вида клиньев, которые Вы найдете на ценовом графике.

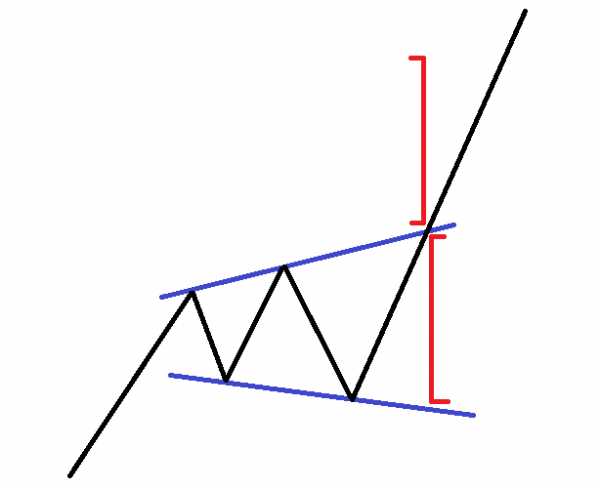
Восходящий клин

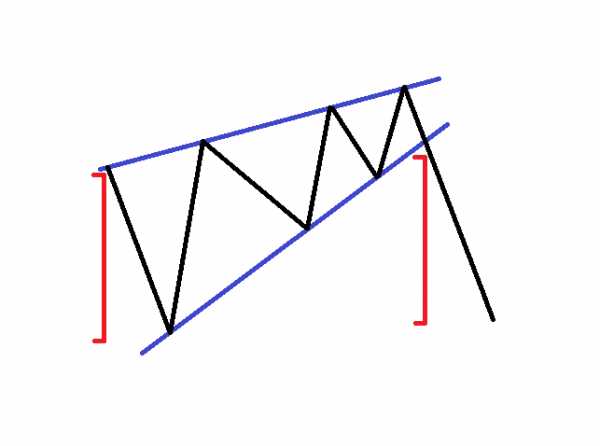
Это модель треугольника, где обе стороны наклонены вверх. Цена создает более высокие вершины и даже более высокие основания. Это приводит к тому, что две восходящие линии взаимодействуют, создавая этот тип треугольника на графике. Восходящий клин имеет сильный медвежий характер. Таким образом, главной стороной клина является нижняя линия. Если вы заметили прорыв через нижний уровень восходящего клина, следует ожидать резкого падения цен равному размеру модели. Таким образом, прорывы через нижний уровень клина используются для открытия коротких позиций. Вот как выглядит формирование восходящего клина:

Нисходящий клин

У Нисходящего клина обе стороны наклонены вниз. Цена создает более низкие днища и еще более низкие вершины. Таким образом, обе стороны треугольника являются нисходящими. В отличие от восходящего клина, нисходящий клин имеет сильный бычий характер. Таким образом, главная сторона формирования нисходящего клина является верхней линией. Когда цена пробивает верхний уровень нисходящего клина, вы должны стремиться к бычьему движению, равному высоте основания клина. По сути, трейдеры используют нисходящий клин, чтобы установить точки входа в длинные позиции на графике. Ниже Вы увидите эскиз нисходящего клина:

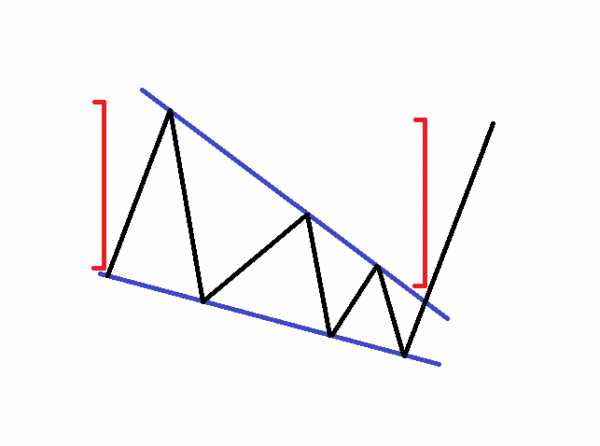
Теперь, когда вы знаете как выглядят восходящие и нисходящие клинья, мы должны выделить еще одну деталь относительно этих формирований. Клинья могут иметь характер продолжения или разворота тренда. При появлении клина после продолжительного ценового движения, мы ожидаем разворот тренда, когда клин появляется в начале тренда, мы ожидаем, что это будет временный откат, который будет продолжать основную тенденцию. Как правило, более мощный клин является формированием потенциального разворота тренда, которое происходит после продолжительного движения тенденции.

Паттерн Симметричного треугольника

Симметричный треугольник является ситуацией на графике, когда вершины ценового действия ниже, а основания выше. Кроме того, обе стороны треугольника наклонены под тем же углом. Это создает симметричный характер треугольника.

Как правило, с симметричной моделью треугольника, ожидаемое направление прорыва неизвестно. Причина этого заключается в том, что бычье и медвежье движение имеют равную силу, что видно на ценовом действии. Когда в конце концов происходит прорыв, это вызывает движение цены, равное размеру модели. Таким образом, вы должны тщательно определить потенциальный прорыв в верхнем и нижнем уровне симметричного треугольника, чтобы заключить правильную позицию на рынке. На рисунке ниже показано формирование симметричного треугольника и возможные сценарии прорыва:

Как видно из приведенного выше примера, потенциальная цель на основании размера формирования треугольника. При этом типе измеренного анализа движения, вы будете знать, что ожидать от прорыва симметричного треугольника, сломан он или вверх или вниз.

Вымпелы

Вымпелы на графике имеют аналогичную форму, что и симметричные треугольники. Как правило, они появляются во время тренда и имеют характер продолжения тенденции.

Бычий вымпел

Бычий вымпел по внешнему виду похож на симметричный треугольник, но формирование Бычьего вымпела происходит после повышения цены. Так как вымпелы имеют характер продолжения тренда, бычий вымпел, вероятно, продолжит бычий тренд на графике. Когда верхняя сторона вымпела сломана вверх, мы увидим увеличение, равное, по меньшей мере размеру вымпела, и, как правило, даже больше. И поэтому при торговле вымпелом, должна использоваться вторая цель, чтобы поймать большее движение. При расчете второй цели, вы должны проанализировать ценовой ход сразу после вымпела.

Вы могли бы поставить перед собой цель на 1:1 предыдущего хода или на уровень Фибоначчи 61.8 этого движения. Когда тенденция кажется сильной и имеет крутой наклон, измеренное движение было бы соответствующей второй целью 1:1, а во всех других случаях могли использоваться уровень 61.8 этого движения. Давайте ниже посмотрим на бычий вымпел:

Смотрите, что здесь у нас есть две цели. Красная мишень является первым, который является столь же большим, как размер вымпела. Зеленый мишень соответствует размеру предыдущего восходящего движения, который должен быть применен, начиная с верхней стороны вымпел.

Посмотрите, что здесь у нас есть две цели. Красная цель — первая, которая является столь же большой как размер вымпела. Зеленая цель соответствует размеру предыдущего, перемещаются, который должен быть применен, начавшись с верхней стороны вымпела.

Медвежий вымпел

Как вы уже, наверное, догадались, медвежий вымпел является зеркальным отражением бычьего вымпела. Медвежьи вымпелы начинаются с понижением цены и заканчиваются симметричным на внешний треугольником. Поскольку вымпелы имеют характер продолжающейся тенденции, медвежьи вымпелы, скорее всего, продолжат медвежий тренд. Когда цена проходит через нижний уровень медвежьего вымпела, вы должны сначала взять первую цель, которая равна размеру самого вымпела. Когда цена завершает эту цель, вы можете попытаться поймать ожидаемое дальнейшее снижение, равное по размеру предыдущему ходу или 61.8 этого движения. На картине ниже изображен медвежий вымпел:

Расширяющийся треугольник

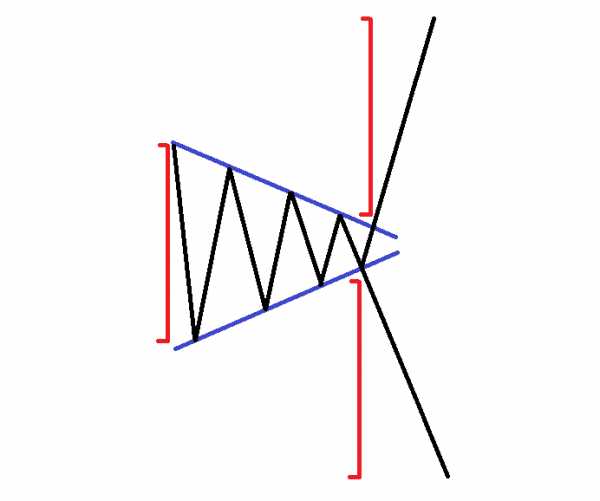
Вряд ли можно ошибиться в расширяющемся треугольнике на графике. Причина этого заключается в том, что он имеет очень уникальные параметры. Обе стороны расширяющегося треугольника наклонены, но в противоположных направлениях.

Направление потенциального ценового движения этой фигуры очень сложно определить. Поэтому мы сейчас введем несколько правил, которые помогут вам определить направление ожидаемого ценового движения.

Симметричные линии

Если Расширяющийся треугольник представляет собой горизонтальный зеркальное отражение симметричного треугольника, то вы должны торговать формированием как моделью продолжения тренда. На рисунке ниже показан эскиз расширяющегося треугольника с симметричными линиями:

Увеличение линий

Если обе стороны расширяющегося треугольника увеличиваются, то модель может иметь медвежий характер.

Снижение линий

Если обе стороны расширяющегося треугольника снижаются, то модель может иметь бычий характер.

Одна сторона сильнее другой
Если вершины ценового действия увеличиваются, но днища уменьшаются с более высокой интенсивностью, то картина имеет медвежий характер. И наоборот, если Днища уменьшаются, а вершины увеличиваются с более высокой интенсивностью, то картина может иметь бычий характер. Другими словами, вы должны торговать в направлении той стороны, которая имеет более высокую склонность.

Торговля треугольниками на Форекс

Теперь, когда мы обсудили большинство важных моделей треугольника на Форекс, теперь я покажу вам, как работает торговая система по треугольникам.

Изображение выше показывает график Н4 пары USD/CHF с января по февраль 2016 года. График иллюстрирует пять примеров треугольников и их потенциальный результат.

График начинается с большого симметрического треугольника. Цена создает три уменьшающихся вершины и три возрастающих основания на графике. Красная стрелка в начале треугольника измеряет его размер. Как вы видите, эта же красная стрелка применяется, когда цена пробивает верхний уровень треугольника. Красная стрелка указывает на потенциальную цель модели, которая будет завершена через неделю.

В то же время, на пути вверх ценовое действие создает восходящую модель клина. Как мы уже говорили, восходящий клин имеет медвежий потенциал. С прорыва через нижний уровень клина мы замечаем небольшую коррекцию. (желтые стрелки)

В конце бычьей тенденции цена создает еще один симметричный треугольник. В дальнейшем цена пробивается через нижний уровень и закрывает прибыль по модели (розовые стрелки).

При снижении ценовое действие фактически создает медвежий вымпел. Это консолидация после первого импульса медвежьего тренда. Впоследствии цена пробивает нижний уровень вымпела. На пути вниз мы видим, что цена завершила первую цель, которая приравнивается размеру вымпел (красные стрелки). Снижение идёт дальше и продолжается до размера, равного предыдущему шагу. (зеленые стрелки).

Затем USD/CHF создает двойное дно модели разворота и переключается на бычье направление. На пути ценовое действие создает расширяющуюся модель треугольника. Обратите внимание на то, как увеличиваются верхний и нижний уровень формирования. В этом случае, ожидаемая цена медвежьего хода должна быть равна размеру модели. Обратите внимание на то, что в этот раз размер модели измеряется от конечной стороны формирования. Причина этого заключается в том, что мы берем самую широкую сторону, когда измеряем ожидаемое движение от треугольного прорыва. Красные стрелки на графике показывают нам, что эта модель также завершает свою цель.

Заключение

Треугольники являются одними из наиболее важных графических моделей в торговле на Форекс.
Мы имеем треугольник на графике, когда верхние и нижние части ценового действия движутся навстречу друг другу.

Также существуют индикаторы для нахождения треугольника, но рекомендуется ручное нахождение паттерна,

Основные треугольники на Форекс:

• Восходящий Треугольник — плоские вершины; высокие основания; бычий потенциал.
• Нисходящий Треугольник — плоские основания; низкие вершины; медвежий потенциал.
• Клинья — стороны увеличения / уменьшения в том же направлении.
• Восходящий Клин — более высокие вершины; еще более высокие основания; медвежий потенциал.
• Нисходящий Клин — более нижние основания; еще более низкие вершины; бычий потенциал.
• Симметричный Треугольник — нижние вершины; высокие основания; стороны имеют один и тот же угол движения.
• Бычий Вымпел — наступает после повышения цены; заканчивается небольшим симметричным треугольником; бычий потенциал.
• Медвежий Вымпел — наступает после снижения цены; заканчивается небольшим симметричным треугольником; медвежий потенциал.
• Расширяющийся Треугольник — стороны двигаются друг против друга.

Потенциал расширяющегося треугольника изменяется в зависимости от угла наклона линий:

• Стороны являются симметричными — потенциальное ценовое движение в направлении тренда.
• Обе стороны Увеличиваются — медвежий потенциал
• Обе стороны Уменьшаются — бычий потенциал
• Одна сторона круче, чем лругая — потенциальное ценовое движение в направлении более крутой стороны.

info-fx.ru

Правила Саррюса (правило треугольников) — Мегаобучалка

ОДОБРЕНО

Протокол заседания ПЦМК

по математике

№ 2 от 29.09.2013

СБОРНИК МЕТОДИЧЕСКИХ УКАЗАНИЙ

ДЛЯ ОБУЧАЮЩИХСЯ ПО ВЫПОЛНЕНИЮ

ПРАКТИЧЕСКИХ ЗАНЯТИЙ

ДИСЦИПЛИНА «ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ»

специальность 230115 ПРОГРАММИРОВАНИЕ В КОМПЬЮТЕРНЫХ СИСТЕМАХ

Актуализировал

преподаватель

ГБОУ СПО «ПГК»

Афонина Н.Е.

Самара, 2013г.

Раздел «ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ»

Тема «МАТРИЦА И ОПРЕДЕЛИТЕЛЬ»

Практическое занятие №1:

«ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ»

Учебная цель:формировать умение вычислять определители 2-го, 3-го и n-го порядка.

Учебные задачи:

1. научиться вычислять определитель 2-го порядка;

2. научиться вычислять определитель 3-го порядка;

3. научиться определять определитель n-го порядка;

4. научиться применять свойства при вычислении определителей.

Образовательные результаты, заявленные во ФГОС третьего поколения

Студент должен

уметь:

— решать системы линейных уравнений;

знать:

— основные понятия линейной алгебры.

Задачи практического занятия №1

1. Повторить теоретический материал по теме практического занятия.
2. Ответить на вопросы для закрепления теоретического материала.
3. Изучить методические рекомендации по выполнению работы.
4. Выполнить задания на нахождение вычисление определителей.
5. Оформить отчет.

Обеспеченность занятия (средства обучения):

1. Справочная литература:

— Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И.Ермакова. – М.: ИНФРА-М, 2005. – 575 с.

2. Рабочие тетради: тетради для практических занятий в клетку.

3. Калькулятор: простой.

4. Ручка.

Краткие теоретические и учебно-методические материалы

По теме практического занятия

Определитель матрицы второго порядка называется число

.

Определитель матрицы третьего порядка называется число

.

Минором элемента определителя n-го порядка называется определитель (n-1)-го порядка, который получается в результате вычёркивания в определителе n-го порядка строки и столбца, содержащих элемент .

Алгебраическим дополнением элемента называется его минор, умноженный на : .

Разложение определителя по элементам ряда. Определитель равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения, т.е.

 

или

 

.

Если в определителе все элементы ряда, кроме одного, равны нулю, то определитель равен произведению отличного от нуля элемента на его алгебраическое дополнение, т.е.

.

Правила Саррюса (правило треугольников).

Три слагаемых, входящих в сумму со знаком «плюс», находятся следующим образом: одно слагаемое состоит из произведения элементов, расположенных на главной диагонали, два других – произведения элементов, лежащих на параллели к этой диагонали с добавлением третьего множителя из противоположного угла. (Получается два треугольника, вершинами которых являются перемножаемые элементы.) (рис. 1).

 

Рис.1 Рис.2

Слагаемые, входящие в сумму со знаком «минус», строятся таким же образом относительно побочной диагонали. (рис.2).

Свойства определителей:

1. При замене каждой строки определителя столбцом с тем же самым номером значение определителя не изменяется.

2. Общий множитель всех элементов ряда определителя можно вынести за знак определителя.

3. Определитель, содержащий две одинаковые строки (столбца), равен нулю.

4. Определитель не изменяется, если к элементам одной из его строк (столбцов) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

5. Если каждый элемент какого-либо столбца определителя представлен в виде суммы двух слагаемых , то этот определитель равен сумме двух определителей, у которого k-й столбец первого определителя состоит из элементов , а k-й столбец второго – из элементов .

 

 

Вопросы для закрепления теоретического материала к практическому занятию:

 

1. Что называется определителем второго порядка?

2. Что называется определителем третьего порядка?

3. Что такое минор элемента определителя?

4. Что такое алгебраическое дополнение элемента определителя?

5. Сформулируйте правило Саррюса.

6. Сформулируйте свойства определителей.

7. Каким образом можно найти определитель 4 порядка?

 

megaobuchalka.ru

Правила треугольника

Треугольное лицо кажется таким непропорциональным! Узкий лоб и широкий подбородок могут приводить вас в отчаяние, но, поверьте, ситуацию можно исправить.

Вообще-то под «треугольным лицом» часто понимают две совершенно противоположные формы. Это может быть «треугольник вершиной вверх» — узкий лоб, широкий подбородок и «треугольник вершиной вниз» — широкие скулы, узкий подбородок. Для каждого из этих типов есть свои способы коррекции.

Лицо треугольник вершиной вверх

Если ваше лицо принадлежит к этому типу, выбирайте короткие стрижки — они зрительно уравновешивают широкий подбородок.

Лучший выбор для треугольного лица — прически с объемными висками, сужающиеся к подбородку. Кстати, верхняя часть может быть многослойной — это добавит необходимый объем». Форму также можно уравновесить с помощью челки — густая челка зрительно расширяет узкую верхнюю часть лица и тем самым делает его более округлым. Так же обратите внимание на стрижку «боб» — тем более что она сегодня очень актуальна!

Окрашивание? Безусловно, оно тоже помогает сгладить недостатки формы лица! «Используйте для всей линии роста волос более темный оттенок, а выше — более светлый. Светлый тон также используется для окрашивания челки.

Беспроигрышный вариант макияжа для лица в форме треугольника вершиной вверх — это макияж с акцентом на глазах. И, конечно, стоит освоить приемы световой коррекции: наносите более темный тон на зону под подбородком и под выступы линии роста волос, более светлый — на скулы.

Лицо треугольник вершиной вниз

Форму такого лица иногда называют «сердечком» — и оно может выглядеть очень мило, особенно если подобрать к нему правильную стрижку! «Для такого лица особенно хороша длина миди. Выбирайте легкие, пышные, слегка растрепанные прически, с отдельными прядями, удлиняющимися к лицу. Отлично будет смотреться также длинная, зачесанная набок челка — она придаст вашему облику сексуальность и шарм».

www.casual-info.ru

No related posts.