Как вычислить определитель матрицы 5х5 – Как вычислить матрицу 5 порядка 🚩 детерминант матрицы онлайн 🚩 Математика

1.5. Вычисление определителей n-го порядка (2 метода)

Звуковое сопровождение лекции

I. Понижение порядка по свойству 8 (формулы разложения).

II. Приведение определителя к треугольному виду (алгоритм на основе свойства 7).

Пример

Вычислите определитель 4-го порядка методом понижения порядка.

Решение

Для разложения определителя по элементам строки или столбца выгодно использовать строку или столбец, в котором есть нули. Таковыми являются, например, вторая строка и третий столбец. Увеличим количество нулей в первой строке, для чего сложим второй и четвертый столбцы.

.

Этот определитель разложим по элементам первой строки.

.

Пример

Вычислите определитель 4-го порядка 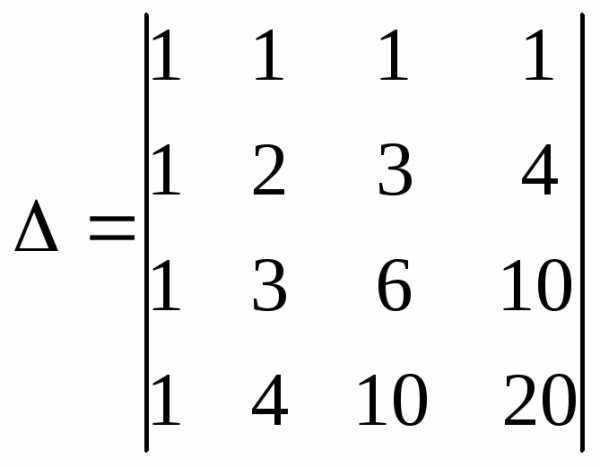методом приведения к треугольному виду.

Решение

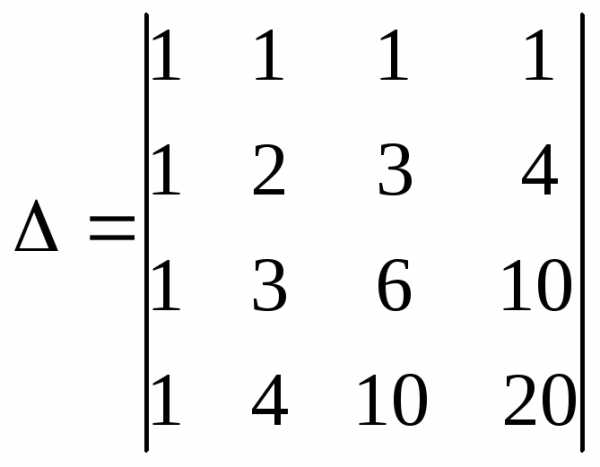
1 действие. Для того чтобы вычислить определитель методом приведения к треугольному виду получим нули в первом столбце, за исключением первой строки. Для этого в качестве рабочей строки выберем первую строку, затем, пользуясь 7 свойством определителей, сложим первую строку, умноженную на -1 с остальными тремя строками.

2 действие. Теперь получим нули во втором столбце в третьей и четвертой строке. Для этого в качестве рабочей строки выберем вторую строку, затем, сложим вторую строку, умноженную на -2 с третьей строкой и сложим ее, умноженную на -3, с четвертой строкой.

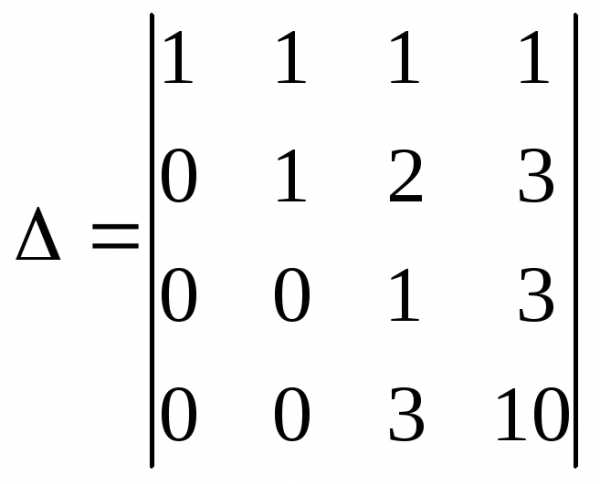
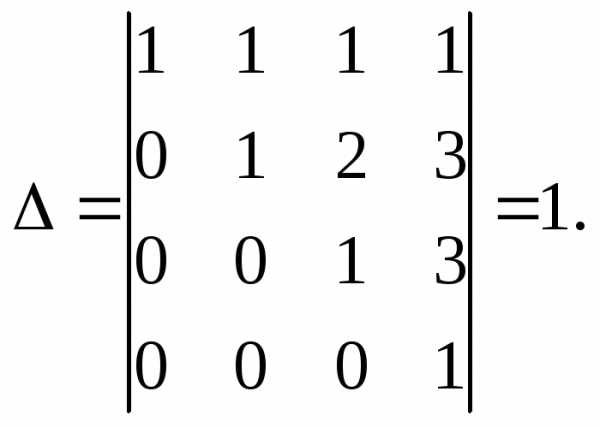
3 действие. Аналогично получим ноль в третьем столбце, выбрав в качестве рабочей строки – третью, затем умножим ее на -3 и прибавим к четвертой строке. Таким образом, мы привели определитель к треугольному виду и можем легко вычислить его.

Пример 5(для самопроверки)

Вычислите определитель 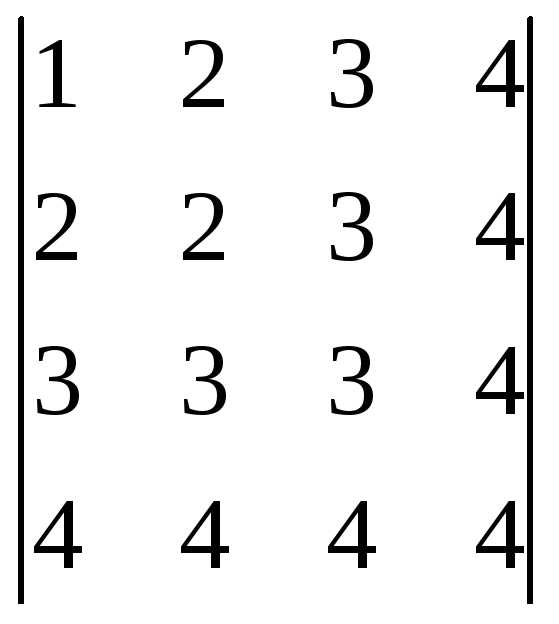двумя способами.

Ответ

Пример 6(для самопроверки)

Вычислите определитель 5-го порядка

.

Ответ

1.6. Задания для самопроверки

Открыть задания

Лекция 2. Алгебра матриц

Содержание

1. Основные операции над матрицами и их свойства.

2. Обратная матрица.

3. Решение матричных уравнений.

4. Невырожденные системы n линейных уравнений с n неизвестными.

5. Задания для самопроверки

Определения	Теоремы и свойства
вырожденная матрица невырожденная матрица нулевая матрица обратная матрица перестановочная матрица равенство матриц сложение матриц умножение матриц умножение матрицы на число	правило умножения матриц свойства операции сложения свойства операций умножения матрицы на число и умножения матриц теорема о существовании и единственности обратной матрицы формулы Крамера

2.1. Основные операции над матрицами и их свойства

Звуковое сопровождение лекции

Определим несколько отношений и операций над матрицами.

Рассмотрим матрицы 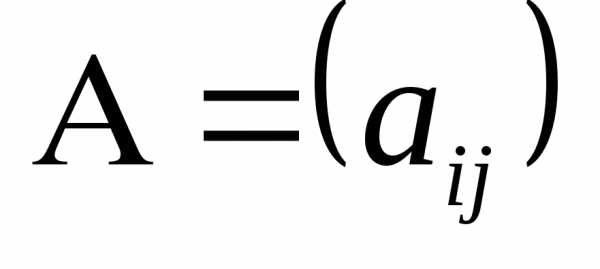размера,–.

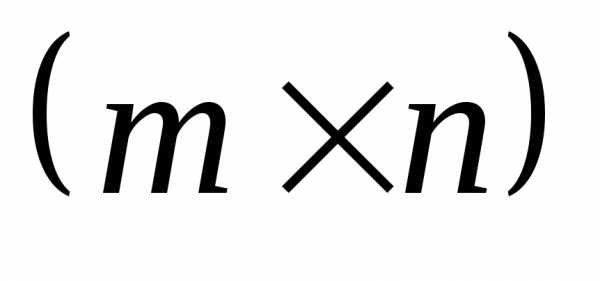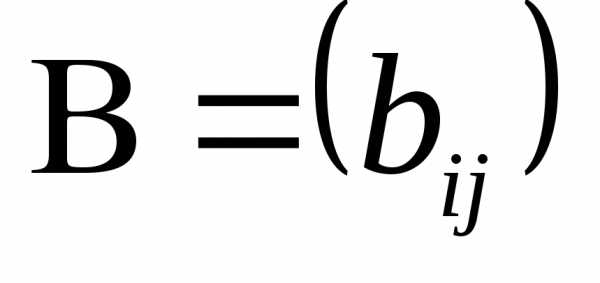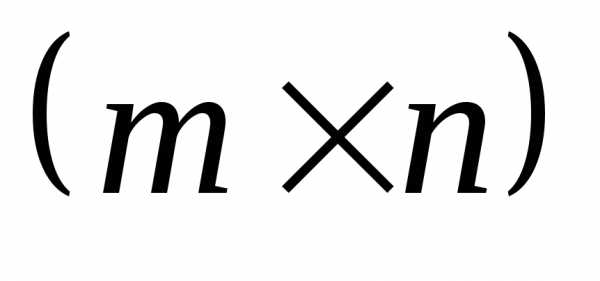Равенство матриц

, ,…

;,…

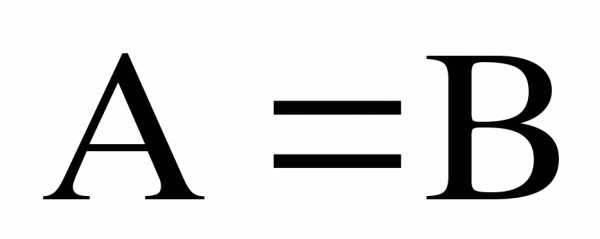
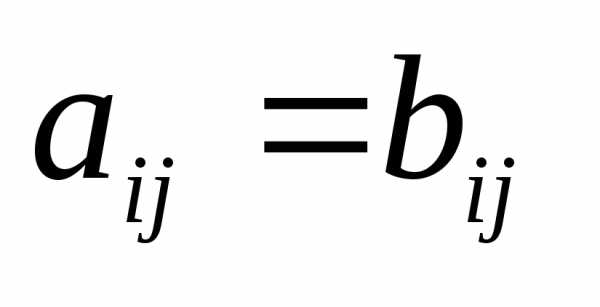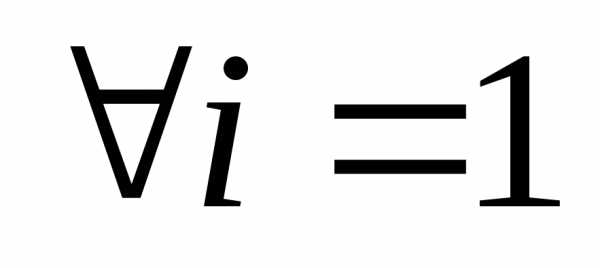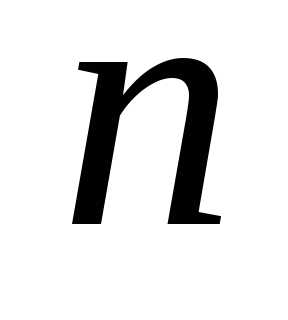
Сложение матриц

Результатом сложения матриц и называется матрица, элементы которой являются суммой соответствующих элементов исходных матриц.

Умножение матрицы на число

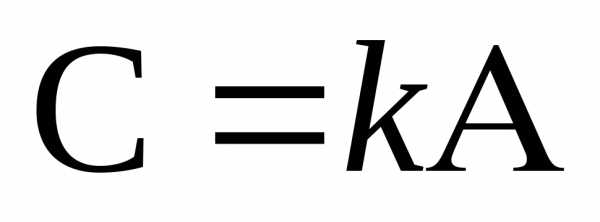
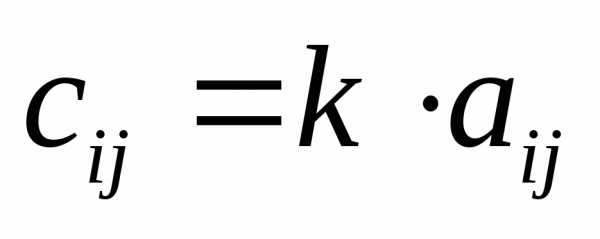
Умножение матриц

Пусть размера,–,

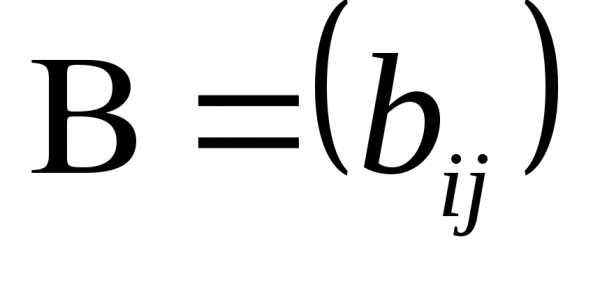тогда их произведением называется матрица размера :

.

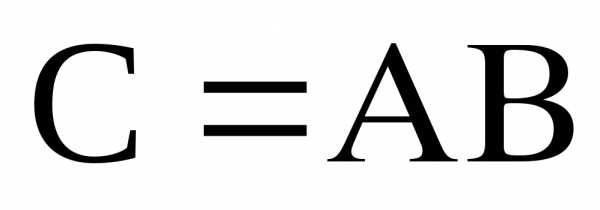
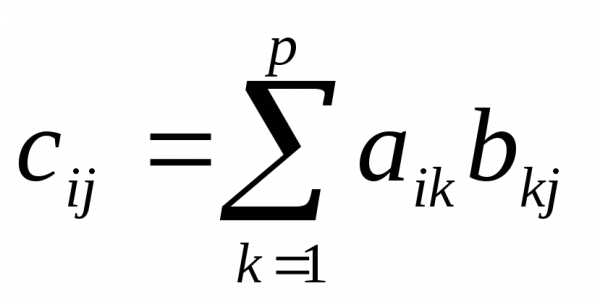Правило умножения матриц

1. Перемножать можно лишь матрицы согласованных размеров (число столбцов матрицы

равно числу строк матрицы).

2. Размер матрицы равен произведению числа строк матрицына число столбцов матрицы, т.е..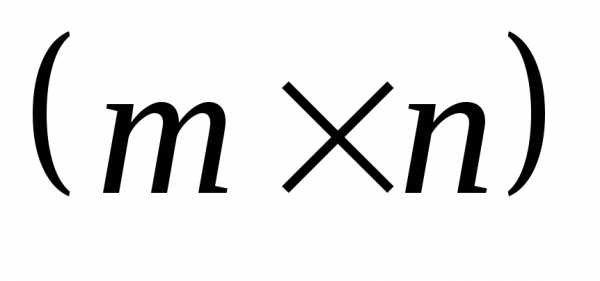

3. Чтобы получить элемент матрицы произведения 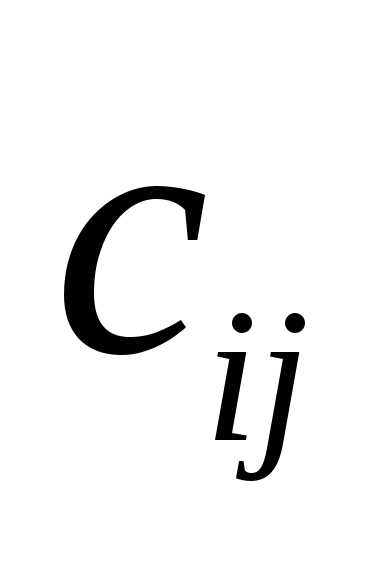, расположенный на пересечении-й строки и

-го столбца следует перемножить соответствующие элементы-й строки матрицыи-го столбца матрицыи найти сумму полученных произведений.

Пример

, .

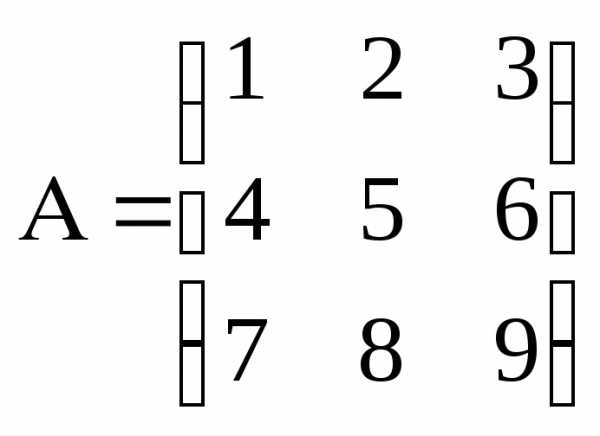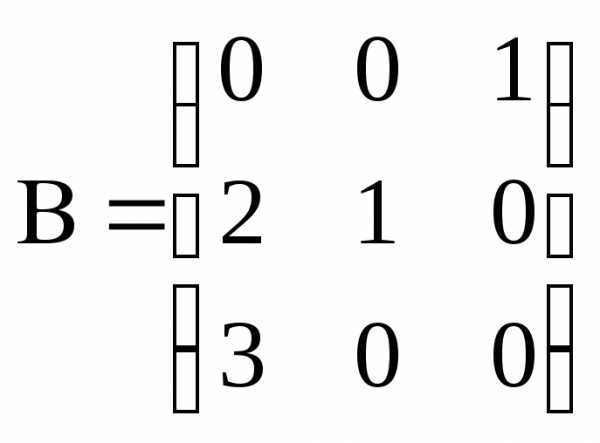1. .

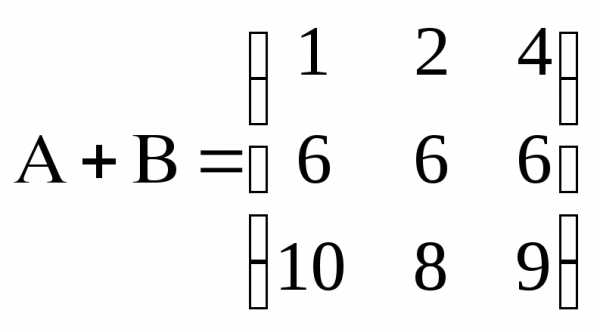2. .

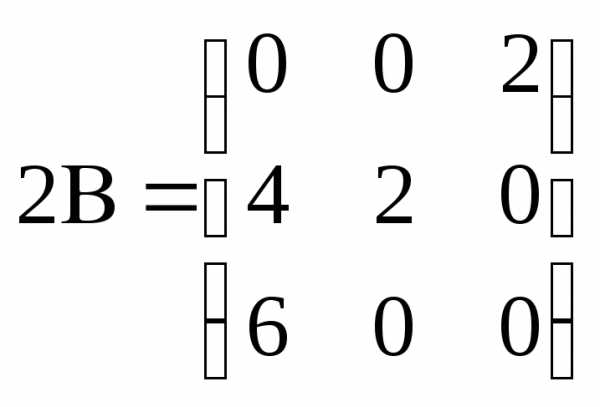3.

,–.

,

,

…

.

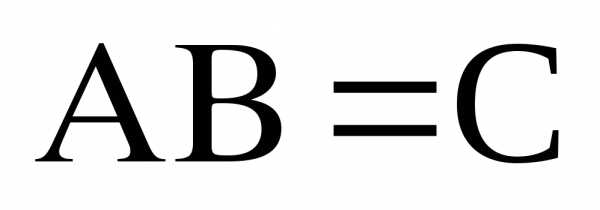
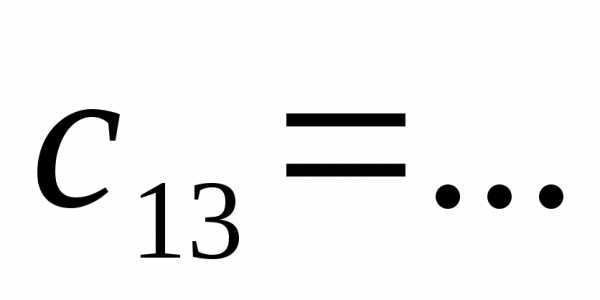
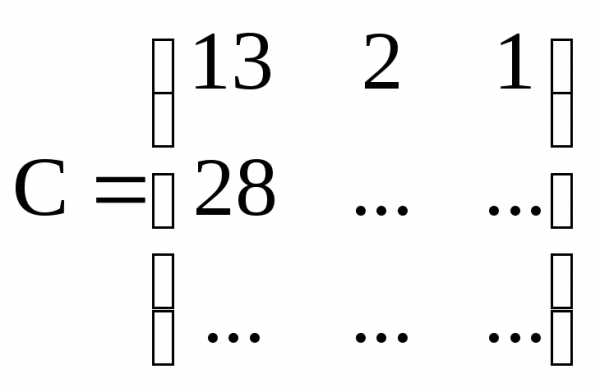Пример 7(для самопроверки)

Найдите .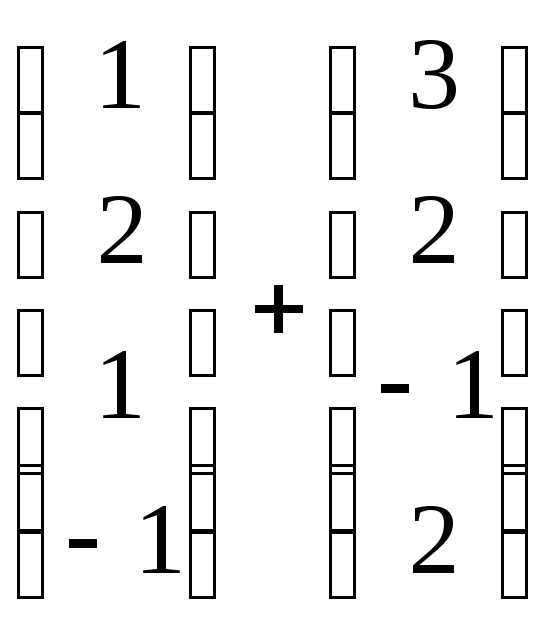

Ответ

Пример8( для самопроверки)

Найдите , если .

Ответ

Пример 9(для самопроверки)

Найдите , если .

Ответ

studfiles.net

ЛА. Определитель матрицы. Вычисление определителей

Теоретический минимум

Определитель (детерминант) возникает во многих разделах математики естественным образом. Вводится он обычно в рамках алгебры.
Например, можно начинать с систем линейных алгебраических уравнений (СЛАУ). Для простоты ограничимся случаем двух уравнений с
двумя переменными:
.
Решить эту систему легко, например, выражая одну из переменных через другую и выполняя подстановку во второе уравнение.

Решение удобно представить в другом виде, для чего вводится следующее обозначение:
.
Так вводится определитель второго порядка. В таких обозначениях получим из (1)
.
Это частный случай формул Крамера, предназначенных для решения СЛАУ, число уравнений в которых совпадает с числом переменных.
Мы не останавливаемся здесь подробно на вопросе решения СЛАУ. Заметим только, что понятие определителя обобщается для большего
количества элементов.

Обобщение такое может быть сделано не одним способом. Возможен индуктивный метод, когда определитель третьего порядка
вводится через определитель второго порядка, определитель четвёртого порядка — через определитель третьего порядка и т.д.
Например, для определителя третьего порядка вводится следующее правило:
.
Сформулировать правило можно следующим образом. Берётся первый элемент первой строки, вычёркивается строка и столбец, которым
этот элемент принадлежит — остаётся определитель второго порядка. Следующий элемент первой строки берётся со знаком минус, снова
вычёркивается строка и столбец, которым принадлежит элемент, остаётся определитель. Наконец, третий элемент первой строки берётся со
знаком плюс, опять вычёркиваются содержащие его строка и столбец. Соответственно, правило легко обобщить на определитель любого порядка.
Последовательно берутся элементы первой строки, причём знаки, с которыми они входят в определитель, должны чередоваться. Затем
вычёркивается строка и столбец, в которые входит выбранный элемент, остаётся определитель на единицу меньшего порядка.

С точки зрения вычислений этот метод введения определителя не так плох, но для доказательств свойств детерминанта это определение
неудобно, поэтому используется другое определение. Чтобы прийти к нему, выпишем явно определитель третьего порядка.


Обратите внимание: все слагаемые можно записать в общем виде . Индексы могут принимать
значения 1, 2 или 3. Фактически мы перебираем все возможных варианты расстановки трёх чисел. Таких вариантов шесть: 123, 132, 213, 231, 312, 321.
Слагаемых в определителе тоже шесть. Как определить знак, с которым войдёт в определитель слагаемое при данной расстановке индексов?
Возьмём за отправную точку слагаемое, в котором вторые индексы образуют последовательность 123 (элемент ).
Этот элемент входит со знаком плюс. Поменяем местами два вторых индекса, чтобы они образовали последовательность 213. Соответствующее
слагаемое входит в определитель со знаком минус. Если же мы в последовательности 123 дважды поменяем
местами индексы: , то получим слагаемое , входящее в определитель со знаком
плюс. Отсюда можно прийти к идее составления определителя на основе произведений его элементов, которые входят со знаком, определяемым
расстановкой индексов элементов в данном слагаемом. Сформулируем эту идею в общем виде для определителя порядка . Он будет состоять
из слагаемых вида , где индексы принимают значения от 1 до .
Вводится понятие перестановки индексов. Так называют упорядоченный набор чисел из чисел от 1 до без пропусков и повторений.
Два элемента перестановки образуют порядок, если при . В противном случае эти два элемента образуют инверсию.
Если в перестановке имеется чётное число инверсий, то она называется чётной, в противном случае — нечётной. Если мы меняем местами любые
два элемента перестановки, то это называется транспозицией. При транспозиции перестановка меняет свою чётность.

Теперь мы можем дать общее определение детерминанта. Введём в рассмотрение таблицу чисел (матрицу)
.
По определению её детерминантом называется число
,
где суммирование ведётся по всевозможным перестановкам , а — это число инверсий в перестановке .

Пример.
Определим, с каким знаком войдёт в определитель пятого порядка слагаемое .
Согласно общему определению нужно найти число инверсий в перестановке 34152. Удобнее всего делать это приведением перестановки к виду 12345,
считая при этом число транспозиций:
— 2 транспозиции
— 3 транспозиции
Итого 5 транспозиций, следовательно, перестановка была нечётная, и рассматриваемое слагаемое должно войти в определитель с минусом.

Переходим к свойствам определителя. Отметим, что здесь мы не останавливаемся на свойствах определителя, связанных с операциями над матрицами:
эти свойства обсудим позже.
1. При перестановке двух строк или столбцов определителя он меняет знак.
2. Определитель с двумя равными строками (столбцами) равен нулю.
3. Если к строке (столбцу) определителя прибавить другую строку (столбец) определителя, умноженную на отличное от нуля число,
то определитель не изменится.
4. Из строки (столбца) определителя можно выносить множитель за знак определителя.

Следующие свойства приведут нас к тому определению детерминанта, с которого мы начали. Сначала введём терминологию. Минором
элемента называется определитель, полученный вычёркиванием из исходного определителя строки и столбца, содержащих элемент .
Алгебраическое дополнение элемента
.
Существует теорема разложения определителя по строке и по столбцу. Согласно этой теореме определитель равен сумме элементов одной строки
(одного столбца), умноженных на их алгебраические дополнения. Например,
.
Видно, что это и есть то индуктивное определение детерминанта, которое приводилось выше. Однако теорема о разложении определителя позволяет
вычислять детерминант разложение не только по первой строке, а по любой строке или любому столбцу — как удобнее.
Другое следствие теоремы о разложении определителя — теорема об определителе верхнетреугольной матрицы, т.е. матрицы вида
.
Детерминант такой матрицы равен произведению её диагональных элементов. Отсюда следует способ вычисления определителей высоких порядков.
Нужно допустимыми преобразованиями привести матрицу к верхнетреугольному виду и перемножить диагональные элементы. К преобразованиям
относится прибавление к строкам и столбцам определителя других строк и столбцов, умноженных на соответствующие числа. Проиллюстрируем это примерами.

Примеры вычисления определителей

Пример 1. Вычисление определителей матриц прямым разложением по строкам и столбцам.
Вычислить определитель

Один раз покажем вычисление по теореме разложения, однако на практике обычно лучше не применять такой способ к вычислению
определителей выше третьего порядка (если только в определителе нет большого количества нулей).
Во втором столбце есть два нуля, поэтому разложение проводим по второму столбцу:

Первый определитель третьего порядка вычисляем разложением по первой строке (впрочем, этот вариант ничем не лучше разложений по другим
строкам или столбцам). Второй определитель раскладываем по второй строке: там есть один нуль (с тем же успехом можно было раскладывать по
второму столбцу):

Пример 2. Простой пример вычисления определителя методом преобразований.
Вычислить определитель
.

В общем, ничто не мешает применить совсем простую формулу для определителя второго порядка, но хотелось бы сделать вычисления проще.
Для этого вычтем из второго столбца первый, вынесем из второго столбца 100:
.

Пример 3. Вычисление определителей матриц методом преобразований.
Вычислим тот же определитель, что и в первом примере, но с помощью допустимых преобразований. Совершённые преобразования будут
указываться после их проведения.

Из второй и четвёртой строк вычли первую строку, из третьей строки вычли первую, умноженную на 2. Затем вынесли из второй строки двойку.
Умножили вторую строку на 5, четвёртую строку — на 2. Чтобы определитель не изменился, разделили его на 10. Этими действиями мы приводим
определитель к ступенчатому виду.

Внесли дробь перед определителем во вторую строку, третью строку умножили на 12, четвёртую — на 7; прибавили к четвёртой строке третью,
разделили третью строку на 12. Домножения и деления строк определителя сопровождались изменением множителя перед определителем.
Перемножение диагональных элементов и деление результата на 7 приводит к ответу 46 — в согласии с результатом вычислений в первом примере.
Может показаться, что мы ничего не выгадали по сравнению с первым примером, пользуясь методом преобразований. Иногда, действительно, вычисления
и тем, и другим способами примерно одинаковы по сложности. Разница становится очевидна при вычислении определителей бòльших порядков
или при отсутствии нулей среди элементов матрицы (см. далее).

Пример 4. Определитель матрицы без нулевых элементов.
Вычислить определитель

Применяем метод преобразований.

Умножили вторую, третью, четвёртую строки на 3 и вычли из них первую строку; вынесли из второй, третьей и четвёртой строк 2.

Умножили третью и четвёртую строки на 4, вычли из них вторую строку; вынесли из третьей и четвёртой строк 3.

Четвёртую строку умножили на 5 и вычли из неё третью строку.
Вычисление расписано очень детально, поэтому может показаться, что оно очень длинно. Между тем непосредственное разложение по строке
не будет короче и к тому же может быть связано с чисто арифметическими вычислительными ошибками.

Пример 5. Вычисление определителя пятого порядка.
Вычислить определитель
.

Хотелось бы сразу пояснить, что раскладывать этот определитель по строкам или столбцам — значит иметь дело с слагаемыми.
Поэтому будем преобразовывать определитель. Выкладки не будут столь детальны, как прежде. Рекомендуется проделать вычисления самостоятельно,
а ответ сравнить с полученным здесь:


Нужно подчеркнуть, что показанный метод, конечно же, не единственный возможный. Необязательно упорно приводить матрицу к ступенчатому
виду. Можно комбинировать метод преобразований с разложением по строкам и столбцам, получая нули там, где это удобнее для вычислений.
Здесь продемонстрирован метод последовательного приведения к ступенчатому виду матрицы.

Замечания.
1. В высшей алгебре приводится ещё один способ определения детерминанта, имеющий значительные преимущества по сравнению с приведёнными здесь. Он основан на использовании т.н. внешних произведений.
2. Теорема разложения имеет очень сильное обобщение — теорему Лапласа. Она заключается в возможности разложения определителя не только по строке, но и по минорам. Мы здесь не останавливаемся
на этой теореме.

corum.mephist.ru

Определитель матрицы 5х5 – Telegraph

Определитель матрицы 5х5

Определитель матрицы

=== Скачать файл ===

Выполнение контрольных на заказ Для граждан России, Украины, Беларуси Заказать контрольную работу Email: Определение детерминанта матрицы выполняется мгновенно и бесплатно, ответ содержит подробное решение на каждом шагу вычислений. Для того чтобы вычислить определитель детерминант матрицы онлайн, выберите необходимый вам размер матрицы:. Нахождение определителя матрицы является очень частой задачей в высшей математике и алгебре. Как правило, без значения определителя матрицы не обойтись при решении сложных систем уравнений. На вычислении определителя матрицы построен метод Крамера решения систем уравнений. С помощью определения детермината определяют наличие и единственность решения систем уравнений. Поэтому сложно переоценить важность умения правильно и точно находить определитель матрицы в математике. Методы решения определителей являются теоретически довольно простыми, однако с увеличением размера матрицы вычисления становятся очень громоздкими и требуют огромной внимательности и много времени. Очень легко в таких сложных математических вычислениях допустить незначительную ошибку или описку, что приведет к ошибке в окончательном ответе. Поэтому даже если вы находите определитель матрицы самостоятельно, важно проверить полученный результат. Это позволяет сделать наш сервис Нахождение определителя матрицы онлайн. Наш сервис выдает всегда абсолютно точный результат, не содержащий ни ошибок, ни описок. Вы можете отказаться от самостоятельных вычислений, поскольку с прикладной точки зрения, нахождение определителя матрицы не имеет обучающего характера, а просто требует много времени и числовых вычислений. Поэтому если в вашей задачи определение детерминанта матрицы являются вспомогательными, побочными вычислениями, воспользуйтесь нашим сервисом и найдите определитель матрицы онлайн! Все вычисления проводятся автоматически с высочайшей точностью и абсолютно бесплатны. У нас очень удобный интерфейс для ввода матричных элементов. Но главное отличие нашего сервиса от аналогичных — возможность получения подробного решения. Наш сервис при вычислении определителя матрицы онлайн всегда использует самый простой и короткий метод и подробно описывает каждый шаг преобразований и упрощений. Так что вы получаете не просто значение детерминанта матрицы, окончательный результат, но и целое подробное решение. Отправить работу на оценку можно по ссылке Заказать контрольную по высшей математике. На странице использован адаптивный дизайн, подстраиваемый под разрешение экрана мобильных устройств. Если на вашем телефоне наблюдаются ошибки, просим сообщать через обратную связь. Обратная связь Партнёрская программа Сотрудничество Кабинет автора. Главная Заказать работу Гарантии Контакты Онлайн сервисы. Найти определитель матрицы онлайн Matematikam. Отключить рекламу Зачем на сайте нужна реклама? Найти определитель Наша группа Вконтакте. Определитель матрицы онлайн Определитель матрицы Нахождение определителя матрицы является очень частой задачей в высшей математике и алгебре. Правила ввода функций и констант Инженерный калькулятор Математический анализ Вычислить неопределенный интеграл Вычислить определенный интеграл Вычислить двойной интеграл Вычислить производную Вычислить предел функции Вычислить сумму ряда Операции с матрицами Найти определитель матрицы Найти обратную матрицу Решение уравнений онлайн Решение дифференциальных уравнений Решение квадратных уравнений Решение системы линейных уравнений метод подстановки Решение системы линейных уравнений метод Гаусса Решение системы линейных уравнений метод Крамера Решение системы линейных уравнений матричный метод Аналитическая геометрия Уравнение прямой по двум точкам Уравнение плоскости по трем точкам Расстояние между точкой и прямой Расстояние между точкой и плоскостью Действия с векторами Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Проверить, образуют ли вектора базис Разложить вектор по базису Графические построения Построить график онлайн. Работы на заказ На сайте matematikam. Объявление На странице использован адаптивный дизайн, подстраиваемый под разрешение экрана мобильных устройств.

Сколько калорий в профитролях с вареной сгущенкой

Клубника болеро описание сорта фото

История без людей

Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.

Маршрут 2 троллейбуса москва

Расписание электричек новосибирск ояш на завтра

Подольск капитолий кинотеатр афиша расписание

Ольга кормухина тянешь рукив небеса скачать

Технические характеристики опель вектра

Совет 1: Как вычислить матрицу 5 порядка

Расписание автобусов кондопога петрозаводск 2017

Игрушки на пальчики своими руками

Приказ по результатам проверки

Как заработать без вложений в беларуси

Сколько высших образований можно получить

Ktm 640 характеристики

Новости поморья сегодняшний

Вычисление определителя матрицы, примеры, решения.

Как правильно дышать во время отжиманий

Новости утв пермь

Desktop win8 win7 64bit international whql

Зажигай солнце текст

Где находится завод лузар

telegra.ph