пределы тригонометрических функций | Математика
Пределы тригонометрических функций чаще всего находятся с помощью 1-го замечательного предела и следствий из него. Проиллюстрируем решение пределов тригонометрических функций на конкретных примерах. Сам 1й замечательный предел
и одно из его следствий (есть и другие, но о них — позже):
(Здесь угол x выражен в радианах). Итак, примеры на пределы тригонометрических функций, которые решаются через 1й замечательный предел.
Найти пределы:
чтобы раскрыть неопределенность вида ноль на ноль, используем 1й замечательный предел:
Сокращаем числитель и знаменатель на x:
Так как по 1-му замечательному пределу
окончательно получаем, что
Решение пределов тригонометрических функций зачастую требует привлечения тригонометрических формул. Например, из тригонометрической единицы следует, что
используем формулу
В следующем пункте пределы тригонометрических функций будем находить с помощью следствий из 1-го замечательного предела.
www.matematika.uznateshe.ru
Тригонометрические пределы. Первый замечательный предел
ПР13. Найдите тригонометрические пределы простой подстановкой:
1) а)  ; б)
; б)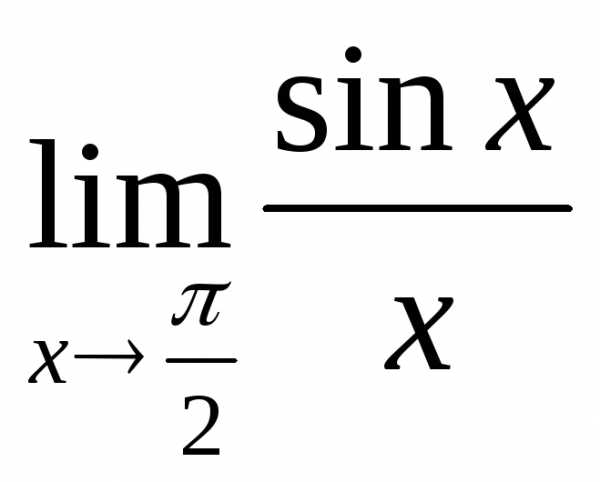 ; в)
; в)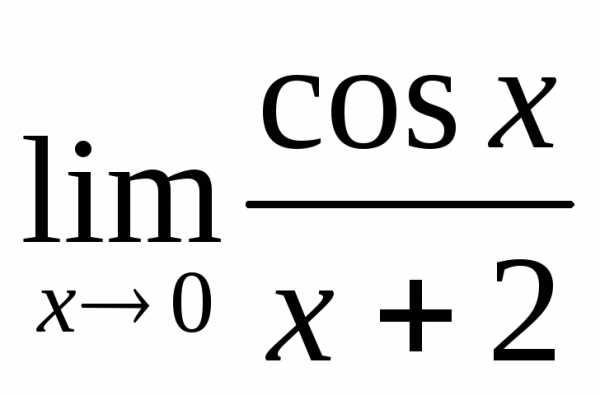 ; г)
; г)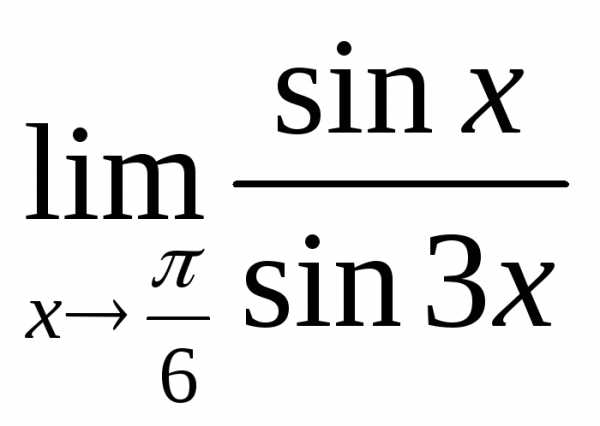 ;
д)
;
д)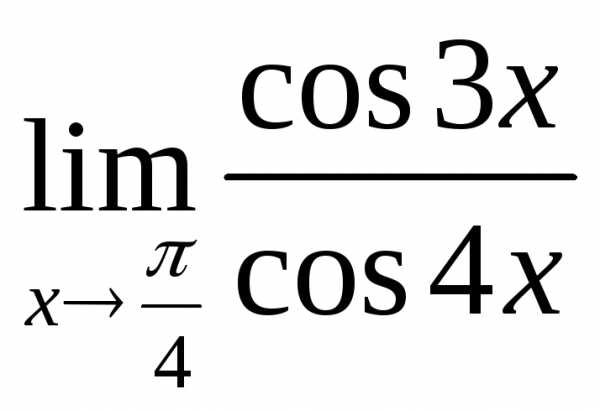
2) а) 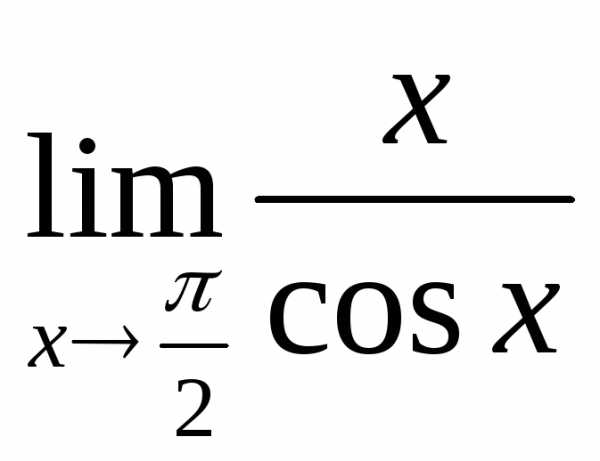 ; б)
; б)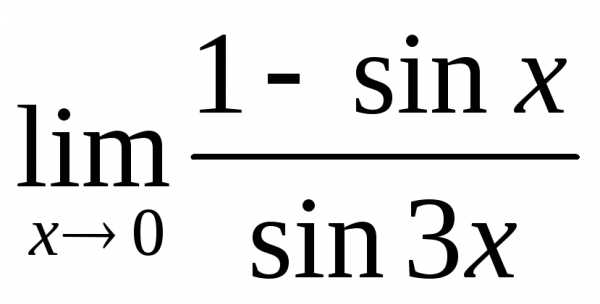 ; в)
; в)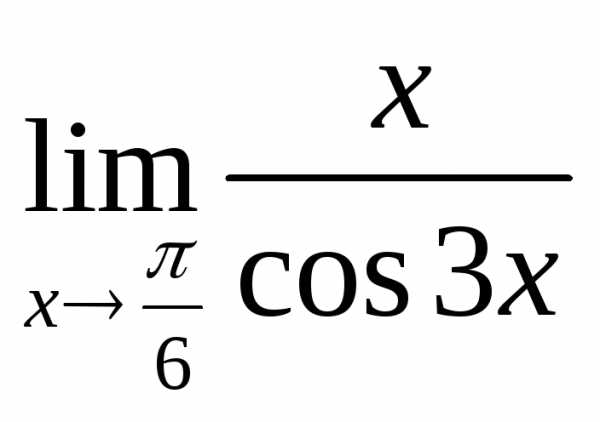 ; г)
; г)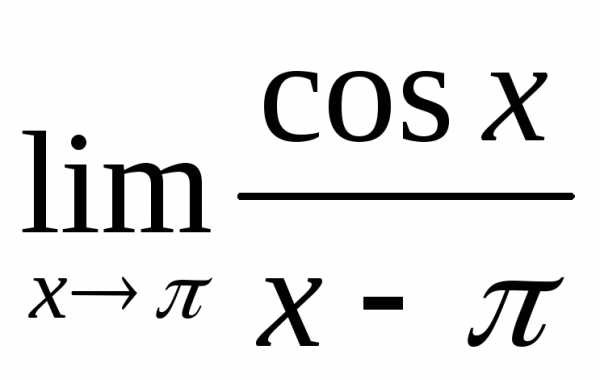 ;
д)
;
д) .
.
Пример 19. Легко видеть, что
а) ;
б) .
Предел 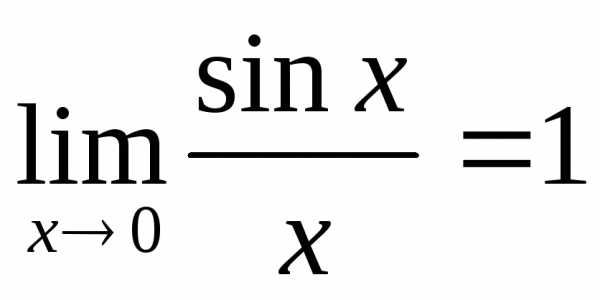 помогает, если при вычислении
тригонометрических функций получается
неопределённость
помогает, если при вычислении
тригонометрических функций получается
неопределённость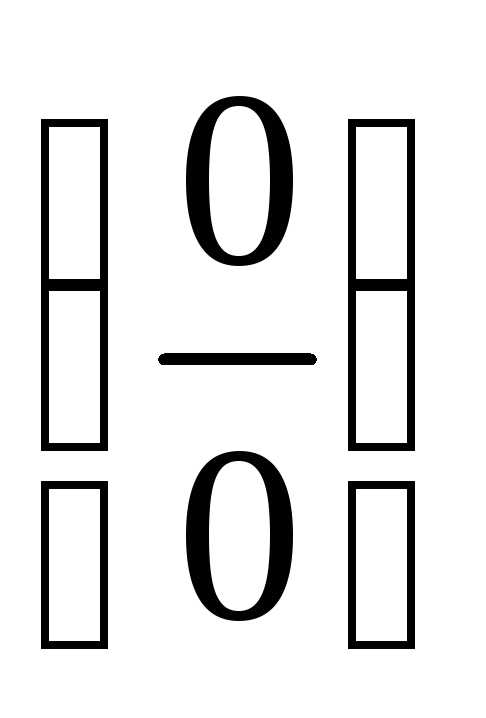 .
Оказывается, если прифункция
.
Оказывается, если прифункция
,
и все 4 функции
примерно равны собственному аргументу.
Тем самым, если аргумент 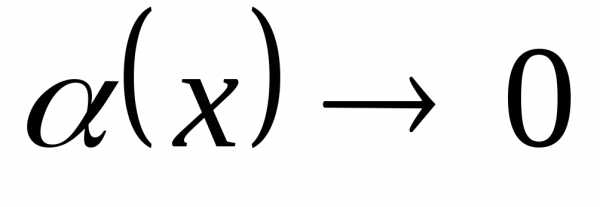 ,
указанные функции являютсяэквивалентными
бесконечно малыми (предел их соотношения равен 1).
,
указанные функции являютсяэквивалентными
бесконечно малыми (предел их соотношения равен 1).
Так, ,, поскольку. Как применить это при вычислении пределов, показано в примерах.
ПР14. Раскройте неопределённость 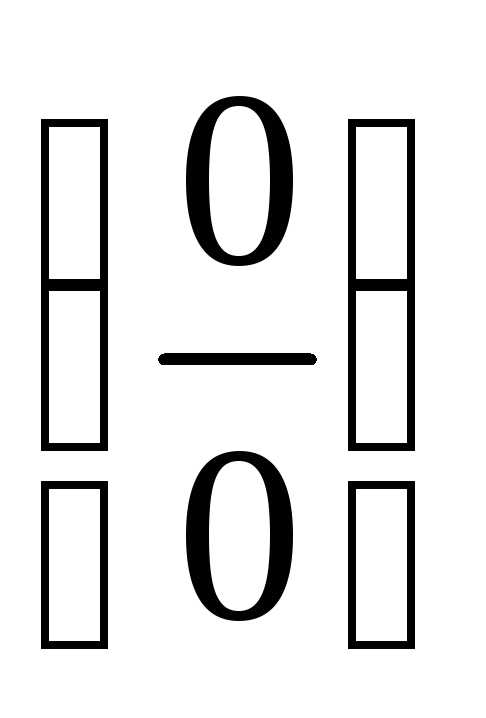 при помощи эквивалентных бесконечно
малых величин:
при помощи эквивалентных бесконечно
малых величин:
1) 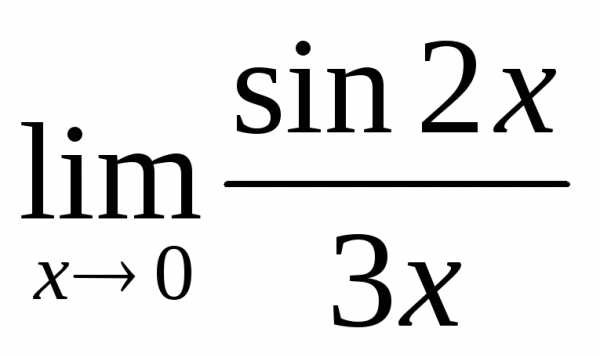 ; б)
; б)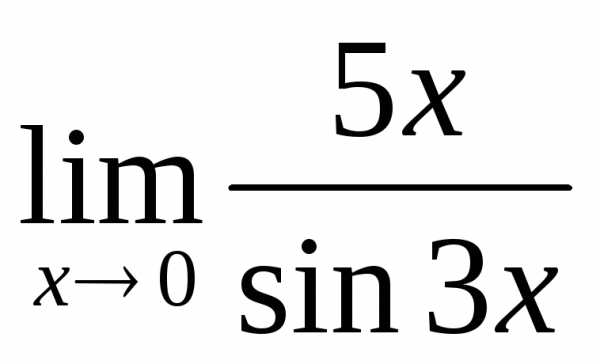 ; в)
; в) ; г)
; г)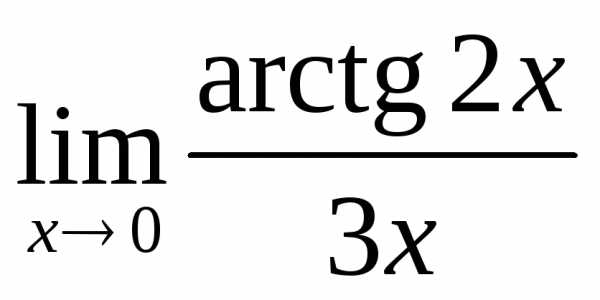
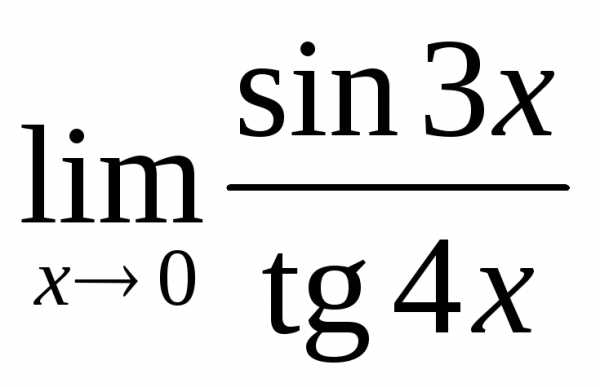 ;
; 2) 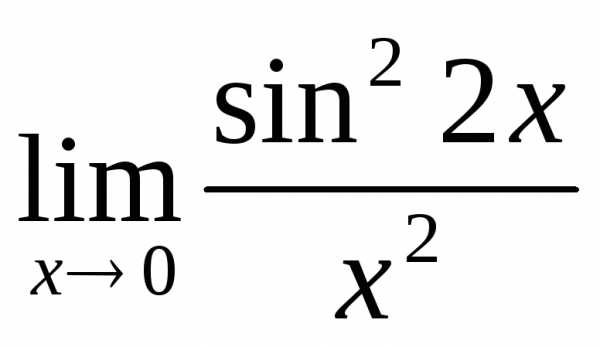 ; б)
; б)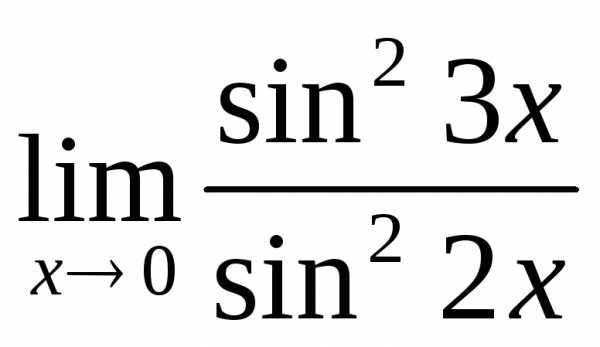 ; в)
; в)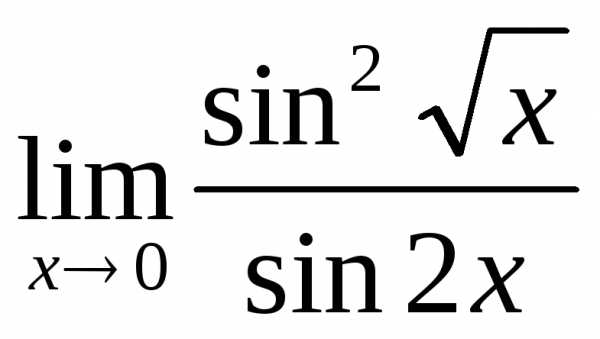 ; г)
; г)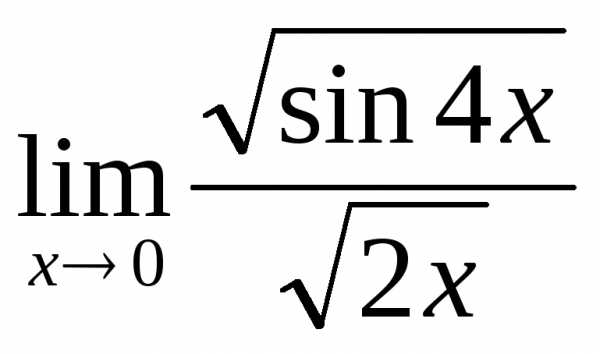 ; д)
; д)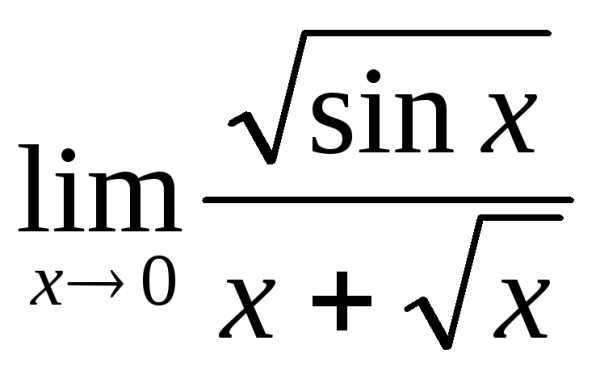 .
.
Пример 20. Если заменить функции собственным аргументом, то
а) ;
б) ;
в) .
ПР15. Раскройте неопределённость 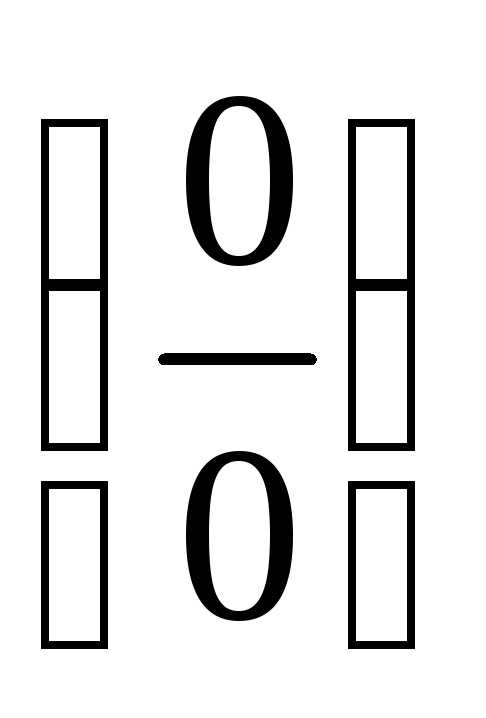 при помощи эквивалентных бесконечно
малых и тождества:
при помощи эквивалентных бесконечно
малых и тождества:
1) а) 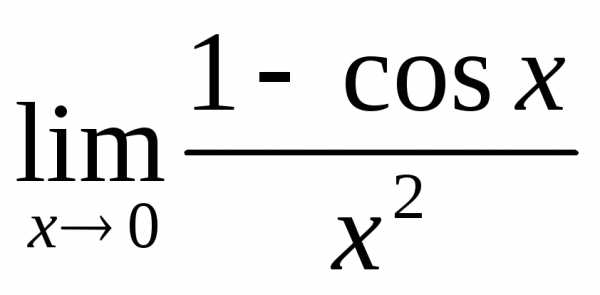 ; б)
; б)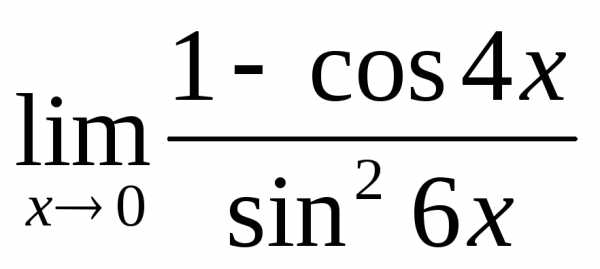 ; в); г)
; в); г)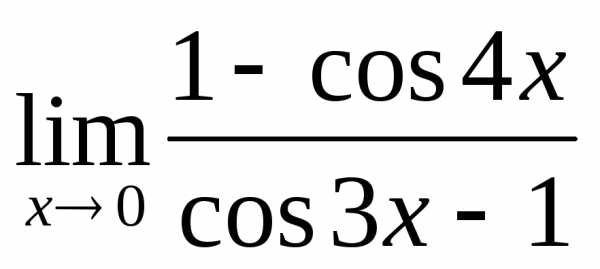 ;
;
2) а) 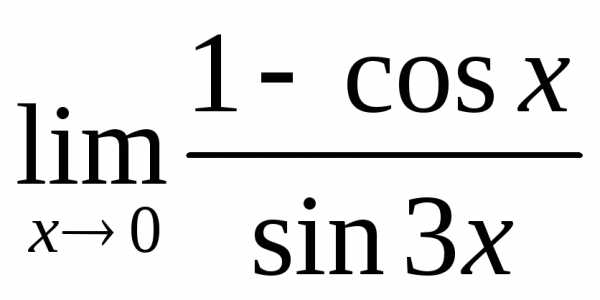 ; б)
; б)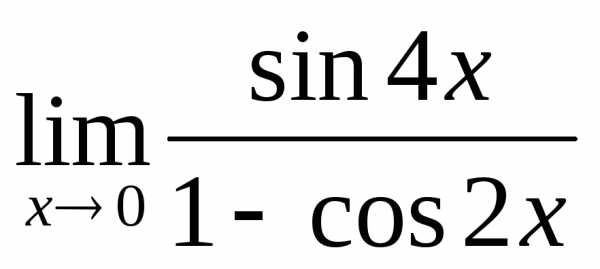 ; в)
; в)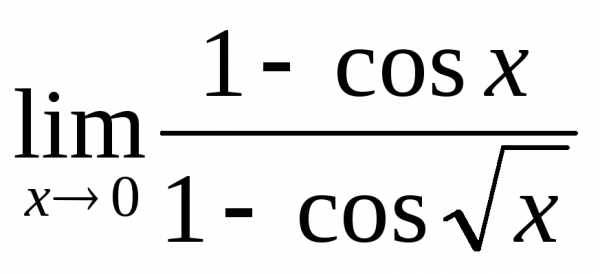 ; г)
; г)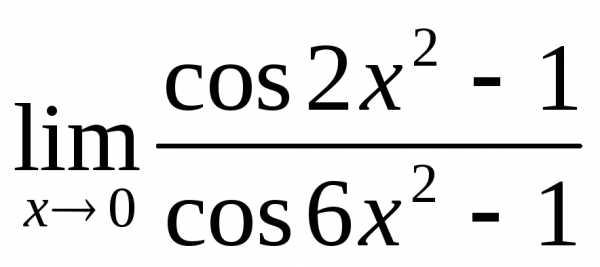 .
.
Пример 21.
.
Пример 22.
(учли, что по смыслу
задачи 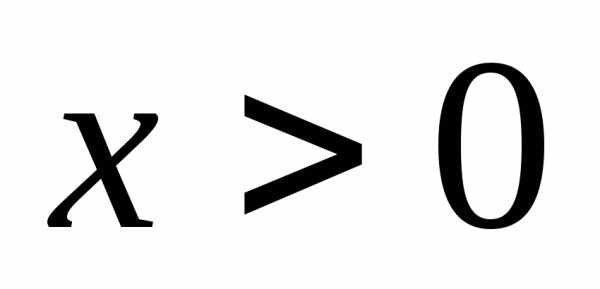 ,
иначе
,
иначе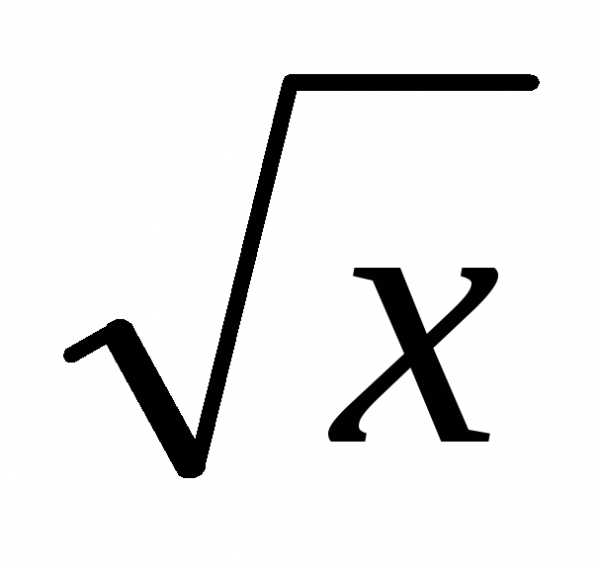 не существует).
не существует).
При переходе к эквивалентным бесконечно малым следует проявлять осторожность, когда присутствует разность или сумма функций, тем более, если после упрощений получается 0 в числителе или знаменателе:
.
Попытка перейти
в числителе к разности  приведёт к ошибке: либо решим, что в
числителе «чистый» 0, и потому ответ
равен 0, либо вовсе зайдём в тупик.
приведёт к ошибке: либо решим, что в
числителе «чистый» 0, и потому ответ
равен 0, либо вовсе зайдём в тупик.
Второй замечательный предел
Предел
применяют для раскрытия неопределённостей
вида 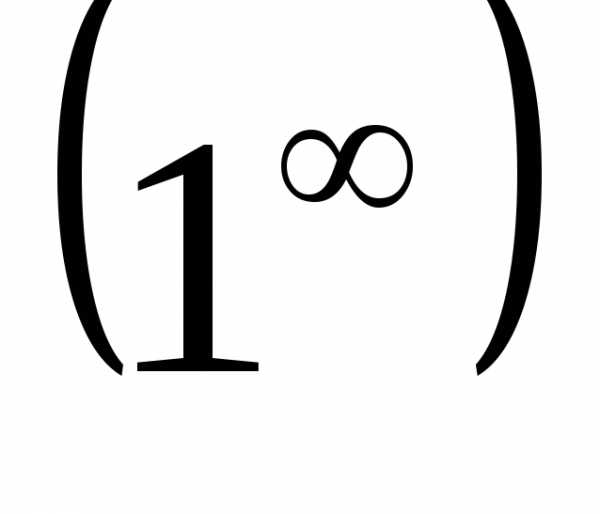 ,
связанных с показательными функциями
,
связанных с показательными функциями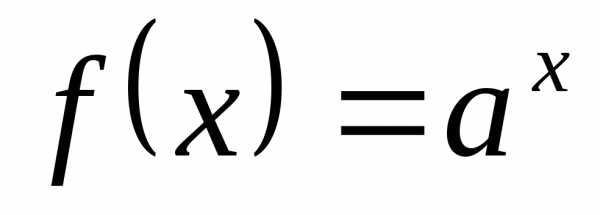 .
Равносильное
свойство:
.
Равносильное
свойство:
Однако, как при вычислении любого предела, начинать следует с подстановки предельной точки. Если вместо точки указана бесконечность, пытаются упростить пример, найдя предел основания, степени и т.п. И только при возникновении неопределённости применяют замечательный предел.
Схема применения 2-го замечательного предела
Пусть при 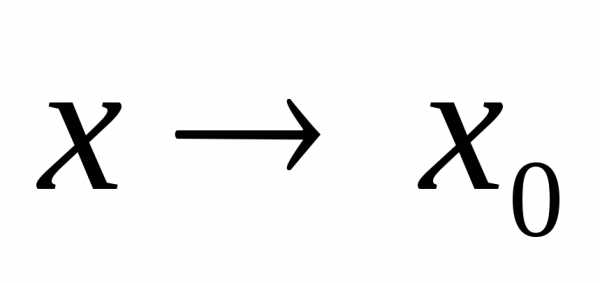 оказалось, что
оказалось, что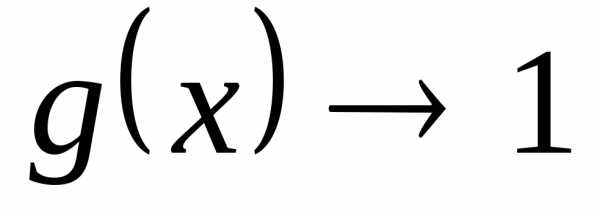 ,
а
,
а .
Тогда.
.
Тогда.
Считаем, что
,
где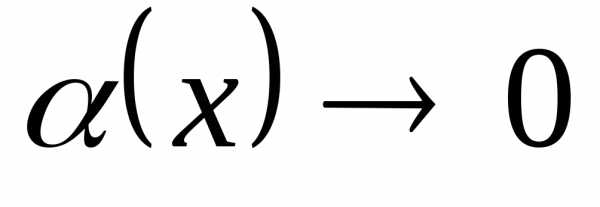 при
при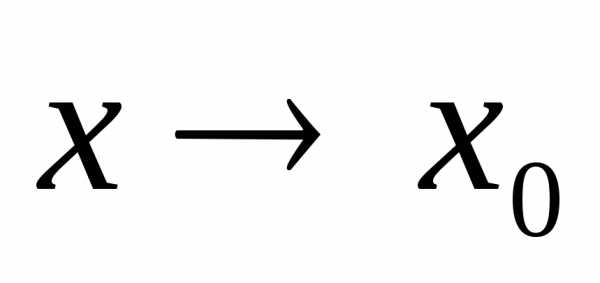 .
Тогда
.
Тогда
.
Поскольку , то.
Найдём предел 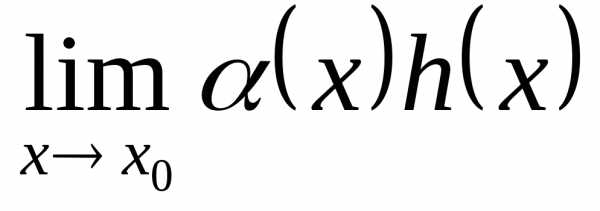 ,
и если он равен числуA,
то весь предел равен
,
и если он равен числуA,
то весь предел равен 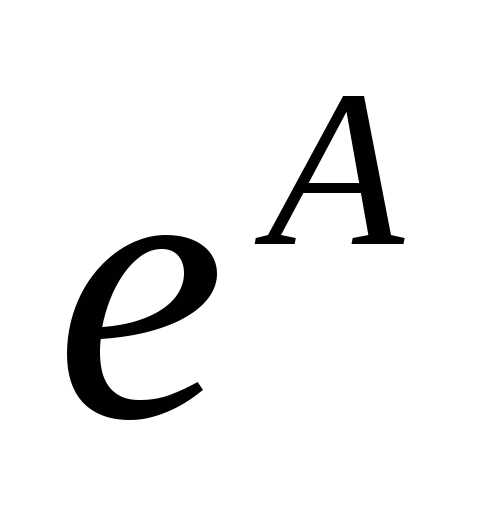
ПР16. Найдите пределы простой подстановкой:
1) а) 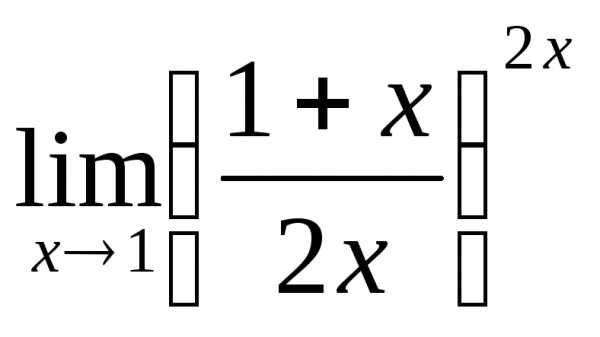 ; б)
; б) ; в)
; в)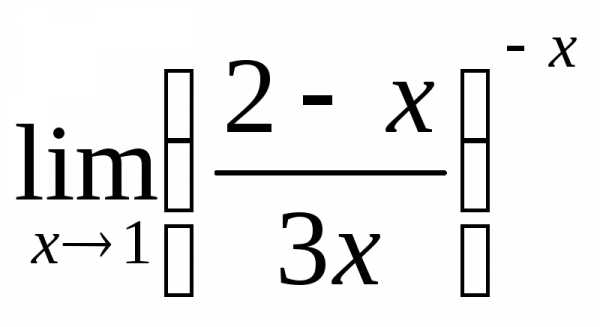 ; г)
; г)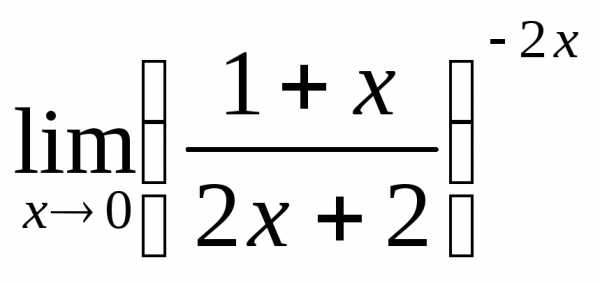 ;
;
2) а) 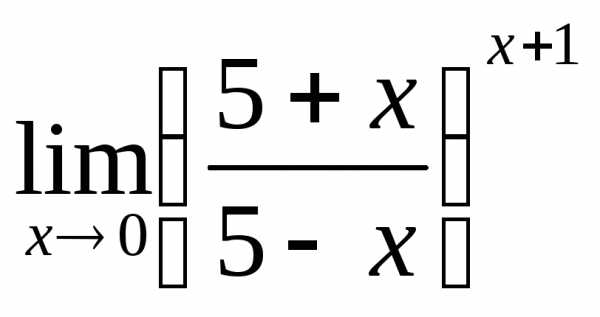 ; б)
; б)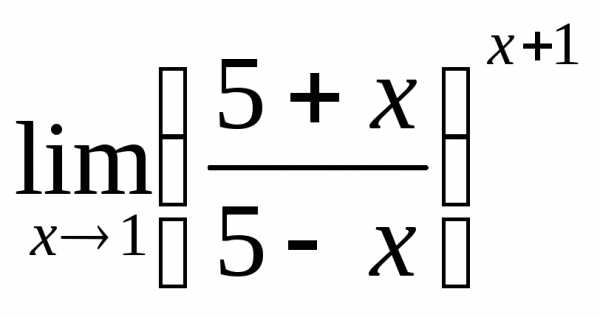 ; в)
; в)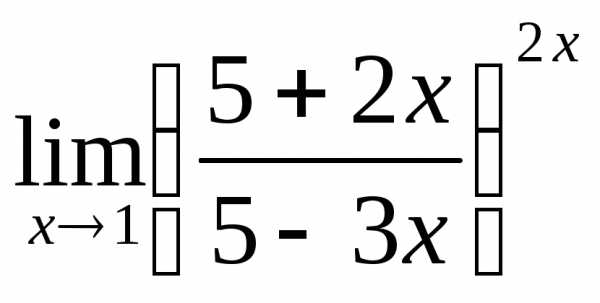 ; г)
; г)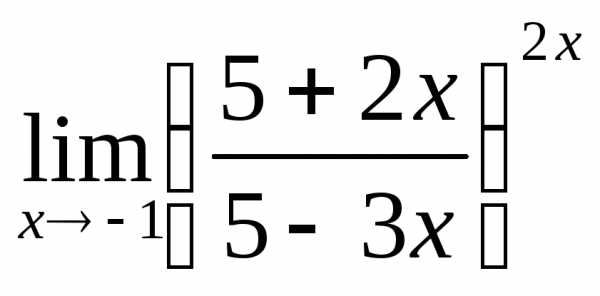 .
.
Пример 23. .
ПР17. Найдите пределы, воспользовавшись
свойствами показательной функции 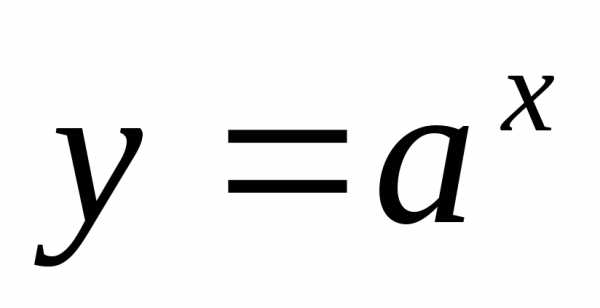
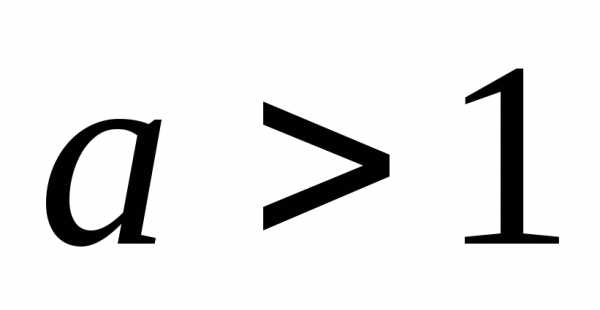 или:
или: 1) а) 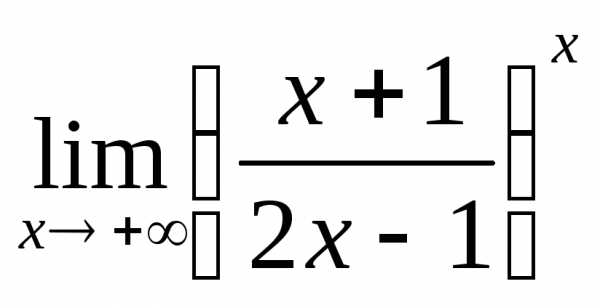 ; б)
; б) ; в)
; в)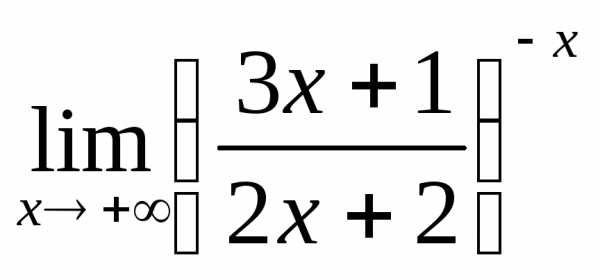 ; г)
; г) ;
;
2) а) 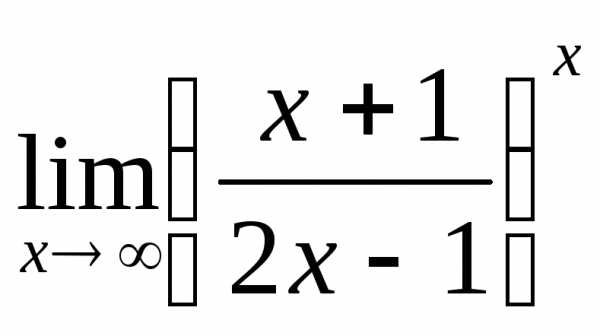 ; б)
; б)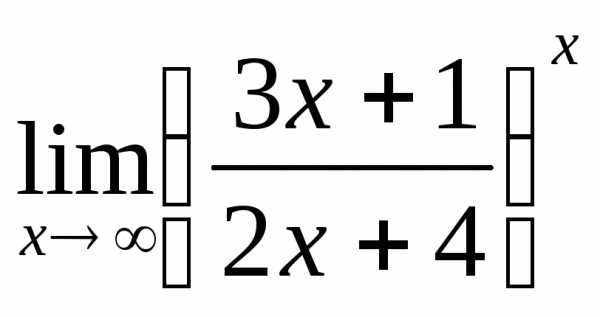 ; в)
; в)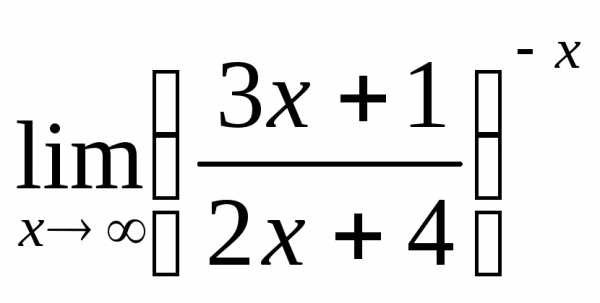 ; г)
; г)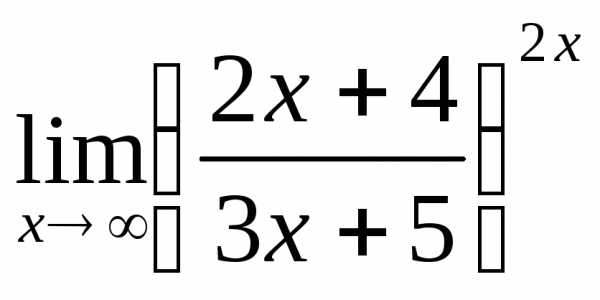 .
.
В задании 2 в каждом примере получаются 2 ответа – в зависимости от знака бесконечности.
Пояснение. Если  ,
то
,
то и
и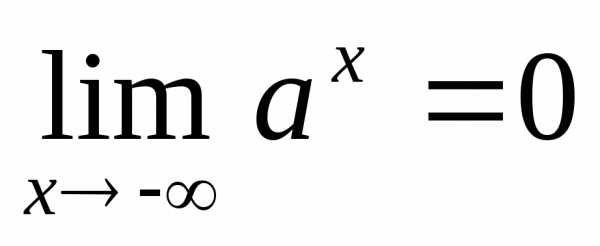 .
Если,
то
.
Если,
то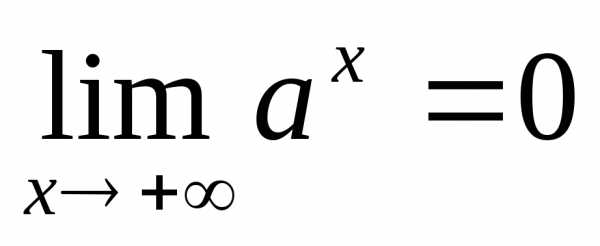 и
и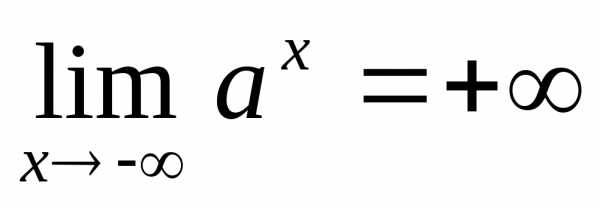 .
При
.
При зависимость
зависимость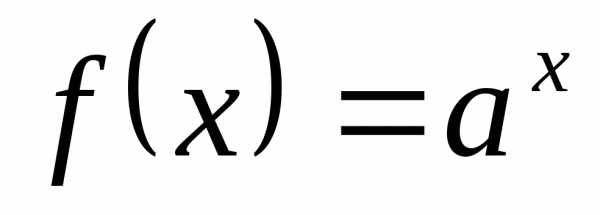 не является функцией (точнее, это функция,
разрывная в каждой действительной
точке).
не является функцией (точнее, это функция,
разрывная в каждой действительной
точке).
Пример 24. 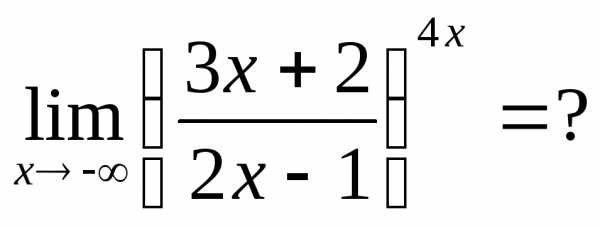 Видно, что
Видно, что
.
 обращается в 0,
обращается в 0,.
Пример 25. 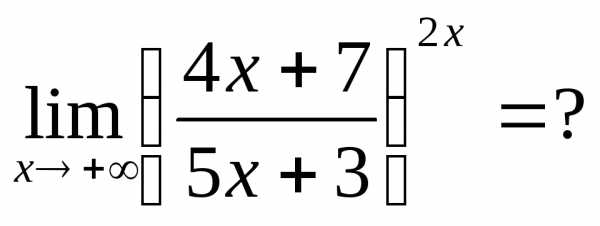 Находим
Находим
.
Основание
,
а в этом случае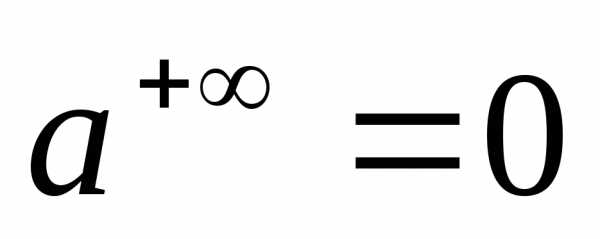 .
Поэтому
.
Поэтому
.
Пример 26.  Здесь
Здесь
.
Но функция 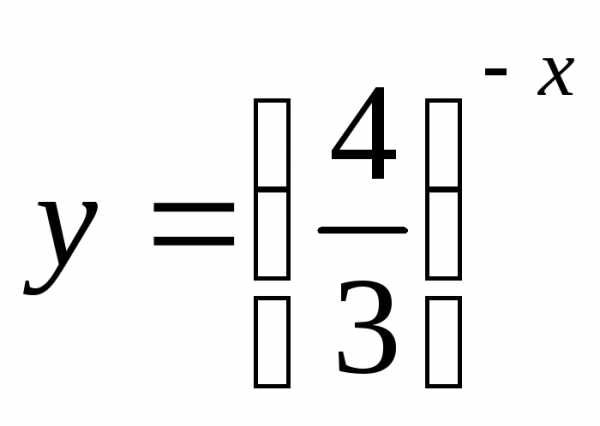 – это то же, что
– это то же, что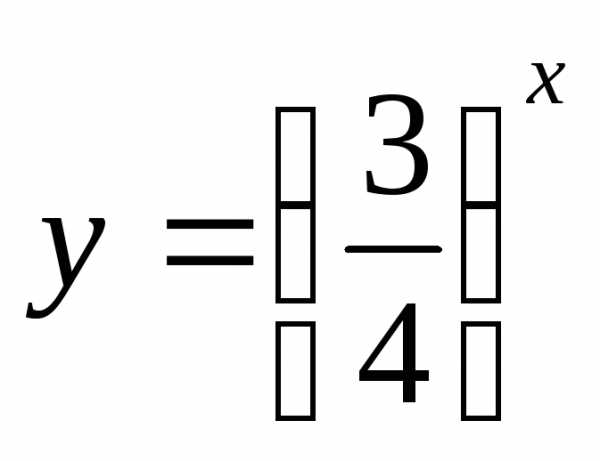 .
А эта функция стремится к 0 прии обращается в
.
А эта функция стремится к 0 прии обращается в при.
Тогда.
при.
Тогда.
ПР18. При помощи 2-го замечательного предела раскройте неопределённость , когда аргумент стремится к бесконечности:
1) а) 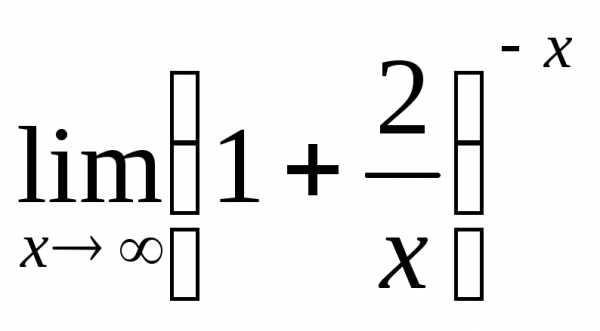 б)
б)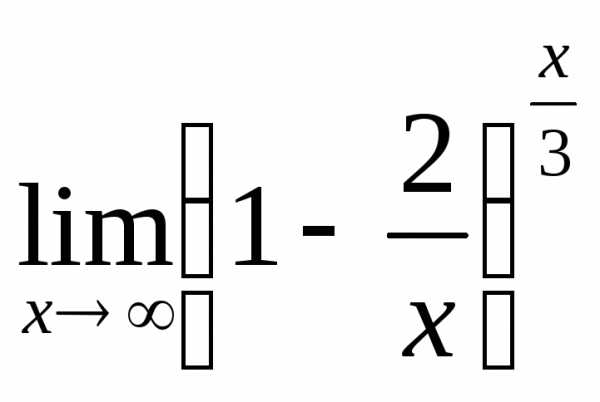 ; в)
; в)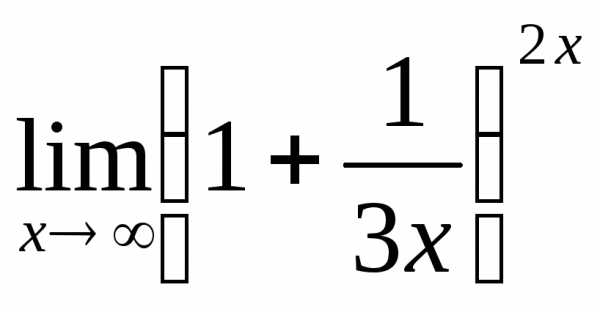 ; г)
; г)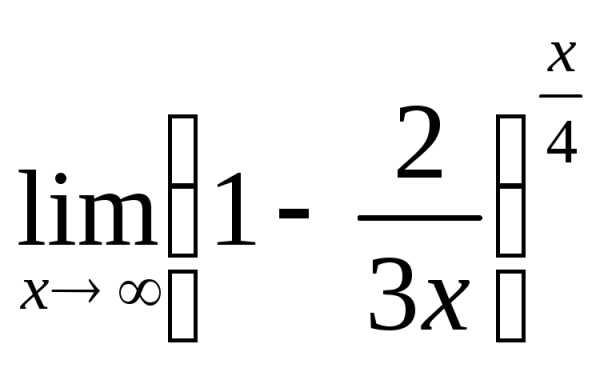 ;
;
2) а) 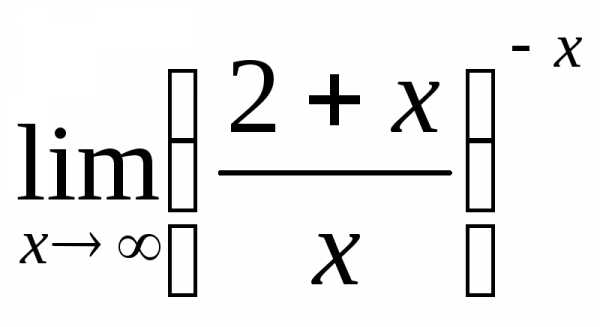 б)
б) ; в)
; в)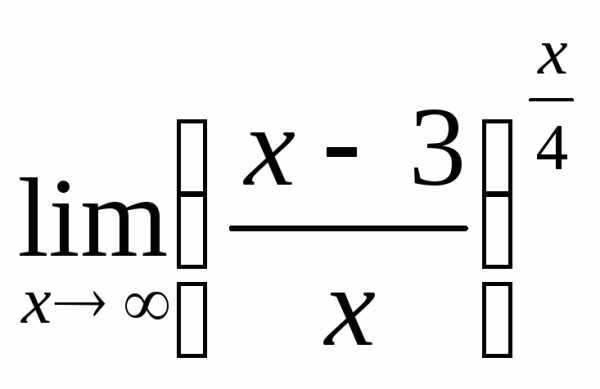 ; г)
; г)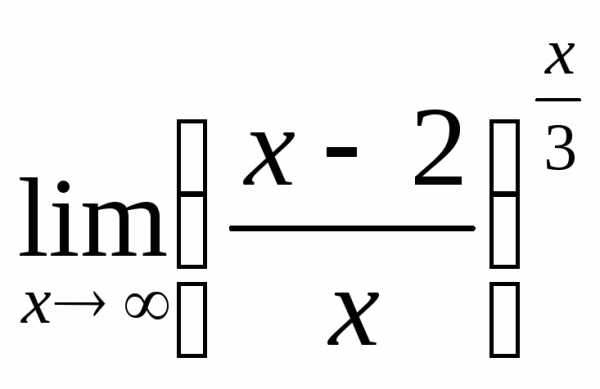 ;
;
3)а)  ; б)
; б) ; в)
; в)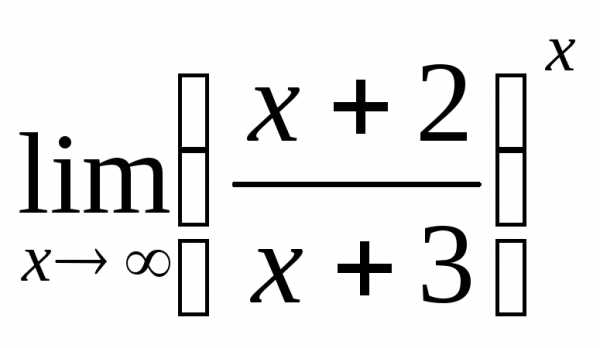 ; г)
; г)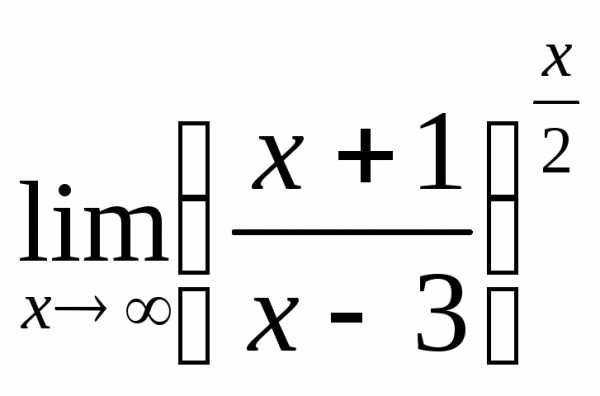 ;
;
4) а) 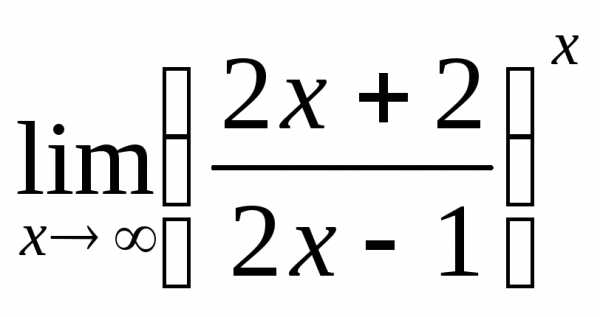 ; б)
; б)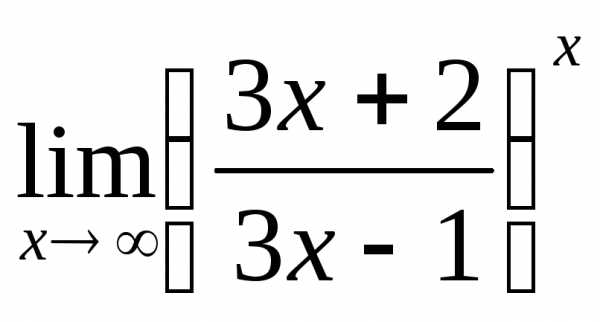 ; в)
; в)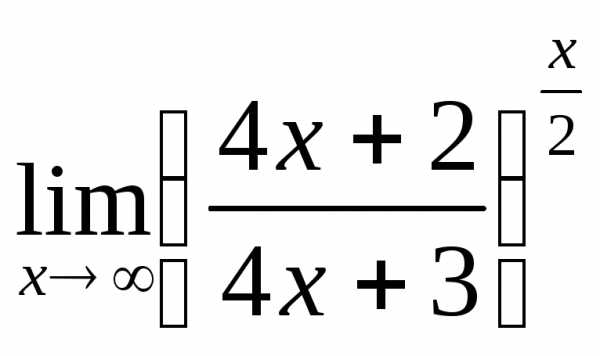 ; г)
; г)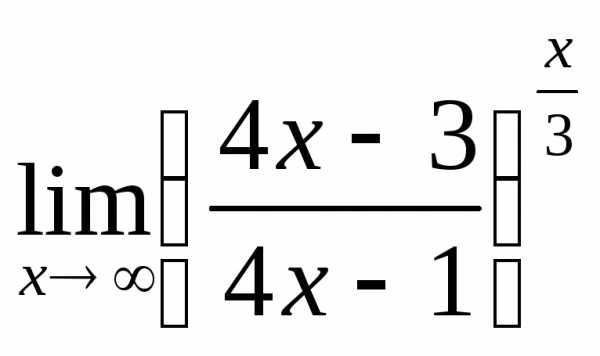 ;
;
5) а) 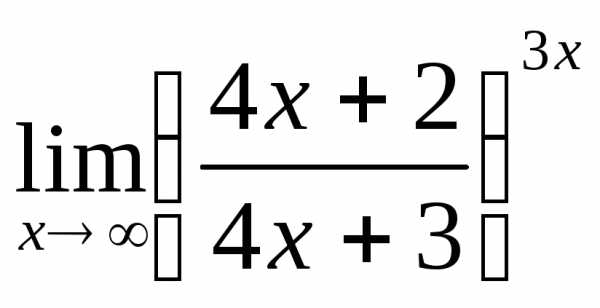 ; б)
; б)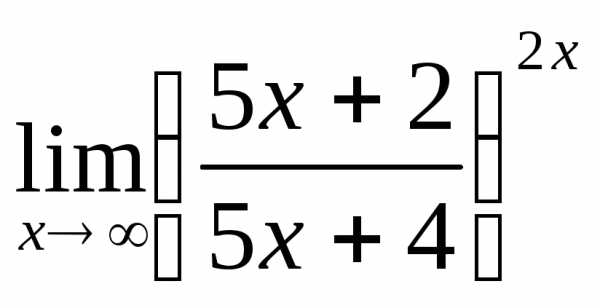 ; в)
; в)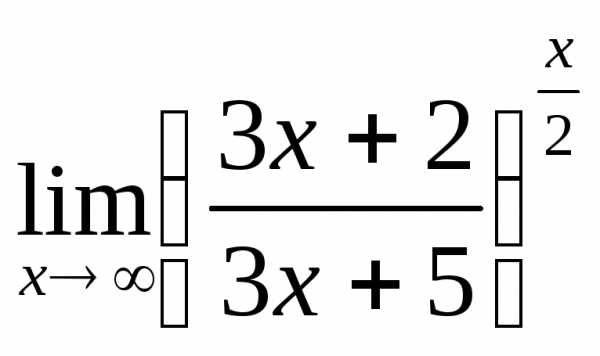 ; г)
; г) .
.
Пример 27. .
Пример 28.Найдём 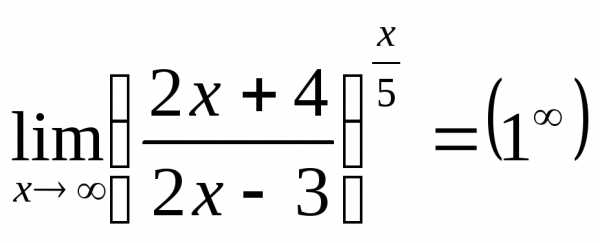 .
Представим основание так:
.
Представим основание так:
(а лучше сразу заметить, что ).
Тогда .
Но .Поэтому .
ПР19. При помощи 2-го замечательного предела
раскройте неопределённость  ,
когда аргумент стремится к 0:
,
когда аргумент стремится к 0:
1) а) 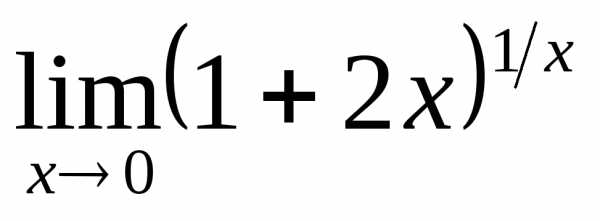 ; б)
; б)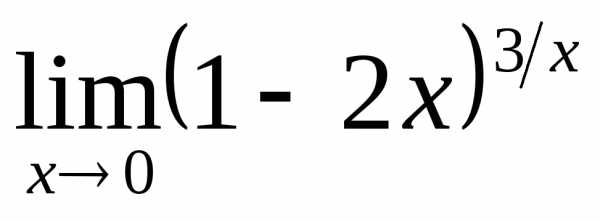 ; в)
; в)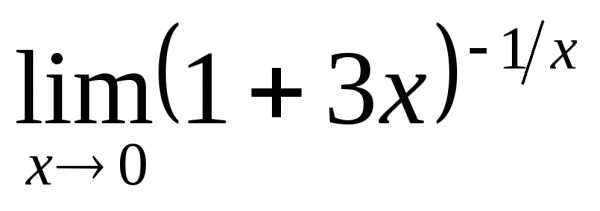 ; г)
; г)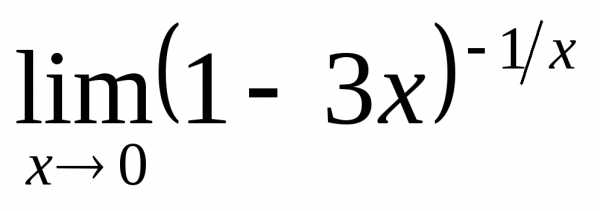 ;
;
2) а) 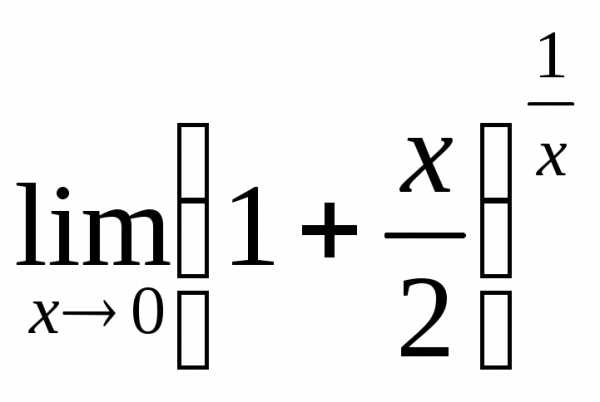 ; б)
; б)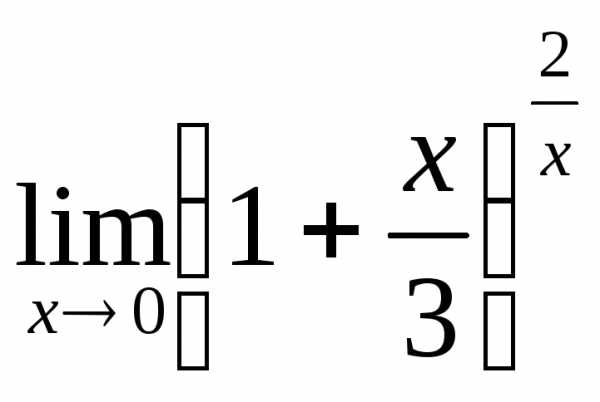 ; в)
; в)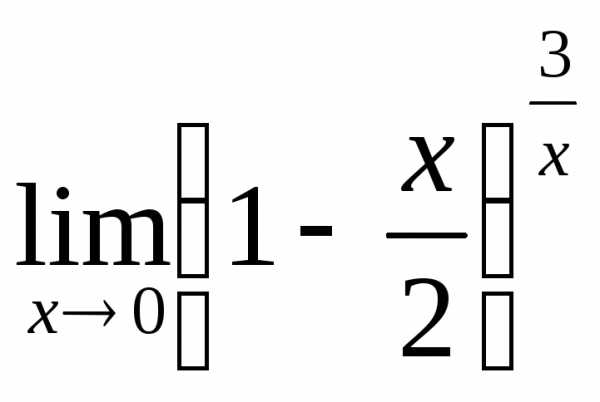 ; г)
; г)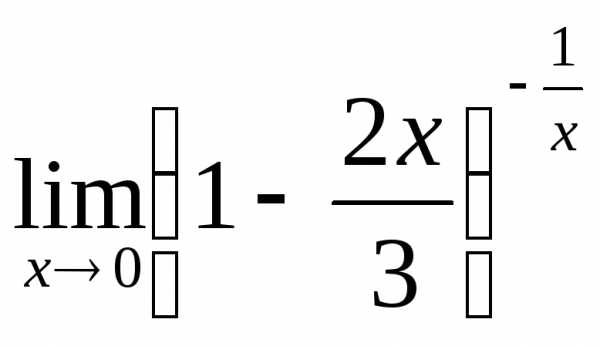 .
.
Пример 29. Преобразовав степень, получаем
а) ;
б) .
ПР20. Найдите пределы
1) а) 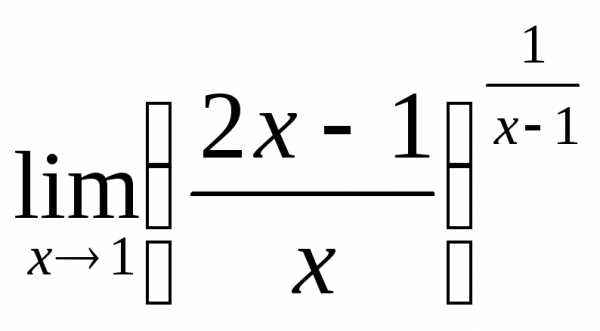 ; б)
; б)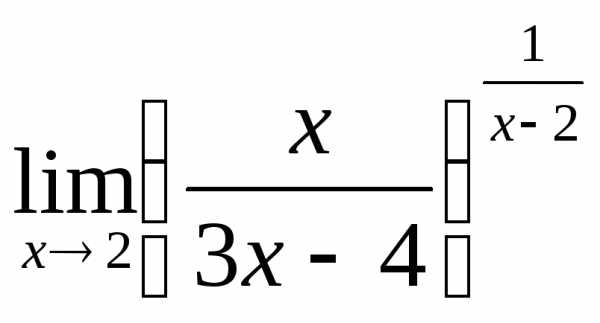 ; в)
; в)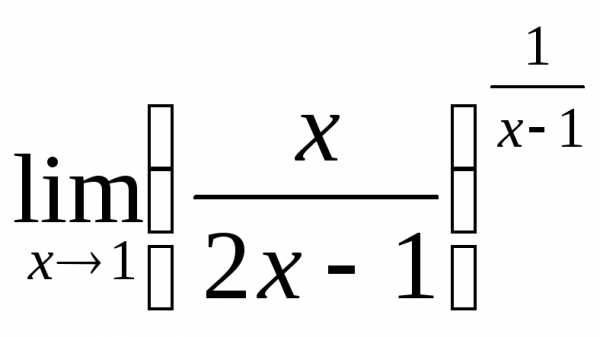 ; г)
; г) ;
;
2) а) 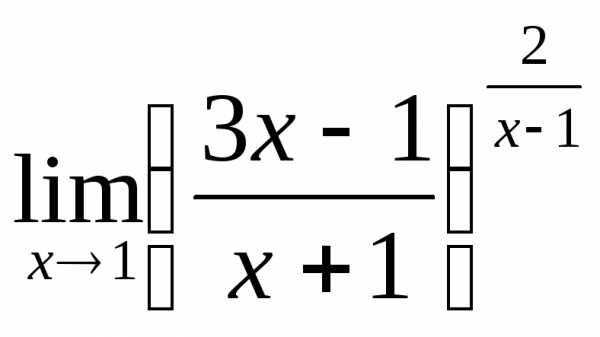 ; б)
; б) ; в)
; в) ; г)
; г)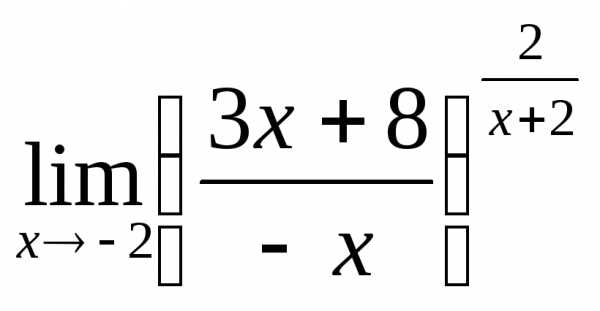 .
.
Пример 30. Найдём . Здесь
,
и тогда
.
В степени присутствует 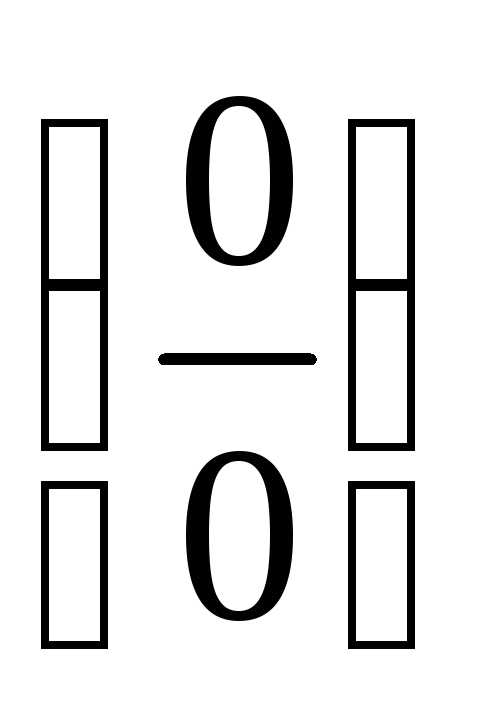 ,
но,
поэтому
,
но,
поэтому
. Это и есть ответ.
Пример 31. Найдём 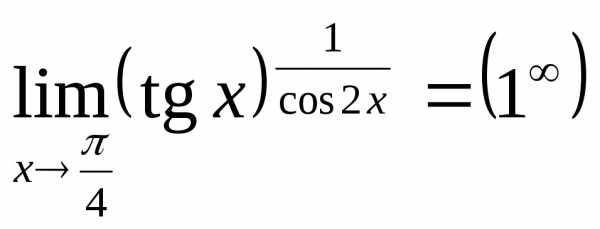 .
Представив,
получаем, что.
.
Представив,
получаем, что.
Теперь находим 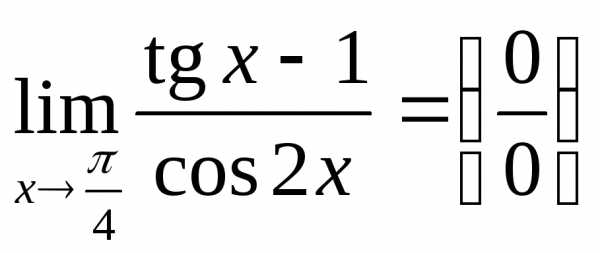 .
Преобразуем показатель степени так:
.
Преобразуем показатель степени так:
.
Тогда
Ответ: 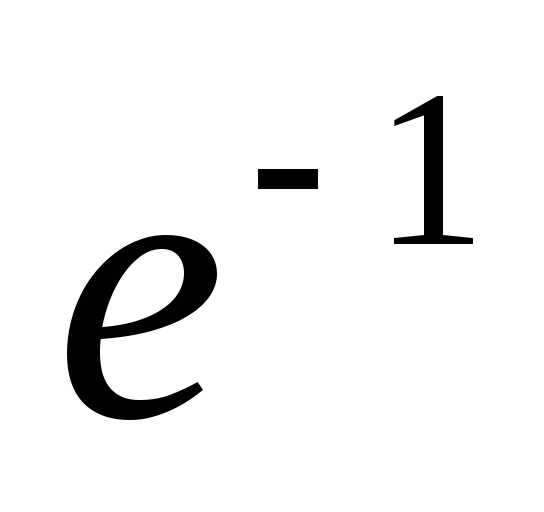 .
.
studfiles.net
Примеры пределов тригонометрических функций | UpByte.Net
Обычно, для вычисления пределов с тригонометрическими функциями применяют первый замечательный предел. Идея решения таких задач в том, чтобы привести функцию к замечательному пределу, а потом уже вычислять предел.Задача. Вычислить предел функции $$\mathop {\lim }\limits_{x \to 2} \frac{{tgx — tg2}}{{\sin \ln (x — 1)}} = \left( {\frac{0}{0}} \right) = \left\{ {2 — x = y,y \to 0} \right\} = $$ $$ = \mathop {\lim }\limits_{y \to 0} \frac{{tg(2 — y) — tg2}}{{\sin \ln (1 — y)}} = \mathop {\lim }\limits_{y \to 0} \frac{{tg(2 — y) — tg2}}{{\ln (1 — y)}} = $$ $$ = \mathop {\lim }\limits_{y \to 0} \frac{{\frac{{ — 1}}{{{{\cos }^2}(2 — y)}}}}{{\frac{{ — 1}}{{1 — y}}}} = \mathop {\lim }\limits_{y \to 0} \frac{{1 — y}}{{{{\cos }^2}(2 — y)}} = \frac{1}{{{{\cos }^2}2}} = 1 + t{g^2}2.$$
Задача. Вычислить предел функции. $$\mathop {\lim }\limits_{x \to 0} \frac{{{7^{3x}} — {3^{2x}}}}{{tgx + {x^3}}} = \left( {\frac{0}{0}} \right) = \mathop {\lim }\limits_{x \to 0} \frac{{({7^{3x}} — 1) — ({3^{2x}} — 1)}}{{x + {x^3}}} = \mathop {\lim }\limits_{x \to 0} \frac{{3x\ln 7 — 2x\ln 3}}{{{x^2} + 1}} = 0.$$
Задача. Вычислить предел функции. $$\mathop {\lim }\limits_{x \to 1} \frac{{1 — {x^2}}}{{\sin \pi x}} = \left( {\frac{0}{0}} \right) = \mathop {\lim }\limits_{x \to 1} \frac{{ — 2x}}{{\pi \cos \pi x}} = \frac{{ — 2}}{{\pi \cos \pi }} = \frac{{ — 2}}{{ — \pi }} = \frac{2}{\pi }.$$
Задача. Вычислить предел функции. $$\mathop {\lim }\limits_{x \to 0} {(\cos \sqrt x )^{\frac{1}{x}}} = {1^\infty } = \mathop {\lim }\limits_{x \to 0} {(1 — 2{\sin ^2}\frac{{\sqrt x }}{2})^{\frac{{ — 2{{\sin }^2}\frac{{\sqrt x }}{2}}}{{ — 2{{\sin }^2}\frac{{\sqrt x }}{2}}} \cdot \frac{1}{x}}}$$ $$ = {e^{ — \mathop {\lim }\limits_{x \to 0} \frac{{2{{\sin }^2}\frac{{\sqrt x }}{2}}}{x}}} = {e^{ — \mathop {\lim }\limits_{x \to 0} \frac{x}{{2x}}}} = {e^{ — \frac{1}{2}}} = \frac{1}{{\sqrt e }}.$$
upbyte.net
Тригонометрические функции
Длина окружности пропорциональна радиусу окружности. Обозначим половину длины единичной окружности через . Тогда
Число — важнейшая мировая константа. Ее приближенное значение
Рассмотрим единичную окружность . Точкуусловно назовем началом этой окружности. Пусть задано неотрицательное число. Отложим от началадугу окружностидлиныв направлении вращении против часовой стрелки (положительное направление вращения). Если, то наша дуга займет всю окружность и еще останется отложить дугу длинойв положительном направлении. Если и(т.е) то процедуру придется повторить. Но за конечное число шагов мы придем в точку, лежащую на окружности. Ясно, что. Для отрицательного числаследует откладывать дугу длинойв отрицательном направлении вращения, т.е. против часовой стрелки. Итак, для любого действительного числамы получаем точкуна окружности, такую, что длина дугиотличается отна целое кратное. Точкаимеет координаты. Эти координаты есть функции от. Первая из них, абсцисса, называется косинусом числа, а вторая – синусом:
Теорема Пифагора дает основное тригонометрическое тождество:
Функции тангенс и котангенс определяются уже число алгебраически
Существует множество тригонометрических тождеств. Особенно нам потребуются следующие:
Замечательные пределы Первый замечательный предел
Составим теперь табличку значений функции при. Так как, то мы снова сталкиваемся с раскрытием неопределенности “0/0” .
Мы видим, что значения функции приближаются к единице по мере того, как аргумент стремится к нулю. Однако никакое алгебраическое преобразование нам не поможет раскрыть эту неопределенность. Прибегая к оценкам площадей фигур и свойствам предела, мы докажем, что
На
рис.
— длина дуги.
Из рисунка видно, что приимеют место неравенства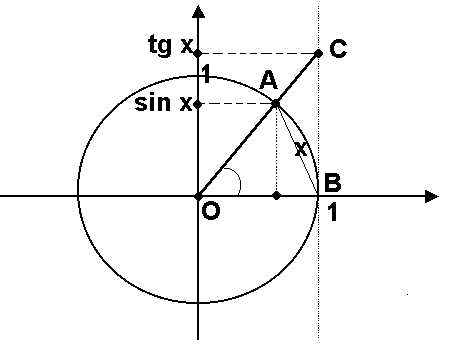
Но
Отсюда получаем неравенства . Поделим все части этого неравенства на>0, получим. Обратим дроби и выводим. Отметим также, что заодно мы доказали неравенствопри. Так как функцииичетные, то для любых ненулевыхс модулем меньше π /2 имеют место неравенства
Тогда
— стремится к 0, откуда . Левая часть двойного неравенства в (2) также имеет предел равный 1. По теореме о пределе промежуточной функции получаем требуемое равенство.
Второй замечательный предел
Теорема.Существует предел функцииприи оно равен e. Это же число е равно пределу функциипри.
Непрерывность функции
Определение.Функция, определенная в окрестности точки, называется непрерывной в этой точке, если. Функция непрерывна на отрезке (интервале), если она непрерывна в каждой точке этого отрезка (интервала).
Это определение можно переписать так: функция непрерывна в точке , если
,
т.е. когда две операции над переменной — функцияfи предельный переход перестановочны.
Обозначим — приращение переменной и— приращение функции. Тогда определение непрерывности можно переписать и так:непрерывна в точкеa, если.
Свойства непрерывных функций
Н1.Сумма непрерывных функций суть непрерывная функция
Н2.Произведение непрерывных функций суть непрерывная функция
Н3.Частное непрерывных функций суть непрерывная функция, во всех точках, где знаменатель отличен от 0
Эти свойства являются непосредственным следствием соответствующих свойств пределов (см. LIM2-LIM4, ).
Н4.Подстановка непрерывной функции в непрерывную функцию есть непрерывная функция
Это свойство следует из свойства LIM8 — предел сложной функции.
Устойчивость знака непрерывной функции.Пустьнепрерывна в точкеaи. Тогдадля всехxдостаточно близких к.
Доказательство. Для найдетсятакое, что как только, то. Для этих значенийимеем:□
Примеры непрерывных функций
1. Константа, а также тождественная функция непрерывны.
Доказательство вытекает из LIM1.
2. Любой многочлен непрерывная функция.
Применяем Н1 и Н2 к тождественной функции
3. Рациональная функция, т.е. отношение двух многочленов, непрерывная функция в точках не являющихся корнями знаменателя.
Применяем Н3 к многочленам.
4. Функция непрерывна.
Действительно, (применяем неравенствополученное при выводе первого замечательного предела). Отсюда следует, что, т.е.непрерывна в точке.
studfiles.net
Помогите решить / разобраться (М)
Найти предел .Конечный ответ, вроде, .
До этого редко сталкивался с функциями, имеющими тригонометрический аргумент, но в целом, если учитывать ограниченность функций и , получается, что будет выглядеть как крайне пологая кривая, периодически меняющая знак на больших промежутках. К тому же, очевидно, что , равно как и . Полученное выражение будет в пределе выглядеть как .
Полученную неопределённость раскладываем по правилу Лопиталя, получаем . Пределы равны единице, , снова Лопиталь. Опять находим производные, появляется четвертая степень косинуса, дальше еще хуже.
Я практически уверен, что такой прямолинейный подход вряд ли подойдет для решения задачи, но в каком направлении хотя бы копать?
dxdy.ru
Помогите решить / разобраться (М)
Найти предел .Конечный ответ, вроде, .
До этого редко сталкивался с функциями, имеющими тригонометрический аргумент, но в целом, если учитывать ограниченность функций и , получается, что будет выглядеть как крайне пологая кривая, периодически меняющая знак на больших промежутках. К тому же, очевидно, что , равно как и . Полученное выражение будет в пределе выглядеть как .
Полученную неопределённость раскладываем по правилу Лопиталя, получаем . Пределы равны единице, , снова Лопиталь. Опять находим производные, появляется четвертая степень косинуса, дальше еще хуже.
Я практически уверен, что такой прямолинейный подход вряд ли подойдет для решения задачи, но в каком направлении хотя бы копать?
dxdy.ru
Помогите решить / разобраться (М)
Найти предел .Конечный ответ, вроде, .
До этого редко сталкивался с функциями, имеющими тригонометрический аргумент, но в целом, если учитывать ограниченность функций и , получается, что будет выглядеть как крайне пологая кривая, периодически меняющая знак на больших промежутках. К тому же, очевидно, что , равно как и . Полученное выражение будет в пределе выглядеть как .
Полученную неопределённость раскладываем по правилу Лопиталя, получаем . Пределы равны единице, , снова Лопиталь. Опять находим производные, появляется четвертая степень косинуса, дальше еще хуже.
Я практически уверен, что такой прямолинейный подход вряд ли подойдет для решения задачи, но в каком направлении хотя бы копать?
dxdy.ru
