Как умножить матрицу на столбец: Умножение матрицы на вектор, формула и примеры

7.1.3. Умножение MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• org/Breadcrumb»>MathCAD 12

• Линейная алгебра
• 7.1. Простейшие матричные операции
  • 7.1.1. Транспонирование
  • 7.1.2. Сложение и вычитание
  • 7.1.3. Умножение
• 7.2. Векторная алгебра
  • 7.2.1. Модуль вектора
  • 7.2.2. Скалярное произведение
  • 7.2.3. Векторное произведение
  • 7.2.4. Векторизация массива
• 7.3. Вычисление определителей и обращение квадратных матриц
  • 7.3.1. Определитель квадратной матрицы
  • 7.3.2. Ранг матрицы
  • 7.3.3. Обращение квадратной матрицы
  • 7.3.4. Возведение квадратной матрицы в степень
  • 7.3.5. Матричные нормы
  • 7.3.6. Число обусловленности квадратной матрицы
• 7.4. Вспомогательные матричные функции
  • 7.4.1. Автоматическая генерация матриц
  • 7.4.2. Разбиение и слияние матриц
  • 7. 4.3. Сортировка элементов матриц
  • 7.4.4. Вывод размера матрицы

При умножении следует помнить, что матрицу размерности MxN допустимо умножать только на матрицу размерности NxP (р может быть любым). В результате получается матрица размерности MхP.

Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*> или воспользоваться панелью инструментов Matrix (Матрица), нажав на ней кнопку Dot Product (Умножение). Умножение матриц обозначается по умолчанию точкой, как показано в листинге 7.5.

Листинг 7.5. Перемножение матриц

Обратите внимание (нижняя строка листинга 7.5), что попытка перемножить матрицы А и В несоответствующего (одинакового 2х3) размера оказалась безрезультатной: после введенного знака равенства находится пустой местозаполнитель, а само выражение в редакторе Mathcad выделяется красным цветом. При установке курсора на это выражение появляется сообщение о несовпадении числа строк первой матрицы с числом столбцов второй матрицы.

Еще один пример, относящийся к умножению вектора на матрицу-строку и, наоборот, строки на вектор, приведен в листинге 7.6.

ВНИМАНИЕ!

Тот же самый оператор умножения действует на два вектора по-другому (см. разд. 7.2.2).

Листинг 7.6. Умножение вектора и строки

Аналогично сложению матриц со скаляром определяется умножение и деление матрицы на скалярную величину (листинг 7.7). Символ умножения вводится так же, как и в случае умножения двух матриц. На скаляр можно умножать матрицу любой размерности.

Листинг 7.7. Умножение матрицы на скалярную величину

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9879 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6917 0

Глава 2 Работа с файлами Mathcad 11

12327 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster. ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2229 s

Вопрос 2.Кольцо матриц над полем действительных чисел. Основные операции над матрицами. Свойства операций. — КиберПедия

Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре… Интересное: Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы. .. Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

⇐ ПредыдущаяСтр 2 из 8Следующая ⇒ Матрицей называется прямоугольная таблица чисел. А – матрица, — элемент матрицы, номер строки, в которой стоит данный элемент, номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов. Определение.Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.   Определение. Матрица вида: = E, называетсяединичной матрицей. Операции над матрицами: Сложение (вычитание) матриц – складывать (вычитать) по элементам и только над матрицами одинаковой размерности. Например: Сложить матрицы и Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы : Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов. 2) Транспонирование матрицы. Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы. Пример: Транспонировать матрицу   Умножение матрицы на число , произведение. Пример: Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку. Умножение матриц. mxnи nxq, называется матрица размерности mxq. Количество столбцов 1-ой матрицы должно совпадать с количеством строк 2-ой матрицы. Умножение происходит таким образом, берется 1 строка 1-ой матрицы и умножается на 1 столбец 2-ой матрицы, далее 1 строка 1-ой матрицы умножается на 2 столбец 2-ой матрицы и т.д и получится 1 строка НОВОЙ МАТРИЦЫ. Пример: Свойства умножения матриц: · 1.ассоциативность (AB)C = A(BC); · 2.некоммутативность (в общем случае): AB BA; · 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA; · 4. дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC; 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB) Коммуникативность: Умножение матриц не коммуникативно, и даже в том случае, когда матрицы квадратные все равно , например имеется 2 матрицы и результатом умножения матрицы А на матрицу Bбудет матрица , а если мы матрицу Bумножим на матрицу А получится . Множество квадратный матриц mxn замкнуто относительно умножения . Множество матриц nxm обладают мультипликативной единицей , , . Действительно, если перемножить матрицу и , то получим => Ассоциативность: Вопрос 3. Определители. Теорема Лапласа. Свойства определителей. Определитель– это число, которое считается по определенному правилу. Минор – это определитель, составленный из первоночального определителя, путем вычеркивания k-строк и k- любых столбцов. Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:   1)Определитель можно посчитать только у квадратной матрицы. 2) Определитель матрицы |An|=An 3)Определитель матрицы 5) Для вычисления матрицы 3×3 существует правило треугольников (Правило Саррюса) Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой . ⇐ Предыдущая12345678Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой. .. Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… 

матриц — умножение матриц на столбцы

спросил 11 лет, 1 месяц назад

Изменено 12 месяцев назад

Просмотрено 12 тысяч раз

$\begingroup$

Yo,

Мне нужна помощь в понимании умножения матриц на столбцы. Рассмотрим две матрицы: 9{th}$ столбец B.

По-видимому, есть другой способ умножения матриц, когда вы работаете с целыми столбцами A, чтобы получить произведение AB. Кто-нибудь знает как это сделать? Если да, не могли бы вы предоставить общий алгоритм? Я никогда о нем не слышал и нигде не могу найти.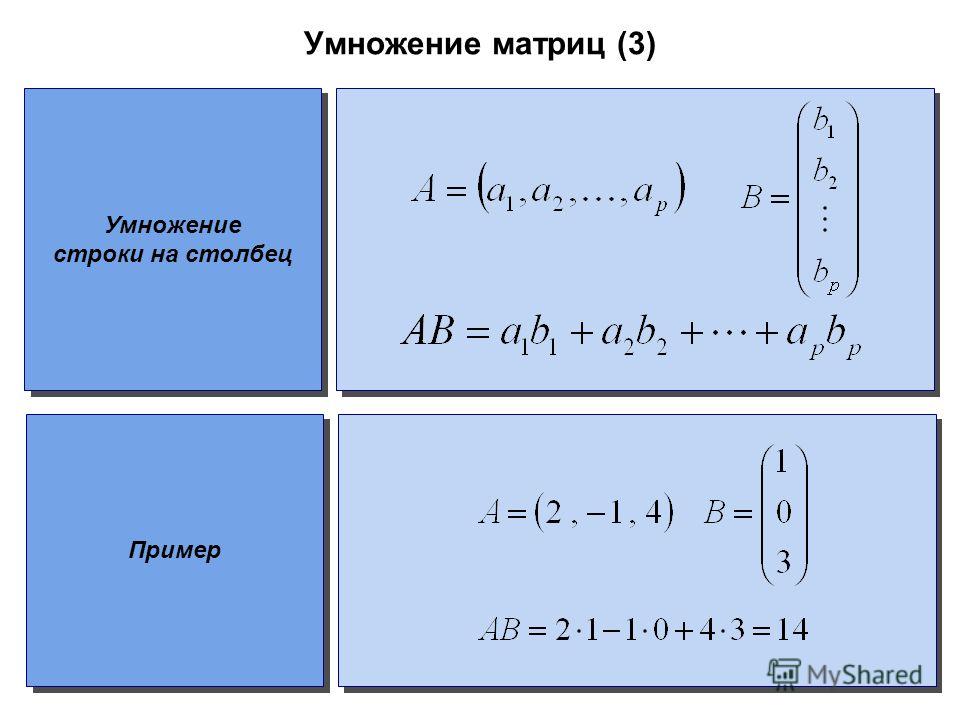

• матрицы

$\endgroup$

$\begingroup$

Вы можете найти его в стартовых лекциях Гилберта Странга. В любом случае, это всего лишь тизер для вас $$ \left( \begin{массив}{ccc} 1 и 2 и 3 \\ 6 и 5 и 4 \\ 7 и 8 и 9\end{массив} \right)\begin{pmatrix}x\\y\\z \end{pmatrix} = \begin{pmatrix} 1\\6\\7 \end{pmatrix}x+ \begin{pmatrix} 2\\5\\8 \end{pmatrix}y+ \begin{pmatrix} 3\\4\\9 \end{pmatrix}z $$ Как насчет этого?

$\endgroup$

2

$\begingroup$

Не ответ, а родственный: то же самое можно сделать, но со строками матрицы:

$$\begin{pmatrix} x & y & z \end{pmatrix} \cdot \left( \begin{array}{ccc} 1 и 2 и 3 \\ 6 и 5 и 4 \\ 7 и 8 и 9 \end{массив} \right) = x\cdot \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} + y\cdot \begin{pmatrix} 6 & 5 & 4 \end{pmatrix } + z\cdot \begin{pmatrix} 7 & 8 & 9 \end{pmatrix}. $$

Это не удивительно, так как вы можете просто транспонировать произведение и использовать метод столбца для вычисления произведения. После этого вы снова транспонируете результат.

Все еще думаю, что стоит поделиться.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

linear алгебра — Матричное умножение столбцов на строки вместо строк на столбцы

Прежде чем говорить об умножении двух матриц, давайте рассмотрим другой способ интерпретации матрицы $A$. Скажем, у нас есть матрица $A$, как показано ниже, $$ \begin{bматрица} 1 и 2 и 3 \\ 1 и 1 и 2 \\ 1 и 2 и 3 \\ \end{bmatrix} $$ легко найти, что столбец $\begin{bmatrix} 3 \\ 2 \\ 3 \\\end{bmatrix}$ является линейной комбинацией первых двух столбцов. $$ 1\begin{bmatrix} 1 \\ 1 \\ 1\\\end{bmatrix} + 1\begin{bmatrix} 2 \\ 1 \\ 2\\\end{bmatrix} = \begin{bmatrix} 3 \\ 2 \\ 3 \\\end{bmatrix} $$ И вы можете сказать, что $\begin{bmatrix} 1 \\ 1 \\ 1 \\\end{bmatrix}$ и $\begin{bmatrix} 2 \\ 1 \\ 2 \\\end{bmatrix}$ — две основы для пространства столбца $A$.

Простите, почему вы хотите сначала разложить матрицу $A$ вот так, $$ \begin{bматрица} 1 и 2 и 3 \\ 1 и 1 и 2 \\ 1 и 2 и 3 \\ \end{bmatrix} = \begin{bматрица} 1 и 0 и 1 \\ 1 и 0 и 1 \\ 1 и 0 и 1 \\ \end{bmatrix} + \begin{bматрица} 0 и 2 и 2 \\ 0 и 1 и 1 \\ 0 и 2 и 2 \\ \end{bmatrix} $$ но вы можете, и, в конце концов, это выглядит разумно.

Если рассматривать это уравнение по столбцам, то каждый $column_j$ матрицы $A$ представляет собой сумму соответствующих $column_j$ каждой матрицы в RHS.

Что особенного в каждой матрице RHS, так это то, что каждая из них является матрицей ранга 1, пространство столбцов которой представляет собой строку, на которой лежит каждое основание пространства столбцов $A$. например. $ \begin{bматрица} 1 и 0 и 1 \\ 1 и 0 и 1 \\ 1 и 0 и 1 \\ \end{bmatrix} $ охватывает только $\begin{bmatrix} 1 \\ 1 \\ 1 \\\end{bmatrix}$. И люди говорят, что матрицы ранга 1 являются строительными блоками любых матриц.

Если теперь вы вернетесь к концепции просмотра $A$ столбец за столбцом, эта декомпозиция на самом деле подчеркивает концепцию линейной комбинации базовых векторов.

Если это имеет смысл, вы можете расширить RHS дальше, $$ \begin{bматрица} 1 и 2 и 3 \\ 1 и 1 и 2 \\ 1 и 2 и 3 \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 1 \\\end{bmatrix} \begin{bmatrix} 1 & 0 & 1 \\\end{bmatrix} + \begin{bmatrix} 2 \\ 1 \\ 2 \\\end{bmatrix} \begin{bmatrix} 0 & 1 & 1 \\\end{bmatrix} $$ Каждый термин в RHS говорит: возьмите эту базу и сделайте ее «похожей» на матрицу ранга 3.