При сложении степеней с одинаковыми основаниями – Что делать со степенями при сложении и вычитании числа? — Любопытная Варвара

Свойства степени с одинаковыми основаниями.

Понятие степени в математике вводится еще в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных своих видах. Степени — достаточно трудная тема, требующая запоминания значений и умения правильно и быстро сосчитать. Для более быстрой и качественной работы со степенями математики придумали свойства степени. Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.

Свойства степени

Мы рассмотрим 12 свойств степени, в том числе и свойства степеней с одинаковыми основаниями, и к каждому свойству приведем пример. Каждое из этих свойств поможет вам быстрее решать задания со степенями, а так же спасет вас от многочисленных вычислительных ошибок.

1-е свойство.

а⁰ = 1

Про это свойство многие очень часто забывают, делают ошибки, представляя число в нулевой степени как ноль.

2-е свойство.

а¹ = а

3-е свойство.

аⁿ * a^m = a^(n+m)

Нужно помнить, что это свойство можно применять только при произведении чисел, при сумме оно не работает! И нельзя забывать, что это, и следующее, свойства применяются только к степеням с одинаковыми основаниями.

4-е свойство.

aⁿ/a^m = a^(n-m)

Если в знаменателе число возведено в отрицательную степень, то при вычитании степень знаменателя берется в скобки для правильной замены знака при дальнейших вычислениях.

Свойство работает только при делении, при вычитании не применяется!

5-е свойство.

(aⁿ)^m = a^(n*m)

6-е свойство.

a^-n = 1/aⁿ

Это свойство можно применить и в обратную сторону. Единица деленная на число в какой-то степени есть это число в минусовой степени.

7-е свойство.

(a*b)^m = a^m * b^m

Это свойство нельзя применять к сумме и разности! При возведении в степень суммы или разности используются формулы сокращенного умножения, а не свойства степени.

8-е свойство.

(a/b)ⁿ = aⁿ/bⁿ

9-е свойство.

а^½ = √а

Это свойство работает для любой дробной степени с числителем, равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.

Также это свойство часто используют в обратном порядке. Корень любой степени из числа можно представить, как это число в степени единица деленная на степень корня. Это свойство очень полезно в случаях, если корень из числа не извлекается.

10-е свойство.

(√а)² = а

Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.

11-е свойство.

ⁿ √aⁿ = a

Это свойство нужно уметь вовремя увидеть при решении, чтобы избавить себя от огромных вычислений.

12-е свойство.

a^m/n = ⁿ √a^m

Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может требовать некоторых преобразований и применения других формул. Поэтому для правильного решения мало знать только свойства, нужно практиковаться и подключать остальные математические знания.

Применение степеней и их свойств

Они активно применяются в алгебре и геометрии. Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.

Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.

Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.

Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.

Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.

Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.

С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.

Показательные уравнения и неравенства

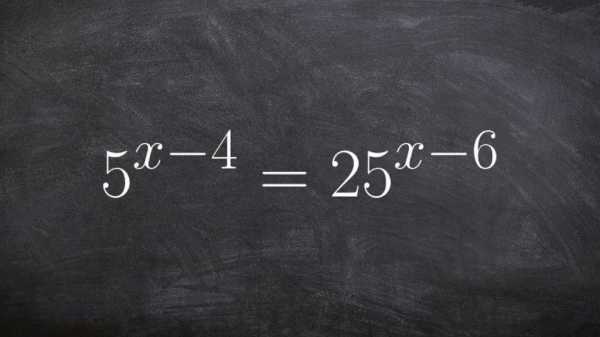
Особое место свойства степени занимают именно в показательных уравнениях и неравенствах. Эти задания очень часто встречаются, как в школьном курсе, так и на экзаменах. Все они решаются за счет применения свойств степени. Неизвестное всегда находится в самой степени, поэтому зная все свойства, решить такое уравнение или неравенство не составит труда.

fb.ru

Что происходит со степенями при сложении цифр?

при сложении — ничего, каждое число так и остается по отдельности, разве что есть с одинакоковыми степенями, тогда можно скомбинировать чтоб запомнить, представь: корень из 3 + корень кубический из 5 + корень из 8 = так они и останутся, если только их в десятичные не перевести

Вроде их складывают

Можно складывать только цифры с одинаковыми степенями

Да ниче не происходит! Они такими же и остаются=)))

А подробнее можно?! Вот, например, 2 в 3-й степени + 2 в 4-ой степени +2 в 5-й степени = 8+16+32=56 То есть никакой закономерности тут нет. Степени они и в Африке степени, а цифры и в Африке цифры:))) То же самое и если 2 в 3-й степени+ 3 в 3-й степени+ 4 в 3-й степени. Тоже нет никакой закономерности!!!

touch.otvet.mail.ru

Ответы@Mail.Ru: матем

С показателями степеней при сложении ничего не делается, просто вычисляется значение числа в степени. Пример 2^2 + 2^3 =4+8=12. Показатели степени складываются если умножаются два числа с одинаковым основанием. Пример 2^2 *2^3 =2^5=32. Умножаются степенные показатели при возведении степени в степень. Пример (2^3)^2=2^6=64.

степени складываются при умножении (основания одинаковые) Например: 3^2 x 3^5=3^7

умножать если «+», делить если «-«, складывать если «х», вычитать если «:»

Ни то ни другое. Это при умножении они складываются. Общую часть вместе с основанием можно вынести за скобку. Для этого примера: 3^15 = 3^(13+2) = 3^13 * 3^2 Значит можно 3^13 вынести за скобку: 3^15 + 3^13 = 3^13 * (3^2 + 1) = 3^13 * (9+1) = 10 * 3^13 В общем случае: a^b * a^c = a^(b+c) (a^b)^c = a^(b*c) Вобщем всё это можно наглядно рассмотреть, если степень расписать через умножение: n^3 = n*n*n — ну и дальше посмтреть что «физически» происходит при сложении и умножении. (только использовать небольшие показатели, чтобы слишком много не писать) &gt^.^&lt

При сложении петрушка получается следующая.. . 3^15+3^13=3^13*(3^2+1) ( ^ — знак степени)…

touch.otvet.mail.ru

Найдите значение выражения (степени, с одинаковыми основаниями) – как решать

Формулировка задачи: Найдите значение выражения (степени, с одинаковыми основаниями).

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 2 (Действия со степенями).

Рассмотрим, как решаются подобные задачи на примерах.

Пример задачи 1:

Найдите значение выражения:

Решение:

Найдем значение выражения. Для этого выполним сложение степеней при умножении чисел с одинаковыми основаниями и вычитание степеней при делении чисел с одинаковыми основаниями:

Ответ: 4

Пример задачи 2:

Найдите значение выражения:

Решение:

Найдем значение выражения. Для этого выполним сложение степеней при умножении чисел с одинаковыми основаниями и вычитание степеней при делении чисел с одинаковыми основаниями. При этом если число в степени возводится в степень, то эти степени перемножаются.

Ответ: 27

Пример задачи 3:

Найдите значение выражения:

Решение:

Найдем значение выражения. Для этого выполним сложение степеней при умножении чисел с одинаковыми основаниями и вычитание степеней при делении чисел с одинаковыми основаниями:

Ответ: 5

Поделитесь статьей с одноклассниками «Найдите значение выражения (степени, с одинаковыми основаниями) – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.

worksbase.ru

Правила вычитания и сложения степеней — Юридический статус

Науколандия

Статьи по естественным наукам и математике

Свойства степеней с одинаковыми основаниями

Существует три свойства степеней с одинаковыми основаниями и натуральными показателями. Это

• Произведение двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть сумма показателей исходных множителей.
• Частное двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть разность показателей исходных множителей.
• Возведение степени числа в степень равно выражению, в котором основание — это то же самое число, а показатель — это произведение двух степеней.

Будьте внимательны! Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует.

Запишем эти свойства-правила в виде формул:

• a m ? a n = a m+n
• a m ? a n = a m–n
• (a m ) n = a mn

Теперь рассмотрим их на конкретных примерах и попробуем доказать.

5 2 ? 5 3 = 5 5 — здесь мы применили правило; а теперь представим как бы мы решали этот пример, если бы не знали правила:

5 2 ? 5 3 = 5 ? 5 ? 5 ? 5 ? 5 = 5 5 — пять в квадрате — это пять умноженное на пять, а в кубе — произведение трех пятерок. В результате получилось произведение пяти пятерок, но это нечто иное как пять в пятой степени: 5 5 .

3 9 ? 3 5 = 3 9–5 = 3 4 . Запишем деление в виде дроби:

Ее можно сократить:

В результате получим:

Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать.

Однако при делении нельзя, чтобы делитель был равен нулю (так как на ноль делить нельзя). Кроме того, поскольку м

yurist-moscow.ru