Николай Лобачевский: параллельные прямые все-таки пересекаются!
Николай Лобачевский известен тем, что создал новую геометрию, в которой параллельные прямые запросто пересекаются. На самом деле все не совсем так. Он просто внимательно изучил имеющуюся на тот момент геометрию Евклида и внес в нее кое-какие коррективы. Учитывая, что этой науке к тому моменту уже исполнилось 2 с лишним тысячи лет, без обновлений было не обойтись…
Николай Иванович Лобачевский родился 20 ноября 1792 года в Нижнем Новгороде. Семья была из простых. Дедушка будущего ученого был поляком, о бабушке известно лишь то, что она была крепостной крестьянкой у князя Михаила Долгорукого. Отец ученого служил чиновником в геодезическом департаменте и умер, когда Николаю было 8 лет.
С деньгами в семье было совсем плохо, и мать отправила Николая и двух его братьев в казанскую гимназию, где они смогли учиться за госсчет. В 16 лет Николай окончил учебу и попробовал поступить в только что открывшийся Казанский университет. С первого раза не выходит, зато со второй попытки Николая зачисляют на первый курс.
Из-за того, что университет только-только открылся, в первые годы там царила неразбериха. Доходило до того, что преподавать математику приходилось самим студентам! Впрочем, Лобачевский к паинькам не относился. Его современники туманно намекают на «студенческие шалости», в которых он участвовал на 1 — 2-м курсах. Но смогли доказать его участие только в одной проделке, когда Николай с приятелями под видом пиротехнических опытов запустили ракету прямо в аудитории! В наказание ему пришлось несколько дней просидеть в карцере.
С тех пор будущий ученый взялся за ум. Засел за учебу, увлекся химией и математикой… Но совсем без приключений не обошлось. Например, в 1811 году Лобачевский чересчур увлекся празднованием Нового года — настолько, что администрация даже хотела его отчислить. А это, как и сейчас, означало для юноши только одно — армию!
«В генваре месяце Лобачевский оказался самого худого поведения, — гласил рапорт, поданный университетскому начальству. — Несмотря на приказание начальства не отлучаться из университета, он в новый год, а потом еще раз ходил в маскарад и многократно в гости, за что опять наказан написанием имени на черной доске и выставлением оной в студентских комнатах на неделю. Несмотря на сие, он после того снова еще был в маскараде»…
Но благодаря заступничеству преподавателей, Лобачевского оставили в университете. Правда, лишили пособия на учебники, так что теперь ему приходилось покупать их за свой счет. Доучиться оставалось всего полгода, так что Лобачевский без особых проблем получил степень магистра по математике и физике с отличием.
Отправлять талантливого студента восвояси никому не хотелось. Поэтому с Лобачевского взяли обещание, что он будет вести себя хорошо, и заставили покаяться во всех прошлых проделках. На этих условиях его взяли преподавать арифметику и геометрию, а также заниматься научной работой.
Сперва карьера пошла вверх: в 1820 году Лобачевский стал деканом физико-математического факультета. Но потом в Казанский университет прислали проверку. Ревизор отчитался об «отсутствии благочестия» в вузе и взялся устанавливать новые порядки. В университете открылась кафедра богословия, все достойные ученые и профессора либо разъехались, либо были уволены.
В такой атмосфере первый труд Лобачевского остался незамеченным. Еще в студенческие годы он пытался доказать пятый постулат Евклида, который звучит так:
«Если на плоскости при пересечении двух прямых третьей сумма внутренних односторонних углов меньше 180, то эти прямые при достаточном продолжении пересекаются».
То есть о параллельных прямых тут речи нет вообще! Речь идет лишь о непересекающихся… Разница в том, что между параллелями должно быть одинаковое расстояние по всей их длине. А для непересекающихся прямых это необязательно!
Над этим постулатом математики бились не одну сотню лет. Дело в том, что доказать его математическими средствами невозможно! Поэтому ученые и пытались создать свою геометрию, которая была бы лишена этого недостатка.
В первом своем учебнике, написанном в 1823 году, Лобачевский попытался это сделать и опровергнуть это утверждение. Но рецензентов возмутили такие вольности. Да и то, что ученый использовал метрическую систему, не добавило ему баллов. После такого разгрома Лобачевский еще долго не брался за написание учебников… Следующее пособие, по алгебре, он опубликовал только через 10 лет.
В 1826 году попечители Казанского университета осознали, что что-то идет не так, и ревизора отстранили «за злоупотребления властью». И в 1827 году новым ректором университета выбрали Николая Лобачевского.
Ученый получает карт-бланш. Он активно погружается во все хозяйственные дела, не забывая при этом и про научные изыскания. Ведет занятия по алгебре, физике, началам анализа, теории вероятностей. И параллельно с этим читает открытые лекции по неевклидовой геометрии.
Одной из главных обязанностей Лобачевский считал наведение порядка в университете. По воспоминаниям современников, профессора сперва жаловались на строгие правила и формализм математика. Но вскоре поняли, что Лобачевский не злоупотребляет властью. «Когда он видел, что члены совета начинали спорить и спору их не предвиделось конца, Лобачевский обыкновенно прерывал заседание, оставлял спорный вопрос открытым до следующего раза; затем он приглашал к себе на дом спорщиков и у себя в кабинете в мирной беседе за чашкой чаю приводил их к соглашению. Этот прием всегда имел хорошие последствия, и на другом совете дело обходилось уже без всяких споров», — отзывался о нем попечитель университета Мусин-Пушкин.

В 1829 году Лобачевский публикует серьезный научный труд «О началах геометрии». Именно он дал старт новому разделу науки — неевклидовой геометрии.
Если говорить просто, то Лобачевский считает неправильным, что непересекающихся прямых может быть только две. И предлагает свою аксиому:
«На плоскости через точку, не лежащую на данной прямой, проходит более, чем одна прямая, не пересекающая данную».
Дело в том, что Евклид в прямом смысле слова плоско мыслил! Свой постулат он сформулировал только для плоскости. Если нарисовать прямую А и точку на листе бумаги, то через эту точку и правда можно провести всего одну прямую В, не пересекающую предыдущую.
А вот на кривой поверхности таких прямых будет гораздо больше. То есть Евклид описал лишь один частный случай, а не все существующие варианты. Пространство может быть и в форме седла, и в форме воронки… И геометрия Лобачевского описывает лучше всего именно такие формы — «с отрицательной кривизной».
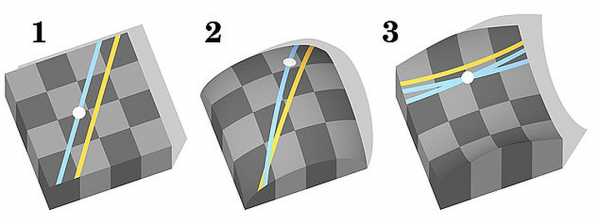
Лобачевский предположил, что в трехмерном пространстве параллельные прямые вполне могут иметь общие точки
Но современники Лобачевского понять этой логики не смогли. На него обрушился целый вал пасквилей и карикатур. Никто не мог поверить, что провинциальный педагог смог всерьез опровергнуть античную аксиому.
В 1832 году ученый женился на Варваре Моисеевой, которая была почти на 20 лет моложе его. В имении жены, недалеко от Казани, он развел большой сад. По преданию, Лобачевский сам посадил кедры и с грустью сказал, что не дождется их плодов. Предсказание сбылось — первые орехи были сняты в год смерти ученого. А кедровая роща на том месте сохранилась до сих пор…
В 1846 году Николая Ивановича отстраняют от должности ректора и лишают профессорской кафедры. Семья лишается значительной части дохода, имение жены приходится продать за долги. Здоровье ученого начинает слабеть, зрение падает. Последний свой труд, «Пангеометрию», Лобачевский создал в 1855 году. Текст записывали под диктовку его ученики — сам Николай Иванович к тому моменту уже ослеп.
Николай Иванович Лобачевский скончался 12 февраля 1856 года, и был похоронен в Казани, на Арском кладбище. Сочинения ученого оценили по достоинству только после его смерти, во второй половине 1860-х годов.
Современная физика Вселенной пришла к выводу, что пространство, где мы с вами живем, обладает отрицательной кривизной. И именно геометрия Лобачевского описывает его лучше всего.
Без геометрии Лобачевского у нас не было бы теории относительности Эйнштейна, исследований Клейна и Пуанкаре. Его работы расширили наше представление о мире и дали возможность составить о нем более точное представление.
Поделиться видео </>Великие ученые: Николай Лобачевский.Русский математик, создатель неевклидовой геометрии, деятель университетского образования и народного просвещения.
www.kp.ru
Ответы@Mail.Ru: параллельные прямые пересекаются?
Теоретически — да
нет, потомучто они паралельны и пересекаться ни как не могут
геометрию учить надо было в школе!!!
Иногда и параллельные прямые пересекаются…
В Евклидовой геометрии нет. В сферической «прямые» — кратчайшее расстояние между точками, меридианы пересекаются. Риманова геометрия включает пространства с любой кривизной. Весь вопрос в том, какое наше пространство. Считается римановым. PS Правильнее сказать на сфере в бытовом, а не строго научном смысле этого слова, так как сфера в неевклидовой геометрии это такое, что и не снилось нашим мудрецам! А возникший ниже терминологический спор связан с тем, что именно Риман дополнил геометрию Лобачевского геометрией на сфере, развил и обобщил
пересекаются! научно доказанный факт
в гиперболической геометрии возможно пересечение параллельных прямых сравним Евклид: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. гиперболическая геометрия: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Да запросто пересекаются 🙂 Например, в искривленном пространстве, в близи черной дыры паралельные прямые вообще могут слится, пересечся и в узел завязаться :))))
Да, это доказано!
Практически абсолютно бесконечные параллельные прямые линии пересекаются друг с другом в точке абсолютной бесконечности, так как каждая из них имеет в реальном пространстве мира вселенной их абсолютно бесконечное конической его формы сужение и расширение, что позволяет обоим этим прямым быть не двумя а одной конически сужающейся и конически расширяющейся общей линией, которая пересекается своими произвольно взятыми коническими прямыми боками в точке абсолютной бесконечности!!! <img src=»//otvet.imgsmail.ru/download/224436214_55646a6e003bf9e5f11100638e4d1ee6_800.png» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/224436214_55646a6e003bf9e5f11100638e4d1ee6_120x120.png» data-big=»1″>
это их воля)))))
Ало, они пересекутся, моему учителю и всем преподавателям обьсняли это, когда они ходили на учебу, в это трудно поверить, и можно ломать голову, но Евклид доказал, что они пересекутся — это факт
touch.otvet.mail.ru
5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
Видеоурок: Параллельные прямые, перпендикулярные к плоскости
Лекция: Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
Пересекающиеся прямые
Если на плоскости имеются несколько прямых, то они либо рано или поздно пересекутся произвольно, либо под прямым углом, или же будут параллельными. Давайте же разберемся с каждым случаем.
Пересекающимися можно назвать те прямые, у которых будет хотя бы одна точка пересечения.

Вы спросите, почему хотя бы одна, не может же прямая пересечь другую прямую две или три раза. Вы правы! Но прямые могут полностью совпасть друг с другом. В таком случае общих точек будет бесконечное множество.
Параллельность
Параллельными можно назвать те прямые, которые никогда не пересекутся, даже на бесконечности.
 Иными словами, параллельные – это те, у которых нет ни одной общей точки. Обратите внимание на то, что данное определение справедливо только в том случае, если прямые находятся в одной плоскости, если же они не имеют общих точек, находясь в разных плоскостях, то они считаются скрещивающимися.
Иными словами, параллельные – это те, у которых нет ни одной общей точки. Обратите внимание на то, что данное определение справедливо только в том случае, если прямые находятся в одной плоскости, если же они не имеют общих точек, находясь в разных плоскостях, то они считаются скрещивающимися.
Примеры параллельных прямых в жизни: два противоположных края экрана монитора, линии в тетрадях, а также многие другие части вещей, имеющих квадратную, прямоугольную и другие формы.
Когда хотят показать на письме, что одна прямая параллельная второй, то используют следующее обозначение a||b. Данная запись говорит, что прямая а параллельна прямой b.
При изучении данной темы важно понять еще одно утверждение: через некоторую точку на плоскости, которая не принадлежит данной прямой, можно провести единственную параллельную прямую. Но обратите внимание, снова поправка – на плоскости. Если рассматривать трехмерное пространство, то можно провести бесконечное множество прямых, которые не будут пересекаться, но будут скрещивающимися.
Утверждение, которое было описано выше, называется аксиомой о параллельности прямых.
Перпендикулярность
Прямые можно назвать только в том случае перпендикулярными, если они пересекаются под углом, равным 90 градусов.
В пространстве через некоторую точку на прямой можно провести бесконечное множество перпендикулярных прямых. Однако, если речь идет о плоскости, то через одну точку на прямой можно провести единственную перпендикулярную прямую.
Скрещенные прямые. Секущая
Если некоторые прямые пересекаются в некоторой точке под произвольным углом, их можно назвать скрещивающимися.
У любых скрещивающихся прямых есть вертикальные углы и смежные.
Если у углов, которые образованы двумя скрещивающимися прямыми, одна сторона общая, то они называются смежными:
Смежные углы в сумме дают 180 градусов.
Если же углы, образованные двумя скрещивающимися прямыми, не имеют общей стороны, то они называются вертикальными:

Вертикальные углы всегда равны.
Если же некоторая прямая пересекает две других прямых, то она называется секущей.
Частным случаем является секущая двух параллельных прямых:
cknow.ru
Пять распространенных мифов о геометрии Лобачевского — Российская газета
7 февраля 1832 года Николай Лобачевский представил на суд коллег свой первый труд по неевклидовой геометрии. Этот день стал началом переворота в математике, а работа Лобачевского — первым шагом к теории относительности Эйнштейна. Сегодня «РГ» собрала пятерку самых распространенных заблуждений о теории Лобачевского, бытующих среди далеких от математической науки людей
Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой.
На самом деле геометрия Лобачевского не слишком сильно отличается от привычной нам Евклидовой. Дело в том, что из пяти постулатов Евклида четыре первых Лобачевский оставил без изменения. То есть он согласен с Евклидом в том, что между двумя любыми точками можно провести прямую, что ее всегда можно продолжить до бесконечности, что из любого центра можно провести окружность с любым радиусом, и что все прямые углы равны между собой. Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.
Миф второй. В теории Лобачевского параллельные прямые пересекаются
Это не так. На самом деле пятый постулат Лобачевского звучит так: «На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную». Иными словами, для одной прямой можно провести как минимум две прямые через одну точку, которые не будут ее пересекать. То есть в этом постулате Лобачевского речи о параллельных прямых вообще не идет! Говорится лишь о существовании нескольких непересекающихся прямых на одной плоскости. Таким образом, предположение о пересечении параллельных прямых родилось из-за банального незнания сути теории великого российского математика.
Миф третий. Геометрия Лобачевского — единственная неевклидова геометрия
Неевклидовы геометрии — это целый пласт теорий в математике, где основой является отличный от Евклидова пятый постулат. Лобачевский, в отличие от Евклида, к примеру, описывает гиперболическое пространство. Существует еще теория, описывающая сферическое пространство — это геометрия Римана. Вот в ней-то как раз параллельные прямые пересекаются. Классический тому пример из школьной программы — меридианы на глобусе. Если посмотреть на лекало глобуса, то окажется, что все меридианы параллельны. Меж тем, стоит нанести лекало на сферу, как мы видим, что все ранее параллельные меридианы сходятся в двух точках — у полюсов. Вместе теории Евклида, Лобачевского и Римана называют «три великих геометрии».
Миф четвертый. Геометрия Лобачевского не применима в реальной жизни
Напротив, современная наука приходит к пониманию, что Евклидова геометрия — лишь частный случай геометрии Лобачевского, и что в реальный мир точнее описывается именно формулами русского ученого. Сильнейшим толчком к дальнейшему развитию геометрии Лобачевского стала теория относительности Альберта Эйнштейна, которая показала, что само пространство нашей Вселенной не является линейным, а представляет собой гиперболическую сферу. Между тем, сам Лобачевский, несмотря на то, что всю жизнь работал над развитием своей теории, называл ее «воображаемой геометрией».
Миф пятый. Лобачевский первым создал неевклидову геометрию
Это не совсем так. Параллельно с ним и независимо от него к подобным выводам пришли венгерский математик Янош Бойяи и знаменитый немецкий ученый Карл Фридрих Гаусс. Однако труды Яноша не были замечены широкой публикой, а Карл Гаусс и вовсе предпочел не издаваться. Поэтому именно наш ученый считается первопроходцем в этой теории. Однако существует несколько парадоксальная точка зрения, что первым неевклидову геометрию придумал сам Евклид. Дело в том, что он самокритично считал свой пятый постулат не очевидным, поэтому большую часть из своих теорем он доказал, не прибегая к нему.
rg.ru
как доказать что 2 параллельные прямые пересекаются в бесконечности?
Есть такая геометрия (математика) Лобачевского, где не так с параллельными прямыми как в классической Эвклидовой геометрии. Француз Понселе получил проективное пространство из обычного, постулировав существование «бесконечно удаленной плоскости» , содержащей «бесконечно удаленную прямую» для каждого пучка параллельных плоскостей, и «бесконечно удаленную точку» для каждого пучка параллельных прямых. Это позволило утверждать, что две параллельные прямые пересекаются в бесконечно удаленной точке.
а параллельные прямые в идеале вроде не пересекаются
Лобачевского потрясите-подскажет
Никак. Есть разные геометрии. В одной геометрии, например, через данную точку на плоскости можно провести прямую, параллельную данной, причем только одну. Это геометрия Евклида. В другой геометрии этого сделать нельзя, параллельных прямых на плоскости в ней вообще нет, все прямые на плоскости пересекаются, это геометрия Римана. В третьей через данную точку на плоскости можно провести бесконечное множество прямых параллельных данной (по крайней мере, две) , это геометрия Лобачевского. Это аксиомы в этих геометриях. Их принимают без доказательств, и на их основе строят свои дальнейшие рассуждения. Аксиомы не доказывают, это не теоремы. Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана — реализуется на поверхностях с постоянной положительной гауссовой кривизной. Есть и другие геометрии, например сферическая.
по свойствам паралельные никогда не пересекаются даже в бесконечности. Пребставь, что рельсы где-нибудь в каком-нибудь населеном пункте пересекутся. Что будет?
Вы не знаете определения параллельности прямых. Посмотрите определение: чтобы прямые можно было назвать параллельными — необходимым условием является их непересекаемость. Раз пересекаются — значит прямые непараллельны…
сегодня я нашел доказательство пересечения двух параллельных прямых в бесконечности!!!
touch.otvet.mail.ru
Теория параллельных прямых. Теория треугольника, страница 14
Если при пересечении двух прямых секущей сумма внутренних односторонних углов не равна 180°, то прямые не параллельны, то есть при достаточном продолжении пересекаются.
Доказательство. Если бы эти прямые не пересекались, то они были бы параллельны, и тогда сумма внутренних односторонних углов равнялась бы 180°, что противоречит условию. Теорема доказана.
Сформулируйте обратную теорему.
3.3. Взаимное расположение четырех прямых.
Мы изучили различные случаи взаимного расположения двух и трёх прямых на плоскости. Теперь изучим взаимное расположения четырёх прямых на плоскости. Изобразим разные случаи.
а) две пересекающиеся прямые пересекают две другие пересекающиеся прямые:
Рис.3.22
б) каждая из двух пересекающиеся прямых пересекает две параллельные прямые:
Рис.3.23
в) две параллельные прямые пересечены двумя параллельными прямыми:
Рис.3.23
г) три параллельные прямые пересечены третьей прямой:
Рис.3.24
д) все четыре прямые параллельны:
Рис.3.25
Какие фигуры вы можете увидеть на этих рисунках? Например, на рис.3.23, слева, видна фигура, состоящая из четырех отрезков, два из которых параллельны. На рис.3.23 видно, что при пересечении двух параллельных прямых двумя другими параллельными прямыми получилась фигура, у которой противоположные стороны попарно параллельны и равны. Докажем это.
Лемма 1. При пересечении двух параллельных прямых двумя другими параллельными между собой прямыми получается фигура, у которой противоположные стороны параллельны.
Доказательство. Пусть параллельные между собой прямые a, b и параллельные между собой прямые c, d пересекаются в точках A, B, C, D (рис.3.26).
Докажем, что АВ=СD и АD=ВС. Проведём отрезок АС (рис.3.27, а). Для начала докажем, что АВ=СD.
Углы ÐACD иÐСAB равны как внутренние накрест лежащие при параллельных прямых a и b и секущей AC. Углы ÐDAC иÐACB равны как внутренние накрест лежащие при параллельных прямых c и d и секущей AC.
На луче АВ отложим отрезок АЕ, равный отрезку CD (рис.3.27, б). Углы ÐACD иÐСAE равны, значит, их соответственные поперечины AD и CE равны. То есть АЕ и DC – соответственные поперечины углов ÐDAC иÐACB, но они равны по построению, а значит, угол ÐACЕ равен углу ÐDAC. Но угол ÐDAC равен углу ÐACB. Это означает, что равны углы ÐACЕ иÐACB, то есть точка Е лежит на луче СВ. По построению точка Е лежит на луче АВ. Но эти лучи пересекаются в точке В, то есть точки В и Е совпадают и АВ=АЕ=CD.
Итак мы доказали, что равны отрезки АВ и СD. Отрезки AD и CB равны как соответственные поперечины равных углов. Утверждение леммы 1 доказано.
Следствие 5: Противоположные углы фигуры ABCD равны (рис.3.27).
vunivere.ru
Параллельные прямые пересекаются: миф или реальность?
Слайд 1
Автор: Панкратов Влад Научный руководитель: Попова Е.А . Параллельные прямые пересекаются: миф или реальность?Слайд 2
Актуальность: параллельные прямые не пересекаются в школьном курсе геометрии, но почему рельсы на горизонте сходятся? И есть предположение , что параллельные прямые пересекаются. Так ли это? Я и решил выяснить.
Слайд 3
Происхождение понятия параллельных прямых . От Евклида Евкли́д ( 300 г. до н. э.) — древнегреческий математик, автор “Начал”. Начала Евклида- это сборник математических трудов, который состоит из 13 книг. В первой книге рассматриваются 5 важных постулатов .
Слайд 4
Рассмотрим примечательные 5 постулатов “Начал” Евклида: 1. От всякой точки до всякой точки можно провести прямую. 2. Ограниченную прямую можно непрерывно продолжать по прямой. 3. Из всякого центра всяким раствором может быть описан круг. 4. Все прямые углы равны между собой. 5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых
Слайд 5
Необычность 5 постулата Евклида В течение двух тысячелетий не прекращались попытки исключить 5 постулат из списка аксиом и вывести как теорему, как получилось с 4 постулатом. Все эти попытки окончились неудачей.
Слайд 6
Источник понятия “ параллельные прямые ” Следствием 5 постулата является понятие параллельных прямых , не пересекающихся на всем их протяжении; и, далее, аксиома параллельности: через точку, не лежащую на заданной прямой, нельзя провести более одной прямой, параллельной этой заданной прямой .
Слайд 7
В результате безуспешных попыток доказать 5 постулат возникли неевклидовые геометрии. Рассмотрим их: Геометрия Николая Ивановича Лобачевского. Сферическая геометрия древних греков. Геометрия Георгия Римана.
Слайд 8
Лобачевский Николай Иванович Годы жизни : 1792 – 1856 ( Нижний Новгород – Казань) Ректор Казанского университета “ Коперник геометрии ”
Слайд 9
Геометрия Лобачевского Ответ с улицы: «Лобачевский доказал, что параллельные прямые пересекаются.» «Лобачевский открыл, что параллельные прямые могут и пересечься». «А что такое параллельные прямые?» «Параллельные — это такие прямые, которые лежат в одной плоскости и не пересекаются». Несовместимые ответы!
Слайд 10
Ф ольклор ( folklore — народная мудрость): Однажды Лобачевский думал, кутаясь в пальто: Как мир прямолинеен, видно, что-то здесь не то! И он вгляделся пристальней в безоблачную высь, И там все параллельные его пересеклись.
Слайд 11
Диалоги на “ Эхе Москвы ” В е н е д и к т о в . Вот вы скажите, параллельные прямые пересекаются? С л у ш а т е л ь . Нет. В е н е д и к т о в . А вот у Лобачевского пересекаются, там другая система отсчёта. Леонид Радзиховский : «Вот когда Лобачевский придумал свою неевклидову геометрию, что две параллельные прямые могут пересечься, — это был действительно переворот в области геометрии и физики».
Слайд 12
Аксиомы о параллельных Правильная формулировка : через точку, не лежащую на заданной прямой, нельзя провести более одной прямой, параллельной этой заданной прямой . В школьном курсе ( Атанасян Л.С.): через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. В версии Лобачевского: через точку, не лежащую на заданной прямой, можно провести более одной прямой, параллельной этой заданной прямой . Правда, как известно, у каждого своя, но истина одна. Истина состоит в том, что параллельные друг другу прямые не пересекаются даже у Лобачевского!
Слайд 13
Важно: А ксиому о параллельных доказать нельзя . В третьем десятилетии XIX в. два великих геометра — российский математик Николай Иванович Лобачевский и венгерский математик Янош Б о йаи —независимо друг от друга построили геометрическую теорию, основанную на отрицании аксиомы о параллельных. Эту теорию за рубежом, как правило, называют геометрией Лобачевского– Бойаи , а в России — геометрией Лобачевского . У нее есть и «обезличенное» название — гиперболическая геометрия . Геометрия Лобачевского применима в космологии, если учесть, что наше пространство искривлено гиперболически .
Слайд 14
“ Плоскость ” Лобачевского — “ седло ” , “ воронка ” Лобачевский Николай Иванович умер, не дожив до признания своей теории 10 лет, осмеянный, больной, в нищете, его уволили из университета. Янош Бойаи сошел с ума, не получив отклика и поддержки своих идей у математиков того времени (у Карла Гаусса – короля математиков)
Слайд 15
Сферическая геометрия Древних Греков. Сферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы. Сферическая геометрия возникла в древности в связи с потребностями географии и астрономии. Сферическая геометрия нужна не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, а также при геодезических съемках больших территорий поверхности Земли, когда становится необходимым учитывать ее шарообразность.
Слайд 16
I век нашей эры Древняя Греция Геометрический труд “ Сферика ” – аналогично “ Началам ” Евклида Менелай Александрийский
Слайд 17
Особенности сферической геометрии Прямые – большие круги (меридианы, экватор, параллели – малые круги ) Есть двуугольник У сферического треугольника могут быть все три угла прямыми Сумма углов треугольника меньше 3П, но больше П Две прямые пересекаются дважды (например, на северном и южном полюсах) Нет понятия параллельности
Слайд 18
Геометрия Римана Геометрия Римана (эллиптическая геометрия) — одна из трёх «великих геометрий» (Евклида, Лобачевского и Римана). Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана реализуется на поверхностях с постоянной положительной гауссовой кривизной, т.е. на сферах. Исторически геометрия Римана появилась позже двух других геометрий (в 1854 г.).
Слайд 19
Годы жизни: 1826 – 1866 (Германия – Италия) Место работы: Гёттингенский университет Научная сфера: математика, механика, физика Основатель римановой геометрии Георг Фридрих Бернхард Риман
Слайд 20
Геометрия Римана похожа на сферическую геометрию, но отличается тем, что любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения. Поэтому иногда геометрией Римана называют геометрию на сфере, в которой противоположные точки отождествлены. В геометрии Римана любые прямые пересекаются , и таким образом, в ней нет параллельных прямых . Геометрия Римана не является абсолютной геометрией, ей нет практического применения.
Слайд 21
Заключение : Итак, подводя итоги, ответим на вопрос: “Параллельные прямые пересекаются”? Нет , в идеале они не пересекаются ни у Евклида (2 параллельные прямые), ни у Лобачевского (прямая и пучок прямых в незримо больших масштабах) – это миф. Но нет дыма без огня: параллельных прямых не существует в сферической геометрии древних греков и в геометрии Римана. А в реальности: нет прямых, как нет и других объектов геометрии, поэтому одна прямая или их несколько, параллельных данной?..
Слайд 22
Спасибо за внимание!!!!!!
nsportal.ru
