При умножении вектора на число – . —

Примечание. Рассмотренные свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, выражение $$ \overrightarrow{р} = 2(\overrightarrow{a} — \overrightarrow{b}) + (\overrightarrow{c} + \overrightarrow{a}) — 3(\overrightarrow{b} — \overrightarrow{c} + \overrightarrow{a}) $$ можно преобразовать так: $$ \overrightarrow{р} = 2\overrightarrow{a} — 2\overrightarrow{b} + \overrightarrow{c} + \overrightarrow{a} — 3\overrightarrow{b} + 3\overrightarrow{c} — 3\overrightarrow{a} = — 5\overrightarrow{b} + 4\overrightarrow{c} $$

Пример 1. Коллинеарны ли векторы $2\overrightarrow{a} \,и\, -\overrightarrow{a}$ ?

Решение. Имеем $2\overrightarrow{a} = -2(-\overrightarrow{a})$ . Значит, данные векторы коллинеарны.

Пример 2. Дан треугольник ABC. Выразите через векторы $\overrightarrow{a} = \overrightarrow{АВ} \,и\, \overrightarrow{b} = \overrightarrow{АС}$ следующие векторы: $а)\, \overrightarrow{ВА}\text{ ; б) }\overrightarrow{СВ}\text{ ; в) }\overrightarrow{СВ} + \overrightarrow{ВА}$ .

Решение

а) Векторы $\overrightarrow{ВА} \,и\, \overrightarrow{АВ}$ — противоположные, поэтому $\overrightarrow{ВА} = -\overrightarrow{АВ}\text{ , или }\overrightarrow{ВА} = -\overrightarrow{a}$ .

б) По правилу треугольника $\overrightarrow{СВ} = \overrightarrow{СА} + \overrightarrow{АВ}$ . Но $\overrightarrow{СА} = -\overrightarrow{АС}$ , поэтому $\overrightarrow{СВ} = \overrightarrow{АВ} + (-\overrightarrow{АС}) = \overrightarrow{АВ} -\overrightarrow{АС} = \overrightarrow{a} — \overrightarrow{b}$ .

в) $\overrightarrow{СВ} + \overrightarrow{ВА} = \overrightarrow{СА} = -\overrightarrow{АС} = -\overrightarrow{b}$.

www.wiki.eduvdom.com

Лекция по математике на тему «Умножение вектора на число»

Лекция по теме «Умножение вектора на число»

Произведение вектора а на число k

Текст

Умножение вектора на число

Рисунок векторов

Для любого числа k и любого вектора а векторы а и ka коллинеарны.

Произведением нулевого вектора на любое число считается нулевой вектор.

Произведение любого вектора на число нуль есть нулевой вектор.

Текст

Умножение вектора на число

││k для любого k.

Рассмотрим основные свойства умножения вектора на число. Для любых векторов а,b и любых чисел k и l справедливы равенства:

Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.

Текст

Свойства умножения вектора на число

1. Сочетательный закон

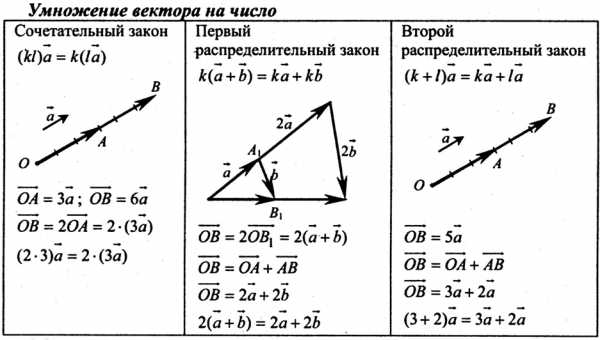
Рисунок векторов

Текст

Второе свойство, первый распределительный закон. Произведение числа k на сумму векторов а и b равно сумме произведений этого числа на векторы а и b.

На рисунке, на примере показано это свойство.

Текст

Свойства умножения вектора на число

2. Первый распределительный закон

Рисунок векторов

Текст

Третье свойство, второй распределительный закон. Произведение суммы чисел k и l на вектор равно сумме произведений чисел k и l на вектор а.

На рисунке, на примере показано это свойство.

Текст

Свойства умножения вектора на число

3. Второй распределительный закон

Рисунок векторов

Текст

Стоит отметить, что произведение числа -1 на любой вектор дает вектор противоположный данному.

Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.

Текст

(-1), так как

и

Для векторов в пространстве, как и в планиметрии, выполняется следующее условие:

Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b равен произведению числа k на вектор а.

Текст

Если ││ , то существует

число k, что

Решим задачу №347 (а)

Необходимо упростить выражение.

Текст

Задача №347(а)

Упростить выражение:

Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.

Текст

Решение:

.

infourok.ru

Умножение — вектор — Большая Энциклопедия Нефти и Газа, статья, страница 3

Умножение — вектор

Cтраница 3

При умножении вектора на число А, все его координаты умножаются на это число.  [31]

При умножении вектора А на У положительный скаляр k получаем новый вектор & А, направление которого совпадает с направлением вектора А, а числовое значение отличается в k раз.  [32]

При умножении вектора А на отрицательный скаляр k получаем новый вектор & А, направление которого противоположно вектору А, а числовое значение отличается в k раз.  [33]

При умножении вектора

При умножении векторов различают два случая: 1) Если перемножаемые векторы параллельны между собою, то умножение их производите. В этом случае величина произведения не зависит от порядка множителей. Если перемножаемые векторы О А и ОВ взаимно перпендикулярны ( черт.  [36]

При умножении вектора А на положительный скаляр k получаем новый вектор k, направление которого совпадает с направлением вектора А, а числовое значение отличается в k раз.  [37]

При умножении вектора на число все его компоненты умножаются на это число.  [38]

При умножении вектора на число все его координаты умножаются на это число.  [41]

При умножении векторов модули их перемножаются, а аргументы складываются.  [42]

При умножении векторов различают скалярное и векторное произведения.  [44]

Страницы:      1    2    3    4

www.ngpedia.ru

УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО (ОПРЕДЕЛЕНИЕ). — КиберПедия

Стр 1 из 5Следующая ⇒ БИЛЕТ № 1. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО (ОПРЕДЕЛЕНИЕ).   Произведением вектора (а1, а2) на число К называется вектор (kа1, kа2), т. е. (а1, а2) k = { ka1; kа2). По определению (а1, а2) k = k(а1, а2). Из определения операции умножения вектора на число следует, что Абсолютная величина вектора равна |. Направление вектора при совпадает с направлением вектора , если , и противоположно направлению вектора , если . Абсолютная величина вектора равна:   ПРИЗНАК ДИАГОНАЛЕЙ ПАРАЛЛЕЛОГРАММ (ДОКАЗАТЕЛЬСТВО). Теорема: Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник — параллелограмм.   Дано: АВСD-четырехугольник. АС∩BD=т.О АО=ОС,DО=ОВ Док-ть: АВСD-параллелограмм Доказательство   БИЛЕТ№2. СВОЙСТВА ДИАГОНАЛЕЙ ПАРАЛЛЕЛОГРАММА. Теорема: Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам   Дано: АВСD-параллелограмм Док-ть АС∩BD=т.О АО=ОС,DО=ОВ Доказательство   БИЛЕТ №3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС. Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние. Определение Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F. Формулы параллельного переноса Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1) то параллельный перенос задаётся формулами: Свойства параллельного переноса 1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние). 2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. 3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя). 4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1. В алгебре параллельный перенос широко используется для построения графиков функций.     СВОЙСТВО ПРОТИВОЛЕЖАЩИХ СТОРОН И УГЛОВ ПАРАЛЛЕЛОГРАММА. Теорема: У параллелограмма противолежащие стороны равны, противолежащие углы равны     Дано: АВСD-параллелограмм Док-ть: ВС=АD, АВ=СD, ∟А=∟В=∟С=∟D Доказательство     БИЛЕТ№4. ПОВОРОТ. Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении. Угол на который поворачивается фигура, относительно точки, называется углом поворота.     ПРИЗНАК ПРОТИВОЛЕЖАЩИХ СТОРОН ПАРАЛЛЕЛОГРАММА. Теорема: Если у четырехугольника две противолежащие стороны параллельны и равны, то он является паралелограммом   Дано: АВСD- четырехугольник ВС=АD, АВ=СD, ВС║АD, АВ║СD Док-ть АВСD-. параллелограмм Доказательство       БИЛЕТ№5. БИЛЕТ №6 БИЛЕТ№7. 1.ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОСИНУСА ДЛЯ ЛЮБОГО УГЛА ОТ 0° ДО 180°. Возьмем окружность на плоскости ху с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси X в верхнюю полуплоскость (полуплоскость, где y>0) угол а. Пусть х и у — координаты точки А. Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно: Определим теперь значения sin а, cos а и tg а этими формулами для любого угла а. (Для tg а угол а = 90° исключается.) При таком определении sin 90° = 1, cos 90° = О, sin 180° = О, cos 180° = — 1, tg 180° = 0. Считая, что совпадающие лучи образуют угол 0°, будем иметь: sinO° = 0, cosO° = l, tgO° = 0. Докажем, что для любого угла а, 0°<:а<:180°, sin (180° — а)=sin а, cos (180° — а) = — cos а. Для угла а ^ 90° tg (180° — а) = — tg а. Действительно, треугольники ОАВ и ОА\В\ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников следует, что АВ=А1В1, т. е. у = у1; ОВ=ОВ1 следовательно, x= —x1. Поэтому разделив почленно равенство sin (180° —а) = sin а на равенство cos (180° — а)=—cos а, получаем: Что и требовалось доказать. СВОЙСТВА ДИАГОНАЛЕЙ РОМБА. Теорема: Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов     Дано: АВСD-ромб Док-ть: АС┴BD, АС-биссектриса ∟А и∟С, BD -биссектриса ∟B и∟D Доказательство     БИЛЕТ№8. БИЛЕТ№9. 1.ЗНАЧЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА НЕКОТОРЫХ УГЛОВ (45°, 30°,60°). 2.ДОКАЖИТЕ, ЧТО ЕСЛИ ДИАГОНАЛИ ПРЯМОУГОЛЬНИКА ПЕРЕСЕКАЮТСЯ ПОД ПРЯМЫМ УГЛОМ, ТО ОН ЯВЛЯЕТСЯ КВАДРАТОМ.   Дано: АВСD-прямоугольник АС┴BD Док-ть АВСD-квадрат Доказательство     БИЛЕТ№10. 1.ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА.   ТЕОРЕМА ФАЛЕСА. Теорема: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.   Дано: ∟COD A1B1 ∥ A2B2 ∥ A3B3, A1, A2, A3 ∈ OC, B1, B2, B3 ∈ OD, A1A2=A2A3. Док-ть B1B2=B2B3. Доказательство 1) Через точку B2 проведем прямую EF, EF ∥ A1A3. 2) Рассмотрим четырехугольник A1FB2A2. — A1F ∥ A2B2 (по условию), — A1A2 ∥ FB2 (по построению).Следовательно, A1FB2A2 — параллелограмм (по определению). По свойству противолежащих сторон параллелограмма, A1A2=FB2. 3) Аналогично доказываем, что A2B2EA3 — параллелограмм и A2A3=B2E. 4) Так как A1A2=A2A3 (по условию), то FB2=B2E. 5) Рассмотрим треугольники B2B1F и B2B3E. — FB2=B2E (по доказанному), — ∠B1B2F=∠B2EB3 (как вертикальные), — ∠B2FB1=∠B2EB3 (как внутренние накрест лежащие при A1B1 ∥ A3B3 и секущей EF). Следовательно, треугольники B2B1F и B2B3E равны (по стороне и двум прилежащим к ней углам). Из равенства треугольников следует равенство соответствующих сторон: B1B2=B2B3. Что и требовалось доказать. Билет№11. 1.СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И УГЛАМИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ (ОПРЕДЕЛЕНИЕ).   2.ДОКАЗАТЬ ТЕОРЕМУ О СРЕДНЕЙ ЛИНИИ ТРАПЕЦИИ. Теорема:   Дано: ΔАВСД-данная трапеция QP-средняя линия Док-ть QP║ BC, QP║AD QP =1/2 (BC+ AD) Доказательство         Билет№12. 1.ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ (ОПРЕДЕЛЕНИЕ).   2. ДОКАЖИТЕ,ЧТО СЕРЕДИНЫ СТОРОН ЧЕТЫРЕХУГОЛЬНИКА ЯВЛЯЮТСЯ ВЕРШИНАМИ ПАРАЛЛЕЛОГРАММА.   Дано: ΔАВС-треугольник ЕД-средняя линия Док-ть ЕД║АВ,ЕД=1/2АВ Доказательство: Проведем диагональ АС в четырехугольнике АВСД.АС разбивает четырехугольник на 2 треугольника АВС и АДС. Проведем средние линии в треугольниках КМ и ОN. КМ — средняя линия ΔАВС(по определению), тогда КМ = АС/2 и КМ ║ АС. ON- средняя линия ΔADC, значит ON = AC/2 и ON ║АС Получаем, что KM=ON и KM параллельна ON(это признак!) Если две стороны четырехуг. равны и параллельны, то четырехуг. — параллелограмм. Значит KMNO параллелограм.       Билет№13. 1.СИНУС, КОСИНУС И ТАНГЕНС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА (ОПРЕДЕЛЕНИЕ).     2.ДОКАЗАТЬ ТЕОРЕМУ О СРЕДНЕЙ ЛИНИИ ТРЕУГОЛЬНИКА. Теорема:   Дано: ΔАВС-треугольник ЕД-средняя линия Док-ть ЕД║АВ,ЕД=1/2АВ Доказательство Билет№14. Билет№15. 1. ОПРЕДЕЛЕНИЕ ТРАПЕЦИИ. ВИДЫ ТРАПЕЦИИ.   Все трапеции можно разделить на три вида: — равнобедренные трапеции; — прямоугольные трапеции; — произвольные трапеции. Равнобедренные трапеции — это трапеции, у которых боковые стороны равны. Прямоугольные трапеции — это трапеции, у которых одна боковая сторона перпендикулярна основаниям. Произвольные трапеции — все остальные трапеции, которые не являются ни равнобедренными, ни прямоугольными. Схематически виды трапеций можно изобразить так:   Билет№16. 1. ОПРЕДЕЛЕНИЕ КВАДРАТА. СВОЙСТВА КВАДРАТА.   2.ТЕОРЕМА ПИФАГОРА (ДОКАЗАТЕЛЬСТВО).   Билет№17. 1. ОПРЕДЕЛЕНИЕ РОМБА. СВОЙСТВА РОМБА.   2.НЕРАВЕНСТВО ТРЕУГОЛЬНИКА (ДОКАЗАТЬ ТЕОРЕМУ).   Билет№18. Билет№19. 1 .ОПРЕДЕЛЕНИЕ ЧЕТЫРЕХУГОЛЬНИКА.   2.СЛОЖЕНИЕ ВЕКТОРОВ (ДОКАЗАТЕЛЬСТВО).ПРАВИЛО ТРЕУГОЛЬНИКА И ПРАВИЛО ПАРАЛЛЕЛОГРАММА (РАССМОТРЕТЬ СПОСОБЫ ПОСТРОЕНИЯ). Билет№20. 1.ОПРЕДЕЛЕНИЕ И СВОЙСТВА ПАРАЛЛЕЛОГРАММА.   2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ (ОПРЕДЕЛЕНИЕ). ДОКАЗАТЬ ТЕОРЕМУ О СКАЛЯРНОМ ПРОИЗВЕДЕНИИ ВЕКТОРОВ. БИЛЕТ № 1. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО (ОПРЕДЕЛЕНИЕ).   Произведением вектора (а1, а2) на число К называется вектор (kа1, kа2), т. е. (а1, а2) k = { ka1; kа2). По определению (а1, а2) k = k(а1, а2). Из определения операции умножения вектора на число следует, что Абсолютная величина вектора равна |. Направление вектора при совпадает с направлением вектора , если , и противоположно направлению вектора , если . Абсолютная величина вектора равна:   

cyberpedia.su

Умножение вектора на число

Материал урока.

Вам уже знакомы правило треугольника, правило параллелограмма и правило многоугольника сложения векторов.

Чтобы сложить неколлинеарные векторы  и  по правилу треугольника, нужно от некоторой точки А отложить вектор , равный вектору . Далее от точки B отложить вектор , равный вектору . Вектор  является вектором суммы двух векторов  и .

Для сложения этих же векторов можно использовать правило параллелограмма. При этом нужно отложить от произвольной точки А векторы  и , равные векторам  и  соответственно, и построить на них параллелограмм ABCD. Тогда вектор равен сумме векторов  и .

Для сложения нескольких векторов применяют правило многоугольника. При этом от некоторой точки последовательно откладывают векторы друг за другом, и вектором их суммы является вектор, проведённый от начала первого вектора к концу последнего. Причём полученный многоугольник может быть не только плоским, но и пространственным.

Также вы владеете двумя способами построения вектора разности.

Можно от некоторой точки О отложить векторы  и , равные векторам  и . При этом вектором их разности будет вектор , направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.

Так же, пользуясь теоремой о разности двух векторов, разность векторов  и  можно представить в виде суммы вектора  и вектора, противоположного вектору  .

Тогда, отложив от некоторой точки О вектор , равный вектору , а от точки А — вектор , равный вектору «- », по правилу треугольника получим вектор .

Он является вектором суммы вектора  и вектора, противоположного вектору . И, соответственно, вектором разности векторов  и .

Как и на плоскости в пространстве вектор можно умножать на число. На этом-то уроке мы и поговорим об умножении вектора на число в пространстве.

Рассмотрим пример, который поможет нам вспомнить, что представляет собой произведение вектора на число.

Парусник дрейфует прямолинейно с одной и той же скоростью, а один из лайнеров движется в попутном направлении со скоростью в пять раз большей. Второй лайнер движется им на встречу, то есть в противоположном направлении, с той же скоростью, что и первый лайнер.

Если изобразить скорость парусника вектором , то скорость первого лайнера, движущегося в попутном направлении, нужно изобразить в виде сонаправленного вектора, длина которого в пять раз больше. И выразить эту скорость можно через скорость  умножением на 5.

Вектор скорости второго лайнера должен иметь такую же длину, как и вектор скорости первого лайнера, но он должен быть ему противоположно направленным. Значит, его можно выразить через вектор  умножением на -5.

Определение. Произведением ненулевого вектора  на число k называется такой вектор , длина которого равна произведению модуля числа k и длины данного вектора . Причем векторы  и  сонаправлены, если k, и противоположно направлены, если k<0.

Произведение числа k на вектор  в пространстве обозначают так же как и на плоскости.

Имеют место такие следствия из определения.

Действительно, по определению длина этого вектора равна произведению длины вектора  на 0, то есть равна 0. Значит, получаем нулевой вектор.

Вторым следствием из определения является то, что ненулевой вектор  коллинеарен вектору, заданному произведением данного вектора  на число k.

Ведь, если k≥0, то полученный вектор сонаправлен вектору , а если k<0, то он противоположно направлен ему. Но в каждом из этих случаев они будут коллинеарны.

Свойства умножения вектора на число, известные нам из планиметрии, имеют место и для векторов в пространстве. Напомним их.

Чтобы умножить вектор  на произведение чисел k и l, можно вектор  сначала умножить на число l, а затем на число k. Этот закон называют сочетательным, и его можно проиллюстрировать так.

Вторым свойством запишем, что произведение вектора  на сумму чисел k и l равно сумме произведений «вектора  на число k» и «вектора  на число l». Это первый распределительный закон.

Запишем второй распределительный закон.

Произведение суммы векторов  и  на число k равно сумме произведений «вектора  на число k» и «вектора  на число k».

Стоит также напомнить, что эти свойства позволяют выполнять преобразования в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, так же как и в числовых выражениях.

Упростим следующие выражения.

Выполним задание, где рассмотрим куб ABCDA₁B₁C₁D₁, диагонали которого пересекаются в точке О. Для каждого из равенств нужно найти такое число k, чтобы равенства были верными.

Рассмотрим первое равенство, .

Для наглядности, изобразим каждый из данных векторов.

Рассмотрим грань ABCD, которая является квадратом, так как перед нами куб.

Это значит, что стороны AB и CD параллельны и равны.

Рассмотрим следующее равенство . Изобразим векторы  и .

Понятно, что диагонали куба точкой пересечения делятся пополам.

Рассмотрим последнее равенство .

Изобразим векторы  и .

Так мы с вами нашли значение числа k для каждого из равенств.

Выполним ещё одно задание.

Задача.  параллелограмм. Точки  и  середины сторон  и  соответственно.

 произвольная точка пространства. Выразить:

а)  через                                              б)  через

Решение.

Обратимся к пункту А.

Обратим своё внимание на пункт Б.

Подведём итоги нашего урока.

Сегодня мы сформулировали определение произведения вектора на число в пространстве, которое ничем не отличается от аналогичного определения для векторов на плоскости.

Произведением ненулевого вектора  на число k называется такой вектор , длина которого равна произведению модуля числа k и длины данного вектора . Причем векторы  и  сонаправлены, если k≥0, и противоположно направлены, если k<0.

Мы вспомнили свойства умножения вектора на число, известные нам из планиметрии, которые имеют место и для векторов в пространстве.

А также отметили, что, как и на плоскости, в пространстве любой ненулевой вектор пространства можно представить в виде произведения коллинеарного ему вектора на некоторое число k.

Все эти знания мы применили при выполнении заданий уже не на плоскости, а в пределах пространства.

videouroki.net

Умножение вектора на число — Мегаобучалка

Свойства

Ортогональность

Векторы являются ортогональными тогда и только тогда, когда их скалярное произведение равно нулю.

Часто вместо этого термина употребляют термин «перпендикулярность», однако следует учитывать, что нулевой вектор ортогонален любому вектору, но понятие перпендикулярности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Пример:
Даны два вектора и , с координатами в ортонормированном базисе. Эти векторы будут ортогональными, если выражение x₁x₂ + y₁y₂ = 0.

Коллинеарность

Два не нулевых вектора называются коллиниарными, если , где

Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.

Часто вместо этого термина употребляют термин «параллельность», однако следует учитывать, что нулевой вектор коллинеарен любому вектору, но понятие параллельности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Сложение геометрических векторов

Два вектора u, v и вектор их суммы

Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.

Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

А модуль (длину) вектора суммы определяют по теореме косинусов где — угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула теперь — угол между векторами выходящими из одной точки.

Умножение вектора на число

Произведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение — нулевой вектор.

• Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .

Из определения произведения вектора на число легко вывести следующие свойства:

megaobuchalka.ru

Умножение вектора на число » Аналитическая геометрия f(x)dx.Ru

п.9. Умножение вектора на число.

Определение. Произведением вектора  на действительное число  называется вектор , удовлетворяющий следующим двум условиям:

1) ;

2) , если  и , если ;

и обозначается .

Теорема. (Свойства умножения вектора на число.)

1. Свойство ассоциативности:  верно

    равенство .

2. Свойство дистрибутивности умножения относительно

   сложения чисел:  верно равенство

                           .

3. Свойство дистрибутивности умножения относительно

   сложения векторов:  верно равенство

                           .

4.  верно равенство .

Доказательство. Свойство 4 вытекает из определения умножения вектора на число. Докажем свойство 1.

   Умножение вектора  на число  можно интерпретировать как гомотетию какой-нибудь плоскости Р, в которой лежит данный вектор, с центром гомотетии в начале вектора и коэффициентом .

   Такая гомотетия плоскости Р оставляет точку А на месте, , а конец вектора – точку В переводит (отображает) в точку С, , причем

и точка С лежит на луче АВ, если  и на

противоположном луче, если . См. рис. 10 и 11.

                      А                  В                            С 

                                      рис. 10.

                С                            А                      В

                                       рис.11.

Теперь свойство 1 следует из того что композиция гомотетий (т.е. последовательное их выполнение) есть гомотетия, причем  и  верно равенство: .

Пусть .

        D           А                  В                            С 

                     |

                                      рис. 12.

Тогда ,  и , т.е. .

   Таким образом,  и ,

следовательно, , ч.т.д.

   Доказательство свойства 2 оставляем читателю в качестве самостоятельного упражнения. Заметим, что если оба числа  и  имеют одинаковый знак, то свойство 2 очевидно. Осталось рассмотреть случай разных знаков чисел  и .

   И, наконец, свойство 3 очевидно из следующего

рисунка, построенного для случая :

                                      рис. 13.

Заметим, что такая картинка возникает, если мы применим к плоскости, в которой лежат оба вектора, отложенные от одной точки О, преобразование гомотетии с центром гомотетии в точке О и коэффициентом .

Теорема доказана.

Теорема. Множество всех векторов  как направленных отрезков в пространстве точек S является векторным пространством над полем действительных чисел.

   Доказательство следует из свойств сложения векторов и их умножения на действительные числа.

Определение. Векторное пространство над полем действительных чисел называется вещественным векторным пространством.

   Пусть L произвольная прямая в пространстве S. Тогда ясно, что , т.е. множество векторов коллинеарных прямой L является подмножеством всех векторов .

  Далее, сумма любых двух векторов коллинеарных прямой L также является вектором коллинеарным прямой L:

 . В этом случае говорят, что множество векторов  замкнуто относительно сложения векторов. Аналогично, , т.е. множество  замкнуто относительно операции умножения вектора на действительное число. Отсюда сразу же следует, что для векторов из множества  справедливы все свойства сложения и умножения на действительные числа, т.е. справедливы все аксиомы вещественного векторного пространства.

   Таким образом, множество  также является вещественным векторным пространством.

   Говорят, что векторное пространство  является векторным подпространством векторного пространства .

   Аналогично и для множества  всех векторов лежащих на некоторой плоскости Р или на параллельной ей плоскости. Множества  также является векторным пространством и векторным подпространством векторного пространства .

   Если прямая L лежит в плоскости Р или параллельна ей, то  и  – подпространство векторного пространства  и одновременно векторного пространства .

   Векторное пространство  мы будем называть пространством векторов на прямой L, а  –пространством векторов на плоскости Р.

п.10. Необходимое и достаточное условие коллинеарности двух векторов.

Определение. Пусть  и  два произвольных вектора. Если верно равенство , где , то говорят, что вектор  линейно выражается через вектор .

Теорема. (О коллинеарности двух векторов.)

Для того, чтобы два вектора были коллинеарными необходимо и достаточно, чтобы либо один из них был нулевым, либо один из них линейно выражался через другой.

   Другими словами, .

   Доказательство. Если , то  по определению. Пусть  и . Тогда из определения умножения вектора на число следует, что либо , либо , в зависимости от знака числа , т.е. , ч.т.д.

   Пусть теперь  и  и . (Если  или , то доказывать нечего.) Рассмотрим два возможных случая.

а) Пусть . Т.к. , то .

   Обозначим буквой  отношение длин этих векторов: . Отсюда следует равенство  и, применяя определение умножения вектора на число, получаем, что .

б) Пусть . Положим по определению . Отсюда следует равенство  и, применяя определение умножения вектора на число, получаем, что .

Теорема доказана.

Возможно найдутся ответы здесь:

fxdx.ru